Оператор троеточие ⫶
Значение символа
Математический оператор кратности, деления без остатка.
Символ «Оператор троеточие» был утвержден как часть Юникода версии 3.2 в 2002 г.
Синонимы
кратно, делится на.
| Версия | 3.2 |
| Блок | Дополнительные математические операторы |
| Тип парной зеркальной скобки (bidi) | Нет |
| Композиционное исключение | Нет |
| Изменение регистра | 2AF6 |
| Простое изменение регистра | 2AF6 |
| Кодировка | hex | dec (bytes) | dec | binary |
|---|---|---|---|---|
| UTF-8 | E2 AB B6 | 226 171 182 | 14855094 | 11100010 10101011 10110110 |
| UTF-16BE | 2A F6 | 42 246 | 10998 | 00101010 11110110 |
| UTF-16LE | F6 2A | 246 42 | 63018 | 11110110 00101010 |
| UTF-32BE | 00 00 2A F6 | 0 0 42 246 | 10998 | 00000000 00000000 00101010 11110110 |
| UTF-32LE | F6 2A 00 00 | 246 42 0 0 | 4129947648 | 11110110 00101010 00000000 00000000 |
Что такое кратное число
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. В этой статье мы расскажем, что такое КРАТНЫЕ ЧИСЛА.
Эту тему каждый школьник в России проходит в 6 классе, когда подробно изучают деление.
Хотя с самой этой математической функцией дети знакомятся гораздо раньше – уже во 2 классе.
Кратное число — это …
Деление – это математическая операция, благодаря которой можно узнать, сколько частей чего-то одного содержится в другом. Или, другими словами, заменяет многократное вычитание из одного числа другое.
Операция деления в математике может обозначаться разными значками. Это двоеточие (:), косая черта (/), горизонтальная черта (-) или специальным значком под названием «обелюс» (÷).
А у чисел, которые участвуют в делении, есть определенные названия:
- Делимое – то число, которое собираются делить;
- Делитель – число, на которое будут делить делимое. Соответственно, делитель чаще всего меньше делимого. Хотя не исключен и другой вариант. Единственное число, которое не может быть делителем, это ноль.
- Частное – результат деления, то есть число, которое получается в результате выполнения математического действия.
Частное, которое получается полным или не полным. Первый вариант, это когда число-делимое, было полностью поделено на делитель. Например, 12 / 3 = 4. Но бывают варианты и с неполным частным, когда появляется некий остаток. Например, 14 / 3 = 4 (2), где 4 – это неполное частное, а 2 – остаток.
Почему мы так подробно рассказали о делении? Это имеет непосредственное отношение к теме статьи.
Одно число называется кратным другому, если его можно на него поделить без остатка.
Но речь идет только о натуральных числах. То есть тех, которые мы используем для счета в обычной жизни. Например, 1, 2, 5, 10, 35, 100 и так далее. При этом дробные числа (например, 2/5 или 0,5) к натуральным не относятся, а значит, в отношении них понятие «кратности» не применяется.
Например, возьмем число 12. Оно может быть кратно сразу нескольким числам.
12 / 3 = 4
12 / 4 = 3
12 / 6 = 2
12 / 2 = 6
Таким образом, можно сказать, что 12 – кратное число 2, 3, 4 и 6. И точно так же можно разложить по кратности любое число.
Внимательный читатель мог бы возразить, что есть еще два числа, на которые можно поделить 12 без остатка. Во-первых, это само 12. А во-вторых, это единица. Что ж, это абсолютная правда, и ее можно даже записать в одном математическом правиле:
Любое натуральное число всегда кратно само себе и единице. В первом случае получается единица, а во втором само число.
Таблицы чисел кратных 2,3,4,5,6,7,9
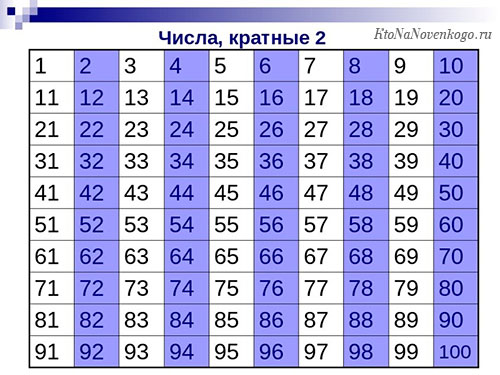
В первую очередь рассмотрим самый простой вариант. Это числа, которые являются кратными двум. Определить их совсем просто, так как к ним относятся все четные числа. Вот, например, как выглядит таблица от 1 до 100.
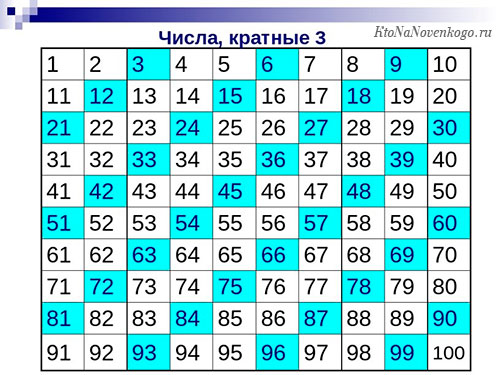
А вот так будет выглядеть таблица чисел кратных трем. Обратите внимание, что все они в результате располагаются по диагонали. Получается весьма красиво.
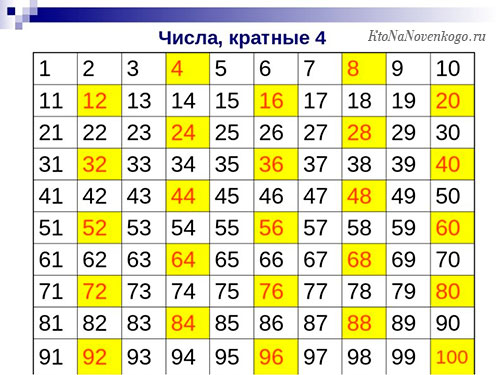
Теперь покажем таблицу чисел, которые можно поделить без остатка на 4. Как можно заметить, это только четные цифры.
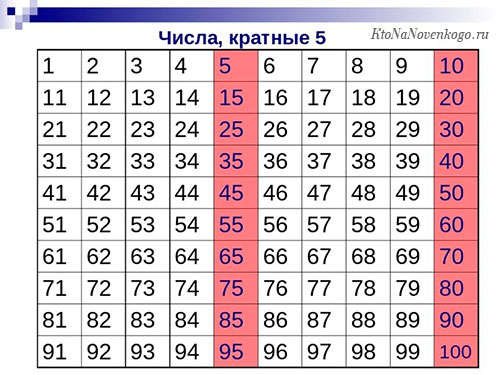
А вот так выглядит таблица чисел, которые кратны пяти. Запомнить их очень просто. Числа, кратные пяти, должны оканчиваться или на 5, или на 0. Других вариантов быть просто не может.
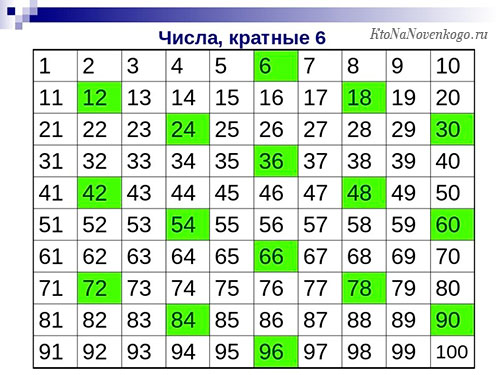
А если взглянуть на таблицу чисел, которые кратны числу 6, то можно сделать интересный вывод. Есть числа, которые никогда не попадут в эту категорию. Они оканчиваются на 1, 3, 5, 7 и 9. Другими словами, только четные числа могут быть кратными 6. Но при этом не все четные числа таковыми являются.
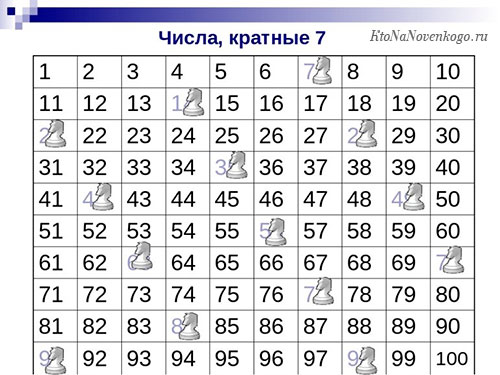
Интересно будет посмотреть и таблицу чисел, которые являются кратными 7. Чтобы определить их, нужно ходить по таблице вниз, как ходить шахматная фигура «конь». В народе это называется «буквой Г», в нашем случае это «шаг влево и два шага вниз».
И наконец, интересно рассмотреть числа, которые кратны 9. Их очень легко определить, это своеобразный математический лайфхак.
Надо просто сложить все цифры в числе, и если в сумме получится 9, то тогда число кратно девятке.
| Числа, кратные 9 | 27 | 198 | 5 877 | 3 816 | 117 | 72 |
|---|---|---|---|---|---|---|
| Сумма | 9 | 18 | 27 | 18 | 9 | 9 |
Да, тут указаны еще и числа 18 и 27. Но они при повторном сложении также дадут девятку.
Вместо заключения
А знаете, что есть число, которое можно назвать кратным всем другим натуральным числам? Это ноль. Ведь если ноль поделить на любое число, то получится опять же ноль. И никакого остатка. А значит, это утверждение верно.
Вот и все, что мы хотели рассказать о КРАТНЫХ ЧИСЛАХ.
B = {9,14,28}
B = {3,9,14},
A = B
B = {1,2,3},
AB = {9,14}
B = {1,2,3},
AB = {9,14}
B = {1,2,3},
A ∆ B = {1,2,9,14}
B = {1,2,3},
A ⊖ B = {1,2,9,14}
принадлежит