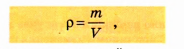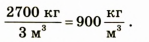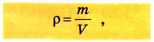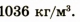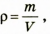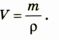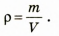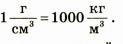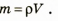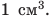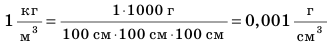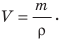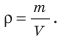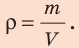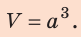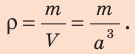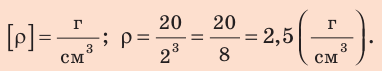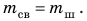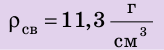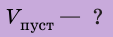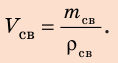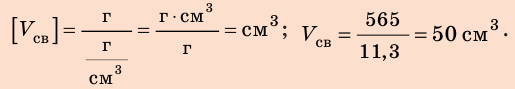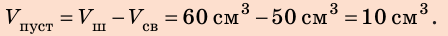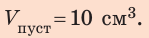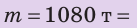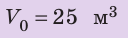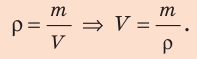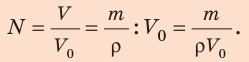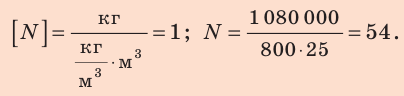Греческая строчная буква ро ρ
Значение символа
Греческая строчная буква ро. Греческое и коптское письмо.
Символ «Греческая строчная буква ро» был утвержден как часть Юникода версии 1.1 в 1993 г.
| Название в Юникоде | Greek Small Letter Rho |
| Номер в Юникоде | |
| HTML-код | |
| CSS-код | |
| Мнемоника | ρ |
| Разделы Юникода | Греческое и коптское письмо |
| Прописная | Ρ |
| Версия Юникода | 1.1 (1993) |
| Версия | 1.1 |
| Блок | Греческое и коптское письмо |
| Тип парной зеркальной скобки (bidi) | Нет |
| Композиционное исключение | Нет |
| Изменение регистра | 03C1 |
| Простое изменение регистра | 03C1 |
| Кодировка | hex | dec (bytes) | dec | binary |
|---|---|---|---|---|
| UTF-8 | CF 81 | 207 129 | 53121 | 11001111 10000001 |
| UTF-16BE | 03 C1 | 3 193 | 961 | 00000011 11000001 |
| UTF-16LE | C1 03 | 193 3 | 49411 | 11000001 00000011 |
| UTF-32BE | 00 00 03 C1 | 0 0 3 193 | 961 | 00000000 00000000 00000011 11000001 |
| UTF-32LE | C1 03 00 00 | 193 3 0 0 | 3238199296 | 11000001 00000011 00000000 00000000 |
Похожие символы
Наборы с этим символом
ρ Греческая строчная буква ро
Нажмите, чтобы скопировать и вставить символ
Значение символа
Греческая строчная буква ро. Греческое и коптское письмо.
Символ «Греческая строчная буква ро» был утвержден как часть Юникода версии 1.1 в 1993 г.
Свойства
| Версия | 1.1 |
| Блок | Греческое и коптское письмо |
| Тип парной зеркальной скобки (bidi) | Нет |
| Композиционное исключение | Нет |
| Изменение регистра | 03C1 |
| Простое изменение регистра | 03C1 |
Похожие символы
-
ω
Греческая строчная буква омега
-
ν
Греческая строчная буква ню
-
δ
Греческая строчная буква дельта
-
ε
Греческая строчная буква эпсилон
-
ζ
Греческая строчная буква дзета
-
η
Греческая строчная буква эта
-
θ
Греческая строчная буква тета
-
ι
Греческая строчная буква йота
-
κ
Греческая строчная буква каппа
-
λ
Греческая строчная буква лямбда
-
μ
Греческая строчная буква мю
-
ξ
Греческая строчная буква кси
-
β
Греческая строчная буква бета
-
ο
Греческая строчная буква омикрон
-
π
Греческая строчная буква пи
Кодировка
| Кодировка | hex | dec (bytes) | dec | binary |
|---|---|---|---|---|
| UTF-8 | CF 81 | 207 129 | 53121 | 11001111 10000001 |
| UTF-16BE | 03 C1 | 3 193 | 961 | 00000011 11000001 |
| UTF-16LE | C1 03 | 193 3 | 49411 | 11000001 00000011 |
| UTF-32BE | 00 00 03 C1 | 0 0 3 193 | 961 | 00000000 00000000 00000011 11000001 |
| UTF-32LE | C1 03 00 00 | 193 3 0 0 | 3238199296 | 11000001 00000011 00000000 00000000 |
| Density | |
|---|---|

A test tube holding four non-miscible colored liquids with different densities |
|
|
Common symbols |
ρ, D |
| SI unit | kg/m3 |
| Extensive? | No |
| Intensive? | Yes |
| Conserved? | No |
|
Derivations from |
 |
| Dimension |  |
Density (volumetric mass density or specific mass) is the substance’s mass per unit of volume. The symbol most often used for density is ρ (the lower case Greek letter rho), although the Latin letter D can also be used. Mathematically, density is defined as mass divided by volume:[1]
where ρ is the density, m is the mass, and V is the volume. In some cases (for instance, in the United States oil and gas industry), density is loosely defined as its weight per unit volume,[2] although this is scientifically inaccurate – this quantity is more specifically called specific weight.
For a pure substance the density has the same numerical value as its mass concentration.
Different materials usually have different densities, and density may be relevant to buoyancy, purity and packaging. Osmium and iridium are the densest known elements at standard conditions for temperature and pressure.
To simplify comparisons of density across different systems of units, it is sometimes replaced by the dimensionless quantity «relative density» or «specific gravity», i.e. the ratio of the density of the material to that of a standard material, usually water. Thus a relative density less than one relative to water means that the substance floats in water.
The density of a material varies with temperature and pressure. This variation is typically small for solids and liquids but much greater for gases. Increasing the pressure on an object decreases the volume of the object and thus increases its density. Increasing the temperature of a substance (with a few exceptions) decreases its density by increasing its volume. In most materials, heating the bottom of a fluid results in convection of the heat from the bottom to the top, due to the decrease in the density of the heated fluid, which causes it to rise relative to denser unheated material.
The reciprocal of the density of a substance is occasionally called its specific volume, a term sometimes used in thermodynamics. Density is an intensive property in that increasing the amount of a substance does not increase its density; rather it increases its mass.
Other conceptually comparable quantities or ratios include specific density, relative density (specific gravity), and specific weight.
History
In a well-known but probably apocryphal tale, Archimedes was given the task of determining whether King Hiero’s goldsmith was embezzling gold during the manufacture of a golden wreath dedicated to the gods and replacing it with another, cheaper alloy.[3] Archimedes knew that the irregularly shaped wreath could be crushed into a cube whose volume could be calculated easily and compared with the mass; but the king did not approve of this. Baffled, Archimedes is said to have taken an immersion bath and observed from the rise of the water upon entering that he could calculate the volume of the gold wreath through the displacement of the water. Upon this discovery, he leapt from his bath and ran naked through the streets shouting, «Eureka! Eureka!» (Εύρηκα! Greek «I have found it»). As a result, the term «eureka» entered common parlance and is used today to indicate a moment of enlightenment.
The story first appeared in written form in Vitruvius’ books of architecture, two centuries after it supposedly took place.[4] Some scholars have doubted the accuracy of this tale, saying among other things that the method would have required precise measurements that would have been difficult to make at the time.[5][6]
Measurement of density
A number of techniques as well as standards exist for the measurement of density of materials. Such techniques include the use of a hydrometer (a buoyancy method for liquids), Hydrostatic balance (a buoyancy method for liquids and solids), immersed body method (a buoyancy method for liquids), pycnometer (liquids and solids), air comparison pycnometer (solids), oscillating densitometer (liquids), as well as pour and tap (solids).[7] However, each individual method or technique measures different types of density (e.g. bulk density, skeletal density, etc.), and therefore it is necessary to have an understanding of the type of density being measured as well as the type of material in question.
Unit
From the equation for density (ρ = m/V), mass density has any unit that is mass divided by volume. As there are many units of mass and volume covering many different magnitudes there are a large number of units for mass density in use. The SI unit of kilogram per cubic metre (kg/m3) and the cgs unit of gram per cubic centimetre (g/cm3) are probably the most commonly used units for density. One g/cm3 is equal to 1000 kg/m3. One cubic centimetre (abbreviation cc) is equal to one millilitre. In industry, other larger or smaller units of mass and or volume are often more practical and US customary units may be used. See below for a list of some of the most common units of density.
Homogeneous materials
The density at all points of a homogeneous object equals its total mass divided by its total volume. The mass is normally measured with a scale or balance; the volume may be measured directly (from the geometry of the object) or by the displacement of a fluid. To determine the density of a liquid or a gas, a hydrometer, a dasymeter or a Coriolis flow meter may be used, respectively. Similarly, hydrostatic weighing uses the displacement of water due to a submerged object to determine the density of the object.
Heterogeneous materials
If the body is not homogeneous, then its density varies between different regions of the object. In that case the density around any given location is determined by calculating the density of a small volume around that location. In the limit of an infinitesimal volume the density of an inhomogeneous object at a point becomes: 


Non-compact materials
In practice, bulk materials such as sugar, sand, or snow contain voids. Many materials exist in nature as flakes, pellets, or granules.
Voids are regions which contain something other than the considered material. Commonly the void is air, but it could also be vacuum, liquid, solid, or a different gas or gaseous mixture.
The bulk volume of a material—inclusive of the void fraction—is often obtained by a simple measurement (e.g. with a calibrated measuring cup) or geometrically from known dimensions.
Mass divided by bulk volume determines bulk density. This is not the same thing as volumetric mass density.
To determine volumetric mass density, one must first discount the volume of the void fraction. Sometimes this can be determined by geometrical reasoning. For the close-packing of equal spheres the non-void fraction can be at most about 74%. It can also be determined empirically. Some bulk materials, however, such as sand, have a variable void fraction which depends on how the material is agitated or poured. It might be loose or compact, with more or less air space depending on handling.
In practice, the void fraction is not necessarily air, or even gaseous. In the case of sand, it could be water, which can be advantageous for measurement as the void fraction for sand saturated in water—once any air bubbles are thoroughly driven out—is potentially more consistent than dry sand measured with an air void.
In the case of non-compact materials, one must also take care in determining the mass of the material sample. If the material is under pressure (commonly ambient air pressure at the earth’s surface) the determination of mass from a measured sample weight might need to account for buoyancy effects due to the density of the void constituent, depending on how the measurement was conducted. In the case of dry sand, sand is so much denser than air that the buoyancy effect is commonly neglected (less than one part in one thousand).
Mass change upon displacing one void material with another while maintaining constant volume can be used to estimate the void fraction, if the difference in density of the two voids materials is reliably known.
Changes of density
In general, density can be changed by changing either the pressure or the temperature. Increasing the pressure always increases the density of a material. Increasing the temperature generally decreases the density, but there are notable exceptions to this generalization. For example, the density of water increases between its melting point at 0 °C and 4 °C; similar behavior is observed in silicon at low temperatures.
The effect of pressure and temperature on the densities of liquids and solids is small. The compressibility for a typical liquid or solid is 10−6 bar−1 (1 bar = 0.1 MPa) and a typical thermal expansivity is 10−5 K−1. This roughly translates into needing around ten thousand times atmospheric pressure to reduce the volume of a substance by one percent. (Although the pressures needed may be around a thousand times smaller for sandy soil and some clays.) A one percent expansion of volume typically requires a temperature increase on the order of thousands of degrees Celsius.
In contrast, the density of gases is strongly affected by pressure. The density of an ideal gas is
where M is the molar mass, P is the pressure, R is the universal gas constant, and T is the absolute temperature. This means that the density of an ideal gas can be doubled by doubling the pressure, or by halving the absolute temperature.
In the case of volumic thermal expansion at constant pressure and small intervals of temperature the temperature dependence of density is
where 


Density of solutions
The density of a solution is the sum of mass (massic) concentrations of the components of that solution.
Mass (massic) concentration of each given component ρi in a solution sums to density of the solution,
Expressed as a function of the densities of pure components of the mixture and their volume participation, it allows the determination of excess molar volumes:
provided that there is no interaction between the components.
Knowing the relation between excess volumes and activity coefficients of the components, one can determine the activity coefficients:
Densities
Various materials
- Selected chemical elements are listed here. For the densities of all chemical elements, see List of chemical elements
Densities of various materials covering a range of values
| Material | ρ (kg/m3)[note 1] | Notes |
|---|---|---|
| Hydrogen | 0.0898 | |
| Helium | 0.179 | |
| Aerographite | 0.2 | [note 2][8][9] |
| Metallic microlattice | 0.9 | [note 2] |
| Aerogel | 1.0 | [note 2] |
| Air | 1.2 | At sea level |
| Tungsten hexafluoride | 12.4 | One of the heaviest known gases at standard conditions |
| Liquid hydrogen | 70 | At approx. −255 °C |
| Styrofoam | 75 | Approx.[10] |
| Cork | 240 | Approx.[10] |
| Pine | 373 | [11] |
| Lithium | 535 | Least dense metal |
| Wood | 700 | Seasoned, typical[12][13] |
| Oak | 710 | [11] |
| Potassium | 860 | [14] |
| Ice | 916.7 | At temperature < 0 °C |
| Cooking oil | 910–930 | |
| Sodium | 970 | |
| Water (fresh) | 1,000 | At 4 °C, the temperature of its maximum density |
| Water (salt) | 1,030 | 3% |
| Liquid oxygen | 1,141 | At approx. −219 °C |
| Nylon | 1,150 | |
| Plastics | 1,175 | Approx.; for polypropylene and PETE/PVC |
| Glycerol | 1,261 | [15] |
| Tetrachloroethene | 1,622 | |
| Sand | 1,600 | Between 1,600 and 2000 [16] |
| Magnesium | 1,740 | |
| Beryllium | 1,850 | |
| Silicon | 2,330 | |
| Concrete | 2,400 | [17][18] |
| Glass | 2,500 | [19] |
| Quartzite | 2,600 | [16] |
| Granite | 2,700 | [16] |
| Gneiss | 2,700 | [16] |
| Aluminium | 2,700 | |
| Limestone | 2,750 | Compact[16] |
| Basalt | 3,000 | [16] |
| Diiodomethane | 3,325 | Liquid at room temperature |
| Diamond | 3,500 | |
| Titanium | 4,540 | |
| Selenium | 4,800 | |
| Vanadium | 6,100 | |
| Antimony | 6,690 | |
| Zinc | 7,000 | |
| Chromium | 7,200 | |
| Tin | 7,310 | |
| Manganese | 7,325 | Approx. |
| Iron | 7,870 | |
| Mild Steel | 7,850 | |
| Niobium | 8,570 | |
| Brass | 8,600 | [18] |
| Cadmium | 8,650 | |
| Cobalt | 8,900 | |
| Nickel | 8,900 | |
| Copper | 8,940 | |
| Bismuth | 9,750 | |
| Molybdenum | 10,220 | |
| Silver | 10,500 | |
| Lead | 11,340 | |
| Thorium | 11,700 | |
| Rhodium | 12,410 | |
| Mercury | 13,546 | |
| Tantalum | 16,600 | |
| Uranium | 18,800 | |
| Tungsten | 19,300 | |
| Gold | 19,320 | |
| Plutonium | 19,840 | |
| Rhenium | 21,020 | |
| Platinum | 21,450 | |
| Iridium | 22,420 | |
| Osmium | 22,570 | Densest element |
Notes:
|
Others
| Entity | ρ (kg/m3) | Notes |
|---|---|---|
| Interstellar medium | 1×10−19 | Assuming 90% H, 10% He; variable T |
| The Earth | 5,515 | Mean density.[20] |
| Earth’s inner core | 13,000 | Approx., as listed in Earth.[21] |
| The core of the Sun | 33,000–160,000 | Approx.[22] |
| White dwarf star | 2.1×109 | Approx.[23] |
| Atomic nuclei | 2.3×1017 | Does not depend strongly on size of nucleus[24] |
| Neutron star | 1×1018 |
Water
Density of liquid water at 1 atm pressure
| Temp. (°C)[note 1] | Density (kg/m3) |
|---|---|
| −30 | 983.854 |
| −20 | 993.547 |
| −10 | 998.117 |
| 0 | 999.8395 |
| 4 | 999.9720 |
| 10 | 999.7026 |
| 15 | 999.1026 |
| 20 | 998.2071 |
| 22 | 997.7735 |
| 25 | 997.0479 |
| 30 | 995.6502 |
| 40 | 992.2 |
| 60 | 983.2 |
| 80 | 971.8 |
| 100 | 958.4 |
Notes:
|
Air
Air density vs. temperature
Density of air at 1 atm pressure
| T (°C) | ρ (kg/m3) |
|---|---|
| −25 | 1.423 |
| −20 | 1.395 |
| −15 | 1.368 |
| −10 | 1.342 |
| −5 | 1.316 |
| 0 | 1.293 |
| 5 | 1.269 |
| 10 | 1.247 |
| 15 | 1.225 |
| 20 | 1.204 |
| 25 | 1.184 |
| 30 | 1.164 |
| 35 | 1.146 |
Molar volumes of liquid and solid phase of elements
Molar volumes of liquid and solid phase of elements
Common units
The SI unit for density is:
- kilogram per cubic metre (kg/m3)
The litre and tonne are not part of the SI, but are acceptable for use with it, leading to the following units:
- kilogram per litre (kg/L)
- gram per millilitre (g/mL)
- tonne per cubic metre (t/m3)
Densities using the following metric units all have exactly the same numerical value, one thousandth of the value in (kg/m3). Liquid water has a density of about 1 kg/dm3, making any of these SI units numerically convenient to use as most solids and liquids have densities between 0.1 and 20 kg/dm3.
- kilogram per cubic decimetre (kg/dm3)
- gram per cubic centimetre (g/cm3)
- 1 g/cm3 = 1000 kg/m3
- megagram (metric ton) per cubic metre (Mg/m3)
In US customary units density can be stated in:
- Avoirdupois ounce per cubic inch (1 g/cm3 ≈ 0.578036672 oz/cu in)
- Avoirdupois ounce per fluid ounce (1 g/cm3 ≈ 1.04317556 oz/US fl oz = 1.04317556 lb/US fl pint)
- Avoirdupois pound per cubic inch (1 g/cm3 ≈ 0.036127292 lb/cu in)
- pound per cubic foot (1 g/cm3 ≈ 62.427961 lb/cu ft)
- pound per cubic yard (1 g/cm3 ≈ 1685.5549 lb/cu yd)
- pound per US liquid gallon (1 g/cm3 ≈ 8.34540445 lb/US gal)
- pound per US bushel (1 g/cm3 ≈ 77.6888513 lb/bu)
- slug per cubic foot
Imperial units differing from the above (as the Imperial gallon and bushel differ from the US units) in practice are rarely used, though found in older documents. The Imperial gallon was based on the concept that an Imperial fluid ounce of water would have a mass of one Avoirdupois ounce, and indeed 1 g/cm3 ≈ 1.00224129 ounces per Imperial fluid ounce = 10.0224129 pounds per Imperial gallon. The density of precious metals could conceivably be based on Troy ounces and pounds, a possible cause of confusion.
Knowing the volume of the unit cell of a crystalline material and its formula weight (in daltons), the density can be calculated. One dalton per cubic ångström is equal to a density of 1.660 539 066 60 g/cm3.
See also
- Densities of the elements (data page)
- List of elements by density
- Air density
- Area density
- Bulk density
- Buoyancy
- Charge density
- Density prediction by the Girolami method
- Dord
- Energy density
- Lighter than air
- Linear density
- Number density
- Orthobaric density
- Paper density
- Specific weight
- Spice (oceanography)
- Standard temperature and pressure
References
- ^ The National Aeronautic and Atmospheric Administration’s Glenn Research Center. «Gas Density Glenn research Center». grc.nasa.gov. Archived from the original on April 14, 2013. Retrieved April 9, 2013.
- ^ «Density definition in Oil Gas Glossary». Oilgasglossary.com. Archived from the original on August 5, 2010. Retrieved September 14, 2010.
- ^ Archimedes, A Gold Thief and Buoyancy Archived August 27, 2007, at the Wayback Machine – by Larry «Harris» Taylor, Ph.D.
- ^ Vitruvius on Architecture, Book IX, paragraphs 9–12, translated into English and in the original Latin.
- ^ «EXHIBIT: The First Eureka Moment». Science. 305 (5688): 1219e. 2004. doi:10.1126/science.305.5688.1219e.
- ^ «Fact or Fiction?: Archimedes Coined the Term «Eureka!» in the Bath». Scientific American. December 2006.
- ^ «Test No. 109: Density of Liquids and Solids». OECD Guidelines for the Testing of Chemicals, Section 1. October 2, 2012. doi:10.1787/9789264123298-en. ISBN 9789264123298. ISSN 2074-5753.
- ^ New carbon nanotube struructure aerographite is lightest material champ Archived October 17, 2013, at the Wayback Machine. Phys.org (July 13, 2012). Retrieved on July 14, 2012.
- ^ Aerographit: Leichtestes Material der Welt entwickelt – SPIEGEL ONLINE Archived October 17, 2013, at the Wayback Machine. Spiegel.de (July 11, 2012). Retrieved on July 14, 2012.
- ^ a b «Re: which is more bouyant [sic] styrofoam or cork». Madsci.org. Archived from the original on February 14, 2011. Retrieved September 14, 2010.
- ^ a b Serway, Raymond; Jewett, John (2005), Principles of Physics: A Calculus-Based Text, Cengage Learning, p. 467, ISBN 0-534-49143-X, archived from the original on May 17, 2016
- ^ «Wood Densities». www.engineeringtoolbox.com. Archived from the original on October 20, 2012. Retrieved October 15, 2012.
- ^ «Density of Wood». www.simetric.co.uk. Archived from the original on October 26, 2012. Retrieved October 15, 2012.
- ^ Bolz, Ray E.; Tuve, George L., eds. (1970). «§1.3 Solids—Metals: Table 1-59 Metals and Alloys—Miscellaneous Properties». CRC Handbook of tables for Applied Engineering Science (2nd ed.). CRC Press. p. 117. ISBN 9781315214092.
- ^ glycerol composition at Archived February 28, 2013, at the Wayback Machine. Physics.nist.gov. Retrieved on July 14, 2012.
- ^ a b c d e f Sharma, P.V. (1997), Environmental and Engineering Geophysics, Cambridge University Press, p. 17, doi:10.1017/CBO9781139171168, ISBN 9781139171168
- ^ «Density of Concrete — The Physics Factbook». hypertextbook.com.
- ^ a b Young, Hugh D.; Freedman, Roger A. (2012). University Physics with Modern Physics. Addison-Wesley. p. 374. ISBN 978-0-321-69686-1.
- ^ «Density of Glass — The Physics Factbook». hypertextbook.com.
- ^ Density of the Earth, wolframalpha.com, archived from the original on October 17, 2013
- ^ Density of Earth’s core, wolframalpha.com, archived from the original on October 17, 2013
- ^ Density of the Sun’s core, wolframalpha.com, archived from the original on October 17, 2013
- ^ Johnson, Jennifer. «Extreme Stars: White Dwarfs & Neutron Stars]» (PDF). lecture notes, Astronomy 162. Ohio State University. Archived from the original (PDF) on September 25, 2007.
- ^ «Nuclear Size and Density». HyperPhysics. Georgia State University. Archived from the original on July 6, 2009.
External links
- «Density» . Encyclopædia Britannica. Vol. 8 (11th ed.). 1911.
- «Density» . The New Student’s Reference Work . 1914.
- Video: Density Experiment with Oil and Alcohol
- Video: Density Experiment with Whiskey and Water
- Glass Density Calculation – Calculation of the density of glass at room temperature and of glass melts at 1000 – 1400°C
- List of Elements of the Periodic Table – Sorted by Density
- Calculation of saturated liquid densities for some components
- Field density test
- Water – Density and specific weight
- Temperature dependence of the density of water – Conversions of density units
- A delicious density experiment
- Water density calculator Archived July 13, 2011, at the Wayback Machine Water density for a given salinity and temperature.
- Liquid density calculator Select a liquid from the list and calculate density as a function of temperature.
- Gas density calculator Calculate density of a gas for as a function of temperature and pressure.
- Densities of various materials.
- Determination of Density of Solid, instructions for performing classroom experiment.
- Lam EJ, Alvarez MN, Galvez ME, Alvarez EB (2008). «A model for calculating the density of aqueous multicomponent electrolyte solutions». Journal of the Chilean Chemical Society. 53 (1): 1393–8. doi:10.4067/S0717-97072008000100015.
- Radović IR, Kijevčanin ML, Tasić AŽ, Djordjević BD, Šerbanović SP (2010). «Derived thermodynamic properties of alcohol+ cyclohexylamine mixtures». Journal of the Serbian Chemical Society. 75 (2): 283–293. CiteSeerX 10.1.1.424.3486. doi:10.2298/JSC1002283R.
| Density | |
|---|---|

A test tube holding four non-miscible colored liquids with different densities |
|
|
Common symbols |
ρ, D |
| SI unit | kg/m3 |
| Extensive? | No |
| Intensive? | Yes |
| Conserved? | No |
|
Derivations from |
 |
| Dimension |  |
Density (volumetric mass density or specific mass) is the substance’s mass per unit of volume. The symbol most often used for density is ρ (the lower case Greek letter rho), although the Latin letter D can also be used. Mathematically, density is defined as mass divided by volume:[1]
where ρ is the density, m is the mass, and V is the volume. In some cases (for instance, in the United States oil and gas industry), density is loosely defined as its weight per unit volume,[2] although this is scientifically inaccurate – this quantity is more specifically called specific weight.
For a pure substance the density has the same numerical value as its mass concentration.
Different materials usually have different densities, and density may be relevant to buoyancy, purity and packaging. Osmium and iridium are the densest known elements at standard conditions for temperature and pressure.
To simplify comparisons of density across different systems of units, it is sometimes replaced by the dimensionless quantity «relative density» or «specific gravity», i.e. the ratio of the density of the material to that of a standard material, usually water. Thus a relative density less than one relative to water means that the substance floats in water.
The density of a material varies with temperature and pressure. This variation is typically small for solids and liquids but much greater for gases. Increasing the pressure on an object decreases the volume of the object and thus increases its density. Increasing the temperature of a substance (with a few exceptions) decreases its density by increasing its volume. In most materials, heating the bottom of a fluid results in convection of the heat from the bottom to the top, due to the decrease in the density of the heated fluid, which causes it to rise relative to denser unheated material.
The reciprocal of the density of a substance is occasionally called its specific volume, a term sometimes used in thermodynamics. Density is an intensive property in that increasing the amount of a substance does not increase its density; rather it increases its mass.
Other conceptually comparable quantities or ratios include specific density, relative density (specific gravity), and specific weight.
History
In a well-known but probably apocryphal tale, Archimedes was given the task of determining whether King Hiero’s goldsmith was embezzling gold during the manufacture of a golden wreath dedicated to the gods and replacing it with another, cheaper alloy.[3] Archimedes knew that the irregularly shaped wreath could be crushed into a cube whose volume could be calculated easily and compared with the mass; but the king did not approve of this. Baffled, Archimedes is said to have taken an immersion bath and observed from the rise of the water upon entering that he could calculate the volume of the gold wreath through the displacement of the water. Upon this discovery, he leapt from his bath and ran naked through the streets shouting, «Eureka! Eureka!» (Εύρηκα! Greek «I have found it»). As a result, the term «eureka» entered common parlance and is used today to indicate a moment of enlightenment.
The story first appeared in written form in Vitruvius’ books of architecture, two centuries after it supposedly took place.[4] Some scholars have doubted the accuracy of this tale, saying among other things that the method would have required precise measurements that would have been difficult to make at the time.[5][6]
Measurement of density
A number of techniques as well as standards exist for the measurement of density of materials. Such techniques include the use of a hydrometer (a buoyancy method for liquids), Hydrostatic balance (a buoyancy method for liquids and solids), immersed body method (a buoyancy method for liquids), pycnometer (liquids and solids), air comparison pycnometer (solids), oscillating densitometer (liquids), as well as pour and tap (solids).[7] However, each individual method or technique measures different types of density (e.g. bulk density, skeletal density, etc.), and therefore it is necessary to have an understanding of the type of density being measured as well as the type of material in question.
Unit
From the equation for density (ρ = m/V), mass density has any unit that is mass divided by volume. As there are many units of mass and volume covering many different magnitudes there are a large number of units for mass density in use. The SI unit of kilogram per cubic metre (kg/m3) and the cgs unit of gram per cubic centimetre (g/cm3) are probably the most commonly used units for density. One g/cm3 is equal to 1000 kg/m3. One cubic centimetre (abbreviation cc) is equal to one millilitre. In industry, other larger or smaller units of mass and or volume are often more practical and US customary units may be used. See below for a list of some of the most common units of density.
Homogeneous materials
The density at all points of a homogeneous object equals its total mass divided by its total volume. The mass is normally measured with a scale or balance; the volume may be measured directly (from the geometry of the object) or by the displacement of a fluid. To determine the density of a liquid or a gas, a hydrometer, a dasymeter or a Coriolis flow meter may be used, respectively. Similarly, hydrostatic weighing uses the displacement of water due to a submerged object to determine the density of the object.
Heterogeneous materials
If the body is not homogeneous, then its density varies between different regions of the object. In that case the density around any given location is determined by calculating the density of a small volume around that location. In the limit of an infinitesimal volume the density of an inhomogeneous object at a point becomes: 


Non-compact materials
In practice, bulk materials such as sugar, sand, or snow contain voids. Many materials exist in nature as flakes, pellets, or granules.
Voids are regions which contain something other than the considered material. Commonly the void is air, but it could also be vacuum, liquid, solid, or a different gas or gaseous mixture.
The bulk volume of a material—inclusive of the void fraction—is often obtained by a simple measurement (e.g. with a calibrated measuring cup) or geometrically from known dimensions.
Mass divided by bulk volume determines bulk density. This is not the same thing as volumetric mass density.
To determine volumetric mass density, one must first discount the volume of the void fraction. Sometimes this can be determined by geometrical reasoning. For the close-packing of equal spheres the non-void fraction can be at most about 74%. It can also be determined empirically. Some bulk materials, however, such as sand, have a variable void fraction which depends on how the material is agitated or poured. It might be loose or compact, with more or less air space depending on handling.
In practice, the void fraction is not necessarily air, or even gaseous. In the case of sand, it could be water, which can be advantageous for measurement as the void fraction for sand saturated in water—once any air bubbles are thoroughly driven out—is potentially more consistent than dry sand measured with an air void.
In the case of non-compact materials, one must also take care in determining the mass of the material sample. If the material is under pressure (commonly ambient air pressure at the earth’s surface) the determination of mass from a measured sample weight might need to account for buoyancy effects due to the density of the void constituent, depending on how the measurement was conducted. In the case of dry sand, sand is so much denser than air that the buoyancy effect is commonly neglected (less than one part in one thousand).
Mass change upon displacing one void material with another while maintaining constant volume can be used to estimate the void fraction, if the difference in density of the two voids materials is reliably known.
Changes of density
In general, density can be changed by changing either the pressure or the temperature. Increasing the pressure always increases the density of a material. Increasing the temperature generally decreases the density, but there are notable exceptions to this generalization. For example, the density of water increases between its melting point at 0 °C and 4 °C; similar behavior is observed in silicon at low temperatures.
The effect of pressure and temperature on the densities of liquids and solids is small. The compressibility for a typical liquid or solid is 10−6 bar−1 (1 bar = 0.1 MPa) and a typical thermal expansivity is 10−5 K−1. This roughly translates into needing around ten thousand times atmospheric pressure to reduce the volume of a substance by one percent. (Although the pressures needed may be around a thousand times smaller for sandy soil and some clays.) A one percent expansion of volume typically requires a temperature increase on the order of thousands of degrees Celsius.
In contrast, the density of gases is strongly affected by pressure. The density of an ideal gas is
where M is the molar mass, P is the pressure, R is the universal gas constant, and T is the absolute temperature. This means that the density of an ideal gas can be doubled by doubling the pressure, or by halving the absolute temperature.
In the case of volumic thermal expansion at constant pressure and small intervals of temperature the temperature dependence of density is
where 


Density of solutions
The density of a solution is the sum of mass (massic) concentrations of the components of that solution.
Mass (massic) concentration of each given component ρi in a solution sums to density of the solution,
Expressed as a function of the densities of pure components of the mixture and their volume participation, it allows the determination of excess molar volumes:
provided that there is no interaction between the components.
Knowing the relation between excess volumes and activity coefficients of the components, one can determine the activity coefficients:
Densities
Various materials
- Selected chemical elements are listed here. For the densities of all chemical elements, see List of chemical elements
Densities of various materials covering a range of values
| Material | ρ (kg/m3)[note 1] | Notes |
|---|---|---|
| Hydrogen | 0.0898 | |
| Helium | 0.179 | |
| Aerographite | 0.2 | [note 2][8][9] |
| Metallic microlattice | 0.9 | [note 2] |
| Aerogel | 1.0 | [note 2] |
| Air | 1.2 | At sea level |
| Tungsten hexafluoride | 12.4 | One of the heaviest known gases at standard conditions |
| Liquid hydrogen | 70 | At approx. −255 °C |
| Styrofoam | 75 | Approx.[10] |
| Cork | 240 | Approx.[10] |
| Pine | 373 | [11] |
| Lithium | 535 | Least dense metal |
| Wood | 700 | Seasoned, typical[12][13] |
| Oak | 710 | [11] |
| Potassium | 860 | [14] |
| Ice | 916.7 | At temperature < 0 °C |
| Cooking oil | 910–930 | |
| Sodium | 970 | |
| Water (fresh) | 1,000 | At 4 °C, the temperature of its maximum density |
| Water (salt) | 1,030 | 3% |
| Liquid oxygen | 1,141 | At approx. −219 °C |
| Nylon | 1,150 | |
| Plastics | 1,175 | Approx.; for polypropylene and PETE/PVC |
| Glycerol | 1,261 | [15] |
| Tetrachloroethene | 1,622 | |
| Sand | 1,600 | Between 1,600 and 2000 [16] |
| Magnesium | 1,740 | |
| Beryllium | 1,850 | |
| Silicon | 2,330 | |
| Concrete | 2,400 | [17][18] |
| Glass | 2,500 | [19] |
| Quartzite | 2,600 | [16] |
| Granite | 2,700 | [16] |
| Gneiss | 2,700 | [16] |
| Aluminium | 2,700 | |
| Limestone | 2,750 | Compact[16] |
| Basalt | 3,000 | [16] |
| Diiodomethane | 3,325 | Liquid at room temperature |
| Diamond | 3,500 | |
| Titanium | 4,540 | |
| Selenium | 4,800 | |
| Vanadium | 6,100 | |
| Antimony | 6,690 | |
| Zinc | 7,000 | |
| Chromium | 7,200 | |
| Tin | 7,310 | |
| Manganese | 7,325 | Approx. |
| Iron | 7,870 | |
| Mild Steel | 7,850 | |
| Niobium | 8,570 | |
| Brass | 8,600 | [18] |
| Cadmium | 8,650 | |
| Cobalt | 8,900 | |
| Nickel | 8,900 | |
| Copper | 8,940 | |
| Bismuth | 9,750 | |
| Molybdenum | 10,220 | |
| Silver | 10,500 | |
| Lead | 11,340 | |
| Thorium | 11,700 | |
| Rhodium | 12,410 | |
| Mercury | 13,546 | |
| Tantalum | 16,600 | |
| Uranium | 18,800 | |
| Tungsten | 19,300 | |
| Gold | 19,320 | |
| Plutonium | 19,840 | |
| Rhenium | 21,020 | |
| Platinum | 21,450 | |
| Iridium | 22,420 | |
| Osmium | 22,570 | Densest element |
Notes:
|
Others
| Entity | ρ (kg/m3) | Notes |
|---|---|---|
| Interstellar medium | 1×10−19 | Assuming 90% H, 10% He; variable T |
| The Earth | 5,515 | Mean density.[20] |
| Earth’s inner core | 13,000 | Approx., as listed in Earth.[21] |
| The core of the Sun | 33,000–160,000 | Approx.[22] |
| White dwarf star | 2.1×109 | Approx.[23] |
| Atomic nuclei | 2.3×1017 | Does not depend strongly on size of nucleus[24] |
| Neutron star | 1×1018 |
Water
Density of liquid water at 1 atm pressure
| Temp. (°C)[note 1] | Density (kg/m3) |
|---|---|
| −30 | 983.854 |
| −20 | 993.547 |
| −10 | 998.117 |
| 0 | 999.8395 |
| 4 | 999.9720 |
| 10 | 999.7026 |
| 15 | 999.1026 |
| 20 | 998.2071 |
| 22 | 997.7735 |
| 25 | 997.0479 |
| 30 | 995.6502 |
| 40 | 992.2 |
| 60 | 983.2 |
| 80 | 971.8 |
| 100 | 958.4 |
Notes:
|
Air
Air density vs. temperature
Density of air at 1 atm pressure
| T (°C) | ρ (kg/m3) |
|---|---|
| −25 | 1.423 |
| −20 | 1.395 |
| −15 | 1.368 |
| −10 | 1.342 |
| −5 | 1.316 |
| 0 | 1.293 |
| 5 | 1.269 |
| 10 | 1.247 |
| 15 | 1.225 |
| 20 | 1.204 |
| 25 | 1.184 |
| 30 | 1.164 |
| 35 | 1.146 |
Molar volumes of liquid and solid phase of elements
Molar volumes of liquid and solid phase of elements
Common units
The SI unit for density is:
- kilogram per cubic metre (kg/m3)
The litre and tonne are not part of the SI, but are acceptable for use with it, leading to the following units:
- kilogram per litre (kg/L)
- gram per millilitre (g/mL)
- tonne per cubic metre (t/m3)
Densities using the following metric units all have exactly the same numerical value, one thousandth of the value in (kg/m3). Liquid water has a density of about 1 kg/dm3, making any of these SI units numerically convenient to use as most solids and liquids have densities between 0.1 and 20 kg/dm3.
- kilogram per cubic decimetre (kg/dm3)
- gram per cubic centimetre (g/cm3)
- 1 g/cm3 = 1000 kg/m3
- megagram (metric ton) per cubic metre (Mg/m3)
In US customary units density can be stated in:
- Avoirdupois ounce per cubic inch (1 g/cm3 ≈ 0.578036672 oz/cu in)
- Avoirdupois ounce per fluid ounce (1 g/cm3 ≈ 1.04317556 oz/US fl oz = 1.04317556 lb/US fl pint)
- Avoirdupois pound per cubic inch (1 g/cm3 ≈ 0.036127292 lb/cu in)
- pound per cubic foot (1 g/cm3 ≈ 62.427961 lb/cu ft)
- pound per cubic yard (1 g/cm3 ≈ 1685.5549 lb/cu yd)
- pound per US liquid gallon (1 g/cm3 ≈ 8.34540445 lb/US gal)
- pound per US bushel (1 g/cm3 ≈ 77.6888513 lb/bu)
- slug per cubic foot
Imperial units differing from the above (as the Imperial gallon and bushel differ from the US units) in practice are rarely used, though found in older documents. The Imperial gallon was based on the concept that an Imperial fluid ounce of water would have a mass of one Avoirdupois ounce, and indeed 1 g/cm3 ≈ 1.00224129 ounces per Imperial fluid ounce = 10.0224129 pounds per Imperial gallon. The density of precious metals could conceivably be based on Troy ounces and pounds, a possible cause of confusion.
Knowing the volume of the unit cell of a crystalline material and its formula weight (in daltons), the density can be calculated. One dalton per cubic ångström is equal to a density of 1.660 539 066 60 g/cm3.
See also
- Densities of the elements (data page)
- List of elements by density
- Air density
- Area density
- Bulk density
- Buoyancy
- Charge density
- Density prediction by the Girolami method
- Dord
- Energy density
- Lighter than air
- Linear density
- Number density
- Orthobaric density
- Paper density
- Specific weight
- Spice (oceanography)
- Standard temperature and pressure
References
- ^ The National Aeronautic and Atmospheric Administration’s Glenn Research Center. «Gas Density Glenn research Center». grc.nasa.gov. Archived from the original on April 14, 2013. Retrieved April 9, 2013.
- ^ «Density definition in Oil Gas Glossary». Oilgasglossary.com. Archived from the original on August 5, 2010. Retrieved September 14, 2010.
- ^ Archimedes, A Gold Thief and Buoyancy Archived August 27, 2007, at the Wayback Machine – by Larry «Harris» Taylor, Ph.D.
- ^ Vitruvius on Architecture, Book IX, paragraphs 9–12, translated into English and in the original Latin.
- ^ «EXHIBIT: The First Eureka Moment». Science. 305 (5688): 1219e. 2004. doi:10.1126/science.305.5688.1219e.
- ^ «Fact or Fiction?: Archimedes Coined the Term «Eureka!» in the Bath». Scientific American. December 2006.
- ^ «Test No. 109: Density of Liquids and Solids». OECD Guidelines for the Testing of Chemicals, Section 1. October 2, 2012. doi:10.1787/9789264123298-en. ISBN 9789264123298. ISSN 2074-5753.
- ^ New carbon nanotube struructure aerographite is lightest material champ Archived October 17, 2013, at the Wayback Machine. Phys.org (July 13, 2012). Retrieved on July 14, 2012.
- ^ Aerographit: Leichtestes Material der Welt entwickelt – SPIEGEL ONLINE Archived October 17, 2013, at the Wayback Machine. Spiegel.de (July 11, 2012). Retrieved on July 14, 2012.
- ^ a b «Re: which is more bouyant [sic] styrofoam or cork». Madsci.org. Archived from the original on February 14, 2011. Retrieved September 14, 2010.
- ^ a b Serway, Raymond; Jewett, John (2005), Principles of Physics: A Calculus-Based Text, Cengage Learning, p. 467, ISBN 0-534-49143-X, archived from the original on May 17, 2016
- ^ «Wood Densities». www.engineeringtoolbox.com. Archived from the original on October 20, 2012. Retrieved October 15, 2012.
- ^ «Density of Wood». www.simetric.co.uk. Archived from the original on October 26, 2012. Retrieved October 15, 2012.
- ^ Bolz, Ray E.; Tuve, George L., eds. (1970). «§1.3 Solids—Metals: Table 1-59 Metals and Alloys—Miscellaneous Properties». CRC Handbook of tables for Applied Engineering Science (2nd ed.). CRC Press. p. 117. ISBN 9781315214092.
- ^ glycerol composition at Archived February 28, 2013, at the Wayback Machine. Physics.nist.gov. Retrieved on July 14, 2012.
- ^ a b c d e f Sharma, P.V. (1997), Environmental and Engineering Geophysics, Cambridge University Press, p. 17, doi:10.1017/CBO9781139171168, ISBN 9781139171168
- ^ «Density of Concrete — The Physics Factbook». hypertextbook.com.
- ^ a b Young, Hugh D.; Freedman, Roger A. (2012). University Physics with Modern Physics. Addison-Wesley. p. 374. ISBN 978-0-321-69686-1.
- ^ «Density of Glass — The Physics Factbook». hypertextbook.com.
- ^ Density of the Earth, wolframalpha.com, archived from the original on October 17, 2013
- ^ Density of Earth’s core, wolframalpha.com, archived from the original on October 17, 2013
- ^ Density of the Sun’s core, wolframalpha.com, archived from the original on October 17, 2013
- ^ Johnson, Jennifer. «Extreme Stars: White Dwarfs & Neutron Stars]» (PDF). lecture notes, Astronomy 162. Ohio State University. Archived from the original (PDF) on September 25, 2007.
- ^ «Nuclear Size and Density». HyperPhysics. Georgia State University. Archived from the original on July 6, 2009.
External links
- «Density» . Encyclopædia Britannica. Vol. 8 (11th ed.). 1911.
- «Density» . The New Student’s Reference Work . 1914.
- Video: Density Experiment with Oil and Alcohol
- Video: Density Experiment with Whiskey and Water
- Glass Density Calculation – Calculation of the density of glass at room temperature and of glass melts at 1000 – 1400°C
- List of Elements of the Periodic Table – Sorted by Density
- Calculation of saturated liquid densities for some components
- Field density test
- Water – Density and specific weight
- Temperature dependence of the density of water – Conversions of density units
- A delicious density experiment
- Water density calculator Archived July 13, 2011, at the Wayback Machine Water density for a given salinity and temperature.
- Liquid density calculator Select a liquid from the list and calculate density as a function of temperature.
- Gas density calculator Calculate density of a gas for as a function of temperature and pressure.
- Densities of various materials.
- Determination of Density of Solid, instructions for performing classroom experiment.
- Lam EJ, Alvarez MN, Galvez ME, Alvarez EB (2008). «A model for calculating the density of aqueous multicomponent electrolyte solutions». Journal of the Chilean Chemical Society. 53 (1): 1393–8. doi:10.4067/S0717-97072008000100015.
- Radović IR, Kijevčanin ML, Tasić AŽ, Djordjević BD, Šerbanović SP (2010). «Derived thermodynamic properties of alcohol+ cyclohexylamine mixtures». Journal of the Serbian Chemical Society. 75 (2): 283–293. CiteSeerX 10.1.1.424.3486. doi:10.2298/JSC1002283R.
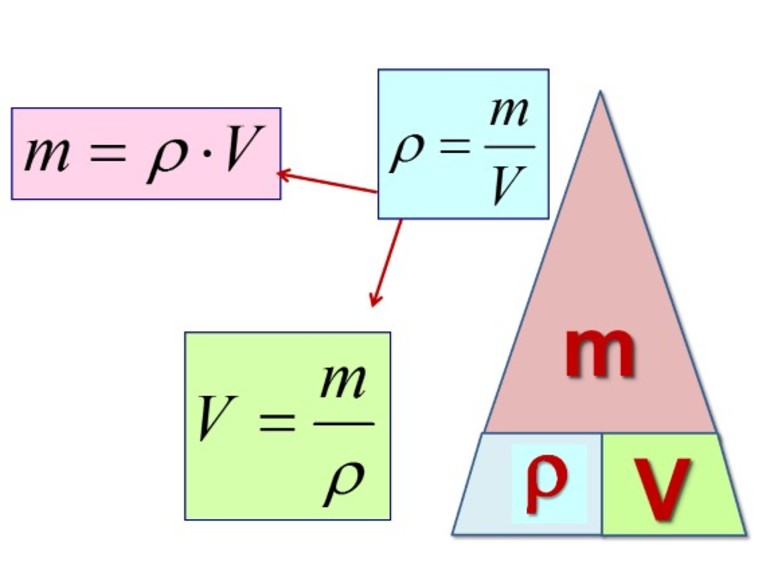
Для обозначения плотности обычно используется символ 
Более точное определение плотности требует уточнение формулировки:
- Средняя плотность тела — отношение массы тела к его объёму. Для однородного тела она также называется просто плотностью тела.
- Плотность вещества — это плотность тел, состоящих из этого вещества.
- Плотность тела в точке — это предел отношения массы малой части тела (
), содержащей эту точку, к объёму этой малой части (
), когда этот объём стремится к нулю[1], или, записывая кратко,
. При таком предельном переходе необходимо помнить, что на атомарном уровне любое тело неоднородно, поэтому необходимо остановиться на объёме, соответствующем используемой физической модели.
Виды плотности и единицы измерения
Исходя из определения плотности, её размерность кг/м³ в системе СИ и в г/см³ в системе СГС.
Для сыпучих и пористых тел различают:
- истинную плотность, определяемую без учёта пустот;
- удельную (кажущуюся) плотность, рассчитываемую как отношение массы вещества ко всему занимаемому им объёму.
Истинную плотность из кажущейся получают с помощью величины коэффициента пористости — доли объёма пустот в занимаемом объёме.
Формула нахождения плотности
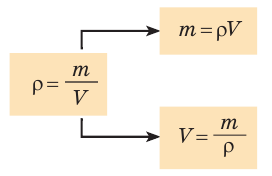
Плотность (плотность однородного тела или средняя плотность неоднородного) находится по формуле:
где m — масса тела, V — его объём; формула является просто математической записью определения термина «плотность», данного выше.
- При вычислении плотности газов эта формула может быть записана и в виде:
- где М — молярная масса газа,
— молярный объём (при нормальных условиях равен 22,4 л/моль).
-
Зависимость плотности от температуры
-
Как правило, при уменьшении температуры плотность увеличивается, хотя встречаются вещества, чья плотность ведёт себя иначе, например, вода, бронза и чугун. Так, плотность воды имеет максимальное значение при 4 °C и уменьшается как с повышением, так и с понижением температуры относительно этого значения.
При изменении агрегатного состояния плотность вещества меняется скачкообразно: плотность растёт при переходе из газообразного состояния в жидкое и при затвердевании жидкости. Вода, кремний, германий и некоторые другие вещества являются исключениями из данного правила, так как их плотность при переходе в твердую фазу уменьшается.
-
-
| Плотность | |
 |
|
| Размерность |
L−3M |
|---|---|
| Единицы измерения | |
| СИ |
кг/м³ |
| СГС |
г/см³ |
| Примечания | |
|
скалярная величина |
Пло́тность — скалярная физическая величина, определяемая как отношение массы тела к занимаемому этим телом объёму. Более строгое определение плотности требует уточнение формулировки:
- Средняя плотность тела — отношение массы тела к его объёму. Для однородного тела она также называется просто плотностью тела.
- Плотность вещества — это плотность тел, состоящих из этого вещества. Отсюда вытекает и короткая формулировка определения плотности вещества: плотность вещества — это масса его единичного объёма.
- Плотность тела в точке — это предел отношения массы малой части тела (
), содержащей эту точку, к объёму этой малой части (
), когда этот объём стремится к нулю[1], или, записывая кратко,
. При таком предельном переходе необходимо помнить, что на атомарном уровне любое тело неоднородно, поэтому необходимо остановиться на объёме, соответствующем используемой физической модели.
Содержание
- 1 Виды плотности и единицы измерения
- 2 Формула нахождения плотности
- 3 Зависимость плотности от температуры
- 4 Диапазон плотностей в природе
- 5 Плотности астрономических объектов
- 6 Плотности некоторых газов
- 7 Плотности некоторых жидкостей
- 8 Плотность некоторых пород древесины
- 9 Измерение плотности
- 10 См. также
- 11 Примечания
- 12 Ссылки
- 13 Источники
Виды плотности и единицы измерения
Исходя из определения плотности, её размерность кг/м³ в системе СИ и в г/см³ в системе СГС.
Для сыпучих и пористых тел различают:
- истинную плотность, определяемую без учёта пустот;
- удельную (кажущуюся) плотность, рассчитываемую как отношение массы вещества ко всему занимаемому им объёму.
Истинную плотность из кажущейся получают с помощью величины коэффициента пористости — доли объёма пустот в занимаемом объёме.
Формула нахождения плотности
Плотность (плотность однородного тела или средняя плотность неоднородного) находится по формуле:
где m — масса тела, V — его объём; формула является просто математической записью определения термина «плотность», данного выше.
- При вычисления плотности газов эта формула может быть записана и в виде:
- где М — молярная масса газа,
— молярный объём (при нормальных условиях равен 22,4 л/моль).
Плотность тела в точке записывается как 
Зависимость плотности от температуры
Как правило, при уменьшении температуры плотность увеличивается, хотя встречаются вещества, чья плотность ведёт себя иначе, например, вода, бронза и чугун. Так, плотность воды имеет максимальное значение при 4 °C и уменьшается как с повышением, так и с понижением температуры относительно этого числа.
При изменении агрегатного состояния плотность вещества меняется скачкообразно: плотность растёт при переходе из газообразного состояния в жидкое и при затвердевании жидкости. Правда, вода является исключением из этого правила, её плотность при затвердевании уменьшается.
Диапазон плотностей в природе
Для различных природных объектов плотность меняется в очень широком диапазоне.
- Самую низкую плотность имеет межгалактическая среда (2·10−31÷5·10−31 кг/м³)[2].
- Плотность межзвёздной среды приблизительно равна 10−23÷10−21 кг/м³.
- Средняя плотность Солнца примерно в 1,5 раза выше плотности воды.
- Средняя плотность красных гигантов на много порядков меньше, чем у Солнца, из-за того, что их радиус в сотни раз больше.
- Средняя плотность Земли равна 5520 кг/м³.
- Жидкий водород при атмосферном давлении и температуре −253 °C имеет плотность 70 кг/м³.
- Плотность жидкого гелия при атмосферном давлении равна 130 кг/м³.
- Плотность пресной воды составляет 1000 кг/м³.
- Гранит имеет плотность 2600 кг/м³.
- Плотность железа равна 7874 кг/м³.
- Наибольшую плотность среди металлов имеет осмий (22 587 кг/м³).
- Плотность атомных ядер приблизительно равна 2·1017 кг/м³.
- Плотность белых карликов составляет 108÷1012 кг/м³.
- Плотность нейтронных звёзд имеет порядок 1017÷1018 кг/м³.
- Теоретически верхнюю границу представляет планковская плотность (современная физика оценивает её в 5,1·1096 кг/м³, хотя не исключено, что она очень сильно завышена).
Плотности астрономических объектов
Средние плотности планет Солнечной системы и Солнца:
Средняя плотность Солнца и планет (в г/см³)[3][4]
- Межпланетная среда в Солнечной системе достаточно неоднородна и может меняться во времени, её плотность в окрестностях Земли ~10−21÷10−20 кг/м³.
- Плотность межзвёздной среды ~10−23÷10−21 кг/м³.
- Плотность межгалактической среды от 2×10−34 до 5×10−34 кг/м³.
- Средняя плотность красных гигантов на много порядков меньше из-за того, что их радиус в сотни раз больше, чем у Солнца.
- Плотность белых карликов 108÷1012 кг/м³
- Плотность нейтронных звёзд имеет порядок 1017÷1018 кг/м³.
- Средняя (по объёму под горизонтом событий) плотность чёрной дыры
- у чёрной дыры с массой порядка солнечной превышает ядерную плотность,
- у сверхмассивной чёрной дыры с массой в 109 солнечных масс (существование таких чёрных дыр подозревается в квазарах) оставляет около 20 кг/м³,
- у сверхмассивной чёрной дыры в центре галактики может быть 0,2 кг/м³.
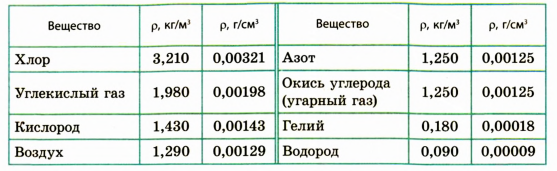
Плотности некоторых газов
Плотность газов и паров (0 °C, 101325 Па), кг/м³
| Азот | 1,250 | Кислород | 1,429 |
| Аммиак | 0,771 | Криптон | 3,743 |
| Аргон | 1,784 | Ксенон | 5,851 |
| Водород | 0,090 | Метан | 0,717 |
| Водяной пар (100 °C) | 0,598 | Неон | 0,900 |
| Воздух | 1,293 | Углекислый газ | 1,977 |
| Хлор | 3,164 | Гелий | 0,178 |
| Этилен | 1,260 |
Плотности некоторых жидкостей
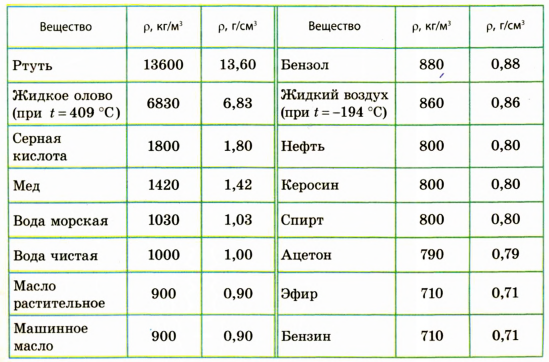
Плотность жидкостей, г/см³
| Бензин | 0,74 | Молоко | 1,04 |
| Вода (4 °C) | 1,00 | Ртуть (0 °C) | 13,60 |
| Керосин | 0,82 | Эфир | 0,72 |
| Глицерин | 1,26 | Спирт | 0,80 |
| Морская вода | 1,03 | Скипидар | 0,86 |
| Масло оливковое | 0,92 | Ацетон | 0,792 |
| Масло машинное | 0,91 | Серная кислота | 1,84 |
| Нефть | 0,81—0,85 | Жидкий водород (−253 °C) | 0,07 |
Плотность некоторых пород древесины
Плотность древесины, г/см³
| Бальса | 0,15 | Пихта сибирская | 0,39 |
| Секвойя вечнозелёная | 0,41 | Ель | 0,45 |
| Ива | 0,46 | Ольха | 0,49 |
| Осина | 0,51 | Сосна | 0,52 |
| Липа | 0,53 | Конский каштан | 0,56 |
| Каштан съедобный | 0,59 | Кипарис | 0,60 |
| Черёмуха | 0,61 | Лещина | 0,63 |
| Грецкий орех | 0,64 | Берёза | 0,65 |
| Вишня | 0,66 | Вяз гладкий | 0,66 |
| Лиственница | 0,66 | Клён полевой | 0,67 |
| Тиковое дерево | 0,67 | Бук | 0,68 |
| Груша | 0,69 | Дуб | 0,69 |
| Свитения (Махагони) | 0,70 | Платан | 0,70 |
| Жостер (крушина) | 0,71 | Тис | 0,75 |
| Ясень | 0,75 | Слива | 0,80 |
| Сирень | 0,80 | Боярышник | 0,80 |
| Пекан (кария) | 0,83 | Сандаловое дерево | 0,90 |
| Самшит | 0,96 | Эбеновое дерево | 1,08 |
| Квебрахо | 1,21 | Бакаут | 1,28 |
| Пробка | 0,48 |
Измерение плотности
Для измерения плотности используются:
- Пикнометр — прибор для измерения истинной плотности
- Ареометр (денсиметр, плотномер) — измеритель плотности жидкостей.
- Бурик Качинского и бур Зайдельмана — приборы для измерения плотности почвы.
- Вибрационный плотномер — прибор для измерения плотности жидкости и газа под давлением.
См. также
- Удельный вес
- Удельная плотность
- Относительная плотность
- Объемная плотность
- Концентрация частиц
- Концентрация растворов
- Плотность заряда
Примечания
- ↑ Подразумевается также, что область стягивается к точке, то есть, не только ее объем стремится к нулю (что могло бы быть не только при стягивании области к точке, но, например, к отрезку), но также стремится к нулю и ее диаметр (максимальный линейный размер).
- ↑ Агекян Т. А. Расширение Вселенной. Модель Вселенной. // Звёзды, галактики, Метагалактика / Под ред. А. Б. Васильева. — 3-е изд. — М.: Наука, 1982. — С. 249. — 416 с.
- ↑ (англ.)Planetary Fact Sheet
- ↑ (англ.)Sun Fact Sheet
Ссылки
- Видео: Эксперимент с маслом и алкоголем
- Видео: Эксперимент с виски и водой
- Плотность элементов (англ.)
- Плотность древесины (рус.)
- Онлайн интерактивная таблица плотности веществ (рус.)
Источники
- Большая советская энциклопедия
- Физическая энциклопедия под. ред. А. М. Прохорова. Москва. Научное издательство «Большая российская энциклопедия», 1992 г. Т.3, стр.637.
Содержание:
Плотность, единицы плотности:
Мы часто употребляем выражение «легкий, как воздух» или «тяжелый. как свинец». Но знаете ли вы. что воздух внутри, скажем, супермаркета, весит больше 400 кг. а груз такой массы не поднять и силачу. Свинцовое же грузило для удочки легко поднимет даже малыш. Выходит, приведенные выше выражения — неправильные? Подождите делать выводы — давайте разберемся.
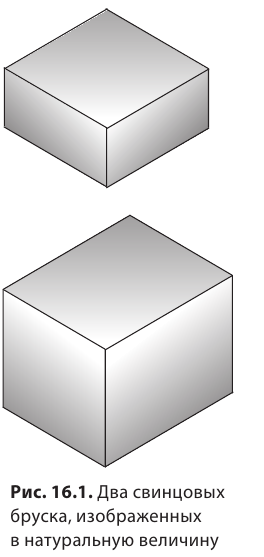
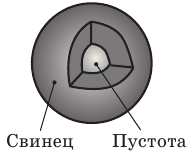
На рис. 2.8 вы видите два бруска, оба бруска изготовлены из одного и того же вещества — свинца, но имеют разные размеры. Наша задача — найти отношение массы каждого бруска к его объему.
Для начала измерьте длину, ширину и высоту брусков и вычислите их объемы. (Если вы правильно выполните измерения и не ошибетесь в расчетах, то вы получите такие результаты: объем меньшего бруска равен 4 см3, большего бруска — 10 см3.)
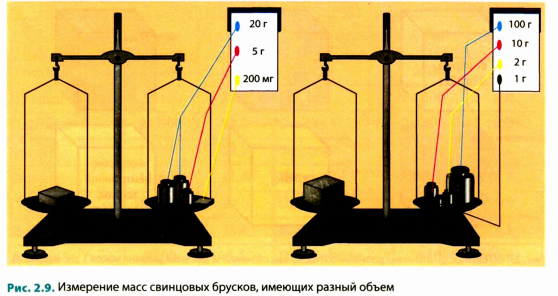
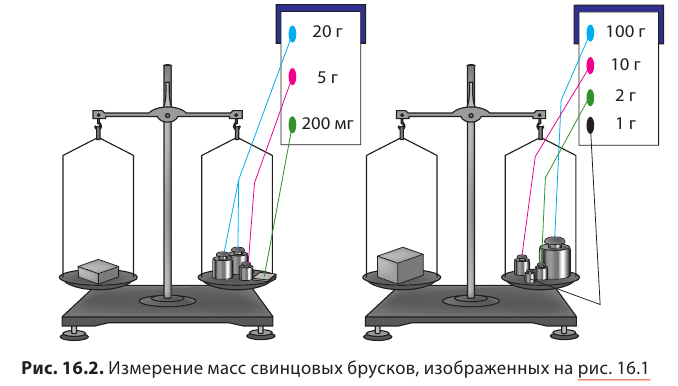
Определив объемы брусков, взвесим их. На левую чашу весов поместим один из брусков, на правую — разновесы (рис. 2.9). Весы находятся в равновесии, ваша задача — сосчитать массу разновесов.
Нам осталось найти отношение массы каждого бруска к его объему, т. е. вычислить, чему равняется масса свинца объемом 1 см3 для меньшего и для большего брусков. Очевидно, что если масса меньшего бруска 45,2 г и он занимает объем 4 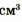
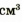
Если теперь взять бруски, изготовленные из другого вещества (например алюминия), и повторить те же действия, то отношение массы алюминиевого бруска к его объему также не будет зависеть от размеров бруска. Мы снова получим постоянное число, но уже другое, чем в опыте со свинцом.
Определение плотности вещества
Физическая величина, характеризующая данное вещество и численно равная массе вещества единичного объема, называется плотностью вещества.
Плотность обозначается символом р и вычисляется по формуле
где V — объем, занятый веществом массой m.
Плотность — это характеристика вещества, не зависящая от массы вещества и его объема. Если увеличить массу вещества, например, в два раза, то объем, который оно займет, также возрастет в два раза*.
Из определения плотности вещества получим единицу плотности. Поскольку в СИ единицей массы является килограмм, а единицей объема — метр кубический, то единицей плотности в СИ будет килограмм на метр кубический (кг/м*).
1 кг/м-* — это плотность такого однородного вещества, масса которого в объеме один кубический метр равняется одному килограмму.
На практике также очень часто применяется единица плотности грамм на сантиметр кубический (г/см*).
Единицы плотности килограмм на метр кубический (кг/м-1) и грамм на сантиметр кубический (г/см3) связаны между собой соотношением:
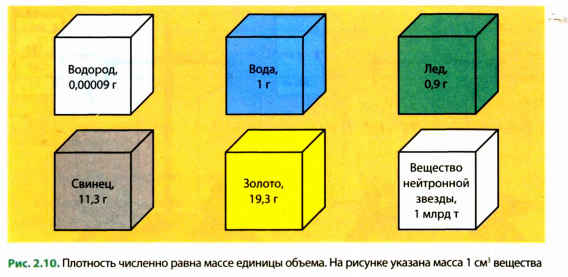
Плотности разных веществ
Плотности разных веществ и материалов могут существенно отличаться друг от друга (рис. 2.10). Рассмотрим несколько примеров. Плотность водорода при температуре О С и давлении 760 мм рт. ст. составляет 0,090 кг/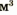
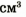
1 м3 имеет массу 11 300 кг, или 11,3 т. Плотность вещества нейтронной звезды достигает 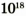
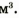

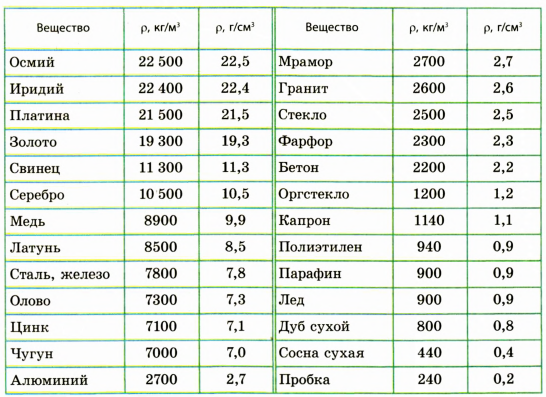
Таблица плотностей некоторых веществ в твердом состоянии
Таблица плотностей некоторых веществ в жидком состоянии
Таблица плотностей некоторых веществ в газообразном состоянии (при температуре О °С и давлении 760 мм рт. ст.)
Вычисление плотности, массы и объема физического тела
На практике часто бывает необходимо определить, из какого вещества состоит то или иное физическое тело. Для этого можно воспользоваться таким способом. Вначале вычислить плотность этого тела, т. е. найти отношение массы тела к его объему. Далее, воспользовавшись данными таблицы плотностей, выяснить, какому веществу соответствует найденное значение плотности.
Например, если глыба объемом 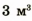
По таблице находим, что глыба состоит из льда.
В приведенных выше примерах мы рассматривали так называемые однородные тела, т. е. тела, не имеющие пустот и состоящие из одного ее щества (ледяная глыба, свинцовый и алюминиевый бруски). В таких случаях плотность тела равна плотности вещества, из которого оно состоит (плотность ледяной глыбы = плотности льда).
Если в теле есть пустоты или оно изготовлено из различных веществ (например, корабль, футбольный мяч, человек), то говорят о средней плотности тела, которая также исчисляется по формуле
где V — объем тела массой m.
Средняя плотность тела человека, например, составляет
Зная плотность вещества, из которого изготовлено тело (или среднюю плотность тела), и объем тела, можно определить массу данного тела без взвешивания. В самом деле, если
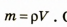
Итоги:
Физическая величина, характеризующая данное вещество и численно равная массе вещества единичного объема, называется плотностью вещества.
Плотность вещества и плотность тела можно рассчитать по формуле
В СИ плотность измеряется в килограммах на метр кубический 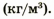
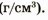
Зная массу тела и его плотность, можно найти объем тела: 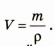
Плотность и единицы плотности
Вы наверняка слышали выражения «легкий, как воздух», «тяжелый, как свинец». При этом воздух внутри, скажем, супермаркета имеет массу более 5000 кг! Поднять груз такой массы не сможет и силач. В то же время свинцовое грузило для удочки легко поднимет даже малыш. Так что же, приведенные выражения ошибочны? Выясним, в чем здесь дело.
На рис. 16.1 изображены два однородных (не имеющих пустот) свинцовых бруска разного объема. Массы брусков тоже разные. Наша задача — найти отношение массы каждого бруска к его объему, то есть определить массу свинца объемом
1)Измерьте длину, ширину, высоту брусков и вычислите их объемы 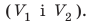
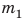
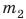
3)Определите отношение массы каждого бруска к его объему 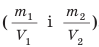
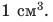
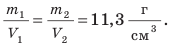
Как вы считаете, изменится ли результат, если для эксперимента взять однородные свинцовые бруски вдвое большей массы? Если изменится, то как?
Определение плотности вещества
Мы провели измерения и расчеты для тел, изготовленных из свинца. Если для эксперимента взять однородные тела, изготовленные из другого вещества, например алюминия, то снова получим одинаковые результаты, но уже другие, чем в опыте со свинцом.
Отношение массы тела к его объему — характеристика не тела, а вещества, из которого это тело изготовлено. Эту величину называют плотность вещества.
Плотность вещества — это физическая величина, которая характеризует вещество и равна отношению массы однородного тела, изготовленного из данного вещества, к объему этого тела: 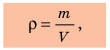
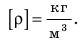
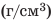
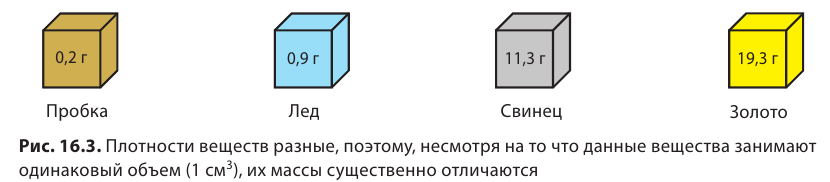
Сравнение плотности разных веществ
Плотности веществ могут существенно отличаться. Именно поэтому одинаковые по размерам однородные тела, изготовленные из разных веществ, будут иметь разную массу. Приведем несколько примеров.
Кубики на рис. 16.3 изображены в натуральную величину и являются однородными. Объем каждого кубика — 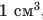
Первый кубик изготовлен из пробки. Плотность пробки составляет 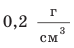
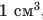
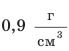
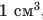
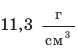
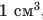
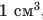
От чего зависит плотность вещества
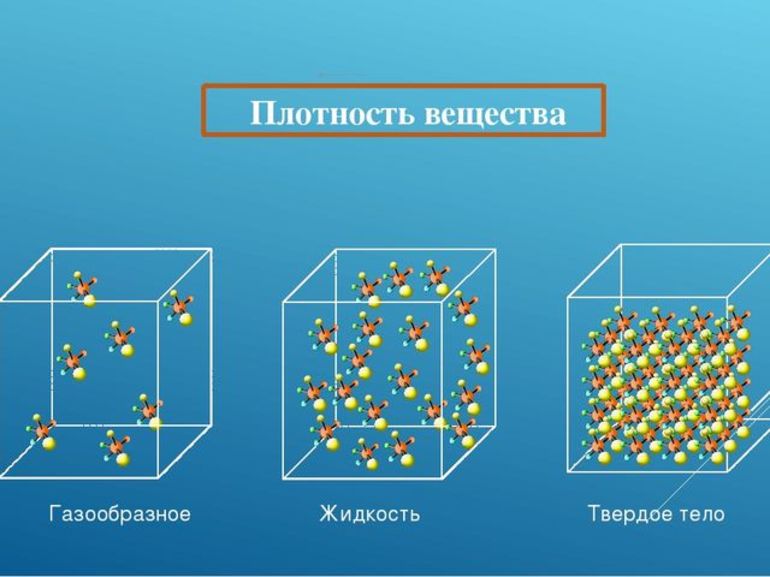
Плотность существенно зависит от агрегатного состояния и температуры вещества. Если вещество изменяет свое агрегатное состояние или температуру, его масса остается неизменной, так как количество частиц (молекул, атомов) и масса каждой из них не изменяются. А вот объем вещества изменяется, поскольку изменяется среднее расстояние между частицами. Так, при переходе вещества из жидкого состояния в газообразное плотность вещества уменьшается, поскольку увеличивается среднее расстояние между частицами, а значит, увеличивается объем, который занимает вещество (рис. 16.4).
С увеличением температуры среднее расстояние между частицами увеличивается, соответственно увеличивается объем вещества и уменьшается его плотность. И наоборот, чем ниже температура вещества, тем меньше межмолекулярные промежутки, а значит, меньше объем вещества и больше — его плотность*. 5
Вычисление и расчёт плотности тела, массы и объем тела
Как выяснить, из какого вещества изготовлено однородное тело? Один из способов — определить плотность этого тела и сравнить полученный результат с данными таблиц плотностей. Чтобы определить плотность тела, достаточно измерить его массу и объем и вычислить отношение массы тела к его объему.
Исключениями являются вода, чугун и некоторые другие вещества. Например, при нагревании воды от О °C до 4 °C ее плотность увеличивается. Плотность — это характеристика вещества, но иногда, например для сокращения записи, употребляют термин «плотность тела».
Например, если однородная фигурка объемом 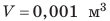
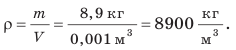
До сих пор речь шла об однородных телах, то есть телах, не имеющих пустот и состоящих из одного вещества (свинцовые бруски, медная фигурка). А вот если в теле есть пустоты или оно состоит из разных веществ (например, корабль, футбольный мяч, человек), то говорят о средней плотности тела; ее вычисляют по формуле: 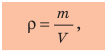
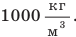
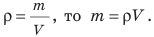
Итоги:
Плотность вещества — это физическая величина, которая характеризует вещество и равна отношению массы однородного тела, изготовленного из данного вещества, к объему этого тела. Плотность можно определить по формуле
Единица плотности в СИ — килограмм на метр кубический 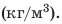
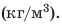
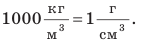
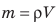
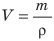
Напомним: приступив к решению задачи по физике, сначала следует несколько раз внимательно прочитать ее условие и понять, какое явление описано в задаче, какое тело рассматривается. Другими словами, нужно четко представить ситуацию, которую описывает задача, а уже потом приступать к поиску ответа. Итак, внимательно читаем, думаем, решаем. Попробуйте сначала поработать над каждой задачей самостоятельно, а уже потом ознакомьтесь с ее решением в учебнике.
- Заказать решение задач по физике
Пример №1
Однородный кубик с ребром 2 см имеет массу 20 г. Из какого вещества изготовлен кубик? Анализ физической проблемы. Для ответа на вопрос определим плотность вещества, из которого изготовлен кубик, а потом воспользуемся таблицей плотностей. Задачу будем решать в единицах, данных в условии.
Дано:

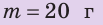
Найти:
Решение:
По определению плотности:
Объем куба вычисляют по формуле:
Следовательно, имеем:
Проверим единицу, найдем значение искомой величины:
Анализ результата. Из таблицы плотностей узнаем, что плотность 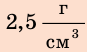
Ответ: кубик, возможно, изготовлен из стекла.
Пример №2
Свинцовый шар объемом 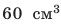
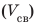
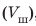
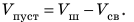
Плотность свинца найдем в таблице плотностей. В данной задаче массу лучше выразить в граммах, объем — в сантиметрах кубических, плотность — в граммах на сантиметр кубический.
Дано:

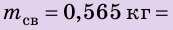

Найти:
Решение:
1. Определим объем свинца.
По определению плотности: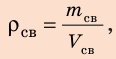
Проверим единицу, найдем значение искомой величины:
Анализ результатов: 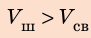
2. Вычислим объем пустоты:
Ответ:
Пример №3
Сколько железнодорожных цистерн емкостью 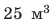
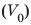
Дано:
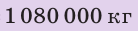
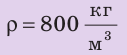
Найти:
Решение:
Из определения плотности найдем общий объем нефти:
Определим общее количество цистерн:
Проверим единицу, найдем значение искомой величины:
Анализ результатов. Количество цистерн, полученное в результате расчетов, вполне реально.
Ответ: N=54.
- Движение молекул в физике в газах, жидкостях и твёрдых телах
- Скорость движения молекул газа
- Газовые законы
- Взаимодействие молекул
- Движение и силы
- Давление в физике
- Строение вещества в физике
- Физическое тело и вещество в физике
Окружающие тела состоят из веществ, масса каждого зависит от размера, объема и других критериев.
Плотность вещества показывает численное выражение массы тела в определенном объеме.
Существуют разные виды скалярной физической величины.
Общая характеристика
Каждый элемент занимает индивидуальную величину. Определение плотности может обозначаться греческой буквой ρ, D или d. Если объемы двух тел одинаковы, а массы различны, тогда плотности не идентичны.
Основные понятия
Определения и характеристики показателя известны с 7 класса школьной программы химии. Плотность представляет собой физическую величину о свойствах вещества. Это удельный вес любого элемента. Существует средняя и относительная плотность. Последняя классификация — это отношение плотности (П) вещества к П эталонного вещества. Часто за эталон принимают дистиллированную воду. Единица измерения П- кг/м3 в интернациональной системе.
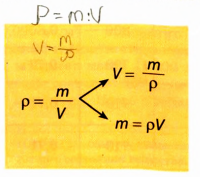
Формула нахождения плотности:
P = m/V
Обозначения:
- m — масса.
- V — объем.
Кроме стандартной формулы плотности, применяемой для твердых состояний веществ, имеется формула для газообразных элементов в нормальных условиях.
ρ (газа) = M/Vm M
Расшифровка:
- М — молярная масса газа [г/моль].
- Vm — объем газа (в норме 22,4 л/моль).
Для сыпучих и пористых тел различают истинную плотность, вычисляемую без учета пустот, и удельную плотность, рассчитываемую как отношение массы вещества ко всему объему. Истинную П получают через коэффициент пористости — доли объема пустот в занимаемом объеме. Для сыпучих тел удельная П называется насыпной.
Низкие показатели П имеет среда между Галактиками (1033 кг/м3).
Способы измерения:
- Пикнометр. Измеряет истинную П.
- Ареометр, денсиметр, плотномер. Используется для жидкого состояния.
- Бурик. Измеряет П почвы.
Вещества состоят из молекулярных структур, масса тела формируется из скопления молекул. Аналогично вес пакета с карамелью складывается из масс всех конфет в мешке. Если все сладости одинаковые, то массу упаковки определяют умножением веса одной конфеты на количество штук.
Молекулярные частицы чистого вещества одинаковы, поэтому вес капли воды равен произведению массы 1 молекулы Н2О на число составляющих молекул в капле. Плотность вещества показывает, чему равна масса одного кубического метра.
Плотность воды — 1000 кг/м³, а масса 1 м³ Н2О равна 1000 килограмм. Это число можно вычислить, умножив массу 1 молекулы воды на количество молекулярных частиц, содержащихся в 1 м3 объема.
П льда составляет 900 кг/м³, это значит, что вес кубического метра льда равна 900 кг. Употребляют единицу измерения плотности г/см3.
При равнозначности физических масс двух тел их объемы различаются. Например, объём льда в девять раз больше объема бруска из металлического сплава. Масса тела распределяется неодинаково, устанавливает П в каждой точке тела.
Влияние факторов
П зависит от давления и температуры. При высоком давлении молекулы плотно прилегают друг к другу, поэтому вещество обладает значительной плотностью.
Зависимость показателей учитывается при расчете П. При повышении температуры П снижается из-за термического расширения, при котором объем вырастает, а масса остается прежней. Если температура снижается, П увеличивается, хотя имеются вещества, П которых при некоторых условиях температурного режима ведет себя иначе. Это вода, бронза, чугун. При фазовом переходе, модифицировании агрегатного состояния П меняется скачками. Условия вычисления зависят от свойств веществ, молекулярных элементов. Для разных природных объектов П изменяется в широком диапазоне.
П воды ниже П льда из-за молекулярной структуры твердой формы жидкости. Вещество, переходя из жидкой в твердую форму, изменяет молекулярную структуру, расстояние между составными частицами сужается и плотность увеличивается. Зимой, если забыть слить воду из труб, их разрывает на части после замерзания. На П Н2О влияют примеси. У морской воды знак П выше, чем у пресной. При соединении в одном стакане двух типов жидкости пресная останется на поверхности. Чем выше концентрация соли, тем больше П воды.
Когда плотность вещества больше П воды, оно полностью погрузится в воду. Предметы, сделанные из материала по низкой П, будут плавать на поверхности воды. На практике эти свойства используются человеком. Сооружая суда, инженеры-проектировщики применяют материалы с высокой П. Корабли, теплоходы, яхты смогут затонуть во время плавания, в корпусах суден создают специальные полости, наполненные воздухом, ведь его П ниже плотности воды.
Чтобы наживка для рыбалки погрузилась в воду, ее обременяют тяжелым по плотности материалом, например, грузиком из металла (чаще свинца). Плотность сплава выше, чем у Н2О.
Жирные пятна масла, нефти, бензина остаются на поверхности воды из-за низкой П маслянистых веществ.
Практическое применение
Из учебников химии и физики вычисляют уровень плотности по формуле. Но также это можно сделать, используя онлайн-систему.
Значение показателя
Окружающий мир состоит из разных веществ.
Скамейка в парке или баня за городом сооружены из древесины, подошва утюга, сковорода выполнены из металла, покрышка колеса, велосипеда — из резины. Каждый предмет имеет свой вес.
Черные дыры Вселенной составляют наибольшую плотность 1014 кг/м3. Самый низкий показатель имеет область между Галактиками (2•10−31—5•10−31 кг/м³).
Таблица плотности веществ
| Вещество | Плотность (кг/м3) |
| Сухой воздух | 1,293 |
| Металлы | |
| Осмий | 22,61 |
| Родий | 12,41 |
| Иридий | 22,56 |
| Плутоний | 19,84 |
| Палладий | 12,02 |
| Свинец | 11,35 |
| Платина | 19,59 |
| Золото | 19,30 |
| Сталь | 7,8 |
| Алюминий | 2,7 |
| Медь | 8,94 |
| Газы | |
| Азот | 1,25 |
| Аммиак | 0,771 |
| Аргон | 1,784 |
| Жидкий водород | 70 |
| Гелий в жидком состоянии | 130 |
| Водород | 0,09 |
| Водяной пар | 0,598 |
| Воздух | 1,293 |
| Хлор | 3,214 |
| О2 | 1,429 |
| Углекислый газ | 1,977 |
| Остальные вещества | |
| Тело человека | На вдохе 940-990, при выдохе — 1010-1070 |
| Пресная вода | 1000 |
| Солнце | 1410 |
| Гранит | 2600 |
| Земля | 5520 |
| Железо | 7874 |
| Бензин | 710 |
| Керосин | 820 |
| Молоко | 1040 |
| Этанол | 789 |
| Ацетон | 792 |
| Морская вода | 1030 |
| Древесина | |
| Пихта | 0,39 |
| Ива | 0,46 |
| Ель | 0,45 |
| Сосна | 0,52 |
| Дуб | 0,69 |
П металлов изменяется от минимального значения у лития, который легче Н2О, до максимального значения у осмия, который тяжелее драгоценных металлов.
Способы расчета и примеры
В сети Интернет существует множество приложений для онлайн-расчета плотности веществ или материалов. В стандартные поля калькулятора вводится основная информация: масса, объем, единицы измерения. Плотность вычисляется автоматически по заданным параметрам и выводится на экран интерфейса. Можно перевести информативные данные в нужную единицу измерения.
Без использования учебной информации показатель П можно определить через физические опыты. Для лабораторных изучений нужны весы, сантиметр, если исследуемое тело находится в твердом состоянии. Для жидкости необходима колба.
Сначала измеряют объем тела, записывая результат по цифровой шкале (в сантиметрах или миллилитрах).
Вычисляя объем деревянного бруска квадратной формы, параметр стороны возводится в третью степень. Измеряя объемные характеристики, тело ставят на весы и записывают значение массы. Рассчитывая жидкое состояние, учитывают массу сосуда, куда помещено исследуемое. В формулу подставляют данные и рассчитывают показатель.
Поскольку П измеряется в кг/л или в г/см³, то иногда приходится пересчитывать одни величины в другие.
В одном грамме содержится 0,001 кг, а один кубический сантиметр (см³) — это 0,000001 м³. В 1 г/(см)3 содержится 1000кг/м3.
Пример 1:
Необходимо найти плотность молока, если 350 г занимают 100 см3. Для решения используют формулу, где масса делится на объем.
Решение: P=m/V = 350/100= 3,5 г/см3.
Пример 2:
Необходимо определить П мела, если масса большого куска объемом 20 см3 составляет 48 грамм. П выразить в кг/м3 и вг/см3.
Решение:
Нужно перевести см3 в кубические метры, а граммы — в килограммы.
V = 20см3= 0,00002 м3.
M= 48 г = 0,048 кг.
Плотность мела составляет 0,048 кг/0,00002 м3 = 2400 кг/м3.
Выражаем в г/см3: 2400 кг/м3 = 2400*1000/1000000 см3 = 2,4 г/см3.
Один килограмм равен 1000 грамм, один кубический метр (1м3) содержит 1000000 см 3. Плотность получится 2,4 г/см3или 2400 кг/м3.
Показатель имеет большое значение в разных сферах жизни и деятельности. Он определяется по таблице или высчитывается расчетным путем.
From Wikipedia, the free encyclopedia
| Density | |
|---|---|

A test tube holding four non-miscible colored liquids with different densities |
|
|
Common symbols |
ρ, D |
| SI unit | kg/m3 |
| Extensive? | No |
| Intensive? | Yes |
| Conserved? | No |
|
Derivations from |
 |
| Dimension |  |
Density (volumetric mass density or specific mass) is the substance’s mass per unit of volume. The symbol most often used for density is ρ (the lower case Greek letter rho), although the Latin letter D can also be used. Mathematically, density is defined as mass divided by volume:[1]
where ρ is the density, m is the mass, and V is the volume. In some cases (for instance, in the United States oil and gas industry), density is loosely defined as its weight per unit volume,[2] although this is scientifically inaccurate – this quantity is more specifically called specific weight.
For a pure substance the density has the same numerical value as its mass concentration.
Different materials usually have different densities, and density may be relevant to buoyancy, purity and packaging. Osmium and iridium are the densest known elements at standard conditions for temperature and pressure.
To simplify comparisons of density across different systems of units, it is sometimes replaced by the dimensionless quantity «relative density» or «specific gravity», i.e. the ratio of the density of the material to that of a standard material, usually water. Thus a relative density less than one relative to water means that the substance floats in water.
The density of a material varies with temperature and pressure. This variation is typically small for solids and liquids but much greater for gases. Increasing the pressure on an object decreases the volume of the object and thus increases its density. Increasing the temperature of a substance (with a few exceptions) decreases its density by increasing its volume. In most materials, heating the bottom of a fluid results in convection of the heat from the bottom to the top, due to the decrease in the density of the heated fluid, which causes it to rise relative to denser unheated material.
The reciprocal of the density of a substance is occasionally called its specific volume, a term sometimes used in thermodynamics. Density is an intensive property in that increasing the amount of a substance does not increase its density; rather it increases its mass.
Other conceptually comparable quantities or ratios include specific density, relative density (specific gravity), and specific weight.
History
In a well-known but probably apocryphal tale, Archimedes was given the task of determining whether King Hiero’s goldsmith was embezzling gold during the manufacture of a golden wreath dedicated to the gods and replacing it with another, cheaper alloy.[3] Archimedes knew that the irregularly shaped wreath could be crushed into a cube whose volume could be calculated easily and compared with the mass; but the king did not approve of this. Baffled, Archimedes is said to have taken an immersion bath and observed from the rise of the water upon entering that he could calculate the volume of the gold wreath through the displacement of the water. Upon this discovery, he leapt from his bath and ran naked through the streets shouting, «Eureka! Eureka!» (Εύρηκα! Greek «I have found it»). As a result, the term «eureka» entered common parlance and is used today to indicate a moment of enlightenment.
The story first appeared in written form in Vitruvius’ books of architecture, two centuries after it supposedly took place.[4] Some scholars have doubted the accuracy of this tale, saying among other things that the method would have required precise measurements that would have been difficult to make at the time.[5][6]
Measurement of density
A number of techniques as well as standards exist for the measurement of density of materials. Such techniques include the use of a hydrometer (a buoyancy method for liquids), Hydrostatic balance (a buoyancy method for liquids and solids), immersed body method (a buoyancy method for liquids), pycnometer (liquids and solids), air comparison pycnometer (solids), oscillating densitometer (liquids), as well as pour and tap (solids).[7] However, each individual method or technique measures different types of density (e.g. bulk density, skeletal density, etc.), and therefore it is necessary to have an understanding of the type of density being measured as well as the type of material in question.
Unit
From the equation for density (ρ = m/V), mass density has any unit that is mass divided by volume. As there are many units of mass and volume covering many different magnitudes there are a large number of units for mass density in use. The SI unit of kilogram per cubic metre (kg/m3) and the cgs unit of gram per cubic centimetre (g/cm3) are probably the most commonly used units for density. One g/cm3 is equal to 1000 kg/m3. One cubic centimetre (abbreviation cc) is equal to one millilitre. In industry, other larger or smaller units of mass and or volume are often more practical and US customary units may be used. See below for a list of some of the most common units of density.
Homogeneous materials
The density at all points of a homogeneous object equals its total mass divided by its total volume. The mass is normally measured with a scale or balance; the volume may be measured directly (from the geometry of the object) or by the displacement of a fluid. To determine the density of a liquid or a gas, a hydrometer, a dasymeter or a Coriolis flow meter may be used, respectively. Similarly, hydrostatic weighing uses the displacement of water due to a submerged object to determine the density of the object.
Heterogeneous materials
If the body is not homogeneous, then its density varies between different regions of the object. In that case the density around any given location is determined by calculating the density of a small volume around that location. In the limit of an infinitesimal volume the density of an inhomogeneous object at a point becomes: 


Non-compact materials
In practice, bulk materials such as sugar, sand, or snow contain voids. Many materials exist in nature as flakes, pellets, or granules.
Voids are regions which contain something other than the considered material. Commonly the void is air, but it could also be vacuum, liquid, solid, or a different gas or gaseous mixture.
The bulk volume of a material—inclusive of the void fraction—is often obtained by a simple measurement (e.g. with a calibrated measuring cup) or geometrically from known dimensions.
Mass divided by bulk volume determines bulk density. This is not the same thing as volumetric mass density.
To determine volumetric mass density, one must first discount the volume of the void fraction. Sometimes this can be determined by geometrical reasoning. For the close-packing of equal spheres the non-void fraction can be at most about 74%. It can also be determined empirically. Some bulk materials, however, such as sand, have a variable void fraction which depends on how the material is agitated or poured. It might be loose or compact, with more or less air space depending on handling.
In practice, the void fraction is not necessarily air, or even gaseous. In the case of sand, it could be water, which can be advantageous for measurement as the void fraction for sand saturated in water—once any air bubbles are thoroughly driven out—is potentially more consistent than dry sand measured with an air void.
In the case of non-compact materials, one must also take care in determining the mass of the material sample. If the material is under pressure (commonly ambient air pressure at the earth’s surface) the determination of mass from a measured sample weight might need to account for buoyancy effects due to the density of the void constituent, depending on how the measurement was conducted. In the case of dry sand, sand is so much denser than air that the buoyancy effect is commonly neglected (less than one part in one thousand).
Mass change upon displacing one void material with another while maintaining constant volume can be used to estimate the void fraction, if the difference in density of the two voids materials is reliably known.
Changes of density
In general, density can be changed by changing either the pressure or the temperature. Increasing the pressure always increases the density of a material. Increasing the temperature generally decreases the density, but there are notable exceptions to this generalization. For example, the density of water increases between its melting point at 0 °C and 4 °C; similar behavior is observed in silicon at low temperatures.
The effect of pressure and temperature on the densities of liquids and solids is small. The compressibility for a typical liquid or solid is 10−6 bar−1 (1 bar = 0.1 MPa) and a typical thermal expansivity is 10−5 K−1. This roughly translates into needing around ten thousand times atmospheric pressure to reduce the volume of a substance by one percent. (Although the pressures needed may be around a thousand times smaller for sandy soil and some clays.) A one percent expansion of volume typically requires a temperature increase on the order of thousands of degrees Celsius.
In contrast, the density of gases is strongly affected by pressure. The density of an ideal gas is
where M is the molar mass, P is the pressure, R is the universal gas constant, and T is the absolute temperature. This means that the density of an ideal gas can be doubled by doubling the pressure, or by halving the absolute temperature.
In the case of volumic thermal expansion at constant pressure and small intervals of temperature the temperature dependence of density is
where 


Density of solutions
The density of a solution is the sum of mass (massic) concentrations of the components of that solution.
Mass (massic) concentration of each given component ρi in a solution sums to density of the solution,
Expressed as a function of the densities of pure components of the mixture and their volume participation, it allows the determination of excess molar volumes:
provided that there is no interaction between the components.
Knowing the relation between excess volumes and activity coefficients of the components, one can determine the activity coefficients:
Densities
Various materials
- Selected chemical elements are listed here. For the densities of all chemical elements, see List of chemical elements
| Material | ρ (kg/m3)[note 1] | Notes |
|---|---|---|
| Hydrogen | 0.0898 | |
| Helium | 0.179 | |
| Aerographite | 0.2 | [note 2][8][9] |
| Metallic microlattice | 0.9 | [note 2] |
| Aerogel | 1.0 | [note 2] |
| Air | 1.2 | At sea level |
| Tungsten hexafluoride | 12.4 | One of the heaviest known gases at standard conditions |
| Liquid hydrogen | 70 | At approx. −255 °C |
| Styrofoam | 75 | Approx.[10] |
| Cork | 240 | Approx.[10] |
| Pine | 373 | [11] |
| Lithium | 535 | Least dense metal |
| Wood | 700 | Seasoned, typical[12][13] |
| Oak | 710 | [11] |
| Potassium | 860 | [14] |
| Ice | 916.7 | At temperature < 0 °C |
| Cooking oil | 910–930 | |
| Sodium | 970 | |
| Water (fresh) | 1,000 | At 4 °C, the temperature of its maximum density |
| Water (salt) | 1,030 | 3% |
| Liquid oxygen | 1,141 | At approx. −219 °C |
| Nylon | 1,150 | |
| Plastics | 1,175 | Approx.; for polypropylene and PETE/PVC |
| Glycerol | 1,261 | [15] |
| Tetrachloroethene | 1,622 | |
| Sand | 1,600 | Between 1,600 and 2000 [16] |
| Magnesium | 1,740 | |
| Beryllium | 1,850 | |
| Silicon | 2,330 | |
| Concrete | 2,400 | [17][18] |
| Glass | 2,500 | [19] |
| Quartzite | 2,600 | [16] |
| Granite | 2,700 | [16] |
| Gneiss | 2,700 | [16] |
| Aluminium | 2,700 | |
| Limestone | 2,750 | Compact[16] |
| Basalt | 3,000 | [16] |
| Diiodomethane | 3,325 | Liquid at room temperature |
| Diamond | 3,500 | |
| Titanium | 4,540 | |
| Selenium | 4,800 | |
| Vanadium | 6,100 | |
| Antimony | 6,690 | |
| Zinc | 7,000 | |
| Chromium | 7,200 | |
| Tin | 7,310 | |
| Manganese | 7,325 | Approx. |
| Iron | 7,870 | |
| Mild Steel | 7,850 | |
| Niobium | 8,570 | |
| Brass | 8,600 | [18] |
| Cadmium | 8,650 | |
| Cobalt | 8,900 | |
| Nickel | 8,900 | |
| Copper | 8,940 | |
| Bismuth | 9,750 | |
| Molybdenum | 10,220 | |
| Silver | 10,500 | |
| Lead | 11,340 | |
| Thorium | 11,700 | |
| Rhodium | 12,410 | |
| Mercury | 13,546 | |
| Tantalum | 16,600 | |
| Uranium | 18,800 | |
| Tungsten | 19,300 | |
| Gold | 19,320 | |
| Plutonium | 19,840 | |
| Rhenium | 21,020 | |
| Platinum | 21,450 | |
| Iridium | 22,420 | |
| Osmium | 22,570 | Densest natural element on Earth |
Notes:
|
Others
| Entity | ρ (kg/m3) | Notes |
|---|---|---|
| Interstellar medium | 1.7×10−26 | Based on 10−5 hydrogen atoms per cubic centimetre[20] |
| Local Interstellar Cloud | 5×10−22 | Based on 0.3 hydrogen atoms per cubic centimetre[20] |
| Interstellar medium | 1.7×10−16 | Based on 105 hydrogen atoms per cubic centimetre[20] |
| The Earth | 5,515 | Mean density.[21] |
| Earth’s inner core | 13,000 | Approx., as listed in Earth.[22] |
| The core of the Sun | 33,000–160,000 | Approx.[23] |
| White dwarf star | 2.1×109 | Approx.[24] |
| Atomic nuclei | 2.3×1017 | Does not depend strongly on size of nucleus[25] |
| Neutron star | 1×1018 |
Water
| Temp. (°C)[note 1] | Density (kg/m3) |
|---|---|
| −30 | 983.854 |
| −20 | 993.547 |
| −10 | 998.117 |
| 0 | 999.8395 |
| 4 | 999.9720 |
| 10 | 999.7026 |
| 15 | 999.1026 |
| 20 | 998.2071 |
| 22 | 997.7735 |
| 25 | 997.0479 |
| 30 | 995.6502 |
| 40 | 992.2 |
| 60 | 983.2 |
| 80 | 971.8 |
| 100 | 958.4 |
Notes:
|
Air
Air density vs. temperature
| T (°C) | ρ (kg/m3) |
|---|---|
| −25 | 1.423 |
| −20 | 1.395 |
| −15 | 1.368 |
| −10 | 1.342 |
| −5 | 1.316 |
| 0 | 1.293 |
| 5 | 1.269 |
| 10 | 1.247 |
| 15 | 1.225 |
| 20 | 1.204 |
| 25 | 1.184 |
| 30 | 1.164 |
| 35 | 1.146 |
Molar volumes of liquid and solid phase of elements
Molar volumes of liquid and solid phase of elements
Common units
The SI unit for density is:
- kilogram per cubic metre (kg/m3)
The litre and tonne are not part of the SI, but are acceptable for use with it, leading to the following units:
- kilogram per litre (kg/L)
- gram per millilitre (g/mL)
- tonne per cubic metre (t/m3)
Densities using the following metric units all have exactly the same numerical value, one thousandth of the value in (kg/m3). Liquid water has a density of about 1 kg/dm3, making any of these SI units numerically convenient to use as most solids and liquids have densities between 0.1 and 20 kg/dm3.
- kilogram per cubic decimetre (kg/dm3)
- gram per cubic centimetre (g/cm3)
- 1 g/cm3 = 1000 kg/m3
- megagram (metric ton) per cubic metre (Mg/m3)
In US customary units density can be stated in:
- Avoirdupois ounce per cubic inch (1 g/cm3 ≈ 0.578036672 oz/cu in)
- Avoirdupois ounce per fluid ounce (1 g/cm3 ≈ 1.04317556 oz/US fl oz = 1.04317556 lb/US fl pint)
- Avoirdupois pound per cubic inch (1 g/cm3 ≈ 0.036127292 lb/cu in)
- pound per cubic foot (1 g/cm3 ≈ 62.427961 lb/cu ft)
- pound per cubic yard (1 g/cm3 ≈ 1685.5549 lb/cu yd)
- pound per US liquid gallon (1 g/cm3 ≈ 8.34540445 lb/US gal)
- pound per US bushel (1 g/cm3 ≈ 77.6888513 lb/bu)
- slug per cubic foot
Imperial units differing from the above (as the Imperial gallon and bushel differ from the US units) in practice are rarely used, though found in older documents. The Imperial gallon was based on the concept that an Imperial fluid ounce of water would have a mass of one Avoirdupois ounce, and indeed 1 g/cm3 ≈ 1.00224129 ounces per Imperial fluid ounce = 10.0224129 pounds per Imperial gallon. The density of precious metals could conceivably be based on Troy ounces and pounds, a possible cause of confusion.
Knowing the volume of the unit cell of a crystalline material and its formula weight (in daltons), the density can be calculated. One dalton per cubic ångström is equal to a density of 1.660 539 066 60 g/cm3.
See also
- Densities of the elements (data page)
- List of elements by density
- Air density
- Area density
- Bulk density
- Buoyancy
- Charge density
- Density prediction by the Girolami method
- Dord
- Energy density
- Lighter than air
- Linear density
- Number density
- Orthobaric density
- Paper density
- Specific weight
- Spice (oceanography)
- Standard temperature and pressure
References
- ^ The National Aeronautic and Atmospheric Administration’s Glenn Research Center. «Gas Density Glenn research Center». grc.nasa.gov. Archived from the original on April 14, 2013. Retrieved April 9, 2013.
- ^ «Density definition in Oil Gas Glossary». Oilgasglossary.com. Archived from the original on August 5, 2010. Retrieved September 14, 2010.
- ^ Archimedes, A Gold Thief and Buoyancy Archived August 27, 2007, at the Wayback Machine – by Larry «Harris» Taylor, Ph.D.
- ^ Vitruvius on Architecture, Book IX, paragraphs 9–12, translated into English and in the original Latin.
- ^ «EXHIBIT: The First Eureka Moment». Science. 305 (5688): 1219e. 2004. doi:10.1126/science.305.5688.1219e.
- ^ «Fact or Fiction?: Archimedes Coined the Term «Eureka!» in the Bath». Scientific American. December 2006.
- ^ «Test No. 109: Density of Liquids and Solids». OECD Guidelines for the Testing of Chemicals, Section 1. October 2, 2012. doi:10.1787/9789264123298-en. ISBN 9789264123298. ISSN 2074-5753.
- ^ New carbon nanotube struructure aerographite is lightest material champ Archived October 17, 2013, at the Wayback Machine. Phys.org (July 13, 2012). Retrieved on July 14, 2012.
- ^ Aerographit: Leichtestes Material der Welt entwickelt – SPIEGEL ONLINE Archived October 17, 2013, at the Wayback Machine. Spiegel.de (July 11, 2012). Retrieved on July 14, 2012.
- ^ a b «Re: which is more bouyant [sic] styrofoam or cork». Madsci.org. Archived from the original on February 14, 2011. Retrieved September 14, 2010.
- ^ a b Serway, Raymond; Jewett, John (2005), Principles of Physics: A Calculus-Based Text, Cengage Learning, p. 467, ISBN 0-534-49143-X, archived from the original on May 17, 2016
- ^ «Wood Densities». www.engineeringtoolbox.com. Archived from the original on October 20, 2012. Retrieved October 15, 2012.
- ^ «Density of Wood». www.simetric.co.uk. Archived from the original on October 26, 2012. Retrieved October 15, 2012.
- ^ Bolz, Ray E.; Tuve, George L., eds. (1970). «§1.3 Solids—Metals: Table 1-59 Metals and Alloys—Miscellaneous Properties». CRC Handbook of tables for Applied Engineering Science (2nd ed.). CRC Press. p. 117. ISBN 9781315214092.
- ^ glycerol composition at Archived February 28, 2013, at the Wayback Machine. Physics.nist.gov. Retrieved on July 14, 2012.
- ^ a b c d e f Sharma, P.V. (1997), Environmental and Engineering Geophysics, Cambridge University Press, p. 17, doi:10.1017/CBO9781139171168, ISBN 9781139171168
- ^ «Density of Concrete — The Physics Factbook». hypertextbook.com.
- ^ a b Young, Hugh D.; Freedman, Roger A. (2012). University Physics with Modern Physics. Addison-Wesley. p. 374. ISBN 978-0-321-69686-1.
- ^ «Density of Glass — The Physics Factbook». hypertextbook.com.
- ^ a b c «Our Local Galactic Neighborhood». Interstellar Probe Project. NASA. 2000. Archived from the original on November 21, 2013. Retrieved August 8, 2012.
- ^ Density of the Earth, wolframalpha.com, archived from the original on October 17, 2013
- ^ Density of Earth’s core, wolframalpha.com, archived from the original on October 17, 2013
- ^ Density of the Sun’s core, wolframalpha.com, archived from the original on October 17, 2013
- ^ Johnson, Jennifer. «Extreme Stars: White Dwarfs & Neutron Stars]» (PDF). lecture notes, Astronomy 162. Ohio State University. Archived from the original (PDF) on September 25, 2007.
- ^ «Nuclear Size and Density». HyperPhysics. Georgia State University. Archived from the original on July 6, 2009.
External links
- «Density» . Encyclopædia Britannica. Vol. 8 (11th ed.). 1911.
- «Density» . The New Student’s Reference Work . 1914.
- Video: Density Experiment with Oil and Alcohol
- Video: Density Experiment with Whiskey and Water
- Glass Density Calculation – Calculation of the density of glass at room temperature and of glass melts at 1000 – 1400°C
- List of Elements of the Periodic Table – Sorted by Density
- Calculation of saturated liquid densities for some components
- Field density test
- Water – Density and specific weight
- Temperature dependence of the density of water – Conversions of density units
- A delicious density experiment
- Water density calculator Archived July 13, 2011, at the Wayback Machine Water density for a given salinity and temperature.
- Liquid density calculator Select a liquid from the list and calculate density as a function of temperature.
- Gas density calculator Calculate density of a gas for as a function of temperature and pressure.
- Densities of various materials.
- Determination of Density of Solid, instructions for performing classroom experiment.
- Lam EJ, Alvarez MN, Galvez ME, Alvarez EB (2008). «A model for calculating the density of aqueous multicomponent electrolyte solutions». Journal of the Chilean Chemical Society. 53 (1): 1393–8. doi:10.4067/S0717-97072008000100015.
- Radović IR, Kijevčanin ML, Tasić AŽ, Djordjević BD, Šerbanović SP (2010). «Derived thermodynamic properties of alcohol+ cyclohexylamine mixtures». Journal of the Serbian Chemical Society. 75 (2): 283–293. CiteSeerX 10.1.1.424.3486. doi:10.2298/JSC1002283R.
From Wikipedia, the free encyclopedia
| Density | |
|---|---|

A test tube holding four non-miscible colored liquids with different densities |
|
|
Common symbols |
ρ, D |
| SI unit | kg/m3 |
| Extensive? | No |
| Intensive? | Yes |
| Conserved? | No |
|
Derivations from |
 |
| Dimension |  |
Density (volumetric mass density or specific mass) is the substance’s mass per unit of volume. The symbol most often used for density is ρ (the lower case Greek letter rho), although the Latin letter D can also be used. Mathematically, density is defined as mass divided by volume:[1]
where ρ is the density, m is the mass, and V is the volume. In some cases (for instance, in the United States oil and gas industry), density is loosely defined as its weight per unit volume,[2] although this is scientifically inaccurate – this quantity is more specifically called specific weight.
For a pure substance the density has the same numerical value as its mass concentration.
Different materials usually have different densities, and density may be relevant to buoyancy, purity and packaging. Osmium and iridium are the densest known elements at standard conditions for temperature and pressure.
To simplify comparisons of density across different systems of units, it is sometimes replaced by the dimensionless quantity «relative density» or «specific gravity», i.e. the ratio of the density of the material to that of a standard material, usually water. Thus a relative density less than one relative to water means that the substance floats in water.
The density of a material varies with temperature and pressure. This variation is typically small for solids and liquids but much greater for gases. Increasing the pressure on an object decreases the volume of the object and thus increases its density. Increasing the temperature of a substance (with a few exceptions) decreases its density by increasing its volume. In most materials, heating the bottom of a fluid results in convection of the heat from the bottom to the top, due to the decrease in the density of the heated fluid, which causes it to rise relative to denser unheated material.
The reciprocal of the density of a substance is occasionally called its specific volume, a term sometimes used in thermodynamics. Density is an intensive property in that increasing the amount of a substance does not increase its density; rather it increases its mass.
Other conceptually comparable quantities or ratios include specific density, relative density (specific gravity), and specific weight.
History
In a well-known but probably apocryphal tale, Archimedes was given the task of determining whether King Hiero’s goldsmith was embezzling gold during the manufacture of a golden wreath dedicated to the gods and replacing it with another, cheaper alloy.[3] Archimedes knew that the irregularly shaped wreath could be crushed into a cube whose volume could be calculated easily and compared with the mass; but the king did not approve of this. Baffled, Archimedes is said to have taken an immersion bath and observed from the rise of the water upon entering that he could calculate the volume of the gold wreath through the displacement of the water. Upon this discovery, he leapt from his bath and ran naked through the streets shouting, «Eureka! Eureka!» (Εύρηκα! Greek «I have found it»). As a result, the term «eureka» entered common parlance and is used today to indicate a moment of enlightenment.
The story first appeared in written form in Vitruvius’ books of architecture, two centuries after it supposedly took place.[4] Some scholars have doubted the accuracy of this tale, saying among other things that the method would have required precise measurements that would have been difficult to make at the time.[5][6]
Measurement of density
A number of techniques as well as standards exist for the measurement of density of materials. Such techniques include the use of a hydrometer (a buoyancy method for liquids), Hydrostatic balance (a buoyancy method for liquids and solids), immersed body method (a buoyancy method for liquids), pycnometer (liquids and solids), air comparison pycnometer (solids), oscillating densitometer (liquids), as well as pour and tap (solids).[7] However, each individual method or technique measures different types of density (e.g. bulk density, skeletal density, etc.), and therefore it is necessary to have an understanding of the type of density being measured as well as the type of material in question.
Unit
From the equation for density (ρ = m/V), mass density has any unit that is mass divided by volume. As there are many units of mass and volume covering many different magnitudes there are a large number of units for mass density in use. The SI unit of kilogram per cubic metre (kg/m3) and the cgs unit of gram per cubic centimetre (g/cm3) are probably the most commonly used units for density. One g/cm3 is equal to 1000 kg/m3. One cubic centimetre (abbreviation cc) is equal to one millilitre. In industry, other larger or smaller units of mass and or volume are often more practical and US customary units may be used. See below for a list of some of the most common units of density.
Homogeneous materials
The density at all points of a homogeneous object equals its total mass divided by its total volume. The mass is normally measured with a scale or balance; the volume may be measured directly (from the geometry of the object) or by the displacement of a fluid. To determine the density of a liquid or a gas, a hydrometer, a dasymeter or a Coriolis flow meter may be used, respectively. Similarly, hydrostatic weighing uses the displacement of water due to a submerged object to determine the density of the object.
Heterogeneous materials
If the body is not homogeneous, then its density varies between different regions of the object. In that case the density around any given location is determined by calculating the density of a small volume around that location. In the limit of an infinitesimal volume the density of an inhomogeneous object at a point becomes: 


Non-compact materials
In practice, bulk materials such as sugar, sand, or snow contain voids. Many materials exist in nature as flakes, pellets, or granules.
Voids are regions which contain something other than the considered material. Commonly the void is air, but it could also be vacuum, liquid, solid, or a different gas or gaseous mixture.
The bulk volume of a material—inclusive of the void fraction—is often obtained by a simple measurement (e.g. with a calibrated measuring cup) or geometrically from known dimensions.
Mass divided by bulk volume determines bulk density. This is not the same thing as volumetric mass density.
To determine volumetric mass density, one must first discount the volume of the void fraction. Sometimes this can be determined by geometrical reasoning. For the close-packing of equal spheres the non-void fraction can be at most about 74%. It can also be determined empirically. Some bulk materials, however, such as sand, have a variable void fraction which depends on how the material is agitated or poured. It might be loose or compact, with more or less air space depending on handling.
In practice, the void fraction is not necessarily air, or even gaseous. In the case of sand, it could be water, which can be advantageous for measurement as the void fraction for sand saturated in water—once any air bubbles are thoroughly driven out—is potentially more consistent than dry sand measured with an air void.
In the case of non-compact materials, one must also take care in determining the mass of the material sample. If the material is under pressure (commonly ambient air pressure at the earth’s surface) the determination of mass from a measured sample weight might need to account for buoyancy effects due to the density of the void constituent, depending on how the measurement was conducted. In the case of dry sand, sand is so much denser than air that the buoyancy effect is commonly neglected (less than one part in one thousand).
Mass change upon displacing one void material with another while maintaining constant volume can be used to estimate the void fraction, if the difference in density of the two voids materials is reliably known.
Changes of density
In general, density can be changed by changing either the pressure or the temperature. Increasing the pressure always increases the density of a material. Increasing the temperature generally decreases the density, but there are notable exceptions to this generalization. For example, the density of water increases between its melting point at 0 °C and 4 °C; similar behavior is observed in silicon at low temperatures.
The effect of pressure and temperature on the densities of liquids and solids is small. The compressibility for a typical liquid or solid is 10−6 bar−1 (1 bar = 0.1 MPa) and a typical thermal expansivity is 10−5 K−1. This roughly translates into needing around ten thousand times atmospheric pressure to reduce the volume of a substance by one percent. (Although the pressures needed may be around a thousand times smaller for sandy soil and some clays.) A one percent expansion of volume typically requires a temperature increase on the order of thousands of degrees Celsius.
In contrast, the density of gases is strongly affected by pressure. The density of an ideal gas is
where M is the molar mass, P is the pressure, R is the universal gas constant, and T is the absolute temperature. This means that the density of an ideal gas can be doubled by doubling the pressure, or by halving the absolute temperature.
In the case of volumic thermal expansion at constant pressure and small intervals of temperature the temperature dependence of density is
where 


Density of solutions
The density of a solution is the sum of mass (massic) concentrations of the components of that solution.
Mass (massic) concentration of each given component ρi in a solution sums to density of the solution,
Expressed as a function of the densities of pure components of the mixture and their volume participation, it allows the determination of excess molar volumes:
provided that there is no interaction between the components.
Knowing the relation between excess volumes and activity coefficients of the components, one can determine the activity coefficients:
Densities
Various materials
- Selected chemical elements are listed here. For the densities of all chemical elements, see List of chemical elements
| Material | ρ (kg/m3)[note 1] | Notes |
|---|---|---|
| Hydrogen | 0.0898 | |
| Helium | 0.179 | |
| Aerographite | 0.2 | [note 2][8][9] |
| Metallic microlattice | 0.9 | [note 2] |
| Aerogel | 1.0 | [note 2] |
| Air | 1.2 | At sea level |
| Tungsten hexafluoride | 12.4 | One of the heaviest known gases at standard conditions |
| Liquid hydrogen | 70 | At approx. −255 °C |
| Styrofoam | 75 | Approx.[10] |
| Cork | 240 | Approx.[10] |
| Pine | 373 | [11] |
| Lithium | 535 | Least dense metal |
| Wood | 700 | Seasoned, typical[12][13] |
| Oak | 710 | [11] |
| Potassium | 860 | [14] |
| Ice | 916.7 | At temperature < 0 °C |
| Cooking oil | 910–930 | |
| Sodium | 970 | |
| Water (fresh) | 1,000 | At 4 °C, the temperature of its maximum density |
| Water (salt) | 1,030 | 3% |
| Liquid oxygen | 1,141 | At approx. −219 °C |
| Nylon | 1,150 | |
| Plastics | 1,175 | Approx.; for polypropylene and PETE/PVC |
| Glycerol | 1,261 | [15] |
| Tetrachloroethene | 1,622 | |
| Sand | 1,600 | Between 1,600 and 2000 [16] |
| Magnesium | 1,740 | |
| Beryllium | 1,850 | |
| Silicon | 2,330 | |
| Concrete | 2,400 | [17][18] |
| Glass | 2,500 | [19] |
| Quartzite | 2,600 | [16] |
| Granite | 2,700 | [16] |
| Gneiss | 2,700 | [16] |
| Aluminium | 2,700 | |
| Limestone | 2,750 | Compact[16] |
| Basalt | 3,000 | [16] |
| Diiodomethane | 3,325 | Liquid at room temperature |
| Diamond | 3,500 | |
| Titanium | 4,540 | |
| Selenium | 4,800 | |
| Vanadium | 6,100 | |
| Antimony | 6,690 | |
| Zinc | 7,000 | |
| Chromium | 7,200 | |
| Tin | 7,310 | |
| Manganese | 7,325 | Approx. |
| Iron | 7,870 | |
| Mild Steel | 7,850 | |
| Niobium | 8,570 | |
| Brass | 8,600 | [18] |
| Cadmium | 8,650 | |
| Cobalt | 8,900 | |
| Nickel | 8,900 | |
| Copper | 8,940 | |
| Bismuth | 9,750 | |
| Molybdenum | 10,220 | |
| Silver | 10,500 | |
| Lead | 11,340 | |
| Thorium | 11,700 | |
| Rhodium | 12,410 | |
| Mercury | 13,546 | |
| Tantalum | 16,600 | |
| Uranium | 18,800 | |
| Tungsten | 19,300 | |
| Gold | 19,320 | |
| Plutonium | 19,840 | |
| Rhenium | 21,020 | |
| Platinum | 21,450 | |
| Iridium | 22,420 | |
| Osmium | 22,570 | Densest natural element on Earth |
Notes:
|
Others
| Entity | ρ (kg/m3) | Notes |
|---|---|---|
| Interstellar medium | 1.7×10−26 | Based on 10−5 hydrogen atoms per cubic centimetre[20] |
| Local Interstellar Cloud | 5×10−22 | Based on 0.3 hydrogen atoms per cubic centimetre[20] |
| Interstellar medium | 1.7×10−16 | Based on 105 hydrogen atoms per cubic centimetre[20] |
| The Earth | 5,515 | Mean density.[21] |
| Earth’s inner core | 13,000 | Approx., as listed in Earth.[22] |
| The core of the Sun | 33,000–160,000 | Approx.[23] |
| White dwarf star | 2.1×109 | Approx.[24] |
| Atomic nuclei | 2.3×1017 | Does not depend strongly on size of nucleus[25] |
| Neutron star | 1×1018 |
Water
| Temp. (°C)[note 1] | Density (kg/m3) |
|---|---|
| −30 | 983.854 |
| −20 | 993.547 |
| −10 | 998.117 |
| 0 | 999.8395 |
| 4 | 999.9720 |
| 10 | 999.7026 |
| 15 | 999.1026 |
| 20 | 998.2071 |
| 22 | 997.7735 |
| 25 | 997.0479 |
| 30 | 995.6502 |
| 40 | 992.2 |
| 60 | 983.2 |
| 80 | 971.8 |
| 100 | 958.4 |
Notes:
|
Air
Air density vs. temperature
| T (°C) | ρ (kg/m3) |
|---|---|
| −25 | 1.423 |
| −20 | 1.395 |
| −15 | 1.368 |
| −10 | 1.342 |
| −5 | 1.316 |
| 0 | 1.293 |
| 5 | 1.269 |
| 10 | 1.247 |
| 15 | 1.225 |
| 20 | 1.204 |
| 25 | 1.184 |
| 30 | 1.164 |
| 35 | 1.146 |
Molar volumes of liquid and solid phase of elements
Molar volumes of liquid and solid phase of elements
Common units
The SI unit for density is:
- kilogram per cubic metre (kg/m3)
The litre and tonne are not part of the SI, but are acceptable for use with it, leading to the following units:
- kilogram per litre (kg/L)
- gram per millilitre (g/mL)
- tonne per cubic metre (t/m3)
Densities using the following metric units all have exactly the same numerical value, one thousandth of the value in (kg/m3). Liquid water has a density of about 1 kg/dm3, making any of these SI units numerically convenient to use as most solids and liquids have densities between 0.1 and 20 kg/dm3.
- kilogram per cubic decimetre (kg/dm3)
- gram per cubic centimetre (g/cm3)
- 1 g/cm3 = 1000 kg/m3
- megagram (metric ton) per cubic metre (Mg/m3)
In US customary units density can be stated in:
- Avoirdupois ounce per cubic inch (1 g/cm3 ≈ 0.578036672 oz/cu in)
- Avoirdupois ounce per fluid ounce (1 g/cm3 ≈ 1.04317556 oz/US fl oz = 1.04317556 lb/US fl pint)
- Avoirdupois pound per cubic inch (1 g/cm3 ≈ 0.036127292 lb/cu in)
- pound per cubic foot (1 g/cm3 ≈ 62.427961 lb/cu ft)
- pound per cubic yard (1 g/cm3 ≈ 1685.5549 lb/cu yd)
- pound per US liquid gallon (1 g/cm3 ≈ 8.34540445 lb/US gal)
- pound per US bushel (1 g/cm3 ≈ 77.6888513 lb/bu)
- slug per cubic foot
Imperial units differing from the above (as the Imperial gallon and bushel differ from the US units) in practice are rarely used, though found in older documents. The Imperial gallon was based on the concept that an Imperial fluid ounce of water would have a mass of one Avoirdupois ounce, and indeed 1 g/cm3 ≈ 1.00224129 ounces per Imperial fluid ounce = 10.0224129 pounds per Imperial gallon. The density of precious metals could conceivably be based on Troy ounces and pounds, a possible cause of confusion.
Knowing the volume of the unit cell of a crystalline material and its formula weight (in daltons), the density can be calculated. One dalton per cubic ångström is equal to a density of 1.660 539 066 60 g/cm3.
See also
- Densities of the elements (data page)
- List of elements by density
- Air density
- Area density
- Bulk density
- Buoyancy
- Charge density
- Density prediction by the Girolami method
- Dord
- Energy density
- Lighter than air
- Linear density
- Number density
- Orthobaric density
- Paper density
- Specific weight
- Spice (oceanography)
- Standard temperature and pressure
References
- ^ The National Aeronautic and Atmospheric Administration’s Glenn Research Center. «Gas Density Glenn research Center». grc.nasa.gov. Archived from the original on April 14, 2013. Retrieved April 9, 2013.
- ^ «Density definition in Oil Gas Glossary». Oilgasglossary.com. Archived from the original on August 5, 2010. Retrieved September 14, 2010.
- ^ Archimedes, A Gold Thief and Buoyancy Archived August 27, 2007, at the Wayback Machine – by Larry «Harris» Taylor, Ph.D.
- ^ Vitruvius on Architecture, Book IX, paragraphs 9–12, translated into English and in the original Latin.
- ^ «EXHIBIT: The First Eureka Moment». Science. 305 (5688): 1219e. 2004. doi:10.1126/science.305.5688.1219e.
- ^ «Fact or Fiction?: Archimedes Coined the Term «Eureka!» in the Bath». Scientific American. December 2006.
- ^ «Test No. 109: Density of Liquids and Solids». OECD Guidelines for the Testing of Chemicals, Section 1. October 2, 2012. doi:10.1787/9789264123298-en. ISBN 9789264123298. ISSN 2074-5753.
- ^ New carbon nanotube struructure aerographite is lightest material champ Archived October 17, 2013, at the Wayback Machine. Phys.org (July 13, 2012). Retrieved on July 14, 2012.
- ^ Aerographit: Leichtestes Material der Welt entwickelt – SPIEGEL ONLINE Archived October 17, 2013, at the Wayback Machine. Spiegel.de (July 11, 2012). Retrieved on July 14, 2012.
- ^ a b «Re: which is more bouyant [sic] styrofoam or cork». Madsci.org. Archived from the original on February 14, 2011. Retrieved September 14, 2010.
- ^ a b Serway, Raymond; Jewett, John (2005), Principles of Physics: A Calculus-Based Text, Cengage Learning, p. 467, ISBN 0-534-49143-X, archived from the original on May 17, 2016
- ^ «Wood Densities». www.engineeringtoolbox.com. Archived from the original on October 20, 2012. Retrieved October 15, 2012.
- ^ «Density of Wood». www.simetric.co.uk. Archived from the original on October 26, 2012. Retrieved October 15, 2012.
- ^ Bolz, Ray E.; Tuve, George L., eds. (1970). «§1.3 Solids—Metals: Table 1-59 Metals and Alloys—Miscellaneous Properties». CRC Handbook of tables for Applied Engineering Science (2nd ed.). CRC Press. p. 117. ISBN 9781315214092.
- ^ glycerol composition at Archived February 28, 2013, at the Wayback Machine. Physics.nist.gov. Retrieved on July 14, 2012.
- ^ a b c d e f Sharma, P.V. (1997), Environmental and Engineering Geophysics, Cambridge University Press, p. 17, doi:10.1017/CBO9781139171168, ISBN 9781139171168
- ^ «Density of Concrete — The Physics Factbook». hypertextbook.com.
- ^ a b Young, Hugh D.; Freedman, Roger A. (2012). University Physics with Modern Physics. Addison-Wesley. p. 374. ISBN 978-0-321-69686-1.
- ^ «Density of Glass — The Physics Factbook». hypertextbook.com.
- ^ a b c «Our Local Galactic Neighborhood». Interstellar Probe Project. NASA. 2000. Archived from the original on November 21, 2013. Retrieved August 8, 2012.
- ^ Density of the Earth, wolframalpha.com, archived from the original on October 17, 2013
- ^ Density of Earth’s core, wolframalpha.com, archived from the original on October 17, 2013
- ^ Density of the Sun’s core, wolframalpha.com, archived from the original on October 17, 2013
- ^ Johnson, Jennifer. «Extreme Stars: White Dwarfs & Neutron Stars]» (PDF). lecture notes, Astronomy 162. Ohio State University. Archived from the original (PDF) on September 25, 2007.
- ^ «Nuclear Size and Density». HyperPhysics. Georgia State University. Archived from the original on July 6, 2009.
External links
- «Density» . Encyclopædia Britannica. Vol. 8 (11th ed.). 1911.
- «Density» . The New Student’s Reference Work . 1914.
- Video: Density Experiment with Oil and Alcohol
- Video: Density Experiment with Whiskey and Water
- Glass Density Calculation – Calculation of the density of glass at room temperature and of glass melts at 1000 – 1400°C
- List of Elements of the Periodic Table – Sorted by Density
- Calculation of saturated liquid densities for some components
- Field density test
- Water – Density and specific weight
- Temperature dependence of the density of water – Conversions of density units
- A delicious density experiment
- Water density calculator Archived July 13, 2011, at the Wayback Machine Water density for a given salinity and temperature.
- Liquid density calculator Select a liquid from the list and calculate density as a function of temperature.
- Gas density calculator Calculate density of a gas for as a function of temperature and pressure.
- Densities of various materials.
- Determination of Density of Solid, instructions for performing classroom experiment.
- Lam EJ, Alvarez MN, Galvez ME, Alvarez EB (2008). «A model for calculating the density of aqueous multicomponent electrolyte solutions». Journal of the Chilean Chemical Society. 53 (1): 1393–8. doi:10.4067/S0717-97072008000100015.
- Radović IR, Kijevčanin ML, Tasić AŽ, Djordjević BD, Šerbanović SP (2010). «Derived thermodynamic properties of alcohol+ cyclohexylamine mixtures». Journal of the Serbian Chemical Society. 75 (2): 283–293. CiteSeerX 10.1.1.424.3486. doi:10.2298/JSC1002283R.
ρ Греческая строчная буква ро
U+03C1
Нажмите, чтобы скопировать и вставить символ
Техническая информация
Значение символа
Греческая строчная буква ро. Греческое и коптское письмо.
Символ «Греческая строчная буква ро» был утвержден как часть Юникода версии 1.1 в 1993 г.
Свойства
| Версия | 1.1 |
| Блок | Греческое и коптское письмо |
| Тип парной зеркальной скобки (bidi) | Нет |
| Композиционное исключение | Нет |
| Изменение регистра | 03C1 |
| Простое изменение регистра | 03C1 |
Похожие символы
Греческая строчная буква омега
Греческая строчная буква ню
Греческая строчная буква дельта
Греческая строчная буква эпсилон
Греческая строчная буква дзета
Греческая строчная буква эта
Греческая строчная буква тета
Греческая строчная буква йота
Греческая строчная буква каппа
Греческая строчная буква лямбда
Греческая строчная буква мю
Греческая строчная буква кси
Греческая строчная буква бета
Греческая строчная буква омикрон
Греческая строчная буква пи
Кодировка
| Кодировка | hex | dec (bytes) | dec | binary |
|---|---|---|---|---|
| UTF-8 | CF 81 | 207 129 | 53121 | 11001111 10000001 |
| UTF-16BE | 03 C1 | 3 193 | 961 | 00000011 11000001 |
| UTF-16LE | C1 03 | 193 3 | 49411 | 11000001 00000011 |
| UTF-32BE | 00 00 03 C1 | 0 0 3 193 | 961 | 00000000 00000000 00000011 11000001 |
| UTF-32LE | C1 03 00 00 | 193 3 0 0 | 3238199296 | 11000001 00000011 00000000 00000000 |
Наборы с этим символом:
© Таблица символов Юникода, 2012–2021.
Юникод® — это зарегистрированная торговая марка консорциума Юникод в США и других странах. Этот сайт никак не связан с консорциумом Юникод. Официальный сайт Юникода располагается по адресу www.unicode.org.
Мы используем 🍪cookie, чтобы сделать сайт максимально удобным для вас. Подробнее
Как в ворде набрать символ плотности (ро)
// PascalABC.NET 3.3, сборка 1583 от 25.11.2017
// Внимание! Если программа не работает, обновите версию!
begin
var (x,y,z):=ReadReal3(‘Введите через пробел три числа:’);
if (x+y>z) and (x+z>y) and (y+z>x) then Writeln(‘Треугольник существует’)
else Writeln(‘Треугольник не существует’)
end.
Примеры
Введите через пробел три числа: 2.34 5.18 9
Треугольник не существует
Введите через пробел три числа: 3 4 5
Треугольник существует
Как поставить знак приблизительно равно в Word и Excel
На клавиатуре отсутствует знак приблизительного равенства, а для вставки часто применяют копирование из другого места. Но есть и более удобные способы, которые помогут быстро напечатать символ в любом месте документа Word или Excel.
Конвертация кода в знак
Первый способ заключается в конвертации юникода символа в знак. В любом месте документа набираем 2248 и одновременно нажимаем «Alt» + «X».
- 2248 ➟ Alt + x = ≈
Вторая возможность связана с ASCII-кодом и преобразование идёт следующим чередом:
- зажимаем Alt ;
- вводим на правой цифровой клавиатуре 8776;
- отпускаем Alt и цифры превращаются в ≈.
Оба варианта работают в Word, Excel и других офисных программах.
Вставка символа без клавиатуры
В Word для вставки символа приблизительно равно можно воспользоваться функцией вставки. На вкладке «Вставка» открываем окно «Другие символы».
Выбираем шрифт «обычный текст» и набор «математические операторы». В первых рядах будет нужный знак.
Похожие знаки равенства
Кроме знака примерного равенства есть много похожих математических и геометрических операндов. Они часто используются в формулах и имеют разную смысловую нагрузку.
К ним также применимы способы вставки в офисных программах.
Ро (буква)
- Ро (буква)
-
Категории:
- Греческие буквы
- Финикийский алфавит
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое «Ро (буква)» в других словарях:
-
Буква А — Буква кириллицы А Кириллица А Б В Г Ґ Д … Википедия
-
Ү (буква) — Буква кириллицы Ү Кириллица А Б В Г Ґ Д … Википедия
-
Ө (буква) — Буква кириллицы Ө Кириллица А Б В Г Ґ Д … Википедия
-
Буква Т — Буква кириллицы Т Кириллица А Б В Г Ґ Д … Википедия
-
Буква Ъ — Буква кириллицы Ъ Кириллица А Б В Г Ґ Д … Википедия
-
Ғ (буква) — Буква кириллицы Ғ Кириллица А Б В Г Ґ Д … Википедия
-
Һ (буква) — Буква кириллицы Һ Кириллица А Б В Г Ґ Д … Википедия
-
Буква — БУКВА. Б. называется графический знак для отдельного звука яз. в так наз. фонетических, или буквенных системах письма (в силлабических, т. е. слоговых системах, напр. в древнем ассирийском письме, графический знак символизирует слог, в… … Литературная энциклопедия
-
Буква И — Буква кириллицы И Кириллица А Б В Г Ґ Д … Википедия
-
Буква З — буква кириллицы З Кириллица А Б В Г Ґ Д … Википедия
-
Буква Н — Буква кириллицы Н Кириллица А Б В Г Ґ Д … Википедия







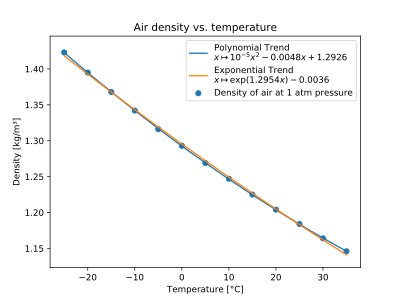

 ), содержащей эту точку, к объёму этой малой части (
), содержащей эту точку, к объёму этой малой части ( ), когда этот объём стремится к нулю[1], или, записывая кратко,
), когда этот объём стремится к нулю[1], или, записывая кратко,  . При таком предельном переходе необходимо помнить, что на атомарном уровне любое тело неоднородно, поэтому необходимо остановиться на объёме, соответствующем используемой физической модели.
. При таком предельном переходе необходимо помнить, что на атомарном уровне любое тело неоднородно, поэтому необходимо остановиться на объёме, соответствующем используемой физической модели.

 — молярный объём (при нормальных условиях равен 22,4 л/моль).
— молярный объём (при нормальных условиях равен 22,4 л/моль).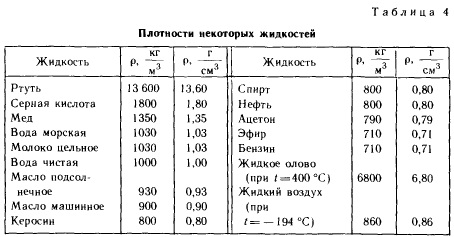
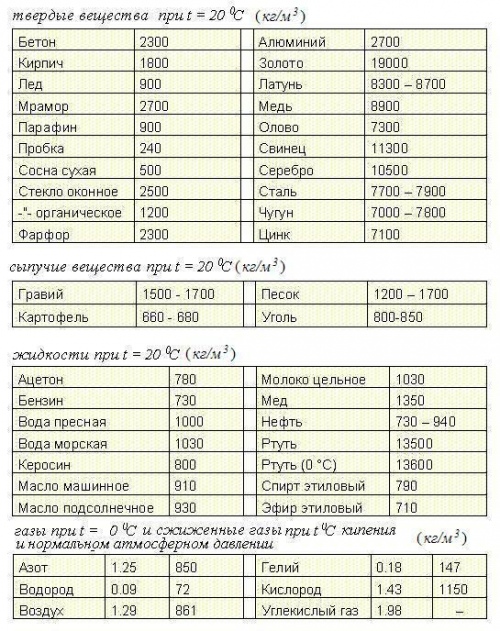
 ), содержащей эту точку, к объёму этой малой части (
), содержащей эту точку, к объёму этой малой части ( ), когда этот объём стремится к нулю[1], или, записывая кратко,
), когда этот объём стремится к нулю[1], или, записывая кратко,  . При таком предельном переходе необходимо помнить, что на атомарном уровне любое тело неоднородно, поэтому необходимо остановиться на объёме, соответствующем используемой физической модели.
. При таком предельном переходе необходимо помнить, что на атомарном уровне любое тело неоднородно, поэтому необходимо остановиться на объёме, соответствующем используемой физической модели.

 — молярный объём (при нормальных условиях равен 22,4 л/моль).
— молярный объём (при нормальных условиях равен 22,4 л/моль).