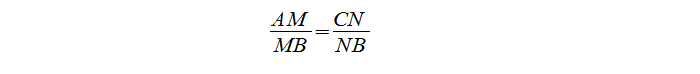В учебниках по геометрии часто встречаются задачи на подобие фигур. Какой знак используется для обозначения подобия фигур? Какие фигуры называются подобными? Поговорим обо всем этом в нашей статье.
Определение и знак подобия в геометрии
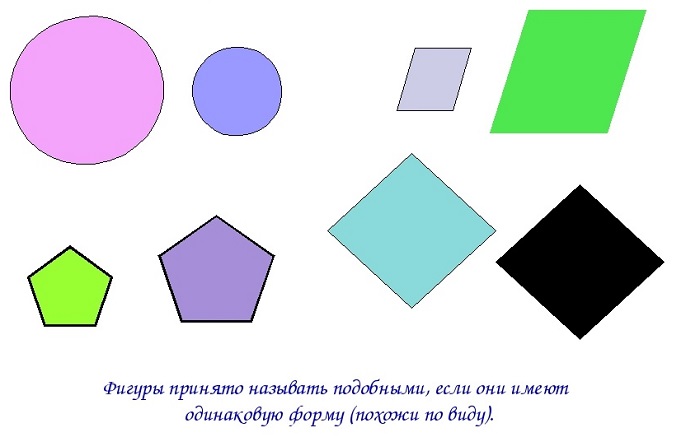
Подобными называются фигуры, если одна из них представляет уменьшенную копию другой.
На нижеприведенном рисунке подобные фигуры: круги, параллелограммы, пятиугольники и ромбы.
Для обозначения термина «подобие» в геометрии используют знак «тильда», который является типографским символом и обозначается волнистой чертой:
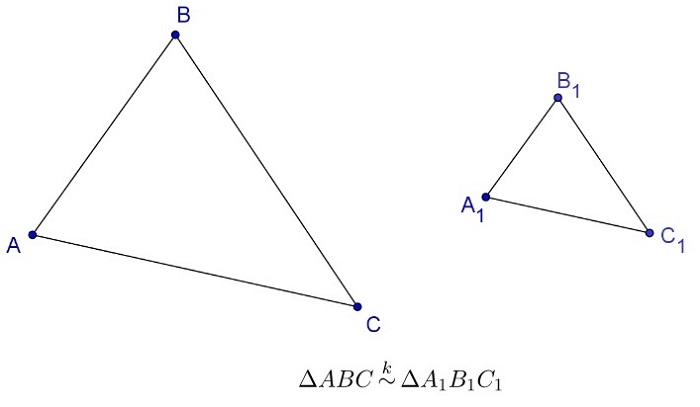
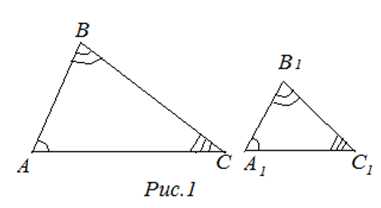
∆ABC ~ ∆A1B1C1
— треугольники ABC и A1B1C1
подобны.
Знак «двойная тильда» ставится около чисел для демонстрации примерности или приблизительности чего-либо:
1,35 ≈ 1,4 — числа 1,35 и 1,4 приблизительно равны.
Коэффициент подобия треугольников и знак подобия
Часто сверху знака подобия выставляют коэффициент подобия треугольников:
В математических задачах и уравнениях «тильду» используют для маркирования разных типов подобия. Часто применяется для обозначения подобия, эквивалентности.
В алгебре высказываний знаком ~ обозначают логическую операцию «эквиваленция».
При сочетании тильды и знака равенства получают обозначение отношения конгруэнтности, определения в геометрии, применяемого в контексте обозначения равенства различных фигур и тел (углов, отрезков):
Признаки подобия прямоугольных треугольников
Острые углы: наличие равного острого угла в прямоугольных треугольниках делает их подобными.
Два катета: общая пропорциональность катетам одного прямоугольного треугольника к катетам второго делает их подобными.
Катет и гипотенуза: пропорциональность катета и гипотенузы одного прямоугольного треугольника к катету и гипотенузе второго прямоугольного треугольника делает их подобными.
Утверждения:
-
треугольник ∆ABC и треугольник ∆A1B1C1 считаются подобными при равнозначности углов и пропорциональности сторон;
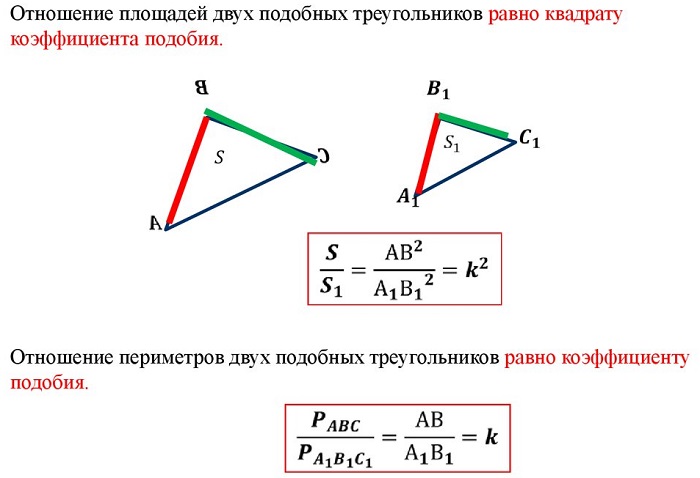
-
отношение площадей подобных треугольников равно квадрату коэффициента подобия.
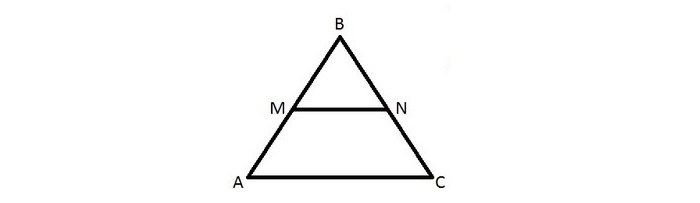
Доказательство подобия треугольников через среднюю линию
Имеется треугольник ∆ABC, mn — средняя линия. M лежит на AB, N лежит на BC.
Требуется доказательство подобия треугольников ∆MBN и ∆ABC.
Посмотрев на ∆MBN и ∆ABC, видим, что угол В — общий, а отношение:
Отсюда делаем вывод, что ∆MBN ~ ∆ABC по II признаку подобия треугольников, что и требовалось доказать.
Примеры решения задач по геометрии на тему «Подобие треугольников»
_____________________________________________________________________
Знак подобия в геометрии
Определение и знак подобия в геометрии
ОПРЕДЕЛЕНИЕ
Два треугольника и называются подобными, если у них равные углы и пропорциональные стороны.
Обозначают подобие треугольников знаком «».
Пример. (читают: треугольник подобен треугольнику ).
Коэффициент подобия треугольников и знак подобия
Иногда над знаком подобия ставят коэффициент подобия треугольников, т.е. .
Знак «» представляет собой типографский знак «тильда», который изображается в виде волнистой черты. Этот знак может быть как надстрочным, так и междустрочным.
В математике «тильда» используется для обозначения различных видов отношений эквивалентности, в частности, отношения подобия.
Знак «тильда» (или «двойная тильда» ), который стоит перед числом может означать «примерно», «приблизительно равно».
В алгебре высказываний знак «» обозначает логическую операцию «эквиваленция».
Если знак «тильда» сочетать со знаком равенства: «», то он будет обозначать отношение конгруэнтности.
Также знак «тильда» активно используется в информатике и вычислительной технике. Например, в редакторе Tex этот знак означает «неразрывный пробел».
ru.solverbook.com
Знак подобия треугольников в геометрии — что значит «~» в геометрии? — 22 ответа
В разделе Школы на вопрос что значит «~» в геометрии? заданный автором Нету лучший ответ это Это знак «Приблизительно»
Ответ от 22 ответа[гуру]
Привет! Вот подборка тем с ответами на Ваш вопрос: что значит «~» в геометрии?
Ответ от Mitternacht[гуру]
Вроде приблизительно
Ответ от Острословить[гуру]
подобие.. . посмотрите в планиметрии в правилах подобия треугольников.. . там этот знак активно используется…
Ответ от Невропатолог
[гуру]
точно не уверенна, но может подобие Для тех кто пишет приблизительно: знак приблизительности похож на знак =,только линии там волнистые, как в вопросе
Ответ от Недоносок[новичек]
Это значит приблизительно
Ответ от МiRaMih[гуру]
Подобие
Ответ от Антон Рзаханов[активный]
это знак подобия)) мы щас проходим)
Ответ от Hip-hop4live[гуру]
Подобие!!!!
Ответ от Ёаша Рощин[активный]
Прекрасных комедий множество. Но одна из лучших «Не упускай из виду! » 1975г. с Пьером Ришаром.
Узнал об этом фильме у него на спектакле в Москве феврале в этом году. Решил посмотреть этот фильм, у меня была истерика, чуть упал под стол от смеха, особенно когда он бегал с унитазом на ноге )) А на самом спектакле Ришар такие байки травил, особенно про Депардье, что я реально устал смеяться )
Ответ от Влад Матвеев[новичек]
подобие
Ответ от Supreme[новичек]
Подобие )
Признаки подобия треугольников на Википедии
Посмотрите статью на википедии про Признаки подобия треугольников
Ответить на вопрос:
22oa.ru
что значит «~» в геометрии?
Вроде приблизительно
подобие.. .
посмотрите в планиметрии в правилах подобия треугольников.. . там этот знак активно используется…
точно не уверенна, но может подобие
Для тех кто пишет приблизительно:
знак приблизительности похож на знак =,только линии там волнистые, как в вопросе
Это значит приблизительно
это знак подобия)) мы щас проходим)
приблизительно
этот символ означает «подобие», а два параллельных (друг под другом) символа означают «приблизительно»
Это «тильда», она обозначает «подобие» в геометрии.
touch.otvet.mail.ru
Что в Геометрий обозначает недорисованная, перевёрнутая 8-ка?
лежащая на боку 8 знак бесконечности …
Перевёрнутая восьмёрка выглядит также как обычная.
Интеграл, параграф. Больше не знаю. У меня была тройка по геометрии (((
в геометрии такой знак обозначает подобие фигур
Я насколько помню так всю жизнь обозначали подобие, НО такого символа фактически нет. Это ~ и она не настолько загнута по краям, как её в школах рисовали.
Перевернутая восьмерка обозначает бесконечность
touch.otvet.mail.ru
Как называется этот знак (Геометрия)???
Дуга выгнута вверх? Тогда это знак пересечения. Если выгнута вниз — объединение…. Если я, конечно, вспомнила правильно
он так и называется дуга. а читается например дуга ОВ
может»принадлежит» ет обуква э ?
Вероятно ето пересечение, если на U похоже.
Это значит точка О получается пересечением АВ и СД. Может это знак пересечения? Больше на ум ничего не идет, что смысл бы имело…
это и есть -дуга — 100%
Если дуга выгнута вниз, значит это «дуга», а если вверх то «пересечение».
touch.otvet.mail.ru
Подобные треугольники в евклидовой геометрии — треугольники, углы у которых соответственно равны, а стороны соответственно пропорциональны. Являются подобными фигурами.
В данной статье рассматриваются свойства подобных треугольников в евклидовой геометрии. Некоторые утверждения являются неверными для неевклидовых геометрий.
Признаки подобия треугольников[править | править код]
Признаки подобия треугольников — геометрические признаки, позволяющие установить, что два треугольника являются подобными без использования всех элементов определения.
Первый признак[править | править код]
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то треугольники подобны.
то есть:
Дано: и
Доказать:
Следствия первого признака подобия[править | править код]
- Если три разные стороны исходного треугольника попарно параллельны (дважды антипараллельны или перпендикулярны) трем разным сходственным сторонам другого треугольника, то указанные два треугольника подобны. Примеры применения этого следствия см. ниже в разделах: «Примеры подобных треугольников» и «Свойства параллельности (антипараллельности) сторон родственных треугольников».
- Под дважды антипараллельными сторонами понимается следующее. Например, стороны данного остроугольного треугольника антипараллельны соответствующим сторонам ортотреугольника, против которых они лежат. В таком случае соответствующие стороны ортотреугольника ортотреугольника (дважды ортотреугольника) дважды антипараллельны соответствующим сторонам исходного треугольника, то есть просто параллельны. Следовательно, подобны, например, ортотреугольник ортотреугольника и исходный треугольник как треугольники с параллельными сторонами.
Второй признак[править | править код]
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.
Дано: и
Доказать:
Третий признак[править | править код]
Если три стороны одного треугольника соответственно пропорциональны трем сторонам другого, то такие треугольники подобны.
Дано: и = = .
Доказать:
Признаки подобия прямоугольных треугольников[править | править код]
- По острому углу — см. первый признак;
- По двум катетам — см. второй признак;
- По катету и гипотенузе — см. третий признак.
Свойства подобных треугольников[править | править код]
- Отношение площадей подобных треугольников равно квадрату коэффициента подобия
- Отношение периметров и длин биссектрис, медиан, высот и серединных перпендикуляров равно коэффициенту подобия.
Примеры подобных треугольников[править | править код]
Подобны следующие виды треугольников:
- Дополнительный треугольник и антидополнительный треугольник подобны; соответственные их стороны параллельны.
- Треугольник ABC подобен своему дополнительному треугольнику; соответственные их стороны параллельны и относятся как 2:1.
- Треугольник ABC подобен своему антидополнительному треугольнику; соответственные их стороны параллельны и относятся как 1:2.
- Исходный треугольник по отношению к ортотреугольнику является треугольником трёх внешних биссектрис[1].
- Ортотреугольник и тангенциальный треугольник подобны (Зетель, следствие 1, § 66, с. 81).
- Ортотреугольник ортотреугольника и исходный треугольник подобны.
- Треугольник трёх внешних биссектрис треугольника трех внешних биссектрис и исходный треугольник подобны.
- Пусть точки касания вписанной в данный треугольник окружности соединены отрезками, тогда получится треугольник Жергонна, и в полученном треугольнике проведены высоты. В этом случае прямые, соединяющие основания этих высот, параллельны сторонам исходного треугольника. Следовательно ортотреугольник треугольника Жергонна и исходный треугольник подобны.
- Выше указанные свойства подобия родственных треугольников являются следствием ниже перечисленных свойств параллельности сторон родственных треугольников.
- Теорема: окружностно-чевианный треугольник подобен подерному[2]. Здесь использованы определения:
- Треугольник с вершинами во вторых точках пересечения прямых, проведённых через вершины и данную точку, с описанной окружностью, называют окружностно-чевианным треугольником.
- Треугольник с вершинами в проекциях данной точки на стороны называется подерным или педальным треугольником этой точки.
Свойства параллельности (антипараллельности) сторон родственных треугольников[править | править код]
- Соответственные стороны дополнительного треугольника, антидополнительного треугольника и исходного треугольника попарно параллельны.
- Стороны данного остроугольного треугольника антипараллельны соответствующим сторонам ортотреугольника, против которых они лежат.
- Стороны тангенциального треугольника антипараллельны соответствующим противоположным сторонам данного треугольника (по свойству антипараллельности касательных к окружности).
- Стороны тангенциального треугольника параллельны соответствующим сторонам ортотреугольника.
- Пусть точки касания вписанной в данный треугольник окружности соединены отрезками, тогда получится треугольник Жергонна, и в полученном треугольнике проведены высоты. В этом случае прямые, соединяющие основания этих высот, параллельны сторонам исходного треугольника. Следовательно ортотреугольник треугольника Жергонна и исходный треугольник подобны.
Подобие в прямоугольном треугольнике[править | править код]
Треугольники, на которые высота, опущенная из прямого угла, делит прямоугольный треугольник, подобны всему треугольнику по первому признаку, а значит:
- Высота прямоугольного треугольника, опущенная на гипотенузу, равна среднему геометрическому проекций катетов на гипотенузу,
- Катет равен среднему геометрическому гипотенузы и проекции этого катета на гипотенузу.
Связанные определения[править | править код]
- Коэффициент подобия — число k, равное отношению сходственных сторон подобных треугольников.
- Сходственные стороны подобных треугольников — стороны, лежащие напротив равных углов.
См. также[править | править код]
- Неравенство Пидо
- Подобие
- Признаки равенства треугольников
- Решение треугольников
- Среднее геометрическое
- Треугольник
Примечания[править | править код]
- ↑ Стариков В. Н. Исследования по геометрии// Сборник публикаций научного журнала Globus по материалам V-й международной научно-практической конференции «Достижения и проблемы современной науки» г. Санкт-Петербург: сборник со статьями (уровень стандарта, академический уровень). С-П.: Научный журнал Globus, 2016. С. 99-100
- ↑ Система задач по геометрии Р. К. Гордина. Задача 6480. Дата обращения: 26 апреля 2016. Архивировано 4 марта 2016 года.
Литература[править | править код]
- Геометрия 7-9/Л. С. Атанасян и др. — 12-е изд. — М.: Просвещение, 2002. — 384 c.:
- Зетель С. И. Новая геометрия треугольника. Пособие для учителей. 2-е издание. М.:Учпедгиз, 1962. 153 с.
Ссылки[править | править код]
- Видео. Подобные треугольники
- Подобие треугольников
- Признаки подобия из учебника за восьмой класс
Ниже представлена таблица с основными математическими символами и знаками, которые используются в геометрии с 7 класса и старше.
| Знак | Название | Значение/описание | Пример |
| ∠ | угол | фигура, состоящая из двух лучей и вершины | ∠ABC = 30° |
| острый угол | угол от 0 до 90 градусов | ∠AOB = 60° | |
| прямой угол | угол, равный 90 граусам | ∠AOB = 90° | |
| тупой угол | угол от 90 до 180 градусов | ∠AOB = 120° | |
 |
развернутый угол | угол, равный 180 градусам | ∠AOB = 180° |
| ° (или deg) |
градус | единица измерения угла, равна 1/360 окружности | 45° |
| ′ | минута | единица измерения угла, 1° = 60′ | α = 70°59′ |
| ″ | секунда | единица измерения угла, 1′ = 60″ | α = 70°59′59″ |
| линия | бесконечная прямая без начала и конца | ||
| отрезок | участок на прямой между точками A и B | ||
| луч | бесконечная прямая, имеющая начало в точке A, но не имеющая конца | ||
| дуга | дуга, образованная между точками A и B | ||
| ⊥ | перпендикулярность | линии (прямые), расположенные под углом 90° по отношению друг к другу | AC ⊥ BC |
| || | параллельность | непересекающиеся прямые (линии) | AB || CD |
| ∩ | пересечение | множество одинаковых элементов, принадлежащих как множеству A, так и B | A ∩ B |
| ∈ / ∉ | принадлежность/ непринадлежность |
элемент является/не является элементом заданного множества | a ∈ S |
| ≅ | конгуэнтность | эквивалентность геометрических форм и размеров | ∆ABC ≅ ∆XYZ |
| ~ | подобие | та же форма, но разные размеры | ∆ABC ~ ∆XYZ |
| Δ | треугольник | фигура треугольника | ΔABC ≅ ΔBCD |
| |x-y| | дистанция | дистанция между точками X и Y | | x-y | = 5 |
| π | константа «Пи» | отношение длины окружности к диаметру круга, π = C/d | π = 3.141592654… |
| рад (rad) или c |
радиан | единица измерения угла | 360° = 2π c |
microexcel.ru

Отношение площадей подобных треугольников равно квадрату коэффициента подобия. Если обозначить площади двух подобных треугольников буквами S и S1, то:
Если два угла одного треугольника равны двум углам другого, то треугольники подобны.

Второй признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то треугольники подобны.
| Если | AB | = | AC | , ∠A = ∠A1, |
| A1B1 | A1C1 | |||
то  ABC ABC
|
Третий признак подобия треугольников
Если три стороны одного треугольника пропорциональны трём сходственным сторонам другого, то треугольники подобны.
Источник
Знак подобия в геометрии — правило и примеры обозначения
В учебниках по геометрии часто встречаются задачи на подобие фигур. Какой знак используется для обозначения подобия фигур? Какие фигуры называются подобными? Поговорим обо всем этом в нашей статье.
Определение и знак подобия в геометрии
Подобными называются фигуры, если одна из них представляет уменьшенную копию другой.
На нижеприведенном рисунке подобные фигуры: круги, параллелограммы, пятиугольники и ромбы.
Для обозначения термина «подобие» в геометрии используют знак «тильда», который является типографским символом и обозначается волнистой чертой:
Знак «двойная тильда» ставится около чисел для демонстрации примерности или приблизительности чего-либо:
1,35 ≈ 1,4 — числа 1,35 и 1,4 приблизительно равны.
Коэффициент подобия треугольников и знак подобия
Часто сверху знака подобия выставляют коэффициент подобия треугольников:
В математических задачах и уравнениях «тильду» используют для маркирования разных типов подобия. Часто применяется для обозначения подобия, эквивалентности.
В алгебре высказываний знаком
обозначают логическую операцию «эквиваленция».
При сочетании тильды и знака равенства получают обозначение отношения конгруэнтности, определения в геометрии, применяемого в контексте обозначения равенства различных фигур и тел (углов, отрезков):
Признаки подобия прямоугольных треугольников
Острые углы: наличие равного острого угла в прямоугольных треугольниках делает их подобными.
Два катета: общая пропорциональность катетам одного прямоугольного треугольника к катетам второго делает их подобными.
Катет и гипотенуза: пропорциональность катета и гипотенузы одного прямоугольного треугольника к катету и гипотенузе второго прямоугольного треугольника делает их подобными.
треугольник ∆ABC и треугольник ∆A1B1C1 считаются подобными при равнозначности углов и пропорциональности сторон;
отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Доказательство подобия треугольников через среднюю линию
Имеется треугольник ∆ABC, mn – средняя линия. M лежит на AB, N лежит на BC.
Требуется доказательство подобия треугольников ∆MBN и ∆ABC.
Посмотрев на ∆MBN и ∆ABC, видим, что угол В — общий, а отношение:
Отсюда делаем вывод, что ∆MBN
∆ABC по II признаку подобия треугольников, что и требовалось доказать.
Примеры решения задач по геометрии на тему «Подобие треугольников»
Еще тесты
Читайте также
Внутренние односторонние углы – теория, правило и свойстваУравнение биссектрисы в треугольнике – формула, свойства и решение задачТеорема Вариньона – формулировка, доказательство и следствияКак доказать, что четырехугольник является параллелограммом?
При изучении геометрии вы непременно обращали внимание, что часть фигур очень похожа на другие. Отличаются только размеры. Но геометрия — наука точная и слово «похожие» не всегда определяет реальное положение вещей. Например, прямоугольный треугольник похож на равносторонний, но при ближайшем рассмотрении легко обнаружить различия, — отличаются углы, длины сторон, конфигурация.
В геометрии применяется другое понятие — «подобие». Это более узкий термин, который определяет фигуры, которые идентичны по всем параметрам, кроме размера. Если увеличить, или уменьшить одну из фигур, то получится другая, с полным соответствием. Знак подобия в геометрии «
» имеет очень большой смысл. Это не просто обозначение «похожести», а специальный термин. Он говорит о том, что из одной фигуры можно получить другую, если преобразовать ее особым образом.
Самый простой способ — увеличение размеров. Но не простое увеличение, а пропорциональное. То есть, каждая сторона фигуры увеличивается на строго определенную величину. Соотношение новой длины и исходной называется коэффициентом подобия. Согласно правилам математики К≠ 0. Смысл ясен, на ноль делить нельзя. В остальном значение К может принимать любое значение, в том числе, и дробное. Если в десятичном исчислении коэффициент находится в диапазоне от ноля до единицы, то фигура уменьшается при проецировании, если К ≥ 1, то фигура получится больше, или идентичной исходной.
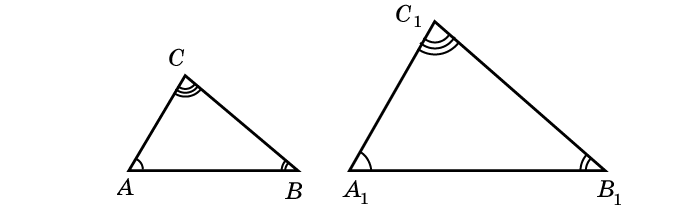
Каждая из геометрических фигур имеет ряд признаков, по которым ее можно сравнить с другой и определить, подобные фигуры, или просто похожие. У треугольников таких признаков три. Рассмотрим их более подробно. В идеале, треугольники называются подобными, если у них три угла одинаковые, а три стороны пропорциональны, согласно коэффициенту К. Но не всегда есть возможность измерить углы и стороны. Есть ряд признаков, требующих меньшего числа измерений, по которым легко определить, подобные треугольники, или нет.
Если два угла произвольного треугольника равны двум углам другого, значит, фигуры подобные. В геометрической графике это записывается так:
ΔА1В1С1 А=∠А1, ∠В=∠В1, ∠С=∠С1.
Доказательство первого признака подобия приводить не будем, ввиду того, что признак проверен и доказан, информация об этом есть в любом учебнике. Намного важнее, что из этого признака вытекает следствие, которое не менее важно, чем сам признак. Во многих задачах на ЕГЭ и в учебниках упор делается именно на знание этого правила. «Если три стороны одного треугольника попарно параллельны трем сторонам другого, то эти фигуры подобны».
Утверждение не менее очевидно, чем первый признак подобия. Формулируется оно так:
Если две соответствующие стороны треугольников пропорциональны, а углы между ними равные, то фигуры подобные.
Это правило называется признаком подобия по двум сторонам и углу между ними. Геометрическая запись выглядит так:
ΔА1В1С1 ↔ ∠ А=∠А1, АВ/А1В1 = АС/А1С1.
Самый простой и наиболее понятный признак подобия: если три стороны одной фигуры пропорциональны трем сторонам другой с одинаковым коэффициентом К, то треугольники подобные. Записывается такое утверждение таким образом:
Доказательство этого утверждения опять же приводить не будем вследствие дефицита размера статьи. Лучше остановимся на следствиях, которые вытекают из этих утверждений. Многие из параметров геометрических фигур можно определить, пользуясь названными правилами.
Один из способов применения признаков подобия демонстрирует теорема об отношении периметров подобных треугольников. В формулировке говорится о том, что отношение периметров подобных треугольников равно коэффициенту пропорциональности сторон. На практике это выглядит так — вам нужно найти периметр треугольника со сторонами в несколько километров, что часто требуется в строительстве, агротехнике и геодезии. Если нарисовать подобный треугольник на бумаге, со сторонами в несколько сантиметров и вычислить периметр, то он будет ровно настолько же меньше, как и стороны треугольников. То есть, коэффициент К работает и в случае с периметром.
Вторая задача — найти соотношение площадей подобных треугольников. Здесь тоже существует определенная пропорция, но уже квадратичная. То есть, соотношение площадей фигур равно квадрату К.
При решении задач поможет также лемма о подобных треугольниках, говорящая о том, что любая прямая, пересекающая треугольник параллельно одной из сторон, отсекает от него подобную фигуру.
Пользуясь полученной информацией, несложно решить любую задачу по определению параметров подобных треугольников.
Теорема 1. Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого.
Прежде всего отметим, что из равенства двух углов данных треугольников следует, что и третьи углы их равны, т. е. ∠C = ∠С’.
Отложим от вершины В, например, на стороне AB треугольника ABC отрезок ВМ, равный отрезку А’В’. Из точки М проведём прямую MN || АС. Мы получили (Delta)MBN, который подобен (Delta)ABC. Но (Delta)MBN = (Delta)А’В’С’, так как ∠В = ∠В’ по условию теоремы; сторона MB = A’B’ по построению; ∠BMN = ∠A’ (∠BMN и ∠А’ порознь равны одному и тому же ∠А).
Если (Delta)MBN (sim) (Delta)AВС, то (Delta)А’В’С’ (sim) (Delta)ABC. Эта теорема выражает 1-й признак подобия треугольников.
Следствия. 1. Равносторонние треугольники подобны.
2. Равнобедренные треугольники подобны, если они имеют по равному углу при вершине или при основании.
3. Два прямоугольных треугольника подобны, если она имеют по равному острому углу.
4. Равнобедренные прямоугольные треугольники подобны.
Пусть в треугольниках ABC и А’В’С’ (frac = frac) и ∠В = ∠В’
Требуется доказать, что (Delta)ABC (sim) (Delta)А’В’С’ (рис. 368).
Для доказательства отложим, например, на стороне AB треугольника ABC от вершины В отрезок ВМ, равный отрезку А’В’. Через точку М проведём прямую MN || АС. Полученный треугольник MBN подобен треугольнику ABC.Докажем, что (Delta)MBN = (Delta)А’В’С’. В этих треугольниках ∠В = ∠В’ по условию теоремы, MB = А’В’ по построению. Чтобы убедиться в равенстве сторон BN и В’С, составим пропорцию AB /MB = BC /BN (она вытекает из параллельности АС и MN) и сравним её с пропорцией, которая дана в условии теоремы: (frac = frac). В этих двух пропорциях имеется по три равных члена, следовательно, равны и четвёртые их члены, т. е. В’С’ = BN. Отсюда следует равенство треугольников MBN и А’В’С’. Так как (Delta)MBN (sim) (Delta)А’В’С’, то, следовательно, и (Delta)А’В’С’ (sim) (Delta)ABС.
Эта теорема выражает 2-й признак подобия треугольников.
Следствие. Прямоугольные треугольники подобны, если катеты одного из них пропорциональны катетам другого.
Теорема 3. Два треугольника подобны, если три стороны одного треугольника пропорциональны трём сторонам другого треугольника.
Пусть в треугольниках ABC и А’В’С’ (frac = frac = frac) (рис. 369).
Требуется доказать, что (Delta)ABC (sim) (Delta)А’В’С’
Для доказательства отложим на стороне AB треугольника ABC от вершины В отрезок BM = А’В’. Из точки M проведём прямую MN || АС. Полученный треугольник MBN подобен треугольнику ABC. Следовательно, (frac = frac = frac).
Эта теорема выражает 3-й признак подобия треугольников.
В учебниках по геометрии часто встречаются задачи на подобие фигур. Какой знак используется для обозначения подобия фигур? Какие фигуры называются подобными? Поговорим обо всем этом в нашей статье.
Определение и знак подобия в геометрии
Подобными называются фигуры, если одна из них представляет уменьшенную копию другой.
На нижеприведенном рисунке подобные фигуры: круги, параллелограммы, пятиугольники и ромбы.
Для обозначения термина «подобие» в геометрии используют знак «тильда», который является типографским символом и обозначается волнистой чертой:
∆A 1 B 1 C 1 — треугольники ABC и A1B1C1 подобны.
Знак «двойная тильда» ставится около чисел для демонстрации примерности или приблизительности чего-либо:
1,35 ≈ 1,4 — числа 1,35 и 1,4 приблизительно равны.
Коэффициент подобия треугольников и знак подобия
Часто сверху знака подобия выставляют коэффициент подобия треугольников:
В математических задачах и уравнениях «тильду» используют для маркирования разных типов подобия. Часто применяется для обозначения подобия, эквивалентности.
В алгебре высказываний знаком
обозначают логическую операцию «эквиваленция».
При сочетании тильды и знака равенства получают обозначение отношения конгруэнтности, определения в геометрии, применяемого в контексте обозначения равенства различных фигур и тел (углов, отрезков):
Признаки подобия прямоугольных треугольников
Острые углы: наличие равного острого угла в прямоугольных треугольниках делает их подобными.
Два катета: общая пропорциональность катетам одного прямоугольного треугольника к катетам второго делает их подобными.
Катет и гипотенуза: пропорциональность катета и гипотенузы одного прямоугольного треугольника к катету и гипотенузе второго прямоугольного треугольника делает их подобными.
треугольник ∆ABC и треугольник ∆A1B1C1 считаются подобными при равнозначности углов и пропорциональности сторон;
отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Доказательство подобия треугольников через среднюю линию
Имеется треугольник ∆ABC, mn — средняя линия. M лежит на AB, N лежит на BC.
Требуется доказательство подобия треугольников ∆MBN и ∆ABC.
Посмотрев на ∆MBN и ∆ABC, видим, что угол В — общий, а отношение:
Отсюда делаем вывод, что ∆MBN
∆ABC по II признаку подобия треугольников, что и требовалось доказать.
Источник
Подобие в геометрии
Смотреть что такое «Подобие в геометрии» в других словарях:
Подобие (значения) — Подобие в геометрии биективное преобразование с особыми свойствами. Подобие в физике равенство отношений каких либо измеряемых величин в двух и более физических системах при их эволюции Подобие в философии и богословии способ связи… … Википедия
Подобие — (в геометрии, Similitude). Два треугольника подобны междусобою, если углы их одинаковы и отношение сторон, противолежащих равнымуглам, имеет одну и ту же величину. Всякие две подобные фигуры и всякиедва подобные тела могут быть рассматриваемы как … Энциклопедия Брокгауза и Ефрона
ПОДОБИЕ — ПОДОБИЕ, подобия, ср. 1. только ед. Образ чего нибудь, нечто похожее, сходное. От него после болезни не осталось и подобия прежнего человека. Даже подобия благородства он не проявил. Осталось жалкое подобие статуи. 2. В геометрии тождество фигур… … Толковый словарь Ушакова
ПОДОБИЕ — ПОДОБИЕ, я, ср. 1. Что н. сходное с чем н. другим, содержащее образ, вид чего н. (книжн.). Создать что н. по своему образу и подобию (т. е. похожим на себя). 2. В геометрии: тождество формы при различии величины. П. двух треугольников. Толковый… … Толковый словарь Ожегова
подобие — ПОДОБИЕ понятие, фундаментальное для характеристики абстрактного мышления. Платон определяет подобное как «такого же рода иное» Платон. Софист. 240а), т.е. как предмет, сходный с другим предметом в родовых и отличный от него в видовых… … Энциклопедия эпистемологии и философии науки
Подобие — геометрическое понятие, характеризующее наличие одинаковой формы у геометрических фигур, независимо от их размеров. Две фигуры F1 и F2 называются подобными, если между их точками можно установить взаимно однозначное соответствие, при… … Большая советская энциклопедия
Подобие (физика) — У этого термина существуют и другие значения, см. Подобие (значения). Две и более физические системы называются подобными, если при их эволюции сохраняется отношение между некоторыми измеряемыми величинами, характеризующими данные системы. Для… … Википедия
Подобие — I ср. 1. Нечто похожее, сходное с чем либо, напоминающее собою что либо. 2. Образ, облик кого либо, чего либо. 3. устар. Сходство. II ср. Тождество фигур по форме при различии их по величине (в геометрии). Толковый словарь Ефремовой. Т. Ф.… … Современный толковый словарь русского языка Ефремовой
Подобие — I ср. 1. Нечто похожее, сходное с чем либо, напоминающее собою что либо. 2. Образ, облик кого либо, чего либо. 3. устар. Сходство. II ср. Тождество фигур по форме при различии их по величине (в геометрии). Толковый словарь Ефремовой. Т. Ф.… … Современный толковый словарь русского языка Ефремовой
Подобие — 1) в широком смысле несколько одинаковых признаков вещей (если совпадают все признаки, то вещи одинаковы); 2) (в философии) в процессе познания движение от познанного к непознанному возможно только в том случае, если между тем и другим заключено… … Начала современного естествознания
Источник
Как пишется знак пересечения в геометрии? Срочно.
Ответы на вопрос

Коэффициент подобия треугольников и знак подобия
Часто сверху знака подобия выставляют коэффициент подобия треугольников:
В математических задачах и уравнениях «тильду» используют для маркирования разных типов подобия. Часто применяется для обозначения подобия, эквивалентности.
В алгебре высказываний знаком
обозначают логическую операцию «эквиваленция».
При сочетании тильды и знака равенства получают обозначение отношения конгруэнтности, определения в геометрии, применяемого в контексте обозначения равенства различных фигур и тел (углов, отрезков):
Определение и знак подобия в геометрии
Подобными называются фигуры, если одна из них представляет уменьшенную копию другой.
На нижеприведенном рисунке подобные фигуры: круги, параллелограммы, пятиугольники и ромбы.
Для обозначения термина «подобие» в геометрии используют знак «тильда», который является типографским символом и обозначается волнистой чертой:
∆A 1 B 1 C 1 — треугольники ABC и A1B1C1 подобны.
Знак «двойная тильда» ставится около чисел для демонстрации примерности или приблизительности чего-либо:
1,35 ≈ 1,4 — числа 1,35 и 1,4 приблизительно равны.
Математические знаки ≈ ∑ ⇒ ∈ ≤ ∞
Нажмите, чтобы скопировать и вставить символ
В разделе собраны математические символы, которые невозможно корректно отобразить с помощью ввода на клавиатуре. Весь представленный набор можно разделить на несколько групп:
Использование данных иконок – единственный вариант корректного отображения ряда математических символов на сайте или в сообщении в любой операционной системе конечного пользователя. Достаточно лишь скопировать закодированный значок. Применение изображений для этих целей значительно усложняет процесс, требует подгонки при разработке и наполнении интернет-ресурса. Кроме того, медиа-контент занимает большой объем дискового пространства.
Математические символы подойдут для публикаций в социальных сетях, создания сообщений в чатах и форумах, разработки интернет-страниц.
Математика, как язык всех наук, не может обходиться без системы записи. Многочисленные понятия, и операторы обрели своё начертание по мере развития этой науки. Так как в стандартные алфавиты эти символы не входят, напечатать их с клавиатуры может оказаться проблематично. Отсюда можно скопировать и вставить.
Консорциуму Юникода не чужды проблемы учёных, поэтому в таблицу было включено множество различных знаков. Если тут нет того, что нужно, воспользуйтесь поиском по сайту или посмотрите в разделах математические символы, разнообразные математические символы-A, разнообразные математические символы-B, дополнительные математические операторы. Буквы для формул можно взять в наборе греческие буквы и блоке математические буквенно-цифровые символы.
Числа для степеней составляются из маленьких цифр. Там же собраны дроби.
Как выглядит в геометрии значок «скрещивается»?
Всемирно принятого значка для скрещивающихся прямых нет. Просто некоторые авторы учебников и справочников придумывают свои, для местного использования.
Источник
Знак подобия в геометрии – правило и примеры обозначения
В учебниках по геометрии часто встречаются задачи на подобие фигур. Какой знак используется для обозначения подобия фигур? Какие фигуры называются подобными? Поговорим обо всем этом в нашей статье.
Определение и знак подобия в геометрии
Подобными называются фигуры, если одна из них представляет уменьшенную копию другой.
На нижеприведенном рисунке подобные фигуры: круги, параллелограммы, пятиугольники и ромбы.
Для обозначения термина «подобие» в геометрии используют знак «тильда», который является типографским символом и обозначается волнистой чертой:
∆A 1 B 1 C 1
— треугольники ABC и A1B1C1
подобны.
Знак «двойная тильда» ставится около чисел для демонстрации примерности или приблизительности чего-либо:
1,35 ≈ 1,4 — числа 1,35 и 1,4 приблизительно равны.
Коэффициент подобия треугольников и знак подобия
Часто сверху знака подобия выставляют коэффициент подобия треугольников:
В математических задачах и уравнениях «тильду» используют для маркирования разных типов подобия. Часто применяется для обозначения подобия, эквивалентности.
В алгебре высказываний знаком
обозначают логическую операцию «эквиваленция».
При сочетании тильды и знака равенства получают обозначение отношения конгруэнтности, определения в геометрии, применяемого в контексте обозначения равенства различных фигур и тел (углов, отрезков):
Признаки подобия прямоугольных треугольников
Острые углы: наличие равного острого угла в прямоугольных треугольниках делает их подобными.
Два катета: общая пропорциональность катетам одного прямоугольного треугольника к катетам второго делает их подобными.
Катет и гипотенуза: пропорциональность катета и гипотенузы одного прямоугольного треугольника к катету и гипотенузе второго прямоугольного треугольника делает их подобными.
треугольник ∆ABC и треугольник ∆A1B1C1 считаются подобными при равнозначности углов и пропорциональности сторон;
отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Доказательство подобия треугольников через среднюю линию
Имеется треугольник ∆ABC, mn – средняя линия. M лежит на AB, N лежит на BC.
Требуется доказательство подобия треугольников ∆MBN и ∆ABC.
Посмотрев на ∆MBN и ∆ABC, видим, что угол В — общий, а отношение:
Отсюда делаем вывод, что ∆MBN
∆ABC по II признаку подобия треугольников, что и требовалось доказать.
Источник статьи: http://sprint-olympic.ru/uroki/geometrija/85548-znak-podobiia-v-geometrii-pravilo-i-primery-oboznacheniia.html
Подобные треугольники
Определение
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.
Коэффициентом подобия называют число k , равное отношению сходственных сторон подобных треугольников.
Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.
Признаки подобия треугольников
I признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
Свойства подобных треугольников
- Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
- Отношение периметров подобных треугольников равно коэффициенту подобия.
- Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.
Примеры наиболее часто встречающихся подобных треугольников
1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.
2. Треугольники и
, образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия –
3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.
Здесь вы найдете подборку задач по теме «Подобные треугольники» .
Источник статьи: http://egemaximum.ru/podobnye-treugolniki/
Как выглядит знак подобия в геометрии?
Как можно доказать, что Земля круглая, кроме как посмотреть на неё из космоса?
Разумному человеку очень просто доказать. Фанатику – невозможно. Итак, доказательство без экспериментов. В Северном полушарии не видно Южный крест. В южном полушарии не видно полярную звезду. Конец доказательства. И вообще даже без пересечения экватора, а просто при перемещении с севера на юг картина созвездий меняется. Одни начинают быть видны, а другие скрываются за горизонтом. На плоской же Земле картина созвездий должна быть одинаковой с любой точки наблюдения. А главное, у них(фанатиков) нет ответа, что находится под диском Земли. Они же гравитацию отрицают. А значит есть верх и низ. А значит, там должна быть некая основа. Но под ней должна быть другая основа. И так бесконечно. Это дурная бесконечность, которая в логике означает ошибочность предпосылок. Но фанатикам плевать на логику и на наблюдения. Это очень обиженные на жизнь люди, которые вокруг себя видят только заговоры: все вокруг заговорщики, одни они – честные и хорошие. Это же касается не только лунатиков и плоскоземельщиков, но и всех альтернативно одарённых хисториков: левашовцев, тартаровцев, фоменковцев, норманистов, укров, неоязычников, славяно-ариев – несть им числа.
Возможен ли не прямоугольный треугольник, в котором сумма квадратов двух сторон равна квадрату третьей стороны?
Я согласен с ответом от Uwe Boll, но постараюсь ответить более детально.
Вообще, если вам даны один угол и длина двух сторон, или два угла и длина одной стороны, или все три стороны, то они определяют остальные три элемента. Однако если вам даны три угла, то они определяют длину сторон с точностью до фактора.
В вашем вопросе, даны длины всех трех сторон с точностью до фактора:
fA, fB, и fC=f sqrt(A^2+B^2). Мы хотим понять почему никакой “гибкости” в этом треугольнике нет.
Обозначим углы напротив каждой из сторон соотвенственно a, b, c .
Мы используем закон косинусов на плоскости:
Косинус угла напротив “длинной” стороны (мы подозреваем, гипотенузы) определен
(фактор f сокращается). (Заметим, что два других угла тоже определены без всякой гибкости, но нам они не интересны.) Дальже идет алгебра – мы знаем длину C(A,B) и подставляем в правую сторону:
(A^2 + B^2 – C^2) / (2AB) = (A^2 + B^2 – sqrt(A^2+B^2)^2) / (2AB) = (A^2 + B^2 – (A^2+B^2)) / (2AB) = 0.
То есть косинус угла c = ноль. Значит это должен быть прямой угол.
Однако закон косинусов так не работает, если ваш треугольник не на плоскости, а, например, на сфере.
Как найти в треугольнике высоту?
Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на противоположную сторону (для тупого угла – на продолжение стороны треугольника).
В зависимости от входных данных, высоту треугольника можно найти разными способами.
- Если известны длины всех сторон
где h – длина высоты треугольника, p – полупериметр, a – длина стороны, на которую падает высота (основание), b и c – длины двух других сторон треугольника.
- Если известна длина одной из сторон треугольника и угол между этой стороной и основанием треугольника
- Если известна длина основания и площадь треугольника
- Если известны длины двух сторон треугольника и радиус описанной вокруг треугольника окружности
Почему кому-то легче даётся алгебра, а кому-то — геометрия?
Вообще если вы будете учиться высшей математике в институте, то вскоре поймёте, что разница между алгеброй и геометрией весьма и весьма условна. Один из самых красивых, абстрактных и продвинутых разделов математики так кстати и называется: алгебраическая геометрия.
Была ещё и геометрическая алгебра. То есть, её так никто из современников не звал, но в целом поздняя математика пифагорейской школы являлась именно чем-то таким – решение уравнений, вытекающих из длин, площадей и объёмов. Именно потому, что греки слишком сильно привязались к наглядной науке, они так и не додумались до уравнений выше третьей степени.
Если смотреть в корень, алгебра и геометрия в целом восходят к двум разным сферам деятельности.
Геометрия по-гречески означает “землемерие” и служила, понятное дело, вполне наглядным и практичным целям – производству нямки. В дальнейшем она нашла своё применение и в архитектуре, и в искусстве. Ну, и померять линейкой или ещё чем-нибудь те вещи довольно легко. Хотя здесь постоянно возникали квадратные-кубические уравнения – и у вас в школьной программе по геометрии они тоже скоро возникнут.
Здесь, кстати, следует сказать, что во многом ограниченность греческой математики – это вина Платона, который несмотря на знаменитую фразу “Не знающий геометрии на да не войдёт [в Академию]”, с самой геометрией не очень-то дружил. Он был больше мистик, считал, что “правильные” приборы – это только циркуль и линейка, и навязал эту точку зрения своим ученикам. Хотя на тот момент греческие учёные уже могли чертить эллипсы, и развивали основы математического анализа. К несчастью, Академию основал именно Платон, а не Архимед, своим авторитетом на два тысячелетия стреножив европейскую науку.
Алгебра, в свою очередь, в первую очередь пошла из области тоже наглядной, но в которой линейкой особо не померяшь, а именно – из астрономии. Как и землемерие, дисциплина эта тоже была тесно связана с производством нямки, а именно – с сотавлением календаря. Ну, и, конечно, астрономия вплоть до Раннего Нового Времени оставалась неотделимой от астрологии, считавшейся (а подавляющим большинством людей и сейчас, к несчастью, считающейся) вещью не менее практичной – будущее всем знать хочется. И вот там-то и требовались сложные уравнения чтобы вычислить, в каком созвездии когда какая будет планета. Появлялись, конечно, и другие применения – посчитать, например, сколько наплодится кроликов (числа Фибоначчи), сколько зерна оставить на посев, сколько набежит процентов по долгам, сколько рисинок положить на шахматную доску и всякое такое.
Так или иначе, геометрия была больше связана с пространством, а алгебра – со временем. Так уж получилось, что геометрия лучше давалась людям на западе, а алгебра – на востоке. Недаром первое из этих слов греческое, а второе – арабское.
Всё начало меняться, когда молодой французский офицер Рене Декарт, будучи на службе у императора Священной Римской Империи, воевал в во время Тридцатилетней Войны в современной Чехии. Как-то раз, лёжа на кровати, он смотрел на солнечные зайчики на стене комнаты, и вдруг понял, что может охарактеризовать положение каждого из них двумя числами: расстоянием от угла комнаты и высотой от пола. То есть точки – в некотором смысле ещё и числа или их последовательности. А последовательности чисел уже можно складывать друг с другом, умножать на число. и вообще много чего интересного с ними делать. Таким образом точка, фундаментальный объект геометрии, долгое время остававшийся вещью в себе, стала обретать алгебраический смысл, и постепенно геометрия и алгебра стали сближаться, обогащая друг друга и давая начало современной математике. Именно алгебраическими методами, в частности, была доказана невозможность решения доставшихся нам по вине всё того же Платона классических проблем геометрии, над которыми люди бились два тысячелетия: квадратуры круга, трисекции угла и удвоения объёма.
В настоящее время разделить алгебру и геометрию можно разве только в школьной программе. Так же, как пространство и время с появлением теории относительности перестали быть чем-то раздельным, превратившись в пространство-время, алгебра и геометрия срослись так, что уже и непонятно, где из них что. Та же точка может означать функцию – только это будет точка уже не в двумерном пространстве стены, на которую смотрел Рене Декарт, а в бесконечномерном пространсвте функций. Уже упомянутая алгебраическая геометрия вообще выворачивает всё наизнанку, задавая точку, грубо говоря, множеством всех функций, обращающихся в этой точке в нуль. А в некоммутативной геометрии – ещё одном разделе современной математики – несмотря на название, вообще точек нет, только алгебры, хотя есть, к примеру, понятие объёма.
Лично мне в школе лучше давалась геометрия. Сейчас я занимаюсь функциональным анализом, но, несмотря на то, что в нашей дисциплине постоянно приходится работать с бесконечномерными пространствами, которые нарисовать нельзя, порой удобно бывает предствить их в виде чего-то геометрического – это порой даёт дать хорошее интуитивное представление о каком-нибудь явлении, а его потом уже можно выразить в строгих формулах.
Источник статьи: http://yandex.ru/q/question/hw.math/kak_vygliadit_znak_podobiia_v_geometrii_81501bed/