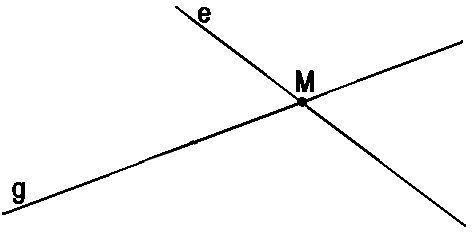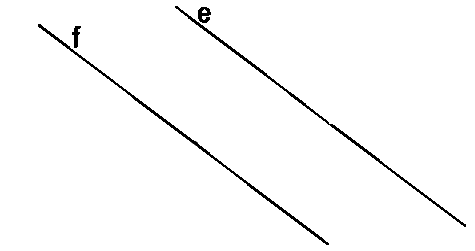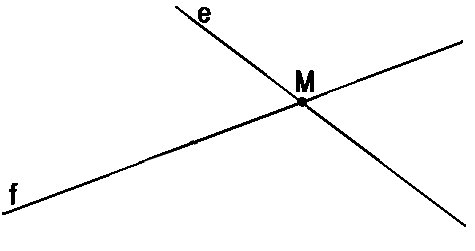Содержание:
- 1 Определение
- 2 Как пишется этот символ пересечения?
- 3 Как быстро запомнить этот знак?
- 4 Как применяется знак ⋂?
- 5 Как выглядит знак «не пересечения» в геометрии?
- 5.1 Пример
- 6 Что обозначает знак пересечения наоборот?
Определение
Знак пересечения – это символ, указывающий на пересечение прямых, углов, лучей, отрезков, плоскостей и других фигур в геометрии, пересечение множеств в математике (алгебре) и информатике.
Как пишется этот символ пересечения?
Этот знак выглядит и пишется так – ⋂
Его достаточно легко запомнить, он похож на русскую букву «П», начальную букву слова «пересечение».
Как быстро запомнить этот знак?
Просто представьте себе и запомните, что этот символ выглядит как буква «П» и похож на подкову, перевернутую вниз ногами.
Как применяется знак ⋂?
Применяется для обозначения пересечения прямых, углов, лучей, отрезков в геометрии, пересечение множеств в математике (алгебре) и информатике.
Как выглядит знак «не пересечения» в геометрии?
Пример
А ∩ С = ∅ — 2 луча или (2 прямые, 2отрезка) А и С не пересекаются.
Что обозначает знак пересечения наоборот?
Это символ выглядит и пишется следующим образом: ∪
Обозначается термином – «объединение».
Ниже представлена таблица с основными математическими символами и знаками, которые используются в геометрии с 7 класса и старше.
| Знак | Название | Значение/описание | Пример |
| ∠ | угол | фигура, состоящая из двух лучей и вершины | ∠ABC = 30° |
| острый угол | угол от 0 до 90 градусов | ∠AOB = 60° | |
| прямой угол | угол, равный 90 граусам | ∠AOB = 90° | |
| тупой угол | угол от 90 до 180 градусов | ∠AOB = 120° | |
 |
развернутый угол | угол, равный 180 градусам | ∠AOB = 180° |
| ° (или deg) |
градус | единица измерения угла, равна 1/360 окружности | 45° |
| ′ | минута | единица измерения угла, 1° = 60′ | α = 70°59′ |
| ″ | секунда | единица измерения угла, 1′ = 60″ | α = 70°59′59″ |
| линия | бесконечная прямая без начала и конца | ||
| отрезок | участок на прямой между точками A и B | ||
| луч | бесконечная прямая, имеющая начало в точке A, но не имеющая конца | ||
| дуга | дуга, образованная между точками A и B | ||
| ⊥ | перпендикулярность | линии (прямые), расположенные под углом 90° по отношению друг к другу | AC ⊥ BC |
| || | параллельность | непересекающиеся прямые (линии) | AB || CD |
| ∩ | пересечение | множество одинаковых элементов, принадлежащих как множеству A, так и B | A ∩ B |
| ∈ / ∉ | принадлежность/ непринадлежность |
элемент является/не является элементом заданного множества | a ∈ S |
| ≅ | конгуэнтность | эквивалентность геометрических форм и размеров | ∆ABC ≅ ∆XYZ |
| ~ | подобие | та же форма, но разные размеры | ∆ABC ~ ∆XYZ |
| Δ | треугольник | фигура треугольника | ΔABC ≅ ΔBCD |
| |x-y| | дистанция | дистанция между точками X и Y | | x-y | = 5 |
| π | константа «Пи» | отношение длины окружности к диаметру круга, π = C/d | π = 3.141592654… |
| рад (rad) или c |
радиан | единица измерения угла | 360° = 2π c |
microexcel.ru
Пересечение в математике
Знак пересечения
Знак пересечения – это символ, указывающий на пересечение прямых, углов, лучей, отрезков, плоскостей и других фигур в геометрии, пересечение множеств в математике (алгебре) и информатике.
Как пишется этот символ пересечения?
Этот знак выглядит и пишется так – ⋂
Его достаточно легко запомнить, он похож на русскую букву «П», начальную букву слова «пересечение».
Как быстро запомнить этот знак?
Просто представьте себе и запомните, что этот символ выглядит как буква «П» и похож на подкову, перевернутую вниз ногами.
Как применяется знак ⋂?
Применяется для обозначения пересечения прямых, углов, лучей, отрезков в геометрии, пересечение множеств в математике (алгебре) и информатике.
Этот знак выглядит и пишется так – ⋂
Как применяется знак.
Sunhi. ru
05.07.2020 0:11:14
2020-07-05 00:11:14
Источники:
Https://sunhi. ru/znak-peresecheniya/
Урок Пересечение и объединение множеств » /> » /> .keyword { color: red; } Пересечение в математике
Урок Пересечение и объединение множеств
Урок «Пересечение и объединение множеств»
«Множество есть многое, мыслимое нами как единое» (основатель теории множеств – Георг Кантор). КАНТОР (Cantor) Георг (1845—1918) — немецкий математик, логик, теолог, создатель теории трансфинитных (бесконечных) множеств, оказавшей определяющее влияние на развитие математических наук на рубеже 19— 20 вв.
Множество — одно из основных понятий современной математики, используемое почти во всех её разделах.
К сожалению, основному понятию теории – понятию множества – нельзя дать строгого определения. Разумеется, можно сказать, что множество – это «совокупность», «собрание», «ансамбль», «коллекция», «семейство», «система», «класс» и т. д. однако всё это было бы не математическим определением, а скорее злоупотреблением словарным богатством русского языка.
Для того чтобы определить какое – либо понятие, нужно, прежде всего, указать, частным случаем какого более общего понятия, оно является, для понятия множества сделать это невозможно, потому что более общего понятия, чем множество, в математике нет.
Часто приходится говорить о нескольких вещах, объединенных некоторым признаком. Так, можно говорить о множестве всех стульев в комнате, о множестве всех клеток человеческого тела, о множестве всех картофелин в данном мешке, о множестве всех рыб в океане, о множестве всех квадратов на плоскости, о множестве всех точек на данной окружности т. д.
Предметы, составляющие данное множество, называются его элементами.
Например, множество дней недели состоит из элементов: понедельник, вторник, среда, четверг, пятница, суббота, воскресенье.
Множество месяцев – из элементов: январь, февраль, март, апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь, декабрь.
Множество арифметических действий — из элементов: сложение, вычитание, умножение, деление.
Например, если А означает множество всех натуральных чисел, то 6 принадлежит к А, а 3 не принадлежит к А.
Если А — множество всех месяцев в году, то май принадлежит к А, а среда не принадлежит к А.
Если множество содержит конечное число элементов, то его называют конечным, а если в нем бесконечно много элементов, то бесконечным. Так множество деревьев в лесу конечно, а множество точек на окружности бесконечно.
Парадокс в логике — это противоречие, имеющее статус логически корректного вывода и, вместе с тем, представляющее собой рассуждение, приводящее к взаимно исключающим заключениям.
Как уже упоминалось, понятие множества лежит в основе математики. Используя простейшие множества и различные математические конструкции, можно построить практически любой математический объект. Идею построения всей математики на основе теории множеств активно пропагандировал Г. Кантор. Однако, при всей своей простоте, понятие множества таит в себе опасность появления противоречий или, как ещё говорят, парадоксов. Появление парадоксов связано с тем, что далеко не всякие конструкции и не всякие множества можно рассматривать.
Самый простой из парадоксов — это «Парадокс брадобрея«.
Одному солдату было приказано брить тех и только тех солдат его взвода, которые сами себя не бреют. Неисполнение приказа в армии, как известно, тягчайшее преступление. Однако возник вопрос, брить ли этому солдату самого себя. Если он побреется, то его следует отнести к множеству солдат, которые сами себя бреют, а таких брить он не имеет права. Если же он себя брить не будет, то попадёт во множество солдат, которые сами себя не бреют, а таких солдат согласно приказу он обязан брить. Парадокс.
Над множествами, как и над многими другими математическими объектами, можно совершать различные операции, которые иногда называют теоретико-множественными операциями или сет-операциями. В результате операций из исходных множеств получаются новые. Множества обозначаются заглавными латинскими буквами, а их элементы – строчными. Запись a R означает, что элемент а принадлежит множеству R, то есть а является элементом множества R. В противном случае, когда а не принадлежит множеству R, пишут a R.
Два множества А и В называются Равными ( А = В ), если они состоят из одних и тех же элементов, то есть каждый элемент множества А является элементом множества В и наоборот, каждый элемент множества В является элементом множества А.
Сравнение множеств.
Множество A содержится во множестве B (множество B включает множество A), если каждый элемент A есть элемент В:
Говорят, что множество А содержится в множестве В или множество Аявляется подмножеством множества В ( в этом случае пишут А В ), если каждый элемент множества А одновременно является элементом множества В. Эта зависимость между множествами называется Включением. Для любого множества А имеют место включения: ØА и А А
В этом случае A называется Подмножеством B, B — Надмножеством A. Если, то A называется Собственным подмножеством В. Заметим, что,
Два множества называются Равными, если они являются подмножествами друг друга
Операции над множествами
Пересечение.
Объединение.
Свойства.
1.Операция объединения множеств коммутативна
2.Операция объединения множеств транзитивна
3. Пустое множество X является нейтральным элементом операции объединения множеств
2. А=, В = . Найдём объединение и пересечение этих множеств:
3. Множество детей является подмножеством всего населения
4. Пересечением множества целых чисел с множеством положительных чисел является множество натуральных чисел.
5. Объединением множества рациональных чисел с множеством иррациональных чисел является множество положительных чисел.
6.Нуль является дополнением множества натуральных чисел относительно множества неотрицательных целых чисел.
Диаграммы Венна (Venn diagrams) — общее название целого ряда методов визуализации и способов графической иллюстрации, широко используемых в различных областях науки и математики: теория множеств, собственно «диаграмма Венна» показывает все возможные отношения между множествами или событиями из некоторого семейства; разновидностями диаграмм Венна служат: диаграммы Эйлера,
Диаграмма Венна четырёх множеств.
Собственно «диаграмма Венна» показывает все возможные отношения между множествами или событиями из некоторого семейства. Обычная диаграмма Венна имеет три множества. Сам Венн пытался найти изящный способ с симметричными фигурами, представляющий на диаграмме большее число множеств, но он смог это сделать только для четырех множеств (см. рисунок справа), используя эллипсы.
Диаграммы Эйлера
Диаграммы Эйлера аналогичны диаграммам Венна. Диаграммы Эйлера можно использовать, для того, чтобы оценивать правдоподобность теоретико-множественных тождеств.
Задача 1. В классе 30 человек, каждый из которых поёт или танцует. Известно, что поют 17 человек, а танцевать умеют 19 человек. Сколько человек поёт и танцует одновременно?
Решение: Сначала заметим, что из 30 человек не умеют петь 30 — 17 = 13 человек.

Все они умеют танцевать, т. к. по условию каждый ученик класса поёт или танцует. Всего умеют танцевать 19 человек, из них 13 не умеют петь, значит, танцевать и петь одновременно умеют 19-13 = 6 человек.
Диаграмма Венна четырёх множеств.
Например, множество дней недели состоит из элементов понедельник, вторник, среда, четверг, пятница, суббота, воскресенье.
Urok.1sept. ru
09.07.2019 7:37:06
2020-12-07 17:08:34
Источники:
Https://urok.1sept. ru/articles/550092
Дополнение (теория множеств) | Математика | Fandom » /> » /> .keyword { color: red; } Пересечение в математике
Дополнение (теория множеств)
Дополнение (теория множеств)
Дополне́ние в теории множеств — это семейство элементов, не принадлежащих данному множеству.
Содержание
Разность множеств
Определение
Разность множества A и множества B — множество, содержащее в себе элементы множества А, но не B.
Пусть даны два множества » width=»» height=»» /> и » width=»» height=»» />. Тогда их (теоретико-множественная) разность определяется следующим образом:
.>» width=»» height=»» />
Примеры
Свойства
Пусть » width=»» height=»» /> — произвольные множества. Тогда
Компьютерные реализации
Дополнение множества
Определение
Если из контекста следует, что все рассматриваемые множества являются подмножествами некоторого фиксированного универсального множества » width=»» height=»» />, то определяется операция дополнения:
=Xsetminus Aequiv .>» width=»» height=»» />
Свойства
См. также
Эта статья содержит материал из статьи Дополнение (теория множеств) русской Википедии.
=Xsetminus Aequiv .>» width=»» height=»» />
Дополнение (теория множеств)
Дополне́ние в теории множеств — это семейство элементов, не принадлежащих данному множеству.
Разность множества A и множества B — множество, содержащее в себе элементы множества А, но не B.
Пусть даны два множества » width=»» height=»» /> и » width=»» height=»» />. Тогда их (теоретико-множественная) разность определяется следующим образом:
.>» width=»» height=»» />
Пусть » width=»» height=»» /> — произвольные множества. Тогда
Width height.
Math. fandom. com
18.09.2020 11:31:39
2020-09-18 11:31:39
Источники:
Https://math. fandom. com/ru/wiki/%D0%94%D0%BE%D0%BF%D0%BE%D0%BB%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5_(%D1%82%D0%B5%D0%BE%D1%80%D0%B8%D1%8F_%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D1%81%D1%82%D0%B2)
From Wikipedia, the free encyclopedia
The red dot represents the point at which the two lines intersect.
In geometry, an intersection is a point, line, or curve common to two or more objects (such as lines, curves, planes, and surfaces). The simplest case in Euclidean geometry is the line–line intersection between two distinct lines, which either is one point or does not exist (if the lines are parallel). Other types of geometric intersection include:
- Line–plane intersection
- Line–sphere intersection
- Intersection of a polyhedron with a line
- Line segment intersection
- Intersection curve
Determination of the intersection of flats – linear geometric objects embedded in a higher-dimensional space – is a simple task of linear algebra, namely the solution of a system of linear equations. In general the determination of an intersection leads to non-linear equations, which can be solved numerically, for example using Newton iteration. Intersection problems between a line and a conic section (circle, ellipse, parabola, etc.) or a quadric (sphere, cylinder, hyperboloid, etc.) lead to quadratic equations that can be easily solved. Intersections between quadrics lead to quartic equations that can be solved algebraically.
On a plane[edit]
Two lines[edit]
For the determination of the intersection point of two non-parallel lines

one gets, from Cramer’s rule or by substituting out a variable, the coordinates of the intersection point 
(If 
Two line segments[edit]
Intersection of two line segments
For two non-parallel line segments 


The line segments intersect only in a common point 


The parameters 
It can be solved for s and t using Cramer’s rule (see above). If the condition 



Example: For the line segments 

and 

Remark: Considering lines, instead of segments, determined by pairs of points, each condition 
A line and a circle[edit]
For the intersection of
one solves the line equation for x or y and substitutes it into the equation of the circle and gets for the solution (using the formula of a quadratic equation) 
if 
If 
If the circle’s midpoint is not the origin, see.[1] The intersection of a line and a parabola or hyperbola may be treated analogously.
Two circles[edit]
The determination of the intersection points of two circles
can be reduced to the previous case of intersecting a line and a circle. By subtraction of the two given equations one gets the line equation:
This special line is the radical line of the two circles.
Intersection of two circles with centers on the x-axis, their radical line is dark red
Special case 
In this case the origin is the center of the first circle and the second center lies on the x-axis (s. diagram). The equation of the radical line simplifies to 

In case of 
In case of 
Any general case as written above can be transformed by a shift and a rotation into the special case.
The intersection of two disks (the interiors of the two circles) forms a shape called a lens.
circle–ellipse intersection
Two conic sections[edit]
The problem of intersection of an ellipse/hyperbola/parabola with another conic section leads to a system of quadratic equations, which can be solved in special cases easily by elimination of one coordinate. Special properties of conic sections may be used to obtain a solution. In general the intersection points can be determined by solving the equation by a Newton iteration. If a) both conics are given implicitly (by an equation) a 2-dimensional Newton iteration b) one implicitly and the other parametrically given a 1-dimensional Newton iteration is necessary. See next section.
Two smooth curves[edit]
A transversal intersection of two curves
touching intersection (left), touching (right)
Two curves in 
have an intersection point, if they have a point of the plane in common and have at this point
- a: different tangent lines (transversal intersection), or
- b: the tangent line in common and they are crossing each other (touching intersection, see diagram).
If both the curves have a point S and the tangent line there in common but do not cross each other, they are just touching at point S.
Because touching intersections appear rarely and are difficult to deal with, the following considerations omit this case. In any case below all necessary differential conditions are presupposed. The determination of intersection points always leads to one or two non-linear equations which can be solved by Newton iteration. A list of the appearing cases follows:
intersection of a parametric curve and an implicit curve
intersection of two implicit curves
- If both curves are explicitly given:
, equating them yields the equation
- If both curves are parametrically given:
- Equating them yields two equations in two variables:
- If one curve is parametrically and the other implicitly given:
- This is the simplest case besides the explicit case. One has to insert the parametric representation of
into the equation
of curve
and one gets the equation:
- If both curves are implicitly given:
- Here, an intersection point is a solution of the system
Any Newton iteration needs convenient starting values, which can be derived by a visualization of both the curves. A parametrically or explicitly given curve can easily be visualized, because to any parameter t or x respectively it is easy to calculate the corresponding point. For implicitly given curves this task is not as easy. In this case one has to determine a curve point with help of starting values and an iteration. See
.[2]
Examples:
- 1:
and circle
(see diagram).
- The Newton iteration
for function
has to be done. As start values one can choose −1 and 1.5.
- The intersection points are: (−1.1073, −1.3578), (1.6011, 4.1046)
- The Newton iteration
- 2:
(see diagram).
- The Newton iteration
has to be performed, where
is the solution of the linear system
at point
. As starting values one can choose(−0.5, 1) and (1, −0.5).
- The linear system can be solved by Cramer’s rule.
- The intersection points are (−0.3686, 0.9953) and (0.9953, −0.3686).
Two polygons[edit]
intersection of two polygons: window test
If one wants to determine the intersection points of two polygons, one can check the intersection of any pair of line segments of the polygons (see above). For polygons with many segments this method is rather time-consuming. In practice one accelerates the intersection algorithm by using window tests. In this case one divides the polygons into small sub-polygons and determines the smallest window (rectangle with sides parallel to the coordinate axes) for any sub-polygon. Before starting the time-consuming determination of the intersection point of two line segments any pair of windows is tested for common points. See.[3]
In space (three dimensions)[edit]
In 3-dimensional space there are intersection points (common points) between curves and surfaces. In the following sections we consider transversal intersection only.
A line and a plane[edit]
The intersection of a line and a plane in general position in three dimensions is a point.
Commonly a line in space is represented parametrically 

for parameter 

If the linear equation has no solution, the line either lies on the plane or is parallel to it.
Three planes[edit]
If a line is defined by two intersecting planes 

Three planes 

For the proof one should establish 
A curve and a surface[edit]
intersection of curve 
Analogously to the plane case the following cases lead to non-linear systems, which can be solved using a 1- or 3-dimensional Newton iteration.[4]
- parametric curve
and
- parametric surface
- parametric curve
and
- implicit surface
Example:
- parametric curve
and
- implicit surface
(s. picture).
- The intersection points are: (−0.8587, 0.7374, −0.6332), (0.8587, 0.7374, 0.6332).
A line–sphere intersection is a simple special case.
Like the case of a line and a plane, the intersection of a curve and a surface in general position consists of discrete points, but a curve may be partly or totally contained in a surface.
A line and a polyhedron[edit]
Two surfaces[edit]
Two transversally intersecting surfaces give an intersection curve. The most simple case is the intersection line of two non-parallel planes.
See also[edit]
- Analytic geometry#Intersections
- Computational geometry
- Equation of a line
- Intersection (set theory)
- Intersection theory
References[edit]
- ^ Erich Hartmann: Geometry and Algorithms for COMPUTER AIDED DESIGN. Lecture notes, Technische Universität Darmstadt, October 2003, p. 17
- ^ Erich Hartmann: Geometry and Algorithms for COMPUTER AIDED DESIGN. Lecture notes, Technische Universität Darmstadt, October 2003, p. 33
- ^ Erich Hartmann: CDKG: Computerunterstützte Darstellende und Konstruktive Geometrie. Lecture notes, TU Darmstadt, 1997, p. 79 (PDF; 3,4 MB)
- ^ Erich Hartmann: Geometry and Algorithms for COMPUTER AIDED DESIGN. Lecture notes, Technische Universität Darmstadt, October 2003, p. 93
Further reading[edit]
- Nicholas M. Patrikalakis and Takashi Maekawa, Shape Interrogation for Computer Aided Design and Manufacturing, Springer, 2002, ISBN 3540424547, 9783540424543, pp. 408. [1]
From Wikipedia, the free encyclopedia
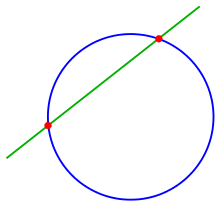
The red dot represents the point at which the two lines intersect.
In geometry, an intersection is a point, line, or curve common to two or more objects (such as lines, curves, planes, and surfaces). The simplest case in Euclidean geometry is the line–line intersection between two distinct lines, which either is one point or does not exist (if the lines are parallel). Other types of geometric intersection include:
- Line–plane intersection
- Line–sphere intersection
- Intersection of a polyhedron with a line
- Line segment intersection
- Intersection curve
Determination of the intersection of flats – linear geometric objects embedded in a higher-dimensional space – is a simple task of linear algebra, namely the solution of a system of linear equations. In general the determination of an intersection leads to non-linear equations, which can be solved numerically, for example using Newton iteration. Intersection problems between a line and a conic section (circle, ellipse, parabola, etc.) or a quadric (sphere, cylinder, hyperboloid, etc.) lead to quadratic equations that can be easily solved. Intersections between quadrics lead to quartic equations that can be solved algebraically.
On a plane[edit]
Two lines[edit]
For the determination of the intersection point of two non-parallel lines

one gets, from Cramer’s rule or by substituting out a variable, the coordinates of the intersection point 
(If 
Two line segments[edit]
Intersection of two line segments
For two non-parallel line segments 


The line segments intersect only in a common point 


The parameters 
It can be solved for s and t using Cramer’s rule (see above). If the condition 



Example: For the line segments 

and 

Remark: Considering lines, instead of segments, determined by pairs of points, each condition 
A line and a circle[edit]
For the intersection of
one solves the line equation for x or y and substitutes it into the equation of the circle and gets for the solution (using the formula of a quadratic equation) 
if 
If 
If the circle’s midpoint is not the origin, see.[1] The intersection of a line and a parabola or hyperbola may be treated analogously.
Two circles[edit]
The determination of the intersection points of two circles
can be reduced to the previous case of intersecting a line and a circle. By subtraction of the two given equations one gets the line equation:
This special line is the radical line of the two circles.
Intersection of two circles with centers on the x-axis, their radical line is dark red
Special case 
In this case the origin is the center of the first circle and the second center lies on the x-axis (s. diagram). The equation of the radical line simplifies to 

In case of 
In case of 
Any general case as written above can be transformed by a shift and a rotation into the special case.
The intersection of two disks (the interiors of the two circles) forms a shape called a lens.
circle–ellipse intersection
Two conic sections[edit]
The problem of intersection of an ellipse/hyperbola/parabola with another conic section leads to a system of quadratic equations, which can be solved in special cases easily by elimination of one coordinate. Special properties of conic sections may be used to obtain a solution. In general the intersection points can be determined by solving the equation by a Newton iteration. If a) both conics are given implicitly (by an equation) a 2-dimensional Newton iteration b) one implicitly and the other parametrically given a 1-dimensional Newton iteration is necessary. See next section.
Two smooth curves[edit]
A transversal intersection of two curves
touching intersection (left), touching (right)
Two curves in 
have an intersection point, if they have a point of the plane in common and have at this point
- a: different tangent lines (transversal intersection), or
- b: the tangent line in common and they are crossing each other (touching intersection, see diagram).
If both the curves have a point S and the tangent line there in common but do not cross each other, they are just touching at point S.
Because touching intersections appear rarely and are difficult to deal with, the following considerations omit this case. In any case below all necessary differential conditions are presupposed. The determination of intersection points always leads to one or two non-linear equations which can be solved by Newton iteration. A list of the appearing cases follows:
intersection of a parametric curve and an implicit curve
intersection of two implicit curves
- If both curves are explicitly given:
, equating them yields the equation
- If both curves are parametrically given:
- Equating them yields two equations in two variables:
- If one curve is parametrically and the other implicitly given:
- This is the simplest case besides the explicit case. One has to insert the parametric representation of
into the equation
of curve
and one gets the equation:
- If both curves are implicitly given:
- Here, an intersection point is a solution of the system
Any Newton iteration needs convenient starting values, which can be derived by a visualization of both the curves. A parametrically or explicitly given curve can easily be visualized, because to any parameter t or x respectively it is easy to calculate the corresponding point. For implicitly given curves this task is not as easy. In this case one has to determine a curve point with help of starting values and an iteration. See
.[2]
Examples:
- 1:
and circle
(see diagram).
- The Newton iteration
for function
has to be done. As start values one can choose −1 and 1.5.
- The intersection points are: (−1.1073, −1.3578), (1.6011, 4.1046)
- The Newton iteration
- 2:
(see diagram).
- The Newton iteration
has to be performed, where
is the solution of the linear system
at point
. As starting values one can choose(−0.5, 1) and (1, −0.5).
- The linear system can be solved by Cramer’s rule.
- The intersection points are (−0.3686, 0.9953) and (0.9953, −0.3686).
Two polygons[edit]
intersection of two polygons: window test
If one wants to determine the intersection points of two polygons, one can check the intersection of any pair of line segments of the polygons (see above). For polygons with many segments this method is rather time-consuming. In practice one accelerates the intersection algorithm by using window tests. In this case one divides the polygons into small sub-polygons and determines the smallest window (rectangle with sides parallel to the coordinate axes) for any sub-polygon. Before starting the time-consuming determination of the intersection point of two line segments any pair of windows is tested for common points. See.[3]
In space (three dimensions)[edit]
In 3-dimensional space there are intersection points (common points) between curves and surfaces. In the following sections we consider transversal intersection only.
A line and a plane[edit]
The intersection of a line and a plane in general position in three dimensions is a point.
Commonly a line in space is represented parametrically 

for parameter 

If the linear equation has no solution, the line either lies on the plane or is parallel to it.
Three planes[edit]
If a line is defined by two intersecting planes 

Three planes 

For the proof one should establish 
A curve and a surface[edit]
intersection of curve 
Analogously to the plane case the following cases lead to non-linear systems, which can be solved using a 1- or 3-dimensional Newton iteration.[4]
- parametric curve
and
- parametric surface
- parametric curve
and
- implicit surface
Example:
- parametric curve
and
- implicit surface
(s. picture).
- The intersection points are: (−0.8587, 0.7374, −0.6332), (0.8587, 0.7374, 0.6332).
A line–sphere intersection is a simple special case.
Like the case of a line and a plane, the intersection of a curve and a surface in general position consists of discrete points, but a curve may be partly or totally contained in a surface.
A line and a polyhedron[edit]
Two surfaces[edit]
Two transversally intersecting surfaces give an intersection curve. The most simple case is the intersection line of two non-parallel planes.
See also[edit]
- Analytic geometry#Intersections
- Computational geometry
- Equation of a line
- Intersection (set theory)
- Intersection theory
References[edit]
- ^ Erich Hartmann: Geometry and Algorithms for COMPUTER AIDED DESIGN. Lecture notes, Technische Universität Darmstadt, October 2003, p. 17
- ^ Erich Hartmann: Geometry and Algorithms for COMPUTER AIDED DESIGN. Lecture notes, Technische Universität Darmstadt, October 2003, p. 33
- ^ Erich Hartmann: CDKG: Computerunterstützte Darstellende und Konstruktive Geometrie. Lecture notes, TU Darmstadt, 1997, p. 79 (PDF; 3,4 MB)
- ^ Erich Hartmann: Geometry and Algorithms for COMPUTER AIDED DESIGN. Lecture notes, Technische Universität Darmstadt, October 2003, p. 93
Further reading[edit]
- Nicholas M. Patrikalakis and Takashi Maekawa, Shape Interrogation for Computer Aided Design and Manufacturing, Springer, 2002, ISBN 3540424547, 9783540424543, pp. 408. [1]
Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне
просто дать определения. Но на практике оказалось, что это не так.
Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так
и не пришли к единому определению.
Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом
их описывают.
Запомните!
Точка — элементарная фигура, не
имеющая частей.
Прямая состоит из множества
точек и простирается бесконечно
в обе стороны.
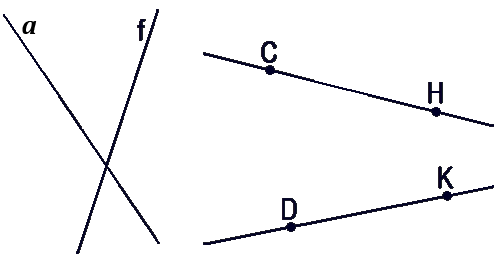
На рисунке изображена прямая a и точки D, F, G и
H. Точки F и G
лежат на прямой a.
Точки D и H
не
лежат на прямой a.
В тексте точку обозначают символом «(·)».
Принадлежность и непринадлежность точки
прямой обозначают символами «∈» и «∉». Знак принадлежности можно запомнить как
зеркальное отображение буквы «Э» или как знак евро «€» .
То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:
- (·)F ∈ a — точка F принадлежит прямой a (другими словами, точка F лежит на прямой a);
- (·)G ∈ a — точка G принадлежит прямой a;
- (·)D ∉ a — точка D не принадлежит прямой a (другими словами, точка D не лежит на прямой a);
- (·)H ∉ a — точка H не принадлежит прямой a.
Как обозначить прямую
Прямую обычно обозначают одной
маленькой латинской буквой.
Прямую, на которой отмечены
две точки, иногда обозначают
по названиям этих точек большими латинскими точками.
- На рисунке изображены:
- Прямая a
- Прямая f
- Прямая CH
- Прямая DK
Точки D, E и F — лежат на одной прямой, поэтому:
прямая DE,
прямая EF и
прямая DF —
это три разных имени одной и той же прямой.
Разбор примера
Проведите прямую, обозначьте её буквой a и
отметьте точки A и B, лежащие на этой прямой, и
точки P, Q и R, не лежащие на ней. Опишите
взаимное расположение точек A, B, P, Q, R и
прямой a, используя символы ∈ и ∉.
Решение задачи
Проведём прямую.
Обозначим её буквой a.
Отметим точки (·)A и (·)B, лежащие на прямой a.
Отметим точки (·)P, (·)Q и (·)R, не лежащие на прямой a.
Опишем взаимное расположение точек и прямой.
- (·)A ∈ a
- (·)B ∈ a
- (·)P ∉ a
- (·)Q ∉ a
- (·)R ∉ a
Задача решена.
Как обозначается пересечение прямых
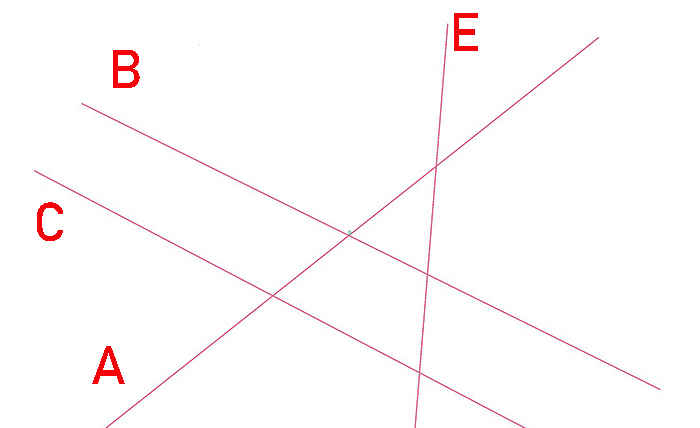
На рисунке прямые a и b
не пересекаются.
Прямые b и
c пересекаются.
Хотя на чертеже не видно, но прямые a и
c тоже пересекаются (это становится ясно, если мысленно
продолжить вниз прямые a и с).
В тексте пересечение прямых обозначают
символом ∩. Информацию на рисунке выше можно записать следующим образом:
- b ∩ c — прямые b и с пересекаются;
- a ∩ c — прямые a и с пересекаются.
Прямые e и g имеют общую точку M.
Другими словами, прямые пересекаются в точке M. Геометрическими обозначениями
пересечение прямых в точке записывается так:
e ∩ g = (·)M
Прямые e и f не имеют общей точки — т.е. они не
пересекаются.
Взаимное расположение прямой и точек
Запомните!
Через любые две точки можно
провести прямую, и притом
только одну.
Через одну точку (·)A можно провести
сколько угодно прямых.
Через две точки
(·)A и (·)B можно провести
только одну прямую.
Сколько общих точек имеют две прямые
Запомните!
Две прямые либо имеют только
одну общую точку, либо не имеют
общих точек.
Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.
Первый случай расположения прямых
На рисунке выше мы видим, что у прямых f и e
нет общих точек, т.к. эти
прямые не пересекаются.
Второй случай расположения прямых
Возможен вариант, что прямые f и e
пересекаются и, значит, имеют одну общую точку (·)M.
Третий случай расположения прямых
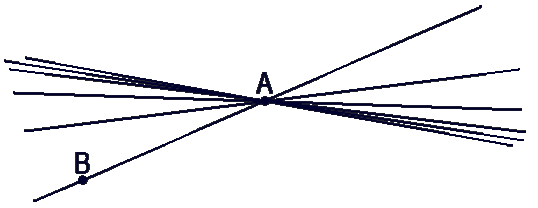
Предположим, что прямые
f и e имеют две или больше общих точек.
Например, точки (·)A и (·)B.
Но мы знаем, что через две
точки можно провести только одну прямую. Значит,
прямые f и e совпадают и наше предположение, что
у двух прямых может быть две или более общих точек неверно.
Вывод: две прямые либо имеют только
одну общую точку, либо не имеют
общих точек.
Разбор примера
Проведите три прямые так, чтобы каждые две из
них пересекались. Обозначьте все точки
пересечения этих прямых. Сколько получилось
точек? Рассмотрите все возможные случаи.
Решение задачи
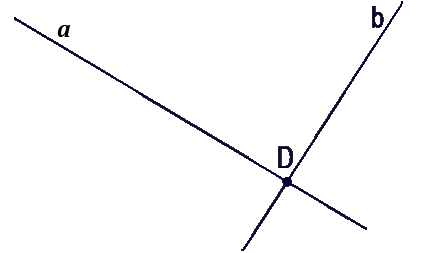
Проведём две прямые a и b так, чтобы эти две
прямые пересекались, и обозначим точку
пересечения.
Как мы видим, точка пересечения только одна. Мы
можем провести третью прямую так, чтобы она
тоже проходила через эту точку пересечения.
Теперь прямая a пересекается
с прямой b,
прямая b пересекается с прямой c и
прямая c пересекается с прямой a.
В этом случае
у нас только одна точка
пересечения всех прямых — точка (·)D.
Но возможен и другой вариант. Мы можем провести третью прямую c так,
чтобы она не проходила через точку (·)D. Тогда
получится
три точки пересечения — (·)D, (·)E и (·)F.
Прямая a пересекается
с прямой b
в точке (·)D,
прямая b пересекается с прямой c в точке (·)F и
прямая c пересекается с прямой a
в точке (·)E. Условие задачи выполнено.
Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.
Ответ: точек пересечения получается одна или
три.
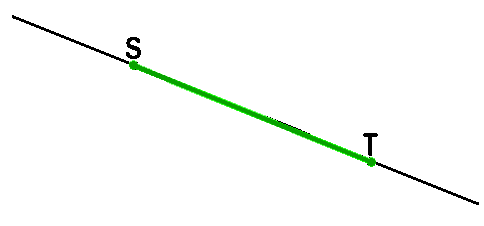
Что такое отрезок
Запомните!
Отрезок —
часть прямой, ограниченная
двумя точками.
Две точки, ограничивающие отрезок, называются
концами отрезка. У отрезка на рисунке выше концы
называются S и
T.
Сам отрезок можно назвать ST
или TS. Когда изображают отрезок, оставшиеся от
прямой хвосты можно не рисовать.
В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.
sthit436
Вопрос по геометрии:
Как пишется знак пересечения в геометрии? Срочно.
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
ncith
Мне кажется так,просто я ещё не изучаю геометрию.
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат — это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи —
смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Аня Колесникова
Ученик
(222),
закрыт
10 лет назад
Лучший ответ
Maxim
Гений
(71098)
10 лет назад
Этот знак используется не только в геометрии и изображается ∩
Остальные ответы
РОМАН ВОРОНЦОВ
Профи
(759)
10 лет назад
∩ знак пересечения
Мери теккозян
Ученик
(136)
6 лет назад
∩ знак
Хо Минхо
Профи
(690)
5 лет назад
∩ — знак пересечения
Мария Стасевич
Ученик
(135)
3 года назад
Перевёрнутая U
Некто никто
Профи
(543)
3 года назад
Этот знак используется не только в геометрии и обозначается ∩
Ҝρนĉ⍡นӈα
Гуру
(3130)
3 года назад
∩
Mihail Dogadov
Ученик
(112)
1 год назад
∩
Определение
Знак пересечения – это символ, указывающий на пересечение прямых, углов, лучей, отрезков, плоскостей и других фигур в геометрии, пересечение множеств в математике (алгебре) и информатике.
Как пишется этот символ пересечения?
Этот знак выглядит и пишется так – ⋂
Его достаточно легко запомнить, он похож на русскую букву «П», начальную букву слова «пересечение».
Как быстро запомнить этот знак?
Просто представьте себе и запомните, что этот символ выглядит как буква «П» и похож на подкову, перевернутую вниз ногами.
Как применяется знак ⋂?
Применяется для обозначения пересечения прямых, углов, лучей, отрезков в геометрии, пересечение множеств в математике (алгебре) и информатике.
Как выглядит знак «не пересечения» в геометрии?
Пример
А ∩ С = ∅ — 2 луча или (2 прямые, 2отрезка) А и С не пересекаются.
Что обозначает знак пересечения наоборот?
Это символ выглядит и пишется следующим образом: ∪
Обозначается термином – «объединение».
Математика | 10 — 11 классы
Как обозначается знак пересечения.
На этой странице сайта размещен вопрос Как обозначается знак пересечения? из категории
Математика с правильным ответом на него. Уровень сложности вопроса
соответствует знаниям учеников 10 — 11 классов. Здесь же находятся ответы по
заданному поиску, которые вы найдете с помощью автоматической системы.
Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по
заданной теме. На этой странице можно обсудить все варианты ответов с другими
пользователями сайта и получить от них наиболее полную подсказку.
Последние ответы

Mandrykina67676767
4 мая 2022 г., 03:27:06
42 + ( — 26) + ( — 16) = 0
Вычитание.
1) 8 — ( — 5) = 8 + 5 = 13.
Раскрываются скобки, знак действия меняется на противоположный, получается пример на сложение.
2) — 9 — 3 = — 12.
Элементы примера складываются и ответ получает общий знак » — «.
..
42 + ( — 26) — ( — 16) = решите пожалуйста)?

Ник14123
4 мая 2022 г., 03:21:31
Пусть второе число = а.
Тогда первое число0, 16а
Пропорция — 0, 16а — 100%
а — х %
0, 16а * х = 100а
х = 100а : 0, 16а = 625%
Ответ 625% составляет второе число от первого…
Первое число составляет 16 процентов от второго?

Gi1g
4 мая 2022 г., 02:52:13
1) 12 руб : 16 = 12 / 16 = 3 / 4 = 75коп / кг — цена 1 кг картофеля
2) 3 / 4 + 1 = 1 3 / 4 руб = 1 руб 75 коп — цена моркови
3) 1 3 / 4 руб * 10 = 70 / 4 = 17 1 / = 17 руб 50 коп — стоимость 10 кг — ОТВЕТ
4) 1 руб 75 коп * 10 = 17 руб 50 коп — стоимо..
На рынке купили картофель и морковь?

Опубликовано — 2 года назад | По предмету
Геометрия |
автор julia2000B
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.