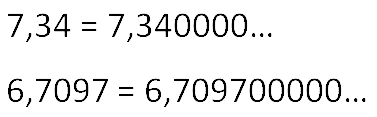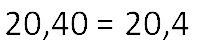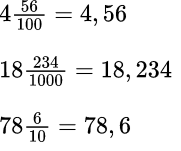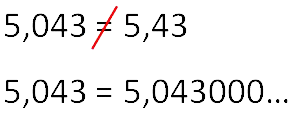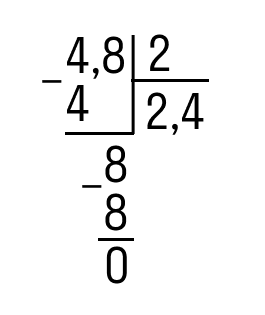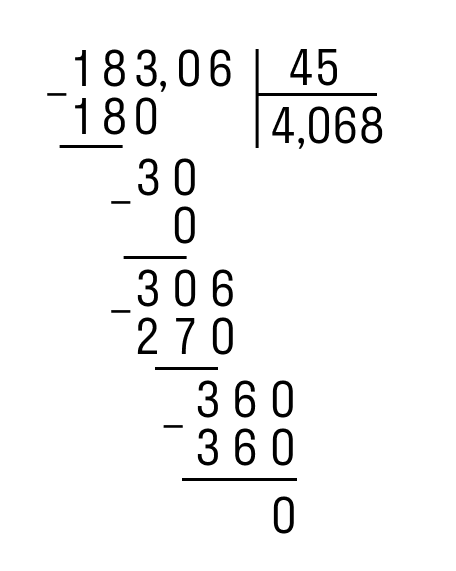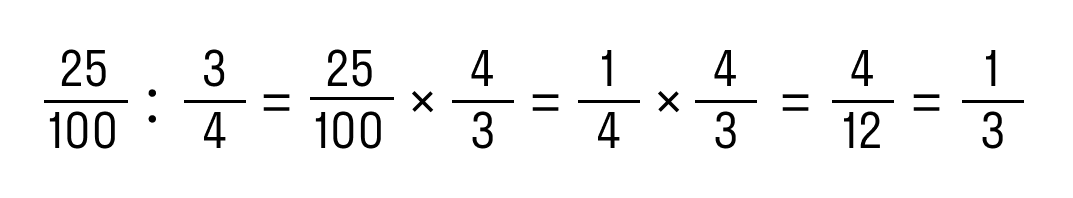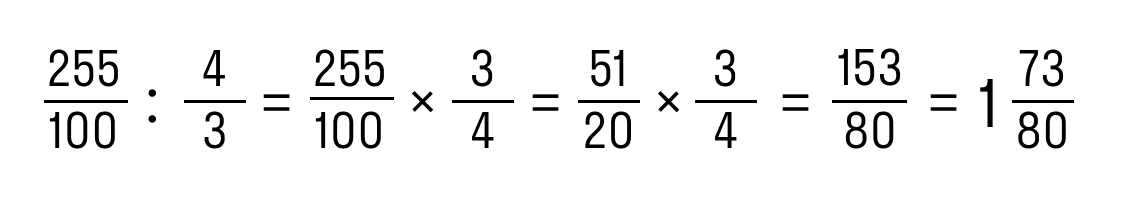Как читать десятичные дроби
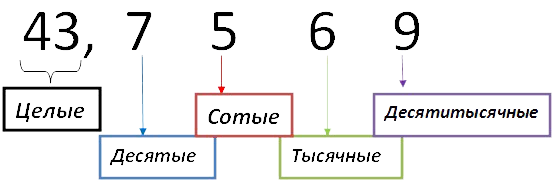
В первую очередь обсудим вид десятичной дроби. Каждая цифра после запятой имеет своё название.
Десятые, сотые, тысячные, десятитысячные…
Десятые, сотые и тысячные
Попробуем прочитать десятичную дробь из примера выше. Чтобы правильно прочитать десятичную дробь нужно:
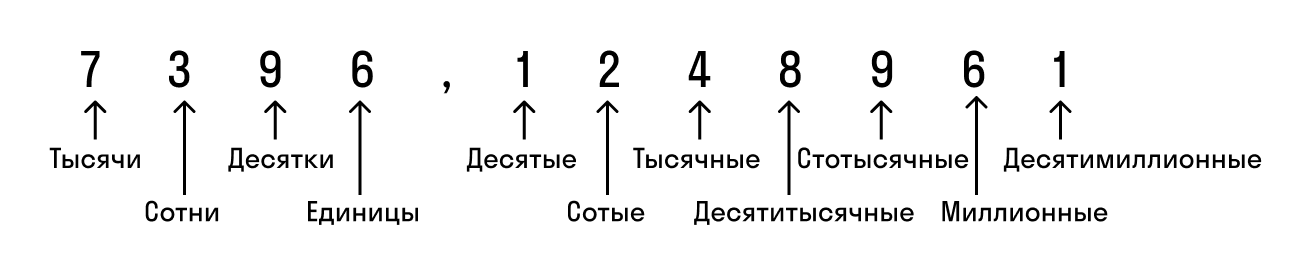
Прочитать число слева от запятой и добавить слово «целыx», так как слева от запятой находится целая часть десятичной дроби. Читаем: «сорок три целых».
Затем прочитать число справа от запятой: «семь тысяч пятьсот шестьдесят девять».
Добавить в конце название самой правой цифры.
У нас это 9 , которая стоит на месте десятитысячных (см. рис. выше): «десятитысячных».
Значит, полное название дроби звучит так:
43,7569 — сорок три целых семь тысяч пятьсот шестьдесят девять десятитысячных.
Справа от запятой после самой последней правой цифры отличной от нуля можно добавлять сколько угодно нулей. От этого значение десятичной дроби не изменится.
Таким же образом если в конце десятичной дроби отбросить ноль, то мы получим такую же по значению десятичную дробь.
Поэтому, если при расчётах получили десятичную дробь 20,40 , отбрасываем ноль на конце и записываем:
Нули можно добавлять (убирать) только после самой последней правой отличной от нуля цифры. Нули между цифрами в числе убирать нельзя.
Источник статьи: http://math-prosto.ru/?page=pages/decimal/decimal2.php
Чтение десятичных дробей
Десятичная дробь в обязательном порядке содержит запятую. Та числовая часть дроби, которая располагается левее запятой, называется целой; правее – дробной:
Дробная часть десятичной дроби состоит из десятичных знаков (десятичных разрядов):
- десятые – 0,1 (одна десятая);
- сотые – 0,01 (одна сотая);
- тысячные – 0,001 (одна тысячная);
- десятитысячные – 0,0001 (одна десятитысячная);
- стотысячные – 0,00001 (одна стотысячная);
- миллионные – 0,000001 (одна миллионная);
- десятимиллионные – 0,0000001 (одна десятимиллионная);
- стомиллионные – 0,00000001 (одна стомиллионная);
- миллиардные – 0,000000001 (одна миллиардная) и т. д.
Как правильно читать десятичную дробь:
- прочитать число, составляющее целую часть дроби и добавить слово “целых“;
- прочитать число, составляющее дробную часть дроби и добавить название младшего разряда.
- 0,25 – ноль целых двадцать пять сотых;
- 9,1 – девять целых одна десятая;
- 18,013 – восемнадцать целых тринадцать тысячных;
- 100,2834 – сто целых две тысячи восемьсот тридцать четыре десятитысячных.
Запись десятичных дробей
Чтобы записать десятичную дробь, необходимо:
- записать целую часть дроби и поставить запятую (число, означающее целую часть дроби всегда заканчивается словом “целых“);
- записать дробную часть дроби таким образом, чтобы последняя цифра попала в нужный разряд (при отсутствии значащих цифр в определенных десятичных разрядах они заменяются нулями).
- двадцать целых девять десятых – 20,9 – в этом примере все просто;
- пять целых одна сотая – 5,01 – слово “сотая” означает, что после запятой должны стоять две цифры, но, поскольку в числе 1 нет разряда десятых, он заменяется нулем;
- ноль целых восемьсот восемь тысячных – 0,808;
- три целых пятнадцать десятых – такую десятичную дробь записать невозможно, потому, что в произношении дробной части допущена ошибка – число 15 содержит два разряда, а слово “десятых” подразумевает только один. Правильно будет три целых пятнадцать сотых (или тысячных, десятитысячных и т. д.).
Сравнение десятичных дробей
Сравнение десятичных дробей проводится аналогично сравнению натуральных чисел.
- сначала сравниваются целые части дробей – больше будет та десятичная дробь у которой больше ее целая часть;
- если целые части дробей равны, сравнивают поразрядно дробные части, слева направо, начиная от запятой: десятые, сотые, тысячные и т.д. Сравнение ведут до первого несовпадения – больше будет та десятичная дробь у которой будет больше неравная цифра в соответствующем разряде дробной части. Например: 1,283 > 1,279, т. к. в сотых разрядах у первой дроби стоит 8, а у второй 7.
Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:
Код кнопки: 
Политика конфиденциальности Об авторе
Источник статьи: http://prosto-o-slognom.ru/matematika/007-desyatichnaya_drob.html
СПАДИЛО.РУ
теория по математике 📈 числа и вычисления
Десятичная дробь — дробь, которая представляет собой способ представление числа в виде записи числа с запятой, где цифры перед запятой называются целой частью, а цифры после запятой – дробной частью (десятичной частью).
Десятичные дроби получают из записи обыкновенных дробей со знаменателем 10, 100, 1000 и так далее. Например, десятичные дроби:
4,56 – четыре целых пятьдесят шесть сотых 18,234 – восемнадцать целых двести тридцать четыре тысячных 78,6 – семьдесят восемь целых шесть десятых
Чтение десятичных дробей
Чтение десятичной части (десятых, сотых и так далее) зависит от количества цифр после запятой. Если цифра одна, то читают – десятых (в числе десять — один нуль, это соответствует одной цифре). Если две цифры после запятой, то читают – сотых (в сотне два нуля).
Десятичные дроби получаются из обыкновенных дробей:
Сложение (вычитание) десятичных дробей
Чтобы сложить (вычесть) в столбик две десятичные дроби нужно:
- Записать их друг под другом так, чтобы при записи запятая оказалась под запятой и соответствующий разряд под соответствующим.
- Уравнять количество знаков после запятой, добавляя недостающие нулями.
- Выполнить сложение (вычитание) в столбик, не обращая внимания на запятую.
- Поставить запятую под запятыми.
Если складывают (вычитают) целое число и десятичную дробь, то нужно поставить запятую после целого числа и приписать необходимое количество нулей после запятой.
Пример №1. Запись, где запятая под запятой и соответствующий разряд под соответствующим.
34,145 + 5,678 = 39,823
Пример №2. Запись, где также запятая под запятой, а во втором числе дописан нуль, чтобы уравнять количество знаков после запятой.
Пример №3. В первом слагаемом нет десятичной части, поэтому, после числа 56 поставили запятую и добавили нужное количество нулей.
Умножение десятичных дробей
При умножении двух десятичных дробей в столбик необходимо:
- Написать числа одно под другим, не обращая внимания на запятую
- Выполнить умножение в столбик
- В ответе отделить столько цифр справа запятой, сколько их в обоих множителях вместе. Если в одном из чисел нет запятой, то считать цифры только в одном числе.
Пример №4. Запись выполнена так, что цифры по правому краю записаны ровно одна под одной, то есть как при обычном умножении чисел в столбик. Умножение выполнено без учета запятой. В ответе справа отделены 4 цифры запятой, так как в первом множителе их 3 после запятой, а во втором – одна, в двух множителях вместе – четыре.
0,125 × 2,3 00375 0250 0,2875
Пример №5. Здесь показано умножение десятичной дроби и целого числа. Умножение выполнено без учета запятой. В ответе отделена справа запятой только одна цифра, так как только в первом множителе есть десятичная часть с одной цифрой после запятой.
Умножение десятичных дробей на 10, 100, 1000…
Чтобы умножить десятичную дробь на 10, 100, 1000 и так далее, нужно перенести запятую вправо на столько цифр, сколько нулей у множителя. Умножение в данном случае выполняется в строчку.
Пример №6. 2,456 × 10 = 24,56 Запятую в десятичной дроби перенесли вправо на 1 цифру, так как у 10 один нуль.
Пример №7. 0,45678 × 100 = 45,678 Запятую перенесли вправо на 2 цифры, так как у 100 два нуля. Нуль, стоящий в начале десятичной дроби, убрали, так как впереди целой части, отличной от нуля он не пишется.
Пример №8. 9,46 × 1000 = 9460 в данном случае при переносе запятой на три цифра не хватило одной, поэтому в конце числа приписали нуль, и в ответе получилось целое число.
Умножение десятичной дроби на разрядную единицу 0,1; 0,01; 0,001…
При умножении десятичной дроби на разрядную единицу 0,1; 0,01; 0,001 (и так далее) нужно перенести запятую на столько цифр влево, сколько цифр в данной разрядной единице после запятой. Умножение обычно выполняется в строчку устно.
Пример №9. 983,7821 × 0,01= 9,837821 Переносим запятые влево на 2 цифры, так как в числе 0,01 две цифры после запятой.
Пример №10. 8,7654 × 0,1 = 0,87654 Перенесли на 1 цифру влево, так как в числе 0,1 одна цифра после запятой. В данном случае перед 8 появился нуль, так как при переносе запятой слева цифр не оказалось.
Пример №11. 7,98 × 0,0001 = 0,000798 При переносе влево на 4 цифры не хватило трех, поэтому впереди поставили нули, а также нуль образуется и в целой части.
Деление десятичных дробей
- При делении десятичной дроби на целое число выполняют сначала деление целой части, а затем десятичной.
- При делении десятичной дроби на другую десятичную дробь необходимо в делителе убрать запятую, а в делимом передвинуть ее вправо на столько цифр, сколько их в делителе после запятой. Затем выполнить деление на целое число.
- Есть случаи, когда цифр после запятой при переносе запятой у дроби не хватает. Тогда необходимо дополнить число нулями.
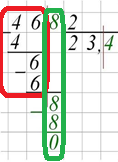
Пример №12. Деление десятичной дроби на целое число. 46,8 : 2 = 23,4
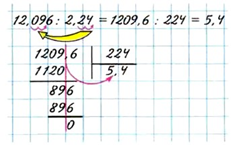
Пример №13. Деление десятичной дроби на десятичную дробь. 12,096 : 2,24 = 5,4 Из данного примера видно, что деление десятичных дробей обязательно сводится к делению на целое число.
Пример №14. 276,3 : 0,003 = 276300 : 3 = 92100. Здесь видно, что не хватает двух цифр в числе 276,3 и поэтому при переносе запятой к нему приписали два нуля. Затем выполнили деление двух целых чисел.
Деление десятичной дроби на 10, 100, 1000…
При делении десятичной дроби на 10,100, 1000 и так далее нужно перенести запятую на столько цифр влево, сколько нулей в данном числе. Деление выполняется в строчку устно.
Пример №16. 134,987 : 1000 = 0,134987 Перенесли запятую на три цифры влево, так как у 1000 три нуля. В целой части поставили нуль, так как цифр не хватило.
Пример №17. 7,234 : 100 = 0,07234 Перенесли запятую влево на две цифры. Так как цифр не хватало, то недостающие заменили нулями.
Деление десятичной дроби на разрядную единицу 0,1; 0,01; 0,001…
При делении десятичной дроби на разрядную единицу 0,1; 0,01; 0,001 и так далее нужно перенести запятую на столько цифр вправо, сколько цифр в данной разрядной единице после запятой. Деление обычно выполняется в строчку устно.
Пример №19. 41,234 : 0,01 = 4123,4 Перенос запятой на 2 цифры вправо, так как в числе 0,01 две цифры после запятой.
Пример №20. 56,91 : 0,001 = 56910 При переносе запятой на три цифры вправо приписали один нуль, так как одной цифры не хватило.
Источник статьи: http://spadilo.ru/desyatichnye-drobi/
Если Вы хотите просто узнать, как пишется число прописью, то можете воспользоваться онлайн сервисом:
Имена числительные в русском языке не имеют единой системы склонения. Изменение по падежам зависит от разряда. Некоторые числительные могут изменяться по родам и числам. При склонении числительных следует уделять внимание и правильности согласования с ним существительного, чтобы не допускать в речи и на письме грамматических ошибок.
Порядковые имена числительные
К разряду порядковых относят числительные, обозначающие порядок при счете и отвечающие на вопросы который? которая? которое? Например: девятый вал, вторая передача, сорок второе открытие. Их делят на простые (состоящие из одного слова) и составные (из двух и более слов).
Склонение порядковых числительных схоже с изменением по числам, родам и падежам имен прилагательных. При склонении составных числительных изменяется только последнее слово. В первом и во втором случае сочетаемое существительное также будет изменяться по падежам. При этом в винительном падеже окончания у числительных, которые согласуются с одушевленными существительными, будут отличаться от тех, которые согласуются с существительными неодушевленными.
|
Падеж |
Простое порядковое |
Составное порядковое |
|---|---|---|
|
Им. |
Первый вагон (неодуш.), пассажир (одуш.) |
Двадцать второй автобус (неодуш.), человек (одуш.) |
|
Род. |
Первого вагона, пассажира |
Двадцать второго автобуса, человека |
|
Дат. |
Первому вагону, пассажиру |
Двадцать второму автобусу, человеку |
|
Вин. |
Первый вагон, первого пассажира |
Двадцать второй автобус, двадцать второго человека |
|
Тв. |
Первым вагоном, пассажиром |
Двадцать вторым автобусом, человеком |
|
Пр. |
О первом вагоне, пассажире |
О двадцать втором автобусе, человеке |
Внимание! При указании даты изменяется только порядковое числительное. Имя существительное, обозначающее название месяца, всегда будет употребляться только в форме родительного падежа: поздравить с восьмым (т. п.) марта (р. п.), подготовиться к первому (д. п.) сентября (р. п.), рассказать о двадцать третьем (п. п.) февраля (р. п.).
Количественные числительные
К этой группе относятся числительные, обозначающие количество предметов: две руки, пять пальцев, тридцать два зуба, четверо друзей. По количеству слов делятся на простые (одно слово) и составные (два и более слов).
Простые количественные числительные представляют собой обширную группу, которая имеет несколько видов склонения.
От 1 до 4
Числительное один имеет падежные окончания прилагательного, бывает единств. и множеств. числа (один – одни), мужского, женского и среднего рода (один, одна, одно).
Следует помнить, что у числительных, которые согласуются с одушевленными существительными единственного и множественного числа мужского рода и среднего рода, а также множественного числа женского рода, окончания совпадают в формах родительного и винительного падежа. Если существительное неодушевленное, то окончания будут совпадать в формах именительного и винительного падежей.
Для единственного числа женского рода этот показатель не будет признаком одушевленности-неодушевленности.
|
Падеж |
Мужской род |
Женский род |
Средний род |
|||
|
Неодушевл. |
Одушевл. |
Неодушевл. |
Одушевл. |
Неодушевл. |
Одушевл. |
|
|
Им. |
Один дом, одни дома |
Один жук, одни жуки |
Одна клетка, одни клетки |
Одна рыба, одни рыбы |
Одно письмо, одни письма |
Одно животное, одни животные |
|
Род. |
Одного дома, одних домов |
Одного жука, одних жуков |
Одной клетки, одних клеток |
Одной рыбы, одних рыб |
Одного письма, одних писем |
Одного животного, одних животных |
|
Вин. |
Один дом, одни дома |
Одного жука, одних жуков |
Одну клетку, одни клетки |
Одну рыбу, одних рыб |
Одно письмо, одни письма |
Одно животное, одних животных |
Числительное два имеет только 2 формы рода: мужского (=среднего) и женского: два стула (м. р.), два окна (ср. р.), две ложки (ж. р.). У числительных три и четыре нет категории рода.
Слова два, три, четыре имеют отличное от остальных склонение. Окончания у числительных, которые согласуются с одушевленными существительными, в родительном и винительном падежах совпадают.
|
Падеж |
Склонение |
||
|
Им. |
Два стола, кота; две руки, собаки |
Три вишни, сестры |
Четыре танка, танкиста |
|
Род. |
Двух столов, котов, рук, собак |
Трех вишен, сестер |
Четырех танков, танкистов |
|
Дат. |
Двум столам, котам, рукам, собакам |
Трем вишням, сестрам |
Четырем танкам, танкистам |
|
Вин. |
Два стола, двух котов; две руки, двух собак |
Три вишни, трех сестер |
Четыре танка, четырех танкистов |
|
Тв. |
Двумя столами, котами, руками, собаками |
Тремя вишнями, сестрами |
Четырьмя танками, танкистами |
|
Пр. |
О двух столах, котах, руках, собаках |
О трех вишнях, сестрах |
О четырех танках, танкистах |
От 5 до 20 и 30
Числительные от пяти до двадцати, а также тридцать изменяются по падежам, как существительные 3-го склонения, поэтому следует обратить внимание на написание окончаний в род., дат. и предл. падежах.
|
Падеж |
Существительное 3 скл. |
Числительное |
|
Род. |
Молодежи |
Пяти, шестнадцати, двадцати, тридцати |
|
Дат. |
Молодежи |
Пяти, шестнадцати, двадцати, тридцати |
|
Пр. |
О молодежи |
О пяти, шестнадцати, двадцати, тридцати |
От 50 до 80 и от 200 до 900
Это сложные числительные, состоящие из двух корней. При склонении будут изменяться корня (при этом числительное пишется слитно): шесть + десять = шестьдесят; р. п. шести + десяти = шестидесяти; т. п. шестью + десятью = шестьюдесятью и так далее.
|
Падеж |
50 |
300 |
500 |
900 |
|
Им. |
Пятьдесят |
Триста |
Пятьсот |
Девятьсот |
|
Род. |
Пятидесяти |
Трехсот |
Пятисот |
Девятисот |
|
Дат. |
Пятидесяти |
Тремстам |
Пятистам |
Девятистам |
|
Вин. |
Пятьдесят |
Триста |
Пятьсот |
Девятьсот |
|
Тв. |
Пятьюдесятью |
Тремястами |
Пятьюстами |
Девятьюстами |
|
Пр. |
Пятидесяти |
Трехстах |
Пятистах |
Девятистах |
40, 90, 100
У слов сорок, девяносто, сто форма именительного падежа совпадает с формой винительного падежа, в остальных падежах используются словоформы сорока, девяноста, ста. Существительные в таких словосочетаниях будут употреблены во множественном числе и склоняться, как обычно.
|
Падеж |
40 |
90 |
100 |
|
Им. |
Сорок ворон |
Девяносто докторов |
Сто морей |
|
Род. |
Сорока ворон |
Девяноста докторов |
Ста морей |
|
Дат. |
Сорока воронам |
Девяноста докторам |
Ста морях |
|
Вин. |
Сорок ворон |
Девяносто докторов |
Сто морей |
|
Тв. |
Сорока воронами |
Девяноста докторами |
Ста морями |
|
Пр. |
О сорока воронах |
О девяноста докторах |
О ста морях |
Полтора, полтораста
Эти числительные склоняются по аналогии с предыдущей группой, то есть имеют всего 2 падежные словоформы: полтора – полутора, полтораста – полутораста.
|
Падеж |
Полтора |
Полтораста |
|
Им. |
Полтора сантиметра |
Полтораста литров |
|
Род. |
Полутора сантиметров |
Полутораста литров |
|
Дат. |
Полутора сантиметрам |
Полутораста литрам |
|
Вин. |
Полтора сантиметра |
Полтораста литров |
|
Тв. |
Полутора сантиметрами |
Полутораста литрами |
|
Пр. |
О полутора сантиметрах |
О полутораста литрах |
Составные количественные числительные
Это имена числительные, состоящие из двух и более слов. Каждое слово здесь будет изменяться отдельно согласно правилам склонения своей группы.
|
Падеж |
Примеры |
||
|
Им. |
Сто девяносто три |
Триста сорок шесть |
Восемьсот семьдесят девять |
|
Род. |
Ста девяноста трех |
Трехсот сорока шести |
Восьмисот семидесяти девяти |
|
Дат. |
Ста девяноста трем |
Тремстам сорока шести |
Восьмистам семидесяти девяти |
|
Вин. |
Сто девяносто три |
Триста сорок шесть |
Восемьсот семьдесят девять |
|
Тв. |
Ста девяноста тремя |
Тремястами сорока шестью |
Восьмьюстами семьюдесятью девятью |
|
Пр. |
Ста девяноста трех |
Трехстах сорока шести |
Восьмистах семидесяти девяти |
Слова тысяча, миллион, миллиард
До сих пор ведутся споры по поводу частеречной принадлежности этих слов. В переносном значении эти слова выступают в роли имени существительного (миллионы людей во всем мире). Если слово обозначает конкретное число или входит в состав числа, его относят к числительному (миллиард лет назад, тысяча девятьсот сорок седьмой год).
В любом случае, слово тысяча склоняется как существительное 1-го скл., миллион и миллиард – как существительные 2-го скл.
Собирательные числительные
Представляют собой небольшую группу, куда входят числительные, обозначающие количество предметов в совокупности: двое, трое, четверо, пятеро, шестеро, семеро, восьмеро, девятеро, десятеро, а также оба и обе.
Собирательные числительные склоняются так же, как прилагательные во множественном числе. При этом у слов, согласующихся с одушевленными существительными, окончания в родительном и винительном падежах совпадают.
|
Падеж |
Примеры |
||
|
Им. |
Двое ворот, ребят |
Четверо ножниц, котят |
Семеро очков, друзей |
|
Род. |
Двоих ворот, ребят |
Четверых ножниц, котят |
Семерых очков, друзей |
|
Дат. |
Двоим воротам, ребятам |
Четверым ножницам, котятам |
Семерым очкам, друзьям |
|
Вин. |
Двое ворот, двоих ребят |
Четверо ножниц, четверых котят |
Семеро очков, семерых друзей |
|
Тв. |
Двоими воротами, ребятами |
Четверыми ножницами, котятами |
Семерыми очками, друзьями |
|
Пр. |
О двоих воротах, ребятах |
О четверых ножницах, котятах |
О семерых очках, друзьях |
Внимание! При склонении собирательных числительных частой ошибкой является переход в другой разряд. Например, правильным вариантом для собирательного числительного будет форма винительного падежа (вижу) девятерых друзей, а не девять друзей, так как в последнем случае употреблено уже количественное числительное. И хотя употребление словосочетания (вижу) девять друзей тоже приемлемо, при задании просклонять именно собирательное числительное этот вариант станет неверным.
|
Падеж |
Собирательные числительные |
Количественные числительные |
|
Им. |
Пятеро суток, медвежат |
Пять суток, медвежат |
|
Род. |
Пятерых суток, медвежат |
Пяти суток, медвежат |
|
Дат. |
Пятерым суткам, медвежатам, |
Пяти суткам, медвежатам |
|
Вин. |
Пятеро суток, пятерых медвежат |
Пять суток, медвежат |
|
Тв. |
Пятерыми суткам, медвежатами |
Пятью сутками, медвежатами |
|
Пр. |
О пятерых сутках, медвежатах |
О пяти сутках, медвежатах |
Обособленно стоит собирательное числительное оба, которое имеет категорию рода: оба – форма мужского и среднего рода (оба товарища, оба окна) и обе – форма женского рода (обе девочки).
|
Падеж |
Примеры |
|
|
Им. |
Оба брата, яблока |
Обе ноги, подруги |
|
Род. |
Обоих братьев, яблок |
Обеих ног, подруг |
|
Дат. |
Обоим братьям, яблокам |
Обеим ногам, подругам |
|
Вин. |
Обоих братьев, оба яблока |
Обе ноги, обеих подруг |
|
Тв. |
Обоими братьями, яблоками |
Обеими ногами, подругами |
|
Пр. |
Об обоих братьях, яблоках |
Об обеих ногах, подругах |
Дробные числительные
В разряд входят имена числительные, называющие дробную величину или количество, часть от целого (¼ – одна четвертая, 0.7 – ноль целых семь десятых, 1 ½ – одна целая одна вторая). Дробные числительные склоняются в зависимости от того, какую дробь они называют – обыкновенную, десятичную или смешанную.
Обыкновенные дроби
В словах, обозначающих обыкновенные дроби, числитель выражается количественным числительным, знаменатель – порядковым (¾ – три четвертых, 7/8 – семь восьмых). По падежам изменяется каждое слово в соответствии со своим типом склонения. При этом согласующиеся с ними имена существительные не склоняются.
|
Падеж |
Примеры |
|
|
Им. |
Две третьих |
Пять шестых |
|
Род. |
Двух третьих |
Пяти шестых |
|
Дат. |
Двум третьим |
Пяти шестым |
|
Вин. |
Две третьих |
Пять шестых |
|
Тв. |
Двумя третьими |
Пятью шестыми |
|
Пр. |
О двух третьих |
О пяти шестых |
Десятичные и смешанные дроби
В числительных, называющих десятичные дроби, склоняются все слова. Сочетающиеся с ними имена существительные не изменяются и остаются в форме родительного падежа.
|
Падеж |
3,5 |
6,54 |
|
Им. |
Три целых пять десятых объема |
Шесть целых пятьдесят четыре сотых гектара |
|
Род. |
Трех целых пяти десятых объема |
Шести целых пятидесяти четырех сотых гектара |
|
Дат. |
Трем целым пяти десятым объема |
Шести целым пятидесяти четырем сотым гектара |
|
Вин. |
Три целых пять десятых объема |
Шесть целых пятьдесят четыре сотых гектара |
|
Тв. |
Тремя целыми пятью десятыми объема |
Шестью целыми пятьюдесятью четырьмя сотыми гектара |
|
Пр. |
О трех целых пяти десятых объема |
О шести целых пятидесяти четырех сотых гектара |
Смешанные дроби склоняются аналогичным способом.
|
Падеж |
7 ¾ |
|
Им. |
Семь целых три четвертых метра |
|
Род. |
Семи целых трех четвертых метра |
|
Дат. |
Семи целым трем четвертым метра |
|
Вин. |
Семь целых три четвертых метра |
|
Тв. |
Семью целыми тремя четвертыми метра |
|
Пр. |
О семи целых трех четвертых метра |
Вы можете воспользоваться автоматическим сервисом, который переведет любое число в пропись.
Если Вы хотите просто узнать как пишется число прописью, то можете воспользоваться онлайн сервисом:
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Как читать десятичные дроби
Поддержать сайт
В первую очередь обсудим вид десятичной дроби.
Каждая цифра после запятой имеет своё название.
Десятые, сотые, тысячные, десятитысячные…
Десятые, сотые и тысячные
Попробуем прочитать десятичную дробь из примера выше.
Чтобы правильно прочитать десятичную дробь нужно:
-
Прочитать число слева от запятой и добавить слово «целыx», так как слева от запятой находится
целая часть десятичной дроби. Читаем: «сорок три целых». -
Затем прочитать число справа от запятой: «семь тысяч пятьсот шестьдесят девять».
-
Добавить в конце название самой правой цифры.
У нас это
9, которая стоит на месте десятитысячных
(см. рис. выше):
«десятитысячных».
Значит, полное название дроби звучит так:
43,7569 — сорок три целых семь тысяч пятьсот шестьдесят девять десятитысячных.
Справа от запятой после самой последней
правой цифры отличной от нуля можно добавлять сколько угодно
нулей. От этого значение десятичной дроби не изменится.
Таким же образом если в конце десятичной дроби отбросить ноль, то мы получим
такую же по значению десятичную дробь.
Поэтому, если при расчётах получили десятичную дробь 20,40 , отбрасываем
ноль на конце и записываем:
Запомните!
Нули можно добавлять (убирать) только после самой последней правой отличной от нуля
цифры. Нули между цифрами в числе убирать нельзя.
Десятичная дробь, как и любое число, состоит из цифр ((0), (1), (2), (3), (4), (5), (6), (7), (8), (9)).
Место каждой цифры в числе важно: оно определяет разряд числа.
Десятичная дробь состоит из целой части (все цифры до запятой) и дробной части (все цифры после запятой).
Целую часть десятичной дроби можно разбить на разряды так же, как и натуральные числа: единицы, десятки, сотни, тысячи и т. д.
Дробную часть десятичной дроби разбивают на разряды так:
десятые (в знаменателе обыкновенной дроби (10)), сотые (в знаменателе обыкновенной дроби (100)), тысячные (в знаменателе обыкновенной дроби (1000)) и т. д.
Таблица разрядов
| Тысячи | Сотни | Десятки | Единицы, | Десятые | Сотые | Тысячные | Десятитысячные |
Таблицу разрядов можно дополнить любым нужным количеством столбцов.
(1)-й разряд после запятой — разряд десятых,
(2)-й разряд после запятой — разряд сотых,
(3)-й разряд после запятой — разряд тысячных,
(4)-й разряд после запятой — разряд десятитысячных,
(5)-й разряд после запятой — разряд стотысячных,
(6)-й разряд после запятой — разряд миллионных,
(7)-й разряд после запятой — разряд десятимиллионных,
(8)-й разряд после запятой — разряд стомиллионных.
Пример:
запишем в таблицу разрядов числа: (25,5701); (13,827); (3,9); (48,65).
| Десятки | Единицы, | Десятые | Сотые | Тысячные | Десятитысячные | |
| (25,5701) |
(2) |
(5) |
(5) |
(7) |
(0) |
(1) |
| (13,827) |
(1) |
(3) |
(8) |
(2) |
(7) |
|
| (48,65) |
(4) |
(8) |
(6) |
(5) |
||
| (3,9) |
(3) |
(9) |
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
- 0,8
- 7,42
- 9,932
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
- 0,600 = 0,6
- 21,10200000 = 21,102
| Основные свойства |
|---|
|
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
- Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
- Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде.
- Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
Обучение на курсах по математике — отличный способ закрепить полученные знания на практике и подтянуть сложные темы.
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
Как решаем:
- Знаменатель равен 10 — это один ноль.
- Отсчитываем справа налево в числителе дробной части один знак и ставим запятую.
- В полученной десятичной дроби цифра 1 — целая часть, цифра 6 — дробная часть.
Ответ: 16/10 = 1,6.
Пример 2. Перевести 37/1000 в десятичную дробь.
Как решаем:
- Знаменатель равен 1000 — это три нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Так как в числителе только две цифры, то на пустующие места пишем нули.
- В полученной десятичной дроби цифра 0 — целая часть, 037 — дробная часть.
Ответ: 37/1000 = 0,037.
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
1% = 1/100 = 0,01
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
0,15 = 0,15 · 100% = 15%.
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%
8/25 = 0,32
0,32 · 100% = 32%
Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:
Преобразование десятичных дробей
Быстрая напоминалка:
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!
Пример 1. Перевести 5,4 в смешанное число.
Как решаем:
- Читаем вслух: пять целых четыре десятых. «Четыре десятых» подсказывают, что в числителе будет 4, а в знаменателе — 10. В смешанном виде эта дробь выглядит так: 5 4/10.
- А теперь сократим числитель и знаменатель на два (потому что можно) и получим: 5 2/5.
Ответ: 5,4 = 5 2/5.
Пример 2. Перевести 4,005 в смешанное число.
Как решаем:
- Читаем вслух: четыре целых пять тысячных. Значит 5 — идет в числитель, а 1000 — в знаменатель. В смешанном виде получается так: 4 5/1000. После сокращения: 4 1/200.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
Как решаем:
- Читаем вслух: пять целых шестьдесят сотых. Отправляем 60 в числитель, а 100 — в знаменатель. В смешанном виде дробь такая: 5 60/100.
- Сократим дробную часть на 10 и получим 5 6/10. Или можно вспомнить про свойство десятичной дроби и просто отбросить нули в числителе и знаменателе.
Ответ: 5,60 = 5 6/10.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:
- Перепишем исходную дробь в новый вид: в числитель поставим исходную десятичную дробь, а в знаменатель — единицу. Например:
- 0,35 = 0,35/1
- 2,34 = 2,34/1
- Умножим числитель и знаменатель на 10 столько раз, чтобы в числителе исчезла запятая. При этом после каждого умножения запятая в числителе сдвигается вправо на один знак, а у знаменателя соответственно добавляются нули. На примере легче:
- 0,35 = 0,35/1 = 3,5/10 = 35/100
- 2,34 = 2,34/1 = 23,4/10 = 234/100
- А теперь сокращаем — то есть делим числитель и знаменатель на кратные им числа:
- 0,35 = 35/100, делим числитель и знаменатель на пять, получаем 6/20, еще раз делим на 2, получаем итоговый ответ 3/10.
- 2,34 = 234/100 = 117/50 = 2 17/50.
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Действия с десятичными дробями
С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.
Как разделить десятичную дробь на натуральное число
- Разделить целую часть десятичной дроби на это число.
- Поставить запятую в частном и продолжить вычисление, как при обычном делении.
Пример 1. Разделить 4,8 на 2.
Как решаем:
- Записать деление уголком.
- Разделить целую часть на два. Записать полученный результат в частное и поставить запятую.
- Умножить частное на делитель, записать, посмотреть на остаток от деления. Но мы еще не закончили, поэтому остаток «ноль» не записываем. Сносим 8 и делим её на 2.
- Делим еще раз. Записываем полученную 4 в частном и умножаем её на делитель:
Ответ: 4,8 : 2 = 2,4.
Пример 2. Разделить 183,06 на 45.
Как решаем:
- Записать деление уголком.
- Разделить целую часть 183 на 45. Записать результат, поставить запятую в частном.
- Записать результат разницы 183 и 180. Снести 0. Записать 0 в частное, чтобы снести 6.
- Записать результат разницы 306 и 270. 36 не делится на 45, поэтому добавляем ноль и производим разницу.
Ответ: 183,06 : 45 = 4,068.
Как разделить десятичную дробь на обыкновенную
Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.
Пример 1. Разделить 0,25 на 3/4.
Как решаем:
- Записать 0,25 в виде обыкновенной дроби: 0,25 = 25/100.
- Разделить дробь по правилам:
Ответ: 0,25 : 3/4 = 1/3.
Пример 2. Разделить 2,55 на 1 1/3.
Как решаем:
- Записать 2,55 в виде обыкновенной дроби: 2,55 = 255/1000.
- Записать 1 1/3 в виде обыкновенной дроби: 1 1/3 = 4/3.
- Разделить дробь по правилам:
Ответ: 2,55 : 1 1/3 = 1 73/80.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить 2/5 на 0,8.
Как решаем:
- Записать 0,8 в виде обыкновенной дроби: 0,8 = 8/10.
- Умножаем по правилам: 2/5 ∗ 8/10 = 2/5 ∗ 4/5 = 8/25 = 0,32.
Ответ: 2/5 ∗ 0,8 = 0,32.
Пример 2. Умножить 0,28 на 6 1/4.
Как решаем:
- Записать 6 1/4 в виде десятичной дроби: 6 1/4 = 6,25.
- Умножаем по правилам: 0,28 ∗ 6,25 = 0,8.
Ответ: 0,28 ∗ 6 1/4 = 0,8.
Правописание счётных числительных в именительном падеже
Для простоты усвоения материала, в данном параграфе мы рассмотрим правила написания
определённо-количественных числительных, т.е. соответствующих числам при счёте: один (1), два (2), тридцать
три (33), сто сорок тысяч пяться двадцать два (140522). Вопросы написания порядковых числительных (первый,
второй, сто восьмидесятый), дробей, а также правила склонения рассмотрены в последующих параграфах.
Для корректной записи имён числительных, нужно запомнить несколько несложных правил.
Базовые слова для выражения числовых значений
Существует ограниченное число базовых слов, посредством которых можно выразить числовые значения. Это:
- слова один (одна, одно), два (две), три, четыре, пять, шесть, семь, восемь, девять, десять;
- слова одиннадцать, двенадцать, тринадцать, четырнадцать, пятнадцать, шестнадцать, семнадцать,
восемнадцать, девятнадцать; - слова двадцать, тридцать, сорок, пятьдесят, шестьдесят, семьдесят, восемьдесят, девяносто;
- слова сто, двести, триста, четыреста, пятьсот, шестьсот, семьсот, восемьсот, девятьсот;
- слова тысяча, миллион, миллиард, триллион, квадриллион, квинтиллион и т.д.
Прим. Конечно слов из списка Д (тысяча, миллион и т.д.) существует больше, но для записи числительных в
повседневной жизни достаточно слов тысяча и миллион. Иногда могут понадобиться миллиард и
триллион, а такие слова как квадриллион и квинтиллион встречаются
совсем уж редко и обычно снабжаются пояснением, например:один квинтиллион, то есть 10 в 18-й степени
Для простоты изложения, далее в тексте будем ограничиваться в этом списке миллиардом.
Правописание мягкого знака в числительных
- у числительных пять — девятнадцать, а также двадцать и
тридцать на конце пишется мягкий знак; - у числительных пятьдесят — восемьдесят, а также пятьсот — девятьсот
в середине слова пишется мягкий знак.
Раздельное и слитное написание числительных
Кратко о написании чисел от 1 до 999
- числа от 1 до 19, целые десятки от 20 до 90, целые сотни от 100 до 900 пишутся в одно слово: один,
двенадцать, тридцать, пятьсот; - числа от 21 до 99, не являющиеся целыми десятками пишутся в два слова:
двадцать один, пятьдесят
пять, восемьдесят один; - для чисел больших ста, не являющимися целыми сотнями, пишутся сначала сотни, а затем оставшееся число,
согласно правилам выше:
сто двадцать три, пятьсот семьдесят один, девятьсот семьдесят девять.
Более подробно
Числительные делятся на четыре группы:
- Простые непроизводные числительные (проще говоря «базовые», не образованные от других числительных):
один — десять, сорок, девяносто, сто, тысяча,
миллион, миллиард. - Простые производные числительные, состоящие из одного корня и суффикса и образованные в свою очередь от
других числительных):
- с помощью суффикса —надцать: один -> одиннадцать, два -> двенадцать, …, девять ->
девятнадцать; - с помощью суффикса —дцать: двадцать, тридцать.
- Сложные числительные, имеющие в своём составе два корня: пятьдесят (корни -пять- и -десят-), шестьдесят,
семьдесят, восемьдесят, двести (корни -дв- и -ст-), триста, четыреста, пятьсот, шестьсот, семьсот,
восемьсот, девятьсот. - Составные числительные, состоящие из двух или более компонентов, каждый из которых, в свою очередь,
является простым или сложным числительным: сто пятьдесят два, двести сорок четыре, два миллиона
пятнадцать тысяч сто сорок четыре и т.д.
Правило раздельного и слитного написания: простые (производные и непроизводные), а также сложные числительные
пишутся слитно. Составные числительные пишутся раздельно. Например:
5 пять
15 пятнадцать
50 пятьдесят
300 триста
119 сто девятнадцать
244 двести сорок
четыре
2015144
два миллиона пятнадцать тысяч сто сорок четыре
Прим. В учебнике Розенталя Д.И. приводится альтернативное деление числительных по группам, а именно
одиннадцать — девятнадцать, двадцать и тридцать отнесены к сложным числительным. В этом случае
-дцать-
является корнем, а на- — приставкой.Исторически слова от одиннадцати до девятнадцати возникли из сочетаний трёх слов: одинъ на десяте, дъвѣ
на десяте, три на десяте и т.д. Числительное десять здесь употреблено в форме местного падежа
(предложный II, на чём?).Впрочем мы можем оставить такие тонкости языка исследователям, ведь на правописание это никак не
влияет.
Слова «тысяча», «миллион», «миллиард»
При написании составных числительных, слова тысяча, миллион и миллиард
склоняются, в зависимости от количества тысяч, миллионов или миллиардов в числе:
- Если количество заканчивается на 1, но не на 11, то употребляются формы тысяча,
миллион, миллиард (одна тысяча, двадцать одна тысяча, пятьсот семьдесят один
миллион). - Если количество заканчивается на 2, 3, 4, но не 12, 13, 14, то употребляются формы тысячи, миллиона,
миллиарда (две тысячи, сорок четыре миллиона, семьсот семьдесят три тысячи). - В остальных случаях, т.е. когда количество заканчивается на 0, 5, 6, 7, 8, 9, а также на 11, 12, 13, 14,
употребляются формы тысяч, миллионов, миллиардов (семь тысяч, сто
пятнадцать тысяч, триста двадцать семь тысяч).
Согласование слов «тысяча», «миллион», «миллиард»
Обратите внимание, что слово тысяча — женского рода, а слова миллион и миллиард — мужского. Поэтому пишется:
одна тысяча, сто тридцать одна тысяча, две тысячи, девятьсот пятьдесят две тысячи, но: один миллион, два
миллиарда, девятьсот пятьдесят два миллиона.
Десятичная дробь в обязательном порядке содержит запятую. Та числовая часть дроби, которая располагается левее запятой, называется целой; правее — дробной:
5,28
5 — целая часть
28 — дробная часть
Дробная часть десятичной дроби состоит из десятичных знаков
(десятичных разрядов):
- десятые — 0,1 (одна десятая);
- сотые — 0,01 (одна сотая);
- тысячные — 0,001 (одна тысячная);
- десятитысячные — 0,0001 (одна десятитысячная);
- стотысячные — 0,00001 (одна стотысячная);
- миллионные — 0,000001 (одна миллионная);
- десятимиллионные — 0,0000001 (одна десятимиллионная);
- стомиллионные — 0,00000001 (одна стомиллионная);
- миллиардные — 0,000000001 (одна миллиардная) и т. д.
- прочитать число, составляющее целую часть дроби и добавить слово «целых
«; - прочитать число, составляющее дробную часть дроби и добавить название младшего разряда.
Например:
- 0,25 — ноль целых двадцать пять сотых;
- 9,1 — девять целых одна десятая;
- 18,013 — восемнадцать целых тринадцать тысячных;
- 100,2834 — сто целых две тысячи восемьсот тридцать четыре десятитысячных.
Запись десятичных дробей
Чтобы записать десятичную дробь, необходимо:
- записать целую часть дроби и поставить запятую (число, означающее целую часть дроби всегда заканчивается словом «целых
«); - записать дробную часть дроби таким образом, чтобы последняя цифра попала в нужный разряд (при отсутствии значащих цифр в определенных десятичных разрядах они заменяются нулями).
Например:
- двадцать целых девять десятых — 20,9 — в этом примере все просто;
- пять целых одна сотая — 5,01 — слово «сотая» означает, что после запятой должны стоять две цифры, но, поскольку в числе 1 нет разряда десятых, он заменяется нулем;
- ноль целых восемьсот восемь тысячных — 0,808;
- три целых пятнадцать десятых — такую десятичную дробь записать невозможно, потому, что в произношении дробной части допущена ошибка — число 15 содержит два разряда, а слово «десятых» подразумевает только один. Правильно будет три целых пятнадцать сотых (или тысячных, десятитысячных и т. д.).
Сравнение десятичных дробей
Сравнение десятичных дробей проводится аналогично сравнению натуральных чисел .
- сначала сравниваются целые части дробей — больше будет та десятичная дробь у которой больше ее целая часть;
- если целые части дробей равны, сравнивают поразрядно дробные части, слева направо, начиная от запятой: десятые, сотые, тысячные и т.д. Сравнение ведут до первого несовпадения — больше будет та десятичная дробь у которой будет больше неравная цифра в соответствующем разряде дробной части. Например: 1,28
3 > 1,27
9, т. к. в сотых разрядах у первой дроби стоит 8, а у второй 7.
Десятичная дробь отличается от обыкновенной дроби тем, что знаменатель у нее — это разрядная единица.
Например:
Десятичные дроби выделены из обыкновенных дробей в отдельный вид, что привело к собственным правилам сравнения, сложения, вычитания, умножения и деления этих дробей. В принципе, с десятичными дробями можно работать и по правилам обыкновенных дробей. Собственные правила преобразования десятичных дробей упрощают вычисления, а правила преобразования обыкновенных дробей в десятичные, и наоборот, служат связкой между этими видами дроби.
Запись и чтение десятичных дробей позволяет их записывать, сравнивать и производить действия над ними по правилам, очень похожим на правила действий с натуральными числами.
Впервые система десятичных дробей и действий над ними была изложена в XV в. самаркандским математиком и астрономом Джемшид ибн-Масудаль-Каши в книге «Ключ к искусству счета».
Целая часть десятичной дроби отделена от дробной части запятой, в некоторых странах (США) ставят точку. Если в десятичной дроби нет целой части, то перед запятой ставят число 0.
К дробной части десятичной дроби справа можно дописывать любое количество нулей, это величину дроби не изменяет. Дробная часть десятичной дроби читается по последнему значащему разряду.
Например:
0,3 — три десятых
0,75 — семьдесят пять сотых
0,000005 — пять миллионных.
Чтение целой части десятичной дроби такое же, как и натуральных чисел.
Например:
27,5 — двадцать семь…;
1,57 — одна…
После целой части десятичной дроби произносится слово «целых».
Например:
10.7 — десять целых семь десятых
0,67 — ноль целых шестьдесят семь сотых.
Десятичные знаки — это цифры дробной части. Дробная часть читается не по разрядам (в отличие от натуральных чисел), а целиком, поэтому дробная часть десятичной дроби определяется последним справа значащим разрядом. Разрядная система дробной части десятичной дроби несколько иная, чем у натуральных чисел.
- 1-й разряд после занятой — разряд десятых
- 2-й разряд после запятой — разряд сотых
- 3-й разряд после запятой — разряд тысячных
- 4-й разряд после запятой — разряд десятитысячных
- 5-й разряд после запятой — разряд стотысячных
- 6-й разряд после запятой — разряд миллионных
- 7-й разряд после запятой — разряд десятимиллионных
- 8-й разряд после запятой — разряд стомиллионных
В вычислениях чаще всего используются первые три разряда. Большая разрядность дробной части десятичных дробей используется только в специфических отраслях знаний, где вычисляются бесконечно малые величины.
Перевод десятичной дроби в смешанную дробь
состоит н следующем: число, стоящее до запятой записать целой частью смешанной дроби; число, стоящее после запятой — числителем ее дробной части, а в знаменателе дробной части записать единицу со столькими нулями, сколько цифр стоит после запятой.
3.4 Правильный порядок
В предыдущем разделе мы сравнивали числа по их положению на числовой прямой. Это хороший способ сравнивать величины чисел в десятичной записи. Этот способ работает всегда, но это трудоемко и неудобно делать всякий раз, когда нужно сравнить два числа. Существует другой хороший способ выяснить, какое из двух чисел больше.
Пример A.
Рассмотрим числа из предыдущего раздела и сравним 0,05 и 0,2.
Чтобы выяснить, какое число больше, сравним сначала их целые части. Оба числа в нашем примере имеют равное количество целых — 0. Сравним тогда их десятые части. Число 0,05 имеет 0 десятых, а число 0,2 имеет 2 десятых. То, что число 0,05 имеет 5 сотых, ни имеет значения, поскольку десятые доли определяют, что число 0,2 больше. Мы можем, таким образом, записать:
Оба числа имеют 0 целых и 6 десятых, и мы пока не можем определить, какое из них больше. Однако, число 0,612 имеет всего 1 сотую часть, а число 0,62 – две. Тогда, мы можем определить, что
0,62 > 0,612
То, что число 0,612 имеет 2 тысячных, не играет роли, оно все равно меньше, чем 0,62.
Мы можем это проиллюстрировать на картинке:

|
0,612 | ||
 |
0,62 |
Для того, чтобы определить, какое из двух чисел в десятичной записи больше, нужно сделать следующее:
1. Сравнить целые части. То число, у которого целая часть больше и будет больше.
2
. Если целые части равны, сравнить десятые части. То число, у которого десятых частей больше, и будет больше.
3
. Если десятые части равны, сравнить сотые части. То число, у которого сотых частей больше, и будет больше.
4
. Если сотые части равны, сравнить тысячные части. То число, у которого тысячных частей больше, и будет больше.
В этой статье мы рассмотрим тему «сравнение десятичных дробей
». Сначала обсудим общий принцип сравнения десятичных дробей. После этого разберемся, какие десятичные дроби являются равными, а какие – неравными. Дальше научимся определять, какая десятичная дробь больше, а какая меньше. Для этого изучим правила сравнения конечных, бесконечных периодических и бесконечных непериодических дробей. Всю теорию снабдим примерами с подробными решениями. В заключение остановимся на сравнении десятичных дробей с натуральными числами, обыкновенными дробями и смешанными числами.
Сразу скажем, что здесь мы будем говорить лишь о сравнении положительных десятичных дробей (смотрите положительные и отрицательные числа). Остальные случаи разобраны в статьях сравнение рациональных чисел и сравнение действительных чисел
.
Навигация по странице.
Общий принцип сравнения десятичных дробей
Исходя из этого принципа сравнения, выводятся правила сравнения десятичных дробей, позволяющие обойтись без перевода сравниваемых десятичных дробей в обыкновенные дроби. Эти правила, а также примеры их применения, мы разберем в следующих пунктах.
По схожему принципу сравниваются конечные десятичные дроби или бесконечные периодические десятичные дроби с натуральными числами , обыкновенными дробями и смешанными числами : сравниваемые числа заменяются соответствующими им обыкновенными дробями, после чего сравниваются обыкновенные дроби.
Что касается сравнения бесконечных непериодических десятичных дробей
, то оно обычно сводится к сравнению конечных десятичных дробей. Для этого рассматривается такое количество знаков сравниваемых бесконечных непериодических десятичных дробей, которое позволяет получить результат сравнения.
Равные и неравные десятичные дроби
Сначала введем определения равных и неравных конечных десятичных дробей
.
Определение.
Две конечные десятичные дроби называются равными
, если равны соответствующие им обыкновенные дроби, в противном случае эти десятичные дроби называются неравными
.
На основании этого определения легко обосновать следующее утверждение: если в конце данной десятичной дроби приписать или отбросить несколько цифр 0
, то получится равная ей десятичная дробь. Например, 0,3=0,30=0,300=…
, а 140,000=140,00=140,0=140
.
Действительно, дописывание или отбрасывание в конце десятичной дроби нуля справа соответствует умножению или делению на 10
числителя и знаменателя соответствующей обыкновенной дроби. А мы знаем основное свойство дроби , которое гласит, что умножение или деление числителя и знаменателя дроби на одно и то же натуральное число дает дробь, равную исходной. Этим доказано, что дописывание или отбрасывание нулей справа в дробной части десятичной дроби дает дробь, равную исходной.
Например, десятичной дроби 0,5
отвечает обыкновенная дробь 5/10
, после дописывания нуля справа получается десятичная дробь 0,50
, которой отвечает обыкновенная дробь 50/100
, а . Таким образом, 0,5=0,50
. Обратно, если в десятичной дроби 0,50
отбросить справа 0
, то мы получим дробь 0,5
, так от обыкновенной дроби 50/100
мы придем к дроби 5/10
, но . Следовательно, 0,50=0,5
.
Переходим к определению равных и неравных бесконечных периодических десятичных дробей
.
Определение.
Две бесконечные периодические дроби равны
, если равны отвечающие им обыкновенные дроби; если же соответствующие им обыкновенные дроби не равны, то сравниваемые периодические дроби тоже не равны
.
Из данного определения следуют три вывода:
- Если записи периодических десятичных дробей полностью совпадают, то такие бесконечные периодические десятичные дроби равны. Например, периодические десятичные дроби 0,34(2987)
и 0,34(2987)
равны. - Если периоды сравниваемых десятичных периодических дробей начинаются с одинаковой позиции, первая дробь имеет период 0
, вторая – период 9
, и значение разряда, предшествующего периоду 0
на единицу больше, чем значение разряда, предшествующего периоду 9
, то такие бесконечные периодические десятичные дроби равны. Например, периодические дроби 8,3(0)
и 8,2(9)
равны, также равны дроби 141,(0)
и 140,(9)
. - Две любые другие периодические дроби не являются равными. Приведем примеры неравных бесконечных периодических десятичных дробей: 9,0(4)
и 7,(21)
, 0,(12)
и 0,(121)
, 10,(0)
и 9,8(9)
.
Осталось разобраться с равными и неравными бесконечными непериодическими десятичными дробями
. Как известно, такие десятичные дроби не могут быть переведены в обыкновенные дроби (такие десятичные дроби представляют иррациональные числа), поэтому сравнение бесконечных непериодических десятичных дробей нельзя свести к сравнению обыкновенных дробей.
Определение.
Две бесконечные непериодические десятичные дроби равны
, если их записи полностью совпадают.
Но есть один нюанс: невозможно увидеть «законченную» запись бесконечных непериодических десятичных дробей, следовательно, невозможно убедиться и в полном совпадении их записей. Как же быть?
При сравнении бесконечных непериодических десятичных дробей рассматривают лишь конечное число знаков сравниваемых дробей, которое позволяет сделать необходимые выводы. Таким образом, сравнение бесконечных непериодических десятичных дробей сводится к сравнению конечных десятичных дробей.
При таком подходе можно говорить о равенстве бесконечных непериодических десятичных дробей лишь с точностью до рассматриваемого разряда. Приведем примеры. Бесконечные непериодические десятичные дроби 5,45839…
и 5,45839…
равны с точностью до стотысячных, так как равны конечные десятичные дроби 5,45839
и 5,45839
; непериодические десятичные дроби 19,54…
и 19,54810375…
равны с точностью до сотых, так как равны дроби 19,54
и 19,54
.
Неравенство бесконечных непериодических десятичных дробей при таком подходе устанавливается вполне определенно. Например, бесконечные непериодические десятичные дроби 5,6789…
и 5,67732…
не равны, так как очевидны различия в их записях (не равны конечные десятичные дроби 5,6789
и 5,6773
). Бесконечные десятичные дроби 6,49354…
и 7,53789…
тоже не равны.
Правила сравнения десятичных дробей, примеры, решения
После установления факта неравенства двух десятичных дробей, часто нужно узнать, какая из этих дробей больше, а какая – меньше другой. Сейчас мы разберем правила сравнения десятичных дробей, позволяющие ответить на поставленный вопрос.
Во многих случаях бывает достаточно сравнить целые части сравниваемых десятичных дробей. Справедливо следующее правило сравнения десятичных дробей
: больше та десятичная дробь, целая часть которой больше, и меньше та десятичная дробь, целая часть которой меньше.
Это правило относится как к конечным десятичным дробям, так и к бесконечным. Рассмотрим решения примеров.
Пример.
Сравните десятичные дроби 9,43
и 7,983023…
.
Решение.
Очевидно, данные десятичные дроби не равны. Целая часть конечной десятичной дроби 9,43
равна 9
, а целая часть бесконечной непериодической дроби 7,983023…
равна 7
. Так как 9>7
(смотрите сравнение натуральных чисел), то 9,43>7,983023
.
Ответ:
9,43>7,983023
.
Пример.
Какая из десятичных дробей 49,43(14)
и 1 045,45029…
меньше?
Решение.
Целая часть периодической дроби 49,43(14)
меньше, чем целая часть бесконечной непериодической десятичной дроби 1 045,45029…
, следовательно, 49,43(14)<1 045,45029…
.
Ответ:
49,43(14)
.
Если целые части сравниваемых десятичных дробей равны, то для выяснения, какая из них больше, а какая — меньше, приходится сравнивать дробные части. Сравнение дробных частей десятичных дробей проводится поразрядно
— от разряда десятых к более младшим.
Для начала рассмотрим пример сравнения двух конечных десятичных дробей.
Пример.
Выполните сравнение конечных десятичных дробей 0,87
и 0,8521
.
Решение.
Целые части данных десятичных дробей равны (0=0
), поэтому переходим к сравнению дробных частей. Значения разряда десятых равны (8=8
), а значение разряда сотых дроби 0,87
больше, чем значение разряда сотых дроби 0,8521
(7>5
). Следовательно, 0,87>0,8521
.
Ответ:
0,87>0,8521
.
Иногда, чтобы выполнить сравнение конечных десятичных дробей с разным количеством десятичных знаков, к дроби с меньшим количеством десятичных знаков приходится дописывать некоторое количество нулей справа. Достаточно удобно уравнивать количество десятичных знаков до начала сравнения конечных десятичных дробей, дописав к одной из них некоторое количество нулей справа.
Пример.
Сравните конечные десятичные дроби 18,00405
и 18,0040532
.
Решение.
Очевидно, данные дроби неравны, так как их записи отличаются, но при этом они имеют равные целые части (18=18
).
Перед поразрядным сравнением дробных частей данных дробей уравняем количество десятичных знаков. Для этого припишем две цифры 0
в конце дроби 18,00405
, при этом получим равную ей десятичную дробь 18,0040500
.
Значения десятичных разрядов дробей 18,0040500
и 18,0040532
равны вплоть до стотысячных, а значение разряда миллионных дроби 18,0040500
меньше значения соответствующего разряда дроби 18,0040532
(0<3
), поэтому, 18,0040500<18,0040532
, следовательно, 18,00405<18,0040532
.
Ответ:
18,00405<18,0040532
.
При сравнении конечной десятичной дроби с бесконечной, конечная дробь заменяется равной ей бесконечной периодической дробью с периодом 0
, после чего проводится сравнение по разрядам.
Пример.
Сравните конечную десятичную дробь 5,27
с бесконечной непериодической десятичной дробью 5,270013…
.
Решение.
Целые части данных десятичных дробей равны. Значения разрядов десятых и сотых данных дробей равны, и чтобы выполнить дальнейшее сравнение, конечную десятичную дробь заменяем равной ей бесконечной периодической дробью с периодом 0
вида 5,270000…
. До пятого знака после запятой значения разрядов десятичных дробей 5,270000…
и 5,270013…
равны, а на пятом знаке имеем 0<1
. Таким образом, 5,270000…<5,270013…
, откуда следует, что 5,27<5,270013…
.
Ответ:
5,27<5,270013…
.
Сравнение бесконечных десятичных дробей также проводится поразрядно
, и заканчивается после того, как только значения какого-то разряда оказываются разными.
Пример.
Сравните бесконечные десятичные дроби 6,23(18)
и 6,25181815…
.
Решение.
Целые части данных дробей равны, также равны значения разряда десятых. А значение разряда сотых периодической дроби 6,23(18)
меньше разряда сотых бесконечной непериодической десятичной дроби 6,25181815…
, следовательно, 6,23(18)<6,25181815…
.
Ответ:
6,23(18)<6,25181815…
.
Пример.
Какая из бесконечных периодических десятичных дробей 3,(73)
и 3,(737)
больше?
Решение.
Понятно, что 3,(73)=3,73737373…
и 3,(737)=3,737737737…
. На четвертом знаке после запятой поразрядное сравнение заканчивается, так как там имеем 3<7
. Таким образом, 3,73737373…<3,737737737…
, то есть, десятичная дробь 3,(737)
больше, чем дробь 3,(73)
.
Ответ:
3,(737)
.
Сравнение десятичных дробей с натуральными числами, обыкновенными дробями и смешанными числами.
Получить результат сравнения десятичной дроби с натуральным числом позволяет сравнение целой части данной дроби с данным натуральным числом. При этом периодические дроби с периодами 0
или 9
нужно предварительно заменить равными им конечными десятичными дробями.
Справедливо следующее правило сравнения десятичной дроби и натурального числа
: если целая часть десятичной дроби меньше данного натурального числа, то и вся дробь меньше этого натурального числа; если целая часть дроби больше или равна данному натуральному числу, то дробь больше данного натурального числа.
Рассмотрим примеры применения этого правила сравнения.
Пример.
Сравните натуральное число 7
с десятичной дробью 8,8329…
.
Решение.
Так как данное натуральное число меньше, чем целая часть данной десятичной дроби, то это число меньше данной десятичной дроби.
Ответ:
7<8,8329…
.
Пример.
Сравните натуральное число 7
и десятичную дробь 7,1
.