From Wikipedia, the free encyclopedia
The system of ancient Egyptian numerals was used in Ancient Egypt from around 3000 BCE[1] until the early first millennium CE. It was a system of numeration based on multiples of ten, often rounded off to the higher power, written in hieroglyphs. The Egyptians had no concept of a place-valued system such as the decimal system.[2] The hieratic form of numerals stressed an exact finite series notation, ciphered one-to-one onto the Egyptian alphabet.[citation needed]
Digits and numbers[edit]
The following hieroglyphs were used to denote powers of ten:
| Value | 1 | 10 | 100 | 1,000 | 10,000 | 100,000 | 1 million, or many |
|---|---|---|---|---|---|---|---|
| Hieroglyph |
|
|
|
|
|
|
|
| Gardiner’s sign list ID | Z1 | V20 | V1 | M12 | D50 | I8 | C11 |
| Description | Single stroke | Cattle hobble | Coil of rope | Water lily (also called lotus) |
Bent finger | Tadpole | Heh[3] |
Multiples of these values were expressed by repeating the symbol as many times as needed. For instance, a stone carving from Karnak shows the number 4,622 as:
Egyptian hieroglyphs could be written in both directions (and even vertically). In this example the symbols decrease in value from top to bottom and from left to right. On the original stone carving, it is right-to-left, and the signs are thus reversed.[citation needed]
Zero and negative numbers[edit]
| nfr |
heart with trachea beautiful, pleasant, good |
|
|---|
By 1740 BCE, the Egyptians had a symbol for zero in accounting texts. The symbol nfr (𓄤), meaning beautiful, was also used to indicate the base level in drawings of tombs and pyramids and distances were measured relative to the base line as being above or below this line.[4]
Fractions[edit]
Rational numbers could also be expressed, but only as sums of unit fractions, i.e., sums of reciprocals of positive integers, except for 2⁄3 and 3⁄4. The hieroglyph indicating a fraction looked like a mouth, which meant «part»:
Fractions were written with this fractional solidus, i.e., the numerator 1, and the positive denominator below. Thus, 1⁄3 was written as:

|
Special symbols were used for 1⁄2 and for the non-unit fractions 2⁄3 and, less frequently, 3⁄4:
If the denominator became too large, the «mouth» was just placed over the beginning of the «denominator»:

|
Addition and subtraction[edit]
For plus and minus signs, the hieroglyphs
(D54, D55) were used: if the feet pointed into the direction of writing, it signified addition, otherwise subtraction.[5]
Written numbers[edit]
As with most modern day languages, the ancient Egyptian language could also write out numerals as words phonetically, just like one can write thirty instead of «30» in English. The word (thirty), for instance, was written as
while the numeral (30) was
This was, however, uncommon for most numbers other than one and two and the signs were used most of the time.[citation needed]
Hieratic numerals[edit]
As administrative and accounting texts were written on papyrus or ostraca, rather than being carved into hard stone (as were hieroglyphic texts), the vast majority of texts employing the Egyptian numeral system utilize the hieratic script. Instances of numerals written in hieratic can be found as far back as the Early Dynastic Period. The Old Kingdom Abusir Papyri are a particularly important corpus of texts that utilize hieratic numerals.[citation needed]
A comparative chart of Egyptian numerals, including hieratic and demotic
Boyer proved 50 years ago[when?] that hieratic script used a different numeral system, using individual signs for the numbers 1 to 9, multiples of 10 from 10 to 90, the hundreds from 100 to 900, and the thousands from 1000 to 9000. A large number like 9999 could thus be written with only four signs—combining the signs for 9000, 900, 90, and 9—as opposed to 36 hieroglyphs. Boyer saw the new hieratic numerals as ciphered, mapping one number onto one Egyptian letter for the first time in human history. Greeks adopted the new system, mapping their counting numbers onto two of their alphabets, the Doric and Ionian.[citation needed]
In the oldest hieratic texts the individual numerals were clearly written in a ciphered relationship to the Egyptian alphabet. But during the Old Kingdom a series of standardized writings had developed for sign-groups containing more than one numeral, repeated as Roman numerals practiced. However, repetition of the same numeral for each place-value was not allowed in the hieratic script. As the hieratic writing system developed over time, these sign-groups were further simplified for quick writing; this process continued into Demotic, as well.[citation needed]
Two famous mathematical papyri using hieratic script are the Moscow Mathematical Papyrus and the Rhind Mathematical Papyrus.[citation needed]
Egyptian words for numbers[edit]
The following table shows the reconstructed Middle Egyptian forms of the numerals (which are indicated by a preceding asterisk), the transliteration of the hieroglyphs used to write them, and finally the Coptic numerals which descended from them and which give Egyptologists clues as to the vocalism of the original Egyptian numbers. A breve (˘) in some reconstructed forms indicates a short vowel whose quality remains uncertain; the letter ‘e’ represents a vowel that was originally u or i (exact quality uncertain) but became e by Late Egyptian.[citation needed]
| Egyptian transliteration | Reconstructed vocalization | English translation | Coptic (Sahidic dialect) | |
|---|---|---|---|---|
| perCalendarr 1975[6] | per Loprieno 1995[7] | |||
| wꜥ(w) (masc.) wꜥt (fem.) |
*wíꜥyaw (masc.) *wiꜥī́yat (fem.) |
*wúꜥꜥuw (masc.) | one | ⲟⲩⲁ (oua) (masc.) ⲟⲩⲉⲓ (ouei) (fem.) |
| snwj (masc.) sntj (fem.) |
*sínwaj (masc.) *síntaj (fem.) |
*sinúwwaj (masc.) | two | ⲥⲛⲁⲩ (snau) (masc.) ⲥⲛ̄ⲧⲉ (snte) (fem.) |
| ḫmtw (masc.) ḫmtt (fem.) |
*ḫámtaw (masc.) *ḫámtat (fem.) |
*ḫámtaw (masc.) | three | ϣⲟⲙⲛ̄ⲧ (šomnt) (masc.) ϣⲟⲙⲧⲉ (šomte) (fem.) |
| jfdw (masc.) jfdt (fem.) |
*j˘fdáw (masc.) *j˘fdát (fem.) |
*jifdáw (masc.) | four | ϥⲧⲟⲟⲩ (ftoou) (masc.) ϥⲧⲟ (fto) or ϥⲧⲟⲉ (ftoe) (fem.) |
| djw (masc.) djt (fem.) |
*dī́jaw (masc.) *dī́jat (fem.) |
*dī́jaw (masc.) | five | ϯⲟⲩ (tiou) (masc.) ϯ (ti) or ϯⲉ (tie) (fem.) |
| sjsw or jsw (?) (masc.) sjst or jst (?) (fem.) |
*j˘ssáw (masc.) *j˘ssát (fem.) |
*sáʾsaw (masc.) | six | ⲥⲟⲟⲩ (soou) (masc.) ⲥⲟ (so) or ⲥⲟⲉ (soe) (fem.) |
| sfḫw (masc.) sfḫt (fem.) |
*sáfḫaw (masc.) *sáfḫat (fem.) |
*sáfḫaw (masc.) | seven | ϣⲁϣϥ̄ (šašf) (masc.) ϣⲁϣϥⲉ (šašfe) (fem.) |
| ḫmnw (masc.) ḫmnt (fem.) |
*ḫ˘mā́naw (masc.) *ḫ˘mā́nat (fem.) |
*ḫamā́naw (masc.) | eight | ϣⲙⲟⲩⲛ (šmoun) (masc.) ϣⲙⲟⲩⲛⲉ (šmoune) (fem.) |
| psḏw (masc.) psḏt (fem.) |
*p˘sī́ḏaw (masc.) *p˘sī́ḏat (fem.) |
*pisī́ḏaw (masc.) | nine | ⲯⲓⲥ (psis) (masc.) ⲯⲓⲧⲉ (psite) (fem.) |
| mḏw (masc.) mḏt (fem.) |
*mū́ḏaw (masc.) *mū́ḏat (fem.) |
*mū́ḏaw (masc.) | ten | ⲙⲏⲧ (mēt) (masc.) ⲙⲏⲧⲉ (mēte) (fem.) |
| mḏwtj, ḏwtj, or ḏbꜥty (?) (masc.) mḏwtt, ḏwtt, or ḏbꜥtt (?) (fem.) |
*ḏubā́ꜥataj (masc.) | *(mu)ḏawā́taj (masc.) | twenty | ϫⲟⲩⲱⲧ (jouōt) (masc.) ϫⲟⲩⲱⲧⲉ (jouōte) (fem.) |
| mꜥbꜣ (masc.) mꜥbꜣt (fem.) |
*máꜥb˘ꜣ (masc.) | *máꜥb˘ꜣ (masc.) | thirty | ⲙⲁⲁⲃ (maab) (masc.) ⲙⲁⲁⲃⲉ (maabe) (fem.) |
| ḥmw | *ḥ˘mí (?) | *ḥ˘méw | forty | ϩⲙⲉ (hme) |
| dyw | *díjwu | *díjjaw | fifty | ⲧⲁⲉⲓⲟⲩ (taeiou) |
| sjsjw, sjsw, or jswjw (?) | *j˘ssáwju | *saʾséw | sixty | ⲥⲉ (se) |
| sfḫjw, sfḫw, or sfḫwjw (?) | *safḫáwju | *safḫéw | seventy | ϣϥⲉ (šfe) |
| ḫmnjw, ḫmnw, or ḫmnwjw (?) | *ḫamanáwju | *ḫamnéw | eighty | ϩⲙⲉⲛⲉ (hmene) |
| psḏjw or psḏwjw (?) | *p˘siḏáwju | *pisḏíjjaw | ninety | ⲡⲥⲧⲁⲓⲟⲩ (pstaiou) |
| št | *šúwat | *ší(nju)t | one hundred | ϣⲉ (še) |
| štj | *šū́taj | *šinjū́taj | two hundred | ϣⲏⲧ (šēt) |
| ḫꜣ | *ḫaꜣ | *ḫaꜣ | one thousand | ϣⲟ (šo) |
| ḏbꜥ | *ḏubáꜥ | *ḏ˘báꜥ | ten thousand | ⲧⲃⲁ (tba) |
| ḥfn | one hundred thousand | |||
| ḥḥ | *ḥaḥ | *ḥaḥ | one million | ϩⲁϩ (hah) «many» |
See also[edit]
- Egyptian language
- Egyptian mathematics
References[edit]
- ^ «Egyptian numerals». MacTutor — School of Mathematics and Statistics. University of St. Andrews. Retrieved January 12, 2023.
- ^ «The Story of Numbers» by John McLeish
- ^ Merzbach, Uta C., and Carl B. Boyer. A History of Mathematics. Hoboken, NJ: John Wiley, 2011, p. 10
- ^ George Gheverghese Joseph (2011). The Crest of the Peacock: Non-European Roots of Mathematics (Third ed.). Princeton. p. 86. ISBN 978-0-691-13526-7.
- ^ Cajori, Florian (1993) [1929]. A History of Mathematical Notations. Dover Publications. pp. pp. 229–230. ISBN 0-486-67766-4.
- ^ Callender, John B. (1975) Middle Egyptian, 1975
- ^ Loprieno, Antonio (1995) Ancient Egyptian: A Linguistic Introduction, Cambridge: Cambridge University Press, p. 71, 255
Bibliography[edit]
- Allen, James Paul (2000). Middle Egyptian: An Introduction to the Language and Culture of Hieroglyphs. Cambridge: Cambridge University Press. Numerals discussed in §§9.1–9.6.
- Gardiner, Alan Henderson (1957). Egyptian Grammar; Being an Introduction to the Study of Hieroglyphs. 3rd ed. Oxford: Griffith Institute. For numerals, see §§259–266.
- Goedicke, Hans (1988). Old Hieratic Paleography. Baltimore: Halgo, Inc.
- Möller, Georg (1927). Hieratische Paläographie: Die Ägyptische Buchschrift in ihrer Entwicklung von der Fünften Dynastie bis zur römischen Kaiserzeit. 3 vols. 2nd ed. Leipzig: J. C. Hinrichs Schen Buchhandlungen. (Reprinted Osnabrück: Otto Zeller Verlag, 1965)
External links[edit]
- Introduction to Hieroglyphs Numbers and Fractions at the Wayback Machine (archived September 29, 2007)
- Numbers and dates at the Wayback Machine (archived March 4, 2001)
- Egyptian Numbers at the Wayback Machine (archived January 12, 2004)
- Egyptian Math History
From Wikipedia, the free encyclopedia
The system of ancient Egyptian numerals was used in Ancient Egypt from around 3000 BCE[1] until the early first millennium CE. It was a system of numeration based on multiples of ten, often rounded off to the higher power, written in hieroglyphs. The Egyptians had no concept of a place-valued system such as the decimal system.[2] The hieratic form of numerals stressed an exact finite series notation, ciphered one-to-one onto the Egyptian alphabet.[citation needed]
Digits and numbers[edit]
The following hieroglyphs were used to denote powers of ten:
| Value | 1 | 10 | 100 | 1,000 | 10,000 | 100,000 | 1 million, or many |
|---|---|---|---|---|---|---|---|
| Hieroglyph |
|
|
|
|
|
|
|
| Gardiner’s sign list ID | Z1 | V20 | V1 | M12 | D50 | I8 | C11 |
| Description | Single stroke | Cattle hobble | Coil of rope | Water lily (also called lotus) |
Bent finger | Tadpole | Heh[3] |
Multiples of these values were expressed by repeating the symbol as many times as needed. For instance, a stone carving from Karnak shows the number 4,622 as:
Egyptian hieroglyphs could be written in both directions (and even vertically). In this example the symbols decrease in value from top to bottom and from left to right. On the original stone carving, it is right-to-left, and the signs are thus reversed.[citation needed]
Zero and negative numbers[edit]
| nfr |
heart with trachea beautiful, pleasant, good |
|
|---|
By 1740 BCE, the Egyptians had a symbol for zero in accounting texts. The symbol nfr (𓄤), meaning beautiful, was also used to indicate the base level in drawings of tombs and pyramids and distances were measured relative to the base line as being above or below this line.[4]
Fractions[edit]
Rational numbers could also be expressed, but only as sums of unit fractions, i.e., sums of reciprocals of positive integers, except for 2⁄3 and 3⁄4. The hieroglyph indicating a fraction looked like a mouth, which meant «part»:
Fractions were written with this fractional solidus, i.e., the numerator 1, and the positive denominator below. Thus, 1⁄3 was written as:

|
Special symbols were used for 1⁄2 and for the non-unit fractions 2⁄3 and, less frequently, 3⁄4:
If the denominator became too large, the «mouth» was just placed over the beginning of the «denominator»:

|
Addition and subtraction[edit]
For plus and minus signs, the hieroglyphs
(D54, D55) were used: if the feet pointed into the direction of writing, it signified addition, otherwise subtraction.[5]
Written numbers[edit]
As with most modern day languages, the ancient Egyptian language could also write out numerals as words phonetically, just like one can write thirty instead of «30» in English. The word (thirty), for instance, was written as
while the numeral (30) was
This was, however, uncommon for most numbers other than one and two and the signs were used most of the time.[citation needed]
Hieratic numerals[edit]
As administrative and accounting texts were written on papyrus or ostraca, rather than being carved into hard stone (as were hieroglyphic texts), the vast majority of texts employing the Egyptian numeral system utilize the hieratic script. Instances of numerals written in hieratic can be found as far back as the Early Dynastic Period. The Old Kingdom Abusir Papyri are a particularly important corpus of texts that utilize hieratic numerals.[citation needed]
A comparative chart of Egyptian numerals, including hieratic and demotic
Boyer proved 50 years ago[when?] that hieratic script used a different numeral system, using individual signs for the numbers 1 to 9, multiples of 10 from 10 to 90, the hundreds from 100 to 900, and the thousands from 1000 to 9000. A large number like 9999 could thus be written with only four signs—combining the signs for 9000, 900, 90, and 9—as opposed to 36 hieroglyphs. Boyer saw the new hieratic numerals as ciphered, mapping one number onto one Egyptian letter for the first time in human history. Greeks adopted the new system, mapping their counting numbers onto two of their alphabets, the Doric and Ionian.[citation needed]
In the oldest hieratic texts the individual numerals were clearly written in a ciphered relationship to the Egyptian alphabet. But during the Old Kingdom a series of standardized writings had developed for sign-groups containing more than one numeral, repeated as Roman numerals practiced. However, repetition of the same numeral for each place-value was not allowed in the hieratic script. As the hieratic writing system developed over time, these sign-groups were further simplified for quick writing; this process continued into Demotic, as well.[citation needed]
Two famous mathematical papyri using hieratic script are the Moscow Mathematical Papyrus and the Rhind Mathematical Papyrus.[citation needed]
Egyptian words for numbers[edit]
The following table shows the reconstructed Middle Egyptian forms of the numerals (which are indicated by a preceding asterisk), the transliteration of the hieroglyphs used to write them, and finally the Coptic numerals which descended from them and which give Egyptologists clues as to the vocalism of the original Egyptian numbers. A breve (˘) in some reconstructed forms indicates a short vowel whose quality remains uncertain; the letter ‘e’ represents a vowel that was originally u or i (exact quality uncertain) but became e by Late Egyptian.[citation needed]
| Egyptian transliteration | Reconstructed vocalization | English translation | Coptic (Sahidic dialect) | |
|---|---|---|---|---|
| perCalendarr 1975[6] | per Loprieno 1995[7] | |||
| wꜥ(w) (masc.) wꜥt (fem.) |
*wíꜥyaw (masc.) *wiꜥī́yat (fem.) |
*wúꜥꜥuw (masc.) | one | ⲟⲩⲁ (oua) (masc.) ⲟⲩⲉⲓ (ouei) (fem.) |
| snwj (masc.) sntj (fem.) |
*sínwaj (masc.) *síntaj (fem.) |
*sinúwwaj (masc.) | two | ⲥⲛⲁⲩ (snau) (masc.) ⲥⲛ̄ⲧⲉ (snte) (fem.) |
| ḫmtw (masc.) ḫmtt (fem.) |
*ḫámtaw (masc.) *ḫámtat (fem.) |
*ḫámtaw (masc.) | three | ϣⲟⲙⲛ̄ⲧ (šomnt) (masc.) ϣⲟⲙⲧⲉ (šomte) (fem.) |
| jfdw (masc.) jfdt (fem.) |
*j˘fdáw (masc.) *j˘fdát (fem.) |
*jifdáw (masc.) | four | ϥⲧⲟⲟⲩ (ftoou) (masc.) ϥⲧⲟ (fto) or ϥⲧⲟⲉ (ftoe) (fem.) |
| djw (masc.) djt (fem.) |
*dī́jaw (masc.) *dī́jat (fem.) |
*dī́jaw (masc.) | five | ϯⲟⲩ (tiou) (masc.) ϯ (ti) or ϯⲉ (tie) (fem.) |
| sjsw or jsw (?) (masc.) sjst or jst (?) (fem.) |
*j˘ssáw (masc.) *j˘ssát (fem.) |
*sáʾsaw (masc.) | six | ⲥⲟⲟⲩ (soou) (masc.) ⲥⲟ (so) or ⲥⲟⲉ (soe) (fem.) |
| sfḫw (masc.) sfḫt (fem.) |
*sáfḫaw (masc.) *sáfḫat (fem.) |
*sáfḫaw (masc.) | seven | ϣⲁϣϥ̄ (šašf) (masc.) ϣⲁϣϥⲉ (šašfe) (fem.) |
| ḫmnw (masc.) ḫmnt (fem.) |
*ḫ˘mā́naw (masc.) *ḫ˘mā́nat (fem.) |
*ḫamā́naw (masc.) | eight | ϣⲙⲟⲩⲛ (šmoun) (masc.) ϣⲙⲟⲩⲛⲉ (šmoune) (fem.) |
| psḏw (masc.) psḏt (fem.) |
*p˘sī́ḏaw (masc.) *p˘sī́ḏat (fem.) |
*pisī́ḏaw (masc.) | nine | ⲯⲓⲥ (psis) (masc.) ⲯⲓⲧⲉ (psite) (fem.) |
| mḏw (masc.) mḏt (fem.) |
*mū́ḏaw (masc.) *mū́ḏat (fem.) |
*mū́ḏaw (masc.) | ten | ⲙⲏⲧ (mēt) (masc.) ⲙⲏⲧⲉ (mēte) (fem.) |
| mḏwtj, ḏwtj, or ḏbꜥty (?) (masc.) mḏwtt, ḏwtt, or ḏbꜥtt (?) (fem.) |
*ḏubā́ꜥataj (masc.) | *(mu)ḏawā́taj (masc.) | twenty | ϫⲟⲩⲱⲧ (jouōt) (masc.) ϫⲟⲩⲱⲧⲉ (jouōte) (fem.) |
| mꜥbꜣ (masc.) mꜥbꜣt (fem.) |
*máꜥb˘ꜣ (masc.) | *máꜥb˘ꜣ (masc.) | thirty | ⲙⲁⲁⲃ (maab) (masc.) ⲙⲁⲁⲃⲉ (maabe) (fem.) |
| ḥmw | *ḥ˘mí (?) | *ḥ˘méw | forty | ϩⲙⲉ (hme) |
| dyw | *díjwu | *díjjaw | fifty | ⲧⲁⲉⲓⲟⲩ (taeiou) |
| sjsjw, sjsw, or jswjw (?) | *j˘ssáwju | *saʾséw | sixty | ⲥⲉ (se) |
| sfḫjw, sfḫw, or sfḫwjw (?) | *safḫáwju | *safḫéw | seventy | ϣϥⲉ (šfe) |
| ḫmnjw, ḫmnw, or ḫmnwjw (?) | *ḫamanáwju | *ḫamnéw | eighty | ϩⲙⲉⲛⲉ (hmene) |
| psḏjw or psḏwjw (?) | *p˘siḏáwju | *pisḏíjjaw | ninety | ⲡⲥⲧⲁⲓⲟⲩ (pstaiou) |
| št | *šúwat | *ší(nju)t | one hundred | ϣⲉ (še) |
| štj | *šū́taj | *šinjū́taj | two hundred | ϣⲏⲧ (šēt) |
| ḫꜣ | *ḫaꜣ | *ḫaꜣ | one thousand | ϣⲟ (šo) |
| ḏbꜥ | *ḏubáꜥ | *ḏ˘báꜥ | ten thousand | ⲧⲃⲁ (tba) |
| ḥfn | one hundred thousand | |||
| ḥḥ | *ḥaḥ | *ḥaḥ | one million | ϩⲁϩ (hah) «many» |
See also[edit]
- Egyptian language
- Egyptian mathematics
References[edit]
- ^ «Egyptian numerals». MacTutor — School of Mathematics and Statistics. University of St. Andrews. Retrieved January 12, 2023.
- ^ «The Story of Numbers» by John McLeish
- ^ Merzbach, Uta C., and Carl B. Boyer. A History of Mathematics. Hoboken, NJ: John Wiley, 2011, p. 10
- ^ George Gheverghese Joseph (2011). The Crest of the Peacock: Non-European Roots of Mathematics (Third ed.). Princeton. p. 86. ISBN 978-0-691-13526-7.
- ^ Cajori, Florian (1993) [1929]. A History of Mathematical Notations. Dover Publications. pp. pp. 229–230. ISBN 0-486-67766-4.
- ^ Callender, John B. (1975) Middle Egyptian, 1975
- ^ Loprieno, Antonio (1995) Ancient Egyptian: A Linguistic Introduction, Cambridge: Cambridge University Press, p. 71, 255
Bibliography[edit]
- Allen, James Paul (2000). Middle Egyptian: An Introduction to the Language and Culture of Hieroglyphs. Cambridge: Cambridge University Press. Numerals discussed in §§9.1–9.6.
- Gardiner, Alan Henderson (1957). Egyptian Grammar; Being an Introduction to the Study of Hieroglyphs. 3rd ed. Oxford: Griffith Institute. For numerals, see §§259–266.
- Goedicke, Hans (1988). Old Hieratic Paleography. Baltimore: Halgo, Inc.
- Möller, Georg (1927). Hieratische Paläographie: Die Ägyptische Buchschrift in ihrer Entwicklung von der Fünften Dynastie bis zur römischen Kaiserzeit. 3 vols. 2nd ed. Leipzig: J. C. Hinrichs Schen Buchhandlungen. (Reprinted Osnabrück: Otto Zeller Verlag, 1965)
External links[edit]
- Introduction to Hieroglyphs Numbers and Fractions at the Wayback Machine (archived September 29, 2007)
- Numbers and dates at the Wayback Machine (archived March 4, 2001)
- Egyptian Numbers at the Wayback Machine (archived January 12, 2004)
- Egyptian Math History
Цифровой мир Египетской Империи завораживает. Сегодня мы можем читать и писать числа так же, как и они. Вы тоже хотите научиться их писать? Продолжайте читать, и вы получите все ключи.
Первое, что мы должны сделать, — это различать представление чисел в иероглифах, с одной стороны, которые использовались для их гравировки на камне, и те, которые мы собираемся научиться писать, а с другой стороны — изображение в иератическом языке, который был совершенно другим и использовался для ежедневного написания на знаменитых папирусах.
Даже сегодня можно найти какой-нибудь древний документ, демонстрирующий еще большие математические знания, но его желание изучать математику с теоретической точки зрения достойно восхищения.
Несмотря на то, что авторы превозносили свою культуру в своем повествовании, великие греческие авторы цитировали египтян как учителей многих математических дисциплин, таких как геометрия или арифметика.
Египтяне использовали эти числа со времен Среднего царства Египта, хотя они действительно мало использовались при ежедневном написании папирусов. С этого времени использовалась иератическая система письма, которая позволяла писцам писать намного быстрее.
Однако, когда дело дошло до резьбы по камню, эти криптограммы использовались.
Мы знаем язык иероглифов благодаря экспедиции под командованием Наполеона Бонапарта в 1799 году. Такая экспедиция обнаружила большую гранитную плиту в Розетте, Египет, которую Англия взяла на себя три года спустя и которая сегодня находится в Британском музее в Лондоне. .
На этом камне есть тексты на 3-х языках: иероглифы, египетский демотический и древнегреческий; известный как Розеттский камень.
В 1822 году Жан-Франсуа Шампольон начал его расшифровывать, а в следующем году Томас Янг также внес свой вклад в эту работу. В последующие годы к делу присоединились многие другие авторы, расшифровав, таким образом, язык иероглифов для всего человечества.
Определенно, самым важным в математике был Генрих Бругш, поскольку в 1849 году он опубликовал «Numerorum apud Veteres Aegyptios», первый трактат, посвященный египетской математике в современной истории ».
Содержание
- 1 Как читать египетские числа: символы и значение
- 2 Правила преобразования египетских чисел в арабские (наши числа)
- 3 Египетская математика
Как читать египетские числа: символы и значение
Эти иероглифические знаки использовались для обозначения различных степеней десяти:
Чтобы хорошо это понять, мы подготовили изображение со списком египетских чисел от 1 до 100, и еще более:
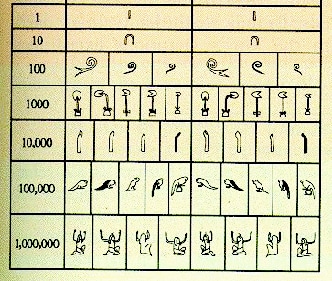
Итак, если представляемое число равно 1.322, мы бы написали
Или мы могли бы также написать:так как это можно писать в любом порядке.
Вы должны знать, что 0 не существовало (до XIII династии в Среднем Египте), и тогда иератический символ «nfr» стал использоваться на папирусе и в иероглифическом представлении. Хотя это стало означать пустое пространство, которое существует до 1 (и которое позже станет пределом между положительными и отрицательными числами). Но это не считалось заполнением цифры, как мы используем ее в нашем арабском письме, поскольку эта система письма появится намного позже.
Правила преобразования египетских чисел в арабские (наши числа)
Мы можем читать и переводить цифровые иероглифы в наши арабские цифры, просто инвертируя приведенную выше формулу. Если мы увидим число, начертанное на камне из Древнего Египта, напримермы можем сделать вывод, что это 45.003.
Египетская математика
Египтяне уже знали математику на определенном уровне, учитывая, что до Среднего Египта у нас не было доказательств того, что они знали число 0. Самый старый известный нам египетский текст, демонстрирующий египетское использование математики, — это Московский папирус, который восходит к временам. с того времени до 2000-1800 гг. до н.э.
Но помните, что для этого они использовали другие символы, чем те, которые используются в иероглифах, которые мы видели выше. Египтяне в своих документах писали (не только числа, но и все другие символы) на своем языке, египетском демотическом, который был написан иератическим.
С помощью этой системы египтяне писали намного быстрее, поскольку им требовалось гораздо меньше символов для представления одного и того же числа.
Вероятно, это происходит гораздо раньше, но мы точно знаем, что еще в 1650 году до нашей эры они знали о сложении и вычитании, умножении и делении, арифметических и геометрических рядах, единичных дробях, составных и простых числах, арифметических, геометрических и гармонических средних, а также о том, как для решения линейных уравнений первого порядка. А также то, что с 1300 г. С. умел решать алгебраические уравнения второго порядка (квадратичные).
Впечатляет, правда? Только подумайте о великих пирамидах: знаете ли вы, что они известны своей математической точностью? Они являются еще одним доказательством изощренности египетской математики, применяемой, в данном случае, к построению.
Что касается дробей в иероглифах, мы знаем , фигура в виде открытого рта. Как будто идеализирующий число, которое метафорически «съедает» себя.
Он символизирует одно совпадение числом, которое вы поставили рядом с ним. Помимо представления единичных дробей, то есть дроби один между любым числом, они также имели две трети (2/3) и три четверти (3/4).
Добавляя эти доли единиц к нескольким футам на гравюре, мы получаем две возможные ситуации: ступни «идут» в направлении письма или ступни идут против него. Если они переходят в ту сторону, в которой выражается, они имеют в виду сложение. Если же стопы идут в противоположном направлении, это означает вычитание.
Числительные в арабский язык пришли из Индии, хотя цифрами привычного нам вида (1, 2, 3 и т.д.) пользуется весь мир, при этом почему-то называя их арабскими. В отличие от слов, пишущихся «справа налево» арабские цифры пишутся наоборот — «слева направо», что является лучшим доказательством заимствованности системы счёта от чуждой арабам культуры, а заодно и выдаёт тайну истоков происхождения цивилизации «серой подрасы» из Индии. При этом весь неарабский мир продолжает упорно не замечать факт чуждости для планеты Земля самой арабской цивилизации, отличающейся не только письменностью, но также устройством общества и семьи, религией, жизненными ценностями, принципами жизни и отношением к другим народам.
Фактов хватает, об этом будет написана отдельная статья, а пока, так как мы продолжаем ездить отдыхать на Красное море, придётся учить арабские цифры и числа на арабском языке.
Числительные, арабские цифры — египетский (каирский) диалект
Арабские цифры от 1 до 10
В египетском языке существуют количественные и порядковые числительные. Количественные числительные свободно употребляются вместо порядковых. Существуют некоторые диалектические вариации произношения, не имеющие принципиального значения и понятные всем арабам (примерно как разница между произношениями украинского и русского языков: одын, один, одыныця, единица) . Для полного раскрытия темы здесь указаны и вариации.
Знак «’» обозначает ударение.
Количественные числительные
- 1 — ва’хид, уа’хид
- 2 — итни’н, этни’н, этни’йн
- 3 — тале’та, таля’та
- 4 — арба’а
- 5 — ха’мса
- 6 — сы’тта, си’тта
- 7 — са’баа
- 8 — тама’ния, тамэ’ния
- 9 — ты’сса, ти’съа
- 10 — а’шара, а’шэра, а’шра
Единица в сочетании с именем мужского рода звучит «ва’хид», в сочетании с именем женского рода — «ва’хида». Остальные количественные числительные применяются без изменений, независимо от рода.
Числительные от 11 до 19 применяются с исчисляемым именем в единственном числе, по родам не изменяются.
- 11 — хэда’шар, хада’шр, хидаа’шар
- 12 — итна’шар, итна’шр, итнаа’шар
- 13 — талята’шар, талята’шр, тляттаа’шар
- 14 — арбаата’шар, арбаата’шр
- 15 — хамста’шар, хамаста’шр, хамастаа’шар
- 16 — ситта’шар, ситта’шр, ситтаа’шар
- 17 — сабаата’шар, сабаата’шр, сабаата’шар
- 18 — таманта’шар, таманта’шр, тмантаа’шар
- 19 — тиссата’шар, тисъата’шр, тэсаата’шар, тсаата’шар
Десятки
- 20 — ашри’н, эшри’н
- 30 — таляти’н, талети’н
- 40 — арбаи’н
- 50 — хамси’н
- 60 — сытти’н, ситти’н
- 70 — сабаи’н
- 80 — тамэни’н, тамани’н
- 90 — тиссаи’н, тисъаи’н
Сотни
- 100 — ми’йя, ме’йа
- 200 — митти’н, мите’йн
- 300 — ту’льта ми’йя, ту’льта ме’йа
- 400 — арба’ ми’йя, арба’ ме’йа, урба’ ми’йя
- 500 — хо’мсу ми’йя, хо’мсу ме’йа
- 600 — си’та ми’йя, си’та ме’йа
- 700 — са’баа ми’йя, са’баа ме’йа
- 800 — то’му ми’йя, то’мму ме’йа
- 900 — ты’сса ми’йя, ти’съа ме’йа
Тысячи
- 1 000 — альф
- 2 000 — альфе’йн, альфе’йин, итне’йн альф
- 3 000 — тале’т тале’ф, таля’т тале’ф, таляталя’ф
- 4 000 — арба’а тале’ф, арбааталя’ф
- 5 000 — ха’мса тале’ф, хамс тале’ф, хама’сталяф
- 6 000 — сит тале’ф, си’тталяф
- 7 000 — са’баа тале’ф, са’бааталяф
- 8 000 — тама’н тале’ф, тама’нияталяф
- 9 000 — ты’сса тале’ф, та’съа тале’ф, ти’сааталяф
- 10 000 — ашр тале’ф, а’шараталяф
- 11 000 — хэда’шр альф, хада’шр альф
- 12 000 — итна’шр альф
- 13 000 — талята’шр альф
- 14 000 — арбата’шр альф
- 15 000 — хамаста’шр альф, хамста’шр альф
- 16 000 — ситта’шр альф
- 17 000 — сабата’шр альф
- 18 000 — таманта’шр альф
- 19 000 — тыссата’шр альф, тисъата’шр альф
- 20 000 — ашри’ин альф, а’шрин альф
- 30 000 — таляти’н альф, т’лятин альф
- 40 000 — арбаи’н альф
- 50 000 — хамси’н альф
- 60 000 — ситти’н альф
- 70 000 — сабаи’н альф
- 80 000 — тамани’н альф
- 90 000 — тыссаи’н альф, тисъаи’н альф
- 100 000 — мит альф
- 200 000 — мите’йн альф
- 300 000 — ту’льту мит альф
- 400 000 — ро’бу мит альф
- 500 000 — хо’мсу мит альф
- 600 000 — си’ту мит альф
- 700 000 — со’бу мит альф
- 800 000 — то’му мит альф
- 900 000 — ты’сса мит альф, ти’съа мит альф
- 1 000 000 — мильу’н, мильё’н
- 2 000 000 — итни’ин мильу’н
- …
- 1 000 000 000 — милиа’р
Множественное число для миллиона — «мильуи’нин».
Чаще говорят «этн’ийн мильуи’нин», «таля’та мильуи’нин», т.е. «два миллионов, три …». Хотя граматически правильно нужно говорить «этни’йн мильу’н».
Правила числительных
Числительные от 21 содержат связующий элемент «уау», встречается произношение «ва», «уи», «уа», «у»:
- 21 — ва’хид ва ашри’н, уа’хид уау (уи) ашри’н, ва’хед у ашри’н
- 22 — этни’н ва ашри’н, этни’йн уау (уи) ашри’н, итнэ’йн у ашри’н
- 23 — тале’та ва ашри’н, таля’та уау (уи) ашри’н
- 24 — арба’ ва ашри’н, арба’ уи (уи) ашри’н
- 25 — ха’мса ва ашри’н, ха’мса уау (уи) ашри’н
- 26 — сы’тта ва ашри’н, си’тта уау (уи) ашри’н
- 27 — са’баа ва ашри’н, са’баа уау (уи) ашри’н
- 28 — тамэ’ния ва ашри’н, тама’ния уау (уи) ашрин
- 29 — ты’сса ва ашри’н, ти’съа уау (уи) ашри’н
- 30 — талети’н, таляти’н
- 31 — ва’хид ва таляти’н, уахид уау (уи) талети’н
- 32 — этни’н ва таляти’н, этнийн уау (уи) талети’н
- …
Числительные сотен:
- 101 — ми’йя у ва’хид, ми’йя ва ва’хид, ме’йя уи уа’хид
- 102 — ми’йя ва итни’н, ме’йя уи этни’йн
- 103 — ми’йя ва тале’та, ме’йя уи таля’та
- 104 — ми’йя ва арба’а, ме’йя уи арба’а
- 105 — ми’йя ва ха’мса, ме’йя уи ха’мса
- 106 — ми’йя ва сы’тта, ме’йя уи си’тта
- 107 — ми’йя ва са’баа, ме’йя уи са’баа
- 108 — ми’йя ва тамэ’ния, ме’йя уи тама’ния
- 109 — ми’йя ва ты’сса, ме’йя уи ти’съа
- 110 — ми’йя ва а’шэра, мейя уи ашра
- 120 — ми’йя ва эшри’н, мейя уи ашрин
- 130 — ми’йя ва талети’н, мейя уи талятин
- 140 — ми’йя ва арбаи’н, мейя уи арбаи’н
- 150 — ми’йя ва хамси’н, мейя уи хамсин
- 160 — ми’йя ва сытти’н, мейя уи ситтин
- 170 — ми’йя ва сабаи’н, мейя уи сабаи’н
- 180 — ми’йя ва тамэни’н, мейя уи тамани’н
- 190 — ми’йя ва тиссаи’н, мейя уи тисъаи’н
- 200 — митти’н, мите’йн
- 201 — митти’н ва ва’хид, мите’йн уи уахид
- 202 — митти’н ва итни’н, мите’йн уи этни’йн
- …
В сложных комбинациях после второй сотни происходит перенос связующего предлога-элемента «уау», «ва», «уи», «уа» и последующего числительного единиц-десятков за пределы числительного сотен-тысяч:
355 — ту’льту ме’йя хамса ва хамси’н
2216 — альфе’йн мите’йн уау ситта’шар
4555 — арба’а тале’ф хомсуме’йя ха’мса уау хамси’н
5555 — хамс тале’ф хомсуме’йя ха’мса ва хамси’н
6890 — сит тале’ф то’му ми’йя уау тисъаи’н
Формы порядковых числительных
- первый — авва’ль, ауа’ль
- первая — у’ля
- второй — та’ни, тэ’ни
- вторая — та’ния
- третий — та’лит
- третья — та’льта
- четвертый — ра’би
- четвертая — ра’биа
- пятый — ха’мис
- пятая — ха’миса
- шестой — са’тис, са’дис
- шестая — са’тса, са’дса, са’диса
- седьмой — са’би
- седьмая — са’биа
- восьмой — та’мин
- восьмая — та’мина, та’мна
- девятый — та’съи, та’си
- девятая — та’съиа, та’сиа
- десятый — а’шир
- десятая — а’шира
- 11-й — ха’ди ашир
- 11-я — ха’дия а’шира
- 12-й — та’ни а’шир
- 12-я — та’ния а’шира
- 13-й — та’лят а’шир, та’лит а’шир
- 13-я — та’лята а’шира, та’лита а’шира
- 14-й — ра’би а’шир
- 14-я — ра’биа а’шира
- 15-й — ха’мис а’шир
- 15-я — ха’миса а’шира
- 16-й — са’тис а’шир, са’дис а’шир
- 16-я — са’тиса а’шира, са’диса а’шира
- 17-й — са’би а’шир
- 17-я — са’биа а’шира
- 18-й — та’мин а’шир
- 18-я — та’мина а’шира
- 19-й — та’съи а’шир, та’си а’шир
- 19-я — та’съиа а’шира, та’сиа а’шира
- …
Дальнейшие числительные по аналогичной схеме.
В десятках женского рода окончание не меняется, изменяются только единицы:
- 21-й — ха’ди уи ашри’н, та’ни у ашри’н
- 21-я — ха’дия уи ашри’н, та’ния у ашри’н
- 22-й — та’ни уи ашри’н, та’ни у ашри’н
- 22-я — та’ниа уи ашри’н, та’ния у ашри’н
- 23-й — та’лит уи ашри’н, та’лит у ашри’н
- 23-я — та’лита уи ашри’н, та’лита у ашри’н
- …
Примечание:
Порядковое числительное «сатиса» — «шестая» может произноситься как «сатса», «тамина» «восьмая» — как «тамна», то есть происходит упущение гласного звука.
Порядковые числительные применяются в качестве вводных слов:
- во-первых — а’вваллян, а’уаллян
- во-вторых — тани’ян
- в-третьих — тали’тян
- в-четвертых — раби’ан
- в-пятых — хамси’ан
- в-шестых — сади’сан, сати’сан
- в-седьмых — саби’ан
- в–восьмых — тами’нан
- в девятых — таси’ан, тисъан
- в-десятых — аши’ран
- в-одиннадцатых — ха’дия аши’ран
Для полноты обзора арабских цифр и египетских числительных назову ещё дробные:
- четверть — ро’ба
- половина — нос
Ну и конечно же важнейшая арабская цифра 0 — ноль — цифр, пишется как наша точка.
Создатель блога Египет web, Олег.
Видеоролик для арабских детей: Арабские цифры от 1 до 10.
Цифры по египетски от 0 до 1000.
Кораллки, шляпу и спасательный круг не считаем… Без языка можно обойтись? Можно!
Без денег можно? Можно. Да пребудет с вами «всё включено». А вот без цифр проблематично. Вы же помните, как в меню были написаны одни цены на арабском для местных, а другие для туристов. Да и на базаре и в маленьких магазинчиках ценники красивые, арабские, с завитушками. И не все таксисты и продавцы говорят на английском и русском.⠀Но, для вас напишу Цифры в Египте с произношением, потому что гугл транслейт не всегда хорошо озвучивает. Даю вам 100 %, что пригодится.
⠀
Цифры в Египте. Сохраняйте!
١ — уАхэт — один
٢- этнИн — два
٣ — талАта — три
٤ — арбА — четыре
٥ — хAмсa — пять
٦ — сЭта — шесть
٧ — сAбa — семь
٨ — тамАнья — восемь
٩ — тЭса — девять
١٠ — Ашара- десять
⠀
١١ — хэдАшер — 11
١٢ — этнАшер — 12
١٣ — талатАшер — 13
١٤ — арбатАшер — 14
١٥ — хамастАшер — 15
١٦ — сэтАшэр — 16
١٧ — сабатАшер — 17
١٨ — тамантАшэр — 18
١٩ — тэсатАшэр — 19
٢٠ — ашрИн — 20
⠀
٢١ — уАхэт уэ ашрИн 21
٢٢ -этнЫн уэ ашрИн 22
٢٣ талАта уэ ашрИн 23
٢٤ — арбА уэ ашрИн 24
٢٥ 25 хамсА уэ ашрИн
٢٦ — сЭта уэ ашрИн 26
٢٧ — сабА уэ ашрИн 27
٢٨- тамАнья ашрин 28
тЭсА уэ ашрИн 29 — ٢٩
٣٠ — талатИн 30
⠀
٣١ уАхэт уэ талатИн 31
٣٢ этнЫн уэ талатИн32
٣٣ талАта у талатИн33
٣٤ арбА уэ талатИн 34
٣٥ хамсА уэ талатИн35
٣٦ сЭта уэ талатИн 36
٣٧ сАба уэ талатИн 37
٣٨ тамАнья уэ талатИн
٣٩ тЭса уэ талатИн 39
٤٠ — арбаИн
⠀
Аналогично дальше
⠀
٥٠ — хамсин 50
٦٠- сэтИн 60
٧٠ — сабАин 70
٨٠- таманИн 80
٩٠ — тэсаин 90
⠀
١٠٠ — мЭя 100
١٥٥ — мэя хАмсА хамсИн 155
и по аналогии дальше
٢٠٠ — 300 толтумЭя
٣٠٠ — 200 мэтЫн
٤٠٠ — 400 арбомЭя
٥٠٠ — 500 хамсомЭя
٦٠٠ — 600 сэтумЭя
٧٠٠ — 700 сэбамЭя
٨٠٠ — 800 тобумЭя
٩٠٠ — 900 тосумЭя
١٠٠٠ — 1000 эльф
- Смотрите также: МАССАЖИСТ.РУ — массажисты Москвы
Зарождение математических знаний у древних египтян связано с развитием хозяйственных потребностей. Без математических навыков древнеегипетские писцы не могли бы обеспечивать проведение землемерных работ, рассчитывать количество рабочих и их содержание или производить раскладку налоговых отчислений. Так что появление математики можно приурочить к эпохе возникновения самых ранних государственных образований на территории Египта.
Египетские числовые обозначения
Десятичная система счета в Древнем Египте сложилась на основе использования для подсчета предметов количества пальцев на обеих руках. Числа от одного до девяти обозначались соответствующим количеством черточек, для десятков, сотен, тысяч и так далее существовали особые иероглифические знаки.
Вероятнее всего, цифровые египетские символы возникли как результат созвучия того или иного числительного и названия какого-либо предмета, ведь в эпоху становления письменности знаки-пиктограммы имели строго предметное значение. Так, например, сотни обозначались иероглифом, изображающим веревку, десятки тысяч — изображением пальца.
В эпоху (начало II тысячелетия до н. э.) появляется более упрощенная, удобная для письма на папирусе иератическая форма письменности, соответствующим образом меняется и написание цифровых знаков. Знаменитые математические папирусы написаны иератическим письмом. Иероглифика применялась в основном для настенных надписей.
Не менялась на протяжении тысяч лет. Позиционного способа записи чисел древние египтяне не знали, поскольку не подошли еще к понятию нуля не только как самостоятельной величины, но и просто как отсутствия количества в определенном разряде (этой начальной ступени достигла математика в Вавилоне).
Дроби в математике Древнего Египта
Египтяне имели понятие о дробях и умели производить некоторые операции с дробными числами. Египетские дроби представляют собой числа вида 1/n (так называемые аликвотные дроби), поскольку дробь представлялась египтянами как одна часть чего-либо. Исключением являются дроби 2/3 и 3/4. Неотъемлемым элементом записи дробного числа был иероглиф, переводимый обычно как «один из (некоторого количества)». Для наиболее употребительных дробей существовали особые знаки.
Дробь, числитель которой отличен от единицы, египетский писец понимал буквально, как несколько частей какого-либо числа, и буквально же записывал. Например, дважды подряд 1/5, если требовалось изобразить число 2/5. Так что египетская система дробей была весьма громоздка.
Интересно, что один из священных символов египтян — так называемое «око Хора» — также имеет математический смысл. Один из вариантов мифа о схватке между божеством ярости и разрушения Сетом и его племянником солнечным богом Хором гласит, что Сет выбил Хору левый глаз и разорвал или растоптал его. Боги восстановили глаз, но не полностью. Око Хора олицетворяло разные аспекты божественного порядка в мироустройстве, такие как идея плодородия или власть фараона.
Изображение ока, почитавшегося как амулет, содержит элементы, обозначающие особый ряд чисел. Это дроби, каждая из которых вдвое меньше предыдущей: 1/2, 1/4, 1/8, 1/16, 1/32 и 1/64. Символ божественного глаза, таким образом, представляет их сумму — 63/64. Некоторые историки-математики полагают, что в этом символе отражено понятие египтян о геометрической прогрессии. Составные части изображения ока Хора использовались в практических расчетах, например при измерении объема сыпучих веществ, таких как зерно.
Принципы арифметических действий
Метод, которым пользовались египтяне при выполнении простейших арифметических операций, состоял в подсчете итогового обозначающих разряды чисел. Единицы складывались с единицами, десятки с десятками и так далее, после чего производилась окончательная запись результата. Если при суммировании получалось более десяти знаков в каком-либо разряде, «лишний» десяток переходил в высший разряд и записывался соответствующим иероглифом. Вычитание производилось таким же способом.
Без применения таблицы умножения, которой египтяне не знали, процесс вычисления произведения двух чисел, особенно многозначных, был чрезвычайно громоздким. Как правило, египтяне пользовались методом последовательного удвоения. Один из множителей раскладывался на сумму чисел, которые мы сегодня назвали бы степенями двух. Для египтянина это означало количество последовательных удвоений второго множителя и итоговое суммирование результатов. Например, умножая 53 на 46, египетский писец разложил бы 46 на сумму 32 + 8 + 4 + 2 и составил бы табличку, которую вы можете видеть ниже.
| * 1 | 53 |
| * 2 | 106 |
| * 4 | 212 |
| * 8 | 424 |
| * 16 | 848 |
| * 32 | 1696 |
Суммируя результаты в отмеченных строках, он получил бы 2438 — столько же, сколько и мы сегодня, но иным способом. Интересно, что такой двоичный метод умножения применяется в наше время в вычислительной технике.
Иногда, помимо удвоения, число могли умножать на десять (поскольку использовалась десятичная система) или на пять, как на половину десятки. Вот еще один пример на умножение с записью египетскими символами (косой черточкой помечались складываемые результаты).
Операция деления производилась также по принципу удвоения делителя. Искомое число при умножении на делитель должно было дать указанное в условии задачи делимое.
Математические знания и навыки египтян
Известно, что египтяне знали возведение в степень, а также применяли обратную операцию — извлечение квадратного корня. Кроме того, они имели представление о прогрессии и решали задачи, сводящиеся к уравнениям. Правда, уравнения как таковые не составлялись, так как еще не сложилось понимание того, что математические отношения между величинами носят универсальный характер. Задачи группировались по тематике: размежевание земель, распределение продуктов и так далее.
В условиях задач присутствует неизвестная величина, которую требуется найти. Она обозначается иероглифом «множество», «куча» и является аналогом величины «икс» в современной алгебре. Условия часто излагаются в форме, которая, казалось бы, просто требует составления и решения простейшего алгебраического уравнения, например: «куча» складывается с 1/4, также содержащей «кучу», и получается 15. Но египтянин не решал уравнение x + x/4 = 15, а подбирал искомую величину, которая удовлетворяла бы условиям.
Значительных успехов математика Древнего Египта достигла в решении геометрических задач, связанных с потребностями строительства и землемерных работ. О круге задач, которые стояли перед писцами, и о способах их решения мы знаем благодаря тому, что сохранилось несколько письменных памятников на папирусе, содержащих примеры вычислений.
Древнеегипетский задачник
Один из наиболее полных источников по истории математики в Египте — так называемый математический папирус Ринда (по имени первого владельца). Он хранится в Британском музее в виде двух частей. Небольшие фрагменты также есть в музее Нью-Йоркского исторического общества. Его также называют папирусом Ахмеса — по имени писца, переписавшего этот документ около 1650 года до н. э.
Папирус представляет собой сборник задач с решениями. Всего он содержит более 80 математических примеров по арифметике и геометрии. Например, задача на равное распределение между 10 работниками 9 хлебов решалась так: 7 хлебов делятся на 3 части каждый, и работникам выдается по 2/3 хлеба, при этом в остатке имеем 1/3. Два хлеба делятся на 5 частей каждый, выдается по 1/5 на человека. Оставшуюся треть хлеба делят на 10 частей.
Есть задача и на неравное распределение 10 мер зерна между 10 людьми. В результате образуется арифметическая прогрессия с разностью 1/8 меры.
Задача на геометрическую прогрессию носит шуточный характер: в 7 домах живет по 7 кошек, каждая из которых съела по 7 мышей. Каждая мышь съела 7 колосков, каждый колос приносит 7 мер хлеба. Нужно вычислить общее количество домов, кошек, мышей, колосьев и хлебных мер. Оно составляет 19607.
Геометрические задачи
Немалый интерес представляют математические примеры, демонстрирующие уровень знаний египтян в области геометрии. Это нахождение объема куба, площади трапеции, вычисление наклона пирамиды. Наклон выражался не в градусах, а рассчитывался как отношение половины основания пирамиды к ее высоте. Эта величина, аналогичная современному котангенсу, называлась «секед». Основными единицами длины служили локоть, составлявший 45 см («царский локоть» — 52,5 см) и хет — 100 локтей, основная единица площади — сешат, равный 100 квадратным локтям (около 0,28 Га).
Египтяне успешно справлялись с вычислением площадей треугольников, применяя способ, аналогичный современному. Вот задача из папируса Ринда: чему равна площадь треугольника, имеющего высоту 10 хет (1000 локтей) и основание 4 хета? В качестве решения предлагается десять умножить на половину от четырех. Мы видим, что метод решения абсолютно верный, подается в конкретном численном виде, а не в формализованном — умножить высоту на половину основания.
Весьма интересна задача на вычисление площади круга. Согласно приведенному решению, она равна величине 8/9 диаметра, возведенной в квадрат. Если теперь из полученной площади вычислить число «пи» (как отношение учетверенной площади к квадрату диаметра), то оно составит около 3,16, то есть довольно близко к истинной величине «пи». Таким образом, египетский способ решения площади круга был достаточно точным.
Московский папирус
Еще один важный источник наших знаний об уровне математики у древних египтян — Московский математический папирус (он же папирус Голенищева), хранящийся в Музее изобразительных искусств им. А. С. Пушкина. Это тоже задачник с решениями. Он не так обширен, содержит 25 задач, но имеет более древний возраст — примерно на 200 лет старше папируса Ринда. Большинство примеров в папирусе — геометрические, в том числе задача на вычисление площади корзины (то есть криволинейной поверхности).
В одной из задач приведен способ нахождения объема усеченной пирамиды, совершенно аналогичный современной формуле. Но поскольку все решения в египетских задачниках имеют «рецептурный» характер и приводятся без промежуточных логических этапов, без всякого объяснения, остается неизвестным, каким образом египтяне нашли эту формулу.
Астрономия, математика и календарь
Древнеегипетская математика связана и с календарными вычислениями, основанными на повторяемости некоторых астрономических явлений. Прежде всего, это предсказание ежегодного подъема Нила. Египетские жрецы заметили, что начало разлива реки на широте Мемфиса обычно совпадает с днем, когда на юге перед восходом Солнца становится виден Сириус (большую часть года эта звезда на данной широте не наблюдается).
Первоначально простейший сельскохозяйственный календарь не был привязан к астрономическим событиям и основывался на простом наблюдении сезонных изменений. Затем он получил точную привязку к восходу Сириуса, а вместе с ней появилась возможность уточнения и дальнейшего усложнения. Без математических навыков жрецы не могли бы уточнять календарь (впрочем, окончательно устранить недостатки календаря египтянам так и не удалось).
Не менее важным было умение выбрать благоприятные моменты для проведения тех или иных религиозных празднеств, также приуроченных к различным астрономическим феноменам. Так что развитие математики и астрономии в Древнем Египте, безусловно, связано с ведением календарных расчетов.
Кроме того, математические знания требуются для хронометрии при наблюдении звездного неба. Известно, что такими наблюдениями занималась особая группа жрецов — «распорядители часов».
Неотъемлемая часть ранней истории науки
При рассмотрении особенностей и уровня развития математики в Древнем Египте видна существенная незрелость, так и не преодоленная за три тысячи лет существования древнеегипетской цивилизации. До нас не дошли сколько-нибудь информативные источники эпохи становления математики, и мы не знаем, как оно происходило. Но ясно, что после некоторого развития уровень знаний и навыков застыл в «рецептурной», предметной форме без признаков прогресса на многие сотни лет.
По-видимому, устойчивый и однообразный круг вопросов, решаемых при помощи уже сложившихся методов, не создавал «спроса» на новые идеи в математике, которая и так справлялась с решением задач строительства, сельского хозяйства, налогообложения и распределения, примитивной торговли и обслуживания календаря и ранней астрономии. Кроме того, архаическое мышление не требует формирования строгой логической, доказательной базы — оно следует рецептуре как ритуалу, и это также сказалось на застойном характере древнеегипетской математики.
Вместе с тем необходимо заметить, что научное знание вообще и математика в частности делали еще первые шаги, а они всегда самые трудные. В примерах, которые демонстрируют нам папирусы с задачами, уже видны начальные ступени обобщения знаний — пока без попыток формализации. Можно сказать, что математика Древнего Египта в том виде, как мы ее знаем (из-за недостаточности источниковой базы по позднему периоду древнеегипетской истории) — это еще не наука в современном понимании, но самое начало пути к ней.
Мало кто задумывается, что те приемы, которые мы используем для письма и счета формировались на протяжении многих тысяч лет. Нам они кажутся очевидными, ну, подумаешь, умножить в столбик, перенести все члены с неизвестным на одну сторону. Ведь это так просто! На самом деле это огромные интеллектуальные завоевания человечества, которые часто были недоступны умнейшим людям прошлого. Я собираюсь (если хватит терпения и времени) написать несколько заметок о том, как считали в прошлом. В этой я расскажу про то, как считали египтяне.
Меня всегда немного интересовал древний Египет. Ну, во-первых, Египет — одно из первых государств, о котором мы много знаем, и кроме того, это очень великое государство, которое оставило огромное наследие. Я не имею в виду огромные размеры пирамид. Даже наша письменность и латинская, и кириллическая восходит к древнему Египту. Мне также всегда нравилась египетская скульптура, и мода брить голову у женщин и мужчин. Это кажется очень современным. Но это статья не о художественной культуре. Так что приступим.
Цифры и числа
Египтяне пользовались непозиционной десятичной системой счисления. Выглядели цифры примерно так:
Эти цифры относятся к т.н. иероглифическому письму, которое позже было заменено иератическим. Я очень люблю иератическое письмо. Оно выглядит весьма стильно. Но здесь я буду использовать иероглифическое начертание.
Все целые числ образовывались путем повторения знаков, приведенных выше (и некоторых других для еще более высоких разрядов). Например, 3215 будет:
Очень ясная система, хотя не слишком лаконичная. Ее просто освоить, но числа получаются не слишком удобными. С первого взгляда трудно уловить точное значение числа. Писали египтяне в разных направлениях, но я здесь пишу как привычно нам слева на право.
Теперь насчет дробей. Для трех дробей существовали специальные значки:
Все остальные дроби, у которых в числителе была единица, обозначались знаменателем и похожим на глаз значком сверху. Например, ниже я написал 1/14
Все правильные дроби записывались как сумма таких дробей. Например:
На одном сайте я прочитал, что «в некоторых случаях» египетские дроби «лучше наших». И даже в английской вики, есть такой чудный пример: «Египетские дроби иногда легче позволяют сравнить размер дробей. Например, если некто хочет знать, больше ли 4/5, чем ¾ он может превратить их в египетские дроби:
4/5= 1/2 + 1/4+ 1/20
3/4= 1/2 +1/4»
Мне этот «легкий способ» напоминает шутку про Фейнмана, который ради какой-то задачи школьного курса просуммировал ряды в уме. Я гуманитарий и особо не умею считать, но сравнивать в уме обычные дроби в их нормальной записи мне кажется гораздо проще, чем переводить их в египетский вид. Возможно, для египтян сравнения такого рода и были более удобны, так как наших дробей они не знали.
Сложение и умножение
Ну, вот мы и переходим к главному. Как египтяне считали? Сложение и вычитание целых чисел у них происходило также как и у нас, а может быть даже проще, им ведь просто нужно было объединить иероглифы и учесть смену разрядов. А как обстоит дело с умножением и делением? В древнеегипетском мире это была вовсе не тривиальная задача.
Египтяне использовали такой алгоритм для умножения. В два столбца писались числа. Первый столбец начинался с единицы, а второй с множимого. Затем каждое число в столбце удваивалось до тех пор, пока из некоторых чисел первого столбца не удастся сложить множитель. Вы поняли? На примере понятно лучше. Например, 7 на 22
1+4+8=13
и 57+228+456=741
Иногда, чтобы ускорить процесс прибегали к умножению на 10.
Может возникнуть вопрос, всегда ли можно представить множитель в таком виде? Да, на самом деле мы фактически имеем дело с двоичной системой счисления: 1*2 0 +0*2 1 +1*2 2 +1*2 3
т.е. 1+100+ 1000=1101
Деление выполнялось при помощи схожего алгоритма. Разделим 238 на 17:
Опять составляем табличку с одной стороны, которой стоит 17 с другой единица. Процесс удвоения останавливается на числе, которое при удвоении будет больше делимого.
Здесь мы останавливемся, ведь 128 на 2 = 256, а это больше 213. 128+64
Мы делим делитель по полам, используя уже привычную таблицу. К счастью 5 это 1+4.
Таким образом, окончательный результат будет
213/8 = 2+8+16+1/2+1/8 =26+1/2+1/8
Сейчас мы имеем удачный случай, но так получается не всегда.
С непозиционной египетской системой счисления, которая употреблялась в Древнем Египте, нас наглядно знакомят немногие сохранившиеся папирусы. Примеры задач и их решения в них настолько интересны, что остается только сожалеть, что их так мало.
Из них видно, что математика и египетская система счисления были тесно связаны с хозяйственными нуждами и практическим применением. Каждый год после разлива Нила приходилось восстанавливать строения, заново межевать земельные наделы, рассчитывая площадь и границы, вести учет урожая, календарь.
Что такое позиционная и непозиционная системы счислений?
Ответ таится в самом названии. Если позиция цифры влияет на результат вычислений, перед нами позиционная система чисел, если нет — непозиционная.
Если мы пишем 12 — это двенадцать, а с теми же цифрами 21 — это двадцать один. По египетской системе счисления: чтобы написать 12, понадобится использовать два раза символ единицы и один раз символ десятки, а 21 будет выглядеть как один знак единицы и два знака десятки, то есть всего надо написать три знака.
К непозиционным относятся: знакомая нам римская система, в которой цифры обозначались римскими буквами, славянская система, где также каждая буква обозначала какую-то цифру или число. Римская система справлялась со своими функциями в Западной Европе до 16 века.
Используемая нами система счисления в современной жизни — позиционная десятичная система.
Непозиционные системы хорошо подходили для выполнения простых арифметических действий, так как сложные вычисления предполагали громоздкие записи, что не мешало в Древнем Египте успешному развитию алгебры и геометрии.
Как считали египтяне?
Что это такое — египетская система счисления? Чтобы написать какое-либо число, использовали иероглифы, обозначавшие определенные числа, сумма которых равнялась нужному значению.
Специальные обозначения имелись для чисел 1, 10, 100, 1000, 10000, 100000, 1000000. При написании нужного числа каждое обозначение использовалось до 9 раз. Запись в египетской системе счисления шла по возрастанию: вначале единицы, потом десятки, сотни и так далее.
Причем писали, как правило, справа налево, но можно было и слева направо, сумма от этого не менялась. Использовалось и вертикальное написание, но тогда отсчет шел сверху вниз.
Использовалось два способа написания:
- Иероглифический, в котором употреблялись принятые иероглифы.
- Иератический, который являлся более схематичным и удобным на практике.
Экскурс в историю
История египетской системы счисления возникла в глубокой древности, первые рукописи с цифрами относятся ко второму тысячелетию до нашей эры. Денег тогда не было, поэтому система использовалась как для невероятных по сложности и величию математических задач, так и для решения ежедневных бытовых вопросов.
Ведь знание математики использовалось и при межевании земель, и при построении календарей, карт в астрономии, мореплавании, при строительстве дворцов, каналов и военных укреплений.
Египетская непозиционная система счисления применялась до 10 века нашей эры.
Она имела и мистическое значение, тайну которого унесли с собой жрецы, но частично приоткрыл миру Пифагор. У него есть труды, в которых он описывает символические значения, которые придаются цифровым иероглифам, написанные им после пребывания в Египте. Поэтому относят их описание к египетской системе счисления.
Сохранилось всего несколько папирусов тех времен, по которым можно понять, что уровень математики был высокий. Достоверно известно, что греки изучали древнеегипетскую математику. Одним из сокровенных знаний является египетская непозиционная система счисления.
Папирус Ахмеса
Папирус Ахмеса датируется 1650 г. до н.э., содержит 84 математические задачи. Он был найден в Фивах, хранится в Британском музее.
Все задачи в папирусе рассмотрены на конкретных примерах египетской системы счисления. В них показываются примеры расчетов с дробями, с целыми числами, делением и умножением.
Даны расчеты для нахождения площадей геометрических фигур: четырехугольника, круга, треугольника.
Сведения из папируса доказывают, что египетские математики умели извлекать корень, составлять арифметическую и геометрическую прогрессию, уравнения с неизвестными.
Аликвотные дроби
Интересно, что в расчетах использовались только аликвотные дроби, в которых числитель равнялся единице и обозначался таким знаком, а под ним писались значения знаменателя, а все другие дроби для расчетов вначале нужно было разложить до аликвотных. Но использовались и имели специальное обозначение дроби 2/3 и 3/4.
Для приведения обычных дробей в состояние аликвотных по египетской системе счисления нужно было потрудиться:
4/5 = 16/20 = 10/20 + 5/20 + 1/20 = 1/2+1/4 + 1/20
2/5 = 1/5 + 1/5, 2/7 = 1/4 + 1/28
3/7 = 12/28 = 24/56 = 14/56+7/56+3/56 = 1/4+1/8+1/18+1/56.
Складывались дроби современным способом: приведением к общему знаменателю, для многих значений имелись многочисленные готовые таблицы.
Умножение
Египтяне узнавали нужный результат, не зная таблицы умножения, но используя знание о том, что, если один множитель увеличить в два раза, а другой уменьшить, то результат не изменится:
32*13=16*26=8*52=4*104=2*208=1*416
Интересно, что этот способ умножения был известен на Руси, и считалось, что он пришел из Древнего Египта, а в Европе его называли русским.
Папирус Голенищева
Благодаря стараниям ученого-египтолога В. С. Голенищева, в Москве хранится папирус еще на 200 лет древнее папируса писца Ахмеса. Ученый купил его во время своей работы в Фивах.
Он был написан иератическим способом, курсивом, в нем рассматривается 25 задач, дано их описание по египетской системе счисления и решение. Его длина более 5 м при ширине 7 см. К этим задачам нет никаких комментариев, как и в предыдущем папирусе, есть только математические расчеты.
Он показывает, что египтяне умели вычислять площади треугольника, трапеции, прямоугольника, круга, а также объёмы пирамиды, призмы, параллелепипеда, цилиндра и усечённой пирамиды с большой точностью, а многие формулы полностью совпадают с современными.
При египетской системе счисления было вычислено число «пи» 3,16, которое почти соответствовало современному значению 3,14, хотя в те времена повсеместно на Востоке использовалось значение, равное 3.
Все вещи — суть числа
Считается, Пифагор прожил в Египте 22 года, глубоко изучая геометрию, философию, мистику цифр. Те открытия, которые позднее делала Пифагорейская школа, вполне могли быть совершены еще в Древнем Египте.
Поэтому считается, что труды Пифагора о мистике цифр, которые он написал позже, основаны на тайных знаниях, полученных им от египетских жрецов. Они не брали на обучение иностранцев, попал он к ним по высокой протекции, после собеседования с главным жрецом, который счел его достойным быть посвященным в тайны.
Числа были живыми сущностями, отражающими свойства пространства, музыки, энергии. Все можно выразить через математику, описав формулами видимые явления предсказать невидимые, опираясь на логику и математические закономерности.
Высота, ширина основания, угол наклона пирамиды Хеопса в Египте соответствуют математическому правилу построения пирамиды Пифагора, что также подтверждает взаимосвязь сделанных им открытий и знаний, полученных от древнеегипетских жрецов, использовавших египетскую систему счисления.
Работая с цифрами, древние мыслители не только понимали суть вещей, но и могли воздействовать на них.
Изучая математику Древнего Египта, использующую египетскую систему счисления, можно только восхищаться тем, как много было открыто людям за тысячи лет до нашей эры.
Официальный язык современного Египта — так называемый «высокий» арабский.
Арабское письмо, включая диалектное, пишется и читается справа налево. Заглавных букв нет нигде — даже в именах собственных и географических названиях. Но будьте осторожны: цифры пишутся и читаются слева направо. Если хотите разобраться в монетах и ценах, лучше выучите арабские числа, а не то, что мы привыкли называть арабскими цифрами.
При более детальном изучении вопроса оказывается, что наши «арабские» цифры частично, но далеко не полностью произошли от настоящих арабских цифр. Как утверждают некоторые источники цифры 2, 3, 7 произошли от арабских путем поворота их на 90 градусов для большего удобства записи. Если сильно не придираться, то похоже на правду. Цифры 1 и 9 также имеют арабское происхождение, и никакие повороты их написание не затронули. Действительно, тут сходство очевидно, чего не скажешь про 4, 5, 6, и 8.
Иногда кажется, что математические символы являются вненациональным научным инструментом, общим и единым для всех стран и народов.
Однако, наши «арабские» цифры отличаются как Вы уже поняли от «арабских» цифр в Египте. Европейская позиционная система записи цифр от старших разрядов к младшим, слева направо, также не единственная. На Востоке используется также система записи цифр справа — налево. В Египте цифры пишутся и читаются слева направо, так же как и у нас.
Автомобильные номера в Египте с настоящими арабскими цифрами.
На дорожных указателях и в названиях улиц часто используется и арабский и латинский шрифт.
Арабский алфавит — алфавит, используемый для записи арабского языка и (чаще всего в модифицированном виде) некоторых других языков, в частности персидского и некоторых тюркских языков. Он состоит из 28 букв и используется для письма справа налево. Арабский алфавит произошёл от финикийского алфавита включив в себя все его буквы и добавив к ним буквы отражающие специфически арабские звуки. Это буквы — са, ха, заль, дад, за, гайн.
Буквы имеют четыре графические позиции (начертания, написания):
- самостоятельную
(обособленную, изолированную от других букв), когда буква не имеет соединения ни справа от себя, ни слева; - начальную
, то есть имеющую соединение только слева (кроме алиф, заль, даль, зейн, pa, вав); - срединную
, то есть имеющую соединение и справа, и слева; - конечную
(с соединением только с правой стороны).
Буква «алиф» в изолированном состоянии не передаёт звуков, то есть не обозначает самостоятельных звуков, не имеет произношения. Она имеет только правостороннее соединение, то есть не имеет левостороннего соединения. Только правостороннее соединение имеют также буквы «вав», «даль», «заль», «pa», «зейн». Те же нормы действуют и в египетском диалекте.
Обозначение согласных
Каждая из 28 букв, кроме буквы алиф, обозначает один согласный. Начертание букв меняется в зависимости от расположения внутри слова. Все буквы одного слова пишутся слитно, за исключением шести букв (алиф, даль, заль, ра, зай, вав), которые не соединяются со следующей буквой.
«Алиф» — единственная буква арабского алфавита, не обозначающая никакой согласный звук. В зависимости от контекста, она может использоваться для обозначения долгого гласного а, либо как вспомогательный орфографический знак, не имеющий собственного звучания.
Обозначение гласных
Три долгих гласных звука арабского языка обозначаются буквами «алиф», «вав», «йа». Краткие гласные на письме, как правило, не передаются. В случаях, когда необходимо передать точное звучание слова (например, в Коране и в словарях), для обозначения гласных звуков используются надстрочные и подстрочные огласовки (харакат).
28 букв, приведённых выше, называются хуруф. Кроме них, в арабском письме используется ещё три дополнительных знака, не являющихся самостоятельными буквами алфавита.
1. Хамза (гортанная смычка) может писаться как отдельная буква, либо на букве-«подставке» («алиф», «вав» или «йа»). Способ написания хамзы определяется её контекстом в соответствии с рядом орфографических правил. Вне зависимости от способа написания, хамза всегда обозначает одинаковый звук.
2. Та-марбута («завязанная та») является формой буквы та. Она пишется только в конце слова и только после огласовки фатха. Когда у буквы та-марбута нет огласовки (например, в конце фразы), она читается как буква ха. Обычная форма буквы та называется «открытая та».
3. Алиф-максура («укороченный алиф») является формой буквы алиф. Она пишется только в конце слова, и сокращается до краткого звука а перед алиф-васла следующего слова (в частности, перед приставкой аль-). Обычная форма буквы алиф называется «удлинённый алиф».
Мало кто задумывается о том, что приемы и формулы, которые мы используем для вычисления простых или сложных чисел, формировались на протяжении многих веков, причем в различных уголках планеты. Современные математические навыки, с которыми знаком даже первоклассник, ранее были непосильными для умнейших людей. Огромный вклад в развитие этой отрасли внесла египетская некоторые элементы которой мы до сих пор используем в первозданном виде.
Краткое определение
Историкам достоверное известно, что в любой древней цивилизации главным образом развивалась письменность, а числовые значения всегда стояли на втором месте. По этой причине в математике былых тысячелетий множество неточностей, и современные эксперты порой ломают голову в подобных ребусах. Не была исключением и египетская система счисления, которая, к слову, являлась еще и непозиционной. Это означает, что положение отдельной цифры в записи числа не меняет общую величину. В качестве примера можно рассмотреть значение 15, где 1 — на первом месте, а 5 — на втором. Если мы поменяем эти цифры местами, получим гораздо большее число. А вот древнеегипетская система счисления таких перемен не предполагала. Даже в самом многозначном числе все его составляющие записывались в произвольном порядке.
Сразу отметим, что современные жители этой жаркой страны пользуются такими же арабскими цифрами, как и мы, записывая их в строгом соответствии с нужным порядком и слева направо.
Какими же были знаки?
Для записи цифр египтяне использовали иероглифы, и при этом их было не так уж и много. Дублируя их по определенному правилу, можно было получить число любой величины, правда, для этого потребовалось бы большое количество папируса. На начальном этапе существования египетская иероглифическая система счисления содержала в себе цифры 1, 10, 100, 1000 и 10000. Позже появились более значимые 10. Если нужно было записать один из вышеперечисленных показателей, использовали такие иероглифы:
Чтобы записать число, не кратное десятке, применялась данная нехитрая техника:
Расшифровка чисел
В результате примера, приведенного выше, мы видим, что на первом месте у нас обозначены 6 сотен, за ними следует два десятка и в конце две единицы. Аналогично записываются любые другие числа, для которых могут быть использованы тысячи и десятки тысяч. Однако этот пример записан слева направо, дабы современный читатель смог правильно его понять, только вот на деле египетская система счисления не являлась столь точной. Такое же значение можно было бы записать справа налево, разобраться в том, где начало, а где конец, приходилось, опираясь на рисунок с наибольшим значением. Аналогичный ориентир потребуется и в том случае, если цифры в записаны вразброс (так как система непозиционная).
Дроби также важны
Египтяне раньше многих других освоили математику. По данной причине в какой-то момент одних только цифр им стало мало, и постепенно были введены дроби. Так как древнеегипетская система счисления считается иероглифической, для записи числителей и знаменателей также использовались символы. Для ½ существовал специальный и неизменный знак, а все остальные показатели формировались таким же путем, который использовался для больших чисел. В числителе всегда фигурировал символ, имитирующий форму человеческого глаза, а в знаменателе указывали уже число.
Математические операции
Если есть цифры, их складывают и вычитают, умножают и делят. Египетская система счисления справлялась с такой задачей на отлично, хотя тут была своя специфика. Проще всего производилось складывание и вычитание. Для этого иероглифы двух чисел записывались в ряд, между ними учитывалась смена разрядов. Сложнее понять, как они умножали, так как процесс этот мало похож на современный. Составляли два столбца, один из них начинался с единицы, а другой — со второго множителя. Потом начинали удваивать каждое из этих чисел, записывая новый результат под предыдущим. Когда из отдельных чисел первого столбца удавалось собрать недостающий множитель, подводились итоги. Точнее понять этот процесс можно, взглянув на таблицу. В данном случае 7 умножаем на 22:
Результат в первой колонке 8 уже превышает 7, поэтому удваивание заканчивается на 4. 1+2+4=7, а 22+44+88=154. Этот ответ верный, хотя получен столь нестандартным для нас путем.
Вычитание и деление производились в обратном сложению и умножению порядке.
Почему сформировалась египетская система счисления?
История возникновения иероглифов, заменяющих числа, так же туманна, как возникновение всей Египетской цивилизации. Ее рождение датируется второй половиной третьего тысячелетия до нашей эры. Принято полагать, что подобная точность в те времена была вынужденной мерой. Египет уже был полноценным государством и с каждым годом становился мощнее и обширнее. Проводилось строительство храмов, велись учеты в главных органах управления, и дабы объединить все это, власти приняли решение ввести данную систему счета. Просуществовала она достаточно долго — вплоть до Х века нашей эры, после чего на смену ей пришла иератика.
Египетская система счисления: достоинства и недостатки
Главное достижение древних египтян в математике — это простота и точность. Глядя на иероглиф, всегда можно было определить, сколько десятков, сотен или тысяч записано на папирусе. Достоинством считалась также система сложения и умножения чисел. Только на первый взгляд она кажется запутанной, но вникнув в суть, вы начнете быстро и просто решать такие задачки. Недостатком была признана большая путаница. Числа могли записываться не только в любом направлении, но и беспорядочно, поэтому требовалось больше времени на их расшифровку. И последний минус, пожалуй, заключается в невероятно длинной шеренге из символов, ведь их постоянно приходилось дублировать.
Загрузка…
Официальный язык современного Египта — так называемый «высокий» арабский.
Арабское письмо, включая диалектное, пишется и читается справа налево. Заглавных букв нет нигде — даже в именах собственных и географических названиях. Но будьте осторожны: цифры пишутся и читаются слева направо. Если хотите разобраться в монетах и ценах, лучше выучите арабские числа, а не то, что мы привыкли называть арабскими цифрами.
При более детальном изучении вопроса оказывается, что наши «арабские» цифры частично, но далеко не полностью произошли от настоящих арабских цифр. Как утверждают некоторые источники цифры 2, 3, 7 произошли от арабских путем поворота их на 90 градусов для большего удобства записи. Если сильно не придираться, то похоже на правду. Цифры 1 и 9 также имеют арабское происхождение, и никакие повороты их написание не затронули. Действительно, тут сходство очевидно, чего не скажешь про 4, 5, 6, и 8.
Иногда кажется, что математические символы являются вненациональным научным инструментом, общим и единым для всех стран и народов.
Однако, наши «арабские» цифры отличаются как Вы уже поняли от «арабских» цифр в Египте. Европейская позиционная система записи цифр от старших разрядов к младшим, слева направо, также не единственная. На Востоке используется также система записи цифр справа — налево. В Египте цифры пишутся и читаются слева направо, так же как и у нас.
Автомобильные номера в Египте с настоящими арабскими цифрами.
На дорожных указателях и в названиях улиц часто используется и арабский и латинский шрифт.
Арабский алфавит — алфавит, используемый для записи арабского языка и (чаще всего в модифицированном виде) некоторых других языков, в частности персидского и некоторых тюркских языков. Он состоит из 28 букв и используется для письма справа налево. Арабский алфавит произошёл от финикийского алфавита включив в себя все его буквы и добавив к ним буквы отражающие специфически арабские звуки. Это буквы — са, ха, заль, дад, за, гайн.
Буквы имеют четыре графические позиции (начертания, написания):
- самостоятельную
(обособленную, изолированную от других букв), когда буква не имеет соединения ни справа от себя, ни слева; - начальную
, то есть имеющую соединение только слева (кроме алиф, заль, даль, зейн, pa, вав); - срединную
, то есть имеющую соединение и справа, и слева; - конечную
(с соединением только с правой стороны).
Буква «алиф» в изолированном состоянии не передаёт звуков, то есть не обозначает самостоятельных звуков, не имеет произношения. Она имеет только правостороннее соединение, то есть не имеет левостороннего соединения. Только правостороннее соединение имеют также буквы «вав», «даль», «заль», «pa», «зейн». Те же нормы действуют и в египетском диалекте.
Обозначение согласных
Каждая из 28 букв, кроме буквы алиф, обозначает один согласный. Начертание букв меняется в зависимости от расположения внутри слова. Все буквы одного слова пишутся слитно, за исключением шести букв (алиф, даль, заль, ра, зай, вав), которые не соединяются со следующей буквой.
«Алиф» — единственная буква арабского алфавита, не обозначающая никакой согласный звук. В зависимости от контекста, она может использоваться для обозначения долгого гласного а, либо как вспомогательный орфографический знак, не имеющий собственного звучания.
Обозначение гласных
Три долгих гласных звука арабского языка обозначаются буквами «алиф», «вав», «йа». Краткие гласные на письме, как правило, не передаются. В случаях, когда необходимо передать точное звучание слова (например, в Коране и в словарях), для обозначения гласных звуков используются надстрочные и подстрочные огласовки (харакат).
28 букв, приведённых выше, называются хуруф. Кроме них, в арабском письме используется ещё три дополнительных знака, не являющихся самостоятельными буквами алфавита.
1. Хамза (гортанная смычка) может писаться как отдельная буква, либо на букве-«подставке» («алиф», «вав» или «йа»). Способ написания хамзы определяется её контекстом в соответствии с рядом орфографических правил. Вне зависимости от способа написания, хамза всегда обозначает одинаковый звук.
2. Та-марбута («завязанная та») является формой буквы та. Она пишется только в конце слова и только после огласовки фатха. Когда у буквы та-марбута нет огласовки (например, в конце фразы), она читается как буква ха. Обычная форма буквы та называется «открытая та».
3. Алиф-максура («укороченный алиф») является формой буквы алиф. Она пишется только в конце слова, и сокращается до краткого звука а перед алиф-васла следующего слова (в частности, перед приставкой аль-). Обычная форма буквы алиф называется «удлинённый алиф».
С непозиционной египетской системой счисления, которая употреблялась в Древнем Египте, нас наглядно знакомят немногие сохранившиеся папирусы. Примеры задач и их решения в них настолько интересны, что остается только сожалеть, что их так мало.
Из них видно, что математика и египетская система счисления были тесно связаны с хозяйственными нуждами и практическим применением. Каждый год после разлива Нила приходилось восстанавливать строения, заново межевать земельные наделы, рассчитывая площадь и границы, вести учет урожая, календарь.
Что такое позиционная и непозиционная системы счислений?
Ответ таится в самом названии. Если позиция цифры влияет на результат вычислений, перед нами позиционная система чисел, если нет — непозиционная.
Если мы пишем 12 — это двенадцать, а с теми же цифрами 21 — это двадцать один. По египетской системе счисления: чтобы написать 12, понадобится использовать два раза символ единицы и один раз символ десятки, а 21 будет выглядеть как один знак единицы и два знака десятки, то есть всего надо написать три знака.
К непозиционным относятся: знакомая нам римская система, в которой цифры обозначались римскими буквами, славянская система, где также каждая буква обозначала какую-то цифру или число. Римская система справлялась со своими функциями в Западной Европе до 16 века.
Используемая нами система счисления в современной жизни — позиционная десятичная система.
Непозиционные системы хорошо подходили для выполнения простых арифметических действий, так как сложные вычисления предполагали громоздкие записи, что не мешало в Древнем Египте успешному развитию алгебры и геометрии.
Как считали египтяне?
Что это такое — египетская система счисления? Чтобы написать какое-либо число, использовали иероглифы, обозначавшие определенные числа, сумма которых равнялась нужному значению.
Специальные обозначения имелись для чисел 1, 10, 100, 1000, 10000, 100000, 1000000. При написании нужного числа каждое обозначение использовалось до 9 раз. Запись в египетской системе счисления шла по возрастанию: вначале единицы, потом десятки, сотни и так далее.
Причем писали, как правило, справа налево, но можно было и слева направо, сумма от этого не менялась. Использовалось и вертикальное написание, но тогда отсчет шел сверху вниз.
Использовалось два способа написания:
- Иероглифический, в котором употреблялись принятые иероглифы.
- Иератический, который являлся более схематичным и удобным на практике.
Экскурс в историю
История египетской системы счисления возникла в глубокой древности, первые рукописи с цифрами относятся ко второму тысячелетию до нашей эры. Денег тогда не было, поэтому система использовалась как для невероятных по сложности и величию математических задач, так и для решения ежедневных бытовых вопросов.
Ведь знание математики использовалось и при межевании земель, и при построении календарей, карт в астрономии, мореплавании, при строительстве дворцов, каналов и военных укреплений.
Египетская непозиционная система счисления применялась до 10 века нашей эры.
Она имела и мистическое значение, тайну которого унесли с собой жрецы, но частично приоткрыл миру Пифагор. У него есть труды, в которых он описывает символические значения, которые придаются цифровым иероглифам, написанные им после пребывания в Египте. Поэтому относят их описание к египетской системе счисления.
Сохранилось всего несколько папирусов тех времен, по которым можно понять, что уровень математики был высокий. Достоверно известно, что греки изучали древнеегипетскую математику. Одним из сокровенных знаний является египетская непозиционная система счисления.
Папирус Ахмеса
Папирус Ахмеса датируется 1650 г. до н.э., содержит 84 математические задачи. Он был найден в Фивах, хранится в Британском музее.
Все задачи в папирусе рассмотрены на конкретных примерах египетской системы счисления. В них показываются примеры расчетов с дробями, с целыми числами, делением и умножением.
Даны расчеты для нахождения площадей геометрических фигур: четырехугольника, круга, треугольника.
Сведения из папируса доказывают, что египетские математики умели извлекать корень, составлять арифметическую и геометрическую прогрессию, уравнения с неизвестными.
Аликвотные дроби
Интересно, что в расчетах использовались только аликвотные дроби, в которых числитель равнялся единице и обозначался таким знаком, а под ним писались значения знаменателя, а все другие дроби для расчетов вначале нужно было разложить до аликвотных. Но использовались и имели специальное обозначение дроби 2/3 и 3/4.
Для приведения обычных дробей в состояние аликвотных по египетской системе счисления нужно было потрудиться:
4/5 = 16/20 = 10/20 + 5/20 + 1/20 = 1/2+1/4 + 1/20
2/5 = 1/5 + 1/5, 2/7 = 1/4 + 1/28
3/7 = 12/28 = 24/56 = 14/56+7/56+3/56 = 1/4+1/8+1/18+1/56.
Складывались дроби современным способом: приведением к общему знаменателю, для многих значений имелись многочисленные готовые таблицы.
Умножение
Египтяне узнавали нужный результат, не зная таблицы умножения, но используя знание о том, что, если один множитель увеличить в два раза, а другой уменьшить, то результат не изменится:
32*13=16*26=8*52=4*104=2*208=1*416
Интересно, что этот способ умножения был известен на Руси, и считалось, что он пришел из Древнего Египта, а в Европе его называли русским.
Папирус Голенищева
Благодаря стараниям ученого-египтолога В. С. Голенищева, в Москве хранится папирус еще на 200 лет древнее папируса писца Ахмеса. Ученый купил его во время своей работы в Фивах.
Он был написан иератическим способом, курсивом, в нем рассматривается 25 задач, дано их описание по египетской системе счисления и решение. Его длина более 5 м при ширине 7 см. К этим задачам нет никаких комментариев, как и в предыдущем папирусе, есть только математические расчеты.
Он показывает, что египтяне умели вычислять площади треугольника, трапеции, прямоугольника, круга, а также объёмы пирамиды, призмы, параллелепипеда, цилиндра и усечённой пирамиды с большой точностью, а многие формулы полностью совпадают с современными.
При египетской системе счисления было вычислено число «пи» 3,16, которое почти соответствовало современному значению 3,14, хотя в те времена повсеместно на Востоке использовалось значение, равное 3.
Все вещи — суть числа
Считается, Пифагор прожил в Египте 22 года, глубоко изучая геометрию, философию, мистику цифр. Те открытия, которые позднее делала Пифагорейская школа, вполне могли быть совершены еще в Древнем Египте.
Поэтому считается, что труды Пифагора о мистике цифр, которые он написал позже, основаны на тайных знаниях, полученных им от египетских жрецов. Они не брали на обучение иностранцев, попал он к ним по высокой протекции, после собеседования с главным жрецом, который счел его достойным быть посвященным в тайны.
Числа были живыми сущностями, отражающими свойства пространства, музыки, энергии. Все можно выразить через математику, описав формулами видимые явления предсказать невидимые, опираясь на логику и математические закономерности.
Высота, ширина основания, угол наклона пирамиды Хеопса в Египте соответствуют математическому правилу построения пирамиды Пифагора, что также подтверждает взаимосвязь сделанных им открытий и знаний, полученных от древнеегипетских жрецов, использовавших египетскую систему счисления.
Работая с цифрами, древние мыслители не только понимали суть вещей, но и могли воздействовать на них.
Изучая математику Древнего Египта, использующую египетскую систему счисления, можно только восхищаться тем, как много было открыто людям за тысячи лет до нашей эры.
Египтяне придумали
эту систему около 5 000 лет тому назад.
Это одна из древнейших систем записи
чисел, известная человеку.
|
1. |
|
|
Если |
|
|
10. |
|
|
Если |
|
|
100. |
|
|
1 000. |
|
|
10 000. |
|
|
100 000. |
|
|
1 000 000. |
|
|
10 000 000. |
Записывались цифры
числа начиная с больших значений и
заканчивая меньшими. Если десятков,
единиц, или какого-то другого разряда
не было, то переходили к следующему
разряду.
—
1207,
—
1 023 029
Попробуйте сложить
эти два числа, зная, что более 9 одинаковых
иероглифов использовать нельзя.
Древняя греческая нумерация
В
древнейшее время в Греции была
распространена так называемая Аттическая
нумерация. В этой нумерации числа 1, 2,
3, 4 изображались соответствующимколичеством
вертикальных полосок:
,
,
,
.
Число 5 записывалось
знаком
(древнее
начертание буквы «Пи», с которой
начиналось слово «пять» — «пенте».
Числа 6, 7, 8, 9 обозначались сочетаниями
этих знаков:.
Число
10 обозначалось
—
заглавной «Дельта» от слова «дека»
— «десять». Числа 100, 1 000 и 10 000
обозначались H, X, M. Числа 50, 500, 5 000
обозначались комбинациями чисел 5 и 10,
5 и 100, 5 и 1 000.
Примерно в третьем
веке до нашей эры аттическая нумерация
в Греции была вытеснена другой, так
называемой «Ионийской» системой.
В ней числа 1 — 9 обозначаются первыми
буквами греческого алфавита:
числа
10, 20, … 90 изображались следующими девятью
буквами:ѓ
числа
100, 200, … 900 последними девятью буквами:
Для обозначения
тысяч и десятков тысяч пользовались
теми же цифрами, но только с добавлением
особого значка «. Любая буква с этим
значком сразу же становилась в тысячу
раз больше.
Для отличия цифр
и букв писали черточки над цифрами.
Примерно по такому
же принципу организованную систему
счисления имели в древности евреи, арабы
и многие другие народы Ближнего Востока.
Зарождение математических знаний у древних египтян связано с развитием хозяйственных потребностей. Без математических навыков древнеегипетские писцы не могли бы обеспечивать проведение землемерных работ, рассчитывать количество рабочих и их содержание или производить раскладку налоговых отчислений. Так что появление математики можно приурочить к эпохе возникновения самых ранних государственных образований на территории Египта.
Египетские числовые обозначения
Десятичная система счета в Древнем Египте сложилась на основе использования для подсчета предметов количества пальцев на обеих руках. Числа от одного до девяти обозначались соответствующим количеством черточек, для десятков, сотен, тысяч и так далее существовали особые иероглифические знаки.
Вероятнее всего, цифровые египетские символы возникли как результат созвучия того или иного числительного и названия какого-либо предмета, ведь в эпоху становления письменности знаки-пиктограммы имели строго предметное значение. Так, например, сотни обозначались иероглифом, изображающим веревку, десятки тысяч — изображением пальца.
В эпоху (начало II тысячелетия до н. э.) появляется более упрощенная, удобная для письма на папирусе иератическая форма письменности, соответствующим образом меняется и написание цифровых знаков. Знаменитые математические папирусы написаны иератическим письмом. Иероглифика применялась в основном для настенных надписей.
Не менялась на протяжении тысяч лет. Позиционного способа записи чисел древние египтяне не знали, поскольку не подошли еще к понятию нуля не только как самостоятельной величины, но и просто как отсутствия количества в определенном разряде (этой начальной ступени достигла математика в Вавилоне).
Дроби в математике Древнего Египта
Египтяне имели понятие о дробях и умели производить некоторые операции с дробными числами. Египетские дроби представляют собой числа вида 1/n (так называемые аликвотные дроби), поскольку дробь представлялась египтянами как одна часть чего-либо. Исключением являются дроби 2/3 и 3/4. Неотъемлемым элементом записи дробного числа был иероглиф, переводимый обычно как «один из (некоторого количества)». Для наиболее употребительных дробей существовали особые знаки.
Дробь, числитель которой отличен от единицы, египетский писец понимал буквально, как несколько частей какого-либо числа, и буквально же записывал. Например, дважды подряд 1/5, если требовалось изобразить число 2/5. Так что египетская система дробей была весьма громоздка.
Интересно, что один из священных символов египтян — так называемое «око Хора» — также имеет математический смысл. Один из вариантов мифа о схватке между божеством ярости и разрушения Сетом и его племянником солнечным богом Хором гласит, что Сет выбил Хору левый глаз и разорвал или растоптал его. Боги восстановили глаз, но не полностью. Око Хора олицетворяло разные аспекты божественного порядка в мироустройстве, такие как идея плодородия или власть фараона.
Изображение ока, почитавшегося как амулет, содержит элементы, обозначающие особый ряд чисел. Это дроби, каждая из которых вдвое меньше предыдущей: 1/2, 1/4, 1/8, 1/16, 1/32 и 1/64. Символ божественного глаза, таким образом, представляет их сумму — 63/64. Некоторые историки-математики полагают, что в этом символе отражено понятие египтян о геометрической прогрессии. Составные части изображения ока Хора использовались в практических расчетах, например при измерении объема сыпучих веществ, таких как зерно.
Принципы арифметических действий
Метод, которым пользовались египтяне при выполнении простейших арифметических операций, состоял в подсчете итогового обозначающих разряды чисел. Единицы складывались с единицами, десятки с десятками и так далее, после чего производилась окончательная запись результата. Если при суммировании получалось более десяти знаков в каком-либо разряде, «лишний» десяток переходил в высший разряд и записывался соответствующим иероглифом. Вычитание производилось таким же способом.
Без применения таблицы умножения, которой египтяне не знали, процесс вычисления произведения двух чисел, особенно многозначных, был чрезвычайно громоздким. Как правило, египтяне пользовались методом последовательного удвоения. Один из множителей раскладывался на сумму чисел, которые мы сегодня назвали бы степенями двух. Для египтянина это означало количество последовательных удвоений второго множителя и итоговое суммирование результатов. Например, умножая 53 на 46, египетский писец разложил бы 46 на сумму 32 + 8 + 4 + 2 и составил бы табличку, которую вы можете видеть ниже.
| * 1 | 53 |
| * 2 | 106 |
| * 4 | 212 |
| * 8 | 424 |
| * 16 | 848 |
| * 32 | 1696 |
Суммируя результаты в отмеченных строках, он получил бы 2438 — столько же, сколько и мы сегодня, но иным способом. Интересно, что такой двоичный метод умножения применяется в наше время в вычислительной технике.
Иногда, помимо удвоения, число могли умножать на десять (поскольку использовалась десятичная система) или на пять, как на половину десятки. Вот еще один пример на умножение с записью египетскими символами (косой черточкой помечались складываемые результаты).
Операция деления производилась также по принципу удвоения делителя. Искомое число при умножении на делитель должно было дать указанное в условии задачи делимое.
Математические знания и навыки египтян
Известно, что египтяне знали возведение в степень, а также применяли обратную операцию — извлечение квадратного корня. Кроме того, они имели представление о прогрессии и решали задачи, сводящиеся к уравнениям. Правда, уравнения как таковые не составлялись, так как еще не сложилось понимание того, что математические отношения между величинами носят универсальный характер. Задачи группировались по тематике: размежевание земель, распределение продуктов и так далее.
В условиях задач присутствует неизвестная величина, которую требуется найти. Она обозначается иероглифом «множество», «куча» и является аналогом величины «икс» в современной алгебре. Условия часто излагаются в форме, которая, казалось бы, просто требует составления и решения простейшего алгебраического уравнения, например: «куча» складывается с 1/4, также содержащей «кучу», и получается 15. Но египтянин не решал уравнение x + x/4 = 15, а подбирал искомую величину, которая удовлетворяла бы условиям.
Значительных успехов математика Древнего Египта достигла в решении геометрических задач, связанных с потребностями строительства и землемерных работ. О круге задач, которые стояли перед писцами, и о способах их решения мы знаем благодаря тому, что сохранилось несколько письменных памятников на папирусе, содержащих примеры вычислений.
Древнеегипетский задачник
Один из наиболее полных источников по истории математики в Египте — так называемый математический папирус Ринда (по имени первого владельца). Он хранится в Британском музее в виде двух частей. Небольшие фрагменты также есть в музее Нью-Йоркского исторического общества. Его также называют папирусом Ахмеса — по имени писца, переписавшего этот документ около 1650 года до н. э.
Папирус представляет собой сборник задач с решениями. Всего он содержит более 80 математических примеров по арифметике и геометрии. Например, задача на равное распределение между 10 работниками 9 хлебов решалась так: 7 хлебов делятся на 3 части каждый, и работникам выдается по 2/3 хлеба, при этом в остатке имеем 1/3. Два хлеба делятся на 5 частей каждый, выдается по 1/5 на человека. Оставшуюся треть хлеба делят на 10 частей.
Есть задача и на неравное распределение 10 мер зерна между 10 людьми. В результате образуется арифметическая прогрессия с разностью 1/8 меры.
Задача на геометрическую прогрессию носит шуточный характер: в 7 домах живет по 7 кошек, каждая из которых съела по 7 мышей. Каждая мышь съела 7 колосков, каждый колос приносит 7 мер хлеба. Нужно вычислить общее количество домов, кошек, мышей, колосьев и хлебных мер. Оно составляет 19607.
Геометрические задачи
Немалый интерес представляют математические примеры, демонстрирующие уровень знаний египтян в области геометрии. Это нахождение объема куба, площади трапеции, вычисление наклона пирамиды. Наклон выражался не в градусах, а рассчитывался как отношение половины основания пирамиды к ее высоте. Эта величина, аналогичная современному котангенсу, называлась «секед». Основными единицами длины служили локоть, составлявший 45 см («царский локоть» — 52,5 см) и хет — 100 локтей, основная единица площади — сешат, равный 100 квадратным локтям (около 0,28 Га).
Египтяне успешно справлялись с вычислением площадей треугольников, применяя способ, аналогичный современному. Вот задача из папируса Ринда: чему равна площадь треугольника, имеющего высоту 10 хет (1000 локтей) и основание 4 хета? В качестве решения предлагается десять умножить на половину от четырех. Мы видим, что метод решения абсолютно верный, подается в конкретном численном виде, а не в формализованном — умножить высоту на половину основания.
Весьма интересна задача на вычисление площади круга. Согласно приведенному решению, она равна величине 8/9 диаметра, возведенной в квадрат. Если теперь из полученной площади вычислить число «пи» (как отношение учетверенной площади к квадрату диаметра), то оно составит около 3,16, то есть довольно близко к истинной величине «пи». Таким образом, египетский способ решения площади круга был достаточно точным.
Московский папирус
Еще один важный источник наших знаний об уровне математики у древних египтян — Московский математический папирус (он же папирус Голенищева), хранящийся в Музее изобразительных искусств им. А. С. Пушкина. Это тоже задачник с решениями. Он не так обширен, содержит 25 задач, но имеет более древний возраст — примерно на 200 лет старше папируса Ринда. Большинство примеров в папирусе — геометрические, в том числе задача на вычисление площади корзины (то есть криволинейной поверхности).
В одной из задач приведен способ нахождения объема усеченной пирамиды, совершенно аналогичный современной формуле. Но поскольку все решения в египетских задачниках имеют «рецептурный» характер и приводятся без промежуточных логических этапов, без всякого объяснения, остается неизвестным, каким образом египтяне нашли эту формулу.
Астрономия, математика и календарь
Древнеегипетская математика связана и с календарными вычислениями, основанными на повторяемости некоторых астрономических явлений. Прежде всего, это предсказание ежегодного подъема Нила. Египетские жрецы заметили, что начало разлива реки на широте Мемфиса обычно совпадает с днем, когда на юге перед восходом Солнца становится виден Сириус (большую часть года эта звезда на данной широте не наблюдается).
Первоначально простейший сельскохозяйственный календарь не был привязан к астрономическим событиям и основывался на простом наблюдении сезонных изменений. Затем он получил точную привязку к восходу Сириуса, а вместе с ней появилась возможность уточнения и дальнейшего усложнения. Без математических навыков жрецы не могли бы уточнять календарь (впрочем, окончательно устранить недостатки календаря египтянам так и не удалось).
Не менее важным было умение выбрать благоприятные моменты для проведения тех или иных религиозных празднеств, также приуроченных к различным астрономическим феноменам. Так что развитие математики и астрономии в Древнем Египте, безусловно, связано с ведением календарных расчетов.
Кроме того, математические знания требуются для хронометрии при наблюдении звездного неба. Известно, что такими наблюдениями занималась особая группа жрецов — «распорядители часов».
Неотъемлемая часть ранней истории науки
При рассмотрении особенностей и уровня развития математики в Древнем Египте видна существенная незрелость, так и не преодоленная за три тысячи лет существования древнеегипетской цивилизации. До нас не дошли сколько-нибудь информативные источники эпохи становления математики, и мы не знаем, как оно происходило. Но ясно, что после некоторого развития уровень знаний и навыков застыл в «рецептурной», предметной форме без признаков прогресса на многие сотни лет.
По-видимому, устойчивый и однообразный круг вопросов, решаемых при помощи уже сложившихся методов, не создавал «спроса» на новые идеи в математике, которая и так справлялась с решением задач строительства, сельского хозяйства, налогообложения и распределения, примитивной торговли и обслуживания календаря и ранней астрономии. Кроме того, архаическое мышление не требует формирования строгой логической, доказательной базы — оно следует рецептуре как ритуалу, и это также сказалось на застойном характере древнеегипетской математики.
Вместе с тем необходимо заметить, что научное знание вообще и математика в частности делали еще первые шаги, а они всегда самые трудные. В примерах, которые демонстрируют нам папирусы с задачами, уже видны начальные ступени обобщения знаний — пока без попыток формализации. Можно сказать, что математика Древнего Египта в том виде, как мы ее знаем (из-за недостаточности источниковой базы по позднему периоду древнеегипетской истории) — это еще не наука в современном понимании, но самое начало пути к ней.
Мало кто задумывается о том, что приемы и формулы, которые мы используем для вычисления простых или сложных чисел, формировались на протяжении многих веков, причем в различных уголках планеты. Современные математические навыки, с которыми знаком даже первоклассник, ранее были непосильными для умнейших людей. Огромный вклад в развитие этой отрасли внесла египетская некоторые элементы которой мы до сих пор используем в первозданном виде.
Краткое определение
Историкам достоверное известно, что в любой древней цивилизации главным образом развивалась письменность, а числовые значения всегда стояли на втором месте. По этой причине в математике былых тысячелетий множество неточностей, и современные эксперты порой ломают голову в подобных ребусах. Не была исключением и египетская система счисления, которая, к слову, являлась еще и непозиционной. Это означает, что положение отдельной цифры в записи числа не меняет общую величину. В качестве примера можно рассмотреть значение 15, где 1 — на первом месте, а 5 — на втором. Если мы поменяем эти цифры местами, получим гораздо большее число. А вот древнеегипетская система счисления таких перемен не предполагала. Даже в самом многозначном числе все его составляющие записывались в произвольном порядке.
Сразу отметим, что современные жители этой жаркой страны пользуются такими же арабскими цифрами, как и мы, записывая их в строгом соответствии с нужным порядком и слева направо.
Какими же были знаки?
Для записи цифр египтяне использовали иероглифы, и при этом их было не так уж и много. Дублируя их по определенному правилу, можно было получить число любой величины, правда, для этого потребовалось бы большое количество папируса. На начальном этапе существования египетская иероглифическая система счисления содержала в себе цифры 1, 10, 100, 1000 и 10000. Позже появились более значимые 10. Если нужно было записать один из вышеперечисленных показателей, использовали такие иероглифы:
Чтобы записать число, не кратное десятке, применялась данная нехитрая техника:
Расшифровка чисел
В результате примера, приведенного выше, мы видим, что на первом месте у нас обозначены 6 сотен, за ними следует два десятка и в конце две единицы. Аналогично записываются любые другие числа, для которых могут быть использованы тысячи и десятки тысяч. Однако этот пример записан слева направо, дабы современный читатель смог правильно его понять, только вот на деле египетская система счисления не являлась столь точной. Такое же значение можно было бы записать справа налево, разобраться в том, где начало, а где конец, приходилось, опираясь на рисунок с наибольшим значением. Аналогичный ориентир потребуется и в том случае, если цифры в записаны вразброс (так как система непозиционная).
Дроби также важны
Египтяне раньше многих других освоили математику. По данной причине в какой-то момент одних только цифр им стало мало, и постепенно были введены дроби. Так как древнеегипетская система счисления считается иероглифической, для записи числителей и знаменателей также использовались символы. Для ½ существовал специальный и неизменный знак, а все остальные показатели формировались таким же путем, который использовался для больших чисел. В числителе всегда фигурировал символ, имитирующий форму человеческого глаза, а в знаменателе указывали уже число.
Математические операции
Если есть цифры, их складывают и вычитают, умножают и делят. Египетская система счисления справлялась с такой задачей на отлично, хотя тут была своя специфика. Проще всего производилось складывание и вычитание. Для этого иероглифы двух чисел записывались в ряд, между ними учитывалась смена разрядов. Сложнее понять, как они умножали, так как процесс этот мало похож на современный. Составляли два столбца, один из них начинался с единицы, а другой — со второго множителя. Потом начинали удваивать каждое из этих чисел, записывая новый результат под предыдущим. Когда из отдельных чисел первого столбца удавалось собрать недостающий множитель, подводились итоги. Точнее понять этот процесс можно, взглянув на таблицу. В данном случае 7 умножаем на 22:
Результат в первой колонке 8 уже превышает 7, поэтому удваивание заканчивается на 4. 1+2+4=7, а 22+44+88=154. Этот ответ верный, хотя получен столь нестандартным для нас путем.
Вычитание и деление производились в обратном сложению и умножению порядке.
Почему сформировалась египетская система счисления?
История возникновения иероглифов, заменяющих числа, так же туманна, как возникновение всей Египетской цивилизации. Ее рождение датируется второй половиной третьего тысячелетия до нашей эры. Принято полагать, что подобная точность в те времена была вынужденной мерой. Египет уже был полноценным государством и с каждым годом становился мощнее и обширнее. Проводилось строительство храмов, велись учеты в главных органах управления, и дабы объединить все это, власти приняли решение ввести данную систему счета. Просуществовала она достаточно долго — вплоть до Х века нашей эры, после чего на смену ей пришла иератика.
Египетская система счисления: достоинства и недостатки
Главное достижение древних египтян в математике — это простота и точность. Глядя на иероглиф, всегда можно было определить, сколько десятков, сотен или тысяч записано на папирусе. Достоинством считалась также система сложения и умножения чисел. Только на первый взгляд она кажется запутанной, но вникнув в суть, вы начнете быстро и просто решать такие задачки. Недостатком была признана большая путаница. Числа могли записываться не только в любом направлении, но и беспорядочно, поэтому требовалось больше времени на их расшифровку. И последний минус, пожалуй, заключается в невероятно длинной шеренге из символов, ведь их постоянно приходилось дублировать.
→
египетских — прилагательное, родительный п., мн. ч.
↳
египетских — прилагательное, винительный п., од., мн. ч.
↳
египетских — прилагательное, предложный п., од., мн. ч.
Часть речи: прилагательное
Положительная степень:
| Единственное число | Множественное число | |||
|---|---|---|---|---|
| Мужской род | Женский род | Средний род | ||
| Им. |
египетский |
египетская |
египетское |
египетские |
| Рд. |
египетского |
египетской |
египетского |
египетских |
| Дт. |
египетскому |
египетской |
египетскому |
египетским |
| Вн. |
египетского египетский |
египетскую |
египетское |
египетские египетских |
| Тв. |
египетским |
египетскою египетской |
египетским |
египетскими |
| Пр. |
египетском |
египетской |
египетском |
египетских |
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Система древнеегипетских цифр использовалась в Древнем Египте примерно с 3000 г. до н.э. [1] до начала первого тысячелетия нашей эры. Это была система счисления, основанная на десятичных числах, часто округленных в высшей степени и написанная иероглифами . У египтян не было понятия о системе счисления знаков, такой как десятичная система . [2] иератическая форма цифр подчеркнуты точные конечный ряд обозначения, зашифровано один-к-одному на египетском алфавит. [ необходима цитата ]
Цифры и числа [ править ]
Следующие иероглифы использовались для обозначения степеней десяти:
Множественные значения этих значений выражались повторением символа столько раз, сколько необходимо. Например, резьба по камню из Карнака показывает число 4622 как:
Египетские иероглифы можно было писать в обоих направлениях (и даже вертикально). В этом примере символы уменьшаются в значении сверху вниз и слева направо. На оригинальной резьбе по камню оно расположено справа налево, и, таким образом, знаки меняются местами. [ необходима цитата ]
Нулевые и отрицательные числа [ править ]
| нфр |
сердце с трахеей красивое, приятное, хорошее |
|---|
К 1740 году до нашей эры у египтян в бухгалтерских текстах был символ нуля. Символ nfr (𓄤), означающий красивый, также использовался для обозначения базового уровня на рисунках гробниц и пирамид, а расстояния измерялись относительно базовой линии как выше или ниже этой линии. [4]
Дроби [ править ]
Рациональные числа также могут быть выражены, но только в виде суммы единичных дробей , то есть , суммы обратных положительных целых чисел, за исключением 2 / 3 и 3 / 4 . Иероглиф, обозначающий дробь, был похож на рот, что означало «часть»:
Фракции были написаны с этим фракционным солидусом , то есть , в числителе 1 и положительный знаменателем ниже. Таким образом, 1 / 3 была написана как:
Специальные символы были использованы для 1 / 2 , и для не-блока фракций 2 / 3 и, реже, 3 / 4 :
Если знаменатель становился слишком большим, «рот» просто помещался над началом «знаменателя»:
Сложение и вычитание [ править ]
Для знаков плюс и минус иероглифы
использовались: если ступни указывали в направлении письма, это означало сложение , в противном случае — вычитание . [5]
Письменные числа [ править ]
Как и в большинстве современных языков дня, древний египетский язык также может выписывать цифры как слова фонетический, так же , как можно написать тридцать вместо «30» на английском языке . Слово ( тридцать ), например, было записано как
в то время как цифра ( 30 ) была
Однако это было необычно для большинства чисел, кроме единицы и двух, и большую часть времени использовались знаки. [ необходима цитата ]
Иератические числа [ править ]
Поскольку административные и бухгалтерские тексты были написаны на папирусе или остраке , а не высечены на твердом камне (как иероглифические тексты), подавляющее большинство текстов, использующих египетскую систему счисления, используют иератический шрифт. Примеры иератического написания числительных можно найти еще в раннединастический период . Abusir Papyri Старого Царства — это особенно важный корпус текстов, в которых используются иератические числа. [ необходима цитата ]
Бойер доказал 50 лет назад [ когда? ] в этом иератическом письме использовалась другая система счисления, с использованием отдельных знаков для чисел от 1 до 9, кратных 10 от 10 до 90, сотен от 100 до 900 и тысяч от 1000 до 9000. Таким образом, большое число, например 9999, могло быть написанным только четырьмя знаками, объединяющими знаки 9000, 900, 90 и 9, в отличие от 36 иероглифов. Бойер увидел новые иератические цифры как зашифрованные, впервые в истории человечества сопоставив одно число с одной египетской буквой. Греки приняли новую систему, нанеся свои счетные числа на два из своих алфавитов, дорический и ионийский. [ необходима цитата ]
В древнейших иератических текстах отдельные цифры явно были написаны в зашифрованном отношении к египетскому алфавиту. Но во времена Древнего Царства была разработана серия стандартизированных писем для групп знаков, содержащих более одной цифры, повторяемой, как это делали римские цифры. Однако повторение одной и той же цифры для каждого значения места в иератическом письме не разрешалось. По мере развития иератической системы письма со временем эти группы знаков были еще более упрощены для быстрого письма; этот процесс продолжился и в Demotic . [ необходима цитата ]
Два известных математических папируса с использованием иератического письма — это Московский математический папирус и Математический папирус Райнда . [ необходима цитата ]
Египетские слова для чисел [ править ]
В следующей таблице показано реконструированные средние египетские формы цифр (которые обозначены предшествующая звездочка), то транслитерации из иероглифов используются для записи их, и , наконец, коптские цифры , которые произошли от них и которые дают египтологам подсказку относительно вокализма оригинальных египетских чисел. Breve (˘) в некоторых реконструированных формах указывает на короткий гласный звук, качество которого остается неопределенным; буква «е» представляет собой гласный звук, который изначально был u или i (точное качество неизвестно), но стал e в позднем египтянине. [ необходима цитата ]
| Египетская транслитерация | Реконструированная вокализация |
Английский перевод | Коптский (сахидский диалект) |
|
|---|---|---|---|---|
| по Каллендеру 1975 [6] | per Loprieno 1995 [7] | |||
| wꜥ (w) ( маск. ) wꜥt ( жен. ) |
* wíꜥyaw (маск.) * wiꜥī́yat (жен.) |
* wúꜥꜥuw (маск.) |
один |
ⲟⲩⲁ ( oua ) (маск.) ⲟⲩⲉⲓ ( ouei ) (жен.) |
| snwj ( маск .) sntj (жен.) |
* sínwaj (маск.) * síntaj (жен.) |
* sinúwwaj (маск.) |
два |
ⲥⲛⲁⲩ ( snau ) (маск.) ⲥⲛ̄ⲧⲉ ( snte ) (fem.) |
| ḫmtw ( маск .) ḫmtt (жен.) |
* ḫámtaw (маск.) * ámtat (жен.) |
* ḫámtaw (маск.) |
три |
ϣ ⲟⲙⲛ̄ⲧ ( šomnt ) (маск.) ϣ ⲟⲙⲧⲉ ( šomte ) (фем.) |
| jfdw ( masc .) jfdt (fem.) |
* j˘fdáw (маск.) * j˘fdát (жен.) |
* jifdáw (маск.) |
четыре |
ϥ ⲧⲟⲟⲩ ( ftoou ) (masc.) ϥ ⲧⲟ ( fto ) или ϥ ⲧⲟⲉ ( ftoe ) (fem.) |
| djw ( маск .) djt (жен.) |
* dī́jaw (маск.) * dī́jat (жен.) |
* dī́jaw (маск.) |
пять |
ϯ ⲟⲩ ( tiou ) (маск.) ϯ ( ti ) или ϯ ⲉ ( галстук ) (жен.) |
| sjsw или jsw (?) (маск.) sjst или jst (?) (фем.) |
* jssáw (маск.) * j˘ssát (жен.) |
* sáʾsaw (маск.) |
шесть |
ⲥⲟⲟⲩ ( soou ) (MASC.) ⲥⲟ ( так ) или ⲥⲟⲉ ( SOE ) (внут.) |
| sfḫw ( маск .) sfḫt (жен.) |
* sáfaw (маск.) * sáfat (жен.) |
* sáfḫaw (маск.) |
Семь |
ϣ ⲁ ϣϥ̄ ( šašf ) (маск.) ϣ ⲁ ϣϥ ⲉ ( šašfe ) (жен.) |
| ḫmnw ( маск .) ḫmnt (жен.) |
* mā́naw (маск.) * mā́nat (жен.) |
* amā́naw (маск.) |
8 |
ϣ ⲙⲟⲩⲛ ( šmoun ) (маск.) ϣ ⲙⲟⲩⲛⲉ ( šmoune ) (жен.) |
| psḏw ( маск .) psḏt (жен.) |
* p˘sī́ḏaw (маск.) * p˘sī́ḏat (жен.) |
* pisī́ḏaw (маск.) |
9 |
ⲯⲓⲥ ( psis ) (masc.) ⲯⲓⲧⲉ ( psite ) (fem.) |
| mḏw ( маск .) mḏt (жен.) |
* mū́ḏaw (маск.) * mū́ḏat (жен.) |
* mū́ḏaw (маск.) |
десять |
ⲙⲏⲧ ( mēt ) (маск.) ⲙⲏⲧⲉ ( mēte ) (жен.) |
| mḏwtj , ḏwtj или ḏbꜥty (?) (маск.) mḏwtt, ḏwtt или ḏbꜥtt (?) (жен.) |
* ubā́ꜥataj (маск.) |
* (му) ḏawā́taj (маск.) |
20 |
ϫ ⲟⲩⲱⲧ ( jouōt ) (маск.) ϫ ⲟⲩⲱⲧⲉ ( jouōte ) (жен.) |
| mꜥbꜣ ( маск .) mꜥbꜣt (жен.) |
* máꜥb˘ꜣ (маск.) |
* máꜥb˘ꜣ (маск.) |
30 |
ⲙⲁⲁⲃ ( maab ) (MASC.) ⲙⲁⲁⲃⲉ ( maabe ) (внут.) |
| ḥmw | * ḥ˘mí (?) |
* ḥ˘méw |
сорок |
ϩ ⲙⲉ ( хмэ ) |
| dyw | * díjwu |
* díjjaw |
50 |
ⲧⲁⲉⲓⲟⲩ ( тэио ) |
| sjsjw , sjsw или jswjw (?) |
* jssáwju |
* saʾséw |
шестьдесят |
ⲥⲉ ( se ) |
| sfḫjw , sfḫw или sfḫwjw (?) |
* safḫáwju |
* safḫéw |
семьдесят |
ϣϥ ⲉ ( šfe ) |
| ḫmnjw , ḫmnw или ḫmnwjw (?) |
* amanáwju |
* amnéw |
восемьдесят |
ϩ ⲙⲉⲛⲉ ( хменэ ) |
| psḏjw или psḏwjw (?) |
* p˘siḏáwju |
* pisḏíjaw |
девяносто |
ⲡⲥⲧⲁⲓⲟⲩ ( pstaiou ) |
| št | * šúwat |
* ší (nju) т |
Сто |
ϣ ⲉ ( še ) |
| štj | * šū́taj |
* šinjū́taj |
двести |
ϣ ⲏⲧ ( šēt ) |
| ḫꜣ | * ḫaꜣ |
* ḫaꜣ |
одна тысяча |
ϣ ⲟ ( šo ) |
| ḏbꜥ | * ubáꜥ |
* ḏ˘báꜥ |
десять тысяч |
ⲧⲃⲁ ( TBA ) |
| ḥfn | сто тысяч |
|||
| ḥḥ | * ḥaḥ |
* ḥaḥ |
один миллион |
ϩ ⲁ ϩ ( ха ) «много» |
См. Также [ править ]
- Египетский язык
- Египетская математика
Ссылки [ править ]
- ^ «Египетские цифры» . Проверено 25 сентября 2013 .
- ^ «История чисел» Джона Маклиша
- ^ Мерцбы, Ут С. , и Карл Б. Бойер. История математики. Хобокен, Нью-Джерси: Джон Вили, 2011, стр. 10
- ^ Джордж Гевергезе Джозеф (2011). Гребень павлина: неевропейские корни математики (Третье изд.). Принстон. п. 86. ISBN 978-0-691-13526-7.
- ^ Каджори, Флориан (1993) [1929]. История математических обозначений . Dover Publications . стр. стр. 229-230. ISBN 0-486-67766-4.
- ^ Каллендер, Джон Б. (1975) Средний египтянин , 1975
- ^ Loprieno, Антонио (1995) Древнеегипетский: лингвистическая Введение , Кембридж: Cambridge University Press, стр. 71, 255
Библиография [ править ]
- Аллен, Джеймс Пол (2000). Среднеегипетский язык: введение в язык и культуру иероглифов . Кембридж: Издательство Кембриджского университета. Цифры обсуждались в §§9.1–9.6.
- Гардинер, Алан Хендерсон (1957). Египетская грамматика; Введение в изучение иероглифов . 3-е изд. Оксфорд: Институт Гриффита. Цифры см. В §§259–266.
- Гедике, Ганс (1988). Древнеиратическая палеография . Балтимор: Halgo, Inc.
- Мёллер, Георг (1927). Hieratische Paläographie: Die aegyptische Buchschrift в ихрере Entwicklung von der Fünften Dynastie bis zur römischen Kaiserzeit. 3 тт. 2-е изд. Лейпциг: JC Hinrichs’schen Buchhandlungen. (Перепечатано Оснабрюк: Отто Целлер Верлаг, 1965)
Внешние ссылки [ править ]
- Вступление
- Египетские цифры
- Цифры и даты
- http://egyptianmath.blogspot.com
Без цифр в Египте никуда. Они вам нужны будут и в магазинах, и на рынках, и в транспорте, и при оплате коммунальных услуг.
1. Десятки
10. عِشرين [эшрИн] – двадцать. ٢٠
11. تلاتين [талятИн] – тридцать. ٣٠
12. اربعين [арбаИн] – сорок. ٤٠
13. خمسين [хамсИн] – пятьдесят. ٥٠
14. ستين [сетИн] – шестьдесят. ٦٠
15. سبعين [сабаИн] – семьдесят. ٧٠
16. تمانين [таманИн] – восемьдесят. ٨٠
17. تسعين [тесаИн] – девяносто. ٩٠
2. Двухзначные числа
Посмотрим, как произносятся двузначные цифры (c 20 до 100). Порядок – обратный привычному нам. Сначала читаются единицы, потом десятки. Между ними используется союз «и», который в Египетском диалекте произносится как [уи] или [уа] (по вашему желанию на выбор).
1. واحِد و عِشرين [уЭхед уи эшрИн] – двадцать один. Пишется: ٢١
2. اِتنين و عشرين [этнИн уи эшрИн] – двадцать два. ٢٢
3. تلاتة و عشرين [тэлЯта уи эшрИн] – двадцать три. ٢٣
4. اربعة و عشرين [арбАа уи эшрИн] – двадцать четыре. ٢٤
5. خمسة و عشرين [хАмса уи эшрИн] – двадцать пять. ٢٥
6. ستّة و عشرين [сЕтта уи эшрИн] – двадцать шесть. ٢٦
7. سبعة و عشرين [сАбаа уи эшрИн] – двадцать семь. ٢٧
8. تمانية و عشرين [тамАнья уи эшрИн] – двадцать восемь. ٢٨
9. تسعة و عشرين [тЕсса уи эшрИн] – двадцать девять. ٢٩
Все остальные двузначные цифры строятся по такому же принципу.
3. Сотни!
А теперь узнаем, как произносятся в Египетском диалекте сотни:
1. مِية [мЕя] – сто, 100. Пишется: ١٠٠
2. مِتين [метИн] – двести, 200. ٢٠٠
3. تُلتُميّة [тольтомЕя] – триста, 300. ٣٠٠
4. رثبعُميّة [робомЕя] – четыреста, 400. ٤٠٠
5. خمسُمِيّة [хомсомЕя] – пятьсот, 500. ٥٠٠
6. سُتُّميّة [соттомЕя] – шестьсот, 600. ٦٠٠
7. سُبعُمِيّة [собомЕя] – семьсот, 700. ٧٠٠
8. تُمنُمِيّة [томномЕя] – весомьсот, 800. ٨٠٠
9. تُسعُمِيّة [тоссомЕя] – девятьсот, 900. ٩٠٠
4. Трехзначные числа
Обратим внимание, как читаются трехзначные числа. В них используется только один союз و. При этом порядок может прямым и частично прямым.
Начнем с чисел, состоящих из сотен и единиц. В этом случае порядок цифр прямой – сначала читаются сотни, потом единицы, соединённые союзом و[уи] – и:
1. مِيّة و واحِد [мЕя уи уЭхед] – сто один. Пишется: ١٠١
2. مِيّة و اِتنين [мЕя уи этнИн] – сто два. ١٠٢
3. مِيّة و تلاتة [мЕя уи тэлЯта] – сто три. ١٠٣
4. مِيّة و ارْبعة [мЕя уи арбАа] – сто четыре. ١٠٤
5. مِيّة و خمْسة [мЕя уи хАмса] – сто пять. ١٠٥
6. مِيّة و سِتّة [мЕя уи сЕтта] – сто шесть. ١٠٥
7. مِيّة و سبعة [мЕя уи сАбаа] – сто семь. ١٠٧
8. مِيّة و تمانسة [мЕя уи тамАнья] – сто восемь. ١٠٨
9. مِيّة و تسعة [мЕя уи тЕсаа] – сто девять. ١٠٩
Точно также обстоит дело с другими сотнями. Примеры:
10. مِتين و واحِد [метИн уи уЭхед] – двести один. ٢٠١
11. تُلتًمية و اِتنين [тольтомЕя уи этнИн] – триста два. ٣٠٢
12. رُبعُميّة و خمْسة [робомЕя уи хАмса] – четыреста пять. ٤٠٥
И так далее.
Цифры от 110 до 120, а также сотни с десятками читаются в прямом порядке.
Примеры:
1. مِيّة و حِداشر [мЕя уи хедАшар] – сто одиннадцать. Пишется: ١١١
2. مِيّة و اِتناشر [мЕя уи этнАшар] – сто двенадцать. ١١٢
3. مِتين و تلتاشر [метИн уи талятАшар] – двести тринадцать. ٢١٣
4. تُلتُميّة و اربعتاشر [тольтомЕя уи арбаатАшар] – триста четырнадцать. ٣١٤
5. رُبعُميّة و خمستاشر [робомЕя уи хамастАшар] – четыреста пятнадцать. ٤١٥
6. خُمسُميّة وسِتّاشر [хомсомЕя уи сеттАшар] – пятьсот шестнадцать. ٥١٦
7. سُتُّميّة و سبعتاشر [сотомЕя уи сабаатАшар] – шестьсот семнадцать. ٦١٧
8. سُبعميّة و تمنتاشر [собомЕя уи тамантАшар] – семьсот восемнадцать. ٧١٨
9. تُمنُميّة و تسعتاشر [томномЕя уи тесаатАшар] – восемьсот девятнадцать. ٨١٩
10. تُسعُميّة و عِشرين [тоссоумЕя уи эшрИн] – девятьсот двадцать. ٩٢٠
11. مِيّة و تلاتين [мЕя уи талятИн] – сто тридцать. ١٣٠
12. مِتين و اربعين [метИн уи арбаИн] – двести сорок.٢٤٠
13. تُلتُمِيّة و خمسين [тольтомЕя уи хамсИн] – триста пятьдесят. ٣٥٠
14. سُتُّمِيّة و سِتّين [соттомЕя уи сеттИн] – шестьсот шестьдесят. ٦٦٠
Сотни с десятками и единицами читаются смешанно – в прямом и обратном порядке. Сначала произносятся сотни, потом единицы, потом союз و [уи], который переводится как «и», затем десятки. Между сотнями и единицами союз و не используется.
Примеры подобных цифр:
1. مِية واحِد و عِشرين [мЕя уЭхед уи эшрИн] – сто двадцать один. Пишется: ١٢١
2. مِية خمْسة و تلاتين [мЕя хАмса уи талятИн] – сто тридцать пять. ١٣٥
3. متين تلاتة و عِشرين [метИн тэлЯта уи эшрИн] – двести двадцать три. ٢٢٣
4. تُلْتُميّة اِتنين و ارْبعين [тольтомЕя этнИн уи арбаИн] – триста сорок два. ٣٤٢
5. رُبعميّة ارْبعة و خمسين [робомЕя арбАа уи хамсИн] – четыреста пятьдесят четыре. ٤٥٤
6. خُمسُميّة سِتّة و سِتين [хомсомЕя сЕтта уи сеттИн] – пятьсот шестьдесят шесть. ٥٦٦
7. سُبعميّة سبعة و سبعين [собомЕя сАбаа уи сабаИн] – семьсот семьдесят семь. ٧٧٧
8. تُمنُميّة خمسة و تِسعين [томномЕя хАмса уи тессаИн] – восемьсот девяносто пять. ٨٩٥
9. تُسعُميّة تِسعة و تمانين [тоссоумЕя тЕсаа уи таманИн] – девятьсот восемьдесят девять. ٩٨٩
10. الْف [альф] – тысяча.١٠٠٠
5. Двойственное число
В отличие от русского языка, в египетском диалекте есть двойственное число, которое означает «два предмета». Образуется оно для существительного мужского рода присоединением к слову окончания ين [ин], для существительного женского рода – добавлением окончания تين [тин].
Примеры двойственного числа для слов мужского рода:
1.مكْتب [мАктаб] офис, مكتبين [мактабИн] – два офиса.
2.مفتاح [муфтЭх] – ключ, مفتاحين [муфтэхИн] – два ключа.
3. شهر[шагхр] – месяц, شهرين [шагхрИн] – два месяца.
Обратите внимание! Нельзя говорить:
اِتنين مكتب [этнИн мАктаб].
Однако допустимо использование числительного اِتنين [этнИн] после существительного в двойственном числе. Пример: اِتنين مكتبين [мактабИн этнИн] – два офиса.
Примеры двойственного числа для слов женского рода:
4. عربية [арабИя] – машина, عربيتين [арабийтИн] – две машины.
5. شنْطة [шАнта] – сумка, سنْطتين [шАнтатИн] – две сумки.
6. سنة [сАна] – год, سنتين [санатИн] – два года.
Какие цифры в Египте и что нужно знать про них туристам
Во время отдыха и путешествия по Египту туристам нужно быть готовыми к тому, что в повседневной и официальной жизни здесь используются не привычные нам современные арабские цифры, а традиционные арабские (или как их называют гиды – египетские цифры, а также они известны как индо-арабские), которые сильно отличаются по написанию. Арабские цифры вы встретите в Египте везде: номера машину казаны с их помощью, ценники в магазинах также часто пишут ими, местные калькуляторы работают на них, и даже банки и обменные пункты иногда используют их, возможно для того, чтобы немного запутать туристов 😃.
Но на самом деле это вовсе не значит, что туристу и путешественнику в Египте без знания индо-арабских цифр не обойтись. Практически везде на курортах в магазинах ценники дублируются на привычных нам современных цифрах, даже на деньгах Египта достоинство купюры продублировано ими с одной стороны. Все даты на товарах и цены в чеках также отпечатываются на привычных цифрах. Тем не менее, знание традиционных индо-арабских цифр позволит вам расширить свой кругозор, в некоторых случаях подстраховаться от обмана в магазине или при обмене валюты, а то и просто блеснуть свой осведомленностью перед местными торговцами.
В отличие от арабской письменности, арабские цифры читаются слева направо, т.е. так же как у нас. Т.е. чтобы перевести число из арабского вида в привычный нам, просто заменяйте последовательно числа по таблице, и все. А вот таблица для замены:
| Современное арабское написание | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Индо-арабские цифры в Египте | ٠ | ١ | ٢ | ٣ | ٤ | ٥ | ٦ | ٧ | ٨ | ٩ |
А вот простой пример перевода: ١٣٩ = 139
А если посмотреть на номер машины на фото, то вы прочитаете там ٩٤٦٤ = 9565
🕒 21 Февраля, 2023