Определение натурального числа
Натуральные числа — это числа, которые мы используем для подсчета чего-то конкретного, осязаемого.
Вот какие числа называют натуральными: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и т. д.
Натуральный ряд — последовательность всех натуральных чисел, расположенных в порядке возрастания. Первые сто можно посмотреть в таблице.
| Особенности натуральных чисел |
|---|
|
Какие операции возможны над натуральными числами
- сложение:
слагаемое + слагаемое = сумма; - умножение:
множитель × множитель = произведение; - вычитание:
уменьшаемое − вычитаемое = разность.При этом уменьшаемое должно быть больше вычитаемого, иначе в результате получится отрицательное число или ноль;
- деление:
делимое : делитель = частное; - деление с остатком:
делимое / делитель = частное (остаток); - возведение в степень:
ab, где a — основание степени, b — показатель степени.
Записывайтесь на курсы обучения математике для учеников с 1 по 11 классы!
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Десятичная запись натурального числа
В школе мы проходим тему натуральных чисел в 5 классе, но на самом деле многое нам может быть интуитивно понятно и раньше. Проговорим важные правила.
Мы регулярно используем цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. При записи любого натурального числа можно использовать только эти цифры без каких-либо других символов. Записываем цифры одну за другой в строчку слева направо, используем одну высоту.
Примеры правильной записи натуральных чисел: 208, 567, 24, 1 467, 899 112. Эти примеры показывают нам, что последовательность цифр может быть разной и некоторые даже могут повторяться.
077, 0, 004, 0931 — это примеры неправильной записи натуральных чисел, потому что ноль расположен слева. Число не может начинаться с нуля. Это и есть десятичная запись натурального числа.
Количественный смысл натуральных чисел
Натуральные числа несут в себе количественный смысл, то есть выступают в качестве инструмента для нумерации.
Представим, что перед нами банан 🍌. Мы можем записать, что видим 1 банан. При этом натуральное число 1 читается как «один» или «единица».
Но термин «единица» имеет еще одно значение: то, что можно рассмотреть, как единое целое. Элемент множества можно обозначить единицей. Например, любое дерево из множества деревьев — единица, любой листок из множества листков — единица.
Представим, что перед нами 2 банана 🍌🍌. Натуральное число 2 читается как «два». Далее, по аналогии:
| 🍌🍌🍌 | 3 предмета («три») |
| 🍌🍌🍌🍌 | 4 предмета («четыре») |
| 🍌🍌🍌🍌🍌 | 5 предметов («пять») |
| 🍌🍌🍌🍌🍌🍌 | 6 предметов («шесть») |
| 🍌🍌🍌🍌🍌🍌🍌 | 7 предметов («семь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌 | 8 предметов («восемь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌🍌 | 9 предметов («девять») |
Основная функция натурального числа — указать количество предметов.
Если запись числа совпадает с цифрой 0, то его называют «ноль». Напомним, что ноль — не натуральное число, но он может обозначать отсутствие. Ноль предметов значит — ни одного.
Однозначные, двузначные и трехзначные натуральные числа
Однозначное натуральное число — это такое число, в составе которого один знак, одна цифра. Девять однозначных натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Двузначные натуральные числа — те, в составе которых два знака, две цифры. Цифры могут повторяться или быть различными. Например: 88, 53, 70.
Если множество предметов состоит из девяти и еще одного, значит, речь идет об 1 десятке («один десяток») предметов. Если один десяток и еще один, значит, перед нами 2 десятка («два десятка») и так далее.
По сути, двузначное число — это набор однозначных чисел, где одно записывается справа, а другое слева. Число слева показывает количество десятков в составе натурального числа, а число справа — количество единиц. Всего двузначных натуральных чисел — 90.
Трехзначные натуральные числа — числа, в составе которых три знака, три цифры. Например: 666, 389, 702.
Одна сотня — это множество, состоящее из десяти десятков. Сотня и еще одна сотня — 2 сотни. Прибавим еще одну сотню — 3 сотни.
Вот как происходит запись трехзначного числа: натуральные числа записываются одно за другим слева направо.
Крайнее правое однозначное число указывает на количество единиц, следующее — на количество десятков, крайнее левое — на количество сотен. Цифра 0 показывает отсутствие единиц или десятков. Поэтому 506 — это 5 сотен, 0 десятков и 6 единиц.
Точно так же определяются четырехзначные, пятизначные, шестизначные и другие натуральные числа.
Многозначные натуральные числа
Многозначные натуральные числа состоят из двух и более знаков.
1 000 — это множество с десятью сотнями, 1 000 000 состоит из тысячи тысяч, а один миллиард — это тысяча миллионов. Тысяча миллионов, только представьте! То есть мы можем рассмотреть любое многозначное натуральное число как набор однозначных натуральных чисел.
Например, 2 873 206 содержит в себе: 6 единиц, 0 десятков, 2 сотни, 3 тысячи, 7 десятков тысяч, 8 сотен тысяч и 2 миллиона.
Сколько всего натуральных чисел?
Однозначных 9, двузначных 90, трехзначных 900 и т.д.
Свойства натуральных чисел
Об особенностях натуральных чисел мы уже знаем. А теперь подробно расскажем про их свойства:
| множество натуральных чисел | бесконечно и начинается с единицы (1) |
| за каждым натуральным числом следует другое | оно больше предыдущего на 1 |
| результат деления натурального числа на единицу (1) | само натуральное число: 5 : 1 = 5 |
| результат деления натурального числа самого на себя | единица (1): 6 : 6 = 1 |
| переместительный закон сложения | от перестановки мест слагаемых сумма не меняется: 4 + 3 = 3 + 4 |
| сочетательный закон сложения | результат сложения нескольких слагаемых не зависит от порядка действий: (2 + 3) + 4 = 2 + (3 + 4) |
| переместительный закон умножения | от перестановки мест множителей произведение не изменится: 4 × 5 = 5 × 4 |
| сочетательный закон умножения | результат произведения множителей не зависит от порядка действий; можно хоть так, хоть эдак: (6 × 7) × 8 = 6 × (7 ×  |
| распределительный закон умножения относительно сложения | чтобы умножить сумму на число, нужно каждое слагаемое умножить на это число и полученные результаты сложить: 4 × (5 + 6) = 4 × 5 + 4 × 6 |
| распределительный закон умножения относительно вычитания | чтобы умножить разность на число, можно умножить на это число отдельно уменьшаемое и вычитаемое, а затем из первого произведения вычесть второе: 3 × (4 − 5) = 3 × 4 − 3 × 5 |
| распределительный закон деления относительно сложения | чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные результаты: (9 +  : 3 = 9 : 3 + 8 : 3 : 3 = 9 : 3 + 8 : 3 |
| распределительный закон деления относительно вычитания | чтобы разделить разность на число, можно разделить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе: (5 − 3) : 2 = 5 : 2 − 3 : 2 |
Разряды натурального числа и значение разряда
Напомним, что от позиции, на которой стоит цифра в записи числа, зависит ее значение. Так, например, 1 123 содержит в себе: 3 единицы, 2 десятка, 1 сотню, 1 тысячу. При этом можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен и 1 служит значением разряда тысяч.
Разряд — это позиция, место расположения цифры в записи натурального числа.
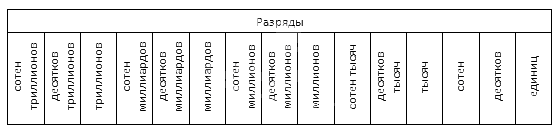
У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.
Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Низший (младший) разряд многозначного натурального числа — разряд единиц.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел. Так делают, чтобы натуральные числа было удобно читать. А еще — чтобы визуально разделить разные классы чисел.
Класс — это группа разрядов, которая содержит в себе три разряда: единицы, десятки и сотни.
Десятичная система счисления
Люди в разные времена использовали разные методы записи чисел. И каждая система счисления имеет свои правила и особенности.
Десятичная система счисления — самая распространенная система счисления, в которой для записи чисел используют десять знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
В десятичной системе значение одной и той же цифры зависит от ее позиции в записи числа. Например, число 555 состоит из трех одинаковых цифр. В этом числе первая слева цифра означает пять сотен, вторая — пять десятков, а третья — пять единиц. Так как значение цифры зависит от ее позиции, десятичную систему счисления называют позиционной.
Вопрос для самопроверки
Сколько натуральных чисел можно отметить на координатном луче между точками с координатами:
-
0 и 15;
-
20 и 50;
-
100 и 130?
Натуральные числа являются привычными человеку и интуитивно понятными, ведь они окружают нас с самого детства. В статье ниже мы дадим базовое представление о смысле натуральных чисел, опишем основные навыки их записи и чтения. Вся теоретическая часть будет сопровождаться примерами.
Общее представление о натуральных числах
На определенном этапе развития человечества возникла задача подсчета неких предметов и обозначение их количества, что, в свою очередь, потребовало нахождения инструмента для решения этой задачи. Таким инструментом и стали натуральные числа. Понятно и основное предназначение натуральных чисел – давать представление о количестве предметов или порядковом номере конкретного предмета, если речь идет о множестве.
Логично, что для использования человеком натуральных чисел, необходимо иметь способ их воспринимать и воспроизводить. Так, натуральное число можно озвучить или изобразить, что является естественными способами передачи информации.
Рассмотрим базовые навыки озвучивания (чтения) и изображения (записи) натуральных чисел.
Десятичная запись натурального числа
Вспомним, как изображаются следующие знаки (укажем их через запятую): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Указанные знаки мы называем цифрами.
Теперь возьмем как правило, что при изображении (записи) любого натурального числа используются только указанные цифры без участия любых других символов. Пусть цифры при записи натурального числа имеют одинаковую высоту, записываются одна за другой в строчку и слева всегда находится цифра, отличная от нуля.
Укажем примеры правильной записи натуральных чисел: 703, 881, 13, 333, 1 023, 7, 500 001. Отступы между цифрами не всегда одинаковы, об этом подробнее будет сказано ниже при изучении классов чисел. Заданные примеры показывают, что при записи натурального числа не обязательно должны присутствовать все цифры из указанного выше ряда. Некоторые из них или все могут повторяться.
Записи вида: 065, 0, 003, 0791 не являются записями натуральных чисел, т.к. слева располагается цифра 0.
Верная запись натурального числа, произведенная с учетом всех описанных требований, называется десятичной записью натурального числа.
Количественный смысл натуральных чисел
Как уже было сказано, натуральные числа изначально несут в себе, в том числе, количественный смысл. Натуральные числа, как инструмент нумерации, рассмотрены в теме о сравнении натуральных чисел.
Приступим к натуральным числам, записи которых совпадают с записями цифр, т.е.: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Представим некий предмет, например, такой: Ψ. Можно записать, что мы видим 1 предмет. Натуральное число 1 читается как «один» или «единица». Термин «единица» имеет также и другое значение: нечто, что можно рассматривать как единое целое. Если есть множество, то любой элемент его можно будет обозначить единицей. К примеру, из множества мышей любая мышь – единица; любой цветок из множества цветов – единица.
Теперь представим: ΨΨ. Мы видим один предмет и еще один предмет, т.е. в записи это будет — 2 предмета. Натуральное число 2 читаем как «два».
Далее, по аналогии: ΨΨΨ – 3 предмета («три»), ΨΨΨΨ – 4 («четыре»), ΨΨΨΨΨ – 5 («пять»), ΨΨΨΨΨΨ – 6 («шесть»), ΨΨΨΨΨΨΨ – 7 («семь»), ΨΨΨΨΨΨΨΨ – 8 («восемь»), ΨΨΨΨΨΨΨΨΨ – 9 («девять»).
С указанной позиции функция натурального числа заключается в указании количества предметов.
Если запись числа совпадает с записью цифры 0, то такое число называют «нуль». Нуль — не натуральное число, но рассматривают его вместе с прочими натуральными числами. Нуль обозначает отсутствие, т.е. нуль предметов означает – ни одного.
Однозначные натуральные числа
Очевидный факт, что, записывая каждое из натуральных чисел, о которых выше велась речь (1, 2, 3, 4, 5, 6, 7, 8, 9), мы используем один знак – одну цифру.
Однозначное натуральное число – натуральное число, при записи которого используется один знак – одна цифра.
Однозначных натуральных чисел девять: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Двузначные и трехзначные натуральные числа
Двузначные натуральные числа – натуральные числа, при записи которых используются два знака – две цифры. При этом используемые цифры могут быть как одинаковые, так и различные.
Например, натуральные числа 71, 64, 11 – двузначные.
Рассмотрим, какой смысл заключен в двузначных числах. Опираться будем на уже известный нам количественный смысл однозначных натуральных чисел.
Введем такое понятие как «десяток».
Представим множество предметов, которое состоит из девяти и еще одного. В таком случае можно говорить об 1 десятке («один десяток») предметов. Если представить один десяток и еще один, то речь пойдёт о 2 десятках («два десятка»). Прибавив к двум десяткам еще один, получим три десятка. И так далее: продолжая добавлять по одному десятку, мы будем получать четыре десятка, пять десятков, шесть десятков, семь десятков, восемь десятков и, наконец, девять десятков.
Посмотрим на двузначное число, как на набор однозначных чисел, одно из которых записывается справа, другое – слева. Число слева будет обозначать количество десятков в составе натурального числа, а число справа – количество единиц. В случае, когда справа расположена цифра 0, то мы говорим об отсутствии единиц. В вышеуказанном и заключается количественный смысл натуральных двузначных чисел. Всего их — 90.
Трехзначные натуральные числа – натуральные числа, при записи которых используются три знака – три цифры. Цифры могут быть различными или повторяющимися в любом сочетании.
Например, 413, 222, 818, 750 – трехзначные натуральные числа.
Чтобы понять количественный смысл трехзначных натуральных чисел, введем понятие «сотня».
Одна сотня (1 сотня) – это множество, состоящее из десяти десятков. Сотня и еще одна сотня составят 2 сотни. Прибавим еще одну сотню и получим 3 сотни. Добавляя постепенно по одной сотне, получим: четыре сотни, пять сотен, шесть сотен, семь сотен, восемь сотен, девять сотен.
Рассмотрим саму запись трехзначного числа: входящие в него однозначные натуральные числа записываются одно за другим слева направо. Крайнее правое однозначное число указывает на количество единиц; следующее однозначное число левее – на количество десятков; крайнее левое однозначное число – на количество сотен. Если в записи участвует цифра 0, она показывает на отсутствие единиц и/или десятков.
Так, трехзначное натуральное число 402 обозначает: 2 единицы, 0 десятков (отсутствуют десятки, не объединенные в сотни) и 4 сотни.
По аналогии дается определение четырёхзначных, пятизначных и так далее натуральных чисел.
Многозначные натуральные числа
От всего вышесказанного теперь возможно перейти к определению многозначных натуральных чисел.
Многозначные натуральные числа – натуральные числа, при записи которых используются два и более знаков. Многозначные натуральные числа – это двухзначные, трехзначные и так далее числа.
Одна тысяча – множество, включающее в себя десять сотен; один миллион состоит из тысячи тысяч; один миллиард – тысяча миллионов; один триллион – тысяча миллиардов. Еще более крупные множества также имеют названия, но использование их редко.
Аналогично принципу выше, мы можем рассмотреть любое многозначное натуральное число, как набор однозначных натуральных чисел, каждое из которых, находясь на определенном месте, свидетельствует о наличии и количестве единиц, десятков, сотен, тысяч, десятков тысяч, сотен тысяч, миллионов, десятков миллионов, сотен миллионов, миллиардов и так далее (справа налево соответственно).
Например, многозначное число 4 912 305 содержит в себе: 5 единиц, 0 десятков, три сотни, 2 тысячи, 1 десяток тысяч, 9 сотен тысяч и 4 миллиона.
Резюмируя, мы рассмотрели навык группировки единиц в различные множества (десятки, сотни и т.д.) и увидели, что цифры в записи многозначного натурального числа являются обозначением количества единиц в каждом из таких множеств.
Чтение натуральных чисел, классы
В теории выше мы обозначили названия натуральных чисел. В таблице 1 укажем, как верно использовать названия однозначных натуральных чисел в речи и при буквенной записи:
| Число | Мужской род | Женский род | Средний род |
|
1 |
Один |
Одна |
Одно |
| Число | Именительнный падеж | Родительный падеж | Дательный падеж | Винительный падеж | Творительный падеж | Предложный падеж |
| 1 2 3 4 5 6 7 8 9 |
Один Два Три Четыре Пять Шесть Семь Восемь Девять |
Одного Двух Трех Четырех Пяти Шести Семи Восьми Девяти |
Одному Двум Трем Четырем Пяти Шести Семи Восьми Девяти |
Один Два Три Четыре Пять Шесть Семь Восемь Девять |
Одним Двумя Тремя Четырьмя Пятью Шестью Семью Восьмью Девятью |
Об одном О двух О трех О четырех О пять О шести О семи О восьми О девяти |
Для грамотного прочтения и написания двузначных чисел, необходимо выучить данные таблицы 2:
| Число |
Мужской, женский и средний род |
| 10 11 12 13 14 15 16 17 18 19 20 30 40 50 60 70 80 90 |
Десять Одиннадцать Двенадцать Тринадцать Четырнадцать Пятнадцать Шестнадцать Семнадцать Восемнадцать Девятнадцать Двадцать Тридцать Сорок Пятьдесят Шестьдесят Семьдесят Восемьдесят Девяносто |
| Число | Именительнный падеж | Родительный падеж | Дательный падеж | Винительный падеж | Творительный падеж | Предложный падеж |
| 10 11 12 13 14 15 16 17 18 19 20 30 40 50 60 70 80 90 |
Десять Одиннадцать Двенадцать Тринадцать Четырнадцать Пятнадцать Шестнадцать Семнадцать Восемнадцать Девятнадцать Двадцать Тридцать Сорок Пятьдесят Шестьдесят Семьдесят Восемьдесят Девяносто |
Десяти |
Десяти Одиннадцати Двенадцати Тринадцати Четырнадцати Пятнадцати Шестнадцати Семнадцати Восемнадцати Девятнадцати Двадцати Тридцати Сорока Пятидесяти Шестидесяти Семидесяти Восьмидесяти Девяноста |
Десять Одиннадцать Двенадцать Тринадцать Четырнадцать Пятнадцать Шестнадцать Семнадцать Восемнадцать Девятнадцать Двадцать Тридцать Сорок Пятьдесят Шестьдесят Семьдесят Восемьдесят Девяносто |
Десятью Одиннадцатью Двенадцатью Тринадцатью Четырнадцатью Пятнадцатью Шестнадцатью Семнадцатью Восемнадцатью Девятнадцатью Двадцатью Тридцатью Сорока Пятидесятью Шестидесятью Семидесятью Восьмидесятью Девяностью |
О десяти Об одиннадцати О двенадцати О тринадцати О четырнадцати О пятнадцати О шестнадцати О семнадцати О восемнадцати О девятнадцати О двадцати О тридцати О сорока О пятидесяти О шестидесяти О семидесяти О восьмидесяти О девяноста |
Для чтения прочих натуральных двузначных чисел будем использовать данные обеих таблиц, рассмотрим это на примере. Допустим, нам необходимо прочитать натуральное двузначное число 21. Это число содержит в себе 1 единицу и 2 десятка, т.е. 20 и 1. Обратившись к таблицам, прочтем указанное число как «двадцать один», при этом союз «и» между словами произносить не нужно. Допустим, нам необходимо использовать указанное число 21 в некотором предложении, указывая на количество предметов в родительном падеже: «нет 21 яблока». Звучать в данном случае произношение будет следующим образом: «нет двадцати одного яблока».
Приведем для наглядности еще пример: число 76, которое прочтется как «семьдесят шесть» и, к примеру – «семьюдесятью шестью тоннами».
Для того, чтобы читать трёхзначные числа, изучим данные таблицы 3:
| Число | Мужской, женский и средний род |
|
100 |
Сто Двести Триста Четыреста Пятьсот Шестьсот Семьсот Восемьсот Девятьсот |
| Число | Именительный падеж | Родительный падеж | Дательный падеж | Винительный падеж | Творительный падеж | Предложный падеж |
| 100 200 300 400 500 600 700 800 900 |
Сто Двести Триста Четыреста Пятьсот Шестьсот Семьсот Восемьсот Девятьсот |
Ста Двухсот Трехсот Четырехсот Пятисот Шестисот Семисот Восьмисот Девятисот |
Ста Двумстам Тремстам Четыремстам Пятистам Шестистам Семистам Восьмистам Девятистам |
Сто Двести Триста Четыреста Пятьсот Шестьсот Семьсот Восемьсот Девятьсот |
Ста Двумстами Тремстами Четыремстами Пятистами Шестистами Семистами Восьмистами Девятистами |
О ста О двухстах О трехстах О четырехстах О пятистах О шестистах О семистах О восьмистах О девятистах |
Чтобы полностью прочитать трехзначное число, также используем данные всех указанных таблиц. Например, дано натуральное число 305. Данному числу соответствует 5 единиц, 0 десятков и 3 сотни: 300 и 5. Взяв за основу таблицы, прочитаем: «триста пять» или в склонении по падежам, к примеру, так: «тремстам пяти метрам».
Прочтем еще одно число: 543. Согласно правилам таблиц, звучать указанное число будет так: «пятьсот сорок три» или в склонении по падежам, к примеру, так: «нет пятисот сорока трех рублей».
Перейдем к общему принципу чтения многозначных натуральных чисел: чтобы прочесть многозначное число, необходимо разбить его справа налево в группы по три цифры, причем в крайней левой группе может быть 1, 2 или 3 цифры. Такие группы называют классами.
Крайний правый класс – класс единиц; затем следующий класс, левее – класс тысяч; далее – класс миллионов; потом следует класс миллиардов, за ним — класс триллионов. Следующие классы также имеют название, но натуральные числа, состоящие из большого количества знаков (16, 17 и более) редко используются на чтении, воспринимать их на слух довольно тяжело.
Для удобства восприятия записи классы отделяют друг от друга небольшим отступом. Например, 31 013 736, 134 678, 23 476 009 434, 2 533 467 001 222.
Чтобы легко прочитать указанные натуральные числа, занесем их в таблицу:
| Класс триллионов |
Класс миллиардов |
Класс миллионов |
Класс тысяч | Класс единиц |
| 134 | 678 | |||
| 31 | 013 | 736 | ||
| 23 | 476 | 009 | 434 | |
| 2 | 533 | 467 | 001 | 222 |
Для прочтения многозначного числа называем по очереди числа, которые его составляют (слева направо по классам, добавляя название класса). Название класса единиц не произносится, а также не произносятся те классы, которые составляют три цифры 0. Если в составе одного класса слева присутствуют одна или две цифры 0, то они при прочтении не используются никак. К примеру, 054 прочтется как «пятьдесят четыре» или 001 – как «один».
Разберем подробно чтение числа 2 533 467 001 222:
— читаем число 2, как составляющую класса триллионов – «два»;
— добавив название класса, получим: «два триллиона»;
— читаем следующее число, добавив название соответствующего класса: «пятьсот тридцать три миллиарда»;
— продолжаем по аналогии, зачитывая следующий класс правее: «четыреста шестьдесят семь миллионов»;
— в следующем классе видим две цифры 0, расположенные слева. Согласно вышеуказанным правилам чтения, цифры 0 отбрасываются и не участвуют в чтении записи. Тогда получим: «одна тысяча»;
— читаем последний класс единиц, не добавляя его название – «двести двадцать два».
Таким образом, число 2 533 467 001 222 будет звучать так: два триллиона пятьсот тридцать три миллиарда четыреста шестьдесят семь миллионов одна тысяча двести двадцать два. Используя указанный принцип, прочтем и прочие заданные числа:
— 31 013 736 – тридцать один миллион тринадцать тысяч семьсот тридцать шесть;
— 134 678 – сто тридцать четыре тысячи шестьсот семьдесят восемь;
— 23 476 009 434 – двадцать три миллиарда четыреста семьдесят шесть миллионов девять тысяч четыреста тридцать четыре.
Таким образом, основой правильного прочтения многозначных чисел является навык разбивать многозначное число на классы, знание соответствующих названий и понимание принципа прочтения двух- и трехзначных чисел.
Разряды натурального числа, значение разряда
Как уже становится понятно из всего вышесказанного, от позиции, на которой стоит цифра в записи числа, зависит ее значение. Т.е., например, цифра 3 в составе натурального числа 314 обозначает количество сотен, а именно – 3 сотни. Цифра 2 – количество десятков (1 десяток), а цифра 4 – количество единиц (4 единицы). При этом мы будем говорить, что цифра 4 находится в разряде единиц и является значением разряда единиц в заданном числе. Цифра 1 стоит в разряде десятков и служит значением разряда десятков. Цифра 3 располагается в разряде сотен и является значением разряда сотен.
Разряд – это позиция цифры в записи натурального числа, а также и значение этой цифры, которое определяется ее позицией в заданном числе.
Разряды имеют свои названия, мы уже использовали их выше. Справа налево следуют разряды: единиц, десятков, сотен, тысяч, десятков тысяч и т.д.
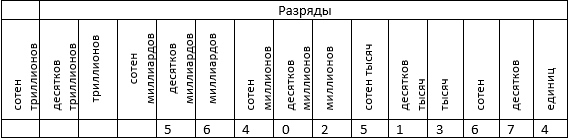
Для удобства запоминания можно использовать следующую таблицу (укажем 15 разрядов):
Уточним такую деталь: количество разрядов в заданном многозначном числе такое же, как количество знаков в составе записи числа. К примеру, данная таблица содержит названия всех разрядов для числа, в котором 15 знаков. Последующие разряды также имеют названия, но используются крайне редко и очень неудобны для восприятия на слух.
При помощи такой таблицы возможно наработать навык определения разряда, записывая заданное натуральное число в таблицу так, чтобы крайняя правая цифра была записана в разряде единиц и далее – в каждый разряд по цифре. К примеру, запишем многозначное натуральное число 56 402 513 674 так:
Обратите внимание на цифру 0, находящуюся в разряде десятков миллионов – она означает отсутствие единиц данного разряда.
Введем также еще понятия низшего и высшего разрядов многозначного числа.
Низший (младший) разряд любого многозначного натурального числа – разряд единиц.
Высший (старший) разряд любого многозначного натурального числа – разряд, соответствующий крайней левой цифре в записи заданного числа.
Так, например, в числе 41 781: низший разряд – разряд единиц; высший разряд – разряд десятков тысяч.
Логически следует, что возможно говорить о старшинстве разрядов относительно друг друга. Каждый последующий разряд при движении слева направо ниже (младше) предыдущего. И наоборот: при движении справа налево каждый следующий разряд выше (старше) предыдущего. К примеру, разряд тысяч старше разряда сотен, но младше разряда миллионов.
Уточним, что при решении некоторых практических примеров используется не само натуральное число, а сумма разрядных слагаемых заданного числа.
Кратко о десятичной системе счисления
Система счисления – метод записи чисел при помощи знаков.
Позиционные системы счисления – такие, в которых значение цифры в составе числа зависит от ее позиции в записи числа.
Согласно данному определению, можно говорить о том, что, изучая выше натуральные числа и способ их записи, мы пользовались позиционной системой счисления. Особое место здесь играет число 10. Счет мы ведем десятками: десять единиц составляют десяток, десяток десятков объединится в сотню и т.д. Число 10 служит основанием этой системы счисления, и саму систему также называют десятичной.
Помимо нее, существуют и прочие системы счисления. Например, информатика использует двоичную систему. Когда же мы ведем счет времени, то задействуем шестидесятеричную систему счисления.
This article is about «positive integers» and «non-negative integers». For all the numbers …, −2, −1, 0, 1, 2, …, see Integer.
Natural numbers can be used for counting (one apple, two apples, three apples, …)
In mathematics, the natural numbers are those numbers used for counting (as in «there are six coins on the table») and ordering (as in «this is the third largest city in the country»).
Numbers used for counting are called cardinal numbers, and numbers used for ordering are called ordinal numbers. Natural numbers are sometimes used as labels, known as nominal numbers, having none of the properties of numbers in a mathematical sense (e.g. sports jersey numbers).[1][2]
Some definitions, including the standard ISO 80000-2,[3][a] begin the natural numbers with 0, corresponding to the non-negative integers 0, 1, 2, 3, …, whereas others start with 1, corresponding to the positive integers 1, 2, 3, …[4][b] Texts that exclude zero from the natural numbers sometimes refer to the natural numbers together with zero as the whole numbers, while in other writings, that term is used instead for the integers (including negative integers).[5]
The natural numbers form a set. Many other number sets are built by successively extending the set of natural numbers: the integers, by including an additive identity 0 (if not yet in) and an additive inverse −n for each nonzero natural number n; the rational numbers, by including a multiplicative inverse 
Properties of the natural numbers, such as divisibility and the distribution of prime numbers, are studied in number theory. Problems concerning counting and ordering, such as partitioning and enumerations, are studied in combinatorics.
In common language, particularly in primary school education, natural numbers may be called counting numbers[6] to intuitively exclude the negative integers and zero, and also to contrast the discreteness of counting to the continuity of measurement—a hallmark characteristic of real numbers.
History[edit]
Ancient roots[edit]
The most primitive method of representing a natural number is to put down a mark for each object. Later, a set of objects could be tested for equality, excess or shortage—by striking out a mark and removing an object from the set.
The first major advance in abstraction was the use of numerals to represent numbers. This allowed systems to be developed for recording large numbers. The ancient Egyptians developed a powerful system of numerals with distinct hieroglyphs for 1, 10, and all powers of 10 up to over 1 million. A stone carving from Karnak, dating back from around 1500 BCE and now at the Louvre in Paris, depicts 276 as 2 hundreds, 7 tens, and 6 ones; and similarly for the number 4,622. The Babylonians had a place-value system based essentially on the numerals for 1 and 10, using base sixty, so that the symbol for sixty was the same as the symbol for one—its value being determined from context.[10]
A much later advance was the development of the idea that 0 can be considered as a number, with its own numeral. The use of a 0 digit in place-value notation (within other numbers) dates back as early as 700 BCE by the Babylonians, who omitted such a digit when it would have been the last symbol in the number.[e] The Olmec and Maya civilizations used 0 as a separate number as early as the 1st century BCE, but this usage did not spread beyond Mesoamerica.[12][13] The use of a numeral 0 in modern times originated with the Indian mathematician Brahmagupta in 628 CE. However, 0 had been used as a number in the medieval computus (the calculation of the date of Easter), beginning with Dionysius Exiguus in 525 CE, without being denoted by a numeral. Standard Roman numerals do not have a symbol for 0; instead, nulla (or the genitive form nullae) from nullus, the Latin word for «none», was employed to denote a 0 value.[14]
The first systematic study of numbers as abstractions is usually credited to the Greek philosophers Pythagoras and Archimedes. Some Greek mathematicians treated the number 1 differently than larger numbers, sometimes even not as a number at all.[f] Euclid, for example, defined a unit first and then a number as a multitude of units, thus by his definition, a unit is not a number and there are no unique numbers (e.g., any two units from indefinitely many units is a 2).[16]
Independent studies on numbers also occurred at around the same time in India, China, and Mesoamerica.[17]
Modern definitions[edit]
In 19th century Europe, there was mathematical and philosophical discussion about the exact nature of the natural numbers. Henri Poincaré stated that axioms can only be demonstrated in their finite application, and concluded that it is «the power of the mind» which allows conceiving of the indefinite repetition of the same act.[18] Leopold Kronecker summarized his belief as «God made the integers, all else is the work of man».[g]
The constructivists saw a need to improve upon the logical rigor in the foundations of mathematics.[h] In the 1860s, Hermann Grassmann suggested a recursive definition for natural numbers, thus stating they were not really natural—but a consequence of definitions. Later, two classes of such formal definitions were constructed; later still, they were shown to be equivalent in most practical applications.
Set-theoretical definitions of natural numbers were initiated by Frege. He initially defined a natural number as the class of all sets that are in one-to-one correspondence with a particular set. However, this definition turned out to lead to paradoxes, including Russell’s paradox. To avoid such paradoxes, the formalism was modified so that a natural number is defined as a particular set, and any set that can be put into one-to-one correspondence with that set is said to have that number of elements.[21]
The second class of definitions was introduced by Charles Sanders Peirce, refined by Richard Dedekind, and further explored by Giuseppe Peano; this approach is now called Peano arithmetic. It is based on an axiomatization of the properties of ordinal numbers: each natural number has a successor and every non-zero natural number has a unique predecessor. Peano arithmetic is equiconsistent with several weak systems of set theory. One such system is ZFC with the axiom of infinity replaced by its negation. Theorems that can be proved in ZFC but cannot be proved using the Peano Axioms include Goodstein’s theorem.[22]
With all these definitions, it is convenient to include 0 (corresponding to the empty set) as a natural number. Including 0 is now the common convention among set theorists[23] and logicians.[24] Other mathematicians also include 0,[a] and computer languages often start from zero when enumerating items like loop counters and string- or array-elements.[25][26] On the other hand, many mathematicians have kept the older tradition to take 1 to be the first natural number.[27]
Notation[edit]
The set of all natural numbers is standardly denoted N or 
Since natural numbers may contain 0 or not, it may be important to know which version is referred to. This is often specified by the context, but may also be done by using a subscript or a superscript in the notation, such as:[3][30]
Alternatively, since the natural numbers naturally form a subset of the integers (often denoted 
Properties[edit]
Addition[edit]
Given the set 


If 1 is defined as S(0), then b + 1 = b + S(0) = S(b + 0) = S(b). That is, b + 1 is simply the successor of b.
Multiplication[edit]
Analogously, given that addition has been defined, a multiplication operator 

Relationship between addition and multiplication[edit]
Addition and multiplication are compatible, which is expressed in the distribution law: a × (b + c) = (a × b) + (a × c). These properties of addition and multiplication make the natural numbers an instance of a commutative semiring. Semirings are an algebraic generalization of the natural numbers where multiplication is not necessarily commutative. The lack of additive inverses, which is equivalent to the fact that 

If the natural numbers are taken as «excluding 0», and «starting at 1», the definitions of + and × are as above, except that they begin with a + 1 = S(a) and a × 1 = a. Furthermore, 
Order[edit]
In this section, juxtaposed variables such as ab indicate the product a × b,[32] and the standard order of operations is assumed.
A total order on the natural numbers is defined by letting a ≤ b if and only if there exists another natural number c where a + c = b. This order is compatible with the arithmetical operations in the following sense: if a, b and c are natural numbers and a ≤ b, then a + c ≤ b + c and ac ≤ bc.
An important property of the natural numbers is that they are well-ordered: every non-empty set of natural numbers has a least element. The rank among well-ordered sets is expressed by an ordinal number; for the natural numbers, this is denoted as ω (omega).
Division[edit]
In this section, juxtaposed variables such as ab indicate the product a × b, and the standard order of operations is assumed.
While it is in general not possible to divide one natural number by another and get a natural number as result, the procedure of division with remainder or Euclidean division is available as a substitute: for any two natural numbers a and b with b ≠ 0 there are natural numbers q and r such that
The number q is called the quotient and r is called the remainder of the division of a by b. The numbers q and r are uniquely determined by a and b. This Euclidean division is key to the several other properties (divisibility), algorithms (such as the Euclidean algorithm), and ideas in number theory.
Algebraic properties satisfied by the natural numbers[edit]
The addition (+) and multiplication (×) operations on natural numbers as defined above have several algebraic properties:
- Closure under addition and multiplication: for all natural numbers a and b, both a + b and a × b are natural numbers.[33]
- Associativity: for all natural numbers a, b, and c, a + (b + c) = (a + b) + c and a × (b × c) = (a × b) × c.[34]
- Commutativity: for all natural numbers a and b, a + b = b + a and a × b = b × a.[35]
- Existence of identity elements: for every natural number a, a + 0 = a and a × 1 = a.
- If the natural numbers are taken as «excluding 0», and «starting at 1», then for every natural number a, a × 1 = a. However, the «existence of additive identity element» property is not satisfied
- Distributivity of multiplication over addition for all natural numbers a, b, and c, a × (b + c) = (a × b) + (a × c).
- No nonzero zero divisors: if a and b are natural numbers such that a × b = 0, then a = 0 or b = 0 (or both).
- If the natural numbers are taken as «excluding 0», and «starting at 1», the «no nonzero zero divisors» property is not satisfied.
Generalizations[edit]
Two important generalizations of natural numbers arise from the two uses of counting and ordering: cardinal numbers and ordinal numbers.
- A natural number can be used to express the size of a finite set; more precisely, a cardinal number is a measure for the size of a set, which is even suitable for infinite sets. This concept of «size» relies on maps between sets, such that two sets have the same size, exactly if there exists a bijection between them. The set of natural numbers itself, and any bijective image of it, is said to be countably infinite and to have cardinality aleph-null (ℵ0).
- Natural numbers are also used as linguistic ordinal numbers: «first», «second», «third», and so forth. This way they can be assigned to the elements of a totally ordered finite set, and also to the elements of any well-ordered countably infinite set. This assignment can be generalized to general well-orderings with a cardinality beyond countability, to yield the ordinal numbers. An ordinal number may also be used to describe the notion of «size» for a well-ordered set, in a sense different from cardinality: if there is an order isomorphism (more than a bijection!) between two well-ordered sets, they have the same ordinal number. The first ordinal number that is not a natural number is expressed as ω; this is also the ordinal number of the set of natural numbers itself.
The least ordinal of cardinality ℵ0 (that is, the initial ordinal of ℵ0) is ω but many well-ordered sets with cardinal number ℵ0 have an ordinal number greater than ω.
For finite well-ordered sets, there is a one-to-one correspondence between ordinal and cardinal numbers; therefore they can both be expressed by the same natural number, the number of elements of the set. This number can also be used to describe the position of an element in a larger finite, or an infinite, sequence.
A countable non-standard model of arithmetic satisfying the Peano Arithmetic (that is, the first-order Peano axioms) was developed by Skolem in 1933. The hypernatural numbers are an uncountable model that can be constructed from the ordinary natural numbers via the ultrapower construction.
Georges Reeb used to claim provocatively that «The naïve integers don’t fill up» 
Formal definitions[edit]
There are two standard methods for formally defining natural numbers. The first one, due to Giuseppe Peano, consists of an autonomous axiomatic theory called Peano arithmetic, based on few axioms called Peano axioms.
The second definition is based on set theory. It defines the natural numbers as specific sets. More precisely, each natural number n is defined as an explicitly defined set, whose elements allow counting the elements of other sets, in the sense that the sentence «a set S has n elements» means that there exists a one to one correspondence between the two sets n and S.
The sets used to define natural numbers satisfy Peano axioms. It follows that every theorem that can be stated and proved in Peano arithmetic can also be proved in set theory. However, the two definitions are not equivalent, as there are theorems that can be stated in terms of Peano arithmetic and proved in set theory, which are not provable inside Peano arithmetic. A probable example is Fermat’s Last Theorem.
The definition of the integers as sets satisfying Peano axioms provide a model of Peano arithmetic inside set theory. An important consequence is that, if set theory is consistent (as it is usually guessed), then Peano arithmetic is consistent. In other words, if a contradiction could be proved in Peano arithmetic, then set theory would by contradictory, and every theorem of set theory would be both true and wrong.
Peano axioms[edit]
The five Peano axioms are the following:[36][i]
- 0 is a natural number.
- Every natural number has a successor which is also a natural number.
- 0 is not the successor of any natural number.
- If the successor of
equals the successor of
, then
equals
.
- The axiom of induction: If a statement is true of 0, and if the truth of that statement for a number implies its truth for the successor of that number, then the statement is true for every natural number.
These are not the original axioms published by Peano, but are named in his honor. Some forms of the Peano axioms have 1 in place of 0. In ordinary arithmetic, the successor of 

Set-theoretic definition[edit]
Intuitively, the natural number n is the common property of all sets that have n elements. So, it seems natural to define n as an equivalence class under the relation «can be made in one to one correspondence». Unfortunately, this does not work in set theory, as such an equivalence class would not be a set (because of Russell’s paradox). The standard solution is to define a particular set with n elements that will be called the natural number n.
The following definition was first published by John von Neumann,[37] although Levy attributes the idea to unpublished work of Zermelo in 1916.[38] As this definition extends to infinite set as a definition of ordinal number, the sets considered below are sometimes called von Neumann ordinals.
The definition proceeds as follows:
- Call 0 = { }, the empty set.
- Define the successor S(a) of any set a by S(a) = a ∪ {a}.
- By the axiom of infinity, there exist sets which contain 0 and are closed under the successor function. Such sets are said to be inductive. The intersection of all inductive sets is still an inductive set.
- This intersection is the set of the natural numbers.
It follows that the natural numbers are defined iteratively as follows:
-
- 0 = { },
- 1 = 0 ∪ {0} = {0} = {{ }},
- 2 = 1 ∪ {1} = {0, 1} = {{ }, {{ }}},
- 3 = 2 ∪ {2} = {0, 1, 2} = {{ }, {{ }}, {{ }, {{ }}}},
- n = n−1 ∪ {n−1} = {0, 1, …, n−1} = {{ }, {{ }}, …, {{ }, {{ }}, …}},
- etc.
It can be checked that the natural numbers satisfies the Peano axioms.
With this definition, given a natural number n, the sentence «a set S has n elements» can be formally defined as «there exists a bijection from n to S. This formalizes the operation of counting the elements of S. Also, n ≤ m if and only if n is a subset of m. In other words, the set inclusion defines the usual total order on the natural numbers. This order is a well-order.
It follows from the definition that each natural number is equal to the set of all natural numbers less than it. This definition, can be extended to the von Neumann definition of ordinals for defining all ordinal numbers, including the infinite ones: «each ordinal is the well-ordered set of all smaller ordinals.»
If one does not accept the axiom of infinity, the natural numbers may not form a set. Nevertheless, the natural numbers can still be individually defined as above, and they still satisfy the Peano axioms.
There are other set theoretical constructions. In particular, Ernst Zermelo provided a construction that is nowadays only of historical interest, and is sometimes referred to as Zermelo ordinals.[38] It consists in defining 0 as the empty set, and S(a) = {a}.
With this definition each natural number is a singleton set. So, the property of the natural numbers to represent cardinalities is not directly accessible; only the ordinal property (being the nth element of a sequence) is immediate. Unlike von Neumann’s construction, the Zermelo ordinals do not extend to infinite ordinals.
See also[edit]
- Canonical representation of a positive integer – Representation of a number as a product of primes
- Countable set – Mathematical set that can be enumerated
- Sequence – Function of the natural numbers in another set
- Ordinal number – Generalization of «n-th» to infinite cases
- Cardinal number – Size of a possibly infinite set
- Set-theoretic definition of natural numbers – constructions of the whole numbers from sets
Complex 
|
|
Notes[edit]
- ^ a b Mac Lane & Birkhoff (1999, p. 15) include zero in the natural numbers: ‘Intuitively, the set
of all natural numbers may be described as follows:
contains an «initial» number 0; …’. They follow that with their version of the Peano’s axioms.
- ^ Carothers (2000, p. 3) says: «
is the set of natural numbers (positive integers)» Both definitions are acknowledged whenever convenient, and there is no general consensus on whether zero should be included in the natural numbers.[1]
- ^ Mendelson (2008, p. x) says: «The whole fantastic hierarchy of number systems is built up by purely set-theoretic means from a few simple assumptions about natural numbers.»
- ^ Bluman (2010, p. 1): «Numbers make up the foundation of mathematics.»
- ^ A tablet found at Kish … thought to date from around 700 BC, uses three hooks to denote an empty place in the positional notation. Other tablets dated from around the same time use a single hook for an empty place.[11]
- ^ This convention is used, for example, in Euclid’s Elements, see D. Joyce’s web edition of Book VII.[15]
- ^ The English translation is from Gray. In a footnote, Gray attributes the German quote to: «Weber 1891–1892, 19, quoting from a lecture of Kronecker’s of 1886.»[19][20]
- ^ «Much of the mathematical work of the twentieth century has been devoted to examining the logical foundations and structure of the subject.» (Eves 1990, p. 606)
- ^ Hamilton (1988, pp. 117 ff) calls them «Peano’s Postulates» and begins with «1. 0 is a natural number.»
Halmos (1960, p. 46) uses the language of set theory instead of the language of arithmetic for his five axioms. He begins with «(I) 0 ∈ ω (where, of course, 0 = ∅» (ω is the set of all natural numbers).
Morash (1991) gives «a two-part axiom» in which the natural numbers begin with 1. (Section 10.1: An Axiomatization for the System of Positive Integers)
References[edit]
- ^ a b c Weisstein, Eric W. «Natural Number». mathworld.wolfram.com. Retrieved 11 August 2020.
- ^ «Natural Numbers». Brilliant Math & Science Wiki. Retrieved 11 August 2020.
- ^ a b c «Standard number sets and intervals». ISO 80000-2:2009. International Organization for Standardization. p. 6.
- ^ «natural number». Merriam-Webster.com. Merriam-Webster. Archived from the original on 13 December 2019. Retrieved 4 October 2014.
- ^ Ganssle, Jack G. & Barr, Michael (2003). «integer». Embedded Systems Dictionary. pp. 138 (integer), 247 (signed integer), & 276 (unsigned integer). ISBN 978-1-57820-120-4. Archived from the original on 29 March 2017. Retrieved 28 March 2017 – via Google Books.
- ^ Weisstein, Eric W. «Counting Number». MathWorld.
- ^ «Introduction». Ishango bone. Brussels, Belgium: Royal Belgian Institute of Natural Sciences. Archived from the original on 4 March 2016.
- ^ «Flash presentation». Ishango bone. Brussels, Belgium: Royal Belgian Institute of Natural Sciences. Archived from the original on 27 May 2016.
- ^ «The Ishango Bone, Democratic Republic of the Congo». UNESCO’s Portal to the Heritage of Astronomy. Archived from the original on 10 November 2014., on permanent display at the Royal Belgian Institute of Natural Sciences, Brussels, Belgium.
- ^ Ifrah, Georges (2000). The Universal History of Numbers. Wiley. ISBN 0-471-37568-3.
- ^ «A history of Zero». MacTutor History of Mathematics. Archived from the original on 19 January 2013. Retrieved 23 January 2013.
- ^ Mann, Charles C. (2005). 1491: New Revelations of the Americas before Columbus. Knopf. p. 19. ISBN 978-1-4000-4006-3. Archived from the original on 14 May 2015. Retrieved 3 February 2015 – via Google Books.
- ^ Evans, Brian (2014). «Chapter 10. Pre-Columbian Mathematics: The Olmec, Maya, and Inca Civilizations». The Development of Mathematics Throughout the Centuries: A brief history in a cultural context. John Wiley & Sons. ISBN 978-1-118-85397-9 – via Google Books.
- ^ Deckers, Michael (25 August 2003). «Cyclus Decemnovennalis Dionysii – Nineteen year cycle of Dionysius». Hbar.phys.msu.ru. Archived from the original on 15 January 2019. Retrieved 13 February 2012.
- ^ Euclid. «Book VII, definitions 1 and 2». In Joyce, D. (ed.). Elements. Clark University. Archived from the original on 5 August 2011.
- ^ Mueller, Ian (2006). Philosophy of mathematics and deductive structure in Euclid’s Elements. Mineola, New York: Dover Publications. p. 58. ISBN 978-0-486-45300-2. OCLC 69792712.
- ^ Kline, Morris (1990) [1972]. Mathematical Thought from Ancient to Modern Times. Oxford University Press. ISBN 0-19-506135-7.
- ^ Poincaré, Henri (1905) [1902]. «On the nature of mathematical reasoning». La Science et l’hypothèse [Science and Hypothesis]. Translated by Greenstreet, William John. VI.
- ^ Gray, Jeremy (2008). Plato’s Ghost: The modernist transformation of mathematics. Princeton University Press. p. 153. ISBN 978-1-4008-2904-0. Archived from the original on 29 March 2017 – via Google Books.
- ^ Weber, Heinrich L. (1891–1892). «Kronecker». Jahresbericht der Deutschen Mathematiker-Vereinigung [Annual report of the German Mathematicians Association]. pp. 2:5–23. (The quote is on p. 19). Archived from the original on 9 August 2018; «access to Jahresbericht der Deutschen Mathematiker-Vereinigung«. Archived from the original on 20 August 2017.
- ^ Eves 1990, Chapter 15
- ^ Kirby, Laurie; Paris, Jeff (1982). «Accessible Independence Results for Peano Arithmetic». Bulletin of the London Mathematical Society. Wiley. 14 (4): 285–293. doi:10.1112/blms/14.4.285. ISSN 0024-6093.
- ^ Bagaria, Joan (2017). Set Theory (Winter 2014 ed.). The Stanford Encyclopedia of Philosophy. Archived from the original on 14 March 2015. Retrieved 13 February 2015.
- ^ Goldrei, Derek (1998). «3». Classic Set Theory: A guided independent study (1. ed., 1. print ed.). Boca Raton, Fla. [u.a.]: Chapman & Hall/CRC. p. 33. ISBN 978-0-412-60610-6.
- ^ Brown, Jim (1978). «In defense of index origin 0». ACM SIGAPL APL Quote Quad. 9 (2): 7. doi:10.1145/586050.586053. S2CID 40187000.
- ^ Hui, Roger. «Is index origin 0 a hindrance?». jsoftware.com. Archived from the original on 20 October 2015. Retrieved 19 January 2015.
- ^ This is common in texts about Real analysis. See, for example, Carothers (2000, p. 3) or Thomson, Bruckner & Bruckner (2008, p. 2).
- ^ «Listing of the Mathematical Notations used in the Mathematical Functions Website: Numbers, variables, and functions». functions.wolfram.com. Retrieved 27 July 2020.
- ^ Rudin, W. (1976). Principles of Mathematical Analysis. New York: McGraw-Hill. p. 25. ISBN 978-0-07-054235-8.
- ^ Grimaldi, Ralph P. (2004). Discrete and Combinatorial Mathematics: An applied introduction (5th ed.). Pearson Addison Wesley. ISBN 978-0-201-72634-3.
- ^ Grimaldi, Ralph P. (2003). A review of discrete and combinatorial mathematics (5th ed.). Boston: Addison-Wesley. p. 133. ISBN 978-0-201-72634-3.
- ^ Weisstein, Eric W. «Multiplication». mathworld.wolfram.com. Retrieved 27 July 2020.
- ^ Fletcher, Harold; Howell, Arnold A. (9 May 2014). Mathematics with Understanding. Elsevier. p. 116. ISBN 978-1-4832-8079-0.
…the set of natural numbers is closed under addition… set of natural numbers is closed under multiplication
- ^ Davisson, Schuyler Colfax (1910). College Algebra. Macmillian Company. p. 2.
Addition of natural numbers is associative.
- ^ Brandon, Bertha (M.); Brown, Kenneth E.; Gundlach, Bernard H.; Cooke, Ralph J. (1962). Laidlaw mathematics series. Vol. 8. Laidlaw Bros. p. 25.
- ^ Mints, G.E. (ed.). «Peano axioms». Encyclopedia of Mathematics. Springer, in cooperation with the European Mathematical Society. Archived from the original on 13 October 2014. Retrieved 8 October 2014.
- ^ von Neumann (1923)
- ^ a b Levy (1979), p. 52
Bibliography[edit]
- Bluman, Allan (2010). Pre-Algebra DeMYSTiFieD (Second ed.). McGraw-Hill Professional. ISBN 978-0-07-174251-1 – via Google Books.
- Carothers, N.L. (2000). Real Analysis. Cambridge University Press. ISBN 978-0-521-49756-5 – via Google Books.
- Clapham, Christopher; Nicholson, James (2014). The Concise Oxford Dictionary of Mathematics (Fifth ed.). Oxford University Press. ISBN 978-0-19-967959-1 – via Google Books.
- Dedekind, Richard (1963) [1901]. Essays on the Theory of Numbers. Translated by Beman, Wooster Woodruff (reprint ed.). Dover Books. ISBN 978-0-486-21010-0 – via Archive.org.
- Dedekind, Richard (1901). Essays on the Theory of Numbers. Translated by Beman, Wooster Woodruff. Chicago, IL: Open Court Publishing Company. Retrieved 13 August 2020 – via Project Gutenberg.
- Dedekind, Richard (2007) [1901]. Essays on the Theory of Numbers. Kessinger Publishing, LLC. ISBN 978-0-548-08985-9.
- Eves, Howard (1990). An Introduction to the History of Mathematics (6th ed.). Thomson. ISBN 978-0-03-029558-4 – via Google Books.
- Halmos, Paul (1960). Naive Set Theory. Springer Science & Business Media. ISBN 978-0-387-90092-6 – via Google Books.
- Hamilton, A.G. (1988). Logic for Mathematicians (Revised ed.). Cambridge University Press. ISBN 978-0-521-36865-0 – via Google Books.
- James, Robert C.; James, Glenn (1992). Mathematics Dictionary (Fifth ed.). Chapman & Hall. ISBN 978-0-412-99041-0 – via Google Books.
- Landau, Edmund (1966). Foundations of Analysis (Third ed.). Chelsea Publishing. ISBN 978-0-8218-2693-5 – via Google Books.
- Levy, Azriel (1979). Basic Set Theory. Springer-Verlag Berlin Heidelberg. ISBN 978-3-662-02310-5.
- Mac Lane, Saunders; Birkhoff, Garrett (1999). Algebra (3rd ed.). American Mathematical Society. ISBN 978-0-8218-1646-2 – via Google Books.
- Mendelson, Elliott (2008) [1973]. Number Systems and the Foundations of Analysis. Dover Publications. ISBN 978-0-486-45792-5 – via Google Books.
- Morash, Ronald P. (1991). Bridge to Abstract Mathematics: Mathematical proof and structures (Second ed.). Mcgraw-Hill College. ISBN 978-0-07-043043-3 – via Google Books.
- Musser, Gary L.; Peterson, Blake E.; Burger, William F. (2013). Mathematics for Elementary Teachers: A contemporary approach (10th ed.). Wiley Global Education. ISBN 978-1-118-45744-3 – via Google Books.
- Szczepanski, Amy F.; Kositsky, Andrew P. (2008). The Complete Idiot’s Guide to Pre-algebra. Penguin Group. ISBN 978-1-59257-772-9 – via Google Books.
- Thomson, Brian S.; Bruckner, Judith B.; Bruckner, Andrew M. (2008). Elementary Real Analysis (Second ed.). ClassicalRealAnalysis.com. ISBN 978-1-4348-4367-8 – via Google Books.
- von Neumann, John (1923). «Zur Einführung der transfiniten Zahlen» [On the Introduction of the Transfinite Numbers]. Acta Litterarum AC Scientiarum Ragiae Universitatis Hungaricae Francisco-Josephinae, Sectio Scientiarum Mathematicarum. 1: 199–208. Archived from the original on 18 December 2014. Retrieved 15 September 2013.
- von Neumann, John (January 2002) [1923]. «On the introduction of transfinite numbers». In van Heijenoort, Jean (ed.). From Frege to Gödel: A source book in mathematical logic, 1879–1931 (3rd ed.). Harvard University Press. pp. 346–354. ISBN 978-0-674-32449-7. – English translation of von Neumann 1923.
External links[edit]
- «Natural number», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- «Axioms and construction of natural numbers». apronus.com.
This article is about «positive integers» and «non-negative integers». For all the numbers …, −2, −1, 0, 1, 2, …, see Integer.
Natural numbers can be used for counting (one apple, two apples, three apples, …)
In mathematics, the natural numbers are those numbers used for counting (as in «there are six coins on the table») and ordering (as in «this is the third largest city in the country»).
Numbers used for counting are called cardinal numbers, and numbers used for ordering are called ordinal numbers. Natural numbers are sometimes used as labels, known as nominal numbers, having none of the properties of numbers in a mathematical sense (e.g. sports jersey numbers).[1][2]
Some definitions, including the standard ISO 80000-2,[3][a] begin the natural numbers with 0, corresponding to the non-negative integers 0, 1, 2, 3, …, whereas others start with 1, corresponding to the positive integers 1, 2, 3, …[4][b] Texts that exclude zero from the natural numbers sometimes refer to the natural numbers together with zero as the whole numbers, while in other writings, that term is used instead for the integers (including negative integers).[5]
The natural numbers form a set. Many other number sets are built by successively extending the set of natural numbers: the integers, by including an additive identity 0 (if not yet in) and an additive inverse −n for each nonzero natural number n; the rational numbers, by including a multiplicative inverse 
Properties of the natural numbers, such as divisibility and the distribution of prime numbers, are studied in number theory. Problems concerning counting and ordering, such as partitioning and enumerations, are studied in combinatorics.
In common language, particularly in primary school education, natural numbers may be called counting numbers[6] to intuitively exclude the negative integers and zero, and also to contrast the discreteness of counting to the continuity of measurement—a hallmark characteristic of real numbers.
History[edit]
Ancient roots[edit]
The most primitive method of representing a natural number is to put down a mark for each object. Later, a set of objects could be tested for equality, excess or shortage—by striking out a mark and removing an object from the set.
The first major advance in abstraction was the use of numerals to represent numbers. This allowed systems to be developed for recording large numbers. The ancient Egyptians developed a powerful system of numerals with distinct hieroglyphs for 1, 10, and all powers of 10 up to over 1 million. A stone carving from Karnak, dating back from around 1500 BCE and now at the Louvre in Paris, depicts 276 as 2 hundreds, 7 tens, and 6 ones; and similarly for the number 4,622. The Babylonians had a place-value system based essentially on the numerals for 1 and 10, using base sixty, so that the symbol for sixty was the same as the symbol for one—its value being determined from context.[10]
A much later advance was the development of the idea that 0 can be considered as a number, with its own numeral. The use of a 0 digit in place-value notation (within other numbers) dates back as early as 700 BCE by the Babylonians, who omitted such a digit when it would have been the last symbol in the number.[e] The Olmec and Maya civilizations used 0 as a separate number as early as the 1st century BCE, but this usage did not spread beyond Mesoamerica.[12][13] The use of a numeral 0 in modern times originated with the Indian mathematician Brahmagupta in 628 CE. However, 0 had been used as a number in the medieval computus (the calculation of the date of Easter), beginning with Dionysius Exiguus in 525 CE, without being denoted by a numeral. Standard Roman numerals do not have a symbol for 0; instead, nulla (or the genitive form nullae) from nullus, the Latin word for «none», was employed to denote a 0 value.[14]
The first systematic study of numbers as abstractions is usually credited to the Greek philosophers Pythagoras and Archimedes. Some Greek mathematicians treated the number 1 differently than larger numbers, sometimes even not as a number at all.[f] Euclid, for example, defined a unit first and then a number as a multitude of units, thus by his definition, a unit is not a number and there are no unique numbers (e.g., any two units from indefinitely many units is a 2).[16]
Independent studies on numbers also occurred at around the same time in India, China, and Mesoamerica.[17]
Modern definitions[edit]
In 19th century Europe, there was mathematical and philosophical discussion about the exact nature of the natural numbers. Henri Poincaré stated that axioms can only be demonstrated in their finite application, and concluded that it is «the power of the mind» which allows conceiving of the indefinite repetition of the same act.[18] Leopold Kronecker summarized his belief as «God made the integers, all else is the work of man».[g]
The constructivists saw a need to improve upon the logical rigor in the foundations of mathematics.[h] In the 1860s, Hermann Grassmann suggested a recursive definition for natural numbers, thus stating they were not really natural—but a consequence of definitions. Later, two classes of such formal definitions were constructed; later still, they were shown to be equivalent in most practical applications.
Set-theoretical definitions of natural numbers were initiated by Frege. He initially defined a natural number as the class of all sets that are in one-to-one correspondence with a particular set. However, this definition turned out to lead to paradoxes, including Russell’s paradox. To avoid such paradoxes, the formalism was modified so that a natural number is defined as a particular set, and any set that can be put into one-to-one correspondence with that set is said to have that number of elements.[21]
The second class of definitions was introduced by Charles Sanders Peirce, refined by Richard Dedekind, and further explored by Giuseppe Peano; this approach is now called Peano arithmetic. It is based on an axiomatization of the properties of ordinal numbers: each natural number has a successor and every non-zero natural number has a unique predecessor. Peano arithmetic is equiconsistent with several weak systems of set theory. One such system is ZFC with the axiom of infinity replaced by its negation. Theorems that can be proved in ZFC but cannot be proved using the Peano Axioms include Goodstein’s theorem.[22]
With all these definitions, it is convenient to include 0 (corresponding to the empty set) as a natural number. Including 0 is now the common convention among set theorists[23] and logicians.[24] Other mathematicians also include 0,[a] and computer languages often start from zero when enumerating items like loop counters and string- or array-elements.[25][26] On the other hand, many mathematicians have kept the older tradition to take 1 to be the first natural number.[27]
Notation[edit]
The set of all natural numbers is standardly denoted N or 
Since natural numbers may contain 0 or not, it may be important to know which version is referred to. This is often specified by the context, but may also be done by using a subscript or a superscript in the notation, such as:[3][30]
Alternatively, since the natural numbers naturally form a subset of the integers (often denoted 
Properties[edit]
Addition[edit]
Given the set 


If 1 is defined as S(0), then b + 1 = b + S(0) = S(b + 0) = S(b). That is, b + 1 is simply the successor of b.
Multiplication[edit]
Analogously, given that addition has been defined, a multiplication operator 

Relationship between addition and multiplication[edit]
Addition and multiplication are compatible, which is expressed in the distribution law: a × (b + c) = (a × b) + (a × c). These properties of addition and multiplication make the natural numbers an instance of a commutative semiring. Semirings are an algebraic generalization of the natural numbers where multiplication is not necessarily commutative. The lack of additive inverses, which is equivalent to the fact that 

If the natural numbers are taken as «excluding 0», and «starting at 1», the definitions of + and × are as above, except that they begin with a + 1 = S(a) and a × 1 = a. Furthermore, 
Order[edit]
In this section, juxtaposed variables such as ab indicate the product a × b,[32] and the standard order of operations is assumed.
A total order on the natural numbers is defined by letting a ≤ b if and only if there exists another natural number c where a + c = b. This order is compatible with the arithmetical operations in the following sense: if a, b and c are natural numbers and a ≤ b, then a + c ≤ b + c and ac ≤ bc.
An important property of the natural numbers is that they are well-ordered: every non-empty set of natural numbers has a least element. The rank among well-ordered sets is expressed by an ordinal number; for the natural numbers, this is denoted as ω (omega).
Division[edit]
In this section, juxtaposed variables such as ab indicate the product a × b, and the standard order of operations is assumed.
While it is in general not possible to divide one natural number by another and get a natural number as result, the procedure of division with remainder or Euclidean division is available as a substitute: for any two natural numbers a and b with b ≠ 0 there are natural numbers q and r such that
The number q is called the quotient and r is called the remainder of the division of a by b. The numbers q and r are uniquely determined by a and b. This Euclidean division is key to the several other properties (divisibility), algorithms (such as the Euclidean algorithm), and ideas in number theory.
Algebraic properties satisfied by the natural numbers[edit]
The addition (+) and multiplication (×) operations on natural numbers as defined above have several algebraic properties:
- Closure under addition and multiplication: for all natural numbers a and b, both a + b and a × b are natural numbers.[33]
- Associativity: for all natural numbers a, b, and c, a + (b + c) = (a + b) + c and a × (b × c) = (a × b) × c.[34]
- Commutativity: for all natural numbers a and b, a + b = b + a and a × b = b × a.[35]
- Existence of identity elements: for every natural number a, a + 0 = a and a × 1 = a.
- If the natural numbers are taken as «excluding 0», and «starting at 1», then for every natural number a, a × 1 = a. However, the «existence of additive identity element» property is not satisfied
- Distributivity of multiplication over addition for all natural numbers a, b, and c, a × (b + c) = (a × b) + (a × c).
- No nonzero zero divisors: if a and b are natural numbers such that a × b = 0, then a = 0 or b = 0 (or both).
- If the natural numbers are taken as «excluding 0», and «starting at 1», the «no nonzero zero divisors» property is not satisfied.
Generalizations[edit]
Two important generalizations of natural numbers arise from the two uses of counting and ordering: cardinal numbers and ordinal numbers.
- A natural number can be used to express the size of a finite set; more precisely, a cardinal number is a measure for the size of a set, which is even suitable for infinite sets. This concept of «size» relies on maps between sets, such that two sets have the same size, exactly if there exists a bijection between them. The set of natural numbers itself, and any bijective image of it, is said to be countably infinite and to have cardinality aleph-null (ℵ0).
- Natural numbers are also used as linguistic ordinal numbers: «first», «second», «third», and so forth. This way they can be assigned to the elements of a totally ordered finite set, and also to the elements of any well-ordered countably infinite set. This assignment can be generalized to general well-orderings with a cardinality beyond countability, to yield the ordinal numbers. An ordinal number may also be used to describe the notion of «size» for a well-ordered set, in a sense different from cardinality: if there is an order isomorphism (more than a bijection!) between two well-ordered sets, they have the same ordinal number. The first ordinal number that is not a natural number is expressed as ω; this is also the ordinal number of the set of natural numbers itself.
The least ordinal of cardinality ℵ0 (that is, the initial ordinal of ℵ0) is ω but many well-ordered sets with cardinal number ℵ0 have an ordinal number greater than ω.
For finite well-ordered sets, there is a one-to-one correspondence between ordinal and cardinal numbers; therefore they can both be expressed by the same natural number, the number of elements of the set. This number can also be used to describe the position of an element in a larger finite, or an infinite, sequence.
A countable non-standard model of arithmetic satisfying the Peano Arithmetic (that is, the first-order Peano axioms) was developed by Skolem in 1933. The hypernatural numbers are an uncountable model that can be constructed from the ordinary natural numbers via the ultrapower construction.
Georges Reeb used to claim provocatively that «The naïve integers don’t fill up» 
Formal definitions[edit]
There are two standard methods for formally defining natural numbers. The first one, due to Giuseppe Peano, consists of an autonomous axiomatic theory called Peano arithmetic, based on few axioms called Peano axioms.
The second definition is based on set theory. It defines the natural numbers as specific sets. More precisely, each natural number n is defined as an explicitly defined set, whose elements allow counting the elements of other sets, in the sense that the sentence «a set S has n elements» means that there exists a one to one correspondence between the two sets n and S.
The sets used to define natural numbers satisfy Peano axioms. It follows that every theorem that can be stated and proved in Peano arithmetic can also be proved in set theory. However, the two definitions are not equivalent, as there are theorems that can be stated in terms of Peano arithmetic and proved in set theory, which are not provable inside Peano arithmetic. A probable example is Fermat’s Last Theorem.
The definition of the integers as sets satisfying Peano axioms provide a model of Peano arithmetic inside set theory. An important consequence is that, if set theory is consistent (as it is usually guessed), then Peano arithmetic is consistent. In other words, if a contradiction could be proved in Peano arithmetic, then set theory would by contradictory, and every theorem of set theory would be both true and wrong.
Peano axioms[edit]
The five Peano axioms are the following:[36][i]
- 0 is a natural number.
- Every natural number has a successor which is also a natural number.
- 0 is not the successor of any natural number.
- If the successor of
equals the successor of
, then
equals
.
- The axiom of induction: If a statement is true of 0, and if the truth of that statement for a number implies its truth for the successor of that number, then the statement is true for every natural number.
These are not the original axioms published by Peano, but are named in his honor. Some forms of the Peano axioms have 1 in place of 0. In ordinary arithmetic, the successor of 

Set-theoretic definition[edit]
Intuitively, the natural number n is the common property of all sets that have n elements. So, it seems natural to define n as an equivalence class under the relation «can be made in one to one correspondence». Unfortunately, this does not work in set theory, as such an equivalence class would not be a set (because of Russell’s paradox). The standard solution is to define a particular set with n elements that will be called the natural number n.
The following definition was first published by John von Neumann,[37] although Levy attributes the idea to unpublished work of Zermelo in 1916.[38] As this definition extends to infinite set as a definition of ordinal number, the sets considered below are sometimes called von Neumann ordinals.
The definition proceeds as follows:
- Call 0 = { }, the empty set.
- Define the successor S(a) of any set a by S(a) = a ∪ {a}.
- By the axiom of infinity, there exist sets which contain 0 and are closed under the successor function. Such sets are said to be inductive. The intersection of all inductive sets is still an inductive set.
- This intersection is the set of the natural numbers.
It follows that the natural numbers are defined iteratively as follows:
-
- 0 = { },
- 1 = 0 ∪ {0} = {0} = {{ }},
- 2 = 1 ∪ {1} = {0, 1} = {{ }, {{ }}},
- 3 = 2 ∪ {2} = {0, 1, 2} = {{ }, {{ }}, {{ }, {{ }}}},
- n = n−1 ∪ {n−1} = {0, 1, …, n−1} = {{ }, {{ }}, …, {{ }, {{ }}, …}},
- etc.
It can be checked that the natural numbers satisfies the Peano axioms.
With this definition, given a natural number n, the sentence «a set S has n elements» can be formally defined as «there exists a bijection from n to S. This formalizes the operation of counting the elements of S. Also, n ≤ m if and only if n is a subset of m. In other words, the set inclusion defines the usual total order on the natural numbers. This order is a well-order.
It follows from the definition that each natural number is equal to the set of all natural numbers less than it. This definition, can be extended to the von Neumann definition of ordinals for defining all ordinal numbers, including the infinite ones: «each ordinal is the well-ordered set of all smaller ordinals.»
If one does not accept the axiom of infinity, the natural numbers may not form a set. Nevertheless, the natural numbers can still be individually defined as above, and they still satisfy the Peano axioms.
There are other set theoretical constructions. In particular, Ernst Zermelo provided a construction that is nowadays only of historical interest, and is sometimes referred to as Zermelo ordinals.[38] It consists in defining 0 as the empty set, and S(a) = {a}.
With this definition each natural number is a singleton set. So, the property of the natural numbers to represent cardinalities is not directly accessible; only the ordinal property (being the nth element of a sequence) is immediate. Unlike von Neumann’s construction, the Zermelo ordinals do not extend to infinite ordinals.
See also[edit]
- Canonical representation of a positive integer – Representation of a number as a product of primes
- Countable set – Mathematical set that can be enumerated
- Sequence – Function of the natural numbers in another set
- Ordinal number – Generalization of «n-th» to infinite cases
- Cardinal number – Size of a possibly infinite set
- Set-theoretic definition of natural numbers – constructions of the whole numbers from sets
Complex 
|
|
Notes[edit]
- ^ a b Mac Lane & Birkhoff (1999, p. 15) include zero in the natural numbers: ‘Intuitively, the set
of all natural numbers may be described as follows:
contains an «initial» number 0; …’. They follow that with their version of the Peano’s axioms.
- ^ Carothers (2000, p. 3) says: «
is the set of natural numbers (positive integers)» Both definitions are acknowledged whenever convenient, and there is no general consensus on whether zero should be included in the natural numbers.[1]
- ^ Mendelson (2008, p. x) says: «The whole fantastic hierarchy of number systems is built up by purely set-theoretic means from a few simple assumptions about natural numbers.»
- ^ Bluman (2010, p. 1): «Numbers make up the foundation of mathematics.»
- ^ A tablet found at Kish … thought to date from around 700 BC, uses three hooks to denote an empty place in the positional notation. Other tablets dated from around the same time use a single hook for an empty place.[11]
- ^ This convention is used, for example, in Euclid’s Elements, see D. Joyce’s web edition of Book VII.[15]
- ^ The English translation is from Gray. In a footnote, Gray attributes the German quote to: «Weber 1891–1892, 19, quoting from a lecture of Kronecker’s of 1886.»[19][20]
- ^ «Much of the mathematical work of the twentieth century has been devoted to examining the logical foundations and structure of the subject.» (Eves 1990, p. 606)
- ^ Hamilton (1988, pp. 117 ff) calls them «Peano’s Postulates» and begins with «1. 0 is a natural number.»
Halmos (1960, p. 46) uses the language of set theory instead of the language of arithmetic for his five axioms. He begins with «(I) 0 ∈ ω (where, of course, 0 = ∅» (ω is the set of all natural numbers).
Morash (1991) gives «a two-part axiom» in which the natural numbers begin with 1. (Section 10.1: An Axiomatization for the System of Positive Integers)
References[edit]
- ^ a b c Weisstein, Eric W. «Natural Number». mathworld.wolfram.com. Retrieved 11 August 2020.
- ^ «Natural Numbers». Brilliant Math & Science Wiki. Retrieved 11 August 2020.
- ^ a b c «Standard number sets and intervals». ISO 80000-2:2009. International Organization for Standardization. p. 6.
- ^ «natural number». Merriam-Webster.com. Merriam-Webster. Archived from the original on 13 December 2019. Retrieved 4 October 2014.
- ^ Ganssle, Jack G. & Barr, Michael (2003). «integer». Embedded Systems Dictionary. pp. 138 (integer), 247 (signed integer), & 276 (unsigned integer). ISBN 978-1-57820-120-4. Archived from the original on 29 March 2017. Retrieved 28 March 2017 – via Google Books.
- ^ Weisstein, Eric W. «Counting Number». MathWorld.
- ^ «Introduction». Ishango bone. Brussels, Belgium: Royal Belgian Institute of Natural Sciences. Archived from the original on 4 March 2016.
- ^ «Flash presentation». Ishango bone. Brussels, Belgium: Royal Belgian Institute of Natural Sciences. Archived from the original on 27 May 2016.
- ^ «The Ishango Bone, Democratic Republic of the Congo». UNESCO’s Portal to the Heritage of Astronomy. Archived from the original on 10 November 2014., on permanent display at the Royal Belgian Institute of Natural Sciences, Brussels, Belgium.
- ^ Ifrah, Georges (2000). The Universal History of Numbers. Wiley. ISBN 0-471-37568-3.
- ^ «A history of Zero». MacTutor History of Mathematics. Archived from the original on 19 January 2013. Retrieved 23 January 2013.
- ^ Mann, Charles C. (2005). 1491: New Revelations of the Americas before Columbus. Knopf. p. 19. ISBN 978-1-4000-4006-3. Archived from the original on 14 May 2015. Retrieved 3 February 2015 – via Google Books.
- ^ Evans, Brian (2014). «Chapter 10. Pre-Columbian Mathematics: The Olmec, Maya, and Inca Civilizations». The Development of Mathematics Throughout the Centuries: A brief history in a cultural context. John Wiley & Sons. ISBN 978-1-118-85397-9 – via Google Books.
- ^ Deckers, Michael (25 August 2003). «Cyclus Decemnovennalis Dionysii – Nineteen year cycle of Dionysius». Hbar.phys.msu.ru. Archived from the original on 15 January 2019. Retrieved 13 February 2012.
- ^ Euclid. «Book VII, definitions 1 and 2». In Joyce, D. (ed.). Elements. Clark University. Archived from the original on 5 August 2011.
- ^ Mueller, Ian (2006). Philosophy of mathematics and deductive structure in Euclid’s Elements. Mineola, New York: Dover Publications. p. 58. ISBN 978-0-486-45300-2. OCLC 69792712.
- ^ Kline, Morris (1990) [1972]. Mathematical Thought from Ancient to Modern Times. Oxford University Press. ISBN 0-19-506135-7.
- ^ Poincaré, Henri (1905) [1902]. «On the nature of mathematical reasoning». La Science et l’hypothèse [Science and Hypothesis]. Translated by Greenstreet, William John. VI.
- ^ Gray, Jeremy (2008). Plato’s Ghost: The modernist transformation of mathematics. Princeton University Press. p. 153. ISBN 978-1-4008-2904-0. Archived from the original on 29 March 2017 – via Google Books.
- ^ Weber, Heinrich L. (1891–1892). «Kronecker». Jahresbericht der Deutschen Mathematiker-Vereinigung [Annual report of the German Mathematicians Association]. pp. 2:5–23. (The quote is on p. 19). Archived from the original on 9 August 2018; «access to Jahresbericht der Deutschen Mathematiker-Vereinigung«. Archived from the original on 20 August 2017.
- ^ Eves 1990, Chapter 15
- ^ Kirby, Laurie; Paris, Jeff (1982). «Accessible Independence Results for Peano Arithmetic». Bulletin of the London Mathematical Society. Wiley. 14 (4): 285–293. doi:10.1112/blms/14.4.285. ISSN 0024-6093.
- ^ Bagaria, Joan (2017). Set Theory (Winter 2014 ed.). The Stanford Encyclopedia of Philosophy. Archived from the original on 14 March 2015. Retrieved 13 February 2015.
- ^ Goldrei, Derek (1998). «3». Classic Set Theory: A guided independent study (1. ed., 1. print ed.). Boca Raton, Fla. [u.a.]: Chapman & Hall/CRC. p. 33. ISBN 978-0-412-60610-6.
- ^ Brown, Jim (1978). «In defense of index origin 0». ACM SIGAPL APL Quote Quad. 9 (2): 7. doi:10.1145/586050.586053. S2CID 40187000.
- ^ Hui, Roger. «Is index origin 0 a hindrance?». jsoftware.com. Archived from the original on 20 October 2015. Retrieved 19 January 2015.
- ^ This is common in texts about Real analysis. See, for example, Carothers (2000, p. 3) or Thomson, Bruckner & Bruckner (2008, p. 2).
- ^ «Listing of the Mathematical Notations used in the Mathematical Functions Website: Numbers, variables, and functions». functions.wolfram.com. Retrieved 27 July 2020.
- ^ Rudin, W. (1976). Principles of Mathematical Analysis. New York: McGraw-Hill. p. 25. ISBN 978-0-07-054235-8.
- ^ Grimaldi, Ralph P. (2004). Discrete and Combinatorial Mathematics: An applied introduction (5th ed.). Pearson Addison Wesley. ISBN 978-0-201-72634-3.
- ^ Grimaldi, Ralph P. (2003). A review of discrete and combinatorial mathematics (5th ed.). Boston: Addison-Wesley. p. 133. ISBN 978-0-201-72634-3.
- ^ Weisstein, Eric W. «Multiplication». mathworld.wolfram.com. Retrieved 27 July 2020.
- ^ Fletcher, Harold; Howell, Arnold A. (9 May 2014). Mathematics with Understanding. Elsevier. p. 116. ISBN 978-1-4832-8079-0.
…the set of natural numbers is closed under addition… set of natural numbers is closed under multiplication
- ^ Davisson, Schuyler Colfax (1910). College Algebra. Macmillian Company. p. 2.
Addition of natural numbers is associative.
- ^ Brandon, Bertha (M.); Brown, Kenneth E.; Gundlach, Bernard H.; Cooke, Ralph J. (1962). Laidlaw mathematics series. Vol. 8. Laidlaw Bros. p. 25.
- ^ Mints, G.E. (ed.). «Peano axioms». Encyclopedia of Mathematics. Springer, in cooperation with the European Mathematical Society. Archived from the original on 13 October 2014. Retrieved 8 October 2014.
- ^ von Neumann (1923)
- ^ a b Levy (1979), p. 52
Bibliography[edit]
- Bluman, Allan (2010). Pre-Algebra DeMYSTiFieD (Second ed.). McGraw-Hill Professional. ISBN 978-0-07-174251-1 – via Google Books.
- Carothers, N.L. (2000). Real Analysis. Cambridge University Press. ISBN 978-0-521-49756-5 – via Google Books.
- Clapham, Christopher; Nicholson, James (2014). The Concise Oxford Dictionary of Mathematics (Fifth ed.). Oxford University Press. ISBN 978-0-19-967959-1 – via Google Books.
- Dedekind, Richard (1963) [1901]. Essays on the Theory of Numbers. Translated by Beman, Wooster Woodruff (reprint ed.). Dover Books. ISBN 978-0-486-21010-0 – via Archive.org.
- Dedekind, Richard (1901). Essays on the Theory of Numbers. Translated by Beman, Wooster Woodruff. Chicago, IL: Open Court Publishing Company. Retrieved 13 August 2020 – via Project Gutenberg.
- Dedekind, Richard (2007) [1901]. Essays on the Theory of Numbers. Kessinger Publishing, LLC. ISBN 978-0-548-08985-9.
- Eves, Howard (1990). An Introduction to the History of Mathematics (6th ed.). Thomson. ISBN 978-0-03-029558-4 – via Google Books.
- Halmos, Paul (1960). Naive Set Theory. Springer Science & Business Media. ISBN 978-0-387-90092-6 – via Google Books.
- Hamilton, A.G. (1988). Logic for Mathematicians (Revised ed.). Cambridge University Press. ISBN 978-0-521-36865-0 – via Google Books.
- James, Robert C.; James, Glenn (1992). Mathematics Dictionary (Fifth ed.). Chapman & Hall. ISBN 978-0-412-99041-0 – via Google Books.
- Landau, Edmund (1966). Foundations of Analysis (Third ed.). Chelsea Publishing. ISBN 978-0-8218-2693-5 – via Google Books.
- Levy, Azriel (1979). Basic Set Theory. Springer-Verlag Berlin Heidelberg. ISBN 978-3-662-02310-5.
- Mac Lane, Saunders; Birkhoff, Garrett (1999). Algebra (3rd ed.). American Mathematical Society. ISBN 978-0-8218-1646-2 – via Google Books.
- Mendelson, Elliott (2008) [1973]. Number Systems and the Foundations of Analysis. Dover Publications. ISBN 978-0-486-45792-5 – via Google Books.
- Morash, Ronald P. (1991). Bridge to Abstract Mathematics: Mathematical proof and structures (Second ed.). Mcgraw-Hill College. ISBN 978-0-07-043043-3 – via Google Books.
- Musser, Gary L.; Peterson, Blake E.; Burger, William F. (2013). Mathematics for Elementary Teachers: A contemporary approach (10th ed.). Wiley Global Education. ISBN 978-1-118-45744-3 – via Google Books.
- Szczepanski, Amy F.; Kositsky, Andrew P. (2008). The Complete Idiot’s Guide to Pre-algebra. Penguin Group. ISBN 978-1-59257-772-9 – via Google Books.
- Thomson, Brian S.; Bruckner, Judith B.; Bruckner, Andrew M. (2008). Elementary Real Analysis (Second ed.). ClassicalRealAnalysis.com. ISBN 978-1-4348-4367-8 – via Google Books.
- von Neumann, John (1923). «Zur Einführung der transfiniten Zahlen» [On the Introduction of the Transfinite Numbers]. Acta Litterarum AC Scientiarum Ragiae Universitatis Hungaricae Francisco-Josephinae, Sectio Scientiarum Mathematicarum. 1: 199–208. Archived from the original on 18 December 2014. Retrieved 15 September 2013.
- von Neumann, John (January 2002) [1923]. «On the introduction of transfinite numbers». In van Heijenoort, Jean (ed.). From Frege to Gödel: A source book in mathematical logic, 1879–1931 (3rd ed.). Harvard University Press. pp. 346–354. ISBN 978-0-674-32449-7. – English translation of von Neumann 1923.
External links[edit]
- «Natural number», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- «Axioms and construction of natural numbers». apronus.com.
Из соседних натуральных чисел, число, которое стоит левее числа n называется предыдущим числу n, а число, которое стоит правее называется следующим за n.
История натуральных чисел началась ещё в первобытные времена.
Издревле люди считали предметы. Например, в торговле нужен был счет товара или в строительстве счет материала. Да даже в быту тоже приходилось считать вещи, продукты, скот. Сначала числа использовались только для подсчета в жизни, на практике, но в дальнейшем при развитии математики стали частью науки.
Натуральные числа
– это числа которые мы используем при счете предметов.
Например: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, ….
Нуль не относится к натуральным числам.
Все натуральные числа или назовем множество натуральных чисел обозначается символом N.
Таблица натуральных чисел.
Натуральный ряд.
Натуральные числа, записанные подряд в порядке возрастания, образуют натуральный ряд
или ряд натуральных чисел.
Свойства натурального ряда:
- Наименьшее натуральное число – единица.
- У натурального ряда следующее число больше предыдущего на единицу. (1, 2, 3, …) Три точки или троеточие ставятся в том случае, если закончить последовательность чисел невозможно.
- Натуральный ряд не имеет наибольшего числа, он бесконечен.
Пример №1:
Напишите первых 5 натуральных числа.
Решение:
Натуральные числа начинаются с единицы.
1, 2, 3, 4, 5
Пример №2:
Нуль является натуральным числом?
Ответ: нет.
Пример №3:
Какое первое число в натуральном ряду?
Ответ: натуральный ряд начинается с единицы.
Пример №4:
Какое последнее число в натуральном ряде? Назовите самое большое натуральное число?
Ответ: Натуральный ряд начинается с единицы. Каждое следующее число больше предыдущего на единицу, поэтому последнего числа не существует. Самого большого числа нет.
Пример №5:
У единицы в натуральном ряду есть предыдущее число?
Ответ: нет, потому что единица является первым числом в натуральном ряду.
Пример №6:
Назовите следующее число в натуральном ряду за числами: а)5, б)67, в)9998.
Ответ: а)6, б)68, в)9999.
Пример №7:
Сколько чисел находится в натуральном ряду между числами: а)1 и 5, б)14 и 19.
Решение:
а) 1, 2, 3, 4,
5 – три числа находятся между числами 1 и 5.
б) 14, 15, 16, 17, 18,
19 – четыре числа находятся между числами 14 и 19.
Пример №8:
Назовите предыдущее число за числом 11.
Ответ: 10.
Пример №9:
Какие числа применяются при счете предметов?
Ответ: натуральные числа.
Простейшее число — это натуральное число
. Их используют в повседневной жизни для подсчета предметов, т.е. для вычисления их количества и порядка.
Что такое натуральное число: натуральными числами
называют числа, которые используются для подсчета предметов либо для указывания порядкового номера любого предмета из всех однородных
предметов.
Натуральные числа
— это числа, начиная с единицы. Они образуются естественным образом при счёте.
Например, 1,2,3,4,5… —
первые натуральные числа.
Наименьшее натуральное число
— один. Наибольшего натурального числа не существует. При счёте число ноль не используют, поэтому ноль натуральное число.
Натуральный ряд чисел
— это последовательность всех натуральных чисел. Запись натуральных чисел:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 …
В натуральном ряду каждое число больше предыдущего на единицу.
Сколько чисел в натуральном ряду? Натуральный ряд бесконечен, самого большого натурального числа не существует.
Десятичной так как 10 единиц всякого разряда образуют 1 единицу старшего разряда. Позиционной так как значение цифры зависит от её места в числе, т.е. от разряда, где она записана.
Классы натуральных чисел.
Всякое натуральное число возможно написать при помощи 10-ти арабских цифр:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Для чтения натуральных чисел их разбивают, начиная справа, на группы по 3 цифры в каждой. 3 первые цифры справа — это класс единиц, 3 следующие — это класс тысяч, далее классы миллионов, миллиардов и
так далее. Каждая из цифр класса называется его
разрядом
.
Сравнение натуральных чисел.
Из 2-х натуральных чисел меньше то число, которое при счете называется ранее. Например
, число 7
меньше
11
(записывают так:
7 ). Когда одно число больше второго, это записывают так:
386 > 99
.
Таблица разрядов и классов чисел.
|
1-й класс единицы |
1-й разряд единицы 2-й разряд десятки 3-й разряд сотни |
|
2-й класс тысячи |
1-й разряд единицы тысяч 2-й разряд десятки тысяч 3-й разряд сотни тысяч |
|
3-й класс миллионы |
1-й разряд единицы миллионов 2-й разряд десятки миллионов 3-й разряд сотни миллионов |
|
4-й класс миллиарды |
1-й разряд единицы миллиардов 2-й разряд десятки миллиардов 3-й разряд сотни миллиардов |
Числа от 5-го класса и выше относятся к большим числам. Единицы 5-го класса — триллионы, 6-го класса — квадриллионы, 7-го класса — квинтиллионы, 8-го класса — секстиллионы, 9-го класса —
ептиллионы.
Основные свойства натуральных чисел.
- Коммутативность сложения. a + b = b + a
- Коммутативность умножения. ab = ba
- Ассоциативность сложения. (a + b) + c = a + (b + c)
- Ассоциативность умножения.
- Дистрибутивность умножения относительно сложения:
Действия над натуральными числами.
4. Деление натуральных чисел — операция, обратная операции умножения.
Если b ∙ с = а
, то
Формулы для деления:
а: 1 = a
a: a = 1, a ≠ 0
0: a = 0, a ≠ 0
(а
∙ b) : c = (a:c) ∙ b
(а
∙ b) : c = (b:c) ∙ a
Числовые выражения и числовые равенства.
Запись, где числа соединяются знаками действий, является числовым выражением
.
Например, 10∙3+4; (60-2∙5):10.
Записи, где знаком равенства объединены 2 числовых выражения, является числовыми равенствами
. У равенства есть левая и правая части.
Порядок выполнения арифметических действий.
Сложение и вычитание чисел — это действия первой степени, а умножение и деление — это действия второй степени.
Когда числовое выражение состоит из действий только одной степени, то их выполняют последовательно
слева направо.
Когда выражения состоят из действия только первой и второй степени, то сначала выполняют действия второй степени, а потом — действия первой степени.
Когда в выражении есть скобки — сначала выполняют действия в скобках.
Например, 36:(10-4)+3∙5= 36:6+15 = 6+15 = 21.
Место нуля
Существуют два подхода к определению натуральных чисел:
- подсчёте (нумерации)
предметов (первый
, второй
, третий
, четвёртый
, пятый
…); - натуральные числа — числа, возникающие при обозначении количества
предметов (0 предметов
, 1 предмет
, 2 предмета
, 3 предмета
, 4 предмета
, 5 предметов
…).
В первом случае ряд натуральных чисел начинается с единицы, во втором — с нуля. Не существует единого для большинства математиков мнения о предпочтительности первого или второго подхода (то есть считать ли ноль натуральным числом или нет). В подавляющем большинстве российских источников традиционно принят первый подход . Второй подход, например, применяется в трудах Николя Бурбаки , где натуральные числа определяются как мощности конечных множеств . Наличие нуля облегчает формулировку и доказательство многих теорем арифметики натуральных чисел, поэтому при первом подходе вводится полезное понятие расширенного натурального ряда
, включающего ноль .
Множество всех натуральных чисел принято обозначать символом . Международные стандарты ISO 31-11 (1992 год) и ISO 80000-2 (2009 год) устанавливают следующие обозначения :
В русских источниках этот стандарт пока не соблюдается — в них символ
N
{displaystyle mathbb {N} }
обозначает натуральные числа без нуля, а расширенный натуральный ряд обозначается
N
0
,
Z
+
,
Z
⩾
0
{displaystyle mathbb {N} _{0},mathbb {Z} _{+},mathbb {Z} _{geqslant 0}}
и т. д.
Аксиомы, позволяющие определить множество натуральных чисел
Аксиомы Пеано для натуральных чисел
Множество
N
{displaystyle mathbb {N} }
будем называть множеством натуральных чисел, если зафиксированы некоторый элемент 1
(единица), функция
S
{displaystyle S}
c областью определения
N
{displaystyle mathbb {N} }
, называемая функцией следования (
S:
N
{displaystyle Scolon mathbb {N} }
), и выполнены следующие условия:
- элемент единица принадлежит этому множеству (
1
∈
N
{displaystyle 1in mathbb {N} }
), то есть является натуральным числом; - число, следующее за натуральным, также является натуральным (если , то
S
(x)
∈
N
{displaystyle S(x)in mathbb {N} }
или, в более короткой записи,
S:
N
→
N
{displaystyle Scolon mathbb {N} to mathbb {N} }
); - единица не следует ни за каким натуральным числом (
∄
x
∈
N
(S
(x)
=
1)
{displaystyle nexists xin mathbb {N} (S(x)=1)}
); - если натуральное число
a
{displaystyle a}непосредственно следует как за натуральным числом
b
{displaystyle b}, так и за натуральным числом
c
{displaystyle c}, то
b
{displaystyle b}и
c
{displaystyle c}— это одно и то же число (если
S
(b)
=
a
{displaystyle S(b)=a}
и
S
(c)
=
a
{displaystyle S(c)=a}
, то
b
=
c
{displaystyle b=c}
); - (аксиома индукции) если какое-либо предложение (высказывание)
P
{displaystyle P}доказано для натурального числа
n
=
1
{displaystyle n=1}
(база индукции
) и если из допущения, что оно верно для другого натурального числа
n
{displaystyle n}, вытекает, что оно верно для следующего за
n
{displaystyle n}натурального числа (индукционное предположение
), то это предложение верно для всех натуральных чисел (пусть
P
(n)
{displaystyle P(n)}
— некоторый одноместный (унарный) предикат , параметром которого является натуральное число
n
{displaystyle n}. Тогда, если
P
(1)
{displaystyle P(1)}
и
∀
n
(P
(n)
⇒
P
(S
(n)))
{displaystyle forall n;(P(n)Rightarrow P(S(n)))}
, то
∀
n
P
(n)
{displaystyle forall n;P(n)}
).
Перечисленные аксиомы отражают наше интуитивное представление о натуральном ряде и числовой линии .
Принципиальным фактом является то, что эти аксиомы по сути однозначно определяют натуральные числа (категоричность системы аксиом Пеано). А именно, можно доказать (см. , а также краткое доказательство ), что если
(N
,
1
,
S)
{displaystyle (mathbb {N} ,1,S)}
и
(N
~
,
1
~
,
S
~)
{displaystyle ({tilde {mathbb {N} }},{tilde {1}},{tilde {S}})}
— две модели для системы аксиом Пеано, то они необходимо изоморфны , то есть существует обратимое отображение (биекция)
f:
N
→
N
~
{displaystyle fcolon mathbb {N} to {tilde {mathbb {N} }}}
такая, что
f
(1)
=
1
~
{displaystyle f(1)={tilde {1}}}
и
f
(S
(x))
=
S
~
(f
(x))
{displaystyle f(S(x))={tilde {S}}(f(x))}
для всех
x
∈
N
{displaystyle xin mathbb {N} }
.
Поэтому, достаточно зафиксировать в качестве
N
{displaystyle mathbb {N} }
какую-либо одну конкретную модель множества натуральных чисел.
Иногда, особенно в иностранной и переводной литературе, в первой и третьей аксиомах Пеано заменяют единицу на ноль. В этом случае ноль считается натуральным числом. При определении через классы равномощных множеств ноль является натуральным числом по определению. Специально отбрасывать его было бы неестественно. Кроме того, это значительно усложнило бы дальнейшее построение и применение теории, так как в большинстве конструкций нуль, как и пустое множество, не является чем-то обособленным. Другим преимуществом считать ноль натуральным числом является то, что при этом
N
{displaystyle mathbb {N} }
образует моноид . Как уже упоминалось , в русской литературе традиционно ноль исключён из числа натуральных чисел.
Теоретико-множественное определение натуральных чисел (определение Фреге — Рассела)
Таким образом, и натуральные числа вводятся, исходя из понятия множества, по двум правилам:
Числа, заданные таким образом, называются ординальными .
Опишем несколько первых ординальных чисел и соответствующих им натуральных чисел:
Величина множества натуральных чисел
Величина бесконечного множества характеризуется понятием «мощность множества », которое является обобщением числа элементов конечного множества на бесконечные множества. По величине (то есть мощности) множество натуральных чисел больше любого конечного множества, но меньше любого интервала, например, интервала
(0
,
1)
{displaystyle (0,1)}
. Множество натуральных чисел по мощности такое же, как множество рациональных чисел. Множество такой же мощности, как множество натуральных чисел, называется счётным множеством . Так, множество членов любой последовательности счётно. В то же время, существует последовательность, в которую каждое натуральное число входит бесконечное число раз, поскольку множество натуральных чисел можно представить как счётное объединение непересекающихся счётных множеств (например ,
N
=
⋃
k
=
0
∞
(⋃
n
=
0
∞
(2
n
+
1)
2
k)
{displaystyle mathbb {N} =bigcup limits _{k=0}^{infty }left(bigcup limits _{n=0}^{infty }(2n+1)2^{k}right)}
).
Операции над натуральными числами
К замкнутым операциям (операциям, не выводящим результат из множества натуральных чисел) над натуральными числами относятся следующие арифметические операции:
Дополнительно рассматривают ещё две операции (с формальной точки зрения не являющиеся операциями над натуральными числами, так как не определены для всех
пар чисел (иногда существуют, иногда нет)):
Следует заметить, что операции сложения и умножения являются основополагающими. В частности, кольцо целых чисел определяется именно через бинарные операции сложения и умножения.
Основные свойства
- Коммутативность сложения:
a
+
b
=
b
+
a
{displaystyle a+b=b+a}
.
- Коммутативность умножения:
a
⋅
b
=
b
⋅
a
{displaystyle acdot b=bcdot a}
.
- Ассоциативность сложения:
(a
+
b)
+
c
=
a
+
(b
+
c)
{displaystyle (a+b)+c=a+(b+c)}
.
- Ассоциативность умножения:
(a
⋅
b)
⋅
c
=
a
⋅
(b
⋅
c)
{displaystyle (acdot b)cdot c=acdot (bcdot c)}
.
- Дистрибутивность умножения относительно сложения:
{
a
⋅
(b
+
c)
=
a
⋅
b
+
a
⋅
c
(b
+
c)
⋅
a
=
b
⋅
a
+
c
⋅
a
{displaystyle {begin{cases}acdot (b+c)=acdot b+acdot c(b+c)cdot a=bcdot a+ccdot aend{cases}}}
.
Алгебраическая структура
Сложение превращает множество натуральных чисел в полугруппу с единицей, роль единицы выполняет 0
. Умножение также превращает множество натуральных чисел в полугруппу с единицей, при этом единичным элементом является 1
. С помощью замыкания относительно операций сложения-вычитания и умножения-деления получаются группы целых чисел
Z
{displaystyle mathbb {Z} }
и рациональных положительных чисел
Q
+
∗
{displaystyle mathbb {Q} _{+}^{*}}
соответственно.
Числа, предназначенные для подсчета предметов и отвечающие на вопрос «сколько?» («сколько
мячей?», «сколько яблок?», «сколько солдатиков?»), называются натуральными.
Если записать их по порядку, от меньшего числа к большему, то получится натуральный ряд чисел:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 99, 100, 101, …, 999, 1000, 1001 …
Натуральный ряд чисел начинается с числа 1.
Каждое следующее натуральное число на 1 больше предыдущего.
Натуральный ряд чисел бесконечен.
Числа бывают четные и нечетные.
Четные числа делятся на два, а нечетные числа не делятся на два.
Ряд нечетных чисел:
1, 3, 5, 7, 9, 11, 13, …, 99, 101, …, 999, 1001, 1003 …
Ряд четных чисел:
2, 4, 6, 8, 10, 12, 14, …, 98, 100, …, 998, 1000, 1002 …
В натуральном ряду нечетные и четные числа чередуются:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …, 99, 100, …, 999, 1000 …
Как сравнивать натуральные числа
При сравнении двух натуральных чисел больше то, которое стоит в натуральном ряду правее:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 …
Так, семь больше трех, а пять больше единицы.
В математике для записи слова «меньше» используют знак « ».
Острый уголок значков «больше» и «меньше» всегда направлен в сторону меньшего из двух чисел.
Запись 7 > 3 читается как «семь больше трех».
Запись 3
Запись 5 > 1 читается как «пять больше одного».
Запись 1
Слово «равно» в математике заменяют знаком «=»:
Когда числа большие, трудно сразу сказать, какое из них стоит правее в натуральном ряду.
При сравнении двух натуральных чисел с разным количеством цифр больше из них то, в котором цифр больше.
Например, 233 000
Многозначные натуральные числа с одинаковым количеством цифр сравниваются поразрядно, начиная со старшего разряда.
Сначала сравниваются единицы самого старшего разряда, потом — следующего за ним, следующего и так далее. Например, сравниваем числа 5401 и 5430:
5401 = 5 тысяч 4 сотни 0 десятков 1 единица;
5430 = 5 тысяч 4 сотни 3 десятка 0 единиц.
Сравниваем единицы тысяч
. В разряде единиц тысяч числа 5401 — 5 единиц, в разряде единиц тысяч числа 5430 — 5 единиц. Сравнив единицы тысяч, еще нельзя сказать, какое из чисел больше.
Сравниваем сотни
. В разряде сотен числа 5401 — 4 единицы, в разряде сотен числа 5430 — тоже 4 единицы. Надо продолжать сравнение.
Сравниваем десятки
. В разряде десятков числа 5401 — 0 единиц, в разряде десятков числа 5430 — 3 единицы.
Сравнив, получим 0
Числа можно располагать в порядке убывания и в порядке возрастания.
Если в записи нескольких натуральных чисел каждое следующее число меньше предыдущего, то говорят, что числа записаны в порядке убывания.
Запишем числа 5, 22, 13, 800 в порядке убывания.
Отыщем большее число. Число 5 — однозначное, 13 и 22 — двузначные, 800 — трехзначное число и, следовательно, самое большое. Пишем на первом месте 800.
Из двузначных чисел 13 и 22 большее 22. Пишем за числом 800 число 22, а затем 13.
Наименьшее число — однозначное число 5. Пишем его последним.
800, 22, 13, 5 — запись данных чисел в порядке их убывания.
Если в записи нескольких натуральных чисел каждое следующее число больше предыдущего, то говорят, что числа записаны в порядке возрастания.
А как записать числа 15, 2, 31, 278, 298 в порядке возрастания?
Среди чисел 15, 2, 31, 278, 298 отыщем меньшее.
Это однозначное число 2. Запишем его на первом месте.
Из двузначных чисел 15 и 31 выбираем меньшее — 15, пишем его на втором месте, а за ним — 31.
Из трехзначных чисел 278 — меньшее, пишем его за числом 31, а последним пишем число 298.
2, 15, 21, 278, 298 — запись данных чисел в порядке возрастания
Натуральные числа
– числа, которые применяют для счета предметов.
Любое натуральное число можно записать с помощью десяти цифр:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Такую записьчисел называют десятичной.
Последовательность всех натуральных чисел называют натуральным рядом.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …
Самое маленькое
натуральное число – единица (1). В натуральном ряду каждое следующее число на 1 больше предыдущего. Натуральный ряд бесконечен,
наибольшего числа в нем нет.
Значение цифры зависит от ее места в записи числа. Например, цифра 4 означает: 4 единицы,если она стоит на последнем месте в записи числа (в разряде единиц);
4 десятка,
если она стоит на предпоследнем месте (в разряде десятков);
4 сотни,
если она стоит на третьем месте от конца (в
разряде сотен).
Цифра0 означает отсутствие единиц данного разряда
в десятичной записи числа.Она служит и для обозначения числа «нуль
». Это число означает «ни одного». Счет 0: 3 футбольного матча говорит о том, что первая команда не забила ни одного гола в ворота противника.
Нуль не относят
к натуральным числам. И действительно счет предметов никогда не начинают с нуля.
Если запись натурального числа состоит из одного знака –
одной цифры, то его называют однозначным.
Т.е. однозначное
натуральное число
– натуральное число, запись которого состоит из одного знака –
одной цифры. Например, числа 1, 6, 8 – однозначные.
Двузначное
натуральное число
– натуральное число, запись которого состоит из двух знаков – двух цифр.
Например, числа 12, 47, 24, 99 – двузначные.
Так же по числу знаков в данном числе дают названия и другим числам:
числа 326, 532, 893 – трехзначные;
числа 1126, 4268, 9999 – четырехзначные
и т.д.
Двузначные, трехзначные, четырехзначные, пятизначные и т.д. числа называют многозначными числами.
Для чтения многозначных чисел их разбивают, начиная справа, на группы по три цифры в каждой (самая левая группа может состоять из одной или двух цифр). Эти группы называют классами.
Миллион
– это тысяча тысяч (1000 тыс.), его записывают 1 млн или 1 000 000.
Миллиард
– это 1000 миллионов. Его записывают 1 млрд или 1 000 000 000.
Три первые цифры справа составляют класс единиц, три следующие – класс тысяч, далее идут классы миллионов, миллиардов и т.д. (рис. 1).
Рис. 1. Класс миллионов, класс тысяч и класс единиц (слева направо)
Число15389000286 записано в разрядной сетке (рис. 2).
Рис. 2. Разрядная сетка: число 15 миллиардов 389 миллионов 286
Это число имеет 286 единиц в классе единиц, нуль единиц в классе тысяч, 389 единиц в классе миллионов и15 единиц в классе миллиардов.
Натуральные числа — одно из старейших
математических понятий.
В далёком прошлом люди не знали чисел и,
когда им требовалось пересчитать предметы
(животных, рыбу и т.д.), они делали это не так, как
мы сейчас.
Количество предметов сравнивали с частями тела, например, с
пальцами на руке и говорили: «У меня столько же орехов, сколько пальцев на руке».
Со временем люди поняли, что пять орехов, пять коз и пять зайцев обладают
общим свойством — их количество равно пяти.
Запомните!
Натуральные числа — это числа, начиная с 1, получаемые
при счете предметов.
1, 2, 3, 4, 5…
Наименьшее натуральное число — 1.
Наибольшего натурального числа не существует.
При счёте число ноль не используется. Поэтому ноль не
считается натуральным числом.
Записывать числа люди научились гораздо позже, чем считать. Раньше
всего они стали изображать единицу одной палочкой, потом
двумя палочками — число 2, тремя — число 3.
| — 1, || — 2, ||| — 3, ||||| — 5 …
Затем появились и особые знаки для обозначения чисел — предшественники современных
цифр. Цифры, которыми мы пользуемся для записи чисел, родились в Индии примерно 1 500
лет назад. В Европу их привезли арабы, поэтому их называют
арабскими цифрами.
Всего цифр десять: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. С помощью этих
цифр можно записать любое натуральное число.
Запомните!
Натуральный ряд — это последовательность всех натуральных чисел:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 …
В натуральном ряду каждое число больше предыдущего на 1.
Натуральный ряд бесконечен, наибольшего натурального числа в нём не существует.
Систему счёта (счисления), который мы пользуемся,
называют десятичной позиционной.
Десятичной потому, что 10 единиц каждого разряда образуют
1 единицу старшего разряда. Позиционной потому, что значение цифры
зависит от её места в записи числа, то есть от
разряда, в котором
она записана.
Важно!
Разряды и классы
(включая класс миллионов) подробно разобраны
на нашем сайте в материалах для начальной школы.
Класс миллиардов
Если взять десять сотен миллионов, то получим новую разрядную единицу —
один миллиард или в записи цифрами.
1 000 миллионов = 1 000 000 000 = 1 млрд
Десять таких единиц — десять миллиардов, десять десятков миллиардов образуют
следующую единицу — сто миллиардов.
Запомните!
Миллиарды, десятки миллиардов и сотни миллиардов образуют четвёртый
класс — класс миллиардов.
Разряды и классы натурального числа
Рассмотрим натуральное число 783 502 197 048
| Название класса |
Миллиарды | Миллионы | Тысячи | Единицы | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Название разряда | Сотни миллиардов | Десятки миллиардов | Миллиарды | Сотни миллионов | Десятки миллионов | Миллионы | Сотни тысяч | Десятки тысяч | Тысячи | Сотни | Десятки | Единицы |
| Цифра (символ) |
7 | 8 | 3 | 5 | 0 | 2 | 1 | 9 | 7 | 0 | 4 | 8 |
| Название класса |
Миллиарды | Миллионы | Тысячи | Единицы | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Название разряда | Сотни миллиардов | Десятки миллиардов | Миллиарды | Сотни миллионов | Десятки миллионов | Миллионы | Сотни тысяч | Десятки тысяч | Тысячи | Сотни | Десятки | Единицы |
| Цифра (символ) |
7 | 8 | 3 | 5 | 0 | 2 | 1 | 9 | 7 | 0 | 4 | 8 |
C помощью таблицы разрядов прочитаем это число. Для этого надо слева направо по очереди
называть количество единиц каждого класса и добавлять название класса.
Название класса
единиц не произносят, также не произносят название класса, если все три
цифры в его разрядах — нули.
Теперь прочтем число 783 502 197 048 из таблицы:
783 миллиарда 502 миллиона 197 тысяч
48.
Числа 1, 10, 100, 1000… называются разрядными единицами. С их помощью натуральное число
записывается в виде разрядных слагаемых. Так, например, число 307 898 будет выглядеть
в виде разрядных слагаемых.
307 898 = 300 000 + 7 000 + 800 + 90 + 8
Проверить свои вычисления
вы можете с помощью нашего
калькулятора разложения числа на разряды онлайн.
Следующие за миллиардом классы названы в соответствии с латинскими
наименованиями чисел. Каждая следующая единица содержит тысячу предыдущих.
- 1 000 миллиардов = 1 000 000 000 000 = 1 триллион («три» — по латыни «три»)
- 1 000 триллионов = 1 000 000 000 000 000 = 1 квадриллион («квадра» — по латыни «четыре»)
- 1 000 квадриллионов = 1 000 000 000 000 000 000 = 1 квинтиллион («квинта» — по латыни «пять»)
Все числа пересчитать невозможно, поскольку за каждым числом следует число на единицу большее,
но очень большие числа в повседневной жизни не нужны.
Однако, физики нашли число, которое превосходит количество всех атомов (мельчайших частиц вещества)
во всей Вселенной.
Это число получило специальное название — гугол. Гугол — число, у которого
100 нулей.