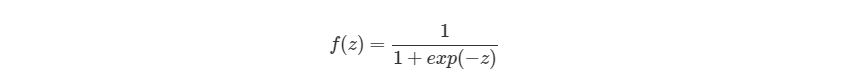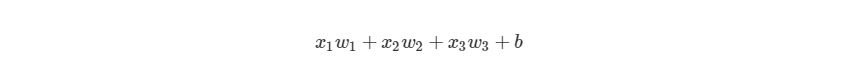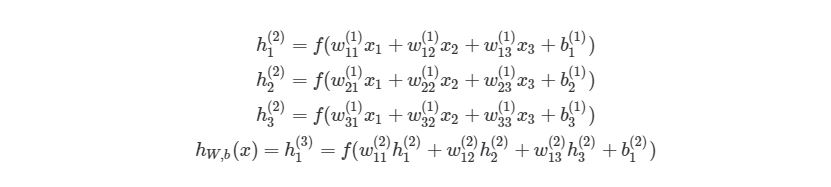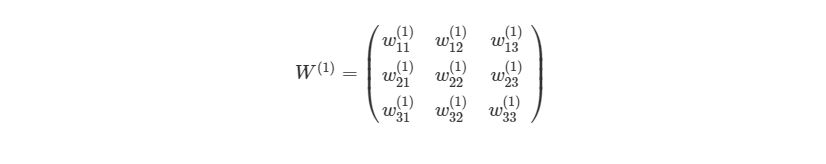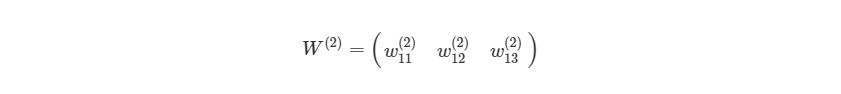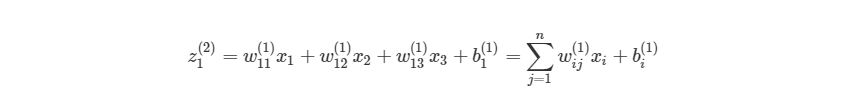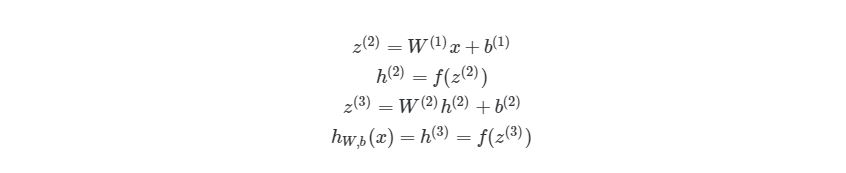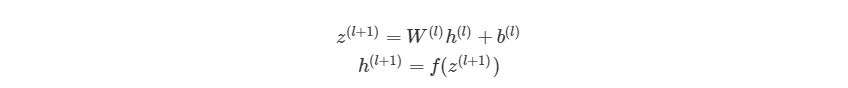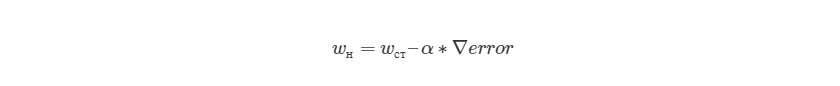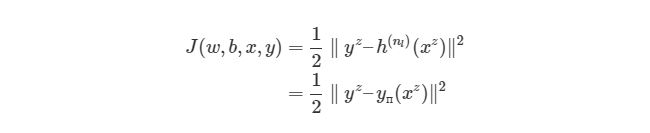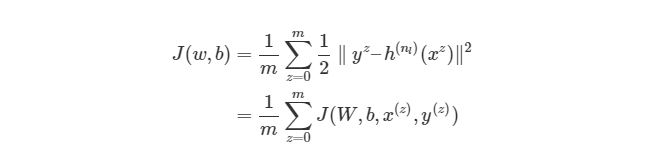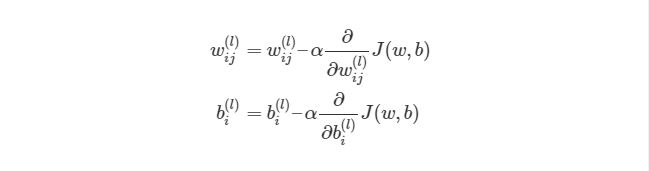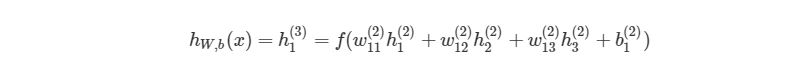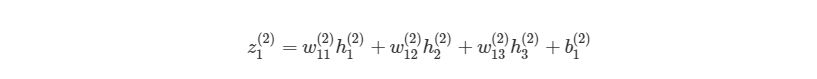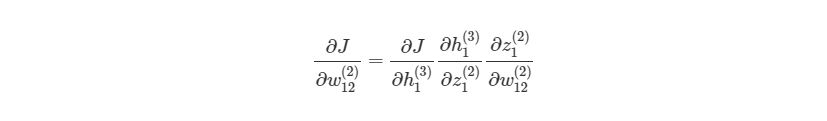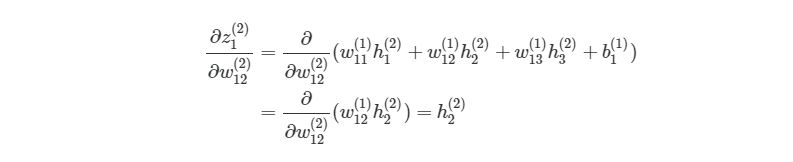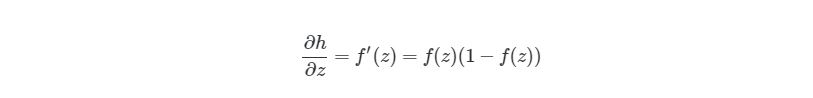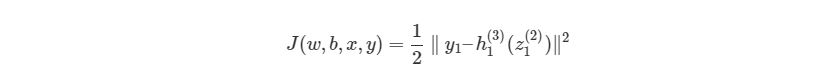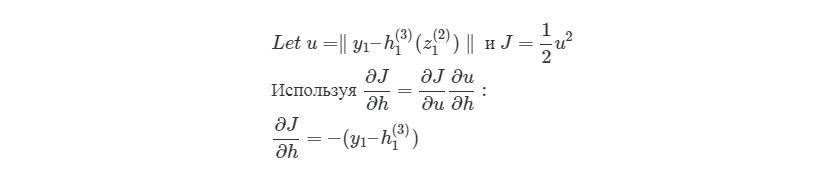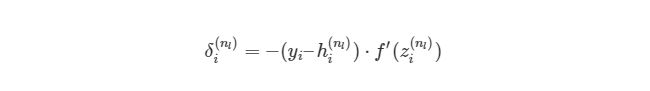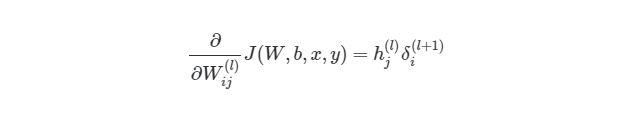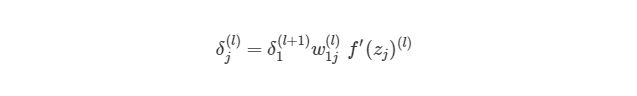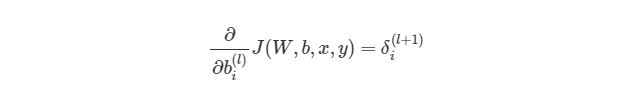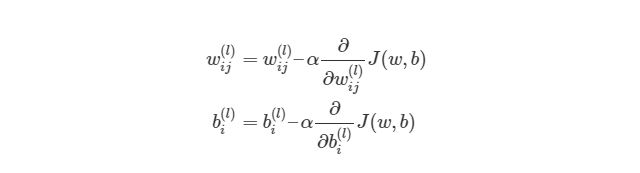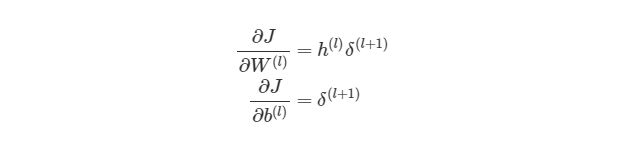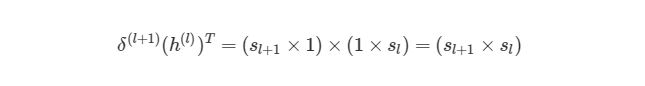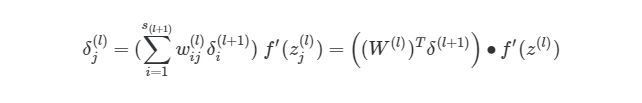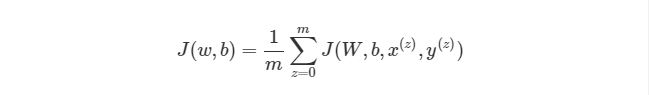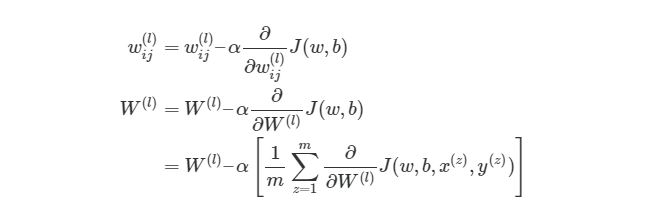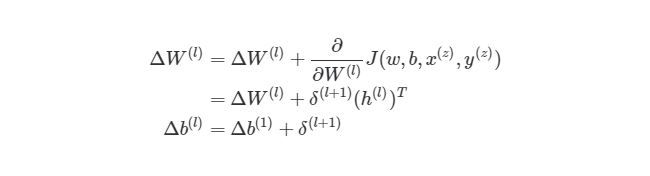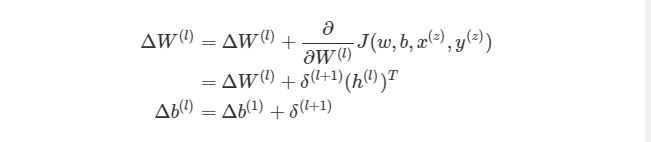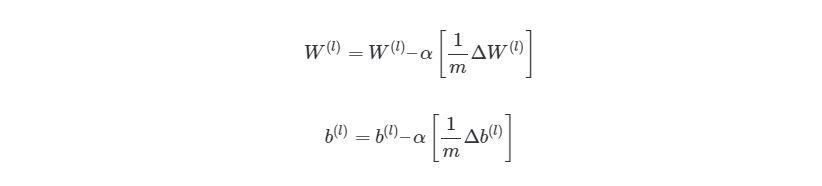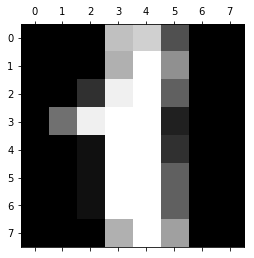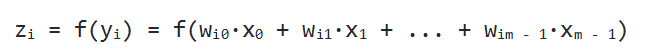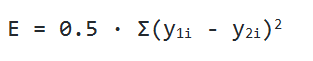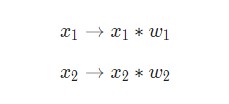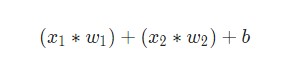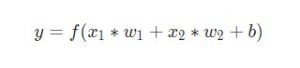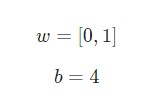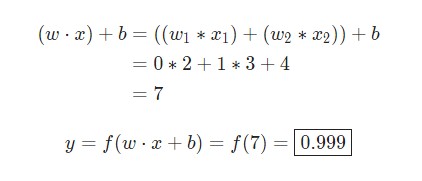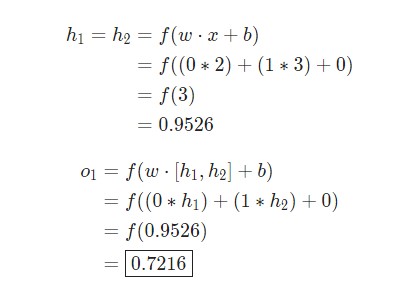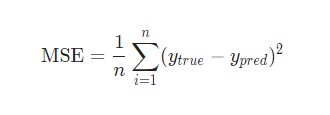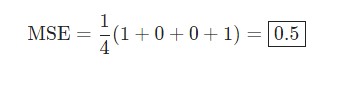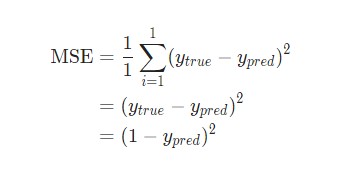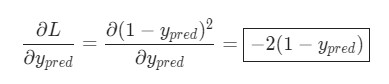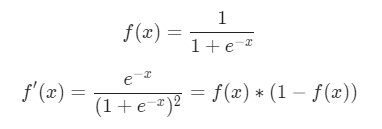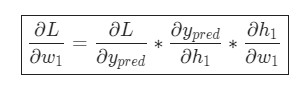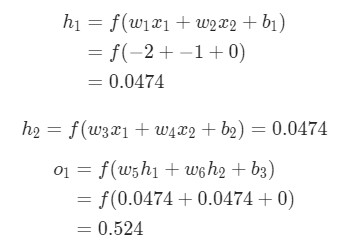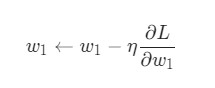Отличный гайд про нейросеть от теории к практике. Вы узнаете из каких элементов состоит ИНС, как она работает и как ее создать самому.
Если вы в поисках пособия по искусственным нейронным сетям (ИНС), то, возможно, у вас уже имеются некоторые предположения относительно того, что это такое. Но знали ли вы, что нейронные сети — основа новой и интересной области глубинного обучения? Глубинное обучение — область машинного обучения, в наше время помогло сделать большой прорыв во многих областях, начиная с игры в Го и Покер с живыми игроками, и заканчивая беспилотными автомобилями. Но, прежде всего, глубинное обучение требует знаний о работе нейронных сетей.
В этой статье будут представлены некоторые понятия, а также немного кода и математики, с помощью которых вы сможете построить и понять простые нейронные сети. Для ознакомления с материалом нужно иметь базовые знания о матрицах и дифференциалах. Код будет написан на языке программирования Python с использованием библиотеки numpy. Вы построите ИНС, используя Python, которая с высокой точностью классифицировать числа на картинках.
1 Что такое искусственная нейросеть?
Искусственные нейросеть (ИНС) — это программная реализация нейронных структур нашего мозга. Мы не будем обсуждать сложную биологию нашей головы, достаточно знать, что мозг содержит нейроны, которые являются своего рода органическими переключателями. Они могут изменять тип передаваемых сигналов в зависимости от электрических или химических сигналов, которые в них передаются. Нейросеть в человеческом мозге — огромная взаимосвязанная система нейронов, где сигнал, передаваемый одним нейроном, может передаваться в тысячи других нейронов. Обучение происходит через повторную активацию некоторых нейронных соединений. Из-за этого увеличивается вероятность вывода нужного результата при соответствующей входной информации (сигналах). Такой вид обучения использует обратную связь — при правильном результате нейронные связи, которые выводят его, становятся более плотными.
Искусственные нейронные сети имитируют поведение мозга в простом виде. Они могут быть обучены контролируемым и неконтролируемым путями. В контролируемой ИНС, сеть обучается путем передачи соответствующей входной информации и примеров исходной информации. Например, спам-фильтр в электронном почтовом ящике: входной информацией может быть список слов, которые обычно содержатся в спам-сообщениях, а исходной информацией — классификация для уведомления (спам, не спам). Такой вид обучения добавляет веса связям ИНС, но это будет рассмотрено позже.
Неконтролируемое обучение в ИНС пытается «заставить» ИНС «понять» структуру передаваемой входной информации «самостоятельно». Мы не будем рассматривать это в данном посте.
2 Структура ИНС
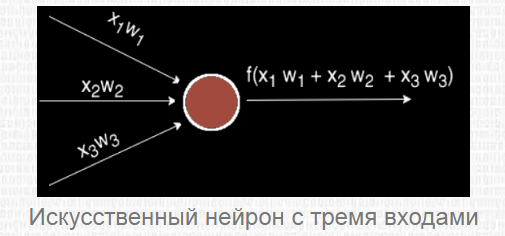
2.1 Искусственный нейрон
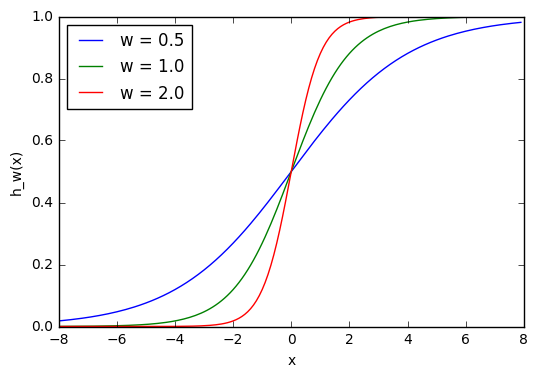
Биологический нейрон имитируется в ИНС через активационную функцию. В задачах классификации (например определение спам-сообщений) активационная функция должна иметь характеристику «включателя». Иными словами, если вход больше, чем некоторое значение, то выход должен изменять состояние, например с 0 на 1 или -1 на 1 Это имитирует «включение» биологического нейрона. В качестве активационной функции обычно используют сигмоидальную функцию:
Которая выглядит следующим образом:
import matplotlib.pylab as plt
import numpy as np
x = np.arange(-8, 8, 0.1)
f = 1 / (1 + np.exp(-x))
plt.plot(x, f)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.show()
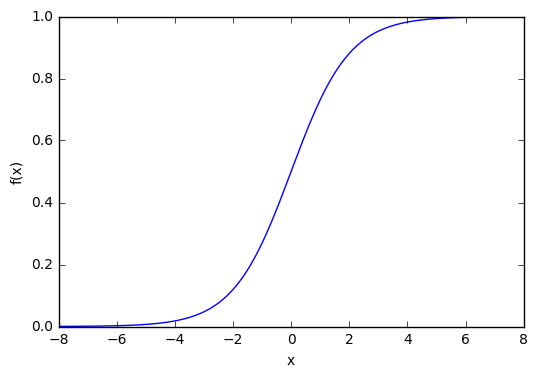
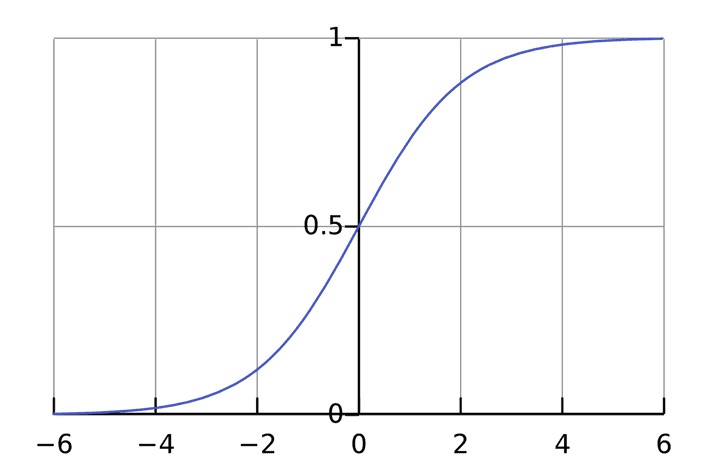
Из графика можно увидеть, что функция «активационная» — она растет с 0 до 1 с каждым увеличением значения х. Сигмоидальная функция является гладкой и непрерывной. Это означает, что функция имеет производную, что в свою очередь является очень важным фактором для обучения алгоритма.
2.2 Узлы
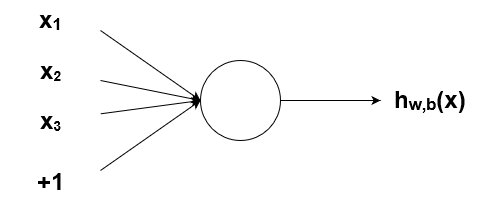
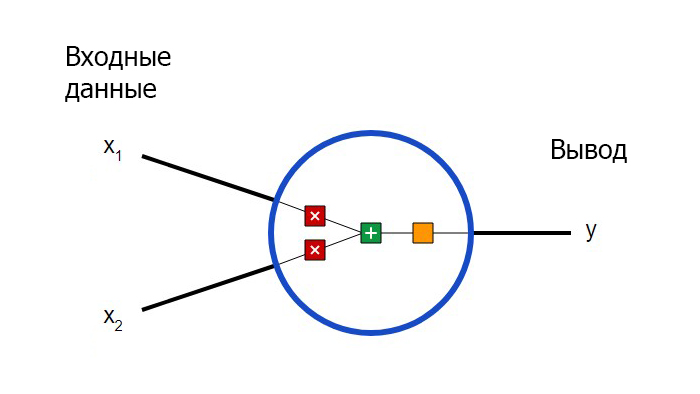
Как было упомянуто ранее, биологические нейроны иерархически соединены в сети, где выход одних нейронов является входом для других нейронов. Мы можем представить такие сети в виде соединенных слоев с узлами. Каждый узел принимает взвешенный вход, активирует активационную функцию для суммы входов и генерирует выход.
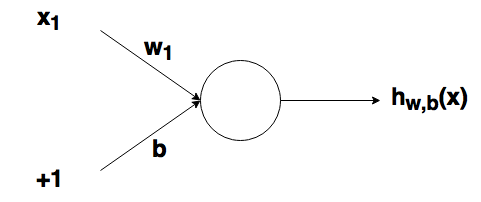
Круг на картинке изображает узел. Узел является «местоположением» активационной функции, он принимает взвешенные входы, складывает их, а затем вводит их в активационную функцию. Вывод активационной функции представлен через h. Примечание: в некоторых источниках узел также называют перцептроном.
Что такое «вес»? По весу берутся числа (не бинарные), которые затем умножаются на входе и суммируются в узле. Иными словами, взвешенный вход в узел имеет вид:
где wi— числовые значения веса ( b мы будем обсудим позже). Весы нам нужны, они являются значениями, которые будут меняться в течение процесса обучения. b является весом элемента смещения на 1, включение веса b делает узел гибким. Проще это понять на примере.
2.3 Смещение
Рассмотрим простой узел, в котором есть по одному входу и выходу:
Ввод для активационной функции в этом узле просто x1w1. На что влияет изменение в w1 в этой простой сети?
w1 = 0.5
w2 = 1.0
w3 = 2.0
l1 = 'w = 0.5'
l2 = 'w = 1.0'
l3 = 'w = 2.0'
for w, l in [(w1, l1), (w2, l2), (w3, l3)]:
f = 1 / (1 + np.exp(-x * w))
plt.plot(x, f, label = l)
plt.xlabel('x')
plt.ylabel('h_w(x)')
plt.legend(loc = 2)
plt.show()
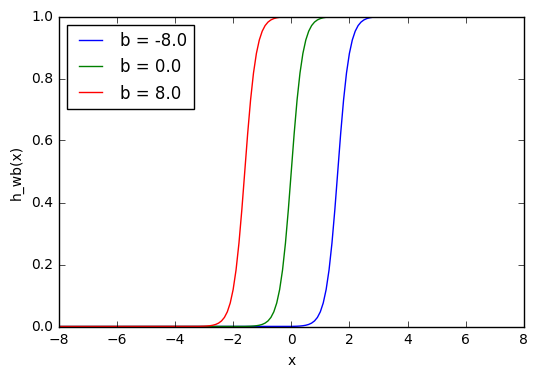
Здесь мы можем видеть, что при изменении веса изменяется также уровень наклона графика активационной функции. Это полезно, если мы моделируем различные плотности взаимосвязей между входами и выходами. Но что делать, если мы хотим, чтобы выход изменялся только при х более 1? Для этого нам нужно смещение. Рассмотрим такую сеть со смещением на входе:
w = 5.0
b1 = -8.0
b2 = 0.0
b3 = 8.0
l1 = 'b = -8.0'
l2 = 'b = 0.0'
l3 = 'b = 8.0'
for b, l in [(b1, l1), (b2, l2), (b3, l3)]:
f = 1 / (1 + np.exp(-(x * w + b)))
plt.plot(x, f, label = l)
plt.xlabel('x')
plt.ylabel('h_wb(x)')
plt.legend(loc = 2)
plt.show()
Из графика можно увидеть, что меняя «вес» смещения b, мы можем изменять время запуска узла. Смещение очень важно в случаях, когда нужно имитировать условные отношения.
2.4 Составленная структура
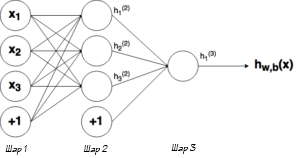
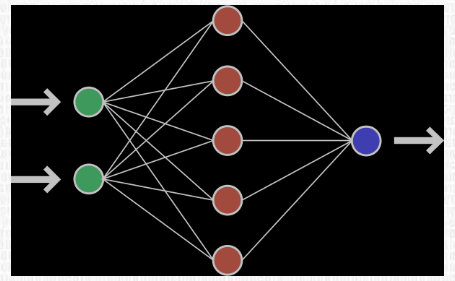
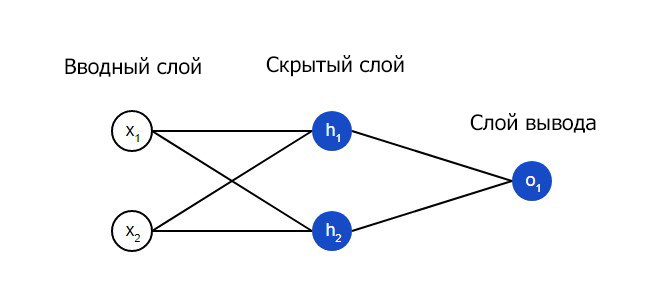
Выше было объяснено, как работает соответствующий узел / нейрон / перцептрон. Но, как вы знаете, в полной нейронной сети находится много таких взаимосвязанных между собой узлов. Структуры таких сетей могут принимать мириады различных форм, но самая распространенная состоит из входного слоя, скрытого слоя и выходного слоя. Пример такой структуры приведены ниже:
Ну рисунке выше можно увидеть три слоя сети — Слой 1 является входным слоем, где сеть принимает внешние входные данные. Слой 2 называют скрытым слоем, этот слой не является частью ни входа, ни выхода. Примечание: нейронные сети могут иметь несколько скрытых слоев, в данном примере для примера был показан лишь один. И наконец, Слой 3 является исходным слоем. Вы можете заметить, что между Шаром 1 (Ш1) и Шаром 2 (Ш2) существует много связей. Каждый узел в Ш1 имеет связь со всеми узлами в Ш2, при этом от каждого узла в Ш2 идет по одной связи к единому выходному узлу в Ш3. Каждая из этих связей должна иметь соответствующий вес.
2.5 Обозначение
Вся математика, приведенная выше, требует очень точной нотации. Нотация, которая используется здесь, используется и в руководстве по глубинному обучению от Стэнфордского Университета. В следующих уравнениях вес соответствующего связи будет обозначаться как w ij(l), где i — номер узла в слое l+1, а j- номер узла в слое l. Например, вес связи между узлом 1 в слое 1 и узлом 2 в слое 2 будет обозначаться как w 21(l). Непонятно, почему индексы 2-1 означают связь 1-2? Такая нотация более понятна, если добавить смещения.
Из графика выше видно, что смещение 1 связано со всеми узлами в соседнем слое. Смещение в Ш1 имеет связь со всеми узлами в Ш2. Так как смещение не является настоящим узлом с активационной функцией, оно не имеет и входов (его входное значение всегда равно константе). Вес связи между смещением и узлом будем обозначать через bi(l), где i- номер узла в слое l+1, так же, как в w ij(l). К примеру с w 21(l) вес между смещением в Ш1 и вторым узлом в Ш2 будет иметь обозначение b2(1).
Помните, что эти значения -w ij(l)и bi(l) — будут меняться в течение процесса обучения ИНС.
Обозначение связи с исходным узлом будет выглядеть следующим образом: hjl, где j- номер узла в слое l. Тогда в предыдущем примере, связью с исходным узлом является h1(2).
Теперь давайте рассмотрим, как рассчитывать выход сети, когда нам известны вес и вход. Процесс нахождения выхода в нейронной сети называется процессом прямого распространения.
3 Процесс прямого распространения
Чтобы продемонстрировать, как находить выход, имея уже известный вход, в нейронных сетях, начнем с предыдущего примера с тремя слоями. Ниже такая система представлена в виде системы уравнений:
, где f(∙) — активационная функция узла, в нашем случае сигмоидальная функция. В первой строке h1(2)— выход первого узла во втором слое, его входами соответственно являются w11(1)x1(1), w12(1)x2(1),w13(1)x3(1) и b1(1). Эти входы было сложены, а затем переданы в активационную функцию для расчета выхода первого узла. С двумя следующими узлами аналогично.
Последняя строка рассчитывает выход единого узла в последнем третьем слое, он является конечной исходной точкой в нейронной сети. В нем вместо взвешенных входных переменных (x1,x2,x3)берутся взвешенные выходы узлов с другой слоя (h1(2),h2(2),h3(2))и смещения. Такая система уравнений также хорошо показывает иерархическую структуру нейронной сети.
3.1 Пример прямого распространения
Приведем простой пример первого вывода нейронной сети языке Python . Обратите внимание, веса w11(1),w12(1),… между Ш1 и Ш2 идеально могут быть представлены в матрице:
Представим эту матрицу через массивы библиотеки numpy.
import numpy as np
w1 = np.array([
[0.2, 0.2, 0.2],
[0.4, 0.4, 0.4],
[0.6, 0.6, 0.6]
])
Мы просто присвоили некоторые рандомные числовые значения весу каждой связи с Ш1. Аналогично можно сделать и с Ш2:
w2 = np.zeros((1, 3))
w2[0, : ] = np.array([0.5, 0.5, 0.5])
Мы можем присвоить некоторые значения весу смещения в Ш1 и Ш2:
b1 = np.array([0.8, 0.8, 0.8])
b2 = np.array([0.2])
Наконец, перед написанием основной программы для расчета выхода нейронной сети, напишем отдельную функцию для активационной функции:
def f(x):
return 1 / (1 + np.exp(-x))
3.2 Первая попытка реализовать процесс прямого распространения
Приведем простой способ расчета выхода нейронной сети, используя вложенные циклы в Python. Позже мы быстро рассмотрим более эффективные способы.
def simple_looped_nn_calc(n_layers, x, w, b):
for l in range(n_layers - 1): #Формируется входной массив - перемножения весов в каждом слое# Если первый слой, то входной массив равен вектору х# Если слой не первый, вход для текущего слоя равен# выходу предыдущего
if l == 0:
node_in = x
else :
node_in = h #формирует выходной массив для узлов в слое l + 1
h = np.zeros((w[l].shape[0], ))#проходит по строкам массива весов
for i in range(w[l].shape[0]): #считает сумму внутри активационной функции
f_sum = 0 #проходит по столбцам массива весов
for j in range(w[l].shape[1]):
f_sum += w[l][i][j] * node_in[j] #добавляет смещение
f_sum += b[l][i]
#использует активационную функцию для расчета
#i - того выхода, в данном случае h1, h2, h3
h[i] = f(f_sum)
return h
Данная функция принимает в качестве входа номер слоя в нейронной сети, х — входной массив / вектор:
w = [w1, w2]
b = [b1, b2] #Рандомный входной вектор x
x = [1.5, 2.0, 3.0]
Функция сначала проверяет, чем является входной массив для соответствующего слоя с узлами / весами. Если рассматривается первый слой, то входом для второго слоя является входной массив xx, Умноженный на соответствующие веса. Если слой не первый, то входом для последующего будет выход предыдущего.
Вызов функции:
simple_looped_nn_calc(3, x, w, b)
возвращает результат 0.8354. Можно проверить правильность, вставив те же значения в систему уравнений:
3.3 Более эффективная реализация
Использование циклов — не самый эффективный способ расчета прямого распространения на языке Python , потому что циклы в этом языке программирования работают довольно медленно. Мы кратко рассмотрим лучшие решения. Также можно будет сравнить работу алгоритмов, используя функцию в IPython:
%timeit simple_looped_nn_calc(3, x, w, b)
В данном случае процесс прямого распространения с циклами занимает около 40 микросекунд. Это довольно быстро, но не для больших нейронных сетей с > 100 узлами на каждом слое, особенно при их обучении. Если мы запустим этот алгоритм на нейронной сети с четырьмя слоями, то получим результат 70 микросекунд. Эта разница является достаточно значительной.
3.4 Векторизация в нейронных сетях
Можно более компактно написать предыдущие уравнения, тем самым найти результат эффективнее. Сначала добавим еще одну переменную zi(l), которая является суммой входа в узел i слоя l, Включая смещение. Тогда для первого узла в Ш2, z будет равна:
, где n- количество узлов в Ш1. Используя это обозначение, систему уравнений можно сократить:
Обратите внимание на W, что означает матричную форму представления весов. Помните, что теперь все элементы в уравнении сверху являются матрицами / векторами. Но на этом упрощение не заканчивается. Данные уравнения можно свести к еще более краткому виду:
Так выглядит общая форма процесса прямого распространения, выход слоя l становится входом в слой l+1. Мы знаем, что h(1) является входным слоем x, а h(nl)(где nl- номер слоя в сети) является исходным слоем. Мы также не стали использовать индексы i и j-за того, что можно просто перемножить матрицы — это даст нам тот же результат. Поэтому данный процесс и называется «векторизацией». Этот метод имеет ряд плюсов. Во-первых, код его реализации выглядит менее запутанным. Во-вторых, используются свойства по линейной алгебре вместо циклов, что делает работу программы быстрее. С numpy можно легко сделать такие подсчеты. В следующей части быстро повторим операции над матрицами, для тех, кто их немного подзабыл.
3.5 Умножение матриц
Распишем z(l+1)=W(l)h(l)+b(l) на выражение из матрицы и векторов входного слоя ( h(l)=x):
Для тех, кто не знает или забыл, как перемножаются матрицы. Когда матрица весов умножается на вектор, каждый элемент в строке матрицы весов умножается на каждый элемент в столбце вектора, после этого все произведения суммируются и создается новый вектор (3х1). После перемножения матрицы на вектор, добавляются элементы из вектора смещения и получается конечный результат.
Каждая строка полученного вектора соответствует аргументу активационной функции в оригинальной НЕ матричной системе уравнений выше. Это означает, что в Python мы можем реализовать все, не используя медленные циклы. К счастью, библиотека numpy дает возможность сделать это достаточно быстро, благодаря функциям-операторам над матрицами. Рассмотрим код простой и быстрой версии функции simple_looped_nn_calc:
def matrix_feed_forward_calc(n_layers, x, w, b):
for l in range(n_layers - 1):
if l == 0:
node_in = x
else :
node_in = h
z = w[l].dot(node_in) + b[l]
h = f(z)
return h
Обратите внимание на строку 7, в которой происходит перемножение матрицы и вектора. Если вместо функции умножения a.dot (b) вы используете символ *, то получится нечто похожее на поэлементное умножение вместо настоящего произведения матриц.
Если сравнить время работы этой функции с предыдущей на простой сети с четырьмя слоями, то мы получим результат лишь на 24 микросекунды меньше. Но если увеличить количество узлов в каждом слое до 100-100-50-10, то мы получим гораздо большую разницу. Функция с циклами в этом случае дает результат 41 миллисекунду, когда у функции с векторизацией это занимает лишь 84 микросекунды. Также существуют еще более эффективные реализации операций над матрицами, которые используют пакеты глубинного обучения, такие как TensorFlow и Theano.
На этом все о процессе прямого распространения в нейронных сетях. В следующих разделах мы поговорим о способах обучения нейронных сетей, используя градиентный спуск и обратное распространение.
4 Градиентный спуск и оптимизация
Расчеты значений весов, которые соединяют слои в сети, это как раз то, что мы называем обучением системы. В контролируемом обучении идея заключается в том, чтобы уменьшить погрешность между входом и нужным выходом. Если у нас есть нейросеть с одним выходным слоем и некоторой вход xx и мы хотим, чтобы на выходе было число 2, но сеть выдает 5, то нахождение погрешности выглядит как abs(2-5)=3. Говоря языком математики, мы нашли норму ошибки L1(Это будет рассмотрено позже).
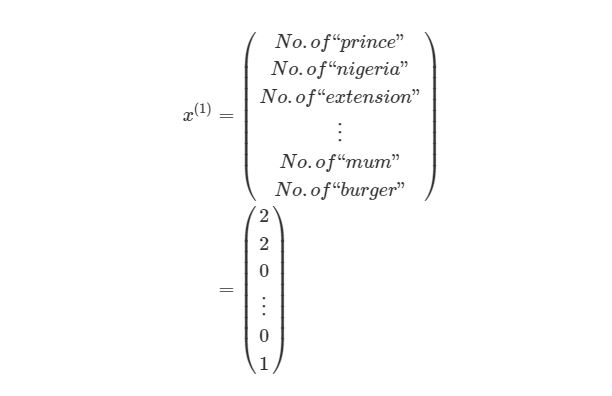
Смысл контролируемого обучения в том, что предоставляется много пар вход-выход уже известных данных и нужно менять значения весов, основываясь на этих примерах, чтобы значение ошибки стало минимальным. Эти пары входа-выхода обозначаются как (x(1),y(1)),…,(x(m),y(m)), где m является количеством экземпляров для обучения. Каждое значение входа или выхода может представлять собой вектор значений, например x(1) не обязательно только одно значение, оно может содержать N-размерный набор значений. Предположим, что мы обучаем нейронную сеть выявлению спам-сообщений — в таком случае x(1) может представлять собой количество соответствующих слов, которые встречаются в сообщении:
y(1) в этом случае может представлять собой единое скалярное значение, например, 1 или 0, обозначающий, было сообщение спамом или нет. В других приложениях это также может быть вектор с K измерениями. Например, мы имеем вход xx, Который является вектором черно-белых пикселей, считанных с фотографии. При этом y может быть вектором с 26 элементами со значениями 1 или 0, обозначающие, какая буква была изображена на фото, например (1,0,…,0)для буквы а, (0,1,…,0) для буквы б и т. д.
В обучении сети, используя (x,y), целью является улучшение нахождения правильного y при известном x. Это делается через изменение значений весов, чтобы минимизировать погрешность. Как тогда менять их значение? Для этого нам и понадобится градиентный спуск. Рассмотрим следующий график:
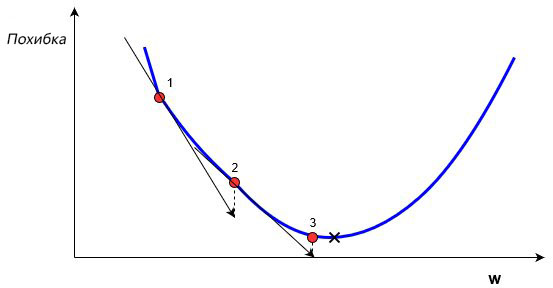
На этом графике изображено погрешность, зависящую от скалярного значения веса, w. Минимально возможная погрешность обозначена черным крестиком, но мы не знаем какое именно значение w дает нам это минимальное значение. Подсчет начинается с рандомного значения переменной w, которая дает погрешность, обозначенную красной точкой под номером «1» на кривой. Нам нужно изменить w таким образом, чтобы достичь минимальной погрешности, черного крестика. Одним из самых распространенных способов является градиентный спуск.
Сначала находится градиент погрешности на «1» по отношению к w. Градиент является уровнем наклона кривой в соответствующей точке. Он изображен на графике в виде черных стрелок. Градиент также дает некоторую информацию о направлении — если он положителен при увеличении w, то в этом направлении погрешность будет увеличиваться, если отрицательный — уменьшаться (см. График). Как вы уже поняли, мы пытаемся сделать, чтобы погрешность с каждым шагом уменьшалась. Величина градиента показывает, как быстро кривая погрешности или функция меняется в соответствующей точке. Чем больше значение, тем быстрее меняется погрешность в соответствующей точке в зависимости от w.
Метод градиентного спуска использует градиент, чтобы принимать решение о следующей смены в w для того, чтобы достичь минимального значения кривой. Он итеративным методом, каждый раз обновляет значение w через:
, где wн означает новое значение w, wст— текущее или «старое» значение w, ∇error является градиентом погрешности на wст и α является шагом. Шаг α также будет означать, как быстро ответ приближается к минимальной погрешности. При каждой итерации в таком алгоритме градиент должен уменьшаться. Из графика выше можно заметить, что с каждым шагом градиент «стихает». Как только ответ достигнет минимального значения, мы уходим из итеративного процесса. Выход можно реализовать способом условия «если погрешность меньше некоторого числа». Это число называют точностью.
4.1 Простой пример на коде
Рассмотрим пример простой имплементации градиентного спуска для нахождения минимума функции f(x)=x4-3x3+2 на языке Python . Градиент этой функции можно найти аналитически через производную f»(x)=4x3-9x2. Это означает, что для любого xx мы можем найти градиент по этой простой формуле. Мы можем найти минимум через производную — x=2.25.
x_old = 0 # Нет разницы, какое значение, главное abs(x_new - x_old) > точность
x_new = 6 # Алгоритм начинается с x = 6
gamma = 0.01 # Размер шага
precision = 0.00001 # Точность
def df(x):
y = 4 * x * * 3 - 9 * x * * 2
return y
while abs(x_new - x_old) > precision:
x_old = x_new
x_new += -gamma * df(x_old)
print("Локальный минимум находится на %f" % x_new)
Вывод этой функции: «Локальный минимум находится на 2.249965», что удовлетворяет правильному ответу с некоторой точностью. Этот код реализует алгоритм изменения веса, о котором рассказывалось выше, и может находить минимум функции с соответствующей точностью. Это был очень простой пример градиентного спуска, нахождение градиента при обучении нейронной сети выглядит несколько иначе, хотя и главная идея остается той же — мы находим градиент нейронной сети и меняем веса на каждом шагу, чтобы приблизиться к минимальной погрешности, которую мы пытаемся найти. Но в случае ИНС нам нужно будет реализовать градиентный спуск с многомерным вектором весов.
Мы будем находить градиент нейронной сети, используя достаточно популярный метод обратного распространения ошибки, о котором будет написано позже. Но сначала нам нужно рассмотреть функцию погрешности более детально.
4.2 Функция оценки
Существует более общий способ изобразить выражения, которые дают нам возможность уменьшить погрешность. Такое общее представление называется функция оценки. Например, функция оценки для пары вход-выход (xz, yz) в нейронной сети будет выглядеть следующим образом:
Выражение является функцией оценки учебного экземпляра zth, где h(nl)является выходом последнего слоя, то есть выход нейронной сети. h(nl) можно представить как yпyп, Что означает полученный результат, когда нам известен вход xz. Две вертикальные линии означают норму L2 погрешности или сумму квадратов ошибок. Сумма квадратов погрешностей является довольно распространенным способом представления погрешностей в системе машинного обучения. Вместо того, чтобы брать абсолютную погрешность abs(ypred(xz)-yz), мы берем квадрат погрешности. Мы не будем обсуждать причину этого в данной статье. 1/2 в начале просто константой, которая нормализует ответ после того, как мы продифференцируем функцию оценки во время обратного распространения.
Обратите внимание, что приведенная ранее функция оценки работает только с одной парой (x,y). Мы хотим минимизировать функцию оценки со всеми mm парами вход-выход:
Тогда как же мы будем использовать функцию J для обучения наших сетей? Конечно, используя градиентный спуск и обратное распространение ошибок. Сначала рассмотрим градиентный спуск в нейронных сетях более детально.
4.3 Градиентный спуск в нейронных сетях
Градиентный спуск для каждого веса w(ij)(l) и смещение bi(l) в нейронной сети выглядит следующим образом:
Выражение выше фактически аналогично представлению градиентного спуска:
wnew=wold-α*∇error. Нет лишь некоторых обозначений, но достаточно понимать, что слева расположены новые значения, а справа — старые. Опять же задействован итерационный метод для расчета весов на каждой итерации, но на этот раз основываясь на функции оценки J(w,b).
Значения ∂/∂wij(l)и ∂/∂bi(l) являются частными производными функции оценки, основываясь на значениях веса. Что это значит? Вспомните простой пример градиентного спуска ранее, каждый шаг зависит от наклона погрешности / оценки по отношению к весу. Производная также имеет значение наклона / градиента. Конечно, производная обозначается как d/dx. x в нашем случае является вектором, а это значит, что наша производная тоже будет вектором, который является градиент каждого измерения x.
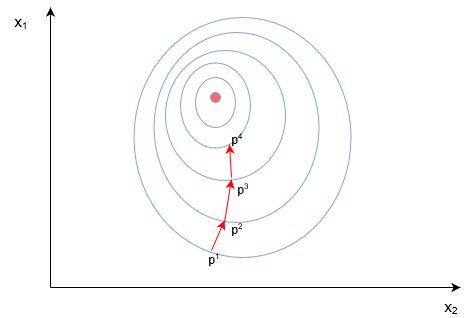
4.4 Пример двумерного градиентного спуска
Рассмотрим пример стандартного двумерного градиентного спуска. Ниже представлены диаграмму работы двух итеративных двумерных градиентных спусков:
Синим обозначены контуры функции оценки, они обозначают области, в которых значение погрешности примерно одинаковы. Каждый шаг (p1→p2→p3) В градиентном спуске используют градиент или производную, которые обозначаются стрелкой / вектором. Этот вектор проходит через два пространства [x1, x2][x1,x2]и показывает направление, в котором находится минимум. Например, производная, исчисленная в p1 может быть d/dx=[2.1,0.7], Где производная является вектором с двумя значениями. Частичная производная ∂/∂x1 в этом случае равна скаляру →[2.1]- иными словами, это значение градиента только в одном измерении поискового пространства (x1).
В нейронных сетях не существует простой полной функции оценки, с которой можно легко посчитать градиент, похожей на функцию, которую мы ранее рассматривали f(x)=x4-3x3+2). Мы можем сравнить выход нейронной сети с нашим ожидаемым значением y(z), После чего функция оценки будет меняться из-за изменения в значениях веса, но как мы это сделаем со всеми скрытыми слоями в сети?
Поэтому нам нужен метод обратного распространения. Этот метод дает нам возможность «делить» функцию оценки или ошибку со всеми весами в сети. Другими словами, мы можем выяснить, как каждый вес влияет на погрешность.
4.5 Углубляемся в обратное распространение
Если математика вам не очень хорошо дается, то вы можете пропустить этот раздел. В следующем разделе вы узнаете, как реализовать обратное распространение языке программирования. Но если вы не против немного больше поговорить о математике, то продолжайте читать, вы получите более глубокие знания по обучению нейронных сетей.
Сначала, давайте вспомним базовые уравнения для нейронной сети с тремя слоями из предыдущих разделов:
Выход этой нейронной сети находится по формуле:
Мы можем упростить это уравнение к h1(3)=f(z1(2)), добавив новое значение z1(2), которое означает:
Предположим, что мы хотим узнать, как влияет изменение в весе w12(2) на функцию оценки. Это означает, что нам нужно вычислить ∂J/∂w12(2). Чтобы сделать это, нужно использовать правило дифференцирования сложной функции:
Если присмотреться, то правая часть полностью сокращается (по принципу 2552=22=1). ∂J∂w12(2) были разбиты на три множителя, два из которых можно прекрасно заменить. Начнем с ∂z1(2)/∂w12(2):
Частичная производная z1(2) по w12(2) зависит только от одного произведения в скобках, w12(1)h2(2), Так как все элементы в скобках, кроме w12(2), не изменяются. Производная от константы всегда равна 1, а ∂/∂w12(2))сокращается до просто h2(2), Что является обычным выходом второго узла из слоя 2.
Следующая частичная производная сложной функции ∂h1(3)/∂z1(2) является частичной производной активационной функции выходного узла h1(3). Так что нам нужно брать производные активационной функции, следует условие ее включения в нейронные сети — функция должна быть дифференцированной. Для сигмоидальной активационной функции производная будет выглядеть так:
, где f(z)является самой активационной функцией. Теперь нам нужно разобраться, что делать с ∂J∂h1(3). Вспомните, что J(w,b,x,y) есть функция квадрата погрешности, выглядит так:
здесь y1 является ожидаемым выходом для выходного узла. Опять используем правило дифференцирования сложной функции:
Мы выяснили, как находить ∂J/∂w12(2)по крайней мере для весов связей с исходным слоем. Перед тем, как перейти к одному из скрытых слоев, введем некоторые новые значения δ, чтобы немного сократить наши выражения:
, где i является номером узла в выходном слое. В нашем примере есть только один узел, поэтому i=1. Напишем полный вид производной функции оценки:
, где выходной слой, в нашем случае, l=2, а i соответствует номеру узла.
4.6 Распространение в скрытых слоях
Что делать с весами в скрытых слоях (в нашем случае в слое 2)? Для весов, которые соединены с выходным слоем, производная ∂J/∂h=-(yi-hi(nl))имела смысл, т.к. функция оценки может быть сразу найдена через сравнение выходного слоя с существующими данными. Но выходы скрытых узлов не имеют подобных уже существующих данных для проверки, они связаны с функцией оценки только через другие слои узлов. Как мы можем найти изменения в функции оценки из-за изменений весов, которые находятся глубоко в нейронной сети? Как уже было сказано, мы используем метод обратного распространения.
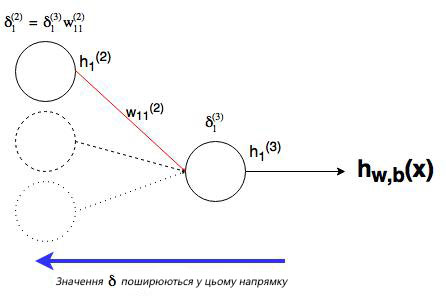
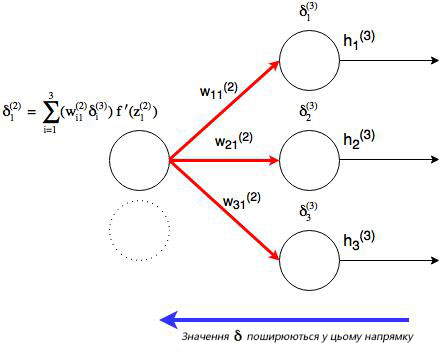
Мы уже сделали тяжелую работу по правилу дифференцирования сложных функций, теперь рассмотрим все более графически. Значение, которое будет обратно распространяться, — δi(nl), т.к. оно в ближайшей связи с функцией оценки. А что с узлом j во втором слое (скрытом слое)? Как он влияет на δi(nl) в нашей сети? Он меняет другие значения из-за веса wij(2)(см. диаграмму ниже, где j=1 i=1).
Как можно понять из рисунка, выходной слой соединяется со скрытым узлом из-за веса. В случае, когда в исходном слое есть только один узел, общее выражение скрытого слоя будет выглядеть так:
, где j номер узла в слое l. Но что будет, если в исходном слое находится много выходных узлов? В этом случае δj(l) находится по взвешенной сумме всех связанных между собой погрешностей, как показано на диаграмме ниже:
На рисунке показано, что каждое значение δ из исходного слоя суммируется для нахождения δ1(2), Но каждый выход δ должен быть взвешенным соответствующими значению wi1(2). Другими словами, узел 1 в слое 2 способствует изменениям погрешностей в трех выходных узлах, при этом полученная погрешность (или значение функции оценки) в каждом из этих узлов должна быть «передана назад» значению δ этого узла. Сформируем общее выражение значение δ для узлов в скрытом слое:
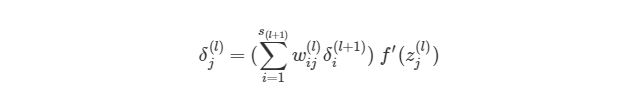
Теперь мы знаем, как находить:
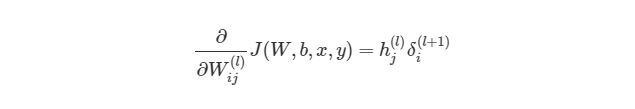
Отлично, теперь мы знаем, как реализовать градиентный спуск в нейронных сетях:
Однако, для такой реализации, нам нужно будет снова применить циклы. Как мы уже знаем из предыдущих разделов, циклы в языке программирования Python работают довольно медленно. Нам нужно будет понять, как можно векторизовать такие подсчеты.
4.7 Векторизация обратного распространения
Для того, чтобы понять, как векторизовать процесс градиентного спуска в нейронных сетях, рассмотрим сначала упрощенную векторизованную версию градиента функции оценки (внимание: это пока неправильная версия!):
Что представляет собой h(l)? Все просто, вектор (sl×1), где sl является количеством узлов в слое l. Как тогда выглядит произведение h(l)δ(l+1)? Мы знаем, что α×∂J/∂W(l) должно быть того же размера, что и матрица весов W(l), Мы также знаем, что результат h(l)δ(l+1) должен быть того же размера, что и матрица весов для слоя l. Иными словами, произведение должно быть размера (sl + 1× sl).
Мы знаем, что δ(l+1) имеет размер (sl+1×1), а h (l)— размер (sl×1). По правилу умножения матриц, если матрицу (n×m)умножить на матрицу (o×p), То мы получим матрицу размера (n×p). Если мы просто перемножим h(l) на δ(l+1), то количество столбцов в первом векторе (один столбец) не будет равно количеству строк во втором векторе (3 строки). Поэтому, для того, чтобы можно было умножить эти матрицы и получить результат размера (sl+1× sl), Нужно сделать трансформирование. Оно меняет в матрице столбцы на строки и наоборот (например матрицу вида (sl×1)на (1×sl)). Трансформирование обозначается как буква T над матрицей. Мы можем сделать следующее:
Используя операцию трансформирования, мы можем достичь результата, который нам нужен.
Еще одно трансформирование нужно сделать с суммой погрешностей в обратном распространении:
символ (∙) в предыдущем выражении означает поэлементное умножение (произведение Адамара), не является умножением матриц. Обратите внимание, что произведение матриц (((W(l))Tδ(l+1))требует еще одного сложения весов и значений δ.
4.8 Реализация этапа градиентного спуска
Как тогда интегрировать векторизацию в этапы градиентного спуска нашего алгоритма? Во-первых, вспомним полный вид нашей функции оценки, который нам нужно сократить:
Из формулы видно, что полная функция оценки состоит из суммы поэтапных расчетов функции оценки. Также следует вспомнить, как находится градиентный спуск (поэлементная и векторизованная версии):
Это означает, что по прохождению через экземпляры обучения нам нужно иметь отдельную переменную, которая равна сумме частных производных функции оценки каждого экземпляра. Такая переменная соберет в себе все значения для «глобального» подсчета. Назовем такую «суммированную» переменную ΔW(l). Соответствующая переменная для смещения будет обозначаться как Δb(l). Следовательно, при каждой итерации в процессе обучения сети нам нужно будет сделать следующие шаги:
Выполняя эти операции на каждой итерации, мы подсчитываем упомянутую ранее сумму Σmz= 1∂/∂W(l)J( w , b , x(z), y(z))(и аналогичная формула для b). После того, как будут проитерированы все экземпляры и получены все значения δ, мы обновляем значения параметров веса:
4.9 Конечный алгоритм градиентного спуска
И, наконец, мы пришли к определению метода обратного распространения через градиентный спуск для обучения наших нейронных сетей. Финальный алгоритм обратного распространения выглядит следующим образом:
Рандомная инициализация веса для каждого слоя W(l). Когда итерация < границы итерации:
01. Зададим ΔW и Δb начальное значение ноль.
02. Для экземпляров от 1 до m: а. Запустите процесс прямого распространения через все nl слоев. Храните вывод активационной функции в h(l)б. Найдите значение δ( nl) выходного слоя. Обновите ΔW(l)и Δb( l ) для каждого слоя.
03. Запустите процесс градиентного спуска, используя:
Из этого алгоритма следует, что мы будем повторять градиентный спуск, пока функция оценки не достигнет минимума. На этом этапе нейросеть считается обученной и готовой к использованию.
Далее мы попробуем реализовать этот алгоритм на языке программирования для обучения нейронной сети распознаванию чисел, написанных от руки.
5 Имплементация нейросети языке Python
В предыдущем разделе мы рассмотрели теорию по обучению нейронной сети через градиентный спуск и метод обратного распространения. В этом разделе мы используем полученные знания на практике — напишем код, который прогнозирует, основываясь на данных MNIST. База данных MNIST — это набор примеров в нейронных сетях и глубинном обучении. Она включает в себя изображения цифр, написанных от руки, с соответствующими ярлыками, которые объясняют, что это за число. Каждое изображение размером 8х8 пикселей. В этом примере мы используем сети данных MNIST для библиотеки машинного обучения scikit learn в языке программирования Python . Пример такого изображения можно увидеть под кодом:
from sklearn.datasets
import load_digits
digits = load_digits()
print(digits.data.shape)
import matplotlib.pyplot as plt
plt.gray()
plt.matshow(digits.images[1])
plt.show()
Код, который мы собираемся написать в нашей нейронной сети, будет анализировать цифры, которые изображают пиксели на изображении. Для начала, нам нужно отсортировать входные данные. Для этого мы сделаем две следующие вещи:
01. Масштабировать данные.
02. Разделить данные на тесты и учебные тесты.
5.1 Масштабирование данных
Почему нам нужно масштабировать данные? Во-первых, рассмотрим представление пикселей одного из сетов данных:
digits.data[0, : ]
Out[2]:
array([0., 0., 5., 13., 9., 1., 0., 0., 0., 0., 13.,
15., 10., 15., 5., 0., 0., 3., 15., 2., 0., 11.,
8., 0., 0., 4., 12., 0., 0., 8., 8., 0., 0.,
5., 8., 0., 0., 9., 8., 0., 0., 4., 11., 0.,
1., 12., 7., 0., 0., 2., 14., 5., 10., 12., 0.,
0., 0., 0., 6., 13., 10., 0., 0., 0.
])
Заметили ли вы, что входные данные меняются в интервале от 0 до 15? Достаточно распространенной практикой является масштабирование входных данных так, чтобы они были только в интервале от [0, 1], или [1, 1]. Это делается для более легкого сравнения различных типов данных в нейронной сети. Масштабирование данных можно легко сделать через библиотеку машинного обучения scikit learn:
from sklearn.preprocessing import StandardScaler
X_scale = StandardScaler()
X = X_scale.fit_transform(digits.data)
X[0,:]
Out[3]:
array([ 0. , -0.33501649, -0.04308102, 0.27407152, -0.66447751,
-0.84412939, -0.40972392, -0.12502292, -0.05907756, -0.62400926,
0.4829745 , 0.75962245, -0.05842586, 1.12772113, 0.87958306,
-0.13043338, -0.04462507, 0.11144272, 0.89588044, -0.86066632,
-1.14964846, 0.51547187, 1.90596347, -0.11422184, -0.03337973,
0.48648928, 0.46988512, -1.49990136, -1.61406277, 0.07639777,
1.54181413, -0.04723238, 0. , 0.76465553, 0.05263019,
-1.44763006, -1.73666443, 0.04361588, 1.43955804, 0. ,
-0.06134367, 0.8105536 , 0.63011714, -1.12245711, -1.06623158,
0.66096475, 0.81845076, -0.08874162, -0.03543326, 0.74211893,
1.15065212, -0.86867056, 0.11012973, 0.53761116, -0.75743581,
-0.20978513, -0.02359646, -0.29908135, 0.08671869, 0.20829258,
-0.36677122, -1.14664746, -0.5056698 , -0.19600752])
Стандартный инструмент масштабирования в scikit learn нормализует данные через вычитание и деление. Вы можете видеть, что теперь все данные находятся в интервале от -2 до 2. По же на счет выходных данных yy, то обычно нет необходимости их масштабировать.
5.2 Создание тестов и учебных наборов данных
В машинном обучении появляется такой феномен, который называется «переобучением». Это происходит, когда модели, во время учебы, становятся слишком запутанными — они достаточно хорошо обучены, но когда им передаются новые данные, которые они никогда на «видели», то результат, который они выдают, становится плохим. Иными словами, модели генерируются не очень хорошо. Чтобы убедиться, что мы не создаем слишком сложные модели, обычно набор данных разбивают на учебные наборы и тестовые наборы. Учебный набором данных, на которых модель будет учиться, а тестовый набор — это данные, на которых модель будет тестироваться после завершения обучения. Количество учебных данных должно быть всегда больше тестовых данных. Обычно они занимают 60-80% от набора данных.
Опять же, scikit learn легко разбивает данные на учебные и тестовые наборы:
from sklearn.model_selection import train_test_split
y = digits.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4)
В этом случае мы выделили 40% данных на тестовые наборы и 60% соответственно на обучение. Функция train_test_split в scikit learn добавляет данные рандомно в различные базы данных — то есть, функция не берет первые 60% строк для учебного набора, а то, что осталось, использует как тестовый.
5.3 Настройка выходного слоя
Для того, чтобы получать результат — числа от 0 до 9, нам нужен выходной слой. Более-менее точная нейросеть, как правило, имеет выходной слой с 10 узлами, каждый из которых выдает число от 0 до 9. Мы хотим научить сеть так, чтобы, например, при цифре 5 на изображении, узел с цифрой 5 в исходном слое имел наибольшее значение. В идеале, мы бы хотели иметь следующий вывод: [0, 0, 0, 0, 0, 1, 0, 0, 0, 0]. Но на самом деле мы можем получить что-то похожее на это: [0.01, 0.1, 0.2, 0.05, 0.3, 0.8, 0.4, 0.03, 0.25, 0.02]. В таком случае мы можем взять крупнейших индекс в исходном массиве и считать это нашим полученным числом.
В данных MNIST нужны результаты от изображений записаны как отдельное число. Нам нужно конвертировать это единственное число в вектор, чтобы его можно было сравнивать с исходным слоем с 10 узлами. Иными словами, если результат в MNIST обозначается как «1», то нам нужно его конвертировать в вектор: [0, 1, 0, 0, 0, 0, 0, 0, 0, 0]. Такую конвертацию осуществляет следующий код:
import numpy as np
def convert_y_to_vect(y):
y_vect = np.zeros((len(y), 10))
for i in range(len(y)):
y_vect[i, y[i]] = 1
return y_vect
y_v_train = convert_y_to_vect(y_train)
y_v_test = convert_y_to_vect(y_test)
y_train[0], y_v_train[0]
Out[8]:
(1, array([ 0., 1., 0., 0., 0., 0., 0., 0., 0., 0.]))
Этот код конвертирует «1» в вектор [0, 1, 0, 0, 0, 0, 0, 0, 0, 0].
5.4 Создаем нейросеть
Следующим шагом является создание структуры нейронной сети. Для входного слоя, мы знаем, что нам нужно 64 узла, чтобы покрыть 64 пикселей изображения. Как было сказано ранее, нам нужен выходной слой с 10 узлами. Нам также потребуется скрытый слой в нашей сети. Обычно, количество узлов в скрытых слоях не менее и не больше количества узлов во входном и выходном слоях. Объявим простой список на языке Python , который определяет структуру нашей сети:
nn_structure = [64, 30, 10]
Мы снова используем сигмоидальную активационную функцию, так что сначала нужно объявить эту функцию и ее производную:
def f(x):
return 1 / (1 + np.exp(-x))
def f_deriv(x):
return f(x) * (1 - f(x))
Сейчас мы не имеем никакого представления, как выглядит наша нейросеть. Как мы будем ее учить? Вспомним наш алгоритм из предыдущих разделов:
Рандомно инициализируем веса для каждого слоя W(l) Когда итерация <границы итерации:
01. Зададим ΔW и Δb начальное значение ноль.
02. Для экземпляров от 1 до m: а. Запустите процесс прямого распространения через все nl слоев. Храните вывод активационной функции в h(l)б. Найдите значение δ( nl) выходного слоя. Обновите ΔW(l)и Δb( l ) для каждого слоя.
03. Запустите процесс градиентного спуска, используя:
Значит первым этапом является инициализация весов для каждого слоя. Для этого мы используем словари в языке программирования Python (обозначается через {}). Рандомные значения предоставляются весам для того, чтобы убедиться, что нейросеть будет работать правильно во время обучения. Для рандомизации мы используем random_sample из библиотеки numpy. Код выглядит следующим образом:
import numpy.random as r
def setup_and_init_weights(nn_structure):
W = {}
b = {}
for l in range(1, len(nn_structure)):
W[l] = r.random_sample((nn_structure[l], nn_structure[l-1]))
b[l] = r.random_sample((nn_structure[l],))
return W, b
Следующим шагом является присвоение двум переменным ΔW и Δb нулевых начальных значений (они должны иметь такой же размер, что и матрицы весов и смещений)
def init_tri_values(nn_structure):
tri_W = {}
tri_b = {}
for l in range(1, len(nn_structure)):
tri_W[l] = np.zeros((nn_structure[l], nn_structure[l-1]))
tri_b[l] = np.zeros((nn_structure[l],))
return tri_W, tri_b
Далее запустим процесс прямого распространения через нейронную сеть:
def feed_forward(x, W, b):
h = {1: x}
z = {}
for l in range(1, len(W) + 1):
#Если первый слой, то весами является x, в противном случае
#Это выход из последнего слоя
if l == 1:
node_in = x
else:
node_in = h[l]
z[l+1] = W[l].dot(node_in) + b[l] # z^(l+1) = W^(l)*h^(l) + b^(l)
h[l+1] = f(z[l+1]) # h^(l) = f(z^(l))
return h, z
И наконец, найдем выходной слой δ (nl) и значение δ (l) в скрытых слоях для запуска обратного распространения:
def calculate_out_layer_delta(y, h_out, z_out):
# delta^(nl) = -(y_i - h_i^(nl)) * f'(z_i^(nl))
return -(y-h_out) * f_deriv(z_out)
def calculate_hidden_delta(delta_plus_1, w_l, z_l):
# delta^(l) = (transpose(W^(l)) * delta^(l+1)) * f'(z^(l))
return np.dot(np.transpose(w_l), delta_plus_1) * f_deriv(z_l)
Теперь мы можем соединить все этапы в одну функцию:
def train_nn(nn_structure, X, y, iter_num=3000, alpha=0.25):
W, b = setup_and_init_weights(nn_structure)
cnt = 0
m = len(y)
avg_cost_func = []
print('Начало градиентного спуска для {} итераций'.format(iter_num))
while cnt 1:
delta[l] = calculate_hidden_delta(delta[l+1], W[l], z[l])
# triW^(l) = triW^(l) + delta^(l+1) * transpose(h^(l))
tri_W[l] += np.dot(delta[l+1][:,np.newaxis], np.transpose(h[l][:,np.newaxis]))
# trib^(l) = trib^(l) + delta^(l+1)
tri_b[l] += delta[l+1]
# запускает градиентный спуск для весов в каждом слое
for l in range(len(nn_structure) - 1, 0, -1):
W[l] += -alpha * (1.0/m * tri_W[l])
b[l] += -alpha * (1.0/m * tri_b[l])
# завершает расчеты общей оценки
avg_cost = 1.0/m * avg_cost
avg_cost_func.append(avg_cost)
cnt += 1
return W, b, avg_cost_func
Функция сверху должна быть немного объяснена. Во-первых, мы не задаем лимит работы градиентного спуска, основываясь на изменениях или точности функции оценки. Вместо этого, мы просто запускаем её с фиксированным числом итераций (3000 в нашем случае), а затем наблюдаем, как меняется общая функция оценки с прогрессом в обучении. В каждой итерации градиентного спуска, мы перебираем каждый учебный экземпляр (range (len (y)) и запускаем процесс прямого распространения, а после него и обратное распространение. Этап обратного распространения является итерацией через слои, начиная с выходного слоя к началу — range (len (nn_structure), 0, 1). Мы находим среднюю оценку на исходном слое (l == len (nn_structure)). Мы также обновляем значение ΔW и Δb с пометкой tri_W и tri_b, для каждого слоя, кроме исходного (исходный слой не имеет никакого связи, который связывает его со следующим слоем).
И наконец, после того, как мы прошлись по всем учебным экземплярам, накапливая значение tri_W и tri_b, мы запускаем градиентный спуск и меняем значения весов и смещений:
После окончания процесса, мы возвращаем полученные вес и смещение со средней оценкой для каждой итерации. Теперь время вызвать функцию. Ее работа может занять несколько минут, в зависимости от компьютера.
W, b, avg_cost_func = train_nn(nn_structure, X_train, y_v_train)
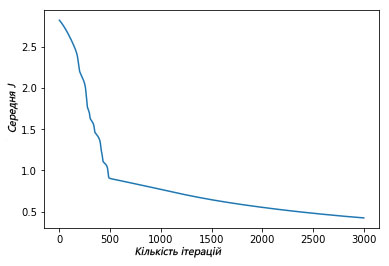
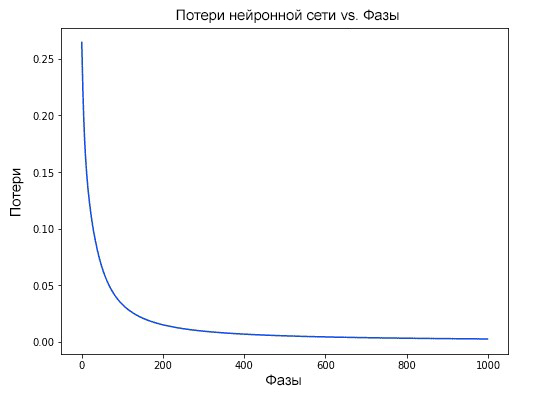
Мы можем увидеть, как функция средней оценки уменьшилась после итерационной работы градиентного спуска:
plt.plot(avg_cost_func)
plt.ylabel('Средняя J')
plt.xlabel('Количество итераций')
plt.show()
Выше изображен график, где показано, как за 3000 итераций нашего градиентного спуска функция средней оценки снизилась и маловероятно, что подобная итерация изменит результат.
5.5 Оценка точности модели
Теперь, после того, как мы научили нашу нейросеть MNIST, мы хотим увидеть, как хорошо она работает на тестах. Дан входной тест (64 пикселя), нам нужно получить вывод нейронной сети — это делается через запуск процесса прямого распространения через сеть, используя наши полученные значения веса и смещения. Как было сказано ранее, мы выбираем результат выходного слоя через выбор узла с максимальным выводом. Для этого можно использовать функцию numpy.argmax, она возвращает индекс элемента массива с наибольшим значением:
def predict_y(W, b, X, n_layers):
m = X.shape[0]
y = np.zeros((m,))
for i in range(m):
h, z = feed_forward(X[i, :], W, b)
y[i] = np.argmax(h[n_layers])
return y
Теперь, наконец, мы можем оценить точность результата (процент раз, когда сеть выдала правильный результат), используя функцию accuracy_score из библиотеки scikit learn:
from sklearn.metrics import accuracy_score
y_pred = predict_y(W, b, X_test, 3)
accuracy_score(y_test, y_pred)*100
Мы получили результат 86% точности. Звучит довольно неплохо? На самом деле, нет, это довольно низкая точностью. В наше время точность алгоритмов глубинного обучения достигает 99.7%, мы немного отстали.
Предлагаем также посмотреть:
- Лучший видеокурс по нейронным сетям на русском
- Подборка материалов по нейронным сетям
- Введение в глубинное обучение
Время на прочтение
6 мин
Количество просмотров 51K
Здравствуйте. Меня зовут Андрей, я frontend-разработчик и я хочу поговорить с вами на такую тему как нейросети. Дело в том, что ML технологии все глубже проникают в нашу жизнь, и о нейросетях сказано и написано уже очень много, но когда я захотел разобраться в этом вопросе, я понял что в интернете есть множество гайдов о том как создать нейросеть и выглядят они примерно следующим образом:
-
Берем Tensorflow
-
Создаем нейросеть
Более подробная информация разбросана кусками по всему интернету. Поэтому я постарался собрать ее воедино и изложить в этой статье. Сразу оговорюсь, что я не являюсь специалистом в области ML или биологии, поэтому местами могу быть не точным. В таком случае буду рад вашим комментариям.
Пока я писал эту статью я понял, что у меня получается довольно объемный лонгрид, поэтому решил разбить ее на несколько частей. В первой части мы поговорим о теории, во второй напишем собственную нейросеть с нуля без использования каких-либо библиотек, в третьей попробуем применить ее на практике.
Так как это моя первая публикация, появляться они будут по мере прохождения модерации, после чего я добавлю ссылки на все части. Итак, приступим.
Нейросеть с нуля своими руками. Часть 2. Реализация
Нейросеть с нуля своими руками. Часть 3. Sad Or Happy?
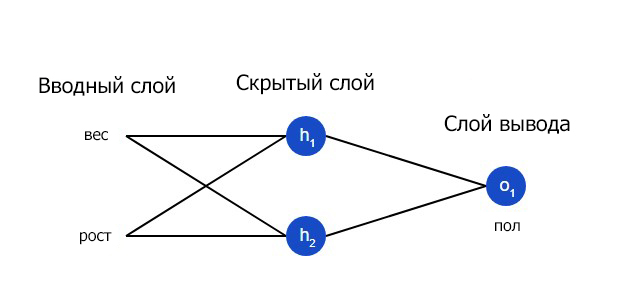
Для чего нужны нейросети
Нейросети встречаются везде. Основная их функция — это управление различными частями организма в зависимости от изменения окружающих условий. В качестве примера можно рассмотреть механизм сужения и расширения зрачка в зависимости от уровня освещения.
В нашем глазу есть сенсоры, которые улавливают количество света попадающего через зрачок на заднюю поверхность глаза. Они преобразуют эту информацию в электрические импульсы и передают на прикрепленные к ним нервные окончания. Далее это сигнал проходит по всей нейронной сети, которая принимает решение о том, не опасно ли такое количество света для глаза, достаточно ли оно для того, чтобы четко распознавать визуальную информацию, и нужно ли, исходя из этих факторов, уменьшить или увеличить количество света.
На выходе этой сети находятся мышцы, отвечающие за расширение или сужение зрачка, и приводят эти механизмы в действие в зависимости от сигнала, полученного из нейросети. И таких механизмов огромное количество в теле любого живого существа, обладающего нервной системой.
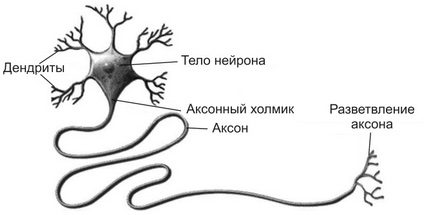
Устройство нейрона
Нейросети встречаются в природе в виде нервной системы того или иного существа. В зависимости от выполняемой функции и расположения, они делятся на различные отделы и органы, такие как головной мозг, спинной мозг, различные проводящие структуры. Но все их объединяет одно — они состоят из связанных между собой структурно-функциональных единиц — клеток нейронов.
Нейрон условно можно разделить на три части: тело нейрона, и его отростки — дендриты и аксон.
Дендриты нейрона создают дендритное дерево, размер которого зависит от числа контактов с другими нейронами. Это своего рода входные каналы нервной клетки. Именно с их помощью нейрон получает сигналы от других нейронов.
Тело нейрона в природе, достаточно сложная штука, но именно в нем все сигналы, поступившие через дендриты объединяются, обрабатываются, и принимается решение о том передавать ли сигнал далее, и какой силы он должен быть.
Аксон — это выходной интерфейс нейрона. Он крепится так называемыми синапсами к дендриту другого нейрона, и по нему сигнал, выходящий из тела нейрона, поступает к следующей клетке нашей нейросети.
Нейросети в IT
Что же, раз механизм нам понятен, почему бы нам не попробовать воспроизвести его с помощью информационных технологий?
Итак, у нас есть входной слои нейронов, которые, по сути, являются сенсорами нашей системы. Они нужны для того, чтобы получить информацию из окружающей среды и передать ее дальше в нейросеть.
Также у нас есть несколько слоев нейронов, каждый из которых получает информацию от всех нейронов предыдущего слоя, каким-то образом ее обрабатывают, и передают на следующий слой.
И, наконец, у нас есть выходные нейроны. Исходя из сигналов, поступающих от них, мы можем судить о принятом нейросетью решении.
Такой простейший вариант нейронной сети называется перцептрон, и именно его мы с вами и попробуем воссоздать.
Все нейроны по сути одинаковы, и принимают решение о том, какой силы сигнал передать далее с помощью одного и того же алгоритма. Это алгоритм называется активационной функцией. На вход она получает сумму значений входных сигналов, а на выход передает значение выходного сигнала.
Но в таком случае, получается, что все нейроны любого слоя будут получать одинаковый сигнал, и отдавать одинаковое значение. Таким образом мы могли бы заменить всю нашу сеть на один нейрон. Чтобы устранить эту проблему, мы присвоим входу каждого нейрона определенный вес. Этот вес будет обозначать насколько важен для каждого конкретного нейрона сигнал, получаемый от другого нейрона. И тут мы подходим к самому интересному.
Обучение нейронной сети — это процесс подбора входных весов для каждого нейрона таким образом, чтобы на выходе получить сигнал максимально соответствующий ожиданиям.
То есть мы подаем на вход нейросети определенные данные, для которых мы знаем, каким должен быть результат. Далее мы сравниваем результат, который нам выдала нейросеть с ожидаемым результатом, вычисляем ошибку, и корректируем веса нейронов таким образом, чтобы эту ошибку минимизировать. И повторяем это действие большое количество раз для большого количества наборов входных и выходных данных, чтобы сеть поняла какие сигналы на каком нейроне ей важны больше, а какие меньше. Чем больше и разнообразнее будет набор данных для обучения, тем лучше нейросеть сможет обучиться и впоследствии давать правильный результат. Этот процесс называется обучением с учителем.
Добавим немного математики.
В качестве активационной функции нейрона может выступать любая функция, существующая на всем отрезке значений, получающихся на выходе нейрона и входных данных. Для нашего примера мы возьмем сигмоиду. Она существует на отрезке от минус бесконечности до бесконечности, плавно меняется от 0 до 1 и имеет значение 0,5 в точке 0. Идеальный кандидат. Выглядит она следующим образом:
Таким образом наш нейрон сможет принимать любую сумму значений всех входящих сигналов и на выходе будет выдавать значение от 0 до 1. Это хорошо подходит для принятия бинарных решений, и мы условимся, что если число на выходе нейросети > 0.5, мы будем расценивать его как истину, иначе — как ложь.
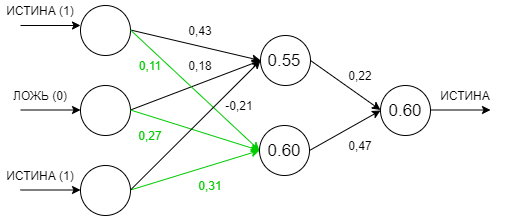
Итак, давайте рассмотрим пример с топологией сети рассмотренной выше. У нас есть три входных нейрона со значениями ИСТИНА, ЛОЖЬ и ИСТИНА соответственно, два нейрона в среднем слое нейросети (эти слои также называют скрытыми), и один выходной нейрон, который сообщит нам о решении, принятом нейросетью. Так как наша сеть еще не обучена, поэтому значения весов на входах нейронов мы возьмем случайными в диапазоне от -0,5 до 0,5.
Таким образом сумма входных значений первого нейрона скрытого слоя будет равна
1 * 0,43 + 0 * 0,18 + 1 * -0,21 = 0,22
Передав это значение в активационную функцию, мы получим значение, которое наш нейрон передаст далее по сети в следующий слой.
sigmoid(0,22) = 1 / (1 + e^-0,22) = 0,55
Аналогичные операции произведём для второго нейрона скрытого слоя и получим значение 0,60.
И, наконец, повторим эти операции для единственного нейрона в выходном слое нашей нейросети и получим значение 0,60, что мы условились считать как истину.
Пока что это абсолютно случайное значение, так как веса мы выбирали случайно. Но, предположим, что мы знаем ожидаемое значение для такого набора входных данных и наша сеть ошиблась. В таком случае нам нужно вычислить ошибку и изменить параметры весов, таким образом немного обучив нашу нейросеть.
Первым делом рассчитаем ошибку на выходе сети. Делается это довольно просто, нам просто нужно получить разницу полученного значения и ожидаемого.
error = 0.60 — 0 = 0.60
Чтобы узнать насколько нам надо изменить веса нашего нейрона, нам нужно величину ошибки умножить на производную от нашей активационной функции в этой точке. К счастью, производная от сигмоиды довольно проста.
Таким образом наша дельта весов будет равна
delta = 0.60 * (1 — 0.60) = 0.24
Новый вес для входа нейрона рассчитывается по формуле
weight = weight — output * delta * learning rate
Где weight — текущий вес, output — значение на выходе предыдущего нейрона, delta — дельта весов, которую мы рассчитали ранее и learning rate — значение, подбираемое экспериментально, от которого зависит скорость обучения нейросети. Если оно будет слишком маленьким — нейросеть будет более чувствительна к деталям, но будет обучаться слишком медленно и наоборот. Для примера возьмем learning rate равным 0,3. Итак новый вес для первого входа выходного нейрона будет равен:
w = 0,22 — 0,55 * 0,24 * 0,3 = 0,18
Аналогичным образом рассчитаем новый вес для второго входа выходного нейрона:
w = 0.47 — 0.60 * 0.24 * 0.3 = 0.43
Итак, мы скорректировали веса для входов выходного нейрона, но чтобы рассчитать остальные, нам нужно знать ошибку для каждого из нейронов нашей нейросети. Это делается не так очевидно как для выходного нейрона, но тоже довольно просто. Чтобы получить ошибку каждого нейрона нам нужно новый вес нейронной связи умножить на дельту. Таким образом ошибка первого нейрона скрытого слоя равна:
error = 0.18 * 0.24 = 0.04
Теперь, зная ошибку для нейрона, мы можем произвести все те же самые операции, что провели ранее, и скорректировать его веса. Этот процесс называется обратным распространением ошибки.
Итак, мы знаем как работает нейрон, что такое нейронные связи в нейросети и как происходит процесс обучения. Этих знаний достаточно чтобы применить их на практике и написать простейшую нейросеть, чем мы и займемся в следующей части статьи.
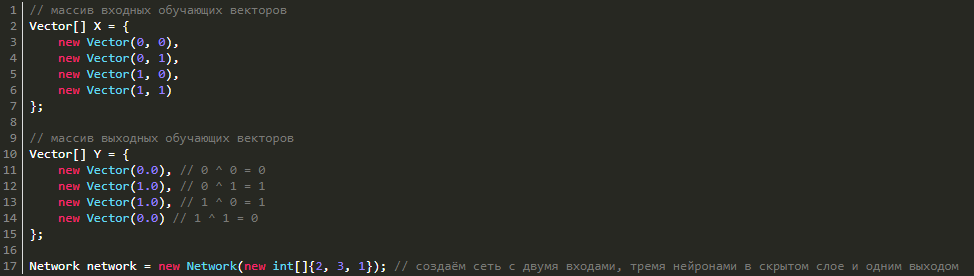
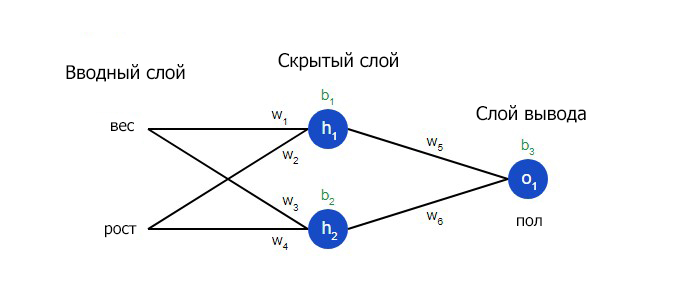
В этой статье поговорим о том, как создавать нейросети и в качестве примера рассмотрим, как сделать нейронную сеть прямого распространения с нуля. Для реализации поставленной задачи воспользуемся языком программирования C#.
Только ленивый не слышал сегодня о существовании и разработке нейронных сетей и такой сфере, как машинное обучение. Для некоторых создание нейросети кажется чем-то очень запутанным, однако на самом деле они создаются не так уж и сложно. Как же их делают? Давайте попробуем самостоятельно создать нейросеть прямого распространения, которую еще называют многослойным перцептроном. В процессе работы будем использовать лишь циклы, массивы и условные операторы. Что означает этот набор данных? Только то, что нам подойдет любой язык программирования, поддерживающий вышеперечисленные возможности. Если же у языка есть библиотеки для векторных и матричных вычислений (вспоминаем NumPy в Python), то реализация с их помощью займет совсем немного времени. Но мы не ищем легких путей и воспользуемся C#, причем полученный код по своей сути будет почти аналогичным и для прочих языков программирования.
Что же такое нейронная сеть?
Под искусственной нейронной сетью (ИНС) понимают математическую модель (включая ее программное либо аппаратное воплощение), которая построена и работает по принципу функционирования биологических нейросетей — речь идет о нейронных сетях нервных клеток живых организмов.
Говоря проще, ИНС можно назвать неким «черным ящиком», превращающим входные данные в выходные данные. Если же посмотреть на это с точки зрения математики, то речь идет о том, чтобы отобразить пространство входных X-признаков в пространство выходных Y-признаков: X → Y. Таким образом, нам надо найти некую F-функцию, которая сможет выполнить данное преобразование. На первом этапе этой информации достаточно в качестве основы.
Какую роль играет искусственный нейрон?
В нашей статье мы не будем вдаваться в лирику и рассказывать об устройстве биологического нейрона в контексте его связи с искусственной моделью. Лучше сразу перейдем к делу.
Искусственный нейрон представляет собой взвешенную сумму векторных значений входных элементов. Эта сумма передается на нелинейную функцию активации f:
Но об активации поговорим после, т. к. сейчас стоит задача узнать, каким образом вместо одного выходного значения можно получить n-значений.
Нейрослой
Один нейрон может превратить в одну точку входной вектор, но по условию мы желаем получить несколько точек, т. к. выходное Y способно иметь произвольную размерность, которая определяется лишь ситуацией (один выход для XOR, десять выходов, чтобы определить принадлежность к одному из десяти классов, и так далее). Каким же образом получить n точек? На деле все просто: для получения n выходных значений, надо задействовать не один нейрон, а n. В результате для каждого элемента выходного Y будет использовано n разных взвешенных сумм от X. В итоге мы придем к следующему соотношению:
Давайте внимательно посмотрим на него. Вышенаписанная формула — это не что иное, как определение умножения матрицы на вектор. И в самом деле, если мы возьмем матрицу W размера n на m и выполним ее умножение на X размерности m, то мы получим другое векторное значение n-размерности, то есть как раз то, что надо.
Таким образом, мы можем записать похожее выражение в более удобной матричной форме:
Но полученный вектор представляет собой неактивированное состояние (промежуточное, невыходное) всех нейронов, а для того, чтобы нам получить выходное значение, нужно каждое неактивированное значение подать на вход вышеупомянутой функции активации. Итогом ее применения и станет выходное значение слоя.
Ниже показан пример нейронной сети, имеющей 2 входа, 5 нейронов и 1 выход:
Последовательность нейрослоев часто применяют для более глубокого обучения нейронной сети и большей формализации имеющихся данных. Именно поэтому, чтобы получить итоговый выходной вектор, нужно проделать вышеописанную операцию пару раз подряд по направлению от одного слоя к другому. В результате для 1-го слоя входным вектором будет являться X, а для последующих входом будет выход предыдущего слоя. То есть нейронная сеть может выглядеть следующим образом:
Функция активации
Речь идет о функции, добавляющей в нейронную сеть нелинейность. В результате нейроны смогут относительно точно сымитировать любую функцию. Широко распространены следующие функции активации:
Каждая из них имеет свои особенности.
Пишем код
Теперь мы знаем достаточно, чтобы создать простую нейронную сеть. Чтобы сделать то, что задумали, нам потребуются:
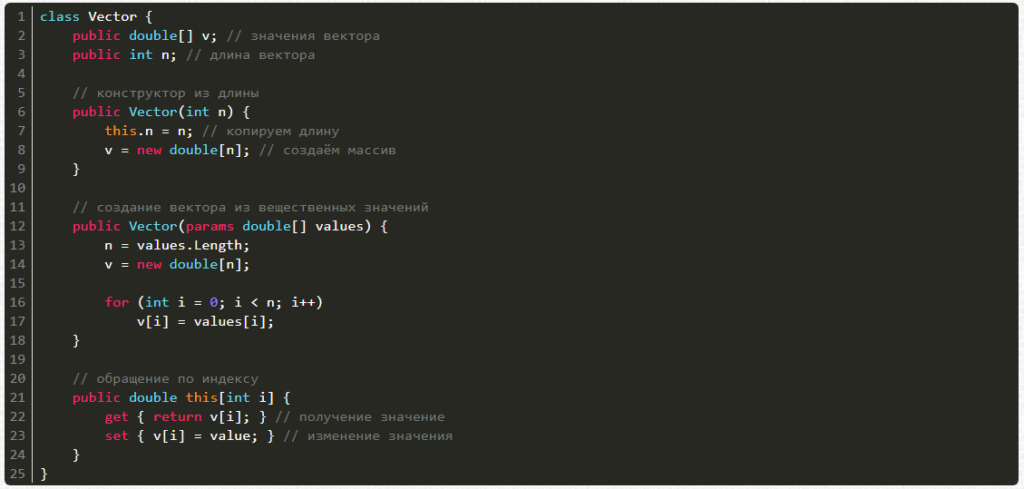
- Вектор.
- Матрица (каждый слой включает в себя матрицу весовых коэффициентов).
- Нейронная сеть.
Начнем с вектора. Создавать его можно:
- из количества элементов;
- из перечисления вещественных чисел.
Также мы можем получать и менять значения по индексу i.
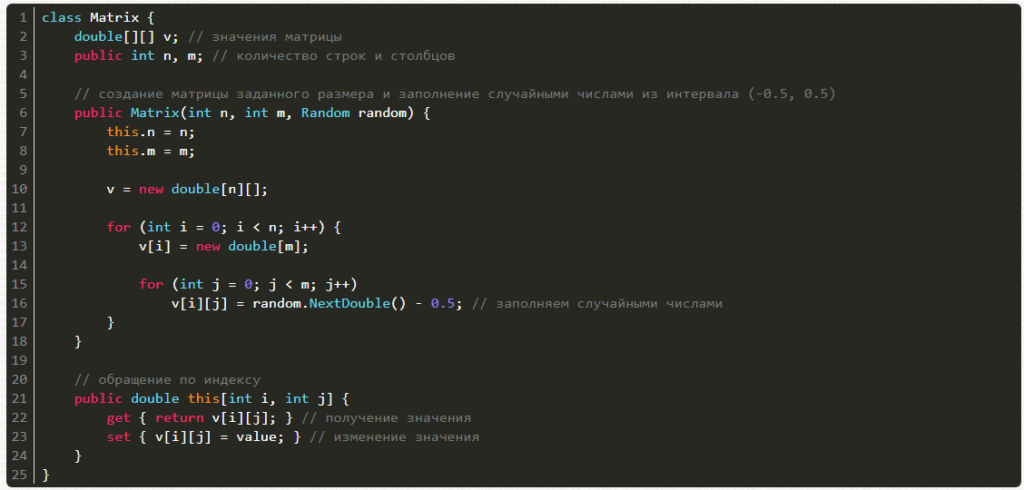
Пишем код:
Теперь очередь матрицы. Ее можно создавать из числа строк и столбцов, а также генератора случайных чисел, причем есть возможность получать и менять значения по индексам i и j.
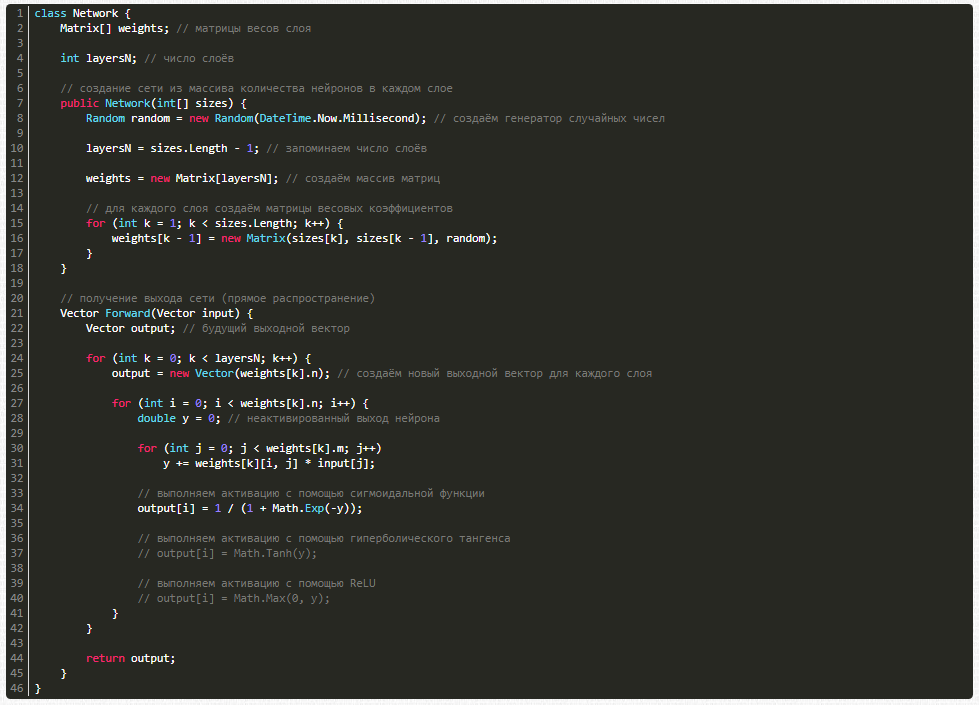
А вот и сама нейронная сеть:
Как будем обучать?
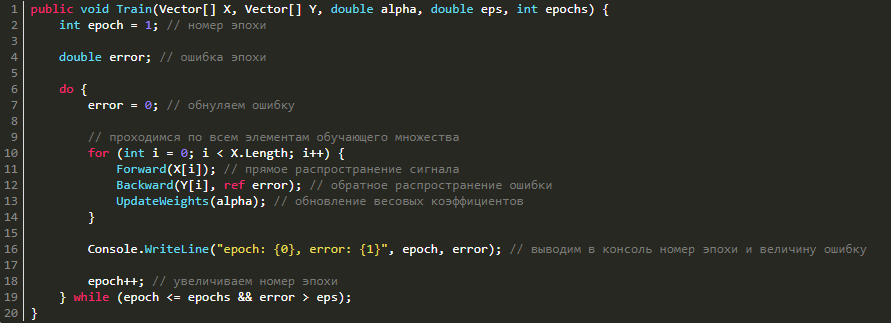
Пусть у нас уже есть нейронная сеть, но ведь ее ответы являются случайными, то есть наша нейросеть не обучена. Сейчас она способна лишь по входному вектору input выдавать случайный ответ, но нам нужны ответы, которые удовлетворяют конкретной поставленной задаче. Дабы этого достичь, сеть надо обучить. Здесь потребуется база тренировочных примеров и множество пар X — Y, на которых и будет происходить обучение, причем с использованием известного алгоритма обратного распространения ошибки.
Некоторые особенности работы этого алгоритма:
- на вход сети подается обучающий пример (1 входной вектор);
- сигнал распространяется по нейросети вперед (получаем выход сети);
- вычисляется ошибка (это разница между получившимся и ожидаемым векторами);
- ошибка распространяется на предыдущие слои;
- происходит обновление весовых коэффициентов в целях уменьшения ошибки.
Вот как выглядит алгоритм обучения:
Переходим к обучению
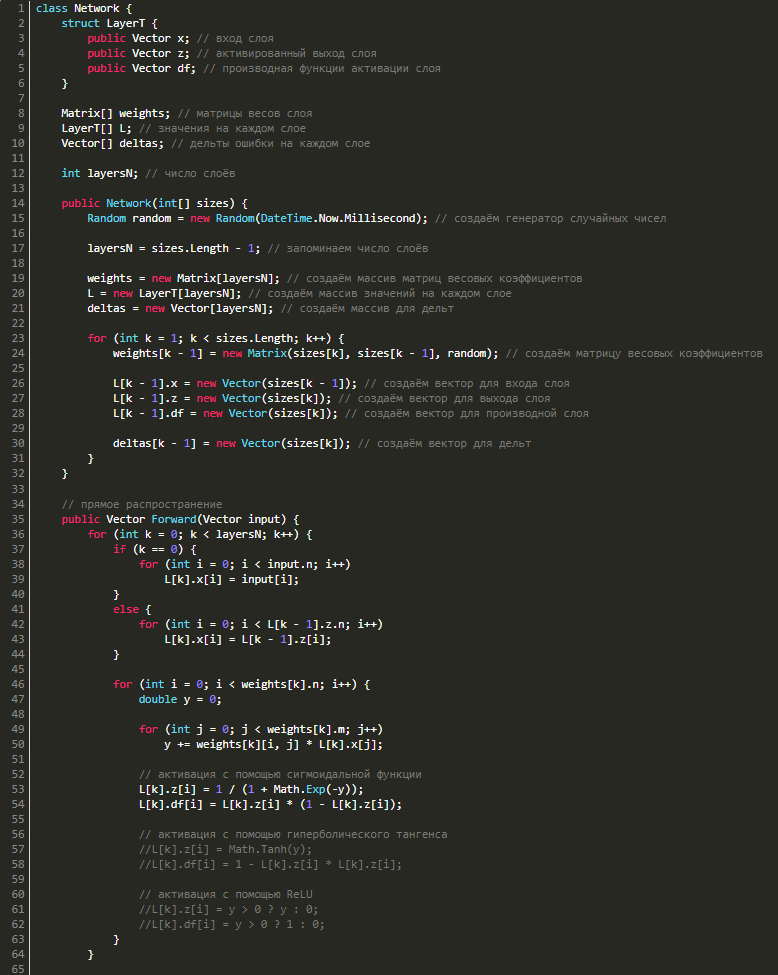
Для обратного распространения ошибки нужно знать значения выходов и входов, а также значения производных функции активации нейросети, причем послойно, следовательно, нужно создать структуру LayerT, где будут три векторных значения:
- x — вход слоя,
- z — выход,
- df — производная функции активации.
Для каждого слоя нам потребуются векторы дельт, в результате чего надо будет добавить в класс еще и их. В итоге класс будет выглядеть следующим образом:
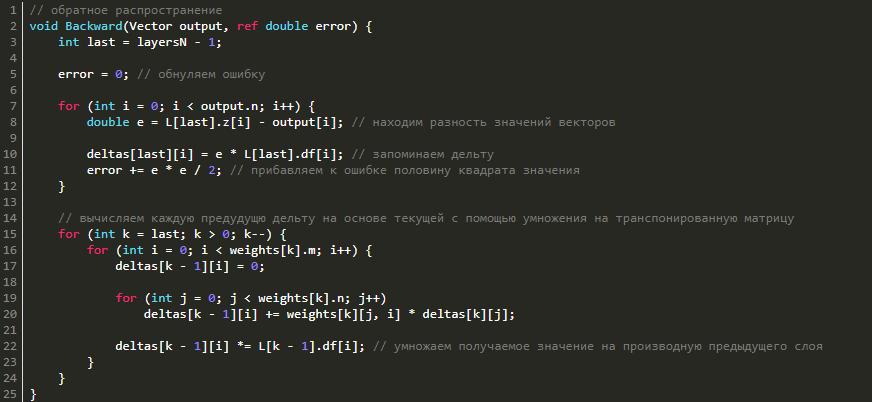
Несколько слов об обратном распространении ошибки
В качестве функции оценки нейросети E(W) мы берем среднее квадратичное отклонение:
Дабы найти значение ошибки E, надо найти сумму квадратов разности векторных значений, которые были выданы нейронной сетью в виде ответа, а также вектора, который ожидается увидеть при обучении. Еще надо будет найти дельту каждого слоя и учесть, что для последнего слоя дельта будет равняться векторной разности фактического и ожидаемого результатов, покомпонентно умноженной на векторное значение производных последнего слоя:
Когда мы узнаем дельту последнего слоя, мы сможем найти дельты и всех предыдущих слоев. Чтобы это сделать, нужно будет лишь перемножить для текущего слоя транспонированную матрицу с дельтой, а потом перемножить результат с вектором производных функции активации предыдущего слоя:
Смотрим реализацию в коде:
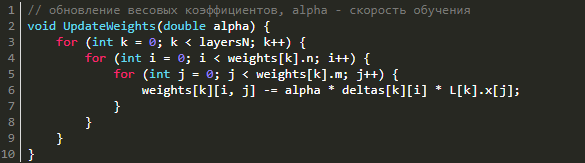
Обновление весовых коэффициентов
Для уменьшения ошибки нейронной сети надо поменять весовые коэффициенты, причем послойно. Каким же образом это осуществить? Ничего сложного в этом нет: надо воспользоваться методом градиентного спуска. То есть нам надо рассчитать градиент по весам и сделать шаг от полученного градиента в отрицательную сторону. Давайте вспомним, что на этапе прямого распространения мы запоминали входные сигналы, а во время обратного распространения ошибки вычисляли дельты, причем послойно. Как раз ими и надо воспользоваться в целях нахождения градиента. Градиент по весам будет равняться не по компонентному перемножению дельт и входного вектора. Дабы обновить весовые коэффициенты, снизив таким образом ошибку нейросети, нужно просто вычесть из матрицы весов итог перемножения входных векторов и дельт, помноженный на скорость обучения. Все вышеперечисленное можно записать в следующем виде:
Вот оно, обучение!
Теперь мы имеем все нужные нам методы, поэтому остается лишь всё это вместе соединить, сформировав единый метод обучения.
Наша сеть готова, но мы пока ее еще ничему не научили. Сейчас это исправим.
Тренировка нейронной сети. Функции XOR
Функция XOR интересна тем, что ее нельзя получить одним нейроном:
Но ее легко получить путем увеличения количества нейронов. Давайте попробуем реализовать обучение с тремя нейронами в скрытом слое и одним выходным (выход ведь у нас только один). Чтобы все получилось, создадим массив X и Y, имеющий обучающие данные и саму нейронную сеть:
Теперь запускаем обучение с параметрами ниже:
- скорость обучения — 0.5,
- количество эпох — 100000,
- значение ошибки — 1e-7.
Выполнив обучение, посмотрим итоги, для чего надо будет сделать прямой проход для всех элементов:
В итоге вывод будет следующим:
Результаты
Мы написали нейронную сеть прямого распространения и не только написали, но и обучили ее функции XOR. Также была обеспечена универсальность, поэтому эту нейросеть можно обучать на любых данных — потребуется лишь:
- подготовить 2 векторных обучающих массива векторов X и Y,
- подобрать параметры,
- запустить само обучение,
- наблюдать за процессом.
Однако помните, что если используется сигмоидальная функция активации, выходные числа не будут больше единицы, что означает, что для обучения данным, которые существенно больше единицы, нужно будет нормировать их, приводя к отрезку [0, 1].
Надеемся, что материал был вам полезен и теперь вы знаете, как сделать нейросеть, и какие нюансы разработки стоит учитывать. Если же интересуют более продвинутые знания, обратите внимание на курсы, которые разработала команда Otus:
По материалам: https://programforyou.ru/poleznoe/pishem-neuroset-pryamogo-rasprostraneniya.
Сегодня мы разберём, зачем нужна библиотека TensorFlow и как её установить, что такое машинное обучение и как научить компьютер решать уравнения. Всё это — в одной статье.
Фреймворк TensorFlow — это относительно простой инструмент, который позволяет быстро создавать нейросети любой сложности. Он очень дружелюбен для начинающих, потому что содержит много примеров и уже готовых моделей машинного обучения, которые можно встроить в любое приложение. А продвинутым разработчикам TensorFlow предоставляет тонкие настройки и API для ускоренного обучения.
TensorFlow поддерживает несколько языков программирования. Главный из них — это Python. Кроме того, есть отдельные пакеты для C/C++, Golang и Java. А ещё — форк TensorFlow.js для исполнения кода на стороне клиента, в браузере, на JavaScript.
Этим возможности фреймворка TensorFlow не ограничиваются. Библиотеку также можно использовать для обучения моделей на смартфонах и умных устройствах (TensorFlow Lite) и создания корпоративных нейросетей (TensorFlow Extended).
Чтобы создать простую нейросеть на TensorFlow, достаточно понимать несколько основных принципов:
- что такое машинное обучение;
- как обучаются нейросети и какие методы для этого используются;
- как весь процесс обучения выглядит в TensorFlow.
О каждом из этих пунктов мы расскажем подробнее ниже.
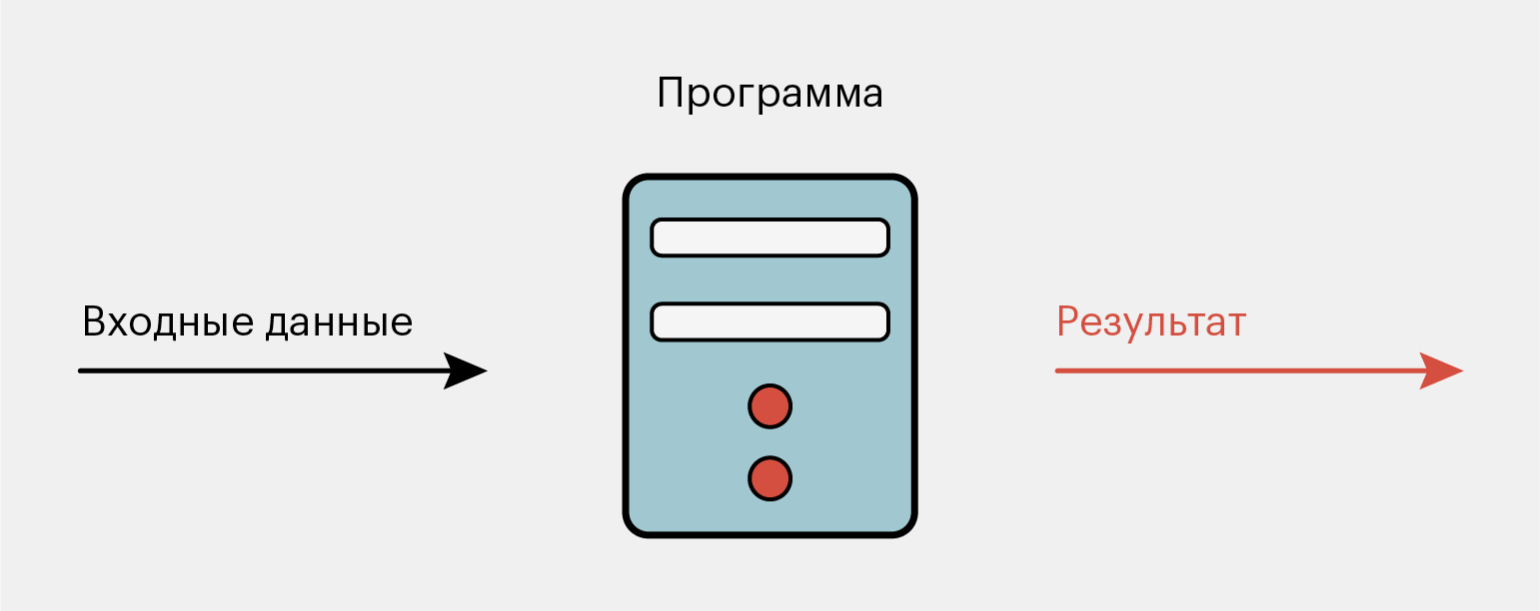
В обычном программировании всё работает по заранее заданным инструкциям. Разработчики их прописывают с помощью выражений, а компьютер строго им подчиняется. В конце выполнения компьютер выдаёт результат.
Например, если описать в обычной программе, как вычисляется площадь квадрата, компьютер будет строго следовать инструкции и всегда выдавать стабильный результат. Он не начнёт придумывать новые методы вычисления и не будет пытаться оптимизировать сам процесс вычисления. Он будет всегда следовать правилам — тому самому алгоритму, выраженному с помощью языка программирования.
Иллюстрация: Оля Ежак для Skillbox Media
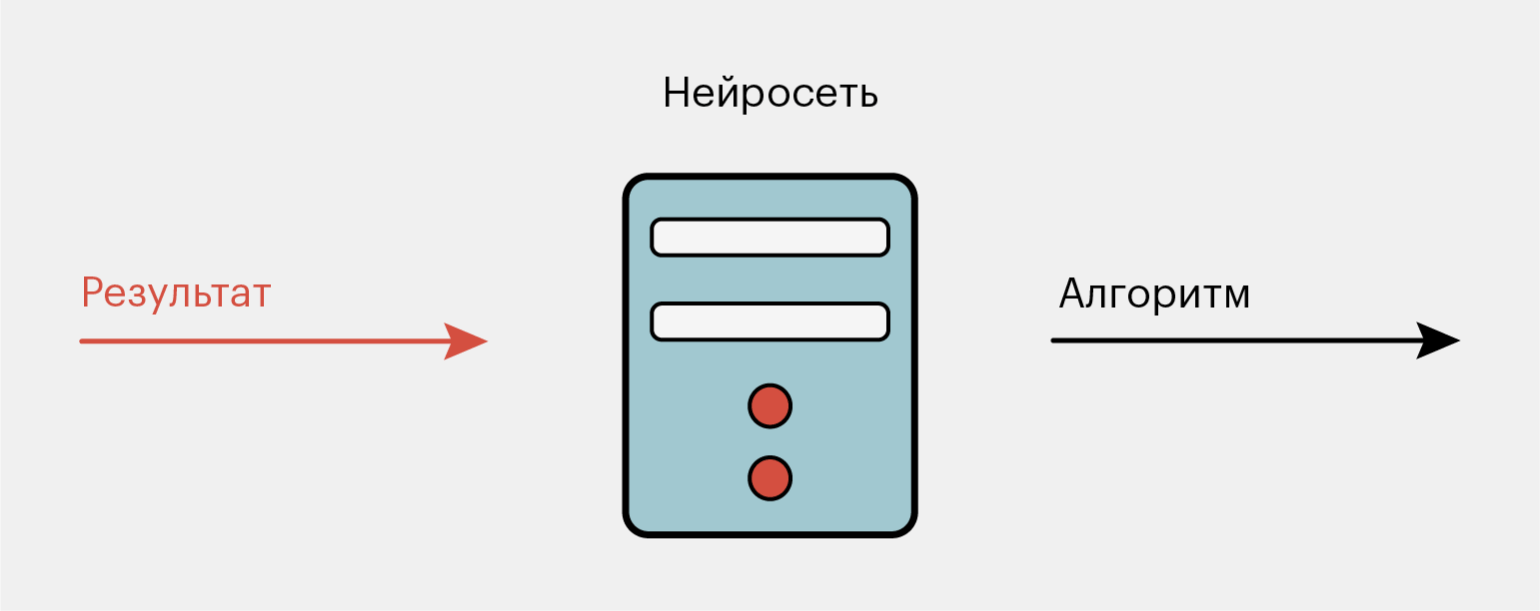
Машинное обучение работает по-другому. Нам нужно отдать компьютеру уже готовые результаты и входные данные и сказать: «Найди алгоритм, который сможет сделать из этих входных данных вот эти результаты». Нам неважно, как он будет это делать. Для нас важнее, чтобы результаты были точными.
Ещё мы должны говорить компьютеру, когда он ответил правильно, а когда — неправильно. Это сделает обучение эффективным и позволит нейросети постепенно двигаться в сторону более точных результатов.
Иллюстрация: Оля Ежак для Skillbox Media
В целом машинное обучение похоже на обучение обычного человека. Например, чтобы различать обувь и одежду, нам нужно посмотреть на какое-то количество экземпляров обуви и одежды, высказать свои предположения относительно того, что именно сейчас находится перед нами, получить обратную связь от кого-то, кто уже умеет их различать, — и тогда у нас появится алгоритм, как отличать одно от другого. Увидев туфли после успешного обучения, мы сразу сможем сказать, что это обувь, потому что по всем признакам они соответствуют этой категории.
Чтобы начать пользоваться фреймворком TensorFlow, можно выбрать один из вариантов:
- установить его на компьютер;
- воспользоваться облачным сервисом Google Colab.
В начале можно попробовать второй вариант, потому что для него не нужно ничего скачивать — всё хранится и работает в облаке. К тому же вычисления не нуждаются в мощностях вашего компьютера, вместо этого используются серверы Google.
Заходим на сайт Google Colab и создаём новый notebook:
Скриншот: Skillbox Media
У нас появится новое пространство, в котором мы и будем писать весь код. Сверху слева можно изменить название документа:
Скриншот: Skillbox Media
Google Colab состоит из ячеек с кодом или текстом. Чтобы создать ячейку с кодом, нужно нажать на кнопку + Code. Ниже появится ячейка, где можно писать Python‑код:
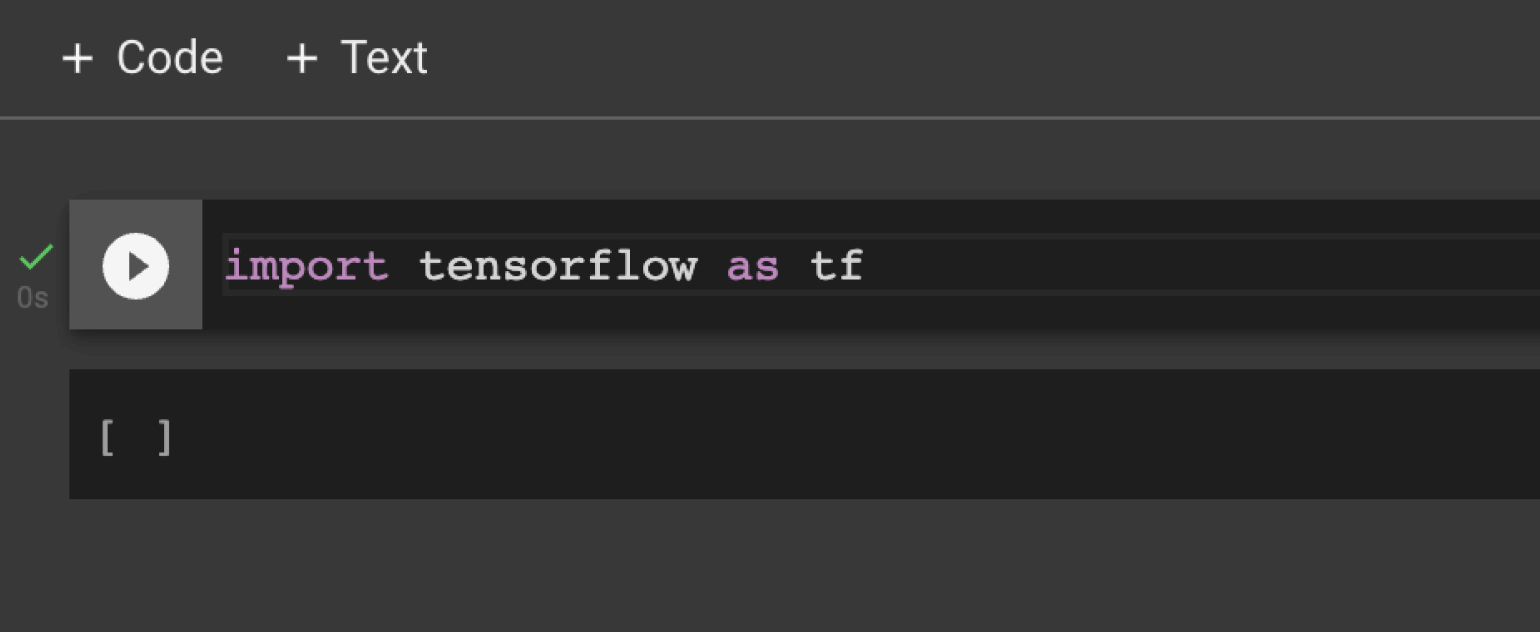
Скриншот: Skillbox Media
Теперь нам нужно проверить, что всё работает. Для этого попробуем экспортировать библиотеку в Google Colab. Делается это через команду import tensorflow as tf:
Скриншот: Skillbox Media
Всё готово. Рассмотрим второй способ, как можно подключить TensorFlow прямо на компьютере.
Чтобы использовать библиотеку TensorFlow на компьютере, её нужно установить через пакетный менеджер PIP.
Открываем терминал и вводим следующую команду:
pip install --upgrade pip
Мы обновили PIP до последней версии. Теперь скачиваем сам TensorFlow:
pip install tensorflow
Если всё прошло успешно, теперь вы можете подключать TensorFlow в Python-коде у вас на компьютере с помощью команды:
import tensorflow as tf
Но если возникли какие-то ошибки, можете прочитать более подробный гайд на официальном сайте TensorFlow и убедиться, что у вас скачаны все нужные пакеты.
Ниже мы будем использовать Google Colab для примеров, но код должен работать одинаково и корректно где угодно.
Допустим, у нас есть два набора чисел X и Y:
X: -1 0 1 2 3 4 Y: -4 1 6 11 16 21
Мы видим, что их значения связаны по какому-то правилу. Это правило: Y = 5X + 1. Но чтобы компьютер это понял, ему нужно научиться сопоставлять входные данные — X — с результатом — Y. У него сначала могут получаться странные уравнения типа: 2X — 5, 8X + 1, 4X + 2, 5X — 1. Но, обучившись немного, он найдёт наиболее близкую к исходной формулу.
Обучается нейросеть итеративно — или поэтапно. На каждой итерации она будет предлагать алгоритм, по которому входные значения сопоставляются с результатом. Затем она проверит свои предположения, вычислив все входные данные по формуле и сравнив с настоящими результатами. Так она узнает, насколько сильно ошиблась. И уже на основе этих ошибок скорректирует формулу на следующей итерации.
Количество итераций ограничено разве что временем разработчика. Главное — чтобы нейросеть на каждом шаге улучшала свои предположения, иначе весь процесс обучения будет бессмысленным.
Теперь давайте создадим модель, которая научится решать поставленную выше задачу. Сперва подключим необходимые зависимости:
import tensorflow as tf import numpy as np from tensorflow import keras
Первая зависимость — это наша библиотека TensorFlow, название которой мы сокращаем до tf, чтобы было удобнее её вызывать в программе. NumPy — это библиотека для эффективной работы с массивами чисел. Можно было, конечно, использовать и обычные списки, но NumPy будет работать намного быстрее, поэтому мы берём его. И последнее — Keras, встроенная в Tensorflow библиотека, которая умеет обучать нейросети.
Теперь создадим самую простую модель:
model = tf.keras.Sequential([keras.layers.Dense(units=1, input_shape=[1])])
Разберём код подробнее. Sequential — это тип нейросети, означающий, что процесс обучения будет последовательным. Это стандартный процесс обучения для простых нейросетей: в нём она сначала делает предсказания, затем тестирует их и сравнивает с результатом, а в конце — корректирует ошибки.
keras.layers.Dense — указывает на то, что мы хотим создать слой в нашей модели. Слой — это место, куда мы будем складывать нейроны, которые запоминают информацию об ошибках и которые отвечают за «умственные способности» нейросети. Dense — это тип слоя, который использует специальные алгоритмы для обучения.
В качестве аргумента нашей нейросети мы передали указания, какой именно она должна быть:
- units=1 означает, что модель состоит из одного нейрона, который будет запоминать информацию о предыдущих предположениях;
- input_shape=[1] говорит о том, что на вход будет подаваться одно число, по которому нейросеть будет строить зависимости двух рядов чисел: X и Y.
Модель мы создали, теперь давайте её скомпилируем:
model.compile(optimizer='sgd', loss='mean_squared_error')
Здесь появляются два важных для машинного обучения элемента: функция оптимизации и функция потерь. Обе они нужны, чтобы постепенно стремиться к более точным результатам.
Функция потерь анализирует, насколько правильно нейросеть дала предсказание. А функция оптимизации исправляет эти предсказания в сторону более корректных результатов.
Мы использовали стандартные функции для большинства моделей — sgd и mean_squared_error. sgd — это метод оптимизации, который работает на формулах математического анализа. Он помогает скорректировать формулу, чтобы прийти к правильной. mean_squared_error — это функция, которая вычисляет, насколько сильно отличаются полученные результаты по формуле, предложенной нейросетью, от настоящих результатов. Эта функция тоже участвует в корректировке формулы.
Теперь давайте зададим наборы данных:
xs = np.array([-1.0, 0.0, 1.0, 2.0, 3.0, 4.0], dtype=float) ys = np.array([-4.0, 1.0, 6.0, 11.0, 16.0, 21.0], dtype=float)
Как видно, это обычные массивы чисел, которые мы передадим модели на обучение:
model.fit(xs, ys, epochs=500)
Функция fit как раз занимается обучением. Она берёт набор входных данных — xs — и сопоставляет с набором правильных результатов — ys. И так нейросеть обучается в течение 500 итераций — epochs=500. Мы использовали 500 итераций, чтобы наверняка прийти к правильному результату. Суть простая: чем больше итераций обучения, тем точнее будут результаты (однако улучшение точности с каждым повтором будет всё меньше и меньше).
На каждой итерации модель проходит следующие шаги:
- берёт весь наш набор входных данных;
- пытается сделать предсказание для каждого элемента;
- сравнивает результат с корректным результатом;
- оптимизирует модель, чтобы давать более точные прогнозы.
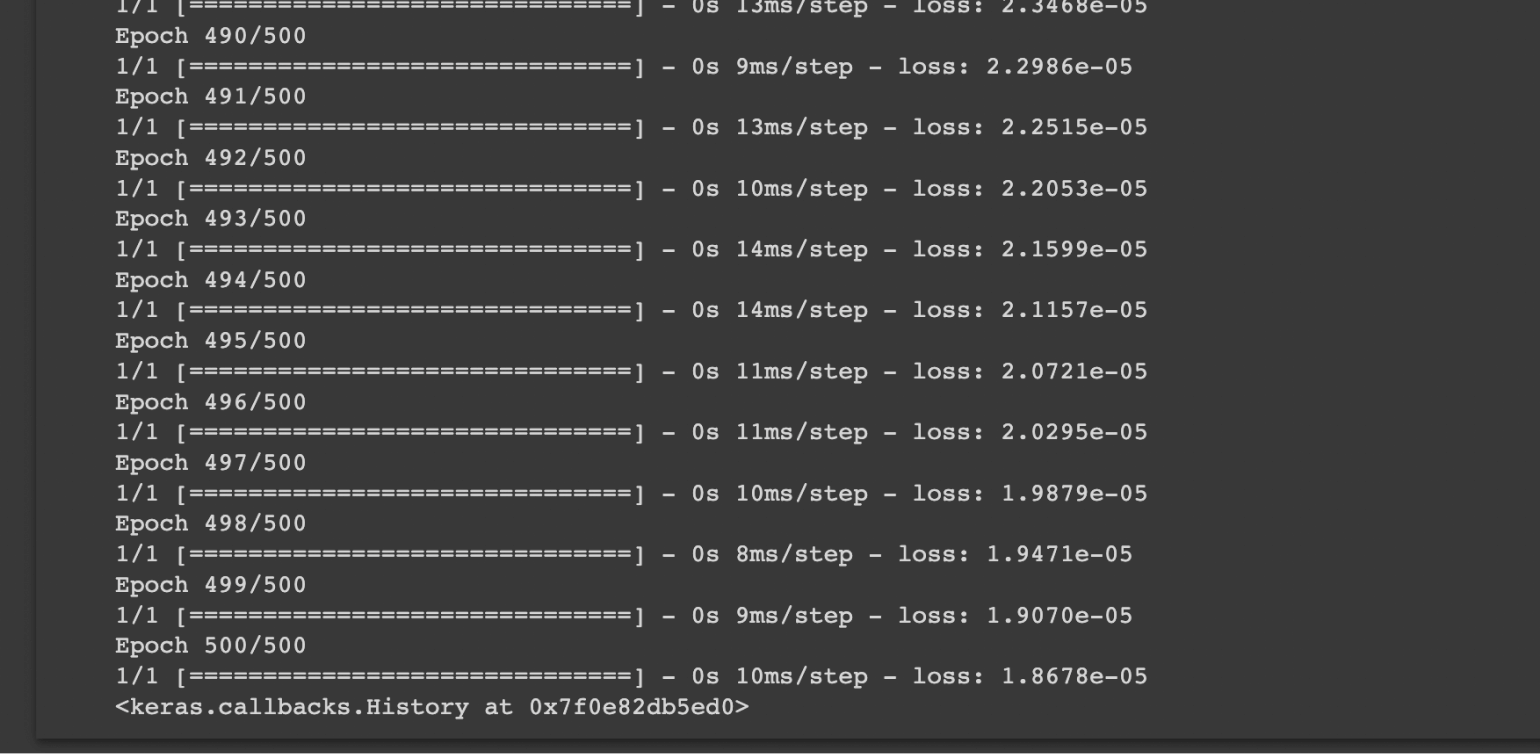
Скриншот: Skillbox Media
Можно заметить, что на каждой итерации TensorFlow выводит, насколько нейросеть сильно ошиблась — loss. Если это число уменьшается, то есть стремится к нулю, значит, она действительно обучается и с каждым шагом улучшает свои прогнозы.
Теперь давайте что-нибудь предскажем и поймём, насколько точно наша нейросеть обучилась:
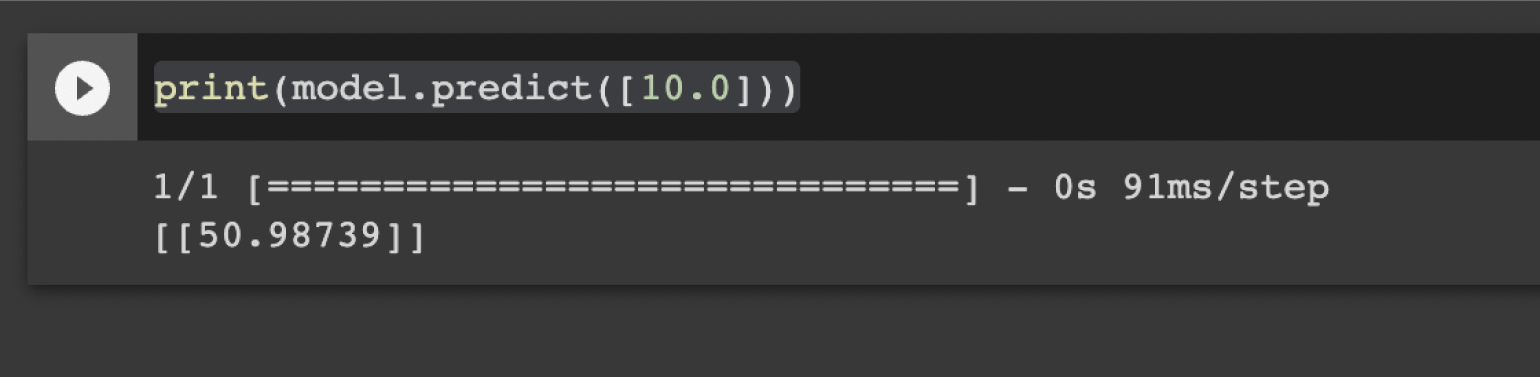
print(model.predict([10.0]))
Мы вызываем у модели метод predict, который получает на вход элемент для предсказания. Результат будет таким:
Скриншот: Skillbox Media
Получилось странно — мы ожидали, что будет число 51 (потому что подставили 10 в выражение 5X + 1) — но на выходе нейросеть выдала число 50.98739. А всё потому, что модель нашла очень близкую, но не до конца точную формулу — например, 4.891X + 0.993. Это одна из особенностей машинного обучения.
А ещё многое зависит от выбранного метода оптимизации — то есть того, как нейросеть корректирует формулу, чтобы прийти к нужным результатам. В библиотеке TensorFlow можно найти разные способы оптимизации, и на выходе каждой из них результаты могут различаться. Однако эта тема выходит за рамки нашей статьи — здесь уже необходимо достаточно глубоко погружаться в процесс машинного обучения и разбираться, как именно устроена оптимизация.
Если вы вдруг подумали, что можно просто увеличить число итераций и точность станет выше, то это справедливо лишь отчасти. У каждого метода оптимизации есть своя точность, до которой нейросеть может дойти. Например, она может вычислять результат с точностью до 0.00000001, однако абсолютно верным и точным результат не будет никогда. А значит, и абсолютно точного значения формулы мы никогда не получим — просто из-за погрешности вычислений и особенности функционирования компьютеров. Но если условно установить число итераций в миллиард, можно получить примерно такую формулу:
4.9999999999997X + 0.9999999999991
Она очень близка к настоящей, хотя и не равна ей. Поэтому математики и специалисты по машинному обучению решили, что будут считать две формулы равными, если значения их вычислений меньше, чем заранее заданная величина погрешности — например, 0.0000001. И если мы подставим в формулу выше и в настоящую вместо X число 5, то получим следующее:
5 · 5 + 1 = 26
4.9999999997 · 5 + 0.9999999991 = 25.9999999976
Если мы из первого числа вычтем второе, то получим:
26 — 25.9999999976 = 0.0000000024
А так как изначально мы сказали, что два числа будут равны, если разница между ними меньше 0.0000001, то обе формулы могут считаться идентичными, потому что получившаяся у нас на практике погрешность 0.0000000024 меньше допустимого значения, о котором мы договорились, — то есть 0.0000001. Вот такая интересная математика.
Рассказываем, как за несколько шагов создать простую нейронную сеть и научить её узнавать известных предпринимателей на фотографиях.
Шаг 0. Разбираемся, как устроены нейронные сети
Проще всего разобраться с принципами работы нейронных сетей можно на примере Teachable Machine — образовательного проекта Google.
В качестве входящих данных — то, что нужно обработать нейронной сети — в Teachable Machine используется изображение с камеры ноутбука. В качестве выходных данных — то, что должна сделать нейросеть после обработки входящих данных — можно использовать гифку или звук.
Например, можно научить Teachable Machine при поднятой вверх ладони говорить «Hi». При поднятом вверх большом пальце — «Cool», а при удивленном лице с открытым ртом — «Wow».
Для начала нужно обучить нейросеть. Для этого поднимаем ладонь и нажимаем на кнопку «Train Green» — сервис делает несколько десятков снимков, чтобы найти на изображениях закономерность. Набор таких снимков принято называть «датасетом».
Теперь остается выбрать действие, которое нужно вызывать при распознании образа — произнести фразу, показать GIF или проиграть звук. Аналогично обучаем нейронную сеть распознавать удивленное лицо и большой палец.
Как только нейросеть обучена, её можно использовать. Teachable Machine показывает коэффициент «уверенности» — насколько система «уверена», что ей показывают один из навыков.
Шаг 1. Готовим компьютер к работе с нейронной сетью
Теперь сделаем свою нейронную сеть, которая при отправке изображения будет сообщать о том, что изображено на картинке. Сначала научим нейронную сеть распознавать цветы на картинке: ромашку, подсолнух, одуванчик, тюльпан или розу.
Для создания собственной нейронной сети понадобится Python — один из наиболее минималистичных и распространенных языков программирования, и TensorFlow — открытая библиотека Google для создания и тренировки нейронных сетей.
Устанавливаем Python
Если у вас Windows: скачиваем установщик с официального сайта Python и запускаем его. При установке нужно поставить галочку «Add Python to PATH».
На macOS Python можно установить сразу через Terminal:
brew install python
Для работы с нейронной сетью подойдет Python 2.7 или более старшая версия.
Устанавливаем виртуальное окружение
Открываем командную строку на Windows или Terminal на macOS и последовательно вводим несколько команд:
pip install —upgrade virtualenv
virtualenv —system-site-packages Название
source Название/bin/activate
На компьютер будет установлен инструмент для запуска программ в виртуальном окружении. Он позволит устанавливать и запускать все библиотеки и приложения внутри одной папки — в команде она обозначена как «Название».
Устанавливаем TensorFlow
Вводим команду:
pip install tensorflow
Всё, библиотека TensorFlow установлена в выбранную папку. На macOS она находится по адресу Macintosh HD/Users/Имя_пользователя/, на Windows — в корне C://.
Можно проверить работоспособность библиотеки последовательно вводя команды:
python
import tensorflow as tf
hello = tf.constant(‘Hello, TensorFlow’)
sess = tf.Session()
print(sess.run(hello))
Если установка прошла успешно, то на экране появится фраза «Hello, Tensorflow».
Шаг 2. Добавляем классификатор
Классификатор — это инструмент, который позволяет методам машинного обучения понимать, к чему относится неизвестный объект. Например, классификатор поможет понять, где на картинке растение, и что это за цветок.
Открываем страницу «Tensorflow for poets» на Github, нажимаем на кнопку «Clone or download» и скачиваем классификатор в формате ZIP-файла.
Затем распаковываем архив в созданную на втором шаге папку.
Шаг 3. Добавляем набор данных
Набор данных нужен для обучения нейронной сети. Это входные данные, на основе которых нейронная сеть научится понимать, какой цветок расположен на картинке.
Сначала скачиваем набор данных (датасет) Google с цветами. В нашем примере — это набор небольших фотографий, отсортированный по папкам с их названиями.
Содержимое архива нужно распаковать в папку /tf_files классификатора.
Шаг 4. Переобучаем модель
Теперь нужно запустить обучение нейронной сети, чтобы она проанализировала картинки из датасета и поняла при помощи классификатора, как и какой тип цветка выглядит.
Переходим в папку с классификатором
Открываем командную строку и вводим команду, чтобы перейти в папку с классификатором.
Windows:
cd C://Название/
macOS:
cd Название
Запускаем процесс обучения
python scripts/retrain.py —output_graph=tf_files/retrained_graph.pb —output_labels=tf_files/retrained_labels.txt —image_dir=tf_files/flower_photos
Что указано в команде:
- retrain.py — название Python-скрипта, который отвечает за запуск процесса обучения нейронной сети.
- output_graph — создаёт новый файл с графом данных. Он и будет использоваться для определения того, что находится на картинке.
- output_labels — создание нового файла с метками. В нашем примере это ромашки, подсолнухи, одуванчики, тюльпаны или розы.
- image_dir — путь к папке, в которой находятся изображения с цветами.
Программа начнет создавать текстовые файлы bottleneck — это специальные текстовые файлы с компактной информацией об изображении. Они помогают классификатору быстрее определять подходящую картинку.
Весь ход обучения занимает около 4000 шагов. Время работы может занять несколько десятков минут — в зависимости от мощности процессора.
После завершения анализа нейросеть сможет распознавать на любой картинке ромашки, подсолнухи, одуванчики, тюльпаны и розы.
Перед тестированием нейросети нужно открыть файл label_image.py, находящийся в папке scripts в любом текстовом редакторе и заменить значения в строках:
input_height = 299
input_width = 299
input_mean = 0
input_std = 255
input_layer = «Mul»
Шаг 5. Тестирование
Выберите любое изображение цветка, которое нужно проанализировать, и поместите его в папку с нейронной сетью. Назовите файл image.jpg.
Для запуска анализа нужно ввести команду:
python scripts/label_image.py —image image.jpg
Нейросеть проверит картинку на соответствие одному из лейблов и выдаст результат.
Например:
Это значит, что с вероятностью 72% на картинке изображена роза.
Шаг 6. Учим нейронную сеть распознавать предпринимателей
Теперь можно расширить возможности нейронной сети — научить её распознавать на картинке не только цветы, но и известных предпринимателей. Например, Элона Маска и Марка Цукерберга.
Для этого нужно добавить новые изображения в датасет и переобучить нейросеть.
Собираем собственный датасет
Для создания датасета с фотографиями предпринимателей можно воспользоваться поиском по картинкам Google и расширением для Chrome, которое сохраняет все картинки на странице.
Папку с изображениями Элона Маска нужно поместить в tf_filesflower_photosmusk. Аналогично все изображения с основателем Facebook — в папку tf_filesflower_photoszuckerberg.
Чем больше фотографий будет в папках, тем точнее нейронная сеть распознает на ней предпринимателя.
Переобучаем и проверяем
Для переобучения и запуска нейронной сети используем те же команды, что и в шагах 4 и 5.
python scripts/retrain.py —output_graph=tf_files/retrained_graph.pb —output_labels=tf_files/retrained_labels.txt —image_dir=tf_files/flower_photos
python scripts/label_image.py —image image.jpg
Шаг 7. «Разгоняем» нейронную сеть
Чтобы процесс обучения не занимал каждый раз много времени, нейросеть лучше всего запускать на сервере с GPU — он спроектирован специально для таких задач.
Процесс запуска и обучения нейронной сети на сервере похож на аналогичный процесс на компьютере.
Создание сервера с Ubuntu
Нам понадобится сервер с операционной системой Ubuntu. Её можно установить самостоятельно, либо — если арендован сервер Selectel — через техподдержку компании.
Установка Python
sudo apt-get install python3-pip python3-dev
Установка TensorFlow
pip3 install tensorflow-gpu
Скачиваем классификатор и набор данных
Аналогично шагам 2 и 3 на компьютере, только архивы необходимо загрузить сразу на сервер.
Переобучаем модель
python3 scripts/retrain.py —output_graph=tf_files/retrained_graph.pb —output_labels=tf_files/retrained_labels.txt —image_dir=tf_files/flower_photos
Тестируем нейросеть
python scripts/label_image.py —image image.jpg
Далее будет представлено максимально простое объяснение того, как работают нейронные сети, а также показаны способы их реализации в Python. Приятная новость для новичков – нейронные сети не такие уж и сложные. Термин нейронные сети зачастую используют в разговоре, ссылаясь на какой-то чрезвычайно запутанный концепт. На деле же все намного проще.
Данная статья предназначена для людей, которые ранее не работали с нейронными сетями вообще или же имеют довольно поверхностное понимание того, что это такое. Принцип работы нейронных сетей будет показан на примере их реализации через Python.
Содержание статьи
- Создание нейронных блоков
- Простой пример работы с нейронами в Python
- Создание нейрона с нуля в Python
- Пример сбор нейронов в нейросеть
- Пример прямого распространения FeedForward
- Создание нейронной сети прямое распространение FeedForward
- Пример тренировки нейронной сети — минимизация потерь, Часть 1
- Пример подсчета потерь в тренировки нейронной сети
- Python код среднеквадратической ошибки (MSE)
- Тренировка нейронной сети — многовариантные исчисления, Часть 2
- Пример подсчета частных производных
- Тренировка нейронной сети: Стохастический градиентный спуск
- Создание нейронной сети с нуля на Python
Создание нейронных блоков
Для начала необходимо определиться с тем, что из себя представляют базовые компоненты нейронной сети – нейроны. Нейрон принимает вводные данные, выполняет с ними определенные математические операции, а затем выводит результат. Нейрон с двумя входными данными выглядит следующим образом:
Здесь происходят три вещи. Во-первых, каждый вход умножается на вес (на схеме обозначен красным):
Затем все взвешенные входы складываются вместе со смещением b (на схеме обозначен зеленым):
Наконец, сумма передается через функцию активации (на схеме обозначена желтым):
Функция активации используется для подключения несвязанных входных данных с выводом, у которого простая и предсказуемая форма. Как правило, в качестве используемой функцией активации берется функция сигмоида:
Функция сигмоида выводит только числа в диапазоне (0, 1). Вы можете воспринимать это как компрессию от (−∞, +∞) до (0, 1). Крупные отрицательные числа становятся ~0, а крупные положительные числа становятся ~1.
Предположим, у нас есть нейрон с двумя входами, который использует функцию активации сигмоида и имеет следующие параметры:
w = [0,1] — это просто один из способов написания w1 = 0, w2 = 1 в векторной форме. Присвоим нейрону вход со значением x = [2, 3]. Для более компактного представления будет использовано скалярное произведение.
С учетом, что вход был x = [2, 3], вывод будет равен 0.999. Вот и все. Такой процесс передачи входных данных для получения вывода называется прямым распространением, или feedforward.
Создание нейрона с нуля в Python
Есть вопросы по Python?
На нашем форуме вы можете задать любой вопрос и получить ответ от всего нашего сообщества!
Telegram Чат & Канал
Вступите в наш дружный чат по Python и начните общение с единомышленниками! Станьте частью большого сообщества!
Паблик VK
Одно из самых больших сообществ по Python в социальной сети ВК. Видео уроки и книги для вас!
Приступим к имплементации нейрона. Для этого потребуется использовать NumPy. Это мощная вычислительная библиотека Python, которая задействует математические операции:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
import numpy as np def sigmoid(x): # Наша функция активации: f(x) = 1 / (1 + e^(-x)) return 1 / (1 + np.exp(—x)) class Neuron: def __init__(self, weights, bias): self.weights = weights self.bias = bias def feedforward(self, inputs): # Вводные данные о весе, добавление смещения # и последующее использование функции активации total = np.dot(self.weights, inputs) + self.bias return sigmoid(total) weights = np.array([0, 1]) # w1 = 0, w2 = 1 bias = 4 # b = 4 n = Neuron(weights, bias) x = np.array([2, 3]) # x1 = 2, x2 = 3 print(n.feedforward(x)) # 0.9990889488055994 |
Узнаете числа? Это тот же пример, который рассматривался ранее. Ответ полученный на этот раз также равен 0.999.
Пример сбор нейронов в нейросеть
Нейронная сеть по сути представляет собой группу связанных между собой нейронов. Простая нейронная сеть выглядит следующим образом:
На вводном слое сети два входа – x1 и x2. На скрытом слое два нейтрона — h1 и h2. На слое вывода находится один нейрон – о1. Обратите внимание на то, что входные данные для о1 являются результатами вывода h1 и h2. Таким образом и строится нейросеть.
Скрытым слоем называется любой слой между вводным слоем и слоем вывода, что являются первым и последним слоями соответственно. Скрытых слоев может быть несколько.
Пример прямого распространения FeedForward
Давайте используем продемонстрированную выше сеть и представим, что все нейроны имеют одинаковый вес w = [0, 1], одинаковое смещение b = 0 и ту же самую функцию активации сигмоида. Пусть h1, h2 и o1 сами отметят результаты вывода представленных ими нейронов.
Что случится, если в качестве ввода будет использовано значение х = [2, 3]?
Результат вывода нейронной сети для входного значения х = [2, 3] составляет 0.7216. Все очень просто.
Нейронная сеть может иметь любое количество слоев с любым количеством нейронов в этих слоях.
Суть остается той же: нужно направить входные данные через нейроны в сеть для получения в итоге выходных данных. Для простоты далее в данной статье будет создан код сети, упомянутая выше.
Создание нейронной сети прямое распространение FeedForward
Далее будет показано, как реализовать прямое распространение feedforward в отношении нейронной сети. В качестве опорной точки будет использована следующая схема нейронной сети:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
import numpy as np # … Здесь код из предыдущего раздела class OurNeuralNetwork: «»» Нейронная сеть, у которой: — 2 входа — 1 скрытый слой с двумя нейронами (h1, h2) — слой вывода с одним нейроном (o1) У каждого нейрона одинаковые вес и смещение: — w = [0, 1] — b = 0 «»» def __init__(self): weights = np.array([0, 1]) bias = 0 # Класс Neuron из предыдущего раздела self.h1 = Neuron(weights, bias) self.h2 = Neuron(weights, bias) self.o1 = Neuron(weights, bias) def feedforward(self, x): out_h1 = self.h1.feedforward(x) out_h2 = self.h2.feedforward(x) # Вводы для о1 являются выводами h1 и h2 out_o1 = self.o1.feedforward(np.array([out_h1, out_h2])) return out_o1 network = OurNeuralNetwork() x = np.array([2, 3]) print(network.feedforward(x)) # 0.7216325609518421 |
Мы вновь получили 0.7216. Похоже, все работает.
Пример тренировки нейронной сети — минимизация потерь, Часть 1
Предположим, у нас есть следующие параметры:
| Имя/Name | Вес/Weight (фунты) | Рост/Height (дюймы) | Пол/Gender |
| Alice | 133 | 65 | F |
| Bob | 160 | 72 | M |
| Charlie | 152 | 70 | M |
| Diana | 120 | 60 | F |
Давайте натренируем нейронную сеть таким образом, чтобы она предсказывала пол заданного человека в зависимости от его веса и роста.
Мужчины Male будут представлены как 0, а женщины Female как 1. Для простоты представления данные также будут несколько смещены.
| Имя/Name | Вес/Weight (минус 135) | Рост/Height (минус 66) | Пол/Gender |
| Alice | -2 | -1 | 1 |
| Bob | 25 | 6 | 0 |
| Charlie | 17 | 4 | 0 |
| Diana | -15 | -6 | 1 |
Для оптимизации здесь произведены произвольные смещения
135и66. Однако, обычно для смещения выбираются средние показатели.
Потери
Перед тренировкой нейронной сети потребуется выбрать способ оценки того, насколько хорошо сеть справляется с задачами. Это необходимо для ее последующих попыток выполнять поставленную задачу лучше. Таков принцип потери.
В данном случае будет использоваться среднеквадратическая ошибка (MSE) потери:
Давайте разберемся:
n– число рассматриваемых объектов, которое в данном случае равно 4. ЭтоAlice,Bob,CharlieиDiana;y– переменные, которые будут предсказаны. В данном случае это пол человека;ytrue– истинное значение переменной, то есть так называемый правильный ответ. Например, дляAliceзначениеytrueбудет1, то естьFemale;ypred– предполагаемое значение переменной. Это результат вывода сети.
(ytrue - ypred)2 называют квадратичной ошибкой (MSE). Здесь функция потери просто берет среднее значение по всем квадратичным ошибкам. Отсюда и название ошибки. Чем лучше предсказания, тем ниже потери.
Лучшие предсказания = Меньшие потери.
Тренировка нейронной сети = стремление к минимизации ее потерь.
Пример подсчета потерь в тренировки нейронной сети
Скажем, наша сеть всегда выдает 0. Другими словами, она уверена, что все люди — Мужчины. Какой будет потеря?
| Имя/Name | ytrue | ypred | (ytrue — ypred)2 |
| Alice | 1 | 0 | 1 |
| Bob | 0 | 0 | 0 |
| Charlie | 0 | 0 | 0 |
| Diana | 1 | 0 | 1 |
Python код среднеквадратической ошибки (MSE)
Ниже представлен код для подсчета потерь:
|
import numpy as np def mse_loss(y_true, y_pred): # y_true и y_pred являются массивами numpy с одинаковой длиной return ((y_true — y_pred) ** 2).mean() y_true = np.array([1, 0, 0, 1]) y_pred = np.array([0, 0, 0, 0]) print(mse_loss(y_true, y_pred)) # 0.5 |
При возникновении сложностей с пониманием работы кода стоит ознакомиться с quickstart в NumPy для операций с массивами.
Тренировка нейронной сети — многовариантные исчисления, Часть 2
Текущая цель понятна – это минимизация потерь нейронной сети. Теперь стало ясно, что повлиять на предсказания сети можно при помощи изменения ее веса и смещения. Однако, как минимизировать потери?
В этом разделе будут затронуты многовариантные исчисления. Если вы не знакомы с данной темой, фрагменты с математическими вычислениями можно пропускать.
Для простоты давайте представим, что в наборе данных рассматривается только Alice:
| Имя/Name | Вес/Weight (минус 135) | Рост/Height (минус 66) | Пол/Gender |
| Alice | -2 | -1 | 1 |
Затем потеря среднеквадратической ошибки будет просто квадратической ошибкой для Alice:
Еще один способ понимания потери – представление ее как функции веса и смещения. Давайте обозначим каждый вес и смещение в рассматриваемой сети:
Затем можно прописать потерю как многовариантную функцию:
Представим, что нам нужно немного отредактировать w1. В таком случае, как изменится потеря L после внесения поправок в w1?
На этот вопрос может ответить частная производная . Как же ее вычислить?
Здесь математические вычисления будут намного сложнее. С первой попытки вникнуть будет непросто, но отчаиваться не стоит. Возьмите блокнот и ручку – лучше делать заметки, они помогут в будущем.
Для начала, давайте перепишем частную производную в контексте :
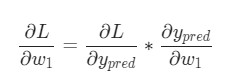
Подсчитать можно благодаря вычисленной выше
L = (1 - ypred)2:
Теперь, давайте определим, что делать с . Как и ранее, позволим
h1, h2, o1 стать результатами вывода нейронов, которые они представляют. Дальнейшие вычисления:
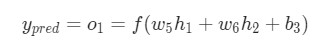
f является функцией активации сигмоида.
Так как w1 влияет только на h1, а не на h2, можно записать:
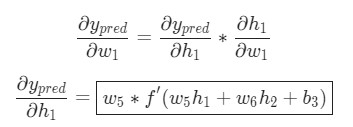
Те же самые действия проводятся для :
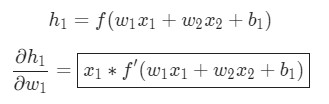
В данном случае х1 — вес, а х2 — рост. Здесь f′(x) как производная функции сигмоида встречается во второй раз. Попробуем вывести ее:
Функция f'(x) в таком виде будет использована несколько позже.
Вот и все. Теперь разбита на несколько частей, которые будут оптимальны для подсчета:
Эта система подсчета частных производных при работе в обратном порядке известна, как метод обратного распространения ошибки, или backprop.
У нас накопилось довольно много формул, в которых легко запутаться. Для лучшего понимания принципа их работы рассмотрим следующий пример.
Пример подсчета частных производных
В данном примере также будет задействована только Alice:
| Имя/Name | Вес/Weight (минус 135) | Рост/Height (минус 66) | Пол/Gender |
| Alice | -2 | -1 | 1 |
Здесь вес будет представлен как 1, а смещение как 0. Если выполним прямое распространение (feedforward) через сеть, получим:
Выдачи нейронной сети ypred = 0.524. Это дает нам слабое представление о том, рассматривается мужчина Male (0), или женщина Female (1). Давайте подсчитаем :
Напоминание: мы вывели
f '(x) = f (x) * (1 - f (x))ранее для нашей функции активации сигмоида.
У нас получилось! Результат говорит о том, что если мы собираемся увеличить w1, L немного увеличивается в результате.
Тренировка нейронной сети: Стохастический градиентный спуск
У нас есть все необходимые инструменты для тренировки нейронной сети. Мы используем алгоритм оптимизации под названием стохастический градиентный спуск (SGD), который говорит нам, как именно поменять вес и смещения для минимизации потерь. По сути, это отражается в следующем уравнении:
η является константой под названием оценка обучения, что контролирует скорость обучения. Все что мы делаем, так это вычитаем из
w1:
Если мы применим это на каждый вес и смещение в сети, потеря будет постепенно снижаться, а показатели сети сильно улучшатся.
Наш процесс тренировки будет выглядеть следующим образом:
- Выбираем один пункт из нашего набора данных. Это то, что делает его стохастическим градиентным спуском. Мы обрабатываем только один пункт за раз;
- Подсчитываем все частные производные потери по весу или смещению. Это может быть
,
и так далее;
- Используем уравнение обновления для обновления каждого веса и смещения;
- Возвращаемся к первому пункту.
Давайте посмотрим, как это работает на практике.
Создание нейронной сети с нуля на Python
Наконец, мы реализуем готовую нейронную сеть:
| Имя/Name | Вес/Weight (минус 135) | Рост/Height (минус 66) | Пол/Gender |
| Alice | -2 | -1 | 1 |
| Bob | 25 | 6 | 0 |
| Charlie | 17 | 4 | 0 |
| Diana | -15 | -6 | 1 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 |
import numpy as np def sigmoid(x): # Функция активации sigmoid:: f(x) = 1 / (1 + e^(-x)) return 1 / (1 + np.exp(—x)) def deriv_sigmoid(x): # Производная от sigmoid: f'(x) = f(x) * (1 — f(x)) fx = sigmoid(x) return fx * (1 — fx) def mse_loss(y_true, y_pred): # y_true и y_pred являются массивами numpy с одинаковой длиной return ((y_true — y_pred) ** 2).mean() class OurNeuralNetwork: «»» Нейронная сеть, у которой: — 2 входа — скрытый слой с двумя нейронами (h1, h2) — слой вывода с одним нейроном (o1) *** ВАЖНО ***: Код ниже написан как простой, образовательный. НЕ оптимальный. Настоящий код нейронной сети выглядит не так. НЕ ИСПОЛЬЗУЙТЕ этот код. Вместо этого, прочитайте/запустите его, чтобы понять, как работает эта сеть. «»» def __init__(self): # Вес self.w1 = np.random.normal() self.w2 = np.random.normal() self.w3 = np.random.normal() self.w4 = np.random.normal() self.w5 = np.random.normal() self.w6 = np.random.normal() # Смещения self.b1 = np.random.normal() self.b2 = np.random.normal() self.b3 = np.random.normal() def feedforward(self, x): # x является массивом numpy с двумя элементами h1 = sigmoid(self.w1 * x[0] + self.w2 * x[1] + self.b1) h2 = sigmoid(self.w3 * x[0] + self.w4 * x[1] + self.b2) o1 = sigmoid(self.w5 * h1 + self.w6 * h2 + self.b3) return o1 def train(self, data, all_y_trues): «»» — data is a (n x 2) numpy array, n = # of samples in the dataset. — all_y_trues is a numpy array with n elements. Elements in all_y_trues correspond to those in data. «»» learn_rate = 0.1 epochs = 1000 # количество циклов во всём наборе данных for epoch in range(epochs): for x, y_true in zip(data, all_y_trues): # — Выполняем обратную связь (нам понадобятся эти значения в дальнейшем) sum_h1 = self.w1 * x[0] + self.w2 * x[1] + self.b1 h1 = sigmoid(sum_h1) sum_h2 = self.w3 * x[0] + self.w4 * x[1] + self.b2 h2 = sigmoid(sum_h2) sum_o1 = self.w5 * h1 + self.w6 * h2 + self.b3 o1 = sigmoid(sum_o1) y_pred = o1 # — Подсчет частных производных # — Наименование: d_L_d_w1 представляет «частично L / частично w1» d_L_d_ypred = —2 * (y_true — y_pred) # Нейрон o1 d_ypred_d_w5 = h1 * deriv_sigmoid(sum_o1) d_ypred_d_w6 = h2 * deriv_sigmoid(sum_o1) d_ypred_d_b3 = deriv_sigmoid(sum_o1) d_ypred_d_h1 = self.w5 * deriv_sigmoid(sum_o1) d_ypred_d_h2 = self.w6 * deriv_sigmoid(sum_o1) # Нейрон h1 d_h1_d_w1 = x[0] * deriv_sigmoid(sum_h1) d_h1_d_w2 = x[1] * deriv_sigmoid(sum_h1) d_h1_d_b1 = deriv_sigmoid(sum_h1) # Нейрон h2 d_h2_d_w3 = x[0] * deriv_sigmoid(sum_h2) d_h2_d_w4 = x[1] * deriv_sigmoid(sum_h2) d_h2_d_b2 = deriv_sigmoid(sum_h2) # — Обновляем вес и смещения # Нейрон h1 self.w1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w1 self.w2 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w2 self.b1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_b1 # Нейрон h2 self.w3 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w3 self.w4 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w4 self.b2 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_b2 # Нейрон o1 self.w5 -= learn_rate * d_L_d_ypred * d_ypred_d_w5 self.w6 -= learn_rate * d_L_d_ypred * d_ypred_d_w6 self.b3 -= learn_rate * d_L_d_ypred * d_ypred_d_b3 # — Подсчитываем общую потерю в конце каждой фазы if epoch % 10 == 0: y_preds = np.apply_along_axis(self.feedforward, 1, data) loss = mse_loss(all_y_trues, y_preds) print(«Epoch %d loss: %.3f» % (epoch, loss)) # Определение набора данных data = np.array([ [—2, —1], # Alice [25, 6], # Bob [17, 4], # Charlie [—15, —6], # Diana ]) all_y_trues = np.array([ 1, # Alice 0, # Bob 0, # Charlie 1, # Diana ]) # Тренируем нашу нейронную сеть! network = OurNeuralNetwork() network.train(data, all_y_trues) |
Вы можете поэкспериментировать с этим кодом самостоятельно. Он также доступен на Github.
Наши потери постоянно уменьшаются по мере того, как учится нейронная сеть:
Теперь мы можем использовать нейронную сеть для предсказания полов:
|
# Делаем предсказания emily = np.array([—7, —3]) # 128 фунтов, 63 дюйма frank = np.array([20, 2]) # 155 фунтов, 68 дюймов print(«Emily: %.3f» % network.feedforward(emily)) # 0.951 — F print(«Frank: %.3f» % network.feedforward(frank)) # 0.039 — M |
Что теперь?
У вас все получилось. Вспомним, как мы это делали:
- Узнали, что такое нейроны, как создать блоки нейронных сетей;
- Использовали функцию активации сигмоида в отношении нейронов;
- Увидели, что по сути нейронные сети — это просто набор нейронов, связанных между собой;
- Создали набор данных с параметрами вес и рост в качестве входных данных (или функций), а также использовали пол в качестве вывода (или маркера);
- Узнали о функциях потерь и среднеквадратичной ошибке (MSE);
- Узнали, что тренировка нейронной сети — это минимизация ее потерь;
- Использовали обратное распространение для вычисления частных производных;
- Использовали стохастический градиентный спуск (SGD) для тренировки нейронной сети.
Подробнее о построении нейронной сети прямого распросранения Feedforward можно ознакомиться в одной из предыдущих публикаций.
Спасибо за внимание!
Являюсь администратором нескольких порталов по обучению языков программирования Python, Golang и Kotlin. В составе небольшой команды единомышленников, мы занимаемся популяризацией языков программирования на русскоязычную аудиторию. Большая часть статей была адаптирована нами на русский язык и распространяется бесплатно.
E-mail: vasile.buldumac@ati.utm.md
Образование
Universitatea Tehnică a Moldovei (utm.md)
- 2014 — 2018 Технический Университет Молдовы, ИТ-Инженер. Тема дипломной работы «Автоматизация покупки и продажи криптовалюты используя технический анализ»
- 2018 — 2020 Технический Университет Молдовы, Магистр, Магистерская диссертация «Идентификация человека в киберпространстве по фотографии лица»
2. Регрессия
Следующий тип задач — это регрессия.
Суть этой задачи — получить на выходе из нейронной сети не класс, а конкретное число, например:
— Определение возраста по фото
— Прогнозирование курса акций
— Оценка стоимости недвижимости
Например, у нас есть данные об объекте недвижимости, такие как: метраж, количество комнат, тип ремонта, развитость инфраструктуры в окрестностях этого объекта, удаленность от метро и т.д.
И нашей задачей является предсказать цену на этот объект, исходя из имеющихся данных. Задачи такого плана — это задачи регрессии, т.к. на выходе мы ожидаем получить стоимость — конкретное число.
3. Прогнозирование временных рядов
Прогнозирование временных рядов — это задача, во многом схожая с регрессией.
Суть её заключается в том, что у нас есть динамический временной ряд значений, и нам нужно понять, какие значения будут идти в нем дальше.
Например, это задачи по предсказанию:
— Курсов акций, нефти, золота, биткойна
— Изменению процессов в котлах (давление, концентрация тех или иных веществ и т.д.)
— Количества трафика на сайте
— Объемов потребления электроэнергии и т.д.
Даже автопилот Tesla отчасти тоже можно отнести к задаче этого типа, ведь видеоряд следует рассматривать как временной ряд из картинок.
Возвращаясь же к примеру с оценкой процессов, происходящих в котлах, задача, по сути, является двойной.
С одной стороны, мы предсказываем временной ряд давления и концентрации тех или иных веществ, а с другой — распознаем по этому временному ряду паттерны, чтобы оценить, критичная ситуация, или нет. И здесь уже идет распознавание образов.
Именно поэтому мы сразу отметили тот факт, что не всегда есть четкая граница между разными типами задач.
4. Кластеризация
Кластеризация — это обучение, когда нет учителя.
В этой ситуации у нас есть много данных и неизвестно, какие из них к какому классу относятся, при этом есть предположение, что там есть некоторое количество классов.
Например, это:
— Выявление классов читателей при email-рассылках
— Выявление классов изображений
Типичная маркетинговая задача — эффективно вести email-рассылку. Допустим, у нас есть миллион email-адресов, и мы ведем некую рассылку.
Разумеется, люди ведут себя совершенно по-разному: кто-то открывает почти все письма, кто-то не открывает почти ничего.
Кто-то постоянно кликает по ссылкам в письмах, а кто-то просто их читает и кликает крайне редко.
Кто-то открывает письма по вечерам в выходные, а кто-то — утром в будние, и так далее.
Задача кластеризации в этом случае — это анализ всего объема данных и выделение нескольких классов подписчиков, обладающих сходными поведенческими паттернами (в рамках, каждого класса, разумеется).
Другая задача этого типа — это, например, выявление классов для изображений. Один из проектов в нашей Лаборатории — это работа с фентези-картинками.
Если передать эти изображения нейронной сети, то, после их анализа, она, к примеру «скажет» нам, что обнаружила 17 различных классов.
Допустим, один класс — это изображение с замками. Другой — это картинки с изображением человека по центру. Третий класс — это когда на картинке дракон, четвертый — это много персонажей на фоне природного ландшафта, происходит какая-нибудь битва, и т.д.
Это примеры типичных задач кластеризации.
5. Генерация
Генеративные сети (GAN) — это самый новый, недавно появившийся тип сетей, который стремительно развивается.
Если говорить кратко, то их задача – машинное творчество. Под машинным творчеством подразумевается генерация любого контента:
— Текстов (стихи, тексты песен, рассказы)
— Изображений (в том числе фотореалистичных)
— Аудио (генерация голоса, музыкальных произведений) и т.д.
Кроме того, в этот список можно добавить и задачи трансформации контента:
— раскрашивание черно-белых фильмов в цветные
— изменение сезона в видеоролике (например, трансформация окружающей среды из зимы в лето) и др.
В случае с «переделкой» сезона изменения затрагивают все важные аспекты. Например, есть видео с регистратора, в котором машина зимой едет по улицам города, вокруг лежит снег, деревья стоят голые, люди в шапках и т.д.
Параллельно с этим роликом идет другой, переделанный в лето. Там уже вместо снега зеленые газоны, деревья с листвой, люди легко одеты и т.д.
Безусловно, есть и некоторые другие типы задач, которые решают нейронные сети, но все основные мы с вами рассмотрели.
1. Самообучение
Косвенно мы уже касались этой момента выше, поэтом сейчас раскроем его чуть больше.
Суть самообучения заключается в том, что мы задаем общий алгоритм, как она будет обучаться, а дальше она сама «понимает», как некое явление или процесс устроены изнутри.
Суть самообучения заключается в том, что нейронной сети для успешной работы нужно дать правильные, подготовленные данные и прописать алгоритм, по которому она будет обучаться.
В качестве иллюстрации для этой особенности можно привести генетический алгоритм, суть которого мы рассмотрим на примере программы с летающими по экрану монитора смайликами.
Одновременно перемещалось 50 смайликов, и они могли замедляться / ускоряться и менять направление своего движения.
В алгоритме мы заложили, что если они вылетают за край экрана или попадают под клик мыши, то «умирают».
После «смерти» тут же создавался новый смайлик, причем на основании того, кто «прожил» дольше всего.
Это была вероятностная функция, которая отдавала приоритет «рождения» новых смайликов тем, кто прожил дольше всех и минимизировала вероятность появления «потомства» у тех, кто быстро улетел за пределы экрана или попался под клик мыши.
Сразу после запуска программы все смайлики начинают летать хаотично и быстро «умирают», улетая за края экрана.
Проходит буквально 1 минута, и они научаются не «умирать», улетая за правый край экрана, но улетают вниз. Еще через минуту они перестают улетать вниз. Через 5 минут они уже вообще не умирают.
Смайлики разбились на несколько групп: кто-то летал вдоль периметра экрана, кто-то топтался в центре, кто-то нарезал восьмерки, и т.д. При этом мышкой мы их еще не кликали.
Теперь мы начали кликать по ним мышкой и, естественно, они тут же умирали, потом что еще не обучались избегать курсора.
Через 5 минут было невозможно поймать ни одного из них. Как только к ним приближался курсор, смайлики делали какой-нибудь кульбит и уходили от клика — поймать их было невозможно.
Самое важное и восхитительное во всем это то, что мы не закладывали в них алгоритм, как не улетать за края экрана и уворачиваться от мышки. И если первый момент реализовать несложно, то со вторым все на порядок сложнее.
Можно было бы потратить примерно неделю времени и создать нечто подобное, но прелесть в том, что мы добились такого же или даже лучшего результата, потратив на программирование пару часов и еще несколько минут на то, чтобы произошло обучение.
Вдобавок к этому, поменяв пару строчек кода, мы могли бы довнести в их алгоритм обучения любую другую функцию. Например, если это происходит на фоне рабочего стола — не залезать на иконки, которые на нем есть.
Или мы хотим, чтобы они не сталкивались друг с другом. Или мы хотим поделить их на 2 группы, раскрашенных в разные цвета и хотим, чтобы они не сталкивались со смайликами другого цвета. И так далее.
И они обучились бы этому за те же самые 5-10 минут по тем же принципам генетических алгоритмов.
Надеюсь, что этот пример показал вам потрясающую силу всего, что связано с искусственным интеллектом и нейронными сетями.
При всем при этом важно иметь компетенцию писать такие генетические алгоритмы и уметь подавать такой сети правильные входные данные.
Так, в рассмотренном выше примере сначала никак не удавалось добиться сколь-нибудь значимого прогресса в обучении смайликов по той причине, что в качестве входных данных им подавалось расстояние до краев экрана и расстояние до курсора мыши.
В результате этого нейронной сети не хватало мощности обучиться на таком типе данных, и прогресса практически не было.
После этого в качестве входных параметров стали передаваться другие значения — единица, деленная на расстояние до края экрана и единица, деленная на расстояние до курсора.
Результат — прекрасное обучение, о котором мы только что говорили. Почему? Потому что когда они подлетали к краю экрана, этот параметр начинал зашкаливать, его изменение происходило очень быстро, и в этой комбинации нейронная сеть смогла выявить важную закономерность и обучиться.
На этом с самообучением всё, двигаемся дальше.
2. Требуется обучающая выборка
Нейронным сетям для обучения требуется обучающая выборка. Это главный минус, т.к. обычно нужно собрать много данных.
К примеру, если мы пишем распознавание лиц в классическом машинном обучении, то нам не нужна база из фотографий – достаточно нескольких фото, по которым человек сам составит алгоритм определения лица, или даже сделает это по памяти, вообще без фото.
В случае с нейронными сетями ситуация иная – нужна большая база того, на чем мы хотим обучить нейронную сеть. При этом важно не только собрать базу, но и определенным образом её предобработать.
Поэтому очень часто сбор базы производится в том числе фрилансерами или крупными бизнесами (классический пример — сбор данных компанией Google для того, чтобы показывать нам капчи).
На своем курсе мы делаем на это упор — в том числе в Лабораториях и во время подготовки дипломных работ. Важно научиться собирать эти данные руками, получив ценный опыт, поняв, как это делается правильно, и на что нужно обратить внимание.
Если вы освоите это сами, то в будущем сможете писать в том числе и правильные ТЗ для подрядчиков, получая качественные, нужные вам результаты.
3. Не требуется понимания явления человеком
Третий пункт — это огромный плюс нейронных сетей.
Можно не быть экспертом в какой-либо предметной области, но, будучи экспертом в нейронных сетях решить практически любую задачу.
Да, экспертность, безусловно влияет в плюс, т.к. мы можем лучше предобработать данные и, возможно, быстрее решить задачу, но в целом это не является критическим фактором.
Если в классическом машинном обучении не являясь экспертом в предметной области (например, атомная энергетика, машиностроение, геологические процессы и т.п.) мы вообще не сможем решить задачу, то здесь это вполне реально.
4. Значительно точнее в большинстве задач
Следующее значимое преимущество нейронных сетей — их высокая точность.
Например, аварийность автопилотов Tesla на пробег в 1 млн. км. примерно в 10 раз ниже, чем аварийность обычного водителя.
Точность предсказания медицинских диагнозов по МРТ также выше, чем у специалистов-врачей.
Нейронные сети обыгрывают людей практически в любые игры: шахматы, покер, го, компьютерные игры и т.д.
Одним словом, их точность значительно выше практически во всех задачах, что и привело к их все более и более активному использованию в самых разных сферах жизни человека, начиная с маркетинга и финансов, и заканчивая медициной, промышленностью и искусством.
5. Непонятно, как работают внутри
Однако, при всех этих возможностях у нейронных сетей есть следующий минус — непонятно, как они работают «внутри».
Мы не можем туда влезть и понять, как там все устроено, как она «мыслит». Это все скрыто в весах, в цифрах.
Более или менее «увидеть» то, что происходит внутри возможно, разве что, в сверточных сетях при работе с изображениями, но даже это не позволяет нам получить полной картины.
Типичный пример того, что нейронная сеть в чем-то похожа на черный ящик — это ситуации, когда, например идет судебный процесс, в ходе которого какие-нибудь компании обращаются в Яндекс и спрашивают, почему именно этот сайт, а не какой-то другой выводится именно на этот позиции в выдаче.
И Яндекс не может ответить на подобные вопросы, т.к. это решение принимается нейронной сетью, а не чётко прописанным алгоритмом, который можно полностью объяснить.
Ответить на такой вопрос — задача столь же нетривиальная, как, например, предсказать точную траекторию, по которой именно с этого стола скатится именно этот металлический шарик, положенный именно в это конкретное место.
Да, законы гравитации нам известны, однако предсказать в точности, как именно будет происходить его движение, практически невозможно.
То же самое с нейронной сетью. Принципы её работы ясны, однако понять, как она сработает в каждом конкретном случае не представляется возможным.
Строение биологического нейрона
Для того, чтобы понять, как устроен искусственный нейрон, начнем с того, что вспомним, как функционирует обычная нервная клетка.
Именно её строение и функционирование Уоррен Мак-Каллок (американский нейропсихолог, нейрофизиолог, теоретик искусственных нейронных сетей и один из основателей кибернетики) и Уолтер Питтс (американский нейролингвист, логик и математик) взяли как основу для модели искусственного нейрона еще в середине прошлого века.
Итак, как выглядит нейрон?
У нейрона есть тело, которое накапливает и некоторым образом преобразует сигнал, приходящий к нему через дендриты – короткие отростки, функция которых заключается в приеме сигналов от других нервных клеток.
Накопив сигнал, нейрон передает его по цепочке дальше, другим нейронам, но уже по длинному отростку – аксону, который, в свою очередь, связан с дендритами других нейронов, и так далее.
Конечно, это крайне примитивная модель, т.к. каждый нейрон в нашем мозге может быть связан с тысячами других нейронов.
Следующий момент, на который нам нужно обратить внимание — это то, каким образом сигнал передается от аксона к дендритам следующего нейрона.
Дендриты с аксонами связаны не напрямую, а через так называемые синапсы, и когда сигнал доходит до конца аксона, в синапсе происходит выброс нейромедиатора, определяющего, как именно сигнал будет передан дальше.
Нейромедиаторы — биологически активные химические вещества, посредством которых осуществляется передача электрохимического импульса от нервной клетки через синаптическое пространство между нейронами, а также, например, от нейронов к мышечной ткани или железистым клеткам.
Иными словами, нейромедиатор является неким мостиком между аксоном и множеством дендритов принимающей сигнал клетки.
Если нейромедиатора выбросится много, то сигнал передастся полностью или даже будет усилен. Если же его выбросится мало, то сигнал будет ослаблен, либо вовсе погашен и не передастся другим нейронам.
Таким образом, процесс формирования устойчивых нейронных дорожек (уникальных цепочек связей между нейронами), являющихся биологической основой процесса обучения, зависит от того, сколько будет выброшено нейромедиатора.
Все наше обучение с самого детства построено именно на этом и образование совсем новых связей происходит достаточно редко.
В основном, все наше обучение и освоение новых навыков связано с настройкой того, сколько выбрасывается нейромедиатора в местах контакта аксонов и дендритов.
Например, у нас в нервной системе может быть установлена связь между понятиями «яблоко» и «груша». Т.е. как только мы видим яблоко, слышим слово «яблоко» или просто думаем о нем, в нашем мозгу по механизму ассоциации возникает образ груши, т.к. между этими понятиями у нас установлена связь — сформирована нейронная дорожка.
При этом между понятиями «яблоко» и подушка такой связи, скорее всего нет, поэтому образ яблока не вызывает у нас ассоциаций с подушкой — соответствующая нейронная связь очень слаба или отсутствует.
Интересный момент, о котором также стоит упомянуть, заключается в том, что у насекомых аксон и дендрит связаны напрямую, без выделения нейромедиатора, поэтому у них не происходит обучения в том виде, как оно происходит у животных и человека.
В течение жизни они не обучаются. Они рождаются уже умея всё, что они будут уметь в течение жизни.
Например, каждая конкретная муха не способна научиться облетать стекла — она всегда будет в них биться, что мы с вами постоянно и наблюдаем.
Все нейронные связи у них уже существуют, а сила передачи каждого сигнала уже отрегулирована определенным образом для всех имеющихся связей.
С одной стороны, такая негибкость в плане обучения имеет свои минусы.
С другой стороны, у насекомых, как правило, очень высокая скорость реакции именно за счет другой организации нервных связей, за счет отсутствия веществ-медиаторов, которые, будучи своеобразными посредниками, естественным образом замедляют процесс передачи сигналов.
При всем при этом обучение у насекомых все же может происходить, но только эволюционно — от поколения к поколению.
Допустим, если способность облетать стекла станет важных фактором, способствующим выживанию вида как такового, то за некоторое количество поколений все мухи в мире научатся их облетать.
Пока этого не могло произойти, т.к. сами стекла существую относительно недавно, а для эволюционного обучения могут потребоваться десятки тысяч лет.
Если же это не играет важной роли для сохранения вида, то данная модель поведения так и не будет ими приобретена.
Обычно при работе математическими нейронами используются следующие обозначения:
X – входные данные
W – веса
H – тело нейрона
Y – выход нейронной сети
Входные данные — это сигналы, поступающие к нейрону.
Веса – это эквиваленты синаптической связи и выброса нейромедиатора, представленные в виде чисел, в том числе отрицательных.
Вес представлен действительным числом, на которое будет умножено значение входящего в нейрон сигнала.
Иными словами, вес показывает, насколько сильно между собой связаны те или иные нейроны — это коэффициент связи между ними.
В теле нейрона накапливается взвешенная сумма от перемножения значений входящих сигналов и весов.
Если говорить кратко, то процесс обучения нейронной сети — это процесс изменения весов, т.е. коэффициентов связи между имеющимися в ней нейронами.
В процессе обучения веса меняются, и, если вес положительный, то идет усиление сигнала в нейроне, к которому он приходит.
Если вес нулевой, то влияние одного нейрона на другой отсутствует. Если же вес отрицательный, то идет погашение сигнала в принимающего нейроне.
И, наконец, выход нейронной сети — это то, что мы получаем в результате обработки нейроном поданного на него сигнала. Это некая функция от накопившейся в теле нейрона взвешенной суммы.
Эти функции бывают разные, например, если мы имеем дело с функцией Хевисайда, то если в теле нейрона накопилась сумма больше определенного порога, то на выходе будет единица. Если же меньше порога — ноль.
На выходе из нейрона возможны разные значения, однако чаще всего их стараются приводить к диапазону от -1 до 1 или, что бывает еще чаще — от 0 до 1.
Еще один пример — это функция ReLU (на иллюстрации не представлена), которая работает иначе: если значение взвешенной суммы в теле нейрона отрицательно, то идет преобразование в 0, а если положительно, то в X.
Так, если значение на нейроне было -100 то после обработки функцией ReLU оно станет равным 0. Если же это значение равно, например, 15,7, то на выходе будут те же 15,7.
Также для обработки сигнала с тела нейрона применяются сигмоидальные функции (логистическая и гиперболический тангенс) и некоторые другие. Обычно они используются для «сглаживания» значений некоторой величины.
К счастью, для написания кода необязательно понимать различные формулы и графики этих функций, т.к. они уже заложены в библиотеках, используемых для работы с нейронными сетями.
Простейший пример классификации 2 объектов
Теперь, когда мы разобрались с общим принципом работы, давайте посмотрим на простейший пример, иллюстрирующий процесс классификации 2 объектов с помощью нейронной сети.
Представим, что нам нужно отличить входной вектор (1,0) от вектора (0,1). Допустим, черное от белого, или белое от черного.
При этом, в нашем распоряжении есть простейшая сеть из 2 нейронов.
Допустим, что мы зададим верхней связи вес «+1», а нижней – «-1». Теперь, если мы подадим на вход вектор (1,0), то на выходе мы получим 1.
Если же мы подадим на вход вектор (0,1), то на выходе получим уже -1.
Для упрощения примера будем считать, что у нас здесь используется тождественная активационная функция, при которой f(x) равно самому x, т.е. функция никак не преобразует аргумент.
Таким образом, наша нейронная сеть может классифицировать 2 разных объекта. Это совсем-совсем примитивный пример.
Обратите внимание на то, что в данном примере мы сами назначаем веса «+1» и «-1», что не совсем неправильно. В действительности они подбираются автоматически в процессе обучения сети.
Обучение нейронной сети – это подбор весов.
Любая нейронная сеть состоит из 2 составляющих:
- Архитектура
- Веса
Архитектура — это её структура и то, как она устроена изнутри (об этом мы поговорим чуть позже).
И когда мы подаем на вход нейронной сети данные, нам нужно её обучить, т.е. подобрать веса между нейронами так, чтобы она действительно выполняла то, что мы от неё ожидаем, допустим, умела отличать фото кошек от фото собак.
На самом деле, обучением нейронной сети можно назвать также и подбор архитектуры в процессе исследования.
Так, например, если мы работаем с генетическими алгоритмами, то в процессе обучения нейронная сеть может менять не только веса, но еще и свою структуру.
Но это скорее исключение, чем правило, поэтому в общем случае под обучением нейронной сети мы будем понимать именно процесс подбора весов.
1. С учителем
Обучение с учителем — это одна из самых частых задач. В этом случае у нас есть выборка, и мы знаем по ней правильные ответы.
Мы точно заранее знаем, что на этих 10 тыс. фото — собаки, а на этих 10 тыс. фото — кошки.
Или мы точно знаем курс каких-нибудь акций на протяжении длительного времени.
Допустим, 5 дней до этого дня были такие цены, а на следующий день цена стала такой-то. Затем смещаемся на день вперед, и мы снова знаем: 5 дней цены были такие, а на следующий день цена стала такой-то, и так далее.
Или мы знаем характеристики домов и их реальные цены, если мы говорим про прогнозирование цен на недвижимость.
Все это — примеры обучения с учителем.
2. Без учителя
Второй тип обучения — это обучение без учителя (кластеризация).
В этом случае мы подаем на вход сети некие данные и предполагаем, что в них можно выделить несколько классов.
Пример: у нас есть большая база email-адресов людей, с которыми мы взаимодействуем.
Они открывают наши письма, читают их, переходят или не переходят по ссылкам. Они делают это в то или иное время суток и т.д.
Обладая этой информацией (например, благодаря статистике почтового рассыльщика), мы можем передать нейронной сети эти данные с «просьбой» выделить несколько классов читателей, которые по тем или иным критериям будут схожи между собой.
Используя эти данные, мы смогли бы выстраивать более эффективную маркетинговую стратегию взаимодействия с каждой из таких групп людей.
Обучение без учителя используется в тех случаях, когда требуется обнаружить внутренние взаимосвязи, зависимости и закономерности, существующие между объектами, но заранее мы не знаем, в чем именно заключаются эти закономерности.
3. С подкреплением
Третий тип обучения — это обучение с подкреплением. Оно немного похоже на обучение с учителем, когда есть готовая база верных ответов. Отличие заключается в том, что в этом случае у нейронной сети нет всей базы сразу, а дополнительные данные приходят в процессе обучения и дают сети обратную связь о том, достигнута цель или нет.
Простой пример: бот проходит некий лабиринт и на 59 шаге получает информацию о том, что он «упал в яму» или после 100 шагов, выделенных на выход из лабиринта, он узнает, что «не дошел до выхода».
Таким образом нейронная сеть понимает, что последовательность её действий не привела к нужному результату и обучается, корректируя свои действия.
Т.е. заранее сеть не знает, что верно, а что – нет, но получает обратную связь, когда происходит некое событие. По этому принципу строятся практически все игры, а также различные агенты и боты.
Кстати, пример с умирающими смайликами, который мы рассматривали выше — это также обучение с подкреплением.
Кроме того, это автопилоты, подбор стиля под пожелания конкретного человека, исходя из его предыдущих выборов и т.д.
Например, нейронная сеть генерирует 20 картинок и человек выбирает из них 3, которые ему больше всего нравятся. Затем нейронная сеть создает еще 20 картинок и человек снова выбирает то, что ему нравится больше всего и т.д.
Таким образом, сеть выявляет предпочтения человека по стилю изображения, цветовой гамме и другим характеристикам, и может создавать изображения под вкусы каждого конкретного человека.
Одной из ключевых задач при создании нейронных сетей является выбор её архитектуры. Он производится разработчиком, исходя из стоящей перед ним задачи и, в общем случае, нейронная сеть обучается только за счет изменения весов.
Исключение – генетические алгоритмы, когда популяция нейронных сетей в процессе обучения самостоятельно пересобирает саму себя и свою архитектуру в том числе.
Однако в подавляющем большинстве случаев в процессе обучения архитектура нейронной сети самопроизвольно не меняется.
Все изменения в нее вносит сам разработчик через добавление или удаление слоев, увеличение или уменьшение количества нейронов на каждом слое и т.д.
Давайте посмотрим на основные архитектуры и начнем с классического примера — полносвязной нейронной сети прямого распространения.
Полносвязная нейронная сеть прямого распространения — это сеть, в которой каждый нейрон связан со всеми остальными нейронами, находящимися в соседних слоях, и в которой все связи направлены строго от входных нейронов к выходным.
Слева на рисунке мы видим входной слой, на который приходит сигнал. Правее находятся два скрытых слоя, и самый правый слой из двух нейронов – выходной слой.
Эта сеть может решить задачу классификации, если нам нужно выделить два любых класса – допустим, кошек и собак.
Например, верхний из этих двух нейронов отвечает за класс «собаки» и может иметь значения 0 или 1. Нижний – за класс «кошки», и имеет возможность принимать те же самые значения – 0 или 1.
Другой вариант — она может, к примеру, прогнозировать 2 параметра — давление и температуру в котле на основании 3 неких входных данных.
Чтобы лучше понять, как это работает, давайте посмотрим, как такая полносвязная сеть может использоваться, допустим, для прогнозирования погоды.
В этом примере мы подаем на вход температурные данные по трем последним дням, а на выходе хотим получить предсказания на два следующих дня.
Между входным и выходным слоями у нас есть 2 скрытых слоя, в которых нейронная сеть будет обобщать данные.
Например, в первом скрытом слое один нейрон будет отвечать за такое простое понятие, как «температура растет».
Другой нейрон будет отвечать за понятие «температура падает».
Третий – за понятие «температура неизменна».
Четвертый – «температура очень высокая».
Пятый – «температура высокая».
Шестой – «температура нормальная».
Седьмой – «температура низкая».
Восьмой – «совсем низкая».
Девятый – «температура скакнула вниз и вернулась».
И так далее.
Мы, разумеется, называет все это словами, понятными нам, в то время как сеть сама в процессе обучения сделает так, что каждый из нейронов будет за что-то отвечать, чтобы эффективно обобщать данные.
И каждый из нейронов первого скрытого слоя (в т.ч. обведенный на картинке) будет отвечать за выделение определенного признака в поступивших данных.
Например, если он отвечает за понятие «температура растет», то нейрон с температурой +17 со входного слоя будет входить в него с положительным весом.
Нейрон с температурой +15 – с нулевым весом, а нейрон с температурой +12 – с отрицательным весом.
Если этот так, т.е. температура реально росла и подавались такие данные, обведенный на рисунке нейрон будет активироваться. Если же температура падала, он останется неактивированным.
Нейроны второго скрытого слоя (например, обведенный на картинке ниже), будут отвечать за более высокоуровневые признаки, например, за то, что это осень. Или за то, что это любое другое время года.
На активацию данного нейрона будет положительно влиять падение температуры, свойственное осени.
Если наблюдается постепенный рост температуры, то, скорее всего, это статистически будет влиять в минус, т.е. не будет активировать данный нейрон.
Понятно, что бывают ситуации, когда осенью температура растет, но, скорее всего, статистически рост температуры в течение 3 дней будет отрицательно влиять на этот нейрон.
То, что температура слишком высокая, точно будет отрицательно влиять на нейрон, отвечающий за осень, т.к. не бывает очень высоких температур в это время года, и так далее.
И, наконец, нейроны 2 скрытого слоя соединяются с двумя выходными нейронами, которые выдают предсказание по температуре.
При этом обратите внимание, что сами мы не задаем, за что будет отвечать каждый из нейронов (это было бы примером классического машинного обучения). Нейронная сеть сама сделает нейроны «ответственными» за те или иные понятия.
Более того, в рамках нейронной сети привычные нам понятия, такие как «весна», «осень», «температура падает» и т.д. не существуют. Мы просто обозначили их так для своего удобства, чтобы нам было понятнее, что примерно происходит внутри во время обучения.
В действительности же нейронная сеть сама в процессе обучения выделит именно те свойства, которые нужны для решения данной конкретной задачи.
Важно понимать, что нейронная сеть именно с такой архитектурой не будет правильно прогнозировать температуру – это упрощенный пример, показывающий, как внутри сети может происходить выделение различных признаков (так называемый процесс feature extraction).
Процесс выделения признаков хорошо иллюстрирует работа свёрточных нейронных сетей.
Допустим, на вход сети мы подаем фото кошек и собак, и сеть начинает их анализировать.
На первых слоях сеть определяет наиболее общие признаки: линия, круг, темное пятно, угол, близкий к прямому, яркое пятно на фоне темного и т.д.
На следующем слое сеть сможет извлечь уже иные признаки: ухо, лапа, голова, нос, хвост и т.д.
Еще дальше, на следующем слое будет идет анализ уже такого плана:
— здесь хвост загнут вверх, это коррелирует с лайкой, значит собака;
— а тут короткие лапы, а у кошек нет коротких лап, поэтому, скорее всего, собака, такса;
— а вот здесь треугольное ухо с белым кончиком, похоже на такую-то породу кошки, и т.д.
Примерно таким образом происходит процесс feature extraction.
Безусловно, чем больше нейронов в сети, тем более детальные, специфические свойства она может выделить.
Если же нейронов немного, она сможет работать только «крупными мазками», т.к. у нее не хватит мощности проанализировать все возможные комбинации признаков.
Таким образом, общий принцип выделения свойств — это все большее обобщение при переходе с одного слоя на другой, от низкого уровня ко все более высокому.
Итак, давайте снова вспомним, что из себя представляет нейронная сеть.
Во-первых, это архитектура.
Она задается разработчиком, т.е. мы сами определяем, сколько у сети слоев, как они связаны, сколько нейронов на каждом слое, есть ли у этой сети память (об этом чуть позже), какие у нее активационные функции и т.д.
Архитектуру сети можно представить, например, как обычный JSON, YAML или XML-файл (текстовые файлы, в которых можно полностью отразить её структуру).
Во-вторых, это обученные веса.
Веса нейронной сети хранятся в совокупности матриц в виде действительных чисел, количество которых (чисел) равно общему количеству связей между нейронами в самой сети.
Количество самих матриц зависит от количества слоев и того, как нейроны разных слоев связаны друг с другом.
Веса задаются в начале обучения (обычно случайным образом) и подбираются в процессе обучения.
Таким образом, сеть можно легко сохранить через сохранение её архитектуры и весов, а в дальнейшем снова использовать её, обратившись к файлам с архитектурой и весами.
Обучение полносвязной сети методом обратного распространения ошибки (градиентного спуска)
Как же обучается полносвязная нейронная сеть прямого распространения? Давайте рассмотрим этот вопрос на примере метода обратного распространения ошибки, являющегося модификацией метода классического градиентного спуска.
Это метод обновления весов нейронной сети, при котором распространение сигналов ошибки происходит от выходов сети к её входам, в направлении, обратном прямому распространению сигналов в обычном режиме работы.
Сразу отметим, что это не самый продвинутый алгоритм, и при работе с библиотекой Keras мы будем использовать более эффективные решения.
Также важно понимать, что в других типах сетей обучение происходит по другим алгоритмам, однако сейчас нам важно понять общий принцип.
Вернемся к примеру про прогнозирование температуры и допустим, что в качестве выходного сигнала у нас есть 2 вещественных числа т.е. значения температуры в градусах по 2 дням.
Таким образом, мы знаем правильные ответы, т.е. какая температура была на самом деле, и знаем те ответы, которые дала нам нейронная сеть.
В качестве способа измерения величины ошибки при обучении сети мы будем использовать так называемую функцию среднеквадратичной ошибки.
Например, в первый день сеть предсказала нам 10 градусов, а реально было 12. Про второй день она сказала, что будет 11 градусов, и реально также было 11.
Среднеквадратичная ошибка в этом случае составит сумму квадратов разностей предсказанной и реальной температур: ((10-12)² + (11-11)²)/2 = 2.
В процессе обучения нейронной сети алгоритмы (в т.ч. Back Propagation – алгоритм обратного распространения ошибки) ориентированы на то, чтобы менять веса так, чтобы уменьшать эту среднеквадратичную ошибку.
Если она будет равна нулю, это значит, что нейронная сеть гарантированно точно распознает, например, все образы в обучающей выборке.
Понятно, что на практике в ноль она никогда не сходится, но близко к нулю — вполне возможно, и точность в этом случае будет очень высокая.
Метод градиентного спуска
Представим теперь, что у нас есть некоторая поверхность ошибки. Допустим, у нас есть нейронная сеть, в которой 2 веса, и мы можем эти веса менять.
Понятно, что разным значениям этих весов будет соответствовать разная ошибка нейронной сети.
Таким образом, взяв эти значения, мы можем создать двухмерную поверхность, на которой видны соотношения значений весов W₁ и W₂ и значений ошибок X₀-X₄ (см. иллюстрацию).
Теперь представим, что у нас в нейронной сети не два, а тысяча весов, и разные комбинации этих тысяч весов соответствуют разным ошибкам при одной и той же обучающей выборке. В этом случае у нас получается уже тысячемерная поверхность.
Мы можем менять тысячу действительных чисел и каждый раз получать новое значение ошибки.
И эту тысячемерную поверхность можно сравнить с поверхностью измятого одеяла со своими локальными максимумами и минимумами (соответственно максимальными и минимальными значениями функции на заданном множестве). Это и будет называться поверхностью ошибки.
Так вот, обучение нейронной сети – это продвижение по этой тысячемерной поверхности разных весов и получение разных ошибок. И где-то на этой поверхности есть глобальный минимум – такая комбинация этой тысячи весов, при которой ошибка минимальна.
Локальных же минимумов может быть много, и в них значение ошибки достаточно низкое.
Поэтому обучение нейронной сети можно представить как это осмысленное перемещение по этой тысячемерной поверхности с целью добиться минимальной ошибки в некоторой точке.
При этом глобальный минимум, как правило, никто не ищет – он один, а пространство для поиска огромное. Именно поэтому нашей целью обычно являются как раз локальные минимумы. При всем при этом стоит отметить, что заранее мы не можем знать, какой именно минимум мы нашли – один из локальных, либо глобальный.
Но как именно происходит перемещение по поверхности ошибки? Давайте разберемся.
Важный момент заключается в том, что мы можем посчитать производную ошибки по весам. Иными словами, мы можем математически просчитать, как изменится ошибка, если мы чуть-чуть изменим в какую-то сторону веса.
Таким образом, мы можем вычислить, куда нам нужно сместить веса, чтобы ошибка у нас гарантированно уменьшилась при следующем шаге обучения.
Именно таким образом мы пошагово ищем необходимое направление спуска по поверхности ошибки.
Если мы шагнем слишком широко, то можем перескочить локальный минимум и подняться выше по поверхности ошибки, что для нас нежелательно.
Если же шаг будет небольшим, то мы шагнем вниз, ближе к локальному минимуму, затем снова пересчитаем направление движения и снова сделаем небольшой шаг.
Да, продвинутые алгоритмы могут, например, «перелезть через горку» и найти более глубокий локальный минимум и т.д., но в целом алгоритм обучения построен именно так.
Мы работаем с многомерной поверхностью ошибки в рамках наших весов и ищем, куда нам двигаться, чтобы прийти в локальный минимум, по возможности, максимально глубокий.
Такая архитектура позволяет поэтапно выделять разные признаки на разных слоях. Первые слои при этом выделяют самые простые признаки, например:
— справа – белое, слева – черное
— по центру – яркое, по краям – тусклое
— линия под 45 градусов
— и т.д.
На иллюстрации ниже изображена одномерная свёрточная сеть, в которой не все нейроны связаны со всеми, а каждый нейрон последующего слоя «смотрит» на два нейрона предыдущего слоя (за исключением входного слоя слева).
При этом вы можете обратить внимание, что в правой части свёрточная сеть переходит в полносвязную, т.е. идет объединение двух архитектур. Для чего это нужно вы узнаете буквально несколькими предложениями ниже.
Выделение признаков происходит постепенно, слой за слоем, например: линия – овал – лапа, что отражено на трех иллюстрациях ниже.
В генеративной сети у нас две нейронных сети: одна генерирует образы, а вторая пытается отличить эти образы от некоторых эталонных.
Например, одна сеть-детектор смотрит на фентези-картинки, а другая пытается создавать новые картинки и говорит: «А попробуй отличить фентези-картинки от моих».
Сначала она генерирует картинки, которые сеть-детектор легко отличает, потому что они не очень похожи на фентези-картинки.
Но потом та сеть, которая создает картинки, обучается все больше, и сеть-детектор уже едва может отличить фентези-картинки, которые мы подали ей на вход сами от тех, что сгенерировала вторая сеть.
И сейчас, когда мы рассмотрели основные архитектуры, давайте вспомним типы задач, которые решаются нейронными сетями и сопоставим их с архитектурами, которые для подходят для их решения.
1. Распознавание образов производится средствами полносвязных, свёрточных, рекуррентных сетей.
2. Языковые задачи чаще всего решаются с помощью рекуррентных сетей с памятью, и иногда — с помощью одномерных свёрточных.
3. Обработка аудио и голоса — это полносвязные, одномерные свёрточные, иногда рекуррентные сети.
4. Задачи регрессии и прогнозирования временных рядов решаются с помощью полносвязных и рекуррентных сетей.
5. Наконец, машинное творчество — это генеративные свёрточные и генеративные полносвязные сети.
Таким образом, мы видим, что стандартные архитектуры пересекаются и используются в задачах разного типа.
Мы будем проходить все эти архитектуры: сначала полносвязные, потом свёрточные, рекуррентные и генеративные. После чего уже будем изучать сложные комбинации архитектур.
На этом шаге мы берем какую-нибудь архитектуру исходя из имеющейся задачи и получаем первичные результаты на обучающей и тестовой выборках.
Допустим, у нас задача распознавания кошек и собак. Значит берем сверточную сеть.
Попробуем простую сеть на 5 слоев по 20 нейронов в каждой, а в конце — 2 слоя полносвязной, и обучим.
В результате мы получаем какие-то базовые результаты, некую первичную точность. И уже после этого начинаем думать, как можно её повысить, например:
— создаем различные варианты архитектур (допустим, несколько десятков вариантов) и собираем статистику по ошибке и точности для каждого из вариантов
— пробуем разные активационные функции
— повышаем качество данных (избавление от зашумленных данных)
— и так далее…
В итоге, путем экспериментов и проверки своих предположений мы доводим качество работы сети до желаемого уровня.
И, наконец, наша production-часть обращается к сервису и производит распознавание.
После вывода в production, разумеется, можно продолжить исследования и постепенно улучшать работу сети и подменять её по мере доработки — либо архитектуру, либо веса, либо и то, и другое.
Скажем, вы обучили сеть на относительно небольшом объеме данных, а через некоторое время вам пришло данных в 10 раз больше. Безусловно, стоит переобучить сеть на большем объеме данных и, вполне возможно, повысить качество её работы.
Для этого мы постоянно сравниваем результаты работы нашей сети по точности распознавания на тестовой выборке.
При этом важно постоянно помнить о том, что в области нейронных сетей даже близко нет детерминированных ответов — это всегда исследование и изобретение.
Итак, мы дошли с вами до нашего главного инструмента в создании нейронных сетей — библиотек.
Что такое библиотека? Это набор функций, которые позволяют нам собрать и обучить нейронную сеть без необходимости глубоко понимать математическую базу, лежащую в основе этих процессов.
Совсем недавно библиотек еще не было, но сейчас уже есть достаточно хороший выбор, существенно облегчающий жизнь разработчика и экономящий его время.
Мы не будем останавливаться на каждой библиотеке отдельно — это, скорее, мини-обзор существующих решений, чтобы вы могли в целом в них ориентироваться.
Так, на настоящее время наиболее известными являются следующие библиотеки:
- TensorFlow (Google)
- CNTK (Microsoft)
- Theano (Монреальский институт алгоритмов обучения (MILA))
- Pytorch (Facebook)
- и так далее
- Сама видеокарта (GPU)
- CUDA (программно-аппаратная архитектура параллельных вычислений, которая позволяет существенно увеличить вычислительную производительность благодаря использованию графических процессоров фирмы Nvidia)
- cuDNN (библиотека, содержащая оптимизированные для GPU реализации сверточных и рекуррентных сетей, различных функций активации, алгоритма обратного распространения ошибки и т.п., что позволяет обучать нейронные сети на GPU в несколько раз быстрее, чем просто CUDA)
- TensorFlow, CNTK, Theano (надстройки над cuDNN)
Keras же, в свою очередь, использует в качестве бэкенда TensorFlow и некоторые другие библиотеками, позволяя нам пользоваться уже готовым кодом, написанными именно для создания нейронных сетей.
Еще один важный момент, который нужно отметить — это вопрос о том, как со всем этим работает Python. Многие говорят, что он работает медленно.
Да, это так, но Keras генерирует не код Python, Keras генерирует код С++, и именно он уже используется непосредственно для работы нейронной сети, поэтому все работает быстро.
Наш учебный процесс будет построен именно вокруг Google Colaboratory (демонстрации кода, домашние задания и т.д.), и в целом это очень удобно, однако, если вы хотите, то можете работать и в своей, привычной вам среде.
Запускать Google Colaboratory рекомендуется под Google Chrome, и при первой попытке открыть ноутбук (так называется любой документ в Google Colaboratory) вам будет предложено установить в браузер приложение Colaboratory, чтобы в будущем оно автоматически «подхватывало» файлы такого типа.
Теперь, после установки Colaboratory мы можем перейти уже непосредственно к практической части.
В первой строке мы импортируем предустановленный датасет MNIST с изображениями рукописных цифр, которые мы будем распознавать.
Затем мы подключаем библиотеки Sequential и Dense т.к. работаем с полносвязной сетью прямого распространения.
Наконец, мы импортируем дополнительные библиотеки, позволяющие нам работать с данными (NumPy, Matplotlib и др.).
Сразу обратите внимание на модульную структуру ноутбука, благодаря которой вы можете в любом порядке чередовать блоки кода и текстовые поля.
Для того, чтобы добавить новую ячейку кода, текстовое поле или поменять порядок их следования воспользуйтесь, кнопками CODE, TEXT и CELL прямо под основным меню.
Ну и, наконец, для запуска фрагмента кода нам нужно просто нажать на значок play слева вверху от кода. Он появляется при выделении блока с кодом, либо при наведении мышки на пустые квадратные скобки, если блок не выделен.
Следующим шагом с помощью функции load_data мы подгружаем данные, необходимые для обучения сети, где x_train_org и y_train_org – данные обучающей выборки, а x_test_org и y_test_org – данные тестовой выборки.
Их названий выборок понятно, что обучающую выборку мы используем для того, чтобы обучить сеть, в то время как тестовая используется для того, чтобы проверить, насколько качественно произошло это обучение.
Смысл тестовой выборки в том, чтобы проверить, насколько точно отработает наша сеть с данными, с которыми она не сталкивалась ранее. Именно это является самой важной метрикой оценки сети.
В x_train_org находятся сами изображения цифр, на которых обучается сеть, а y_train_org – правильные ответы, какая именно цифра изображена на том или ином изображении.
Сразу важно отметить, что формат представления правильных ответов на выходе из сети — one hot encoding. Это одномерный массив (вектор), хранящий 10 цифр – 0 или 1. При этом положение единицы в этом векторе и говорит нам о верном ответе.
Например, если цифра на картинке изображен 0, то вектор будет выглядеть как в первой строке на картинке ниже.
Если на изображении цифра 2, то единица в векторе будет стоять в 3 позиции (как в строке 2).
Если же на изображении цифра 9, то единица в векторе будет стоять в последней, десятой позиции.
Это объясняется тем, что нумерация в массивах по умолчанию начинается с нуля.
Изначально на вход сети в обучающей выборке подается 60 тыс. изображений размером 28 на 28 пикселей. В тестовой выборке таких изображений 10 тыс. штук.
Наша задача — привести их к одномерному массиву (вектору), размерность которого будет не 28 на 28, а 1 на 784, что мы и делаем в коде выше.
Следующий наш шаг – это так называемая нормализация данных, их «выравнивание» с целью привести их значения к диапазону от 0 до 1.
Дело в том, что до нормализации изображение каждой рукописной цифры (все они представлены в градациях серого) представлено числами от 0 до 255, где 0 представляет собой чёрный цвет, а 255 — белый).
Однако для эффективной работы сети нам необходимо привести их к другому диапазону, что мы и делаем, разделив каждое значение на 255.
В данном случае количество нейронов (800) уже подобрано эмпирически. При таком количестве нейронная сеть обучается лучше всего (безусловно, на старте своих исследований мы можем пробовать самые разные варианты, постепенно приходя к оптимальному).
В качестве выходного слоя у нас будет полносвязный слой из 10 нейронов – по количеству рукописных цифр, которые мы распознаём.
И наконец, функция softmax будет преобразовывать вектор из 10 значений в другой вектор, в котором каждая координата представлена вещественным числом в интервале [0,1] и сумма этих координат равна 1.
Эта функция применяется в машинном обучении для задач классификации, когда количество классов больше двух, при этом полученные координаты трактуются как вероятности того, что объект принадлежит к определенному классу.
После этого мы компилируем сеть и выходим на экран ее архитектуру.
Сначала мы записываем сеть в файл, затем можем проверить, что он сохранился, после чего сохраняем файл на компьютер с помощью метода download.
Ну что ж, теперь настало время проверить, как наша сеть распознает рукописные цифры, которые она еще не видела. Для этого нам понадобится тестовая выборка, которая, наряду с обучающей, также входит в датасет MNIST.
Для начала выберем произвольную цифру из набора тестовых данных и выведем её на экран:
Теперь, когда мы получили некие первичные результаты, мы можем продолжить процесс исследования, меняя различные параметры нашей нейронной сети.
Например, мы можем поменять количество нейронов во входном слое и уменьшить их количество с 800, например, до 10.
Для того, чтобы запустить сеть обучаться повторно после внесенных изменений с нуля, нам необходимо заново пересобрать модель, запустить код с измененными параметрами сети и снова её скомпилировать (в противном случае сеть будет дообучаться, что требуется далеко не всегда).
Для этого мы просто заново нажимаем на play последовательно во всех трех блоках кода (см. ниже).
В результате этих действий вы увидите, что исходные данные изменились, и сеть теперь имеет 2 слоя по 10 нейронов, вместо 800 и 10, которые были ранее.
Как мы видим, даже при одном нейроне в скрытом слое сеть достигла точности почти в 38%. Понятно, что с таким результатом она едва ли найдет практическое применение, однако мы делаем это просто для понимания того, как могут разниться результаты при изменении архитектуры.
Итак, завершая разбор кода, следует сделать важную оговорку: то, что мы смотрим точность на обучающей выборке – это просто пример для понимания того, как это работает.
В действительности, качество работы сети нужно замерять исключительно на тестовой выборке с данными, с которыми нейронная сеть еще не сталкивалась ранее.
И теперь, когда мы немного поэкспериментировали, давайте подведем небольшой итог и посмотрим, как подойти к проведению экспериментов с нейронными сетями системно, чтобы получать действительно статистически значимые результаты.
Итак, мы берем одну модель сети, и в цикле формируем из имеющихся данных 100 разных обучающих и тестовых выборок в пропорции 80% — обучающая выборка, и 20% — тестовая.
Далее на всех этих данных мы проводим 100 обучений нейронной сети со случайной точки (каждый раз сеть стартует со случайными весами) и получаем некую ошибку на тестовой выборке — среднюю за эти 100 обучений на данной конкретной архитектуре (но с разными комбинациями обучающей и тестовой выборок).
Потом берется другая архитектура и делается то же самое. Таким образом мы можем проверить, например несколько десятков вариантов архитектур по 100 обучений на каждой, в результате чего получим статистически значимые результаты своих экспериментов и сможем выбрать самую точную сеть.
Ну что ж, на этом мы завершаем данный обзор и надеемся, что он помог вам лучше понять как работают нейронные сети, и как можно быстро написать свою первую нейронную сеть на Python.