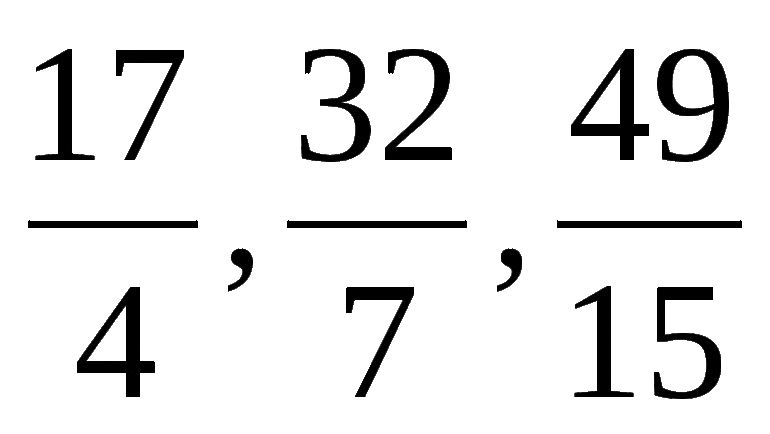Мы можем использовать неправильные дроби и смешанные числа для представления одних и тех же значений. Рассмотрим на примере равенство неправильной дроби и смешанного числа 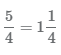
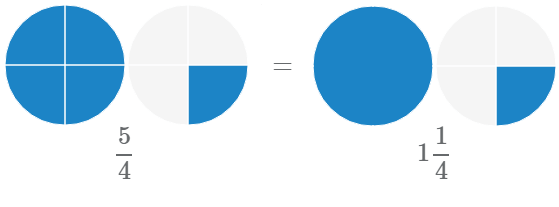
Перевод неправильной дроби в смешанное число
Для перевода неправильной дроби 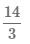
- 1 Разделим числитель на знаменатель 14 ÷ 3, в результате получим 4 целых и 2 в остатке.
- 2 Число 4 будет целой частью смешанного числа.
-
3 Остаток от деления 2 будет числителем дроби, а знаменатель останется прежним, равным 3. В результате получаем
Рассмотрим на примерах как переводить неправильные дроби в смешанные числа.
Пример Перевести неправильные дроби  в смешанные числа.
в смешанные числа.
Перевод смешанного числа в неправильную дробь
Для перевода смешанного числа 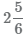
- 1 Умножим целую часть на знаменатель 2×6 и прибавим числитель 5. Полученное число 17=2×6+5запищем в числитель неправильной дроби.
- 2 Запищем в знаменатель неправильной дроби число 6, знаменатель при преобразование в неправильную дробь остается неизменным.
-
3 В результате шагов 1-2 получаем неправильную дробь
Пример Перевести смешанные числа  в неправильные дроби.
в неправильные дроби.
Перейти к содержанию
Правильная и неправильная дроби
Опубликовано 04.06.2021
Дадим определение правильной и неправильной дроби. Эти понятия часто используются в математике. Как понять – какая дробь правильная, а какая неправильная – даем определения. Пример правильной дроби и пример неправильной дроби – в этом материале.
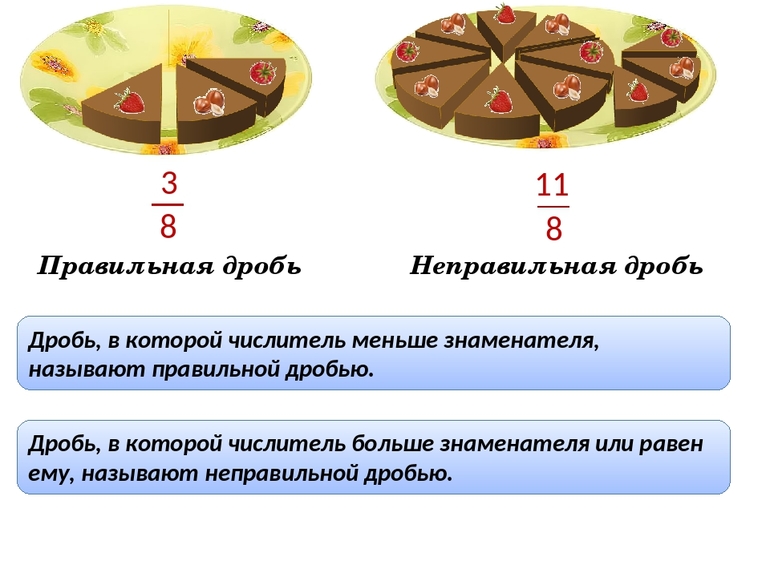
Правильная дробь
Определение правильной дроби:
Дробь, в которой числитель меньше знаменателя, называется правильной. Например,
– правильная дробь.
Неправильная дробь
Определение неправильной дроби:
Дробь, в которой числитель равен знаменателю или больше его, называется неправильной дробью. Например,
,
– неправильные дроби.
Обращение числа с целой и дробной частями в неправильную дробь
Число, состоящее из целой и дробной частей, можно обратить в неправильную дробь. Например, .
.
Вообще, чтобы записать число в виде неправильной дроби, нужно умножить его целую часть на знаменатель дробной части и к произведению прибавить числитель дробной части. Полученная сумма будет числителем дроби, а знаменателем будет знаменатель дробной части.
Как выделить целую часть из неправильной дроби
Из любой неправильной дроби можно выделить целую часть. Для этого нужно разделить с остатком числитель на знаменатель. Частное от деления будет целой частью числа, остаток – числителем, а делитель – знаменателем. Например, .
( 8 оценок, среднее 4.25 из 5 )
Общие сведения
Слово «дробь» в обиход ввёл математик средневековой Европы Фибоначчи. На Руси под этим понятием понимались доли чисел. В дословном переводе на русский с арабского термин обозначает «ломать» или «раздроблять». Вид записи выражения, который применяется и сегодня, предложили арабы. Но фундамент теории заложили греческие и индийские учёные.
В математике под дробным отношением понимают число, образованное из некоторой части единицы. Простыми словами это можно объяснить на наглядном примере. Пусть на столе лежит две круглые пиццы. Каждую из них разрезали на восемь равных частей. Всего получилось шестнадцать долей. Через какое-то время было съедено одиннадцать кусков. Соответственно на столе осталось пять. В математической записи такое действие будет выглядеть как 11 / 8.
Это легко проверить: 11/ 8 пиццы — это тоже что 8 / 8 плюс 3 / 8. То есть одна была полностью съедена, а с другой взяли только три кусочка. Так как отношение 8 / 8 — это целое (единица), то можно утверждать, что 8 / 8 = 1. Значит, произошедшее можно представить в виде равенства: 11 / 8 = 1 + 3 / 8.
Число, стоящее в верхней части выражения, называют делимым или числителем, а в нижней делителем или знаменателем. В зависимости от их числового значения все дроби разделяют на три класса:
- Правильные. Рациональные выражения, в которых числитель меньше или неравен делителю. Например, 1 / 16; 4 / 45; -78 / 123.
- Неправильные. Обыкновенные дроби, у которых знаменатель количественно меньше значения делимого или равен ему по численности. Например, 7 / 6; 19 / 19; 453 / 21.
- Смешанные. Отношения, включающие в свою запись как натуральное число, так и правильную дробь. Фактически они представляют собой их сумму: 4 (4 / 5) = 4 + 4 / 5
Кроме этого, выделяют ещё одну группу выражений. Дроби, относящиеся к ней, называют десятичными. Это такие отношения, у которых знаменатель — это десятичное число, стоящее в любой натуральной степени. Для записи десятичных выражений используют не дробную черту, а запятую. Например, 12 / 10 = 1,2.
Так как, по сути, дроби — это числа, только чаще всего не целые, над ними можно выполнять любые операции. Для того чтобы школьника научить правильно решать дроби, в 5 классе, кроме теоретического материала несколько уроков уделяют практике. На ней, кроме непосредственного выполнения арифметических операций, учат преобразовывать дробные отношения из одного вида в другой.
Суть отношения
Обыкновенная дробь может быть правильной или неправильной. Например, 19 / 21 — правильное выражение, так как результат деления будет меньше единицы. В то же время обыкновенные числа 32 / 6 и 90 / 90 — неправильные, так как ответ, получаемый при делении, будет больше единицы в первом случае и равен ей во втором.
Чтобы разобраться, почему же дробные выражения, у которых числитель превосходит или равняется знаменателю называют «неправильными» можно порассуждать следующим образом.
Пусть имеется неправильная дробь 10 / 10. Эта запись обозначает, что взято десять долей чего-то состоящего из такого же числа частей. Иными словами, из имеющихся десяти долей можно сложить целый предмет. Неправильное выражение вида 10 / 10, по сути, означает целый предмет. Значит, можно записать, что 10 / 10 =1. Следовательно, такое отношение можно заменить натуральным числом.
Теперь можно рассмотреть неправильные отношения 7 / 3 и 12 / 4. Совершенно очевидно, что из этих семи третьих долей легко составляется два целых числа. Одно из них будет содержать три части. Значит, для оставшихся двух долей понадобится шесть частей: 3 + 3 = 6. При этом останется ещё одна доля — третья. Таким образом, выражение семь третьих означает две целые части и ещё одну третью от них. Аналогично из двенадцати четвёртых можно сформировать три целых числа по четыре доли в каждом. То есть дробное отношение 12 / 4 означает, по сути, три целых предмета.
Если провести анализ полученных результатов, то можно сделать вывод о том, что неправильные дроби, могут быть представлены в двух видах:
- натуральным числом — в случае когда числитель количественно совпадает со знаменателем;
- суммой правильной дроби и простого числа — если делимое не делится нацело на делитель.
Как и любое число, дробь может быть положительной и отрицательной. В первом случае она обозначает изменение чего-то в сторону увеличения, а во втором — уменьшения. Например, -6 / 5 может обозначать недостачу равную шесть пятых.
Особенный интерес вызывает представление неправильной дроби в виде суммы натурального числа и правильной части. Это действие называется выделением целой доли из неправильного отношения. Причём такая операция может быть выполнена и в обратном направлении — трансформация выражения в смешанное.
Превращение дробей
По смыслу неправильные выражения представляют собой целую и дробную часть, записанную в виде отношения. Поэтому любую смешанную дробь можно превратить в правильную, и наоборот. Деление целого числа на такое же можно объяснить так. Пусть нужно разделить четыре на пять. Значит, единицу понадобится разделить на пять равных частей, то есть 1 / 5. Четыре же единицы дадут 1 / 5 + 1/ 5 + 1 / 5 + 1 / 5 = 4 / 5. В этом случае получается правильное выражение. Но бывает, что числитель количественно превышает знаменатель. Значит, для более понятной формы записи нужно из такого выражения выделить целую часть.
Например, нужно преобразовать число 25 / 8. Это действие подразумевает нахождение целых единиц, содержащихся в выражении. Рассуждать нужно следующим образом. Одна единица может быть представлена как 8 / 8, две — 16 / 8, три — 24 / 8. Значит, число состоит из трёх единиц и оставшейся 1 / 8 части. Поэтому записать его можно так: 3 (1 / 8).
Поняв смысл такого перехода, можно выполнить превращение и в обратную сторону. Чтобы разобраться, как это сделать лучше, проще рассмотреть пример. Пусть имеется смешанное число 4 (5/8), его нужно превратить в неправильную дробь. Иными словами, определить, сколько восьмых долей содержится в четырёх и пяти восьмых. Так как одной единице соответствует 8 / 8, то четырём — 8 * 4 / 8 = 32 / 8. Соответственно в четырёх и 5 / 8 будет 37 / 8 долей.
Такого вида преобразования часто приходится выполнять при решении примеров с дробями в 5 классе. Поэтому понять принцип превращения лучше всего на конкретное задание. При этом можно использовать следующий алгоритм:
- перемножить единицы целой части со знаменателем дробного числа;
- сложить полученное произведение и числитель дроби;
- результат сложения записать в числитель, а знаменатель оставить без изменений.
Итак, пусть имеется выражение 3 (5 / 7). Так как фактически это сумма трёх и пяти седьмых, то следуя алгоритму, можно решение расписать так: 3 + 5 / 7 = (3 * 7 + 5) / 7 = (21 + 5) / 7 = 26 / 7. Аналогичный результат мог быть получен при простом сложении двух частей смешанного числа: 3 / 1 + 5 / 7 = (3 * 7) / 1 * 7 + 5 / 7 = 21 / 7 + 5 / 7 = (21 + 5) / 7 = 26 / 7. Первый вариант, конечно же, более удобен. Его можно выразить формулой: a (c / d) = (a * d + c) / d.
Эту выражение нужно обязательно запомнить, так как его придётся довольно часто использовать при решении задач различной сложности.
Выполнение действий
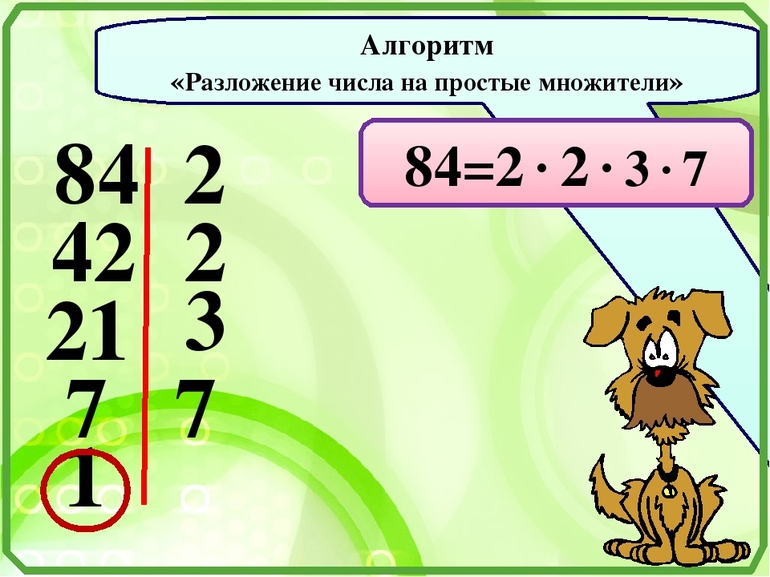
Отличие неправильной дроби от правильной заключается в том, что первая равна или больше единицы, а вторая меньше её. Поэтому правило выполнения арифметических действий одинаковое для этих двух групп. Для того чтобы ребёнок понял, как правильно решать простые и сложные задания объяснение в 5 классе неправильных дробей и действий над ними начинают с повторения правила разложения числа на простые множители.
Выполняется оно за несколько шагов. Вначале ищут минимальную величину, на которую можно разделить исходное без остатка. Далее, находят результат деления и повторяют действие, но уже для полученного числа. Операцию повторяют до тех пор, пока в ответе не получится единица.
Разложение на простые множители используется при поиске наименьшего знаменателя при сложении или вычитании неправильных дробей с разными делителями. Существует алгоритм, придерживаясь которого можно выполнить любое арифметическое действие над двумя и более дробными выражениями. Он заключается в следующем:
- исследовать числитель и знаменатель на возможность сокращения;
- определить наименьший общий знаменатель (НОЗ) среди делителей;
- найти дополнительные множители;
- выполнить умножение числителей на найденные аргументы;
- в знаменатель записать НОЗ, а в числитель сумму или разность произведений делимых.
Например, 4 / 3 + 9 / 7 = (7 * 4) / 21 + (3 * 9) / 21 = 28 / 21 + 27 / 21 = (28 + 27) / 21 = 55 / 21 = 2 (13 / 21) и 56 / 9 — 6 / 9 = (56 — 6) / 9 = 50 / 9 = 5 (5 / 9).
Неправильные выражения можно не только складывать, но и вычитать. Для того чтобы их перемножить следует отдельно найти произведение делимых и делителей. Затем в числитель записать первый результат, а в знаменатель второй. То есть действие нужно выполнять по формуле: f / n * s / m = (f * s) / (n * m). Выполнить деление также просто. Для этого действия в вычитаемом выражении меняется местами аргументы и выполняется умножение: (f / n) / (s / m) = (f * m) / (n * s).
Возведение в степень и извлечение корня выполняют способом разделения. То есть, делимое от делителя возводится или извлекается отдельно: (s / m) j = sj / mj и √(s / m) = √s / √m. Например, 3 / 2 * 9 / 6 : 7 / 5 * (3 / 2)3. С какого действия начинать решение не принципиально, но следует обратить внимание, что 9 / 6 можно сократить на три. В итоге получится 9 / 6 = 3 / 2. Далее, решение будет выглядеть следующим образом: 3 / 2 * 3 / 2 : 7 / 5 * 3 3 / 23 = (3 * 3) / (2 * 2): 7 / 5 * 27 / 8 = 9 / 4 * 5 / 7 * 27 / 8 = (9 * 5 * 27) / (4* 7 * 
Дроби
Содержание:
- Что такое дробь
- Основные свойства дробей
-
Виды
- Правильные дроби
- Неправильные дроби
- Смешанные дроби
- Как перевести правильную дробь в неправильную
-
Действия с дробями, как решать примеры
- Приведение к общему знаменателю
- Сравнение
- Сложение и вычитание
- Умножение и деление
Что такое дробь
Дробь — это число, состоящее из одной или нескольких частей единицы. Обыкновенные дроби записываются в формате (frac mn), где «—» — это дробная черта; n — знаменатель; а m — числитель. Такая запись читается как «m-энных».
Дроби нужны для обозначения нецелых количеств. Они образуются как результат деления натуральных чисел, когда делимое не кратно делителю.
Дробная черта равносильна знаку деления. То есть (4:6=frac46) (четыре шестых), (7:2=frac72) (семь вторых). Числитель дроби играет роль делимого, а знаменатель — делителя.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Знаменатель дроби не может быть нулем.
Основные свойства дробей
- Дробь является видом записи числа. Одно и то же число можно записать в виде разных дробей.
- Если умножить числитель и знаменатель на одинаковую величину, то значение дроби останется прежним, хотя дроби разные: (frac pr=frac{ccdot p}{ccdot r}.)
Например, (frac34=frac68=frac9{12}.) - И обратно, если числитель и знаменатель имеют общий делитель, то обе части можно разделить на него. Такая операция называется сокращением дроби: (frac{12}{16}=frac{12:4}{16:4}=frac34.)
Определение
Несократимой называют дробь, числитель и знаменатель которой взаимно просты, то есть не имеют общих делителей, кроме 1 (-1).
Виды
Существует два вида дробей: правильные и неправильные.
Неправильные дроби всегда больше правильных: (frac{39}{40}<frac32, frac67<frac33.)
Правильные дроби
Определение
Правильная дробь — это обыкновенная дробь, числитель которой меньше знаменателя.
Правильная дробь называется так, поскольку выражает «правильную» часть единицы, то есть часть, которая меньше целого:( frac25<1, frac{99}{100}<1.)
Пример:
Рассмотрим дробь (frac56), у которой 5 — это числитель, а 6 — знаменатель.Сравним числитель со знаменателем: 5<6. Так как числитель меньше знаменателя, дробь является правильной.
Неправильные дроби
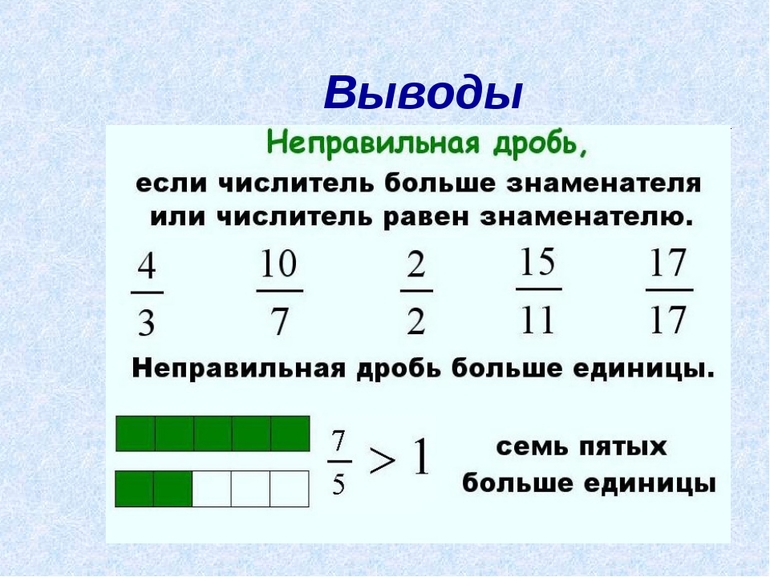
Неправильная дробь — это обыкновенная дробь, числитель которой больше или равен знаменателю. Эти дроби всегда больше или равны единице: (frac73>1, frac{14}8>1, frac55=1.)
Пример:
Рассмотрим дробь (frac65), у которой 6 — это числитель, а 5 — знаменатель. 6>5, значит, данная дробь является неправильной.
Таким образом, отличить правильную дробь от неправильной можно при сравнении дробей с единицей. Это различие не влияет на арифметические действия, но важно при сравнении дробей.
Смешанные дроби
Неправильные дроби не принято оставлять в результате вычислений. Лучше преобразовывать их в смешанные числа. Любую неправильную дробь можно представить в виде смешанного числа.
Определение
Смешанное число — это число, содержащее целую и дробную часть.
Для составления смешанной дроби необходимо:
- Выделить наибольшее целое число, содержащееся в неправильной дроби. Для этого нужно разделить числитель на знаменатель. Получившееся частное без остатка является целой частью смешанной дроби: (frac{40}5=40:5=8).
- Если в результате деления есть остаток, то этот остаток становится числителем дробной части. Знаменатель дробной части останется частным. (frac{42}5=8frac25)
Задача
Записать неправильную дробь (frac{18}4) в виде смешанной.
Решение
Выделим целую часть смешанной дроби. Чтобы сделать это, необходимо числитель дроби, 18, поделить на ее знаменатель, 4:
Итак, получаем, что (frac{18}4=18:4=4), остаток 2.
Тогда искомая смешанная дробь (frac{18}4=4frac24.) Эту дробь можно сократить, поделив числитель и знаменатель дробной части на общий делитель 2:
(4frac24=4frac{2:2}{4:2}=4frac12)
Ответ: (4frac12.)
Примечание
Смешанное число можно записать в виде неправильной дроби. Для этого необходимо целую часть умножить на знаменатель дробной части. К полученному числу нужно прибавить числитель дробной части. Эту сумму записать в числитель, а знаменатель дробной части оставить без изменений.
Задача
Смешанное число (6frac25) записать в виде неправильной дроби.
Решение
(6frac25=frac{6cdot5+2}5=frac{32}5)
Ответ: (frac{32}5)
Как перевести правильную дробь в неправильную
Перевести правильную дробь в неправильную или наоборот невозможно. Это разные категории чисел.
Любое натуральное число можно представить в виде неправильной дроби: (2=frac21.)
Дробь с числителем p и знаменателем 1 — это другая форма записи натурального числа p. Это правило можно представить в виде формулы: (p=frac p1.)
Число 0 считают равным дроби вида (frac0q), где q — любое натуральное число:
(0=frac01=frac02=dots=frac0q)
Действия с дробями, как решать примеры
Приведение к общему знаменателю
Определение
Чтобы решать большинство примеров с дробями, необходимо приводить их к общему знаменателю. Чтобы привести дроби (frac ab) и (frac cd) к общему знаменателю, необходимо:
- Найти наименьшее общее кратное (НОК) обоих знаменателей: (M=left[b,dright].)
- Умножить числитель и знаменатель первой дроби на M/b: (frac{acdotfrac Mb}{bcdotfrac Mb}.)
- Умножить числитель и знаменатель второй дроби на M/d: (frac{ccdotfrac Md}{dcdotfrac Md}.)
Пример:
Необходимо привести к общему знаменателю дроби (frac34) и (frac13). Действуем по алгоритму:
- Находим НОК. У чисел 4 и 3 им является число 12.
- Умножаем числитель и знаменатель первой дроби на (frac{12}4), то есть 3: (frac{3cdot3}{4cdot3}=frac9{12}).
- Умножаем числитель и знаменатель второй дроби на (frac{12}3), то есть 4: (frac{1cdot4}{3cdot4}=frac4{12}).
Ответ: (frac9{12}, frac4{12}.)
Сравнение
Определение
Чтобы сравнить обыкновенные дроби, следует привести их к общему знаменателю и сравнить числители. Дробь с большим числителем больше.
Пример:
(frac34>frac13,) поскольку (frac9{12}>frac4{12}.)
Примечание
Если сравниваются смешанные числа, в первую очередь необходимо смотреть на целую часть. Больше то число, целая часть которого больше.
К примеру, (8frac16>5frac23.)
Если целые части смешанных чисел равны, то сравнивают дробные части по правилу сравнения обыкновенных дробей. Число с наибольшей дробной частью будет больше: (5frac23>5frac13.)
Сложение и вычитание
Определение
Чтобы сложить обыкновенные дроби, необходимо привести их к общему знаменателю, сложить числители, а знаменатели оставить без изменений. При необходимости привести дробь в вид смешанного числа.
Пример:
(frac34+frac13=frac9{12}+frac4{12}=frac{13}{12}=1frac1{12})
Примечание
При сложении смешанных чисел целые и дробные части складываются отдельно.
(5frac13+4frac16=9frac{2cdot1+1}6=9frac36=9frac12)
Определение
Чтобы вычесть одну дробь из другой, также необходимо привести их к общему знаменателю, после чего вычесть числители, а знаменатели оставить без изменений.
Пример:
(frac12-frac13=frac{3-2}6=frac16)
Умножение и деление
Определение
Чтобы умножить обыкновенные дроби, необходимо перемножить их числители и знаменатели.
(frac abcdotfrac cd=frac{ac}{bd})
Задача
Умножить дробь (frac35) на (frac23.)
Решение
(frac35cdotfrac23=frac{3cdot2}{5cdot3}=frac6{15}=frac25)
Ответ: (frac25)
При умножении дроби на натуральное число, нужно умножить числитель на это число, а знаменатель оставить тем же. Так происходит, поскольку любое натуральное число можно представить в виде (p=frac p1.)
(frac abcdot p=frac abcdotfrac p1=frac{ap}b.)
Примечание
Чтобы умножить смешанные числа, необходимо сперва представить их в виде обыкновенных дробей и лишь затем совершать действие.
(2frac13cdot3frac12=frac73cdotfrac72=frac{49}6=8frac16)
Определение
Чтобы поделить одну дробь на другую, нужно умножить первую дробь на дробь, обратную второй. При этом оба знаменателя и числитель второй дроби не должны быть равны нулю.
(frac ab:frac cd=frac abcdotfrac dc=frac{ad}{bc}.)
Задача
Поделить дробь (frac34) на (frac23.)
Решение
(frac34:frac23=frac34cdotfrac32=frac{3cdot3}{4cdot2}=frac98=1frac18)
Ответ: (1frac18)
Примечание
При делении смешанных чисел, как и при умножении, их необходимо сперва привести к виду обыкновенной дроби.
(2frac13:1frac16=frac73:frac76=frac{7cdot6}{3cdot7}=frac63=2)
Содержание:
- Правильные и неправильные дроби
- Смешанные дроби
Правильные и неправильные дроби
Например. Дробь $frac{11}{23}$ является правильной,
так как ее числитель, равный 11, меньше, чем знаменатель, который равен 23: 11
Определение
Дробь называется неправильной, если ее числитель больше знаменателя или равен ему.
Например. Дробь $frac{23}{11}$ — неправильная,
так как 23 > 11 . Дробь $frac{3}{3}$ — неправильная, так как числитель дроби равен ее знаменателю.
Смешанные дроби
Определение
Числа, в состав которых входит целое число и правильная дробь, называются смешанными числами.
Целое число называют целой частью смешанного числа, а правильная дробь называется дробной частью смешанного числа.
Например. Для смешанной дроби $3 frac{11}{23}=3+frac{11}{23}$
число 3 — целая часть, $frac{11}{23}$ — дробная.
Неправильную дробь можно записать в виде смешанного числа, для этого нужно
числитель поделить на
знаменатель.
Полученное неполное частное будет целой частью смешанной дроби, остаток — числителем дробной части, а знаменатель
исходной неправильной дроби — знаменателем дробной части.
Пример
Задание. Записать неправильную дробь
$frac{20}{3}$ в виде смешанной.
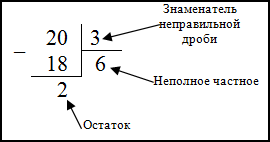
Решение. Поделим числитель дроби — 20 на ее знаменатель — 3 (то есть выделим целую часть):
Итак, получаем, что $frac{20}{3}=20 : 3=$ 6 (остаток 2).
А тогда искомая смешанная дробь
$frac{20}{3}=6 frac{2}{3}$
Ответ. $frac{20}{3}=6 frac{2}{3}$
Чтобы смешанное число записать в виде неправильной дроби, надо целую часть умножить на знаменатель
дробной части, к полученному числу прибавить числитель дробной части и записать эту сумму в числитель,
а знаменатель дробной части оставить без изменений.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Смешанное число
8$frac{2}{3}$ записать в виде неправильной дроби.
Решение. $8 frac{2}{3}=frac{8 cdot 3+2}{3}=frac{26}{3}$
Ответ. $8 frac{2}{3}=frac{26}{3}$
Читать следующую тему: сравнение дробей.

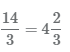
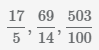 в смешанные числа.
в смешанные числа.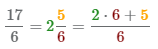
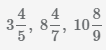 в неправильные дроби.
в неправильные дроби.