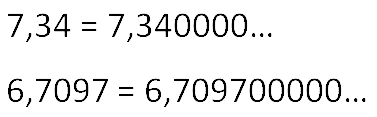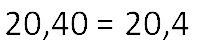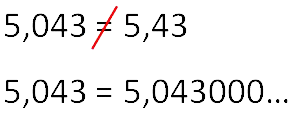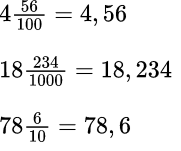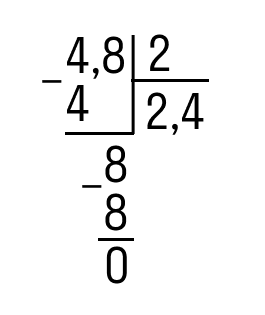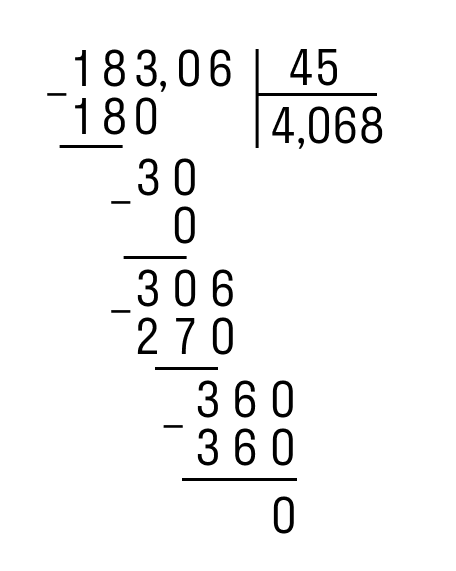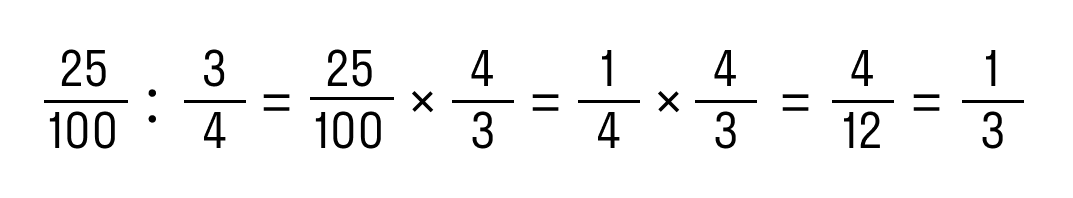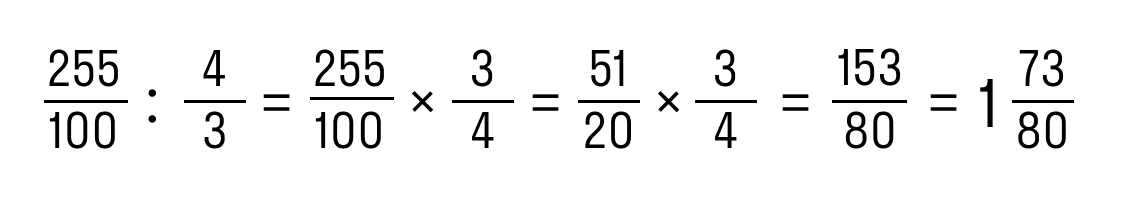Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Как читать десятичные дроби
Поддержать сайт
В первую очередь обсудим вид десятичной дроби.
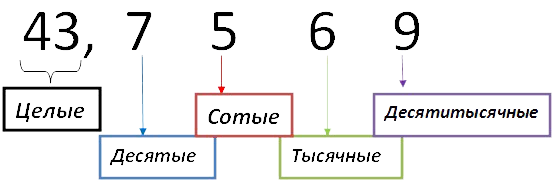
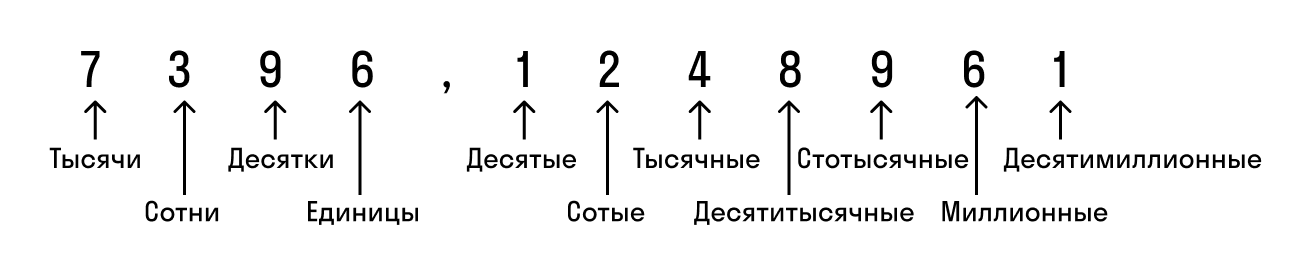
Каждая цифра после запятой имеет своё название.
Десятые, сотые, тысячные, десятитысячные…
Десятые, сотые и тысячные
Попробуем прочитать десятичную дробь из примера выше.
Чтобы правильно прочитать десятичную дробь нужно:
-
Прочитать число слева от запятой и добавить слово «целыx», так как слева от запятой находится
целая часть десятичной дроби. Читаем: «сорок три целых». -
Затем прочитать число справа от запятой: «семь тысяч пятьсот шестьдесят девять».
-
Добавить в конце название самой правой цифры.
У нас это
9, которая стоит на месте десятитысячных
(см. рис. выше):
«десятитысячных».
Значит, полное название дроби звучит так:
43,7569 — сорок три целых семь тысяч пятьсот шестьдесят девять десятитысячных.
Справа от запятой после самой последней
правой цифры отличной от нуля можно добавлять сколько угодно
нулей. От этого значение десятичной дроби не изменится.
Таким же образом если в конце десятичной дроби отбросить ноль, то мы получим
такую же по значению десятичную дробь.
Поэтому, если при расчётах получили десятичную дробь 20,40 , отбрасываем
ноль на конце и записываем:
Запомните!
Нули можно добавлять (убирать) только после самой последней правой отличной от нуля
цифры. Нули между цифрами в числе убирать нельзя.
Как читать десятичные дроби
В первую очередь обсудим вид десятичной дроби. Каждая цифра после запятой имеет своё название.
Десятые, сотые, тысячные, десятитысячные…
Десятые, сотые и тысячные
Попробуем прочитать десятичную дробь из примера выше. Чтобы правильно прочитать десятичную дробь нужно:
Прочитать число слева от запятой и добавить слово «целыx», так как слева от запятой находится целая часть десятичной дроби. Читаем: «сорок три целых».
Затем прочитать число справа от запятой: «семь тысяч пятьсот шестьдесят девять».
Добавить в конце название самой правой цифры.
У нас это 9 , которая стоит на месте десятитысячных (см. рис. выше): «десятитысячных».
Значит, полное название дроби звучит так:
43,7569 — сорок три целых семь тысяч пятьсот шестьдесят девять десятитысячных.
Справа от запятой после самой последней правой цифры отличной от нуля можно добавлять сколько угодно нулей. От этого значение десятичной дроби не изменится.
Таким же образом если в конце десятичной дроби отбросить ноль, то мы получим такую же по значению десятичную дробь.
Поэтому, если при расчётах получили десятичную дробь 20,40 , отбрасываем ноль на конце и записываем:
Нули можно добавлять (убирать) только после самой последней правой отличной от нуля цифры. Нули между цифрами в числе убирать нельзя.
Источник статьи: http://math-prosto.ru/?page=pages/decimal/decimal2.php
Чтение десятичных дробей
Десятичная дробь в обязательном порядке содержит запятую. Та числовая часть дроби, которая располагается левее запятой, называется целой; правее – дробной:
Дробная часть десятичной дроби состоит из десятичных знаков (десятичных разрядов):
- десятые – 0,1 (одна десятая);
- сотые – 0,01 (одна сотая);
- тысячные – 0,001 (одна тысячная);
- десятитысячные – 0,0001 (одна десятитысячная);
- стотысячные – 0,00001 (одна стотысячная);
- миллионные – 0,000001 (одна миллионная);
- десятимиллионные – 0,0000001 (одна десятимиллионная);
- стомиллионные – 0,00000001 (одна стомиллионная);
- миллиардные – 0,000000001 (одна миллиардная) и т. д.
Как правильно читать десятичную дробь:
- прочитать число, составляющее целую часть дроби и добавить слово “целых“;
- прочитать число, составляющее дробную часть дроби и добавить название младшего разряда.
- 0,25 – ноль целых двадцать пять сотых;
- 9,1 – девять целых одна десятая;
- 18,013 – восемнадцать целых тринадцать тысячных;
- 100,2834 – сто целых две тысячи восемьсот тридцать четыре десятитысячных.
Запись десятичных дробей
Чтобы записать десятичную дробь, необходимо:
- записать целую часть дроби и поставить запятую (число, означающее целую часть дроби всегда заканчивается словом “целых“);
- записать дробную часть дроби таким образом, чтобы последняя цифра попала в нужный разряд (при отсутствии значащих цифр в определенных десятичных разрядах они заменяются нулями).
- двадцать целых девять десятых – 20,9 – в этом примере все просто;
- пять целых одна сотая – 5,01 – слово “сотая” означает, что после запятой должны стоять две цифры, но, поскольку в числе 1 нет разряда десятых, он заменяется нулем;
- ноль целых восемьсот восемь тысячных – 0,808;
- три целых пятнадцать десятых – такую десятичную дробь записать невозможно, потому, что в произношении дробной части допущена ошибка – число 15 содержит два разряда, а слово “десятых” подразумевает только один. Правильно будет три целых пятнадцать сотых (или тысячных, десятитысячных и т. д.).
Сравнение десятичных дробей
Сравнение десятичных дробей проводится аналогично сравнению натуральных чисел.
- сначала сравниваются целые части дробей – больше будет та десятичная дробь у которой больше ее целая часть;
- если целые части дробей равны, сравнивают поразрядно дробные части, слева направо, начиная от запятой: десятые, сотые, тысячные и т.д. Сравнение ведут до первого несовпадения – больше будет та десятичная дробь у которой будет больше неравная цифра в соответствующем разряде дробной части. Например: 1,283 > 1,279, т. к. в сотых разрядах у первой дроби стоит 8, а у второй 7.
Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:
Код кнопки: 
Политика конфиденциальности Об авторе
Источник статьи: http://prosto-o-slognom.ru/matematika/007-desyatichnaya_drob.html
СПАДИЛО.РУ
теория по математике 📈 числа и вычисления
Десятичная дробь — дробь, которая представляет собой способ представление числа в виде записи числа с запятой, где цифры перед запятой называются целой частью, а цифры после запятой – дробной частью (десятичной частью).
Десятичные дроби получают из записи обыкновенных дробей со знаменателем 10, 100, 1000 и так далее. Например, десятичные дроби:
4,56 – четыре целых пятьдесят шесть сотых 18,234 – восемнадцать целых двести тридцать четыре тысячных 78,6 – семьдесят восемь целых шесть десятых
Чтение десятичных дробей
Чтение десятичной части (десятых, сотых и так далее) зависит от количества цифр после запятой. Если цифра одна, то читают – десятых (в числе десять — один нуль, это соответствует одной цифре). Если две цифры после запятой, то читают – сотых (в сотне два нуля).
Десятичные дроби получаются из обыкновенных дробей:
Сложение (вычитание) десятичных дробей
Чтобы сложить (вычесть) в столбик две десятичные дроби нужно:
- Записать их друг под другом так, чтобы при записи запятая оказалась под запятой и соответствующий разряд под соответствующим.
- Уравнять количество знаков после запятой, добавляя недостающие нулями.
- Выполнить сложение (вычитание) в столбик, не обращая внимания на запятую.
- Поставить запятую под запятыми.
Если складывают (вычитают) целое число и десятичную дробь, то нужно поставить запятую после целого числа и приписать необходимое количество нулей после запятой.
Пример №1. Запись, где запятая под запятой и соответствующий разряд под соответствующим.
34,145 + 5,678 = 39,823
Пример №2. Запись, где также запятая под запятой, а во втором числе дописан нуль, чтобы уравнять количество знаков после запятой.
Пример №3. В первом слагаемом нет десятичной части, поэтому, после числа 56 поставили запятую и добавили нужное количество нулей.
Умножение десятичных дробей
При умножении двух десятичных дробей в столбик необходимо:
- Написать числа одно под другим, не обращая внимания на запятую
- Выполнить умножение в столбик
- В ответе отделить столько цифр справа запятой, сколько их в обоих множителях вместе. Если в одном из чисел нет запятой, то считать цифры только в одном числе.
Пример №4. Запись выполнена так, что цифры по правому краю записаны ровно одна под одной, то есть как при обычном умножении чисел в столбик. Умножение выполнено без учета запятой. В ответе справа отделены 4 цифры запятой, так как в первом множителе их 3 после запятой, а во втором – одна, в двух множителях вместе – четыре.
0,125 × 2,3 00375 0250 0,2875
Пример №5. Здесь показано умножение десятичной дроби и целого числа. Умножение выполнено без учета запятой. В ответе отделена справа запятой только одна цифра, так как только в первом множителе есть десятичная часть с одной цифрой после запятой.
Умножение десятичных дробей на 10, 100, 1000…
Чтобы умножить десятичную дробь на 10, 100, 1000 и так далее, нужно перенести запятую вправо на столько цифр, сколько нулей у множителя. Умножение в данном случае выполняется в строчку.
Пример №6. 2,456 × 10 = 24,56 Запятую в десятичной дроби перенесли вправо на 1 цифру, так как у 10 один нуль.
Пример №7. 0,45678 × 100 = 45,678 Запятую перенесли вправо на 2 цифры, так как у 100 два нуля. Нуль, стоящий в начале десятичной дроби, убрали, так как впереди целой части, отличной от нуля он не пишется.
Пример №8. 9,46 × 1000 = 9460 в данном случае при переносе запятой на три цифра не хватило одной, поэтому в конце числа приписали нуль, и в ответе получилось целое число.
Умножение десятичной дроби на разрядную единицу 0,1; 0,01; 0,001…
При умножении десятичной дроби на разрядную единицу 0,1; 0,01; 0,001 (и так далее) нужно перенести запятую на столько цифр влево, сколько цифр в данной разрядной единице после запятой. Умножение обычно выполняется в строчку устно.
Пример №9. 983,7821 × 0,01= 9,837821 Переносим запятые влево на 2 цифры, так как в числе 0,01 две цифры после запятой.
Пример №10. 8,7654 × 0,1 = 0,87654 Перенесли на 1 цифру влево, так как в числе 0,1 одна цифра после запятой. В данном случае перед 8 появился нуль, так как при переносе запятой слева цифр не оказалось.
Пример №11. 7,98 × 0,0001 = 0,000798 При переносе влево на 4 цифры не хватило трех, поэтому впереди поставили нули, а также нуль образуется и в целой части.
Деление десятичных дробей
- При делении десятичной дроби на целое число выполняют сначала деление целой части, а затем десятичной.
- При делении десятичной дроби на другую десятичную дробь необходимо в делителе убрать запятую, а в делимом передвинуть ее вправо на столько цифр, сколько их в делителе после запятой. Затем выполнить деление на целое число.
- Есть случаи, когда цифр после запятой при переносе запятой у дроби не хватает. Тогда необходимо дополнить число нулями.
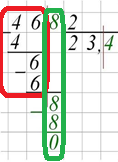
Пример №12. Деление десятичной дроби на целое число. 46,8 : 2 = 23,4
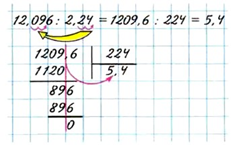
Пример №13. Деление десятичной дроби на десятичную дробь. 12,096 : 2,24 = 5,4 Из данного примера видно, что деление десятичных дробей обязательно сводится к делению на целое число.
Пример №14. 276,3 : 0,003 = 276300 : 3 = 92100. Здесь видно, что не хватает двух цифр в числе 276,3 и поэтому при переносе запятой к нему приписали два нуля. Затем выполнили деление двух целых чисел.
Деление десятичной дроби на 10, 100, 1000…
При делении десятичной дроби на 10,100, 1000 и так далее нужно перенести запятую на столько цифр влево, сколько нулей в данном числе. Деление выполняется в строчку устно.
Пример №16. 134,987 : 1000 = 0,134987 Перенесли запятую на три цифры влево, так как у 1000 три нуля. В целой части поставили нуль, так как цифр не хватило.
Пример №17. 7,234 : 100 = 0,07234 Перенесли запятую влево на две цифры. Так как цифр не хватало, то недостающие заменили нулями.
Деление десятичной дроби на разрядную единицу 0,1; 0,01; 0,001…
При делении десятичной дроби на разрядную единицу 0,1; 0,01; 0,001 и так далее нужно перенести запятую на столько цифр вправо, сколько цифр в данной разрядной единице после запятой. Деление обычно выполняется в строчку устно.
Пример №19. 41,234 : 0,01 = 4123,4 Перенос запятой на 2 цифры вправо, так как в числе 0,01 две цифры после запятой.
Пример №20. 56,91 : 0,001 = 56910 При переносе запятой на три цифры вправо приписали один нуль, так как одной цифры не хватило.
Источник статьи: http://spadilo.ru/desyatichnye-drobi/
Десятичная дробь, как и любое число, состоит из цифр ((0), (1), (2), (3), (4), (5), (6), (7), (8), (9)).
Место каждой цифры в числе важно: оно определяет разряд числа.
Десятичная дробь состоит из целой части (все цифры до запятой) и дробной части (все цифры после запятой).
Целую часть десятичной дроби можно разбить на разряды так же, как и натуральные числа: единицы, десятки, сотни, тысячи и т. д.
Дробную часть десятичной дроби разбивают на разряды так:
десятые (в знаменателе обыкновенной дроби (10)), сотые (в знаменателе обыкновенной дроби (100)), тысячные (в знаменателе обыкновенной дроби (1000)) и т. д.
Таблица разрядов
| Тысячи | Сотни | Десятки | Единицы, | Десятые | Сотые | Тысячные | Десятитысячные |
Таблицу разрядов можно дополнить любым нужным количеством столбцов.
(1)-й разряд после запятой — разряд десятых,
(2)-й разряд после запятой — разряд сотых,
(3)-й разряд после запятой — разряд тысячных,
(4)-й разряд после запятой — разряд десятитысячных,
(5)-й разряд после запятой — разряд стотысячных,
(6)-й разряд после запятой — разряд миллионных,
(7)-й разряд после запятой — разряд десятимиллионных,
(8)-й разряд после запятой — разряд стомиллионных.
Пример:
запишем в таблицу разрядов числа: (25,5701); (13,827); (3,9); (48,65).
| Десятки | Единицы, | Десятые | Сотые | Тысячные | Десятитысячные | |
| (25,5701) |
(2) |
(5) |
(5) |
(7) |
(0) |
(1) |
| (13,827) |
(1) |
(3) |
(8) |
(2) |
(7) |
|
| (48,65) |
(4) |
(8) |
(6) |
(5) |
||
| (3,9) |
(3) |
(9) |
Как прописать сумму в тысячах?
Сумма пишется с заглавной буквы, значение суммы в рублях и копейках не разделяется запятой или другим знаком препинания (точка, скобка). Например: «Двадцать тысяч пятьсот один рубль 51 копейка”. Если нужно указать число копеек в сумме, пишите их после запятой или точки в составе числа.
Как миллион записать в тысячах рублей?
1 миллион = 1000 тысяч
Смотрите также — универсальный калькулятор чисел.
Как правильно читать тыс руб?
традиционно тысяча сокращается до тыс., а рубли до руб. Поэтому лучше написать 100 тыс. руб.
Что такое число с одним десятичным знаком?
ДЕСЯТИЧНЫЙ ЗНАК, число знаков справа от десятичной запятой, необходимое для представления действительного числа (см. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА) с определенной точностью. Например, число 4,893302 с точностью до третьего знака записывается как 4,893. С точностью до пятого десятичного знака оно будет записано как 4,89330.
Как написать сумму в рублях?
Сумма пишется с заглавной буквы, значение суммы в рублях и копейках не разделяется запятой или другим знаком препинания (точка, скобка). Например: “Двадцать тысяч пятьсот один рубль 51 копейка”. Если нужно указать число копеек в сумме, пишите их после запятой или точки в составе числа.
Как правильно писать цифры словами?
Основные правила написания числительных словами
- В конце всех числительных от 5 до 20 и 30 пишется буква ь. …
- В числительном 4 при написании прописью используется две буквы е: четыре.
- Числительные от 9 до 19 заканчиваются на –ять, -ать: девять, двадцать, восемнадцать.
Как сократить миллион в цифрах?
Что касается сокращений счетных числительных, то устойчивые написания существуют: «млн» вместо «миллиона» или «млрд» вместо «миллиарда».
Сколько будет нулей в миллионе?
В десятичной системе счисления изображается единицей с шестью нулями (1000000), и 106.
Как правильно написать сумму прописью в скобках?
Сумма пишется с заглавной буквы, значение суммы в рублях и копейках не разделяется запятой или другим знаком препинания (точка, скобка). Например: “Двадцать тысяч пятьсот один рубль 51 копейка”. Если нужно указать число копеек в сумме, пишите их после запятой или точки в составе числа.
Какие цифры есть?
Цифры
- римские цифры: I V X L C D M.
- шестнадцатеричные цифры: 0 1 2 3 4 5 6 7 8 9 A B C D E F.
- цифры майя: от 0 до 19.
- в некоторых языках, например, в церковнославянском, древнегреческом, иврите и др., существует система записи чисел буквами
Как правильно написать дробное число прописью?
Дробные числительные словами
Слова данной группы записываются так же, как аналогичные им количественные и порядковые числительные: одна целая две сотых, две третьи, три четвёртых, семь восьмых, двенадцать пятнадцатых и т. д. Порядковые числительные в обозначениях дробных чисел употребляются в форме Р. п.
Округление числа означает введение ограничения числа цифр (отдельных чисел), которые используются при учетной записи числа. Существуют определенные правила, которые помогают решить, в каких случаях числа должны быть округлены, и как они должны быть округлены. Этот раздел поможет Вам понять эти правила и корректно применять их.
Проводя вычисления, числа, которые Вы используете в своей работе, будут представляться в одной из следующих форм:
- Целые числа 1;32;512
- Десятичные дроби с целой частью 2,5;40,67;600,2
- Простые десятичные дроби 0,1;0,03;0,007
- Обыкновенные дроби
Для удобства простые дроби будут использоваться только при получении результатов вычислений в разделе «Алгебра» данного модуля. Обыкновенные дроби могут быть преобразованы в десятичные дроби, путем деления числа, находящегося выше черты (числитель), на число, находящееся ниже черты (знаменатель). Например, могут быть записаны, как 3 ¸ 4 = 0,75.
В данном материале десятичные знаки будут обозначаться запятой ‘ , ‘, например, 2,1 (в англоязычной литературе используется ‘ . ’). Тысячи будут отмечаться интервалом между цифрами, изображающими сотни и тысячи, например, 13 456 означает тринадцать тысяч четыреста пятьдесят шесть.
1.1 Значащие цифры
Число цифр, которые должны быть оставлены для выражения результата вычисления, зависит от типа (этапа) вычисления и от его необходимой точности. Одним из способов ее установления является принятие решения о числе значащих цифр, подлежащих сохранению. ‘0’ не является значащей цифрой, если только он не стоит между двумя другими числами, например, 103, или если он не является последним десятичным знаком, например, 2,10. (Оба эти числа являются примерами чисел с тремя значащими цифрами). Например, число 13 456 с точностью до двух значащих чисел может быть записано как 13 000 (отметим, что нули не являются здесь значащими цифрами). Этот способ записи является удобным для представления результата, однако он не указывает на размер ответа. Например, 13 000 и 2,1 могут оба представлять результат округления до двух значащих цифр. Число значащих цифр может, однако, быть показателем точности задания числа. Это является одним из основных факторов, определяющих сколько значащих цифр следует удерживать.
1.2 Как пользоваться округлением
Округление может быть осуществлено путем учета необходимого количества значащих цифр, как это обсуждалось в последнем параграфе, либо как резервирование десятичных разрядов. Число десятичных разрядов есть число десятичных знаков после запятой. Например, число 2,10 имеет два десятичных разряда (но три значащие цифры).
В обычной практике округление производится с повышением, если цифра, подлежащая округлению, больше, либо равна пяти. Например, числа 2,55, 2,56, 2,57, 2,58 and 2,59 запишутся как 2,6 при округлении до двух значащих цифр. (или одного десятичного разряда). Числа 2,50, 2,51, 2,52, 2,53 и 2,54 запишутся как 2,5 при округлении до двух значащих цифр (или одного десятичного разряда). Такая операция называется округлением с понижением, и обычно применяется, если цифры не превышают значение 5.
В табл. 1 показано, как используются значащие цифры, десятичные разряды при округлении.
Значащие цифры, десятичные разряды и округление
| Рассчитанноезначение | Число значащих цифр | Число десятичных разрядов | ||||
| Четыре | Три | Два | Четыре | Три | Два | |
| 525,7910 | 525,8 | 526 | 530 | 525,7910 | 525,791 | 525,79 |
| 0,003417 | 0,003417 | 0,00342 | 0,0034 | 0,0034 | 0,003 | 0,00 |
1.3 Когда использовать округление
Существуют две принципиальных причины, почему следует округлять числа, а именно, чтобы
дать ответ, имеющий смысл,
показать точность измерения.
Для некоторых расчетов ответ приобретает смысл, только если результат соотносится с предварительно установленным уровнем значимости. Простым примером этого может служить случай, когда Вы хотите рассчитать число человек, которые могут сидеть вокруг стола в 345 см в окружности. Если каждому отвести по 75 см, то разделив 345 на 75, получится 4,6 человек! Очевидно, 0,6 человека не имеют никакого смысла в случае, когда необходимо знать, сколько человек могут сидеть вокруг стола. Если применить правила округления, приведенные в разделе 1.2, ответ получится равным 5. Но это пример «обычной практики», и не дает очень осмысленный ответ. Пятерым сидеть будет тесно; в этом случае 4 будет лучшим ответом.
Всегда следует думать, что означает ответ с практической точки зрения.
Точность числа может следовать из числа десятичных разрядов значащих цифр, данных в числе. Например, если длина футбольного поля определяется в 110 м, это означает, что это поле измерено с точностью до 10 м. Его действительная длина может иметь значение между 105 м и 114 м. Если же длина поля зарегистрирована как 108,54 м, это означает, что она измерена с точностью до одной сотой метра (сантиметра). Это представляет собой очень точное измерение. Число десятичных разрядов, удерживаемое в этом случае, определяется методом измерения. Очевидно, на имеет смысла принимать 108,54 м за длину футбольного поля, если измерение произведено с помощью мерной ленты, на которой метр является наименьшим делением. Больше смысла будет говорить о величине 109 м, т.е. округлить до одного метра.
1.4 Как определить число десятичных знаков
Существует несколько простых правил, применяемых при установлении, сколько десятичных разрядов или значащих цифр должно быть сохранено в числе. Эти правила таковы:
- Подумайте о смысле полученного ответа. (Как в примере с числом людей, которых можно усадить вокруг стола).
- Если число есть результат расчета, то в нем должно быть сохранено столько десятичных разрядов или значащих цифр, сколько их содержится в наименее точном числе, использованном при вычислении. Например,
2,1 x 3,45 x 1.3 = 9,4185 = 9,4 (округленно)
- Если число является результатом измерения, обратите внимание, как оно получено и какая точность может быть. (Как в примере с футбольным полем.)
- Рассмотрите, с какой точностью необходимо получить результат. (Например, Ответ может быть округлен до ближайшего десятка.)
Научно-технический энциклопедический словарь .
Смотреть что такое «ДЕСЯТИЧНЫЙ ЗНАК» в других словарях:
десятичный знак — десятичная дробь десятичный — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность Синонимы десятичная дробьдесятичный EN decimal … Справочник технического переводчика
Десятичный разделитель — Десятичный разделитель знак, используемый для разделения целой и дробной частей вещественного числа в форме десятичной дроби в системе десятичного исчисления. Для дробей в иных системах счисления может использоваться термин разделитель… … Википедия
Знак процента — % Знак процента Пунктуация апостроф (’ … Википедия
Знак деления — ÷ Знак деления Пунктуация апостроф (’ ) … Википедия
Знак охраны авторского права — © Знак охраны авторского права Пунктуация апостроф ( … Википедия
Знак правовой охраны товарного знака — ® Знак правовой охраны товарного знака Пунктуация апостроф (’ … Википедия
Знак умножения — × • Знак умножения (×) математический знак операции умножения. Знак умножения изображают как крестик (×), точку … Википедия
Десятичный логарифм — График десятичного логарифма Десятичный логарифм логарифм по основанию 10. Другими словами, десятичный логарифм числа … Википедия
Знак градуса — У этого термина существуют и другие значения, см. Градус. ° Знак градуса Пунктуация апостроф … Википедия
Знак равенства — … Википедия
Код по океи 384
Автор Наталья Малеина задал вопрос в разделе Бухгалтерия, Аудит, Налоги
В документе статистики графа «Код по ОКЕИ: тысяча рублей – 384 (с одним десятичным знаком)». и получил лучший ответ
Ответ от Е К[гуру]Все данные в этой отчетности заполняются в тыс. руб с одним знаком после запятой. Например у Вас 1 523 601 в таблицу заносите 1 523,6
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
- 0,8
- 7,42
- 9,932
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
- 0,600 = 0,6
- 21,10200000 = 21,102
| Основные свойства |
|---|
|
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
- Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
- Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде.
- Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
Обучение на курсах по математике — отличный способ закрепить полученные знания на практике и подтянуть сложные темы.
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
Как решаем:
- Знаменатель равен 10 — это один ноль.
- Отсчитываем справа налево в числителе дробной части один знак и ставим запятую.
- В полученной десятичной дроби цифра 1 — целая часть, цифра 6 — дробная часть.
Ответ: 16/10 = 1,6.
Пример 2. Перевести 37/1000 в десятичную дробь.
Как решаем:
- Знаменатель равен 1000 — это три нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Так как в числителе только две цифры, то на пустующие места пишем нули.
- В полученной десятичной дроби цифра 0 — целая часть, 037 — дробная часть.
Ответ: 37/1000 = 0,037.
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
1% = 1/100 = 0,01
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
0,15 = 0,15 · 100% = 15%.
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%
8/25 = 0,32
0,32 · 100% = 32%
Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:
Преобразование десятичных дробей
Быстрая напоминалка:
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!
Пример 1. Перевести 5,4 в смешанное число.
Как решаем:
- Читаем вслух: пять целых четыре десятых. «Четыре десятых» подсказывают, что в числителе будет 4, а в знаменателе — 10. В смешанном виде эта дробь выглядит так: 5 4/10.
- А теперь сократим числитель и знаменатель на два (потому что можно) и получим: 5 2/5.
Ответ: 5,4 = 5 2/5.
Пример 2. Перевести 4,005 в смешанное число.
Как решаем:
- Читаем вслух: четыре целых пять тысячных. Значит 5 — идет в числитель, а 1000 — в знаменатель. В смешанном виде получается так: 4 5/1000. После сокращения: 4 1/200.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
Как решаем:
- Читаем вслух: пять целых шестьдесят сотых. Отправляем 60 в числитель, а 100 — в знаменатель. В смешанном виде дробь такая: 5 60/100.
- Сократим дробную часть на 10 и получим 5 6/10. Или можно вспомнить про свойство десятичной дроби и просто отбросить нули в числителе и знаменателе.
Ответ: 5,60 = 5 6/10.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:
- Перепишем исходную дробь в новый вид: в числитель поставим исходную десятичную дробь, а в знаменатель — единицу. Например:
- 0,35 = 0,35/1
- 2,34 = 2,34/1
- Умножим числитель и знаменатель на 10 столько раз, чтобы в числителе исчезла запятая. При этом после каждого умножения запятая в числителе сдвигается вправо на один знак, а у знаменателя соответственно добавляются нули. На примере легче:
- 0,35 = 0,35/1 = 3,5/10 = 35/100
- 2,34 = 2,34/1 = 23,4/10 = 234/100
- А теперь сокращаем — то есть делим числитель и знаменатель на кратные им числа:
- 0,35 = 35/100, делим числитель и знаменатель на пять, получаем 6/20, еще раз делим на 2, получаем итоговый ответ 3/10.
- 2,34 = 234/100 = 117/50 = 2 17/50.
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Действия с десятичными дробями
С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.
Как разделить десятичную дробь на натуральное число
- Разделить целую часть десятичной дроби на это число.
- Поставить запятую в частном и продолжить вычисление, как при обычном делении.
Пример 1. Разделить 4,8 на 2.
Как решаем:
- Записать деление уголком.
- Разделить целую часть на два. Записать полученный результат в частное и поставить запятую.
- Умножить частное на делитель, записать, посмотреть на остаток от деления. Но мы еще не закончили, поэтому остаток «ноль» не записываем. Сносим 8 и делим её на 2.
- Делим еще раз. Записываем полученную 4 в частном и умножаем её на делитель:
Ответ: 4,8 : 2 = 2,4.
Пример 2. Разделить 183,06 на 45.
Как решаем:
- Записать деление уголком.
- Разделить целую часть 183 на 45. Записать результат, поставить запятую в частном.
- Записать результат разницы 183 и 180. Снести 0. Записать 0 в частное, чтобы снести 6.
- Записать результат разницы 306 и 270. 36 не делится на 45, поэтому добавляем ноль и производим разницу.
Ответ: 183,06 : 45 = 4,068.
Как разделить десятичную дробь на обыкновенную
Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.
Пример 1. Разделить 0,25 на 3/4.
Как решаем:
- Записать 0,25 в виде обыкновенной дроби: 0,25 = 25/100.
- Разделить дробь по правилам:
Ответ: 0,25 : 3/4 = 1/3.
Пример 2. Разделить 2,55 на 1 1/3.
Как решаем:
- Записать 2,55 в виде обыкновенной дроби: 2,55 = 255/1000.
- Записать 1 1/3 в виде обыкновенной дроби: 1 1/3 = 4/3.
- Разделить дробь по правилам:
Ответ: 2,55 : 1 1/3 = 1 73/80.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить 2/5 на 0,8.
Как решаем:
- Записать 0,8 в виде обыкновенной дроби: 0,8 = 8/10.
- Умножаем по правилам: 2/5 ∗ 8/10 = 2/5 ∗ 4/5 = 8/25 = 0,32.
Ответ: 2/5 ∗ 0,8 = 0,32.
Пример 2. Умножить 0,28 на 6 1/4.
Как решаем:
- Записать 6 1/4 в виде десятичной дроби: 6 1/4 = 6,25.
- Умножаем по правилам: 0,28 ∗ 6,25 = 0,8.
Ответ: 0,28 ∗ 6 1/4 = 0,8.
A Decimal Number consists of a whole number part and a fractional part separated by a decimal point. If you wish to learn completely about Decimal Places and How to Learn to Count Decimal Places. Know about Decimal Place Value Chart Definition, Facts, Solved Examples in the further modules. We are sure you will be familiar with the Decimal Places by the end of this article.
What is meant by Decimal Places?
A Decimal Number consists of both whole number part and decimal number part. The digits right to the decimal point are called the Decimal Part and the digits left to the decimal point are called the whole number part. The Number of Digits present in the decimal part of the given decimal number is known as Decimal Places.
Based on the position of the digit in the number it has a value named place value. For Example, the Place Value of the digit 2 in 1234.45 is 200 as 2 is in the hundreds place. However, if you interchange the digits 3 and 2 we get a new number i.e. 1324.45. In 1324.45 the place value of a digit is 20 as it is in the tens place.
How to Learn to Count Decimal Places?
The number of digits present in the decimal part of the given decimal number is nothing but the Decimal Places. Check out the below-listed examples to understand how to read and count the decimal places for the given decimal number.
For Example:
Decimal Number 5.34 has 2 decimal places.
Decimal Number 0.376 has 3 decimal places.
The Number 86.261 has 3 decimal places.
The Number 912.67 has 2 decimal places.
To better understand the Decimal Numbers you need to be aware of the Place Value.
For Example Decimal Number 51.048053 Place Value is explained clearly below.
In the above-illustrated example, 51 is the whole number part and 048053 is the decimal or fractional part.
Whole Number Part
Place of 1 is Ones and its place value is 1
Place of 5 is Tens and its place value is 50
Decimal Number Part
Place of 0 is Tenths and its place value is 0*(frac { 1 }{ 10 } ) = 0
Place of 4 is hundredths and its place value is 4*(frac { 1 }{ 100 } ) = (frac { 4 }{ 100 } ) = 0.04
Place of 8 is Thousandths and its place value is 8*(frac { 1 }{ 1000 } ) = (frac { 8 }{ 1000 } ) = 0.008
Place of 0 is Ten Thousandths and its place value is 0*(frac { 1 }{ 10,000 } ) = 0
Place of 5 is Hundred Thousandths and its place value is 5*(frac { 1 }{ 100,000 } ) = (frac { 5 }{ 100,000 } ) = 0.00005
Place of 3 is Millionths and its place value is 3*(frac { 1 }{ 1000000 } ) = (frac { 3 }{ 1000000 } ) = 0.000003
= 5*10+1*1+0*10-1+4*10-2+8*10-3+0*10-4+5*10-5+3*10-6
= 51.048053
FAQs on Decimal Places
1. What are Decimal Places?
Decimal Places are nothing but the number of digits next to the decimal point or in the decimal part.
2. How do you find the Decimal Places?
Firstly, count the number of digits after the decimal point and the number itself tells the Decimal Places for a particular decimal number.
3. How many decimal places are there in the Decimal Number 32.4356?
The number of Decimal Places in the Decimal Number 32.4356 is 4.
A Decimal Number consists of a whole number part and a fractional part separated by a decimal point. If you wish to learn completely about Decimal Places and How to Learn to Count Decimal Places. Know about Decimal Place Value Chart Definition, Facts, Solved Examples in the further modules. We are sure you will be familiar with the Decimal Places by the end of this article.
What is meant by Decimal Places?
A Decimal Number consists of both whole number part and decimal number part. The digits right to the decimal point are called the Decimal Part and the digits left to the decimal point are called the whole number part. The Number of Digits present in the decimal part of the given decimal number is known as Decimal Places.
Based on the position of the digit in the number it has a value named place value. For Example, the Place Value of the digit 2 in 1234.45 is 200 as 2 is in the hundreds place. However, if you interchange the digits 3 and 2 we get a new number i.e. 1324.45. In 1324.45 the place value of a digit is 20 as it is in the tens place.
How to Learn to Count Decimal Places?
The number of digits present in the decimal part of the given decimal number is nothing but the Decimal Places. Check out the below-listed examples to understand how to read and count the decimal places for the given decimal number.
For Example:
Decimal Number 5.34 has 2 decimal places.
Decimal Number 0.376 has 3 decimal places.
The Number 86.261 has 3 decimal places.
The Number 912.67 has 2 decimal places.
To better understand the Decimal Numbers you need to be aware of the Place Value.
For Example Decimal Number 51.048053 Place Value is explained clearly below.
In the above-illustrated example, 51 is the whole number part and 048053 is the decimal or fractional part.
Whole Number Part
Place of 1 is Ones and its place value is 1
Place of 5 is Tens and its place value is 50
Decimal Number Part
Place of 0 is Tenths and its place value is 0*(frac { 1 }{ 10 } ) = 0
Place of 4 is hundredths and its place value is 4*(frac { 1 }{ 100 } ) = (frac { 4 }{ 100 } ) = 0.04
Place of 8 is Thousandths and its place value is 8*(frac { 1 }{ 1000 } ) = (frac { 8 }{ 1000 } ) = 0.008
Place of 0 is Ten Thousandths and its place value is 0*(frac { 1 }{ 10,000 } ) = 0
Place of 5 is Hundred Thousandths and its place value is 5*(frac { 1 }{ 100,000 } ) = (frac { 5 }{ 100,000 } ) = 0.00005
Place of 3 is Millionths and its place value is 3*(frac { 1 }{ 1000000 } ) = (frac { 3 }{ 1000000 } ) = 0.000003
= 5*10+1*1+0*10-1+4*10-2+8*10-3+0*10-4+5*10-5+3*10-6
= 51.048053
FAQs on Decimal Places
1. What are Decimal Places?
Decimal Places are nothing but the number of digits next to the decimal point or in the decimal part.
2. How do you find the Decimal Places?
Firstly, count the number of digits after the decimal point and the number itself tells the Decimal Places for a particular decimal number.
3. How many decimal places are there in the Decimal Number 32.4356?
The number of Decimal Places in the Decimal Number 32.4356 is 4.