Аня Колесникова
Ученик
(222),
закрыт
10 лет назад
Лучший ответ
Maxim
Гений
(71098)
10 лет назад
Этот знак используется не только в геометрии и изображается ∩
Остальные ответы
РОМАН ВОРОНЦОВ
Профи
(759)
10 лет назад
∩ знак пересечения
Мери теккозян
Ученик
(136)
6 лет назад
∩ знак
Хо Минхо
Профи
(690)
5 лет назад
∩ — знак пересечения
Мария Стасевич
Ученик
(135)
3 года назад
Перевёрнутая U
Некто никто
Профи
(543)
3 года назад
Этот знак используется не только в геометрии и обозначается ∩
Ҝρนĉ⍡นӈα
Гуру
(3130)
3 года назад
∩
Mihail Dogadov
Ученик
(112)
1 год назад
∩
3
Какие бывают углы в геометрии?
11 ответов:
3
0
Углы в геометрии бывают следующие:
Во-первых, это прямой угол, равный 90 градусов.
Во-вторых, это тупой угол, равный более 90 градусов.
В- третьих, это острый угол, равный менее 90 градусов.
В-четвёртых, это развёрнутый угол, равный 180 градусов.
В-пятых, вертикальные углы, скрещивающиеся, смежные, накрестлежащие, односторонние.
Геометрия — наука не самая простая, чтобы ее понять нужен талант и конечно, замечательный учитель.
1
0
Скрещивающиеся, вертикальные, накрест лежащие, смежные, тупые, острые, прямоугольные…
1
0
Углом в геометрии, называют геометрическую фигуру, которую образуют вершина и два луча. Виды углов бывают следующие —
Прямой — равен 90 градусов.
Острый — менее 90 градусов.
Тупой — более 90 градусов.
Есть ещё угол, равный 180 градусов, который называют развёрнутым.
1
0
Вот что я помню из геометрии:
углы бывают прямые(90 градусов), углы бывают тупыми (более 90 градусов, но менее 180), углы бывают острыми (менее 90 градусов), развёрнутыми — это когда он равен 180 градусам.
1
0
в геометрии бывают 5 углов насколько я помню(давно закончила школу так что не осуждайте если не права) ПРЯМЫМ-90 градусов, РАЗВЁРНУТЫМ он равен 180 градусам, ТУПЫМ больше 90 градусов но меньше 180 градусов, ОСТРЫМ меньше 90 градусов и много разновидностей названий:вертикальные углы, скрещивающиеся, смежные, накрестлежащие, односторонние.
1
0
Угол в геометрии-это геометрическая фигура, которая образует вершину и два угла. Вот какими бывают углы, вспомним, так сказать, школьные годы.
- прямой угол, он равен 90 градусам
- острый угол, он равен менее 90 градусов
- тупой угол, он более 90 градусов
- развернутый угол, он как раз составит 180 градусов
1
0
Если говорить о геометрических углах, то они делятся по градусам на:
Острые углы (меньше 90 градусов),
Прямые углы (равны 90 градусам),
Тупые углы (больше 90 градусов).
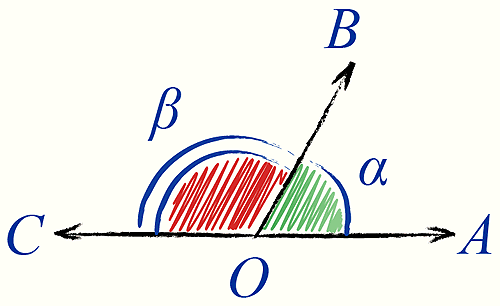
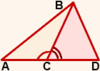
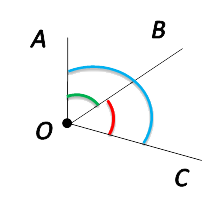
Кроме того в геометрии есть такое понятие, как смежные углы – это два угла, которые имеют одну общую сторону, а другие их стороны являются дополнительными лучами, как на картинке красный угол СОВ и зелёный угол АОВ:
1
0
В геометрии бывают углы острые, это те, что меньше 90 градусов от 0 до 90(не включая 90), прямые, те что ровно составляют 90 градусов, и тупые, которые больше 90 градусов и до 180( они развернутые )
Изучение геометрии как раз начинается с углов
1
0
Геометрия предмет сложный когда учились в школе давался многим с трудом. Но вот когда пришлось столкнуться с этой наукой в жизни то эта наука оказалась не столь уж и сложна. Поэтому как говорится на практике становится все просто и очевидно и не только с углами.
Углы бывают такие ;
острый угол это угол меньше 90 градусов .
прямой угол это 90 градусов.
тупой угол больше 90 градусов.
есть развернутый угол это 180 градусов.
В жизни взрослой человек постоянно сталкивается с углами и порой даже не замечает этого феномена.
1
0
Из Евклидовой геометрии мы знаем,что углы бывают следующие: прямой угол,равный 90°;тупой,велина которого превышает 90°;острый,величина — менее 90°; и наконец развернутый угол,равняющийся 180°.углов ,как мы видим,немного и запомнить их нетрудно
0
0
Я в геометрии не сильна, могу припомнить только такие углы, которые, в принципе, известны всем. Вот они:
- прямой угол, равный 90 градусам, такие углы имеют наши квартиры.
- острый угол, он меньше 90 градусов, название говорит само за себя.
- тупой угол, он, конечно же, бол ше 90 градусов, тоже, весьма говорящее название.
Читайте также
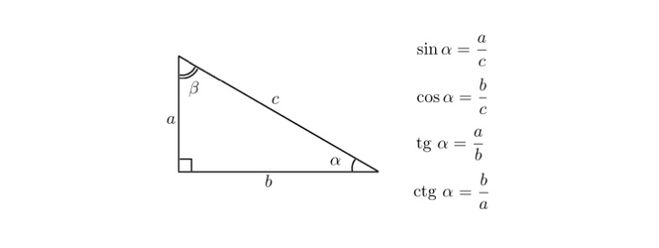
Совсем несложно найти угол между катетом и гипотенузой.
Сумма углов в треугольнике равна 180 градусам, один из них равен 90 градусам и если известно значение второго острого угла, нужно от 90 градусов отнять это значение.
если известны величины сторон прямоугольного треугольника, тогда угол можно найти по этим формулам, используя при этом таблицы значений синусов, косинусов и тангенсов.
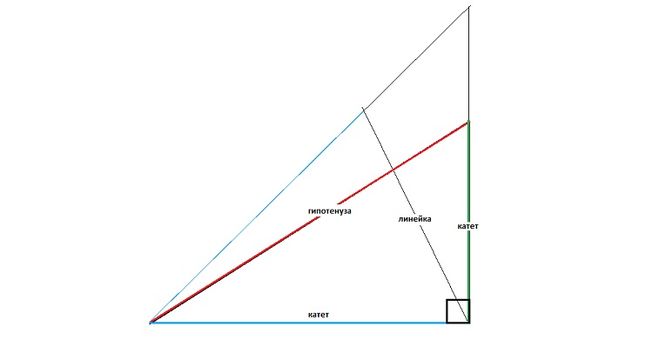
Но бывает и такое. что под рукой как назло нет этих табличек, тогда угол между катетом и гипотенузой можно просто измерить с помощью транспортира, но если и его нет, тогда
угол в прямоугольном треугольнике между катетом и гипотенузой можно определить с помощью обычной линейки и карандаша
меньший катет удлиняем к размеру большого. соединяем, откладываем на новой гипотенузе длину большего катета.
С вершины прямого угла прикладываем линейку и измеряем расстояние между синими отрезками и между вершиной треугольника и гипотенузой.
Большее расстояние делим на 45 и умножаем на меньшее расстояние — получим значение нашего угла (будет небольшая погрешность, но она будет совсем незначительной).
Сравнить два угла на глаз невозможно, ведь отличаться они могут совсем на немного и тогда нам будет казаться, что углы равные, хотя на самом деле один больше другого. Поэтому обычно сравнивают углы либо измерением с помощью например транспортира, или наложением если такое возможно.
И тот и другой вариант имеют свою погрешность, но если абсолютная точность не требуется, то они вполне годятся.
При наложении углы просто накладываются друг на друга, чтобы совместились вершина угла и одна сторона обоих углов. Тогда по взаимоположению второй стороны этих углов можно сделать вывод о равенстве или неравенстве углов.
Смотря с какой силой и в каким направленни ударить кием по шару. Если удар достаточно сильный и направлен перпендикулярно к борту, то шар докотится до противоположного борта и вернется по той же траектории, и далее повторяя движение сначала до своей остановки. В этом случае ответ утвердительный.
К счастью, угол 15 ° — это четвёртая часть угла в 60 °, который строится элементарно.Чертите прямую, на ней отмечаете две точки (А и В). Циркулем отмеряете расстояние АВ, не меняя раствора циркуля, последовательно ставите ножку циркуля в точки А и В, и проводите дуги до их пересечения. Точку пересечения обозначаете С. Точку С соединяете отрезками прямых с точками А и В. Получился равносторонний треугольник, каждый угол которого равен 60 °.
Другой способ. Чертите циркулем окружность. Ставите ножку циркуля в любую точку этой окружности (пусть это точка А), и делаете засечку на окружности. Получаете точку В. Далее, ставите ножку циркуля в точку В и делаете следующую засечку (С) и так далее, пока очередная (шестая) засечка не «придёт» в точку А. Соединяете через одну любые три точки и получаете равносторонний треугольник с углами по 60 °.
<hr />
Деление угла пополам. Пусть дан угол в вершиной А. Ставите ножку циркуля в вершину угла и проводите дугу, так, чтобы она пересекла обе стороны угла. Обозначаете точки пересечения В и С. Теперь, ставите ножку циркуля последовательно в точки В и С и проводите дуги одинакового радиуса (не обязательно равного АВ и АС), до их пересечения. Точку пересечения этих дуг обозначаете D. Через точки А и D проводите прямую линию. Она является биссектрисой заданного угла), т.е. делит его пополам.
<hr />
Таким образом, разделив угол 60 ° пополам, получите угол в 30 °, а разделив пополам его, получите угол в 15 °.
Биссектриса — это крыса, которая бегает по углам и делит угол пополам.
© старая поговорка школьников и студентов.
Благодаря ей нетрудно запомнить, что биссектриса проводится так, чтобы, например, угол в 90 градусов разделился на два угла в 45 градусов. А сделать это можно с помощью транспортира (хотя в данном случае, рисуя в тетрадке в клеточку, можно нарисовать и проще — если угол проведен точно по линии клеточек, а не под наклоном, биссектриса будет делить и клеточки по диагонали.
Вот пример биссектрисы прямого угла (увы, рисунка на листе в клеточку не нашла). Но можно представить, что линии — это границы тетрадной клеточки, и станет понятно, как в таком случае её нарисовать в тетрадке)
Как построить биссектрису?
Как по мне, проще всего это сделать с помощью транспортира, но в школах обычно учат строить её с помощью циркуля.
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Найти репетитора
Поддержать сайт
Запомните!
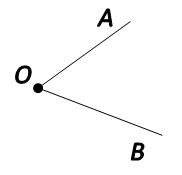
Угол — это геометрическая фигура, которая состоит из двух лучей и вершины.
Вершина угла — это точка, в которой два луча берут начало.
Стороны угла — это лучи, которые образуют угол.
Например:
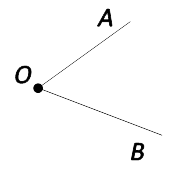
Вершина угла — точка «O».
Стороны угла — «OA» и «OB».
Для обозначения угла в тексте используется символ:

Способы обозначения углов
-
Одной заглавной латинской буквой, указывающей его вершину.
Угол:O
-
Тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные
на сторонах угла.
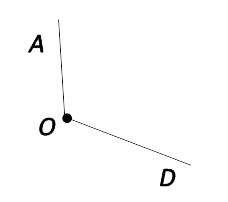
Угол:AOD
Называть угол можно с любого края, но НЕ с вершины.
Угол с рисунка выше имеет два названия:
AOD
иDOA.
Запомните!
При таком обозначении вершина угла должна всегда находиться в середине названия.
Единица измерения углов — градусы. Углы измеряют с помощью специального прибора — транспортира.
Для обозначения градусов в тексте используется символ: °
50 градусов обозначаются так: «50°»
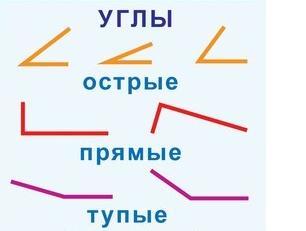
Виды углов
Запомните!
Два угла могут иметь одну общую сторону.
Обратите внимание на рисунок ниже. Попробуйте сосчитать и назвать все углы на изображении.
Если насчитали три угла, то вы правы. Давайте их назовём:
Углы 

имеют общую сторону OB.
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Геометрия
- Угол. Обозначение углов
Угол — геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
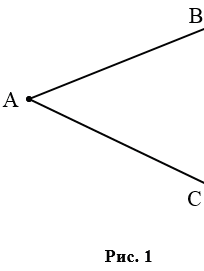
На рис. 1 лучи АВ и АС — стороны угла, точка А — вершина угла.
При записи угла в середине пишут букву, обозначающую его вершину. Сам угол на рис. 1 обозначают так: 






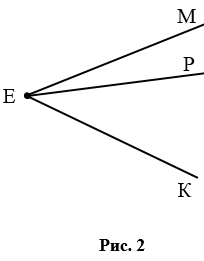
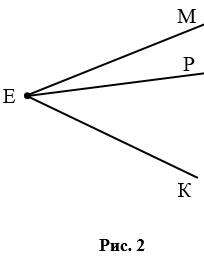
Если углы имеют общую вершину, то их нельзя обозначить одной буквой. Так на рис. 2 углы имеют общую вершину Е, поэтому мы можем использовать для данных углов только следующие обозначения: 











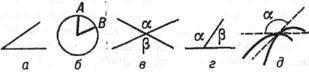
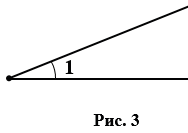
Также иногда углы обозначают цифрами, например, на рис.3 мы имеем 
Углы, как и отрезки, можно сравнивать между собой. Чтобы сравнить два угла можно наложить один угол на другой. Если при наложении одного угла на другой они совпадут, то эти углы равны.
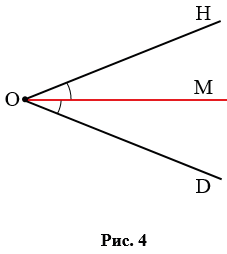
Биссектриса — луч, который делит угол на два равных угла. На рис. 4 углы НОМ и DОМ равны, значит, луч ОМ — биссектриса угла НОD.
Прямой угол — угол, который можно построить с помощью угольника (рис. 5).
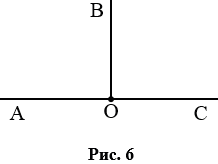
Если начертить два прямых угла с общей вершиной и одной общей стороной, то две другие стороны этих углов составят прямую (рис. 6). Считают, что лучи, составляющие прямую, также образуют угол, который называют развернутым.
На рис. 6 


Развернутый угол равен двум прямым углам, а прямой угол составляет половину развернутого.
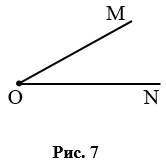
Острый угол — угол, который меньше прямого угла. На рис. 7 
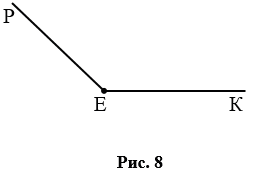
Тупой угол — угол, который больше прямого угла, но меньше развернутого. На рис. 8 
Советуем посмотреть:
Отрезок
Ломаная
Четырехугольники
Единицы измерения площадей. Свойства площадей
Прямоугольник, его периметр и площадь. Ось симметрии фигуры
Квадрат. Периметр и площадь квадрата.
Многоугольники. Правильные многоугольники. Равенство фигур.
Плоскость
Прямая
Луч
Шкалы и координаты
Прямоугольный параллелепипед. Пирамида.
Объем прямоугольного параллелепипеда
Куб. Площадь поверхности куба
Куб. Объем куба
Прямой и развернутый угол
Чертежный треугольник
Измерение углов. Транспортир. Виды углов
Треугольник и его виды
Окружность, круг, шар
Цилиндр, конус
Отрезок-xx
Геометрия
Правило встречается в следующих упражнениях:
5 класс
Задание 1651,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1652,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1661,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1701,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1702,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1710,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1772,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 309,
Мерзляк, Полонский, Якир, Учебник
Номер 13,
Мерзляк, Полонский, Якир, Учебник
Номер 1,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 206,
Мерзляк, Полонский, Якир, Учебник
Номер 220,
Мерзляк, Полонский, Якир, Учебник
Номер 391,
Мерзляк, Полонский, Якир, Учебник
Номер 1217,
Мерзляк, Полонский, Якир, Учебник
Номер 1234,
Мерзляк, Полонский, Якир, Учебник
Номер 1236,
Мерзляк, Полонский, Якир, Учебник
Задание 773,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1375,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1385,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1571,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 759,
Мерзляк, Полонский, Якир, Учебник
Задание 81,
Атанасян, Бутузов, Кадомцев, Юдина, Позняк, Учебник
Русский
Морфологические и синтаксические свойства
| падеж | ед. ч. | мн. ч. |
|---|---|---|
| Им. | у́гол | углы́ |
| Р. | угла́ | угло́в |
| Д. | углу́ | угла́м |
| В. | у́гол | углы́ |
| Тв. | угло́м | угла́ми |
| Пр. | угле́ | угла́х |
| М. | в углу́ | — |
у́·гол
Существительное, неодушевлённое, мужской род, 2-е склонение (тип склонения 1*b по классификации А. А. Зализняка). В сочетаниях типа на́ угол, за́ угол ударение может падать на предлог; слово «угол» при этом превращается в клитику.
Корень: -угол- [Тихонов, 1996].
Произношение
- МФА: ед. ч. [ˈuɡəɫ] мн. ч. [ʊˈɡɫɨ]
Семантические свойства
Значение
- место соединения, пересечения чего-либо (двух стен, граней здания или сооружения и т. п.), выступающее или, наоборот, находящееся в углублении ребро конструкции с примыкающими к нему гранями ◆ Отсутствует пример употребления (см. рекомендации).
- геометр. геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (вершины угла). ◆ Из теоремы о сумме смежных углов следует, что угол, смежный с прямым углом, есть прямой угол. А. В. Погорелов, «Геометрия, учебник для 7—11 классов», 1999 г.
- перен. пристанище, приют ◆ Отсутствует пример употребления (см. рекомендации).
- карт. четверть ставки, при объявлении которой загибается край карты ◆ Отсутствует пример употребления (см. рекомендации).
- истор., прост. кредитный билет или сумма в двадцать пять рублей ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы
- частичные: выступ, пересечение
- —
- пристанище, приют, обиталище, обитель, кров, крыша над головой
Антонимы
- —
- —
Гиперонимы
- —
- фигура
Гипонимы
- клин
Родственные слова
| Ближайшее родство | |
|
Этимология
Происходит от праслав. *ǫgъlъ, от кот. в числе прочего произошли: др.-русск. уг(ъ)лъ, ст.-слав. ѫгълъ (γωνία; Зогр., Мар., Ассем., Рs. Sin., Еuсh. Sin.), русск. угол, укр. ву́гол, белор. ву́гол, болг. ъ́гъл, сербохорв. диал. у̏гал (род. п. у̏гла), словенск. vọ̑gǝl (род. п. vȏgla), чешск. úhel, словацк. uhol, польск. węgieł (род. п. węgła), в.-луж. nuhł, н.-луж. nugeł. Родственно лат. angulus — то же, умбр. anglom-e Ώаd аngulum᾽, арм. ankiun, angiun — то же, др.-инд. áŋgam, ср. р., «член», aŋgúliṣ, aŋgúriṣ «палец», аŋgulīуаm «перстень»; наряду с и.-е. *аŋg- представлено *аŋk- «изогнутый»; лат. аnсus «кривой, изогнутый», uncus — то же, греч. ἀγκών м. «изгиб, локоть», ἀγκύλος «кривой», др.-инд. aŋkás м. «крюк». Использованы данные словаря М. Фасмера. См. Список литературы.
Фразеологизмы и устойчивые сочетания
- прямой угол
- косой угол
- острый угол
- тупой угол
- развёрнутый угол
- вершина угла
- внешний угол
- внутренний угол
- во главу угла
- голландский угол
- дальний угол (души, сознания, памяти)
- загнать в угол
- зажать в угол
- зажать в углу
- за́ угол (завернуть / заворачивать, зайти / заходить, забежать / забегать и т. п.)
- искать пятый угол
- красный угол
- медвежий угол
- на углу (находиться, стоять, высадить и т. п.)
- нейтральный угол (ринга)
- обходить острые углы / обойти острые углы
- сглаживать острые углы / сгладить острые углы
- поставить кого-либо в угол
- по чужим углам (скитаться, мыкаться, ютиться)
- свой угол (иметь)
- снять угол / снимать угол
- ставить во главу угла / поставить во главу угла
- сшибать углы
- съёмный угол
- угол атаки
- угол возвышения
- угол зрения
- угол места
- угол обзора
- угол обстрела
- угол стрельбы
- угол отражения
- угол падения
- угол съёмки
Пословицы и поговорки
- красна изба не углами, а пирогами
- угол падения равен углу отражения
Перевод
| место схождения, пересечения сторон или стен дома, комнаты и т. п. | |
|
| геометрическая фигура | |
|
| пристанище, приют | |
|
Анаграммы
- Гуло, оглу
Библиография
- Левонтина И. Б. Пристанище, приют 1, угол 3, обиталище, обитель 2, кров, крыша над головой // Апресян Ю. Д. (рук.) Новый объяснительный словарь синонимов русского языка. Проспект. — М.: Русские словари, 1995. — С. 393—400.
|
|
Для улучшения этой статьи желательно:
|
Углом называется геометрическая фигура, которая состоит из двух различных лучей, исходящих из одной точки. В данном случае, эти лучи называются сторонами угла. Точка, являющаяся началом лучей, называется вершиной угла. На рисунке вы можете увидеть угол с вершиной в точке О
, и сторонами k
и m
.
На сторонах угла отмечены точки А и С. Этот угол можно обозначить как угол AOC. В середине обязательно должно стоять название точки, в которой находится вершина угла. Также существуют и другие обозначения, угол О или угол km. В геометрии вместо слова угол часто пишут специальный значок.
Развернутый и неразвернутый угол
Если у угла обе стороны лежат на одной прямой, то такой угол называется развернутым
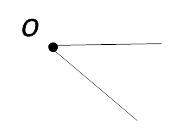
углом. То есть одна сторона угла является продолжением другой стороны угла. На рисунке нижк представлен развернутый угол О.
Следует отметить, что любой угол, разделяет плоскость на две части. Если угол не является развернутым, то одна из частей называется внутренней областью угла, а другая внешней областью этого угла. На рисунке ниже представлен неразвернутый угол и отмечены внешняя и внутренняя области этого угла.
В случае с развернутым углом любую из двух частей, на которые он делит плоскость, можно считать внешней областью угла. Можно говорить о положении точки относительно угла. Точка может лежать вне угла (во внешней области), может находится на одной из его сторон, либо может лежать внутри угла (во внутренней области).
На рисунке ниже, точка А лежит вне угла О, точка B лежит на одной из сторон угла, а точка С лежит внутри угла.
Измерение углов
Для измерения углов существует прибор называемый транспортиром. Единицей измерения угла является градус
. Следует отметить, что каждый угол имеет определенную градусную меру, которая больше нуля.
В зависимости от градусной меры углы делятся на несколько групп.
Угловая мера
Угол в измеряют в градусной мере (градус, минута, секунда), в оборотах — отношение длины дуги s к длине окружности L , в радианах — отношение длины дуги s к радиусу r ; исторически применялась также градовая мера измерения углов, в настоящее время она почти нигде не используется.
1 оборот = 2π радианам = 360° = 400 градам .
В морской терминологии углы обозначаются румбами .
Типы углов
Смежные углы — острый (a) и тупой (b). Развёрнутый угол (c)
Кроме этого, рассматривается угол между гладкими кривыми в точке касания: по определению, его величина равна величине угла между касательными к кривым.
Wikimedia Foundation
.
2010
.
Смотреть что такое «Развернутый угол» в других словарях:
Угол, равный двум прямым. *РАЗВЕРТКА поверхности фигура, получающаяся в плоскости при таком совмещении точек данной поверхности с этой плоскостью, при котором длины линий остаются неизменными. Развертка кривой см. Эвольвента … Большой Энциклопедический словарь
угол
— ▲ разность направление (в пространстве) угол протяженность поворота от одного направления к другому; разность направлений; часть полного оборота (# наклона. образовывать #). наклон. наклонный. отклонение. уклониться (дорога уклонилась вправо).… …
Угол
— Углы: 1 общего вида; 2 смежные; 3 прилежащие; 4 вертикальные; 5 развернутый; 6 прямой, острый и тупой; 7 между кривыми; 8 между прямой и плоскостью; 9 между скрещивающимися прямыми (не лежащими в одной плоскостью) прямыми. УГОЛ, геометрическая… … Иллюстрированный энциклопедический словарь
Геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки. Лучи наз. сторонами У., а их общее начало вершиной У. Пусть [ ВА),[ ВС) стороны угла, В его вершина, плоскость, определяемая сторонами У. Фигура делит плоскость… … Математическая энциклопедия
Угол, равный двум прямым. * * * РАЗВЕРНУТЫЙ УГОЛ РАЗВЕРНУТЫЙ УГОЛ, угол, равный двум прямым … Энциклопедический словарь
Раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера
1) Замкнутая ломаная линия, именно: если различные точки, никакие последовательные три из к рых не лежат на одной прямой, то совокупность отрезков наз. многоугольником (см. рис. 1). М. могут быть пространственными или плоскими (ниже… … Математическая энциклопедия
поперек
— ▲ под углом максимум, косой угол поперечный. поперек под прямым углом. . прямой угол угол максимального отклонения; угол, равный своему смежному; четверть оборота. перпендикуляр. перпендикулярный находящийся под прямым углом. перпендикулярно.… … Идеографический словарь русского языка
градус
— а, м. 1) Единица измерения плоского угла, равная 1/90 прямого угла или соответственно 1/360 окружности. Угол в 90 градусов называется прямым углом. Развернутый угол составляет 180 градусов. 2) Единица измерения температурного интервала, имеющая… … Популярный словарь русского языка
Теорема Шварца Кристоффеля важная теорема в теории функций комплексного переменного, носит название немецких математиков Карла Шварца и Элвина Кристоффеля. Очень важной с практической точки зрения является проблема о конформном… … Википедия
Давайте начнем с определения того, что такое угол. Во-первых, он является Во-вторых, он образован двумя лучами, которые называются сторонами угла. В-третьих, последние выходят из одной точки, которую называют вершиной угла. Исходя из этих признаков, мы можем составить определение: угол — геометрическая фигура, которая состоит из двух лучей (сторон), выходящих из одной точки (вершины).
Их классифицируют по градусной величине, по расположению относительно друг друга и относительно окружности. Начнем с видов углов по их величине.
Существует несколько их разновидностей. Рассмотрим подробнее каждый вид.
Основных типов углов всего четыре — прямой, тупой, острый и развернутый угол.
Прямой
Он выглядит так:
Его градусная мера всегда составляет 90 о, иначе говоря, прямой угол — это угол 90 градусов. Только они есть у таких четырехугольников, как квадрат и прямоугольник.
Тупой
Он имеет такой вид:
Градусная мера всегда больше 90 о, но меньше 180 о. Он может встречаться в таких четырехугольниках, как ромб, произвольный параллелограмм, во многоугольниках.
Острый
Он выглядит так:
Градусная мера острого угла всегда меньше 90 о. Он встречается во всех четырехугольниках, кроме квадрата и произвольного параллелограмма.
Развернутый
Развернутый угол имеет такой вид:
В многоугольниках он не встречается, но не менее важен, чем все остальные. Развернутый угол — это геометрическая фигура, градусная мера которой всегда равняется 180º. На нем можно построить проведя из его вершины один или несколько лучей в любых направлениях.
Есть еще несколько второстепенных видов углов. Их не изучают в школах, но знать хотя бы об их существовании необходимо. Второстепенных видов углов всего пять:
1. Нулевой
Он выглядит так:
Само название угла уже говорит о его величине. Его внутренняя область равняется 0 о, а стороны лежат друг на друге так, как показано на рисунке.
2. Косой
Косым может быть и прямой, и тупой, и острый, и развернутый угол. Главное его условие — он не должен равняться 0 о, 90 о, 180 о, 270 о.
3. Выпуклый
Выпуклыми являются нулевой, прямой, тупой, острый и развернутый углы. Как вы уже поняли, градусная мера выпуклого угла — от 0 о до 180 о.
4. Невыпуклый
Невыпуклыми являются углы с градусной мерой от 181 о до 359 о включительно.
5. Полный
Полным является угол с градусной мерой 360 о.
Это все типы углов по их величине. Теперь рассмотрим их виды по расположению на плоскости относительно друг друга.
1. Дополнительные
Это два острых угла, образовывающие один прямой, т.е. их сумма 90 о.
2. Смежные
Смежные углы образуются, если через развернутый, точнее, через его вершину, провести луч в любом направлении. Их сумма равна 180 о.
3. Вертикальные
Вертикальные углы образуются при пересечении двух прямых. Их градусные меры равны.
Теперь перейдем к видам углов, расположенным относительно окружности. Их всего два: центральный и вписанный.
1. Центральный
Центральным является угол с вершиной в центре окружности. Его градусная мера равна градусной мере меньшей дуги, стянутой сторонами.
2. Вписанный
Вписанным называется угол, вершина которого лежит на окружности, и стороны которого ее пересекают. Его градусная мера равна половине дуги, на которую он опирается.
Это все, что касается углов. Теперь вы знаете, что помимо наиболее известных — острого, тупого, прямого и развернутого — в геометрии существует много других их видов.
С понятием угол учащиеся знакомятся еще в начальной школе. Но как геометрическую фигуру, имеющую определенные свойства, начинают изучать его с 7-го класса в геометрии. Кажется, довольно простая фигура
, что о ней можно сказать. Но, приобретая новые знания, школьники всё больше понимают, что можно узнать о ней довольно интересные факты.
Вконтакте
Когда изучаются
Школьный курс геометрии разделён на два раздела: планиметрию и стереометрию. В каждом из них немалое внимание уделяется углам
:
- В планиметрии дается их основное понятие, происходит знакомство с их видами по величине. Более подробно изучаются свойства каждого вида треугольников. Появляются новые определения для учащихся – это геометрические фигуры, образованные при пересечении двух прямых между собой и пересечении нескольких прямых секущей.
- В стереометрии изучаются пространственные углы – двугранные и трехгранные.
Внимание!
В данной статье рассматриваются все виды и свойства углов именно в планиметрии.
Определение и измерение
Приступая к изучению, первоначально определяют, что такое угол
в планиметрии.
Если на плоскости взять определённую точку и провести от нее два произвольных луча, то получим геометрическую фигуру – угол, состоящую из следующих элементов:
- вершина – та точка, из которой и проводились лучи, обозначается заглавной буквой латинского алфавита;
- стороны – полупрямые, проведенные из вершины.
Все элементы, образующие рассматриваемую нами фигуру, разбивают плоскость на две части
:
- внутренняя — в планиметрии не превышает 180 градусов;
- внешняя.
Принцип измерения углов в планиметрии
объясняют на интуитивной основе. Для начала знакомят учащихся с понятием развернутый угол.
Важно!
Угол называется развернутым, если полупрямые, выходящие из его вершины, образуют прямую линию. Неразвернутый угол это все остальные случаи.
Если его разделить на 180 равных частей, то принято считать меру одной части равной 10. В таком случае говорят, что измерение производится в градусах, а градусная мера такой фигуры составляет 180 градусов.
Основные виды
Виды углов подразделяются по таким критериям, как градусная мера, характер их образования и представленные ниже категории.
По величине
Учитывая величину, углы разделяют на:
- развернутый;
- прямой;
- тупой;
- острый.

Его можно получить при делении развернутого на две равные части. В этом случае легко ответить на вопрос: прямой угол, сколько градусов составляет?
180 градусов развернутого делим на 2 и получаем, что прямой угол равен 90 градусам
. Это замечательная фигура, так как многие факты в геометрии связаны именно с ней.
Имеет она и свои особенности в обозначении. Чтобы на рисунке показать прямой угол, его обозначают не дугой, а квадратиком.
Углы, которые получаются при делении произвольным лучом прямого, называют острыми.
По логике вещей следует, что острый угол меньше прямого, но его мера отлична от 0 градусов. То есть, он имеет величину от 0 до 90 градусов.
Тупой угол больше прямого, но меньше развернутого. Его градусная мера варьируется в интервале от 90 до 180 градусов.
Данный элемент можно разбить на разные виды рассматриваемых фигур, исключая развёрнутый.
Вне зависимости от того, как разбивается неразвернутый угол, всегда пользуются базовой аксиомой планиметрии — «основное свойство измерения».
При разделении угла одним лучом
или несколькими, градусная мера данной фигуры равна сумме мер углов, на которые она разбита.
На уровне 7-го класса виды углов по их величине на этом заканчиваются. Но для повышения эрудиции можно добавить, что существуют и другие разновидности, которые обладают градусной мерой больше 180 градусов.Их называют выпуклыми.
Фигуры при пересечении прямых
Следующие типы углов, с которыми знакомятся учащиеся – элементы, образованные при пересечении двух прямых. Фигуры, которые размещаются друг напротив друга, называют вертикальными. Их отличительное свойство – они равны.
Элементы, которые прилегают к одной и той же прямой, называют смежными. Теорема, отображающая их свойство, говорит о том, что смежные углы в сумме дают 180 градусов
.
Элементы в треугольнике
Если рассматривать фигуру как элемент в треугольнике, то углы подразделяют на внутренний и внешний. Треугольник ограничен тремя отрезками и состоит из трёх вершин. Углы, расположенные внутри треугольника при каждой вершине, называют внутренними
.
Если взять любой внутренний элемент при любой вершине и продлить любую сторону, то угол, который образовался и является смежным с внутренним, называется внешним. Эта пара элементов имеет следующее свойство: их сумма равна 180 градусам.
Пересечение двух прямых секущей
Пересечение прямых
При пересечении двух прямых секущей также образуются углы
, которые принято распределять по парам. Каждая пара элементов имеет свое название. Выглядит это следующим образом:
- внутренние накрест лежащие:∟4 и ∟6, ∟3 и ∟5;
- внутренние односторонние: ∟4 и ∟5, ∟3 и ∟6;
- соответствующие: ∟1 и ∟5, ∟2 и ∟6, ∟4 и ∟8, ∟3 и ∟7.
В том случае, когда секущая пересекает две
«Крошка сын к отцу пришел, и спросила Кроха: «А какие бывают углы?». Но отец, ответ забыл. Это очень плохо!».
В нашей статье мы предлагаем вспомнить уроки математики и найти ответы на вопросы Крохи.
Что такое угол
Что такое угол конечно легче показать, чем объяснить. Из начальных классов мы знаем, что плоский угол:
- Это геометрическая фигура.
- Она образована двумя сторонами – лучами.
- Лучи выходят из одной вершины – точки.
- Измеряется в градусах.
То есть, если на любой плоскости поставить точку, а затем из этой точки вывести два луча (луч – прямая имеющая начало, но не имеющая конца), то получим угол, и не один, а два. Это потому что, лучи поделили плоскость на две части. У нас образовалось два угла — внутренний и внешний.
Обозначение углов
Обозначается угол в математике вот таким значком – «˪» и греческими буквами: β, δ, φ. Так же обозначать углы можно маленькими или большими латинскими буквами. Строчными (d, c, b) обозначают лучи образующие угол, следовательно, название будет складываться из двух букв и значка — ˪ab. Большие латинские буквы обозначают три точки угла: две на сторонах и одна вершина (˪ DEF). Причем, буква вершины всегда будет находиться в середине названия, а как читать DEF или FED, это уже разницы не имеет.
Виды углов
В зависимости от градусов (мерной величины) углы разделяют на:
- Острые (> 90 градусов);
- Прямые (ровно 90);
- Тупые (180);
- Развернутый (равен 180);
- Невыпуклый (более 180, но менее 360);
- Полный (360);
Все углы, которые не являются прямыми или развернутыми, называются косыми.
Еще, какие есть углы?
- Смежные – одна сторона у них общая, а другие лежат, не совпадая, на одной плоскости. Сумма таких углов всегда будет равна 180.
- Вертикальные – углы образованные двумя пересекающимися прямыми и общих сторон они не имеют, но их лучи выходят с одной точки. То есть, сторона одного угла есть продолжение другого. Такие углы равны.
- Центральный – угол, вершина которого является центром окружности.
- Вписанный угол. Его вершина находится на окружности, а лучи, образующие его, пересекают эту окружность.
Теперь вы знаете, какой прямой угол, а акже сможете отличить, какой угол острый. Запомнить это не сложно, да и другие виды углов тоже имеют характерные названия.
Углом называется геометрическая фигура, которая состоит из двух различных лучей, исходящих из одной точки. В данном случае, эти лучи называются сторонами угла. Точка, являющаяся началом лучей, называется вершиной угла. На рисунке вы можете увидеть угол с вершиной в точке О
, и сторонами k
и m
.
На сторонах угла отмечены точки А и С. Этот угол можно обозначить как угол AOC. В середине обязательно должно стоять название точки, в которой находится вершина угла. Также существуют и другие обозначения, угол О или угол km. В геометрии вместо слова угол часто пишут специальный значок.
Развернутый и неразвернутый угол
Если у угла обе стороны лежат на одной прямой, то такой угол называется развернутым
углом. То есть одна сторона угла является продолжением другой стороны угла. На рисунке нижк представлен развернутый угол О.
Следует отметить, что любой угол, разделяет плоскость на две части. Если угол не является развернутым, то одна из частей называется внутренней областью угла, а другая внешней областью этого угла. На рисунке ниже представлен неразвернутый угол и отмечены внешняя и внутренняя области этого угла.
В случае с развернутым углом любую из двух частей, на которые он делит плоскость, можно считать внешней областью угла. Можно говорить о положении точки относительно угла. Точка может лежать вне угла (во внешней области), может находится на одной из его сторон, либо может лежать внутри угла (во внутренней области).
На рисунке ниже, точка А лежит вне угла О, точка B лежит на одной из сторон угла, а точка С лежит внутри угла.
Измерение углов
Для измерения углов существует прибор называемый транспортиром. Единицей измерения угла является градус
. Следует отметить, что каждый угол имеет определенную градусную меру, которая больше нуля.
В зависимости от градусной меры углы делятся на несколько групп.
Угловая мера
Угол в измеряют в градусной мере (градус, минута, секунда), в оборотах — отношение длины дуги s к длине окружности L , в радианах — отношение длины дуги s к радиусу r ; исторически применялась также градовая мера измерения углов, в настоящее время она почти нигде не используется.
1 оборот = 2π радианам = 360° = 400 градам .
В морской терминологии углы обозначаются румбами .
Типы углов
Смежные углы — острый (a) и тупой (b). Развёрнутый угол (c)
Кроме этого, рассматривается угол между гладкими кривыми в точке касания: по определению, его величина равна величине угла между касательными к кривым.
Wikimedia Foundation
.
2010
.
Смотреть что такое «Полный угол» в других словарях:
Неузаконенная внесистемная ед. плоского угла. 1 П. у.= 2ПИ рад 6.283 185 рад (см. Радиан) … Большой энциклопедический политехнический словарь
Угол вертикальной наводки ствола орудия при стрельбе с учетом углов качки корабля. Определяется приборами центрального артиллерийского поста. EdwART. Толковый Военно морской Словарь, 2010 … Морской словарь
Угол горизонтальной наводки ствола орудия при стрельбе с учетом углов качки корабля. Определяется ߑؐѐޑАܐؠцентрального артиллерийского поста. EdwART. Толковый Военно морской Словарь, 2010 … Морской словарь
полный механический угол поворота подвижной системы переменного резистора
— полный механический угол поворота Полный угол поворота подвижной системы переменного резистора от упора до упора. Примечание Для резисторов, не имеющих упоров, полный механический угол равен максимальному углу между двумя положениями подвижной… … Справочник технического переводчика
Полный механический угол поворота подвижной системы переменного резистора
— 52. Полный механический угол поворота подвижной системы переменного резистора Полный механический угол поворота D. Mechanischer Drehwinkel E. Total mechanical rotation F. Course mécanique totale Полный угол поворота подвижной системы переменного… … Словарь-справочник терминов нормативно-технической документации
УГОЛ
— (1) атаки угол между направлением воздушного потока, набегающего на крыло самолёта, и хордой сечения крыла. От этого угла зависит значение подъёмной силы. Угол, при котором подъёмная сила максимальна, называется критическим углом атаки. У… … Большая политехническая энциклопедия
УГОЛ, мера наклона между двумя прямыми линиями или плоскостями, а также величины вращательного движения. Полный круг делится на 360° (градусов) иди на 2p радиан. Прямой угол составляет 90° или p/2 радиан. Один градус подразделяется на 60 (минут) … Научно-технический энциклопедический словарь
Элементы: Drop прыжок с высоты, выполняется с места или из позиции cat leap. Амортизировать падение можно только ногами, или ногами и руками (ну или одной рукой). Spring прыжок через какое либо препятствие, не касаясь его. Например, перелёт через … Википедия
Идти в полную. Жарг. угол. Признаваться в совершении преступления. Балдаев 1, 169. Два полных, третий не целый. Новг. Ирон. О небольшом количестве людей где л. НОС 2, 76 …
Жарг. угол. Одобр. Всё в порядке, дела идут хорошо. Б., 159; Быков, 202. /i> Вероятно, из идиш или иврита, где слово является оценкой высшего качества. Елистратов 1994, 537 … Большой словарь русских поговорок
Что такое угол?
Углом называют фигуру, образованную двумя лучами, выходящими из одной точки (рис. 160).
Лучи, образующие угол
, называют сторонами угла, а точку, из которой они выходят, — вершиной угла.
На рисунке 160 сторонами угла являются лучи ОА и ОБ, а его вершиной — точка О. Этот угол обозначают так: АОВ.
При записи угла в середине пишут букву, обозначающую его вершину. Угол можно обозначить и одной буквой — названием его вершины.
Например, вместо «угол АОВ» пишут короче: «угол О».
Вместо слова «угол» пишут знак .
Например, AОВ, O.
На рисунке 161 точки С и D лежат внутри угла АОВ, точки X и У лежат вне этого угла, а точки
М и Н — на сторонах угла.
Как и все геометрические фигуры, углы сравниваются с помощью наложения.
Если один угол можно наложить на другой так, что они совпадут, то эти углы равны.
Например, на рисунке 162 ABC = MNK.
Из вершины угла СОК (рис. 163) проведен луч ОР. Он разбивает угол СОК на два угла — СОР и РОК. Каждый из этих углов меньше угла СОК.
Пишут: COP
Прямой и развернутый угол
Два дополнительных друг другу луча
образуют развернутый угол. Стороны этого угла вместе составляют прямую линию, на которой лежит вершина развернутого угла (рис. 164).
Часовая и минутная стрелки часов образуют в 6 ч развернутый угол (рис. 165).
Согнем два раза пополам лист бумаги, а потом развернем его (рис. 166).
Линии сгиба образуют 4 равных угла. Каждый из этих углов равен половине развернутого угла. Такие углы называют прямыми.
Прямым углом называют половину развернутого угла.
Чертежный треугольник
Для построения прямого угла пользуются чертежным треугольником
(рис. 167). Чтобы построить прямой угол, одной из сторон которого является луч ОЛ, надо:
а) расположить чертежный треугольник так, чтобы вершина его прямого угла совпала с точкой О, а одна из сторон пошла по лучу ОА;
б) провести вдоль второй стороны треугольника луч ОВ.
В результате получим прямой угол АОВ.
Вопросы к теме
1.Что такое угол?
2.Какой угол называют развернутым?
3.Какие углы называют равными?
4.Какой угол называют прямым?
5.Как строят прямой угол с помощью чертежного треугольника?
Нам с вами уже известно, что любой угол делит плоскость на две части. Но, в случае, если у угла его обе стороны лежат на одной прямой, то такой угол называется развернутым. То есть, у развернутого угла одна его сторона является продолжением его другой стороны угла.
Теперь давайте посмотрим на рисунок, на котором как раз и изображен развернутый угол О.
Если мы возьмем и проведем из вершины развернутого угла луч, то он разделит данный развернутый угол еще на два угла, которые будут иметь одну общую сторону, а другие два угла будут составлять прямую. То есть, с одного развернутого угла мы получили два смежных.
Если мы возьмем развернутый угол и проведем биссектрису, то эта биссектриса разделит развернутый угол на два прямых угла.
А, в том случае, если мы из вершины развернутого угла проведем произвольный луч, который не является биссектрисой, то такой луч разделит развернутый угол на два угла, один из которых будет острым, а другой тупым.
Свойства развернутого угла
Развернутый угол обладает такими свойствами:
Во-первых, стороны развёрнутого угла являются антипараллельными и образуют прямую;
во-вторых, развернутый угол равен 180°;
в-третьих, два смежных угла образуют развернутый угол;
в-четвертых, развернутый угол составляет половину полного угла;
в-пятых, полный угол будет равен сумме двух развёрнутых углов;
в-шестых, половина развернутого угла составляет прямой угол.
Измерение углов
Чтобы измерить любой угол, для этих целей чаще всего используют транспортир, у которого единица измерения равна одному градусу. При измерении углов следует помнить, что любой угол имеет свою определенную градусную меру и естественно эта мера больше нуля. А развернутый угол, как нам уже известно, равен 180 градусам.
То есть, если мы с вами возьмем любую плоскость круга и разделим ее радиусами на 360 равных частей, то 1/360 часть данного круга будет являться угловым градусом. Как вы уже знаете, что градус обозначается определенным значком, который имеет такой вид:
« ° ».
Теперь мы также знаем, что один градус 1° = 1/360 части круга. Если угол равен плоскости круга и составляет 360 градусов, то такой угол является полным.
А теперь мы возьмем, и плоскость круга поделим с помощью двух радиусов, лежащих на одной прямой линии, на две равные части. То в этом случае, плоскость полукруга составит половину полного угла, то есть 360: 2 = 180°. Мы с вами получили угол, который равен полуплоскости круга и имеет 180°. Это и есть развернутый угол.
Практическое задание
1613. Назовите углы, изображенные на рисунке 168. Запишите их обозначения.
1614. Начертите четыре луча: ОА, ОВ, ОС и OD. Запишите названия шести углов, сторонами которых являются эти лучи. На сколько частей эти лучи делят плоскость
?
1615. Укажите, какие точки на рисунке 169 лежат внутри угла КОМ, Какие точки лежат вне этого угла? Какие точки лежат на стороне OK, a какие — на стороне ОМ?
1616. Начертите угол MOD и проведите внутри него луч ОТ. Назовите и обозначьте углы, на которые этот луч делит угол MOD.
1617. Минутная стрелка за 10 мин повернулась на угол АОВ, за следующие 10 мин — на угол ВОС, а еще за 15 мин — на угол COD. Сравните углы АОВ и ВОС, ВОС и COD, АОС и АОВ, АОС и COD (рис. 170).
1618. Изобразите с помощью чертежного треугольника 4 прямых угла в разных положениях.
1619. С помощью чертежного треугольника найдите на рисунке 171 прямые углы. Запишите их обозначения.
1620. Укажите прямые углы в классной комнате.
а) 0,09 200; б) 208 0,4; в) 130 0,1 + 80 0,1.
1629. Сколько процентов от 400 составляет число 200; 100; 4; 40; 80; 400; 600?
1630. Найдите пропущенное число:
а) 2 5 3 б) 2 3 5
13 6 12 1
2 3? 42?
1631. Начертите квадрат, сторона которого равна длине 10 клеток тетради. Пусть этот квадрат изображает поле. Рожь занимает 12% поля, овес — 8%, пшеница — 64%, а остальная часть поля занята гречихой. Покажите на рисунке часть поля, занятую каждой культурой. Сколько процентов поля занимает гречиха?
1632. За учебный год Петя израсходовал 40% купленных в начале года тетрадей, и у него осталось 30 тетрадей. Сколько тетрадей было куплено для Пети в начале учебного года?
1633. Бронза является сплавом олова и меди. Сколько процентов сплава составляет медь в куске бронзы, состоящем из 6 кг олова и 34 кг меди?
1634. Построенный в древности Александрийский маяк, который называли одним из семи чудес света, выше башен Московского Кремля в 1,7 раза, но ниже здания Московского университета на 119 м. Найдите высоту каждого из этих сооружений, если башни Московского Кремля на 49 м ниже Александрийского маяка.
1635. Найдите с помощью микрокалькулятора:
а) 4,5% от 168; в) 28,3% от 569,8;
б) 147,6% от 2500; г) 0,09% от 456 800.
1636. Решите задачу:
1) Площадь огорода 6,4 а. В первый день вскопали 30% огорода, а во второй день — 35% огорода. Сколько аров осталось еще вскопать?
2) У Сережи было 4,8 ч свободного времени. 35% этого времени он потратил на чтение книги, а 40% на просмотр передач по телевизору. Сколько времени у него еще осталось?
1637. Выполните действия:
1) ((23,79: 7,8 — 6,8: 17) 3,04 — 2,04) 0,85;
2) (3,42: 0,57 9,5 — 6,6) : ((4,8 — 1,6) (3,1 + 0,05)).
1638. Начертите угол ВАС и отметьте по одной точке внутри угла, вне угла и на сторонах угла.
1639. Какие из отмеченных на рисунке 172 точек лежат внутри угла АМК.Какая точка лежит внутри угла АМВ> но вне угла АМК.Какие точки лежат на сторонах угла АМК?
1640. Найдите с помощью чертежного треугольника прямые углы на рисунке 173.
1641. Постройте квадрат со стороной 43 мм. Вычислите его периметр и площадь.
1642. Найдите значение выражения:
а) 14,791: а + 160,961: b, если а = 100, b = 10;
б) 361,62с + 1848: d, если с = 100, d =100.
1643. Рабочий должен был изготовить 450 деталей. В первый день он изготовил 60% деталей, а остальные — во второй. Сколько деталей изготовил рабочий
во второй день?
1644. В библиотеке было 8000 книг. Через год число их увеличилось на 2000 книг. На сколько процентов увеличилось число книг в библиотеке?
1645. Грузовики в первый день проехали 24% намеченного пути, во второй день — 46% пути, а в третий — остальные 450 км. Сколько километров проехали эти грузовики?
1646. Найдите, сколько составляют:
а) 1% от тонны; в) 5% от 7 т;
б) 1% от литра; г) 6% от 80 км.
1647. Масса детеныша моржа в 9 раз меньше массы взрослого моржа. Какова масса взрослого моржа, если вместе с детенышем их масса равна 0,9 т?
1648. Во время маневров командир оставил 0,3 всех своих солдат охранять переправу, а остальных разделил на 2 отряда для обороны двух высот. В первом отряде было в 6 раз больше солдат, чем во втором. Сколько солдат было в первом отряде, если всего было 200 солдат?
Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений
В этой статье будет рассматриваться одна из основных геометрических фигур — угол. После общего введения в это понятие мы уделим основное внимание отдельному виду такой фигуры. Развернутый угол — важное понятие геометрии, которое и будет основной темой этой статьи.
Введение в понятие геометрического угла
В геометрии существует ряд объектов, которые составляют основу всей науки. Угол как раз относиться к ним и определяется с помощью понятия луча, поэтому начнем именно с него.
Также перед тем, как приступать к определению самого угла, нужно вспомнить о нескольких не менее важных объектах в геометрии — это точка, прямая на плоскости и собственно сама плоскость. Прямой называют самую простую геометрическую фигуру, у которой нет ни начала, ни конца. Плоскостью — поверхность, которая имеет два измерения. Ну и луч (или же полупрямая) в геометрии — это часть прямой, у которой есть начало, но нет конца.
Используя данные понятия, можем составить утверждение, что углом является геометрическая фигура, которая полностью лежит в некоторой плоскости и состоит из двух несовпадающих лучей с общим началом. Такие лучи называются сторонами угла, а общее начало сторон — это его вершина.
Виды углов и геометрии
Мы знаем о том, что углы могут быть совсем разными. А потому немного ниже будет приведена небольшая классификация, которая поможет лучше разобраться в видах углов и их главных особенностях. Итак, существует несколько видов углов в геометрии:
- Прямой угол. Он характеризируется величиной в 90 градусов, а значит, его стороны всегда перпендикулярны между собой.
- Острый угол. К таким углам относятся все их представители, имеющие размер меньше 90 градусов.
- Тупой угол. Здесь же могут быть все углы с величиной от 90 до 180 градусов.
- Развернутый угол. Имеет размер строго 180 градусов и внешне его стороны составляют одну прямую.
Понятие развернутого угла
Теперь давайте рассмотрим развернутый угол более подробно. Это тот случай, когда обе стороны лежат на одной прямой, что можно четко увидеть на рисунке немного ниже. Значит, мы можем с уверенностью сказать, что у развернутого угла одна из его сторон по сути есть продолжением другой.
Стоит запомнить тот факт, что такой угол всегда можно разделить с помощью луча, который выходит из его вершины. В результате мы получим два угла, которые в геометрии называются смежными.
Также развернутый угол имеет несколько особенностей. Для того, чтобы рассказать о первой из них, нужно вспомнить понятие «биссектриса угла». Напомним, что это луч, который делит любой угол строго пополам. Что касается развернутого угла, то его биссектриса разделяет его таким образом, что образуется два прямых угла по 90 градусов. Это очень легко просчитать математически: 180˚ (градус развернутого угла) : 2 = 90˚.
Если же разделять развернутый угол совсем произвольным лучом, то в результате мы всегда получаем два угла, один из которых будет острым, а другой — тупым.
Свойства развернутых углов
Будет удобно рассматривать этот угол, собрав воедино все его главные свойства, что мы и сделали в данном списке:
- Стороны развернутого угла антипараллельны и составляют прямую.
- Величина развернутого угла всегда составляет 180˚.
- Два смежных угла вместе всегда составляют развернутый угол.
- Полный угол, который составляет 360˚, состоит из двух развернутых и равен их суме.
- Половина развернутого угла — это прямой угол.
Итак, зная все эти характеристики данного вида углов, мы можем использовать их для решения ряда геометрических задач.
Задачи с развернутыми углами
Для того, чтобы понять, усвоили ли вы понятие развернутого угла, попытайтесь ответить на несколько следующих вопросов.
- Чему равен развернутый угол, если его стороны составляют вертикальную прямую?
- Будут ли два угла смежными, если величина первого 72˚, а другого — 118˚?
- Если полный угол состоит из двух развернутых, то сколько в нем прямых углов?
- Развернутый угол разделили лучом на два таких угла, что их градусные меры относятся как 1:4. Вычислите полученные углы.
Решения и ответы:
- Как бы ни был расположен развернутый угол, он всегда по определению равен 180˚.
- Смежные углы имеют одну общую сторону. Поэтому, чтобы вычислить размер угла, который они составляю вместе, нужно просто прибавить значение их градусных мер. Значит, 72 +118 = 190. Но по определению развернутый угол составляет 180˚, а значит, два данных угла не могут быть смежными.
- Развернутый угол вмещает два прямых угла. А так как в полном имеется два развернутых, значит, прямых в нем будет 4.
- Если мы назовем искомые углы а и b, то пусть х — это коэффициент пропорциональности для них, а это значит, что а=х, и соответственно b=4х. Развернутый угол в градусах равен 180˚. И согласно своим свойствам, что градусная мера угла всегда равна сумме градусных мер тех углов, на которые он разбивается любым произвольным лучом, что проходит между его сторонами, можем сделать вывод, что х + 4х = 180˚, а значит, 5х = 180˚. Отсюда находим: х=а=36˚ и b = 4х = 144˚. Ответ: 36˚ и 144˚.
Если у вас получилось ответить на все эти вопросы без подсказок и не подглядывая в ответы, значит вы готовы переходить к следующему уроку по геометрии.
В этой статье мы всесторонне разберем одну из основных геометрических фигур – угол. Начнем со вспомогательных понятий и определений, которые нас приведут к определению угла. После этого приведем принятые способы обозначения углов. Далее подробно разберемся с процессом измерения углов. В заключении покажем как можно отметить углы на чертеже. Все теорию мы снабдили необходимыми чертежами и графическими иллюстрациями для лучшего запоминания материала.
Навигация по странице.
Определение угла.
Угол является одной из важнейших фигур в геометрии. Определение угла дается через определение луча. В свою очередь представление о луче невозможно получить без знания таких геометрических фигур как точка, прямая и плоскость. Поэтому, перед знакомством с определением угла, рекомендуем освежить в памяти теорию из разделов и .
Итак, будем отталкиваться от понятий точки, прямой на плоскости и плоскости.
Дадим сначала определение луча.
Пусть нам дана некоторая прямая на плоскости. Обозначим ее буквой a
. Пусть O
– некоторая точка прямой a
. Точка O
разделяет прямую a
на две части. Каждая из этих частей вместе с точкой О
называется лучом
, а точка О
называется началом луча
. Еще можно услышать, что луч называют полупрямой
.
Для краткости и удобства ввели следующие обозначения для лучей: луч обозначают либо малой латинской буквой (например, луч p
или луч k
), либо двумя большими латинскими буквами, первая из которых соответствует началу луча, а вторая обозначает некоторую точку этого луча (например, луч ОА
или луч СD
). Покажем изображение и обозначение лучей на чертеже.
Теперь мы можем дать первое определение угла.
Определение.
Угол
– это плоская геометрическая фигура (то есть целиком лежащая в некоторой плоскости), которую составляют два несовпадающих луча с общим началом. Каждый из лучей называют стороной угла
, общее начало сторон угла называют вершиной угла
.
Возможен случай, когда стороны угла составляют прямую линию. Такой угол имеет свое название.
Определение.
Если обе стороны угла лежат на одной прямой, то такой угол называется развернутым
.
Предлагаем Вашему вниманию графическую иллюстрацию развернутого угла.
Для обозначения угла используют значок угла «». Если стороны угла обозначены малыми латинскими буквами (например, одна сторона угла k
, а другая h
), то для обозначения этого угла после значка угла записывают подряд буквы, соответствующие сторонам, причем порядок записи значения не имеет (то есть, или ). Если стороны угла обозначены двумя большими латинскими буквами (к примеру, одна сторона угла OA
, а вторая сторона угла OB
), то угол обозначают следующим образом: после значка угла записывают три буквы, участвующие в обозначении сторон угла, причем буква, отвечающая вершине угла, располагается посередине (в нашем случае угол будет обозначен как или ). Если вершина угла не является вершиной еще какого-нибудь угла, то такой угол можно обозначать буквой, соответствующей вершине угла (например, ). Иногда можно видеть, что углы на чертежах отмечают цифрами (1
, 2
и т.д.), обозначают эти углы как и так далее. Для наглядности приведем рисунок, на котором изображены и обозначены углы.
Любой угол разделяет плоскость на две части. При этом если угол не развернутый, то одну часть плоскости называют внутренней областью угла
, а другую – внешней областью угла
. Следующее изображение разъясняет, какая часть плоскости отвечает внутренней области угла, а какая — внешней.
Любую из двух частей, на которые развернутый угол разделяет плоскость, можно считать внутренней областью развернутого угла.
Определение внутренней области угла приводит нас ко второму определению угла.
Определение.
Угол
– это геометрическая фигура, которую составляют два несовпадающих луча с общим началом и соответствующая внутренняя область угла.
Следует отметить, что второе определение угла строже первого, так как содержит больше условий. Однако не следует отметать первое определение угла, также не следует рассматривать первое и второе определения угла по отдельности. Поясним этот момент. Когда речь идет об угле как о геометрической фигуре, то под углом понимается фигура, составленная двумя лучами с общим началом. Если же возникает необходимость провести какие-либо действия с этим углом (например, измерение угла), то под углом уже следует понимать два луча с общим началом и внутренней областью (иначе возникла бы двоякая ситуация из-за наличия как внутренней так и внешней области угла).
Дадим еще определения смежных и вертикальных углов.
Определение.
Смежные углы
– это два угла, у которых одна сторона общая, а две другие образуют развернутый угол.
Из определения следует, что смежные углы дополняют друг друга до развернутого угла.
Определение.
Вертикальные углы
– это два угла, у которых стороны одного угла являются продолжениями сторон другого.
На рисунке изображены вертикальные углы.
Очевидно, что две пересекающиеся прямые образуют четыре пары смежных углов и две пары вертикальных углов.
Сравнение углов.
В этом пункте статьи мы разберемся с определениями равных и неравных углов, а также в случае неравных углов разъясним, какой угол считается большим, а какой меньшим.
Напомним, что две геометрические фигуры называются равными, если их можно совместить наложением.
Пусть нам даны два угла. Приведем рассуждения, которые помогут нам получить ответ на вопрос: «Равны эти два угла или нет»?
Очевидно, что мы всегда можем совместить вершины двух углов, а также одну сторону первого угла с любой из сторон второго угла. Совместим сторону первого угла с той стороной второго угла, чтобы оставшиеся стороны углов оказались по одну сторону от прямой, на которой лежат совмещенные стороны углов. Тогда, если две другие стороны углов совместятся, то углы называются равными
.
Если же две другие стороны углов не совместятся, то углы называются неравными
, причем меньшим
считается тот угол, который составляет часть другого (большим
является тот угол, который полностью содержит другой угол).
Очевидно, что два развернутых угла равны. Также очевидно, что развернутый угол больше любого неразвернутого угла.
Измерение углов.
Измерение углов основывается на сравнении измеряемого угла с углом, взятым в качестве единицы измерения. Процесс измерения углов выглядит так: начиная от одной из сторон измеряемого угла, его внутреннюю область последовательно заполняют единичными углами, плотно укладывая их один к другому. При этом запоминают количество уложенных углов, которое и дает меру измеряемого угла.
Фактически, в качестве единицы измерения углов может быть принят любой угол. Однако существует множество общепринятых единиц измерения углов, относящихся к различным областям науки и техники, они получили специальные названия.
Одной из единиц измерения углов является градус
.
Определение.
Один градус
– это угол, равный одной сто восьмидесятой части развернутого угла.
Градус обозначают символом «», следовательно, один градус обозначается как .
Таким образом, в развернутом угле мы можем уложить 180
углов в один градус. Это будет выглядеть как половинка круглого пирога, разрезанная на 180
равных кусочков. Очень важно: «кусочки пирога» плотно укладываются один к другому (то есть, стороны углов совмещаются), причем сторона первого угла совмещается с одной стороной развернутого угла, а сторона последнего единичного угла совпадет с другой стороной развернутого угла.
При измерении углов выясняют, сколько раз градус (или другая единица измерения углов) укладывается в измеряемом угле до полного покрытия внутренней области измеряемого угла. Как мы уже убедились, в развернутом угле градус укладывается ровно 180
раз. Ниже приведены примеры углов, в которых угол в один градус укладывается ровно 30
раз (такой угол составляет шестую часть развернутого угла) и ровно 90
раз (половина развернутого угла).
Для измерения углов, меньших одного градуса (или другой единицы измерения углов) и в случаях, когда угол не удается измерить целым числом градусов (взятых единиц измерения), приходится использовать части градуса (части взятых единиц измерения). Определенные части градуса получили специальные названия. Наибольшее распространение получили, так называемые, минуты и секунды.
Определение.
Минута
– это одна шестидесятая часть градуса.
Определение.
Секунда
– это одна шестидесятая часть минуты.
Иными словами, в минуте содержится шестьдесят секунд, а в градусе – шестьдесят минут (3600
секунд). Для обозначения минут используют символ «», а для обозначения секунд – символ «» (не путайте со знаками производной и второй производной). Тогда при введенных определениях и обозначениях имеем , а угол, в котором укладываются 17
градусов 3
минуты и 59
секунд, можно обозначить как .
Определение.
Градусной мерой угла
называется положительное число, которое показывает сколько раз градус и его части укладываются в данном угле.
Например, градусная мера развернутого угла равна ста восьмидесяти, а градусная мера угла равна .
Для измерения углов существуют специальные измерительные приборы, наиболее известным из них является транспортир.
Если известно и обозначение угла (к примеру, ) и его градусная мера (пусть 110
), то используют краткую запись вида и говорят: «Угол АОВ
равен ста десяти градусам».
Из определений угла и градусной меры угла следует, что в геометрии мера угла в градусах выражается действительным числом из интервала (0, 180]
(в тригонометрии рассматривают углы с произвольной градусной мерой, их называют ). Угол в девяносто градусов имеет специальное название, его называют прямым углом
. Угол меньший 90
градусов называется острым углом
. Угол больший девяноста градусов называется тупым углом
. Итак, мера острого угла в градусах выражается числом из интервала (0, 90)
, мера тупого угла – числом из интервала (90, 180)
, прямой угол равен девяноста градусам. Приведем иллюстрации острого угла, тупого угла и прямого угла.
Из принципа измерения углов следует, что градусные меры равных углов одинаковы, градусная мера большего угла больше градусной меры меньшего, а градусная мера угла, который составляют несколько углов, равна сумме градусных мер составляющих углов. На рисунке ниже показан угол АОВ
, который составляют углы АОС
, СОD
и DОВ
, при этом .
Таким образом, сумма смежных углов равна ста восьмидесяти градусам
, так как они составляют развернутый угол.
Из этого утверждения следует, что . Действительно, если углы АОВ
и СОD
– вертикальные, то углы АОВ
и ВОС
— смежные и углы СОD
и ВОС
также смежные, поэтому, справедливы равенства и , откуда следует равенство .
Наряду с градусом удобна единица измерения углов, называемая радианом
. Радианная мера широко используется в тригонометрии. Дадим определение радиана.
Определение.
Угол в один радиан
– это центральный угол
, которому соответствует длина дуги, равная длине радиуса соответствующей окружности.
Дадим графическую иллюстрацию угла в один радиан. На чертеже длина радиуса OA
(как и радиуса OB
) равна длине дуги AB
, поэтому, по определению угол AOB
равен одному радиану.
Для обозначения радианов используют сокращение «рад». Например, запись 5 рад означает 5 радианов. Однако на письме обозначение «рад» часто опускают. К примеру, когда написано, что угол равен пи, то имеется в виду пи рад.
Стоит отдельно отметить, что величина угла, выраженная в радианах, не зависит от длины радиуса окружности. Это связано с тем, что фигуры, ограниченные данным углом и дугой окружности с центром в вершине данного угла, подобны между собой.
Измерение углов в радианах можно выполнять так же, как и измерение углов в градусах: выяснить, сколько раз угол в один радиан (и его части) укладываются в данном угле. А можно вычислить длину дуги соответствующего центрального угла, после чего разделить ее на длину радиуса.
Для нужд практики полезно знать, как соотносятся между собой градусная и радианная меры, так как довольно часть приходится осуществлять . В указанной статье установлена связь между градусной и радианной мерой угла, и приведены примеры перевода градусов в радианы и обратно.
Обозначение углов на чертеже.
На чертежах для удобства и наглядности углы можно отмечать дугами, которые принято проводить во внутренней области угла от одной стороны угла до другой. Равные углы отмечают одинаковым количеством дуг, неравные углы – различным количеством дуг. Прямые углы на чертеже обозначают символом вида «», который изображают во внутренней области прямого угла от одной стороны угла до другой.
Если на чертеже приходится отмечать много различных углов (обычно больше трех), то при обозначении углов кроме обычных дуг допустимо использование дуг какого-либо специального вида. К примеру, можно изобразить зубчатые дуги, или нечто подобное.
Следует отметить, что не стоит увлекаться с обозначением углов на чертежах и не загромождать рисунки. Рекомендуем обозначать только те углы, которые необходимы в процессе решения или доказательства.
Список литературы.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. Геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы.
- Погорелов А.В., Геометрия. Учебник для 7-11 классов общеобразовательных учреждений.
Толковый словарь Ушакова.
Д.Н. Ушаков.
1935-1940.
Как правильно пишется слово «угол»
у́гол
у́гол, угла́, предл. в (на) углу́ и (матем.) в угле́
Источник: Орфографический
академический ресурс «Академос» Института русского языка им. В.В. Виноградова РАН (словарная база
2020)
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать
Карту слов. Я отлично
умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: чумак — это что-то нейтральное, положительное или отрицательное?
Ассоциации к слову «угол»
Синонимы к слову «угол»
Предложения со словом «угол»
- В дальнем углу комнаты стоял довольно большой шкаф с резными дверцами – видимо, для одежды.
- В дальнем углу комнаты стояла ещё и целая колонна, выложенная из круглых и, похоже, однотипных щитов.
- Казалось, будто какой-то унылый жилец, которому лучше всего было бы запереться в самом дальнем углу дома, вдруг пробил крышу и высунулся наружу, чтобы показаться всему свету.
- (все предложения)
Цитаты из русской классики со словом «угол»
- Гостиная в доме Торцова. У задней стены диван, перед диваном круглый стол и шесть кресел, по три на стороне; в левом углу дверь; на стенах по зеркалу и под ними маленькие столики; в боковых стенах по двери и дверь на задней в углу. На сцене темно; из левой двери свет.
- У первого окна, ближе к авансцене, высокое кресло и столик, на нем раскрытая старинная книга и колокольчик; в глубине, в правом углу, двустворчатая дверь в большую переднюю; в левом — дверь в комнату Мурзавецкого; между дверями печь; на левой стороне, в углу, дверь в коридор, ведущий во внутренние комнаты; ближе к авансцене двери в гостиную; между дверями придвинут к стене большой обеденный стол.
- Часть столовой — скучный угол со старинными часами на стене. Солидный буфет и большой стол, уходящий наполовину за пределы сцены. Широкая арка, занавешенная тёмной драпировкой, отделяет столовую от гостиной; гостиная глубже столовой, тесно заставлена старой мебелью. В правом углу горит небольшая электрическая лампа; под нею на кушетке Вера с книгой в руках. Между стульев ходит Пётр, точно ищет чего-то. В глубине у окна Любовь, она встала коленями на стул, держится за спинку и смотрит в окно.
- (все
цитаты из русской классики)
Каким бывает «угол»
Значение слова «угол»
-
У́ГОЛ, угла́, предл. об угле́, в углу́ и (мат.) в угле́, м. 1. Мат. Часть плоскости между двумя прямыми линиями, исходящими из одной точки. Измерение угла. Прямой угол (равный 90°). Тупой угол (более 90°). Острый угол (менее 90°). Дополнительный угол. (Малый академический словарь, МАС)
Все значения слова УГОЛ
Афоризмы русских писателей со словом «угол»
- За все, что есть в тебе, за все, что слышу, вижу,
За тихий твой простор, за красоту твою,
За то, что нет в тебе того, что ненавижу,
Родимый угол мой, тебя я так люблю. - Молчанье — это будущее слов,
Уже пожравших гласными всю вещность,
Страшащуюся собственных углов;
Волна, перекрывающая вечность. - У больных появляется страстная привязанность именно к своему углу…
- (все афоризмы русских писателей)
Отправить комментарий
Дополнительно
Смотрите также
У́ГОЛ, угла́, предл. об угле́, в углу́ и (мат.) в угле́, м. 1. Мат. Часть плоскости между двумя прямыми линиями, исходящими из одной точки. Измерение угла. Прямой угол (равный 90°). Тупой угол (более 90°). Острый угол (менее 90°). Дополнительный угол.
Все значения слова «угол»
-
В дальнем углу комнаты стоял довольно большой шкаф с резными дверцами – видимо, для одежды.
-
В дальнем углу комнаты стояла ещё и целая колонна, выложенная из круглых и, похоже, однотипных щитов.
-
Казалось, будто какой-то унылый жилец, которому лучше всего было бы запереться в самом дальнем углу дома, вдруг пробил крышу и высунулся наружу, чтобы показаться всему свету.
- (все предложения)
- закуток
- уголок
- уголочек
- закоулок
- дом
- (ещё синонимы…)
- закуток
- наказание
- геометрия
- углы
- треугольник
- (ещё ассоциации…)
- в дальний угол
- в углу комнаты
- во главу угла
- забиться в угол
- (полная таблица сочетаемости…)
- медвежий
- неестественный
- немыслимый
- юго-восточный
- дальний
- (ещё…)
- Склонение
существительного «угол» - Разбор по составу слова «угол»
Угол. Обозначение углов
Угол — геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
На рис. 1 лучи АВ и АС — стороны угла, точка А — вершина угла.
При записи угла в середине пишут букву, обозначающую его вершину. Сам угол на рис. 1 обозначают так: 






Если углы имеют общую вершину, то их нельзя обозначить одной буквой. Так на рис. 2 углы имеют общую вершину Е, поэтому мы можем использовать для данных углов только следующие обозначения: 











Также иногда углы обозначают цифрами, например, на рис.3 мы имеем 
Углы, как и отрезки, можно сравнивать между собой. Чтобы сравнить два угла можно наложить один угол на другой. Если при наложении одного угла на другой они совпадут, то эти углы равны.
Биссектриса — луч, который делит угол на два равных угла. На рис. 4 углы НОМ и DОМ равны, значит, луч ОМ — биссектриса угла НОD.
Прямой угол — угол, который можно построить с помощью угольника (рис. 5).
Если начертить два прямых угла с общей вершиной и одной общей стороной, то две другие стороны этих углов составят прямую (рис. 6). Считают, что лучи, составляющие прямую, также образуют угол, который называют развернутым.
На рис. 6 


Развернутый угол равен двум прямым углам, а прямой угол составляет половину развернутого.
Острый угол — угол, который меньше прямого угла. На рис. 7 
Тупой угол — угол, который больше прямого угла, но меньше развернутого. На рис. 8 
Поделись с друзьями в социальных сетях:
Как написать углы треугольника
Треугольник
Треугольник — это замкнутая ломаная линия, состоящая из трёх звеньев:
Вершины ломаной называются вершинами треугольника, а её звенья — сторонами треугольника. Углы, образованные двумя сторона треугольника, называются углами треугольника:
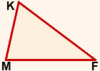
В треугольнике ABC вершины A, B и C — это вершины треугольника, звенья AB, BC и CA — стороны треугольника. Три угла — ∠ABC, ∠BCA и ∠CAB — углы треугольника. Часто углы треугольника обозначаются только одной буквой: ∠A, ∠B, ∠C.
Треугольник обычно обозначается тремя буквами, стоящими при его вершинах. Например, треугольник ABC, или BCA, или CBA. Вместо слова треугольник часто используется знак 

У каждого треугольника 3 вершины, 3 стороны и 3 угла.
Высота
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на его основание. Высота треугольника может быть опущена и на продолжение основания.
Отрезок BN — это высота 

Длина высоты — это длина отрезка от вершины угла до пересечения с основанием.
Каждый треугольник имеет три высоты.
Биссектриса
Биссектриса угла треугольника — прямая, делящая угол треугольника пополам. Длина отрезка этой прямой от вершины угла до точки пересечения с противоположной стороной называется длиной биссектрисы.
Отрезок BN — это биссектриса 
Каждый треугольник имеет три биссектрисы.
Медиана
Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Длина этого отрезка называется длиной медианы.
Отрезок BN — это медиана 
Как называются углы треугольника
Как называются углы треугольника? Ответ может зависеть от того, сколько углов имеется при вершине треугольника.
Если при вершине треугольника есть только один угол, то его можно назвать одной буквой, по названию вершины.
Например, в треугольнике MKF (рисунок 1) при каждой вершине есть только один угол. Следовательно, каждый из углов можно назвать одной буквой, по названию вершины, из которой исходят образующие этот угол лучи:
Угол M, угол K и угол F.
Для обозначения угла существует специальный знак: ∠
Запись ∠ M читают как «угол M».
Каждый из углов треугольника MKF можно назвать также тремя буквами. При этом вершина в названии угла должна стоять посередине.
Угол M также можно назвать углом KMF или углом FMK,
В треугольниках, изображенных на рисунке 2, одной буквой могут быть названы только углы при вершинах A и D: ∠A и ∠D.
При вершине B есть три угла, поэтому каждый из этих углов нужно назвать тремя буквами: ∠ABC, ∠CBD и ∠ABD.
Аналогично, углы при вершине C могут быть названы только тремя буквами: ∠ACB, ∠BCD и ∠ACD. Назвать какой-либо из этих углов ∠C нельзя.
Каждый из углов треугольников, изображенных на рисунке 3, может быть назван только тремя буквами.
Треугольник. Формулы и свойства треугольников.
Типы треугольников
По величине углов
По числу равных сторон
Вершины углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°:
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
если α > β , тогда a > b
если α = β , тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 — 2 bc · cos α
b 2 = a 2 + c 2 — 2 ac · cos β
c 2 = a 2 + b 2 — 2 ab · cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Медианы треугольника
Свойства медиан треугольника:
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
Медиана треугольника делит треугольник на две равновеликие части
Треугольник делится тремя медианами на шесть равновеликих треугольников.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 1 2 √ 2 b 2 +2 c 2 — a 2
mb = 1 2 √ 2 a 2 +2 c 2 — b 2
mc = 1 2 √ 2 a 2 +2 b 2 — c 2
Биссектрисы треугольника
Свойства биссектрис треугольника:
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
la = 2√ bcp ( p — a ) b + c
lb = 2√ acp ( p — b ) a + c
lc = 2√ abp ( p — c ) a + b
где p = a + b + c 2 — полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
la = 2 bc cos α 2 b + c
lb = 2 ac cos β 2 a + c
lc = 2 ab cos γ 2 a + b
Высоты треугольника
Свойства высот треугольника
Формулы высот треугольника
ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Окружность вписанная в треугольник
Свойства окружности вписанной в треугольник
Формулы радиуса окружности вписанной в треугольник
r = ( a + b — c )( b + c — a )( c + a — b ) 4( a + b + c )
Окружность описанная вокруг треугольника
Свойства окружности описанной вокруг треугольника
Формулы радиуса окружности описанной вокруг треугольника
R = S 2 sin α sin β sin γ
R = a 2 sin α = b 2 sin β = c 2 sin γ
Связь между вписанной и описанной окружностями треугольника
Средняя линия треугольника
Свойства средней линии треугольника
MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC
MN || AC KN || AB KM || BC
Периметр треугольника
Периметр треугольника ∆ ABC равен сумме длин его сторон
Формулы площади треугольника
Формула Герона
Равенство треугольников
Признаки равенства треугольников
Первый признак равенства треугольников — по двум сторонам и углу между ними
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Третий признак равенства треугольников — по трем сторонам
Подобие треугольников
∆MNK => α = α 1, β = β 1, γ = γ 1 и AB MN = BC NK = AC MK = k ,
где k — коэффициент подобия
Признаки подобия треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Треугольник
Треугольник — это замкнутая ломаная линия, состоящая из трёх звеньев:
Вершины ломаной называются вершинами треугольника, а её звенья — сторонами треугольника. Углы, образованные двумя сторона треугольника, называются углами треугольника:
В треугольнике ABC вершины A, B и C — это вершины треугольника, звенья AB, BC и CA — стороны треугольника. Три угла — ∠ABC, ∠BCA и ∠CAB — углы треугольника. Часто углы треугольника обозначаются только одной буквой: ∠A, ∠B, ∠C.
Треугольник обычно обозначается тремя буквами, стоящими при его вершинах. Например, треугольник ABC, или BCA, или CBA. Вместо слова треугольник часто используется знак 

У каждого треугольника 3 вершины, 3 стороны и 3 угла.
Высота
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на его основание. Высота треугольника может быть опущена и на продолжение основания.
Отрезок BN — это высота 

Длина высоты — это длина отрезка от вершины угла до пересечения с основанием.
Каждый треугольник имеет три высоты.
Биссектриса
Биссектриса угла треугольника — прямая, делящая угол треугольника пополам. Длина отрезка этой прямой от вершины угла до точки пересечения с противоположной стороной называется длиной биссектрисы.
Отрезок BN — это биссектриса 
Каждый треугольник имеет три биссектрисы.
Медиана
Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Длина этого отрезка называется длиной медианы.
Отрезок BN — это медиана 
источники:
http://b4.cooksy.ru/articles/kak-napisat-ugly-treugolnika
http://izamorfix.ru/matematika/planimetriya/treugolnik.html
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Углы в геометрии
Поддержать сайт
Запомните!
Угол — это геометрическая фигура, которая состоит из двух лучей и вершины.
Вершина угла — это точка, в которой два луча берут начало.
Стороны угла — это лучи, которые образуют угол.
Например:
Вершина угла — точка «O».
Стороны угла — «OA» и «OB».
Для обозначения угла в тексте используется символ:

Способы обозначения углов
-
Одной заглавной латинской буквой, указывающей его вершину.
Угол:O
-
Тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные
на сторонах угла.
Угол:AOD
Называть угол можно с любого края, но НЕ с вершины.
Угол с рисунка выше имеет два названия:
AOD
иDOA.
Запомните!
При таком обозначении вершина угла должна всегда находиться в середине названия.
Единица измерения углов — градусы. Углы измеряют с помощью специального прибора — транспортира.
Для обозначения градусов в тексте используется символ: °
50 градусов обозначаются так: «50°»
Виды углов
| Вид угла | Размер в градусах | Пример |
|---|---|---|
| Прямой | Равен 90° | 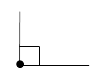 |
| Острый | Меньше 90° |
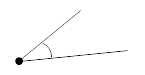 |
| Тупой | Больше 90° |
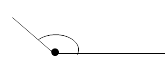 |
| Развернутый | Равен 180° |
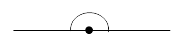 |
Запомните!
Два угла могут иметь одну общую сторону.
Обратите внимание на рисунок ниже. Попробуйте сосчитать и назвать все углы на изображении.
Если насчитали три угла, то вы правы. Давайте их назовём:
Углы 

имеют общую сторону OB.