Перейти к содержанию
«Преобразовать» или «приобразовать» — как правильно?
На чтение 2 мин Просмотров 1.9к. Опубликовано 29.11.2021
При написании приставок глаголов нередки ошибки. Попробуем разобраться, как верно – «преобразовать» или «приобразовать», и почему.
Как пишется правильно: «преобразовать» или «приобразовать»?
Какое применяется правило
Чтобы понять правописание нашего слова, следует выяснить его часть речи, задав для этого вопрос: «что делать?» – «преобразовать». Перед нами глагол. Произведем его морфемный разбор:
- «пре» – приставка;
- «образова» – корень;
- «ть» – суффикс.
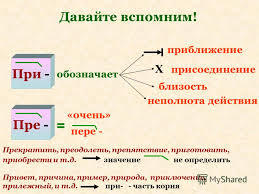
У нас вызывает сомнение написание приставки. В глаголах приставка «пре» пишется для обозначения:
- усиления,
- «пере».
«Преобразовать» используется в значении «переделать что-либо», поэтому пишется с приставкой «пре».
Примеры предложений
Встав на должность генерального директора, Андрей решил полностью преобразовать производство.
Мне необходимо преобразовать информацию из неэлектронного варианта в электронный.
Как неправильно писать
Это идет вразрез с принятыми орфографическими требованиями.
Равносильные уравнения
Два или более уравнений называются равносильными, если они имеют одни и те же корни. Например, уравнения:
равносильные, потому что имеют одни и те же корни (2 и 1 — это можно проверить подстановкой).
Уравнения, не имеющие корней, также считаются равносильными.
Преобразование уравнений
Если одно уравнение заменяется другим уравнением, равносильным данному, то такая замена называется преобразованием уравнения. Например, уравнение
можно преобразовать в такое:
Если одно уравнение заменяется другим, равносильным данному и при этом более простым, то такое преобразование называется упрощением уравнения. Например, упростим следующее уравнение:
заменив его равносильным уравнением
Все преобразования уравнений основаны на двух свойствах равенств, и следствиях, которые вытекают из данных свойств.
Если к обеим частям уравнения прибавить или отнять одно и то же число или алгебраическое выражение, то получится уравнение, равносильное данному.
Рассмотрим уравнение x — 5 = 7. Прибавив к обеим частям уравнения число 5
получим уравнение x = 12. Если в уравнение x — 5 = 7 вместо x подставить число 12, то можно удостовериться, что, прибавив к обеим частям уравнения число 5, мы не только получили равносильное уравнение, но и нашли его корень.
Из данного свойства можно вывести три следствия:
- Если в обеих частях уравнения есть одинаковые члены с одинаковыми знаками, то эти члены можно опустить (сократить).
Возьмём уравнение x + 13 = 10 + 13. Отняв от обеих частей по 13, получим
Любой член уравнения можно перенести из одной части в другую, изменив его знак на противоположный.
Рассмотрим уравнение 5x — 4 = 12 + x. Прибавим к обеим частям уравнения по 4:
5x — 4 + 4 = 12 + x + 4.
то есть член 4 перешёл в другую часть с обратным знаком. Теперь вычтем из обеих частей уравнения 5x — 4 = 12 + x по x:
то есть член x перешёл в другую часть с обратным знаком.
Знаки всех членов уравнения можно заменить на противоположные.
Перенесём все члены левой части уравнения 5x — 4 = 12 + x в правую, а все члены правой в левую:
И, учитывая, что части любого равенства ( в том числе и любого уравнения) можно менять местами, то, поменяв левую часть с правой, получим:
то есть получилось, что мы просто заменили знаки всех членов уравнения на противоположные.
Данное преобразование можно также рассматривать как умножение обеих частей уравнения на -1.
Если обе части уравнения умножить или разделить на одно и то же число или алгебраическое выражение, то получится уравнение, равносильное данному.
Рассмотрим уравнение 3x = 12. Разделив обе части уравнения на число 3:
получим уравнение x = 4. Если в уравнение 3x = 12 вместо x подставить число 4, то можно удостовериться, что, разделив обе части уравнения на 3, мы не только получили равносильное уравнение, но и нашли его корень.
Из данного свойства можно вывести два следствия:
- Если все члены уравнения имеют общий множитель, то можно разделить на него все члены уравнения, таким образом, упростив его.
Возьмём уравнение 16x + 8 = 40. Разделив все члены на общий множитель 8, получим:
Если в уравнении есть дробные члены, то от них можно освободить уравнение, приведя все члены к одному знаменателю и затем отбросить его.
| x + | 12 — x | = | 26 — x | . |
| 4 | 2 |
После приведения всех членов к общему знаменателю получим:
| 4x | + | 12 — x | = | 2(26 — x) | . |
| 4 | 4 | 4 |
Теперь, умножив все члены уравнения на 4, или, что то же самое, просто отбросив знаменатель, получим:
Общие методы преобразования уравнений
Разделы: Математика
Цели и задачи урока:
- обобщить и углубить знания по теме;
- сформировать представление о методах и способах решения алгебраических уравнений на уровне, превышающем уровень государственных образовательных стандартов;
- формирование навыков умственного труда;
- развивать качества мышления: гибкость, рациональность, критичность;
- развитие внимания, логического мышления, аргументированной математической речи, самостоятельности, познавательной активности;
- воспитание ответственности, воли, упорства в достижении поставленной цели, умение контролировать внимание на всех этапах урока.
Оборудование: кодоскоп, слайды, доклады-сообщения учащихся.
Тип урока: урок формирования знаний, умений и навыков.
Формы обучения: общеклассная, групповая, индивидуальная.
Методы обучения: словесный, наглядный, практические задания, самостоятельная деятельность, проблемно-поисковый.
I. Организационный момент
Мотивационная беседа с учащимися пропедевтической направленности через осознание ими практической значимости изучаемых и применяемых знаний, умений и навыков.
Эпиграф урока: «Час, затраченный на понимание, экономит год жизни». (В. Босс)
II. Актуализация опорных знаний учащихся
1. Работа по основным определениям, понятиям, относящимся к уравнениям (вопросы, составленные на основе курса лекций 1-4 «Уравнения и неравенства в школьном курсе математики» автора П.В. Чулкова, М. Шабунин «Уравнения» – библиотека приложения к газете 1 сентября, дополнительные главы по курсу математики 10 под редакцией З.А. Скопеца);
2. Ответить на вопросы:
– Верно ли, что 5х = 10 

– Верно ли, что 2х = 10 
3. Алгоритм решения уравнения или как мы решаем уравнения?
III. Решение уравнений
Рассмотрим наиболее часто встречаемые преобразования уравнений.
а) разложение на множители (или расщепление уравнений):
1. х 3 – 4х 2 – 16х + 64 = 0
(х 3 – 4х 2 ) – (16х – 64) = 0
х 2 (х – 4) – 16(х – 4) = 0
(х – 4)(х 2 – 16) = 0
(х – 4) 2 (х + 4) = 0
х1 = 4 или х2 = – 4
2. х 3 + х – 10 = 0 (заслушать предлагаемые учащимися способы)
х 3 + х – 8 – 2 = 0
(х 3 – 
(х – 2)(х 2 + 2х + 4) + (х – 2) = 0
(х – 2)( х 2 + 2х + 5) = 0
(х – 2) = 0 или х 2 + 2х + 5= 0
х1 = 2 т.к. D = –16 2 + х + 1)(х 2 + х + 2) = 12 (Заслушать предлагаемые учащимися способы. Очевидно, что ученики предложат выполнить умножение многочлена на многочлен)
– А какова степень уравнения? А нет ли более рационального способа решения? Посмотрите, как «звучит» способ в заголовке? Что вы заметили?
Возможны варианты: x 2 + x = t или x 2 + x + 1 = t
Пусть x 2 + x + 1 = t
Тогда t (t + 1) = 12
t 2 + t – 12 = 0, получаем t1 = – 4; t2 = 3.
Отсюда: х 2 + х + 1 = – 4 или х 2 + х + 1 = 3
х 2 + х + 5 = 0 х 2 + х – 2 = 0
т.к. D = –19 0 
Т.к. сумма коэффициентов a + b + c = 0, то х1 = 1; х2 = c/a х2 = – 2
2. Используйте этот приём для решения следующего уравнения:
; ОДЗ: х =/= 0, х =/= – 4, х =/= – 2.
Запишем уравнение иначе:
Пусть x 2 + 4x = t, тогда
Получим: 1 . 5(t + 4) – 1 . t . 5 = 4 . t . (t + 4)
5t + 20 – 5t = 4t 2 + 16t
4t 2 + 16t – 20 = 0
t 2 + 4t – 5 = 0 D = 36 > 02 корня. По сумме коэффициентов: 1 + 4 – 5 = 0 имеем: t1 = 1; t2 = c/a t2 = – 5. Оба корня принадлежат ОДЗ уравнения с переменной t.
Отсюда: x 2 + 4x = 1 или x 2 + 4x = – 5
x 2 + 4x – 1 = 0 x 2 + 4x + 5 = 0
D = 20 > 02 корня т.к. D = – 4 2 + 3х + 3)(х 2 – 2х + 3) = 24х 2
(Посмотреть на реакцию учащихся)
Для введения новой переменной «мешает» х 2 в правой части, нет никакого смысла применять замену х 2 = t. Как же преобразовать уравнение? Причём так преобразовать, чтобы правая часть не содержала х 2 . (как в уравнении 1) этого метода) Выслушать мнение учащихся. Достаточно разделить почленно уравнение на х 2 , т.к. х = 0 не является корнем данного уравнения!
(х 2 + 3х + 3)(х 2 – 2х + 3) = 24х 2
х 2 =/= 0

Вот теперь пусть, тогда (t + 3)(t – 2) = 24
t 2 + t – 30 = 0, получаем: t1 = – 6; t2 = 5.
Отсюда:= – 6 или
= 5
х 2 + 6х + 3 = 0 или х 2 – 5х + 3 = 0
D = 24 > 02 корня D = 13 > 0
2 корня
Ответ:
;
.
4. А вот ещё одно очень интересное уравнение:
–1 и + 3 можно представить в виде сумм, одно из слагаемых которых будет 1 : – 1 = – 2 + 1 и 3 = 2 + 1.
Тогда х – 1 = х – 2 + 1 = (х + 1) – 2
х + 3 = х + 2 + 1 = (х + 1) + 2, получим уравнение:
((х +1) – 2) 4 + ((х +1) + 2) 4 = 82, пусть х + 1 = t,
Тогда (t – 2) 4 + (t + 2) 4 = 82.
На первый взгляд, новое уравнение не отличается принципиально от данного: мы получили четвёртую степень двучлена, но вторые слагаемые двучлена отличаются только знаками, что намного упрощает конечный вид и преобразования полученного уравнения.
В результате преобразований получается биквадратное уравнение относительно переменной t: t 4 + 24 t 2 – 25 = 0; пусть t 2 = y, тогда y 2 + 24y – 25 = 0
Корни этого уравнения 1 и – 25.
Отсюда: t 2 = 1 или t 2 = – 25
t1,2 = ± 
Свойства симметрических уравнений:
а) если дано уравнение нечётной степени, то х = – 1 – корень уравнения;
б) уравнение чётной степени 2n с помощью подстановки v = x + 1/x сводится к уравнению степени n.
Рассмотрим решение на конкретном уравнении:
2х 5 + 5х 4 – 13х 3 – 13х 2 + 5х + 2 = 0 да, по определению это симметрическое уравнение нечётной степени. Значит х = – 1 – корень исходного уравнения; разложим его на множители:
(х + 1)(2х 4 + 3х 3 – 16х 2 + 3х + 2) = 0;
работаем со вторым множителем:
2х 4 + 3х 3 – 16х 2 + 3х + 2 = 0 ¦: х2 =/= 0 2х 2 + 3х – 16 + 3 . 1/х + 2 . 1/х 2 = 0.
Группируем: 2(х 2 + 1/х 2 ) + 3(х + 1/х) – 16 = 0. Пусть х + 1/х =, тогда х 2 + 1/х 2 = t 2 – 2,
отсюда: 2(t 2 – 2) + 3t – 16 = 0 и далее 2t 2 + 3t – 20 = 0,
решая это уравнение, получим: t1= – 4 и t2 = – 5/2; откуда х + 1/х = – 4 или х + 1/х = – 5/2.
Решая эти уравнения, получим: х1,2 = – 2 ±, х3 = 2, х4 = 1/2.
Ответ: – 1, – 2 ±
, 2, 1/2.
2. Определение. Уравнение вида a0(u(x)) n + a1(u(x)) n – 1 v(x) + a2(u(x)) n – 2 (v(x)) 2 +…+ ak(u(x)) n – k (v(x)) k +…+ a0(v(x)) n = 0 называют однородным уравнением степени n относительно u(x) иv(x).
Решите уравнение: (х – 2) 2 (х + 1) 2 – (х – 2)(х 2 – 1) – (х – 1) 2 = 0
Пусть u = (х – 2)(х + 1) и v = х – 1, получаем: u 2 – uv – 2v 2 = 0.
Рассмотрим все возможные случаи:
а) v = 0, тогда х = 1, но 1 не является корнем исходного уравнения (была проверка!);
б) v =/= 0, тогда заменой p = u/v получаем уравнение: p 2 – p – 2 = 0, откуда p1 = –1, p2 = 2. т.е. 
Решаем эти уравнения, получаем: х1 = 0; х2 = 3; х3,4 = + 
Ответ: 0; 3; + 
VI. Итог урока
Рефлексия: беседа с учащимися о занятии, что необходимо школьнику, чтобы заметить тот или иной приём, рациональный в данном конкретном случае, что было трудно, какой приём требуется ещё повторить?
VII. Домашнее задание:
Решите уравнения:
- х 4 + (1 – х) 4 = 1/8;
- (х + 2)(х – 3)(х – 1)(х + 6) = 40х 2
- х 2 (х – 1) 2 + х(х 2 – 1) = 2(х + 1) 2 .
Проверочная работа.
1) Равносильны ли уравнения
2) Какое из двух уравнений является следствием другого: х 2 = 9 или х = 3?
3) Решите уравнения:
- х 3 – 6х 2 + 11х – 6 = 0;
- х 6 – 9х 3 + 8 = 0;
- (х 2 – 6х) 2 – 2(х – 3) 2 = 81;
- х(х + 3)(х + 5)(х +
= 10;
- х 4 – 4х 3 + 5х 2 – 4х + 1 = 0;
;
- (х 2 + х + 4) 2 + 8х(х 2 + х + 4) + 15х 2 = 0;
.
1) нет,
2) первое,
3)
- 1; 2; 3,
- 1; 2,
- 3; 3 + 2
,
- – 4 +
,
,
- 0,
- – 2; – 3 +
,
- 7 +
.
Равносильные уравнения, преобразование уравнений
Некоторые преобразования позволяют нам перейти от решаемого уравнения к равносильным, а также к уравнениям-следствиям, благодаря чему упрощается решение первоначального уравнения. В данном материале мы расскажем, что из себя представляют эти уравнения, сформулируем основные определения, проиллюстрируем их наглядными примерами и поясним, как именно осуществляется вычисление корней исходного уравнения по корням уравнения-следствия или равносильного уравнения.
Понятие равносильных уравнений
Равносильными называются такие уравнения, имеющие одни и те же корни, или же те, в которых корней нет.
Определения такого типа часто встречаются в различных учебниках. Приведем несколько примеров.
Уравнение f ( x ) = g ( x ) считается равносильным уравнению r ( x ) = s ( x ) , если у них одинаковые корни или у них обоих нет корней.
Уравнения с одинаковыми корнями считаются равносильными. Также ими считаются два уравнения, одинаково не имеющие корней.
Если уравнение f ( x ) = g ( x ) имеет то же множество корней, что и уравнение p ( x ) = h ( x ) , то они считаются равносильными по отношению друг к другу.
Когда мы говорим о совпадающем множестве корней, то имеем в виду, что если определенное число будет корнем одного уравнения, то оно подойдет в качестве решения и другому уравнению. Ни одно из уравнений, являющихся равносильными, не может иметь такого корня, который не подходит для другого.
Приведем несколько примеров таких уравнений.
Например, равносильными будут 4 · x = 8 , 2 · x = 4 и x = 2 , поскольку каждое из них имеет только один корень – двойку. Также равносильными будут x · 0 = 0 и 2 + x = x + 2 , поскольку их корнями могут быть любые числа, то есть множества их решений совпадают. Также равносильными будут уравнения x = x + 5 и x 4 = − 1 , каждое из которых не имеет ни одного решения.
Для наглядности рассмотрим несколько примеров неравносильных уравнений.
К примеру, таковыми будут x = 2 и x 2 = 4 , поскольку их корни отличаются. То же относится и к уравнениям x x = 1 и x 2 + 5 x 2 + 5 , потому что во втором решением может быть любое число, а во втором корнем не может быть 0 .
Определения, данные выше, подойдут и для уравнений с несколькими переменными, однако в том случае, когда мы говорим о двух, трех и более корнях, более уместно выражение «решение уравнения». Таким образом, подытожим: равносильные уравнения – это те уравнения, у которых одни и те же решения или их совсем нет.
Возьмем примеры уравнений, которые содержат несколько переменных и являются равносильными друг другу. Так, x 2 + y 2 + z 2 = 0 и 5 · x 2 + x 2 · y 4 · z 8 = 0 включают в себя по три переменных и имеют только одно решение, равное 0 , во всех трех случаях. А пара уравнений x + y = 5 и x · y = 1 равносильной по отношению друг к другу не будет, поскольку, например, значения 5 и 3 подойдут для первого, но не будут решением второго: при подстановке их в первое уравнение мы получим верное равенство, а во второе – неверное.
Понятие уравнений-следствий
Процитируем несколько примеров определений уравнений-следствий, взятых из учебных пособий.
Следствием уравнения f ( x ) = g ( x ) будет уравнение p ( x ) = h ( x ) при условии, что каждый корень первого уравнения будет в то же время корнем второго.
источники:
http://urok.1sept.ru/articles/578198
http://zaochnik.com/spravochnik/matematika/systems/ravnosilnye-uravnenija-preobrazovanie-uravnenij/
-
Главная
- Правописание слова «преобразовать»
Неверные варианты написания
приобразовать
Верный вариант написания
преобразовать
приставка имеет значение, близкое к «пере», а в этом случае пишется пре-.
Похожие слова по данному правилу
пришить
преспокойный
премилый
4
Преобразить или приобразить? Как пишется?
10 ответов:
14
0
Что касается данного слова, то здесь конечно, нужно писать приставку -ПРЕ-, так как налицо значение пере, то есть превосходная степень преобразования.
Однако если брать в целом, то может быть по разному и все зависит от семантике слова.
13
0
Какую приставку писать, ПРЕ- или ПРИ-, зависит от значения слова.
Проанализируем значение приставки в заданном слове: она имеет значение приставки «пере-«, поэтому пишется ПРЕОБРАЗИТЬ.
Преобразить — сделать по-иному, переделать образ, форму или вид чего-нибудь.
5
0
Преобразить или «приобразить»?
Чтобы выбрать правильный вариант написания пре- или при-, укажу, что эти приставки они являются смысловыми. Их написание зависит от значения, которое они привносят в слово. Приставка пре- может обозначать превосходную степень признака. Она чаще всего используются в составе качественных прилагательных:
добрый — предобрый = очень добрый;
сильный — пресильный = очень сильный.
Приставка пре- может употребляться в значении приставки пере-. Рассматриваемое слово — это, на мой взгляд, как раз такой случай. Начальное пре-, которое входит в современном русском языке уже в корень (преобраз-и-ть), вносит смысл «переделать, переиначить свой образ».
Поэтому выбираю выриант написания анализируемого слова преобразить.
Слова «приобразить» просто не существует в русском языке.
4
0
В великом и могучем нашем русском языке случаются ситуации, когда у глагола любая приставка из пары ПРИ- и ПРЕ- хороша, просто значение меняется (претворить и притворить, к примеру),
но в случае с «преобразить» — только ПРЕ-, слова «приобразить» нет в языке.
3
0
Поскольку значение этого слова — сделать что-то иначе, по-иному, здесь используется приставка пре-. У нее как раз имеется такое же значение. Так что правильно писать преобразить, тем более что слова приобразить вообще нет в русском языке.
3
0
Глагол «преобразить» пишется с буквой «Е» в первом слоге. Используется при этом только приставка «пре-«. Всегда. Во всех случаях. В любой ситуации.
_
Считаю, что начинать рассуждения нужно именно с этого, а уже потом, на десерт, путать читателя «пре-«, «при-«, «разными семантиками» и так далее.
_
Итак, глагол «преобразовать» имеет значение радикальных изменений. Например, если зайти в дом, переложить авторучку с полки на письменный стол, то это не преобразование и не преображение.
Если переставить мебель, перекрасить пол и побелить потолок — то это уже самое настоящее преображение интерьера.
Поэтому и используется только «пре-«, имеющая именно «радикальное» значение.
_
А теперь десерт.
Слово «приобразить» авторы используют в ничтожно редчайших случаях, стилизуя слой текст под просторечный и преображая просторечный (читайте — несуществующий) глагол «обрАзить» (придать некий положительный внешний образ) до значения неполноты — «немножко приобрАзить» (ударение на «А»). Но нас это не касается, так писать нельзя.
2
0
Добрый день, «»преобразить» — у вас написано, верно. Глагол «преобразить» пишется с буквой «Е», однако не с «И». Приставка «Пре».
Если написать вместо преобразить – приобразить это будет грамматической ошибкой. Вот сейчас написал это слово, и на меня «ВОРД» начал ругаться.
1
0
Если мы можем заменить «сомнительную» приставку ПРЕ или ПРИ, на слово с приставкой «пере» (переделать, переложить), то пишем в приставке букву Е.
В слове ПРЕОБРАЗИТЬ, мы может применить это — «переделать Образ», значит пишем через буку Е
Ответ: правильно пишется ПРЕОБРАЗИТЬ.
1
0
А я бы произвел аналогию со словами приукрасить и преукрасить. Ведь именно эти слова ближе всего по счыслу к словам преобразить и приобразить. Да в значении пере пишется преобразить, а вот в смысловом значении приукрасить и пишется приобразить. Конечно слово приобразить встречается редко и даже компьютер, а вернее сказать данная система его не распознает и подчеркивает красной волнистой чертой.
0
0
Очень часто для того, чтобы определить какую из приставок ПРЕ или ПРИ выбрать для написания того или иного слова, приходится вспоминать правила их использования.
В данном слове Преобразить мы используем приставку ПРЕ и вот почему:
Приставка ПРЕ используется, если слово можно заменить синонимом с приставкой ПЕРЕ, а слово Преобразить легко заменяется словом Переделать. Следовательно здесь эта приставка близка по значению к приставке Пере.
Преобразить свой образ можно очень легко, достаточно прогуляться поздно вечером по спальному району любого города.
Читайте также
Все ранее отвечающие на Ваш вопрос совершенно правильно связали написание двойного согласного н
в заданном слове с окончанием его на -ованный. Все слова на «-ованный (-ёванный)» пишутся с двумя «н».
Например: командированный, премированный, унифицированный, корчёванный.
Однако, если это правило не вспоминается или не знается, такое написание легко вывести из правила образования причастий и отглагольных прилагательных.
Давайте разберем заданное слово по составу: сервир/ова/нн/ый (корень/суффикс/суффикс/окончание).
Здесь два суффикса — -ова- и -нн-. Первый суффикс остается от глагола сервир/ова/ть, а второй — суффикс -нн-, при помощи которого обычно образуются причастия страдательные прошедшего времени от глаголов переходных с основой на а(я), как и в причастиях, например, сдела/ть — сдела/нн/ый; связа/ть — связа/нн/ый;
сказа/ть — сказа/нн/ый; рассея/ть — рассея/нн/ый.
Рассматриваемое слово является существительным «душа» в творительном падеже единственного числа.
В данном слове ставится под сомнение, какую из букв О или Ё следует писать после буквы Ш.
Чтобы выяснить, к какому правилу русского языка относится данное правописание, надо определиться, к какой морфеме относится сомнительная буква. Поэтому следует разобрать его по составу: ДУШ — корень, ОЙ — окончание.
Следовательно, сомнительная буква подпадает под правило русского языка, которое гласит: В окончаниях существительных после шипящих под ударением пишется буква О: душой. По аналогии: межой, вожжой, плечом, калачом.
Правильное написание » артобстрел», так как это сложносокращённое слово.
Написание глагольной формы «колышется» осложнено тем, что:
- В ней есть безударное окончание «-ЕТ-» (которое можно ошибочно принять за «-ИТ-«).
- После личного окончания имеется ещё и постфикс «-СЯ«, который несколько запутывает орфографическую картину, усугубляя редукцию заударной «Е» до «ъ«, в результате чего иностранец может написать даже «колыштся».
- Отбрасывание «-СЯ» в методических целях (чтобы проверить «-ет«) ничего точного не даст. В форме «колышет» ударение по-прежнему будет падать на «Ы«, поэтому никакой проверки не состоится.
Нам необходима форма глагола, которая бы стала проверочной. Ею будет инфинитив. Ударение в неопределённой форме («колыхаться» либо, если мешает «-СЯ«, то «колыхать») попадает на «-АТЬ«. Это нужное место, которое определяет спряжение глагола (1-е спряжение).
Грамматический признак, который мы только что определили, не позволяет писать «колышится».
Например:
- «Взволнованно колышется грудь», «лениво колышется туман», беспомощно колышется лепесток», «соблазнительно колышется юбка», «торжественно колышется занавес».
Слово «любящая» является действительным причастием настоящего времени и ошибиться здесь можно в правописании суффикса -ащ/ющ-.
Все зависит от спряжения глагола, от которого образовано причастие «любящая».
Любящая — (что делать?) любить, оканчивается на -ить- не является исключением, значит — 2-ое спряжение: любит, любят, любящая.
Правильный ответ — любящая.
|
Слово преобразовать доставит хлопоты в написании из-за большого количества безударных гласных в приставке и корне: пре-образова-ть — приставка/корень/окончание. Ведь при произношении этого глагола в форме инфинитива ударным является только пятый гласный по счету: преобразовать. Разобрав слово по составу, увидим, что в его начале имеется смысловая приставка пре-, поскольку она используется в значении приставки пере- и придает данному глаголу значение «что-то переделать». Значит, напишем в приставке букву «е». Первый безударный гласный корня проверяем словами: образ, образный. Написание буквы а в корне докажут слово «образчик». В современном делении слова на морфемы не выделяется суффикс ова-. Написание буквы «о» проверим родственными словами: образовывать, образовываться. автор вопроса выбрал этот ответ лучшим majestikmolsent 7 лет назад В данном слове «преобразовать» можно совершить сразу несколько ошибок,если не знать достоверно,как же оно пишется правильно на самом деле.Чтобы этого избежать,нужно просто вспомнить на мгновение правила русского языка.Первой ошибкой может быть само написание приставки «пре» в слове,так как иногда ее пишут с «и»,но данное проверяемое слово образованно именно от приставки «прЕ». Второй значимой ошибкой тут может служить корневая ошибка первой гласной,где есть сомнения в написании буквы «о» или «а». Это достоверно можно проверить словом «Образ» ,где ударение падает на как раз проверяемую гласную «о»,чего мы и добивались.И последней ошибкой может быть написание буквы «о» или «а» в самом суффиксе,но проверочное слово «преобразОвывать» дает понять,что нужно писать именно гласную «о»,так как именно она стоит под ударением.Соответственно,правильное написание слова будет таким — «прЕОбразОвать». Go Green 2 года назад Слово, о котором вы спрашиваете, состоит из пяти слогов. Последний слог ударный, значит, нужно проверить первые четыре слога и безударных гласных. Первый слог — это приставка пре- (проверим путем возможности замены приставкой пере-). Второй слог — однокоренное слово «образ» станет проверочным, пишем слог -об-. Третий слог — проверочным станет слово «образчик». Пишем слог правильно так: -ра-. Четвертый слог: проверяем словом «преобразованный», значит, правильно его писать -зо-. В итоге, правильное написание всего слова такое: преобразовать. Проверочные слова следующие: образ, образчик, преобразованный. КорнетОболенский 3 года назад Сначала проясним, в чём могут быть сомнения в написании данного слова. Можно усомниться, какую писать приставку ПРИ или ПРЕ. Поскольку она синонимична приставке ПЕРЕ, то писать нужно ПРЕ, ну а в корне ОБРАЗ безударную гласную напишет через О совсем уж малообразованный человек. Правильный вариант: преобразовать. Цветрана 8 лет назад Так и пишется: преобразовать, никаких сомнений. Глагол Преобразовать следует отнести к инфинитиву, то есть мы сразу можем выделить в его составе окончание ТЬ, которое не будет включаться в основу, хотя часто это окончание считают и суффиксом, формообразующим, не входящим в основу. Далее выделим в составе слова приставку ПРЕ, корень ОБРАЗ и суффикс глагола ОВА. Это морфемы которые входят в основу слова. Ударение в этом слове падает на последний слог: преобразовАть. Таким образом безударными оказываются гласные Е в приставке, А и О в корне и О в суффиксе. Приставка ПРЕ пишется, так как ее можно заменить приставкой ПЕРЕ, суффикса АВА не бывает. Гласную О можно проверить словом Образ. Пашенька 8 лет назад Слово ПРЕОБРАЗОВАТЬ — это глагол. Данный глагол образован с помощью приставки прЕ- (преобразовать — перЕобразовать, переделать). В корне слова пишем гласную О, так как слово имеет корень -Образ-. ПреобразОвать — преобразОвывать. Пишем гласную О. Людвиго 6 лет назад ПРЕОБРАЗОВАТЬ. В приставке ПРЕ- мы пишем Е, так как приставку можно заменить аналогичной по значению приставкой ПЕРЕ-: переобразовать. В корне ОБРАЗ- мы пишем безударные гласные О и А, подберем проверочные слова: Образ, обрАзчик. В суффиксе -ОВА- пишем гласную О, ее можно проверить: преобразОванный, преобразОвывать. Знаете ответ? |
преобразова́ть(ся)
преобразова́ть(ся), -зу́ю, -зу́ет(ся)
Источник: Орфографический
академический ресурс «Академос» Института русского языка им. В.В. Виноградова РАН (словарная база
2020)
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать
Карту слов. Я отлично
умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова взвешенно (наречие):
Ассоциации к слову «преобразовать»
Синонимы к слову «преобразовать»
Предложения со словом «преобразовать»
- Но именно поэтому человеческая мысль провозглашается русскими космистами силой, которая может преобразовать мир.
- Ты плохо двигаешься и плохо преобразуешь энергию из одного вида в другой.
- В общем, это не типичная история о революционном стартапе или гении-одиночке, которому удалось преобразовать мир, прославиться и по ходу дела заработать много денег.
- (все предложения)
Цитаты из русской классики со словом «преобразовать»
- Влияние путешествия за границей раньше всего проявилось у Петра желанием преобразовать формы некоторых общественных отношений.
- Решено было воспользоваться существующим уже журналом «Новый путь», введя в него новые элементы и преобразовав его.
- Получив верховную власть, он задумал, между прочим, преобразовать к лучшему русское общество, введением в него рыцарских элементов.
- (все
цитаты из русской классики)
Значение слова «преобразовать»
-
ПРЕОБРАЗОВА́ТЬ, —зу́ю, —зу́ешь; прич. страд. прош. преобразо́ванный, —ван, -а, -о; сов., перех. (несов. преобразовывать). 1. Внести коренные изменения во что-л., переделать, перестроить. (Малый академический словарь, МАС)
Все значения слова ПРЕОБРАЗОВАТЬ
Смотрите также
ПРЕОБРАЗОВА́ТЬ, —зу́ю, —зу́ешь; прич. страд. прош. преобразо́ванный, —ван, -а, -о; сов., перех. (несов. преобразовывать). 1. Внести коренные изменения во что-л., переделать, перестроить.
Все значения слова «преобразовать»
-
Но именно поэтому человеческая мысль провозглашается русскими космистами силой, которая может преобразовать мир.
-
Ты плохо двигаешься и плохо преобразуешь энергию из одного вида в другой.
-
В общем, это не типичная история о революционном стартапе или гении-одиночке, которому удалось преобразовать мир, прославиться и по ходу дела заработать много денег.
- (все предложения)
- преобразовывать
- трансформировать
- усвоить
- изучить
- возродить
- (ещё синонимы…)
- преобразование
- (ещё ассоциации…)
- Спряжение глагола «преобразовать»
- Разбор по составу слова «преобразовать»
На чтение 2 мин Просмотров 350 Опубликовано 29.11.2021
При написании приставок глаголов нередки ошибки. Попробуем разобраться, как верно – «преобразовать» или «приобразовать», и почему.
Как пишется правильно: «преобразовать» или «приобразовать»?
Какое применяется правило
Чтобы понять правописание нашего слова, следует выяснить его часть речи, задав для этого вопрос: «что делать?» – «преобразовать». Перед нами глагол. Произведем его морфемный разбор:
- «пре» – приставка;
- «образова» – корень;
- «ть» – суффикс.
У нас вызывает сомнение написание приставки. В глаголах приставка «пре» пишется для обозначения:
- усиления,
- «пере».
«Преобразовать» используется в значении «переделать что-либо», поэтому пишется с приставкой «пре».
Примеры предложений
Встав на должность генерального директора, Андрей решил полностью преобразовать производство.
Мне необходимо преобразовать информацию из неэлектронного варианта в электронный.
Как неправильно писать
Это идет вразрез с принятыми орфографическими требованиями.
Все категории
- Фотография и видеосъемка
- Знания
- Другое
- Гороскопы, магия, гадания
- Общество и политика
- Образование
- Путешествия и туризм
- Искусство и культура
- Города и страны
- Строительство и ремонт
- Работа и карьера
- Спорт
- Стиль и красота
- Юридическая консультация
- Компьютеры и интернет
- Товары и услуги
- Темы для взрослых
- Семья и дом
- Животные и растения
- Еда и кулинария
- Здоровье и медицина
- Авто и мото
- Бизнес и финансы
- Философия, непознанное
- Досуг и развлечения
- Знакомства, любовь, отношения
- Наука и техника
1
Как пишется слово «преобразовать»?
8 ответов:
4
0
Слово преобразовать доставит хлопоты в написании из-за большого количества безударных гласных в приставке и корне:
пре-образова-ть — приставка/корень/окончание.
Ведь при произношении этого глагола в форме инфинитива ударным является только пятый гласный по счету:
преобразовать.
Разобрав слово по составу, увидим, что в его начале имеется смысловая приставка пре-, поскольку она используется в значении приставки пере- и придает данному глаголу значение «что-то переделать». Значит, напишем в приставке букву «е».
Первый безударный гласный корня проверяем словами:
образ, образный.
Написание буквы а в корне докажут слово «образчик».
В современном делении слова на морфемы не выделяется суффикс ова-. Написание буквы «о» проверим родственными словами:
образовывать, образовываться.
2
0
Так и пишется: преобразовать, никаких сомнений.
2
0
В данном слове «преобразовать» можно совершить сразу несколько ошибок,если не знать достоверно,как же оно пишется правильно на самом деле.Чтобы этого избежать,нужно просто вспомнить на мгновение правила русского языка.Первой ошибкой может быть само написание приставки «пре» в слове,так как иногда ее пишут с «и»,но данное проверяемое слово образованно именно от приставки «прЕ». Второй значимой ошибкой тут может служить корневая ошибка первой гласной,где есть сомнения в написании буквы «о» или «а». Это достоверно можно проверить словом «Образ» ,где ударение падает на как раз проверяемую гласную «о»,чего мы и добивались.И последней ошибкой может быть написание буквы «о» или «а» в самом суффиксе,но проверочное слово «преобразОвывать» дает понять,что нужно писать именно гласную «о»,так как именно она стоит под ударением.Соответственно,правильное написание слова будет таким — «прЕОбразОвать».
2
0
Сначала проясним, в чём могут быть сомнения в написании данного слова.
Можно усомниться, какую писать приставку ПРИ или ПРЕ. Поскольку она синонимична приставке ПЕРЕ, то писать нужно ПРЕ, ну а в корне ОБРАЗ безударную гласную напишет через О совсем уж малообразованный человек. Правильный вариант: преобразовать.
2
0
Слово, о котором вы спрашиваете, состоит из пяти слогов.
Последний слог ударный, значит, нужно проверить первые четыре слога и безударных гласных.
Первый слог — это приставка пре- (проверим путем возможности замены приставкой пере-).
Второй слог — однокоренное слово «образ» станет проверочным, пишем слог -об-.
Третий слог — проверочным станет слово «образчик». Пишем слог правильно так: -ра-.
Четвертый слог: проверяем словом «преобразованный», значит, правильно его писать -зо-.
В итоге, правильное написание всего слова такое: преобразовать.
Проверочные слова следующие: образ, образчик, преобразованный.
1
0
Слово ПРЕОБРАЗОВАТЬ — это глагол.
Данный глагол образован с помощью приставки прЕ- (преобразовать — перЕобразовать, переделать).
В корне слова пишем гласную О, так как слово имеет корень -Образ-.
ПреобразОвать — преобразОвывать. Пишем гласную О.
1
0
Глагол Преобразовать следует отнести к инфинитиву, то есть мы сразу можем выделить в его составе окончание ТЬ, которое не будет включаться в основу, хотя часто это окончание считают и суффиксом, формообразующим, не входящим в основу. Далее выделим в составе слова приставку ПРЕ, корень ОБРАЗ и суффикс глагола ОВА. Это морфемы которые входят в основу слова.
Ударение в этом слове падает на последний слог: преобразовАть.
Таким образом безударными оказываются гласные Е в приставке, А и О в корне и О в суффиксе. Приставка ПРЕ пишется, так как ее можно заменить приставкой ПЕРЕ, суффикса АВА не бывает. Гласную О можно проверить словом Образ.
0
0
ПРЕОБРАЗОВАТЬ.
В приставке ПРЕ- мы пишем Е, так как приставку можно заменить аналогичной по значению приставкой ПЕРЕ-: переобразовать.
В корне ОБРАЗ- мы пишем безударные гласные О и А, подберем проверочные слова:
Образ, обрАзчик.
В суффиксе -ОВА- пишем гласную О, ее можно проверить: преобразОванный, преобразОвывать.
Читайте также
Слово инквизиция — иностранного происхождение, поэтому его написание нельзя проверить проверочными словами, нужно всего лишь свериться с орфографическим словарем.
Слово это происходит от лат. inquīsītiō, перевести его можно как поиск, розыск, что несомненно отражает характер деятельности инквизиции.
Правильно пишется — инквизиция.
Как часто мы задумываемся о правописании того или иного слова, но на этот вопрос нам всегда только поможет ответить наш могучий русский язык, в котором есть именно правила по написанию слов, а есть и слова исключения. Чтобы нам с вами правильно ответить на данный поставленный вопрос, я снова полистала учебник русского языка, и могу вам с уверенностью сказать, что к данному слову применимо такое правило, как: «чередование гласных в корнях «бер» и «бир», «тер» и «тир» и так далее, эти слова и данное правило нужно обязательно запомнить, чтобы в дальнейшем вы смогли его применять к правописанию похожих слов.
Слово «аудиокурс» является сложным существительным, состоящим из двух слов «аудио» и «курс». Первое слово можно отнести к иноязычным, по правилу сложные слова с иноязычными корнями-приставками правильно писать слитно.
Подобные слова: суперобложка, инфракрасный, радиоэфир, аудиозапись.
При произнесении этого глагола ударение падает на первый гласный корня, а гласная в окончании оказывается безударной.
Чтобы правильно написать безударное окончание глагола, необходимо сначала определить, к какому спряжению относится спрягаемый глагол. А для того, чтобы определить спряжение, следует узнать начальную форму глагола.
Начальной же формой глагола (обычно в такой форме глагол дается в толковых словарях) считается неопределенная форма (инфинитив). Итак, в неопределенной форме искомый глагол выглядит таким образом: ЕХАТЬ.
И пусть никого не смущает, что при спряжении этого глагола изменяется вид. Это происходит чередование согласных Х-Д.
По суффиксу и окончанию инфинитива (-ать) можно легко определить, к какому спряжению (первому или второму) относится глагол ехать.
Поскольку ко второму спряжению относятся все глаголы на -ить и четыре глагола на -ать (гнать, держать, слышать, дышать), в число которых не входит глагол ЕХАТЬ, то его без всякого сомнения можно (и даже нужно!) отнести к первому спряжению.
А глаголы первого спряжения в настоящем времени имеют окончания с гласной Е:
он едет, мы едем, вы едете и, наконец, добрались до формы, приведенной в вопросе, — (ты) ЕДЕШЬ.
Вот так правильно писать. Ты куда ПОЕДЕШЬ летом отдыхать?
Глаголы с приставками имеют те же окончания, что и глаголы без приставок.
Сызмальства мы бегали на речку искупаться.
Сызмальства или сизмальства?
Чтобы выбрать правильный вариант написания, определю часть речи, к которой принадлежит данное слово:
Бегали когда? сызмальства.
Это слово обозначает признак действия и отвечает на обстоятельственный вопрос. Значит, это наречие, которое имеет следующий морфемный состав:
с-ыз-маль-ств-а — приставка/приставка/корень/суффикс/суффикс.
Первая приставка выражена согласным, значит далее происходит чередование гласных и//ы, поэтому выберу написание сызмальства как единственно верное.
Аналогично после русской приставки на согласный пишется ы в словах:
сымпровизировать;
небезынтересный;
безынициативный;
предыстория;
предыюньский.
Только после приставок меж- и сверх- сохраняется начальное и в корне:
межинститутский;
сверхинтересный.
Разбор слова «Преобразовать»
На чтение 1 мин.
Значение слова «Преобразовать»
— смотри: преобразовывать
Содержание
- Транскрипция слова
- MFA Международная транскрипция
- Цветовая схема слова
Транскрипция слова
[пр’иабразава́т’]
MFA Международная транскрипция
[prʲɪəbrəzɐˈvatʲ]
| п | [п] | согласный, глухой парный, твердый парный |
| р | [р’] | согласный, звонкий непарный (сонорный), мягкий парный |
| е | [и] | гласный, безударный |
| о | [а] | гласный, безударный |
| б | [б] | согласный, звонкий парный, твердый парный |
| р | [р] | согласный, звонкий непарный (сонорный), твердый парный |
| а | [а] | гласный, безударный |
| з | [з] | согласный, звонкий парный, твердый парный |
| о | [а] | гласный, безударный |
| в | [в] | согласный, звонкий парный, твердый парный |
| а | [́а] | гласный, ударный |
| т | [т’] | согласный, глухой парный, мягкий парный |
| ь | [-] |
Букв: 13 Звуков: 12
Цветовая схема слова
преобразовать
Как правильно пишется «Преобразовать»
преобразова́ть(ся)
преобразова́ть(ся), -зу́ю, -зу́ет(ся)
Как правильно перенести «Преобразовать»
пре—об—ра—зо—ва́ть
Часть речи
Часть речи слова «преобразовать» — Глагол
Морфологические признаки.
- Начальная форма — преобразовать
- Лемма — преобразовать
Постоянные признаки:
- Спряжение — 1-е спряжение
- Вид — совершенный
- Переходность — переходный
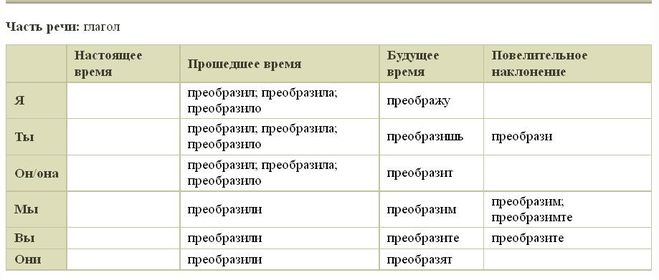
Склонение слова «Преобразовать»
| будущ. | прош. | повелит. | ||
|---|---|---|---|---|
| Я | муж. р. | преобразую | преобразовал | |
| жен. р. | преобразовала | |||
| Ты | муж. р. | преобразуешь | преобразовал | преобразуй |
| жен. р. | преобразовала | |||
| Он | преобразует | преобразовал | ||
| Она | преобразовала | |||
| Оно | преобразовало | |||
| Мы | преобразуем | преобразовали | ||
| Вы | преобразуете | преобразовали | преобразуйте | |
| Они | преобразуют | преобразовали |
Разбор по составу слова «Преобразовать»
Проверьте свои знания русского языка
Категория: Русский язык
Русский язык
Тест на тему “Мягкие согласные”
1 / 5
Какие буквы всегда обозначают мягкие согласные звуки?
ж, ц, ш
б, в, г
й, ч, щ
с, т, ф
2 / 5
Какие буквы не выражают мягкость согласных звуков?
3 / 5
Укажите верное утверждение.
В русском языкознании нет термина «мягкие согласные буквы»
В русском языкознании нет термина «мягкие согласные звуки»
Термин «мягкие согласные буквы» равнозначен термину «мягкие согласные звуки»
В русском языкознании есть только термин «мягкие согласные»
4 / 5
Что можно сказать про буквы б, в, г, д, з, к, л, м, н, п, р, с, т, ф, х?
Обозначают всегда мягкие звуки
Обозначают всегда твердые звуки
Обозначают и мягкие, и твердые звуки
Не обозначают звуки
5 / 5
Почему согласные звуки называются мягкими?
Потому что после согласных звуков стоят гласные буквы я, е, ё, и, ю
Потому что после согласных звуков стоит мягкий знак (ь)
Потому что после согласных звуков стоят гласные буквы а, э, о, ы, у
Потому что при произношении таких согласных средняя спинка языка поднята к твердому нёбу
Синонимы к слову «преобразовать»
Ассоциации к слову «преобразовать»
Предложения со словом «преобразовать»
- Но именно поэтому человеческая мысль провозглашается русскими космистами силой, которая может преобразовать мир.
Борис Гройс, Русский космизм. Антология, 2015
- В общем, это не типичная история о революционном стартапе или гении-одиночке, которому удалось преобразовать мир, прославиться и по ходу дела заработать много денег.
Натаниел Поппер, Цифровое золото: невероятная история Биткойна, или Как идеалисты и бизнесмены изобретают деньги заново, 2015
- – О сэр! Она преобразует энергию белков, жиров и углеводов в продукт структурной неустойчивости определённой цветовой гаммы!
Сборник, Самые смешные отпадные анекдоты. Смешнее не бывает!, 2017
Преобразовать как пишется?
→
преобразовать — инфинитив,
Часть речи: инфинитив — преобразовать
Часть речи: глагол
Часть речи: деепричастие
| Несовершенный вид | Совершенный вид |
|---|---|
|
преобразовавши преобразовав |
Часть речи: причастие
Действительное причастие:
| Настоящее время | ||||
|---|---|---|---|---|
| Единственное число | Множественное число | |||
| Мужской род | Женский род | Средний род | ||
| Им. | ||||
| Рд. | ||||
| Дт. | ||||
| Вн. | ||||
| Тв. | ||||
| Пр. |
Страдательное причастие:
| Настоящее время | ||||
|---|---|---|---|---|
| Единственное число | Множественное число | |||
| Мужской род | Женский род | Средний род | ||
| Им. | ||||
| Рд. | ||||
| Дт. | ||||
| Вн. | ||||
| Тв. | ||||
| Пр. |
Часть речи: кр. причастие
Страдательное причастие:
| Прошедшее время | |||
|---|---|---|---|
| Единственное число | Множественное число | ||
| Мужской род | Женский род | Средний род | |
|
преобразован |
преобразована |
преобразовано |
преобразованы |
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Содержание
- Уравнения
- Как решать уравнения?
- Тождественные преобразования уравнений.
- Примеры тождественных преобразований уравнений. Основные проблемы.
- Как выразить одну переменную через другую? Как выразить переменную из формулы?
- Если Вам нравится этот сайт.
Уравнения
Как решать уравнения?
В этом разделе мы вспомним (или изучим – уж кому как) самые элементарные уравнения. Итак, что такое уравнение? Говоря человеческим языком, это какое-то математическое выражение, где есть знак равенства и неизвестное. Которое, обычно, обозначается буквой «х». Решить уравнение — это найти такие значения икса, которые при подстановке в исходное выражение, дадут нам верное тождество. Напомню, что тождество – это выражение, которое не вызывает сомнения даже у человека, абсолютно не отягощенного математическими знаниями. Типа 2=2, 0=0, ab=ab и т.д. Так как решать уравнения? Давайте разберёмся.
Уравнения бывают всякие (вот удивил, да?). Но всё их бесконечное многообразие можно разбить всего на четыре типа.
4. Все остальные.)
Всех остальных, разумеется, больше всего, да. ) Сюда входят и кубические, и показательные, и логарифмические, и тригонометрические и всякие другие. С ними мы в соответствующих разделах плотно поработаем.
Сразу скажу, что иногда и уравнения первых трёх типов так накрутят, что и не узнаешь их… Ничего. Мы научимся их разматывать.
И зачем нам эти четыре типа? А затем, что линейные уравнения решаются одним способом, квадратные другим, дробные рациональные — третьим, а остальные не решаются вовсе! Ну, не то, чтобы уж совсем никак не решаются, это я зря математику обидел.) Просто для них существуют свои специальные приёмы и методы.
Но для любых (повторяю — для любых!) уравнений есть надёжная и безотказная основа для решения. Работает везде и всегда. Эта основа — тождественные преобразования уравнений. Звучит страшно, но штука очень простая. И очень (очень!) важная.
Собственно, решение уравнения и состоит из этих самых преобразований. На 99%. Ответ на вопрос: «Как решать уравнения?» лежит, как раз, в этих преобразованиях. Намёк понятен?)
Тождественные преобразования уравнений.
В любых уравнениях для нахождения неизвестного надо преобразовать и упростить исходный пример. Причем так, чтобы при смене внешнего вида суть уравнения не менялась. Такие преобразования называются тождественными или равносильными.
Отмечу, что эти преобразования относятся именно к уравнениям. В математике ещё имеются тождественные преобразования выражений. Это другая тема.
Сейчас мы с вами повторим все-все-все базовые тождественные преобразования уравнений.
Первое тождественное преобразование: к обеим частям любого уравнения можно прибавить (отнять) любое (но одно и то же!) число или выражение (в том числе и выражение с неизвестным!). Суть уравнения от этого не меняется.
Вы, между прочим, постоянно пользовались этим преобразованием, только думали, что переносите какие-то слагаемые из одной части уравнения в другую со сменой знака. Типа:
Дело знакомое, переносим двойку вправо, и получаем:
На самом деле вы отняли от обеих частей уравнения двойку. Результат получается тот же самый:
х+2 — 2 = 3 — 2
Перенос слагаемых влево-вправо со сменой знака есть просто сокращённый вариант первого тождественного преобразования. И зачем нам такие глубокие познания? – спросите вы. В уравнениях низачем. Переносите, ради бога. Только знак не забывайте менять. А вот в неравенствах привычка к переносу может и в тупик поставить….
Второе тождественное преобразование: обе части уравнения можно умножить (разделить) на одно и то же отличное от нуля число или выражение. Здесь уже появляется понятное ограничение: на ноль умножать глупо, а делить и вовсе нельзя. Это преобразование вы используете, когда решаете что-нибудь крутое, типа
Понятное дело, х = 2. А вот как вы его нашли? Подбором? Или просто озарило? Чтобы не подбирать и не ждать озарения, нужно понять, что вы просто поделили обе части уравнения на 5. При делении левой части (5х) пятёрка сократилась, остался чистый икс. Чего нам и требовалось. А при делении правой части (10) на пять, получилась, знамо дело, двойка.
Забавно, но эти два (всего два!) тождественных преобразования лежат в основе решения всех уравнений математики. Во как! Имеет смысл посмотреть на примерах, что и как, правда?)
Примеры тождественных преобразований уравнений. Основные проблемы.
Начнём с первого тождественного преобразования. Перенос влево-вправо.
Пример для младшеньких.)
Допустим, надо решить вот такое уравнение:
Вспоминаем заклинание: «с иксами — влево, без иксов — вправо!» Это заклинание — инструкция по применению первого тождественного преобразования.) Какое выражение с иксом у нас справа? 3х? Ответ неверный! Справа у нас —3х! Минус три икс! Стало быть, при переносе влево, знак поменяется на плюс. Получится:
Так, иксы собрали в кучку. Займёмся числами. Слева стоит тройка. С каким знаком? Ответ «с никаким» не принимается!) Перед тройкой, действительно, ничего не нарисовано. А это значит, что перед тройкой стоит плюс. Так уж математики договорились. Ничего не написано, значит, плюс. Следовательно, в правую часть тройка перенесётся с минусом. Получим:
Остались сущие пустяки. Слева — привести подобные, справа — посчитать. Сразу получается ответ:
В этом примере хватило одного тождественного преобразования. Второе не понадобилось. Ну и ладно.)
Пример для старшеньких.)
Это логарифмическое уравнение. Ну и что? Первым шагом всё равно будет базовое тождественное преобразование. «С иксами — влево». ) Надо выражение с иксом (-lgx) перенести из правой части в левую. Со сменой знака:
А выражение без икса (lg2) переносим вправо. Со сменой знака:
Справа получилась готовая формула. Кто понимает логарифмы, тот уже запросто дорешает пример. В уме. Без переноса влево-вправо это было бы затруднительно. )
Эти два примера показывают универсальность первого тождественного преобразования. Нигде его не обойти. Стало быть, надо уметь легко и непринуждённо его делать.) Собственно, ошибиться здесь можно только в одном. Забыть сменить знак при переносе. Что и происходит сплошь и рядом. Внимательнее надо быть, да. )
Приступим ко второму тождественному преобразованию. С умножением-делением. Оно так же универсально и популярно, как и первое. Но простора для ошибок в нём побольше. Разберёмся, что к чему?)
Пример для младшеньких.)
Пусть нам надо решить вот такое суровое уравнение:
Смотрим и соображаем: что нам не нравится в этом примере? Что нам мешает? Да тройка мешает! Нам в ответе всегда чистый икс нужен! Икс равен чему-то. А тройка мешает! Как можно от неё избавиться? Перенести вправо? Э-э-э нет! Тройка с иксом умножением связана. Нельзя её оторвать и вправо перенести. Вот всё выражение 3х можно переносить (только зачем?), а тройку отдельно — нельзя.
Самое время про умножение-деление вспомнить! Чтобы слева остался чистый икс, надо левую часть разделить на три. Это НАМ надо. Получим икс, чего и требовалось. Правую часть тоже придётся разделить на три. Это МАТЕМАТИКА требует. Что уж там получится, то и получится. Но пример хороший. Я старался.) 12 на 3 замечательно делится. Получится четыре. Ответ:
Пример для старшеньких.)
Здесь без логарифмов обойдёмся. Решаем:
Вполне солидно, правда?) Кое-кто и запутается…. Понятно, что надо делить обе части на дробь 1/5. Именно она нам мешает. Это не очень в уме удобно… Можно поступить гораздо проще. Не делить обе части на 1/5, а умножить на 5. Слева всё равно чистый икс получится, а умножать на 5 — не самая трудная работа.)
Умножение обеих частей на нужное число, позволяет сразу избавляться от дробей, минуя промежуточные выкладки, в которых, между прочим, вполне можно и ошибок наляпать. Короче дорога – меньше ошибок!
Как видите, тождественные преобразования уравнений — штука не самая сложная. Перенос, да умножение-деление. Однако, не у всех они получаются. Почему? Есть две главные причины.
Причина первая (для начинающих):
Иногда человек думает, что упрощение примеров делается по одному, раз и навсегда установленному правилу. И никак не может понять это правило. В одном примере начинают с переноса. В другом с домножения. В третьем три раза домножают и ни разу не переносят. Тоскует человек от неопределённости.)
А правила никакого нет.
Есть разрешённые математикой преобразования (целых два!), которые мы применяем по своему усмотрению. В удобном нам порядке. Порядок зависит исключительно от исходного примера и личных привычек решающего.
Причина вторая (почти для всех. ):
Ошибки в вычислениях. В преобразованиях постоянно приходится перемножать скобки. Заключать выражения в скобки и раскрывать их. Складывать и вычитать дроби. Умножать и делить дроби. Короче, в наличии весь набор элементарных вычислений. Дальше понятно.
Обе эти причины замечательно устраняются практикой. Исчезают сомнения и ошибки. Примеры становятся проще, задания — легче.)
Как выразить одну переменную через другую?
Как выразить переменную из формулы?
Умение делать такие вещи крайне необходимо в математике. Во всех разделах, без исключения. По этой причине, задания подобного рода обязательно присутствуют в выпускных экзаменах. И в ГИА, и в ЕГЭ. И в базовом уровне, и в профильном.
Имеет смысл разобраться, правда?) Тем более, что ничего сложного здесь нет. Есть применение тождественных преобразований уравнений и. всё!
Вся теоретическая часть подобных заданий заключается в одной фразе. Вот она, эта фраза: любая формула, любое равенство с буквами — это тоже уравнение. Усвоили эту сложную теорию?) Тогда остаётся правильно применять тождественные преобразования на практике.
Начнём с простого. Как выразить одну переменную через другую? Такая задача постоянно возникает при решении систем уравнений. Например, имеется уравнение:
Здесь две переменные. Икс и игрек.
Допустим, нам нужно выразить х через у.
Что означает это задание? Она означает, что в итоге мы должны получить какое-то равенство, где в левой части стоит чистый х, без всяких букв и чисел. В гордом одиночестве. А в правой части — что уж получится. И как добраться до этого результата? Легко! С помощью тождественных преобразований.
Напоминаю: преобразования можно применять в каком угодно порядке! Вот и применяем, шаг за шагом добираясь до чистого икса.
Смотрим на левую часть уравнения:
Здесь нам мешаются двойка перед иксом и -3у. Начнём с -3у, это проще будет.
Перебрасываем -3у в правую часть, со сменой знака, разумеется:
Осталась двойка перед иксом. Как от неё избавится? Разделить обе части уравнения на 2! Получим:
Вот и всё. Мы выразили х через у. Можно ли было сразу делить обе части исходного уравнения на двойку, а уж потом переносить? Запросто! Но это привело бы к появлению дробей в процессе решения, что не очень удобно. А так дробь появилась только в самом конце.
А можно ли из этого же уравнения
выразить у через х? Можно, конечно. Только теперь слева нам нужен чистый у, а не х. Вот и «очищаем» игрек от соседей.) Сначала избавляемся от выражения 2x. Переносим его в правую часть:
Теперь мешает тройка с минусом. Делим обе части на -3:
Вот и всё. Мы выразили у через х. Переходим к более хитрым примерам.
Как выразить переменную из формулы? Не вопрос!) Точно так же!
К примеру, имеется задание:
выразить переменную b.
Формула — тоже уравнение! Стало быть, нам надо получить новую формулу, где слева — чистая b, а справа — то, что уж получится в результате «очищения» b.
Однако. Как же эту b вытаскивать-то!?
Как, как. По шагам! Выделить чистую b сразу невозможно. Она в дроби сидит. А дробь умножается на h. Значит, очищаем, для начала, выражение с b, т.е. дробь, целиком. Если можно, разумеется. Здесь — можно поделить обе части формулы на h. Получим:
Следующий шаг — выдернуть b из числителя дроби. Это делается просто. Избавимся от дроби. Нет дроби — нет числителя!) Умножим обе части формулы на 2. Вот так:
Остались сущие пустяки. Оставляем b в гордом одиночестве, т.е. переносим a в левую часть:
Ответ почти готов. Осталось переписать его в привычном нам виде. Равенство, оно, что слева-направо, что справа-налево — всё едино:
Надеюсь, общая идея понятна. Делаем элементарные тождественные преобразования с целью уединить интересующую нас переменную. Главное здесь — не последовательность шагов (она может быть любой), а их правильность.
Разные последовательности дадут разные пути к одному и тому же результату. Путь может получиться простым, может получиться сложным. Тут практика рулит. Решите десяток-другой примеров, сами почувствуете, как проще.
В данном разделе рассматриваются только два базовых тождественных преобразования уравнений. Кроме этой парочки существует множество других преобразований, которые тоже будут тождественными, но, при определённых условиях. Скажем, возведение обеих частей уравнения (или формулы) в квадрат будет тождественным преобразованием, если обе части уравнения заведомо неотрицательны. Подобные преобразования рассматриваются в соответствующих темах.
А здесь и сейчас — примеры для тренировки по элементарным преобразованиям.
выразите переменную t и найдите её значение при v=7, v=16, a=3.
выразите переменную m и найдите её значение при x=1, n=2.
А вот задание на основе реального варианта ГИА:
Мощность постоянного тока (в ваттах) вычисляется по формуле P = J 2 R, где J — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление (в омах), если мощность составляет 80 Вт, а сила тока равна 4 А.
Задание на основе реального варианта ЕГЭ:
Локатор батискафа, равномерно погружающегося вертикально вниз со скоростью v (в м/сек), испускает ультразвуковые импульсы частотой f=374 МГц. Частота отражённого от дна сигнала f, регистрируемая приёмником (в МГц), определяется по формуле 
где c =1500 м/с — скорость звука в воде, f — частота испускаемых импульсов (в МГц). Определите скорость погружения батискафа v в м/с, если частота отражённого от дна сигнала f составляет 376 Мгц.
В реальных заданиях «многа букафф», да. ) Но тема та же.
Ответы (в беспорядке):
А где числа, омы, метры в секунду — это уж сами. )
В следующих уроках вы сможете познакомиться с практикой тождественных преобразований в конкретных уравнениях. В линейных, квадратных и дробных. С пояснениями что, как, зачем и почему мы делаем. Очень помогает!)
Если Вам нравится этот сайт.
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Вот здесь можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
А вот здесь можно познакомиться с функциями и производными.
Источник
Толковый словарь русского языка. Поиск по слову, типу, синониму, антониму и описанию. Словарь ударений.
преобразовать
ТОЛКОВЫЙ СЛОВАРЬ
ТОЛКОВЫЙ СЛОВАРЬ УШАКОВА
ПРЕОБРАЗОВА́ТЬ, преобразую, преобразуешь, совер. (к преобразовывать), кого-что (книжн.).
1. В корне изменить, переделать на другой лад. «…Укрупнить сельское хозяйство, сделать его способным к накоплению, к расширенному воспроизводству и преобразовать таким образом сельско-хозяйственную базу народного хозяйства.» Сталин (1929 г.). Преобразовать учреждение.
2. Придать кому-чему-нибудь другой вид, образ, преобразить кого-что-нибудь (устар.). «Волшебницей зимой весь мир преобразован.» Вяземский.
3. Превратить из одного вида, качества в другой вид, в другое качество (спец.). Преобразовать переменный ток в постоянный. Преобразовать уравнение (мат.).
ТОЛКОВЫЙ СЛОВАРЬ ОЖЕГОВА
ПРЕОБРАЗОВА́ТЬ, -зую, -зуешь; -ованный; совер.
1. что. Совершенно переделать, изменить к лучшему. П. систему управления.
2. что. Превратить из одного вида в другой, из одной формы в другую (спец.). П. переменный ток в постоянный. П. алгебраическое выражение.
| несовер. преобразовывать, -аю, -аешь.
| сущ. преобразование, -я, ср.
| прил. преобразовательный, -ая, -ое.
ЭНЦИКЛОПЕДИЧЕСКИЙ СЛОВАРЬ
ПРЕОБРАЗОВА́ТЬ -зу́ю, -зу́ешь; преобразо́ванный; -ван, -а, -о; св. что.
1. Внести коренные изменения во что-л., переделать, перестроить. П. общество. П. систему управления.
2. во что. Перестраивая, изменяя, превратить во что-л., сделать чем-л. другим. Коммуна была преобразована в сельскохозяйственную артель. // Спец. Превратить из одного вида, качества в другой вид, качество. П. кинетическую энергию в тепловую. П. переменный ток в постоянный.
◁ Преобразо́вывать, -аю, -аешь; нсв. Преобразо́вываться, -ается; страд. Преобразова́ние (см.).
АКАДЕМИЧЕСКИЙ СЛОВАРЬ
-зу́ю, -зу́ешь; прич. страд. прош. преобразо́ванный, -ван, -а, -о; сов., перех.
(несов. преобразовывать).
1. Внести коренные изменения во что-л., переделать, перестроить.
Силы человека растут вслед за ростом его знаний о жизни и его сознания необходимости преобразовать жизнь. М. Горький, О борьбе с природой.
2. во что.
Перестраивая, изменяя, превратить во что-л., сделать чем-л. другим.
[Я] преобразовал ее [лабораторию] с помощью своих сотрудников в существующий теперь Государственный научный институт имени Лесгафта. Морозов, Повести моей жизни.
[Коммуна] была преобразована в сельскохозяйственную артель и стала называться колхозом имени Мичурина. Овечкин, [Автобиография].
|| спец.
Превратить из одного вида, качества в другой вид, в другое качество.
Преобразовать кинетическую энергию в тепловую. Преобразовать переменный ток в постоянный.
ПУНКТУАЦИЯ И УПРАВЛЕНИЕ В РУССКОМ ЯЗЫКЕ
что во что. Преобразовать кинетическую энергию в тепловую. Преобразовать переменный ток в постоянный.
ОРФОГРАФИЧЕСКИЙ СЛОВАРЬ
преобразова́ть, -зу́ю, -зу́ет
СИНОНИМЫ
изменить, обновить, модернизировать, модифицировать, трансформировать, переработать, реформировать, переустроить, реорганизовать, реконструировать; перестроить, переделать, модулировать, превратить, преобразить, перекроить, переиначить, переустраивать, переменить, пересоздать, конвертировать, разнообразить
гл. сов.
реорганизовать
реформировать
перестроить
переустроить
переделать
ТЕЗАУРУС РУССКОЙ ДЕЛОВОЙ ЛЕКСИКИ
Syn: изменить, обновить, модернизировать, модифицировать, трансформировать, переработать, реформировать (полит.), переустроить, реорганизовать (кн.), реконструировать
ИДИОМАТИКА
в корне преобразовать
до неузнаваемости преобразовать
коренным образом преобразовать
полностью преобразовать
радикально преобразовать
совсем преобразовать
ГРАММАТИЧЕСКИЙ СЛОВАРЬ
преобразова́ть св [но в наст.-буд. также нсв] 2a ◑нсв также I
ПОЛЕЗНЫЕ СЕРВИСЫ
преобразовать(ся)
СЛОВАРЬ УДАРЕНИЙ
преобразова́ть(ся), -зу́ю, -зу́ешь, -зу́ет(ся)
МОРФЕМНО-ОРФОГРАФИЧЕСКИЙ СЛОВАРЬ
ПОЛЕЗНЫЕ СЕРВИСЫ
преобразоваться
ТОЛКОВЫЙ СЛОВАРЬ
ТОЛКОВЫЙ СЛОВАРЬ УШАКОВА
ПРЕОБРАЗОВА́ТЬСЯ, преобразуюсь, преобразуешься, совер. (к преобразовываться) (книжн.).
1. Подвергнуться коренному изменению, реформе. Учреждение совершенно преобразовалось.
2. Претерпеть изменение своего вида, образа, преобразиться, перемениться (устар.).
3. Превратиться из одного вида, качества в другой вид, в другое качество, перейти в иное состояние (спец.). Переменный ток преобразовался в постоянный.
ЭНЦИКЛОПЕДИЧЕСКИЙ СЛОВАРЬ
ПРЕОБРАЗОВА́ТЬСЯ -зу́ется; св.
1. Претерпеть коренные изменения. Как преобразовалось искусство кино за последние годы!
2. во что. Превратиться во что-л., стать чем-л. в результате перестройки, изменений. Небольшой посёлок преобразовался в крупный районный центр. // Спец. Превратиться, перейти из одного вида, качества, состояния в другой вид, качество, состояние. Переменный ток преобразовался в постоянный.
◁ Преобразо́вываться, -ается; нсв. Преобразова́ние (см.).
АКАДЕМИЧЕСКИЙ СЛОВАРЬ
-зу́ется; сов.
(несов. преобразовываться).
1. Претерпеть коренные изменения.
Страна преобразовалась.
◊
Бажов совершил своего рода открытие, показав, как преобразуется народное творчество в нашем советском мире. Б. Полевой, Секрет вечности.
2. во что.
Превратиться во что-л., стать чем-л. в результате перестройки, изменений.
Постепенно колхозные деревни и села преобразуются в укрупненные населенные пункты городского типа. Программа КПСС.
|| спец.
Превратиться, перейти из одного вида, качества, состояния в другой вид, в другое качество, состояние.
Переменный ток преобразовался в постоянный.
ОРФОГРАФИЧЕСКИЙ СЛОВАРЬ
преобразова́ться, -зу́ется
ФОРМЫ СЛОВ
преобразова́ться, преобразуюсь, преобразуемся, преобразуешься, преобразуетесь, преобразуется, преобразуются, преобразуясь, преобразова́лся, преобразова́лась, преобразова́лось, преобразова́лись, преобразуйся, преобразуйтесь, преобразующийсяа́, преобразующаясяа́, преобразующеесяа́, преобразующиесяа́, преобразующегося́, преобразующейсяа́, преобразующихсяа́, преобразующемуся́, преобразующимсяа́, преобразующуюсяа́, преобразующеюсяа́, преобразующимися́, преобразующемсяа́, преобразова́вшийся, преобразова́вшаяся, преобразова́вшееся, преобразова́вшиеся, преобразова́вшегося, преобразова́вшейся, преобразова́вшихся, преобразова́вшемуся, преобразова́вшимся, преобразова́вшуюся, преобразова́вшеюся, преобразова́вшимися, преобразова́вшемся
СИНОНИМЫ
гл. сов.
реорганизоваться
реформироваться
перестроиться
переустроиться
переделаться
ТЕЗАУРУС РУССКОЙ ДЕЛОВОЙ ЛЕКСИКИ
Syn: реорганизоваться (кн.), реформироваться (кн.), перестроиться (обр.), переустроиться
ГРАММАТИЧЕСКИЙ СЛОВАРЬ
преобразова́ться св [но в наст.-буд. также нсв] 2a ◑нсв также I
ПОЛЕЗНЫЕ СЕРВИСЫ
При решении уравнений мы переходим от одного уравнения к другому, пока не придем к уравнению вида 

Прибавляя к обеим частям этого уравнения 

А теперь умножим обе части уравнения (2) на и получим, что

В процессе решения этого уравнения мы прибавляли к обеим частям уравнения некоторое алгебраическое выражение (а именно, 


Однако не всегда одинаковые преобразования обеих частей уравнения приводят к уравнению, равносильному первоначальному. Рассмотрим уравнение:

Его решением является 


Это уравнение, кроме решения 

С другой стороны, если мы возьмем уравнение (5), имеющее решения 





Не является «безобидным» и прибавление к обеим частям уравнения одного и того же алгебраического выражения. Например, уравнение

имеет решение 


для которого 

Эти примеры наглядно показывают, что при преобразовании уравнений необходима осторожносгь — неправильно преобразуя уравнение, мы можем как приобрести лишние решения, так и потерять решения данного уравнения. При этом надо иметь в виду, что приобретение лишних решений не столь опасно, как потеря существующих. Ведь после того, как уравнение решено, можно подставить все найденные решения в заданное уравнение и отобрать те из решений, которые ему удовлетворяют. А потерянные решения восстановить уже нельзя.
Из изложенного видно, что, прежде чем решать конкретные виды уравнений, надо познакомиться с общей теорией уравнений, выяснить, какие преобразования приводят к равносильным уравнениям, какие дают посторонние решения, а при каких решения могут быть потеряны. Только после этого мы сможем решать уравнения «с открытыми глазами».

 ; ОДЗ: х =/= 0, х =/= – 4, х =/= – 2.
; ОДЗ: х =/= 0, х =/= – 4, х =/= – 2. 


 х 2 =/= 0
х 2 =/= 0 

 , тогда (t + 3)(t – 2) = 24
, тогда (t + 3)(t – 2) = 24  = – 6 или
= – 6 или 

 ;
;  .
.
 ;
; .
. ,
, ,
, ,
, .
.