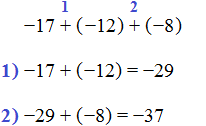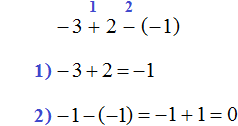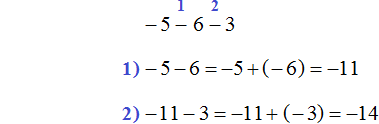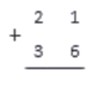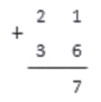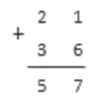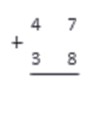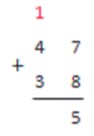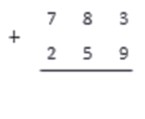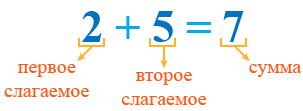Чтобы выполнить сложение целых чисел, нужно учитывать знаки, которые стоят перед этими числами. Рассмотрим примеры:
Сложение целых чисел с одинаковыми знаками.
Сложение целых чисел с одинаковым знаком есть число, полученное в результате сложения модуля этих целых чисел, перед полученной суммой ставим знак слагаемых.
Сложение положительных целых чисел.
Выполним сложение чисел 4+3.
Рассмотри на числовой прямой пример 4+3=(+4)+(+3).
Сначала в положительную сторону от нуля пройдем (+4) единицы, а потом еще (+3) единицы и окажемся в точке (+7).
Сумма целых положительных чисел есть число положительное.
Сложение отрицательных целых чисел.
Рассмотрим еще пример -3+(-4).
Наглядно разберем на числовой прямой пример.
Идем в отрицательную сторону от 0 на (-3) единицы, потом еще на (-4) единицы и оказываемся в точке (-7).
Сумма целых отрицательных чисел есть число отрицательное.
Сложение целых чисел с разными знаками.
Следующий пример (-4)+(+3).
Смотрим на координатную прямую.
От нуля в отрицательную сторону отступаем на (-4) единицы, потом в положительную сторону идем на (+3) единицы и попадаем в точку (-1).
Правило:
Чтобы сложить целые числа с разными знаками, нужно из модуля большего числа вычесть модуль меньшего числа, а в результат поставить тот знак модуль числа, которого больше.
Рассмотрим пример:
Выполните сложение целых чисел (+25)+(-23).
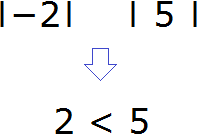
Посчитаем модули чисел: |-23|=23 и |25|=25.
Сравним результат 23<25. Число 25 больше, оно имеет знак “+”, поэтому ответ будет с положительным знаком.
(+25)+(-23)=25-23=+2=2
Еще пример: (-9)+(+6).
Посчитаем модули чисел: |-9|=9 и |+6|=6.
Сравним результат 6<9. Число 9 больше, оно имеет знак “-”, поэтому ответ будет с отрицательным знаком.
(-9)+(+6)=-(9-6)=-3
Сложение противоположных целых чисел.
Сумма противоположных чисел равна нулю.
Пример:
(+10)+(-10)=0
Сложение целых чисел с нулем.
Если к нулю прибавить целое положительное или отрицательное число в результате получим то же самое целое число.
0+(+1)=+1 или 0+(-1)=-1
(+2)+0=+2 или (-2)+0=-2
Получим:
a+0=a или 0+a=a
Сложение нескольких целых чисел.
Чтобы сложить несколько чисел, нужно сначала сложить два числа, потом к их сумме добавить третье число и так далее.
Пример:
(+3)+(-1)+(+4)=+(3-1)+(+4)=(+2)+(+4)=+(2+4)=+6=6
Примечание: знак “+” и скобки, обычно, у положительных чисел опускают.
Например: (+3)+(-2)=3+(-2)
Вопросы по теме:
Как сложить два числа с одинаковыми знаками?
Ответ: складываем модули чисел и перед полученным результатом ставим знак слагаемых.
Как сложить два числа с разными знаками?
Ответ: у слагаемых из большего модуля вычитаем меньший, а в ответ пишем знак наибольшего числа по модулю.
Измениться ли число если к нему прибавить 0?
Ответ: нет.
Чему равна сумма противоположных числе?
Ответ: 0.
Пример №1:
Найдите сумму:
а) (+7)+(+5)
б) (+10)+(-8)
в) (-12)+(+8)
г) (-7)+(-3)
д) (-8)+(+8)
е) (+9)+0
ж) 0+(-12)
Решение:
а) (+7)+(+5)=7+5=12
б) (+10)+(-8)=10+(-8)=+(10-8)=+2=2, так как |+10|>|-8|
в) (-12)+(+8)=(-12)+8=-(12-8)=-4, так как |-12|>|+8|
г) (-7)+(-3)=-(7+3)=-10
д) (-8)+(+8)=(-8)+8=0
е) (+9)+0=9+0=9
ж) 0+(-12)=-12
В данном уроке мы изýчим сложение и вычитание целых чисел.
Напомним, что целые числа — это все положительные и отрицательные числа, а также число 0. Например, следующие числа являются целыми:
−3, −2, −1, 0, 1, 2, 3
Положительные числа легко складываются и вычитаются, умножаются и делятся. К сожалению, этого нельзя сказать об отрицательных числах, которые смущают многих новичков своими минусами перед каждой цифрой.
Примеры сложения и вычитания целых чисел
Первое чему следует научиться это складывать и вычитать целые числа с помощью координатной прямой. Совсем необязательно рисовать координатную прямую. Достаточно воображать её в своих мыслях и видеть, где располагаются отрицательные числа и где положительные.
Рассмотрим следующее простейшее выражение
1 + 3
Значение данного выражения равно 4
1 + 3 = 4
Этот пример можно понять с помощью координатной прямой. Для этого из точки, где располагается число 1, нужно сдвинуться вправо на три шага. В результате мы окажемся в точке, где располагается число 4. На рисунке можно увидеть, как это происходит:
Знак плюса в выражении 1 + 3 указывает нам, что нужно двигаться вправо в сторону увеличения чисел.
Пример 2. Найдём значение выражения 1 − 3
Значение данного выражения равно −2
1 − 3 = −2
Этот пример опять же можно понять с помощью координатной прямой. Для этого из точки, где располагается число 1 нужно сдвинуться влево на три шага. В результате мы окажемся в точке, где располагается отрицательное число −2. На рисунке можно увидеть, как это происходит:
Знак минуса в выражении 1 − 3 указывает нам, что нужно двигаться влево в сторону уменьшения чисел.
Вообще, если осуществляется сложение, то нужно двигаться вправо в сторону увеличения. Если же осуществляется вычитание, то нужно двигаться влево в сторону уменьшения.
Пример 3. Найти значение выражения −2 + 4
Значение данного выражения равно 2
−2 + 4 = 2
Этот пример опять же можно понять с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −2 нужно сдвинуться вправо на четыре шага. В результате мы окажемся в точке, где располагается положительное число 2
Видно, что мы сдвинулись из точки где располагается отрицательное число −2 в правую сторону на четыре шага, и оказались в точке, где располагается положительное число 2.
Пример 4. Найти значение выражения −1 − 3
Значение данного выражения равно −4
−1 − 3 = −4
Этот пример опять же можно решить с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −1 нужно сдвинуться влево на три шага. В результате мы окажемся в точке, где располагается отрицательное число −4
Видно, что мы сдвинулись из точки где располагается отрицательное число −1 в левую сторону на три шага, и оказались в точке, где располагается отрицательное число −4.
Пример 5. Найти значение выражения −2 + 2
Значение данного выражения равно 0
−2 + 2 = 0
Этот пример можно решить с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −2 нужно сдвинуться вправо на два шага. В результате мы окажемся в точке, где располагается число 0
Видно, что мы сдвинулись из точки где располагается отрицательное число −2 в правую сторону на два шага и оказались в точке, где располагается число 0.
Правила сложения и вычитания целых чисел
Чтобы сложить или вычесть целые числа, вовсе необязательно каждый раз воображать координатную прямую, и тем более рисовать её. Можно воспользоваться готовыми правилами.
Применяя правила, нужно обращать внимания на знак операции и знаки чисел, которые нужно сложить или вычесть. От этого будет зависеть какое правило применять.
Пример 1. Найти значение выражения −2 + 5
Здесь к отрицательному числу прибавляется положительное число. Другими словами, осуществляется сложение чисел с разными знаками, потому что −2 это отрицательное число, а 5 — положительное. Для таких случаев применяется следующее правило:
Чтобы сложить числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше.
Итак, посмотрим какой модуль больше:
Модуль числа 5 больше, чем модуль числа −2. Правило требует из большего модуля вычесть меньший. Поэтому мы должны из 5 вычесть 2, и перед полученным ответом поставить знак того числа, модуль которого больше.
У числа 5 модуль больше, поэтому знак этого числа и будет в ответе. То есть ответ будет положительным:
−2 + 5 = 5 − 2 = 3
Обычно записывают покороче: −2 + 5 = 3
Пример 2. Найти значение выражения 3 + (−2)
Здесь как и в предыдущем примере, осуществляется сложение чисел с разными знаками. 3 это положительное число, а −2 — отрицательное. Обратите внимание, что число −2 заключено в скобки, чтобы сделать выражение понятнее. Это выражение намного проще для восприятия, чем выражение 3 + −2.
Итак, применим правило сложения чисел с разными знаками. Как и в прошлом примере, из большего модуля вычитаем меньший модуль и перед ответом ставим знак того числа, модуль которого больше:
3 + (−2) = |3| − |−2| = 3 − 2 = 1
Модуль числа 3 больше, чем модуль числа −2, поэтому мы из 3 вычли 2, и перед полученным ответом поставили знак того числа, модуль которого больше. У числа 3 модуль больше, поэтому знак этого числа и поставлен в ответе. То есть ответ положительный.
Обычно записывают покороче 3 + (−2) = 1
Пример 3. Найти значение выражения 3 − 7
В этом выражении из меньшего числа вычитается большее. Для такого случая применяется следующее правило:
Чтобы из меньшего числа вычесть большее, нужно из большего числа вычесть меньшее, и перед полученным ответом поставить минус.
3 − 7 = 7 − 3 = −4
В этом выражении есть небольшая загвоздка. Вспомним, что знак равенства (=) ставится между величинами и выражениями тогда, когда они равны между собой.
Значение выражения 3 − 7 как мы узнали равно −4. Это означает, что любые преобразования которые мы будем совершать в данном выражении, должны быть равны −4
Но мы видим, что на втором этапе располагается выражение 7 − 3, которое не равно −4.
Чтобы исправить эту ситуацию, выражение 7 − 3 нужно взять в скобки и перед этой скобкой поставить минус:
3 − 7 = − (7 − 3) = − (4) = −4
В этом случае равенство будет соблюдаться на каждом этапе:
После того, как выражение вычислено, скобки можно убрать, что мы и сделали.
Поэтому, чтобы быть более точным, решение должно выглядеть так:
3 − 7 = − (7 − 3) = − (4) = − 4
Данное правило можно записать с помощью переменных. Выглядеть оно будет следующим образом:
a − b = − (b − a)
Большое количество скобок и знаков операций могут усложнять решение, казалось бы совсем простой задачи, поэтому целесообразнее научиться записывать такие примеры коротко, например 3 − 7 = − 4.
На самом деле сложение и вычитание целых чисел сводится только к сложению. Это означает, что если требуется осуществить вычитание чисел, эту операцию можно заменить сложением.
Итак, знакомимся с новым правилом:
Вычесть одно число из другого означает прибавить к уменьшаемому такое число, которое будет противоположно вычитаемому.
Например, рассмотрим простейшее выражение 5 − 3. На начальных этапах изучения математики мы ставили знак равенства и записывали ответ:
5 − 3 = 2
Но сейчас мы прогрессируем в изучении, поэтому надо приспосабливаться к новым правилам. Новое правило говорит, что вычесть одно число из другого означает прибавить к уменьшаемому такое число, которое будет противоположно вычитаемому.
На примере выражения 5 − 3 попробуем понять это правило. Уменьшаемое в данном выражении это 5, а вычитаемое это 3. Правило говорит, что для того, чтобы из 5 вычесть 3 , нужно к 5 прибавить такое число, которое будет противоположно 3. Противоположное для числа 3 это число −3. Записываем новое выражение:
5 + (−3)
А как находить значения для таких выражений мы уже знаем. Это сложение чисел с разными знаками, которое мы рассмотрели ранее. Чтобы сложить числа с разными знаками, мы из большего модуля вычитаем меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше:
5 + (−3) = |5| − |−3| = 5 − 3 = 2
Модуль числа 5 больше, чем модуль числа −3. Поэтому мы из 5 вычли 3 и получили 2. У числа 5 модуль больше, поэтому знак этого числа и поставили в ответе. То есть ответ положителен.
Поначалу быстро заменять вычитание сложением удаётся не всем. Это связано с тем, что положительные числа записываются без знака плюс.
Например, в выражении 3 − 1 знак минуса, указывающий на вычитание, является знаком операции и не относится к единице. Единица в данном случае является положительным числом, и у неё есть свой знак плюса, но мы его не видим, поскольку плюс перед положительными числами не записывают.
А стало быть, для наглядности данное выражение можно записать следующим образом:
(+3) − (+1)
Для удобства числа со своим знаками заключают в скобки. В таком случае заменить вычитание сложением намного проще.
В выражении (+3) − (+1) вычитаемое это число (+1), а противоположное ему число это (−1).
Заменим вычитание сложением и вместо вычитаемого (+1) записываем противоположное ему число (−1)
(+3) − (+1) = (+3) + (−1)
Дальнейшее вычисление не составит особого труда.
(+3) − (+1) = (+3) + (−1) = |3| − |−1| = 3 − 1 = 2
На первый взгляд покажется, какой смысл в этих лишних телодвижениях, если можно старым добрым методом поставить знак равенства и сразу записать ответ 2. На самом деле это правило ещё не раз нас выручит.
Решим предыдущий пример 3 − 7, используя правило вычитания. Сначала приведём выражение к понятному виду, расставив каждому числу свои знаки.
У тройки знак плюса, поскольку она является положительным числом. Минус, указывающий на вычитание не относится к семёрке. У семёрки знак плюса, поскольку она является положительным числом:
(+3) − (+7)
Заменим вычитание сложением:
(+3) − (+7) = (+3) + (−7)
Дальнейшее вычисление не составляет труда:
(+3) − (−7) = (+3) + (-7) = −(|−7| − |+3|) = −(7 − 3) = −(4) = −4
Пример 7. Найти значение выражения −4 − 5
Приведём выражение к понятному виду:
(−4) − (+5)
Перед нами снова операция вычитания. Эту операцию нужно заменить сложением. К уменьшаемому (−4) прибавим число, противоположное вычитаемому (+5). Противоположное число для вычитаемого (+5) это число (−5).
(−4) − (+5) = (−4) + (−5)
Мы пришли к ситуации, где нужно сложить отрицательные числа. Для таких случаев применяется следующее правило:
Чтобы сложить отрицательные числа, нужно сложить их модули, и перед полученным ответом поставить минус.
Итак, сложим модули чисел, как от нас требует правило, и поставим перед полученным ответом минус:
(−4) − (+5) = (−4) + (−5) = |−4| + |−5| = 4 + 5 = −9
Запись с модулями необходимо заключить в скобки и перед этими скобками поставить минус. Так мы обеспечим минус, который должен стоять перед ответом:
(−4) − (+5) = (−4) + (−5) = −(|−4| + |−5|) = −(4 + 5) = −(9) = −9
Решение для данного примера можно записать покороче:
−4 − 5 = −(4 + 5) = −9
или ещё короче:
−4 − 5 = −9
Пример 8. Найти значение выражения −3 − 5 − 7 − 9
Приведём выражение к понятному виду. Здесь все числа, кроме числа −3 являются положительными, поэтому у них будут знаки плюса:
(−3) − (+5) − (+7) − (+9)
Заменим вычитания сложениями. Все минусы, кроме минуса, стоящего перед тройкой, поменяются на плюсы, и все положительные числа поменяются на противоположные:
(−3) − (+5) − (+7) − (+9) = (−3) + (−5) + (−7) + (−9)
Теперь применим правило сложения отрицательных чисел. Чтобы сложить отрицательные числа, нужно сложить их модули и перед полученным ответом поставить минус:
(−3) − (+5) − (+7) − (+9) = (−3) + (−5) + (−7) + (−9) =
= −( |−3| + |−5| + |−7| + |−9| ) = −(3 + 5 + 7 + 9) = −(24) = −24
Решение данного примера можно записать покороче:
−3 − 5 − 7 − 9 = −(3 + 5 + 7 + 9) = −24
или ещё короче:
−3 − 5 − 7 − 9 = −24
Пример 9. Найти значение выражения −10 + 6 − 15 + 11 − 7
Приведём выражение к понятному виду:
(−10) + (+6) − (+15) + (+11) − (+7)
Здесь сразу две операции: сложение и вычитание. Сложение оставляем без изменения, а вычитание заменяем сложением:
(−10) + (+6) − (+15) + (+11) − (+7) = (−10) + (+6) + (−15) + (+11) + (−7)
Соблюдая порядок действий, выполним поочерёдно каждое действие, опираясь на ранее изученные правила. Записи с модулями можно пропустить:
Первое действие:
(−10) + (+6) = − (10 − 6) = − (4) = − 4
Второе действие:
(−4) + (−15) = − (4 + 15) = − (19) = − 19
Третье действие:
(−19) + (+11) = − (19 − 11) = − (8) = −8
Четвёртое действие:
(−8) + (−7) = − (8 + 7) = − (15) = − 15
Таким образом, значение выражения −10 + 6 − 15 + 11 − 7 равно −15
Примечание. Приводить выражение к понятному виду, заключая числа в скобки, вовсе необязательно. Когда происходит привыкание к отрицательным числам, это действие можно пропустить, поскольку оно отнимает время и может запутать.
Итак, для сложения и вычитания целых чисел необходимо запомнить следующие правила:
Чтобы сложить числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше.
Чтобы из меньшего числа вычесть большее, нужно из большего числа вычесть меньшее и перед полученным ответом поставить минус.
Вычесть одно число из другого означает, прибавить к уменьшаемому такое число, которое противоположно вычитаемому.
Чтобы сложить отрицательные числа, нужно сложить их модули, и перед полученным ответом поставить минус.
Задания для самостоятельного решения
Задание 1. Найдите значение выражения:
−50 + 40
Задание 2. Найдите значение выражения:
25 + (−5)
Задание 3. Найдите значение выражения:
−20 + 60
Задание 4. Найдите значение выражения:
20 + (−8)
Задание 5. Найдите значение выражения:
30 + (−50)
Задание 6. Найдите значение выражения:
27 + (−19)
Задание 7. Найдите значение выражения:
−17 + (−12) + (−8)
Решение
Задание 8. Найдите значение выражения:
−6 − 4
Решение
−6 − 4 = −6 + (−4) = −10
Задание 9. Найдите значение выражения:
−6 − (−4)
Решение
−6 − (−4) = −6 + 4 = −2
Задание 10. Найдите значение выражения:
−15 − (−15)
Решение
−15 − (−15) = −15 + 15 = 0
Задание 11. Найдите значение выражения:
−11 − (−14)
Решение
−11 − (−14) = −11 + 14 = 3
Задание 12. Найдите значение выражения:
−3 + 2 − (−1)
Решение
Задание 13. Найдите значение выражения:
−5 − 6 − 3
Решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

Как правильно пишется «сложение»?
Буквы а — о в корне -лаг- — -лож-
В корне -лаг- — -лож- в безударном положении буква а пишется, если за корнем стоит суффикс -а-; буква о пишется, если за корнем нет суффикса -а-.
Пример
Предполагать (есть -а- за корнем), предположение (нет -а- за корнем).
Не пользуйтесь проверочным словом при написании слов с чередованием гласных в корне.
УМК под редакцией Т. А. Ладыженской, 5 класс.
Проверить правописание любого слова
Результаты поиска
Слово/Фраза
Правило
сложение Буквы а — о в корне -лаг- — -лож-
Буквы а — о в корне -лаг- — -лож-
Записи 1-1 из 1
Как правильно пишется словосочетание «складывать числа»
- Как правильно пишется слово «сложить»
- Как правильно пишется слово «число»
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать
Карту слов. Я отлично
умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: ласина — это что-то нейтральное, положительное или отрицательное?
Ассоциации к слову «сложить»
Ассоциации к слову «число»
Синонимы к словосочетанию «складывать числа»
Предложения со словосочетанием «складывать числа»
- Числовое чутьё позволяет примерно понимать, что такое сложение, поэтому ещё до школы дети находят простые способы складывать числа.
- Может ли при этом парафреник правильно складывать числа?
- Число судьбы: складываем число имени 2 и число рождения 7, получаем 9.
- (все предложения)
Цитаты из русской классики со словосочетанием «складывать числа»
- В числе этих любителей преферанса было: два военных с благородными, но слегка изношенными лицами, несколько штатских особ, в тесных, высоких галстухах и с висячими, крашеными усами, какие только бывают у людей решительных, но благонамеренных (эти благонамеренные люди с важностью подбирали карты и, не поворачивая головы, вскидывали сбоку глазами на подходивших); пять или шесть уездных чиновников, с круглыми брюшками, пухлыми и потными ручками и скромно неподвижными ножками (эти господа говорили мягким голосом, кротко улыбались на все стороны, держали свои игры у самой манишки и, козыряя, не стучали по столу, а, напротив, волнообразно роняли карты на зеленое сукно и, складывая взятки, производили легкий, весьма учтивый и приличный скрип).
- Он любил цифры, выучился у меня складывать и умножать их, но терпеть не мог деления. Увлеченно умножал многозначные числа, храбро ошибался при этом и, написав длинную линию цифр палкой на песке, смотрел на них пораженно, вытаращив детские глаза, восклицая:
- Купец, то есть шляпа, борода, крутое брюхо и сапоги, смотрел, как рабочие, кряхтя, складывали мешки хлеба в амбар; там толпились какие-то неопределенные личности у кабака, а там проехала длинная и глубокая телега, с насаженным туда невероятным числом рослого, здорового мужичья, в порыжевших шапках без полей, в рубашках с синими заплатами, и в бурых армяках, и в лаптях, и в громадных сапожищах, с рыжими, седыми и разношерстными бородами, то клином, то лопатой, то раздвоенными, то козлинообразными.
- (все
цитаты из русской классики)
Значение слова «сложить»
-
СЛОЖИ́ТЬ, сложу́, сло́жишь; прич. страд. прош. сло́женный, —жен, -а, -о; сов., перех. 1. (несов. складывать). Положить в определенном порядке, придав какой-л. вид, форму. Сложить сено в копны. Сложить дрова в поленницу. (Малый академический словарь, МАС)
Все значения слова СЛОЖИТЬ
Значение слова «число»
-
ЧИСЛО́, -а́, мн. чи́сла, —сел, —слам, ср. 1. Понятие, служащее выражением количества, при помощи которого производится счет. Простые числа. Целое число. Положительные числа. Теория чисел (наука о целых числах). (Малый академический словарь, МАС)
Все значения слова ЧИСЛО
Афоризмы русских писателей со словом «сложить»
- Много дум я в тишине продумал,
Много песен про себя сложил,
И на этой на земле угрюмой
Счастлив тем, что я дышал и жил. - Но, погребальной грусти внемля,
Я для себя сложил бы так:
Любил он родину и землю,
Как любит пьяница кабак. - Иному век случается прожить,
А он не может значащее слово
Из пережитых горестей сложить. - (все афоризмы русских писателей)
Отправить комментарий
Дополнительно
Смотрите также
СЛОЖИ́ТЬ, сложу́, сло́жишь; прич. страд. прош. сло́женный, —жен, -а, -о; сов., перех. 1. (несов. складывать). Положить в определенном порядке, придав какой-л. вид, форму. Сложить сено в копны. Сложить дрова в поленницу.
Все значения слова «сложить»
ЧИСЛО́, -а́, мн. чи́сла, —сел, —слам, ср. 1. Понятие, служащее выражением количества, при помощи которого производится счет. Простые числа. Целое число. Положительные числа. Теория чисел (наука о целых числах).
Все значения слова «число»
-
Числовое чутьё позволяет примерно понимать, что такое сложение, поэтому ещё до школы дети находят простые способы складывать числа.
-
Может ли при этом парафреник правильно складывать числа?
-
Число судьбы: складываем число имени 2 и число рождения 7, получаем 9.
- (все предложения)
- сложение чисел
- записывать числа
- однозначное число
- полученное число
- двузначное число
- (ещё синонимы…)
- сложение
- штабель
- несложный
- доски
- сумма
- (ещё ассоциации…)
- сто
- цифра
- десять
- третий
- двенадцать
- (ещё ассоциации…)
- сложить руки на груди
- сложить руки на коленях
- сложить оружие
- (полная таблица сочетаемости…)
- задним число
- число людей
- увеличение числа
- число делится
- принадлежать к числу
- (полная таблица сочетаемости…)
- Разбор по составу слова «сложить»
- Разбор по составу слова «число»
- Как правильно пишется слово «сложить»
- Как правильно пишется слово «число»
А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я
сложе́ние, -я
Рядом по алфавиту:
слого́вость , -и
слогоделе́ние , -я
слогообразу́ющий
слогоразде́л , -а
слоеви́ще , -а
слоевищеподо́бный
слоеви́щный
слоево́й
слоевцо́вый
слоёк , слойка́
слое́ние , -я
слоённый , кр. ф. -ён, -ена́, прич.
слоёный , прил.
сло́ечка , -и, р. мн. -чек
сложа́ ру́ки , (сиде́ть)
сложе́ние , -я
сло́женный , кр. ф. -ен, -ена, прич.
сложённый , кр. ф. -ён, -ена́, прил. (о человеке)
сложи́ть(ся) , сложу́(сь), сло́жит(ся)
сложне́йший
сло́жно , нареч. и в знач. сказ.
сложнова́то , нареч. и в знач. сказ.
сложнова́тый
сложнокоординацио́нный
сложноорганизо́ванный* , [изменено, ср. РОС 2012: сложноорганизо́ванный]
сложноподчинённый
сложнопостано́вочный
сложнопро́фильный
сложносокращённый
сложносоставно́й
сложносочинённый
– как правильно пишется слово?Написание – «сложить» или «слажить» – определено правилом «Буквы «о» и «а» в корне «-лаг-/-лож-».
Как пишется правильно: «сложить» или «слажить»?
Какое правило применяется?
«Сложить» – глагол совершенного вида в форме инфинитива. Употребляется в значении – разместить что-либо в определенном порядке или месте; согнуть что-либо гибкое, изменяя его прежнюю форму; суммировать несколько чисел; сочинить стих.
Лексема славянского происхождения, происходит от праславянского «ložiti», далее от древнерусского «ложити».
В глаголе часто допускается ошибка: вместо гласной «о» в безударном корне «-лож-» пишут – «а».
Проверить написание гласной в корне нельзя. При написании нужно руководствоваться названной выше орфограммой, в которой сказано, что гласная «а» в корне с чередованием «-лаг-/-лож-» пишется в слабой позиции, когда корень оканчивается на «-г», а «о», когда корень оканчивается на – «-ж».
В слове, нас интересующем, гласная безударная, корень оканчивается на «ж», следовательно, пишем в нём гласную «о».
Примеры предложений
От тебя требуется только одно – сложить аккуратно свои вещи.
Он мог даже сложить стихотворение к какой-нибудь знаменательной дате.
Как неправильно писать
Ответ:
Правильное написание слова — сложение
Ударение и произношение — слож`ение
Значение слова -== телосложение
Пример:
Богатырское с.
Выберите, на какой слог падает ударение в слове — РЕВЕНЬ?
Слово состоит из букв:
С,
Л,
О,
Ж,
Е,
Н,
И,
Е,
Похожие слова:
словосложение
сложением
стихосложение
стопосложение
телосложение
Рифма к слову сложение
приложение, предложение, расположение, изложение, предположение, положение, нерасположение, разложение, брожение, уничтожение, раздражение, сражение, движение, приближение, выражение, передвижение, отражение, уважение, пренебрежение, служение, унижение, сожжение, продолжение, воображение, поражение, вооружение, сближение, самоотвержение, соображение, постижение, достижение, богослужение, одолжение, изображение, противодвижение, учреждение, убеждение, падение, нападение, мгновение, обхождение, благословение, утверждение, нововведение, поведение, хождение, объедение, побуждение, пробуждение, провидение, столкновение, рассуждение, суждение, повиновение, соблюдение, постигновение, благоговение, сновидение, заблуждение, освобождение, препровождение, прикосновение, происхождение, обсуждение, ведение, наблюдение, подтверждение, сведение, произведение, совпадение, владение, съедение, предвидение, выпадение, подведение, распадение, возрождение, овладение, наслаждение, возникновение, несоблюдение, возбуждение, местопребывание, предание, следование, завывание, колебание, негодование, подтрунивание, добивание, преследование, укладывание, разрывание, существование, содрогание, название, приставание, звание, выговаривание, приказывание, всачивание, комплектование, образование, поругание, командование, наименование, фехтование, царствование, ознаменование, воззвание, пребывание, бомбардирование, сондирование, отрезывание, всхлипывание, именование, обмундирование, усовершенствование, сострадание, оправдание, самопожертвование, преобладание, толкование, призвание, жертвование, очарование, требование, соборование, празднование, соревнование, основание, страдание, сословие, препятствие, шествие, богословие, нашествие, царствие, долгие, орудие, приветствие, неудовольствие, людие, воздействие, строгие, дорогие, пособие, усердие, предисловие, условие, молебствие, действие, происшествие, бедствие, свежие, насильствие, удовольствие, спокойствие, многие, следствие, самолюбие, бездействие, другие, высокоблагородие, отсутствие, благородие, противудействие, тщеславие, вследствие, подобие, добронравие, предчувствие, властолюбие, путешествие, содействие, сумасшествие, милосердие, странствие, продовольствие, присутствие, сочувствие, высокородие
Толкование слова. Правильное произношение слова. Значение слова.
Содержание
- Как пишется «сложение» или «слажение». Почему?
- Значение слова «сложение»
- сложе́ние
- Делаем Карту слов лучше вместе
- Связанные словари
- Сложение
- Как правильно пишется слово «слагаемое»
- Делаем Карту слов лучше вместе
- Ассоциации к слову «слагаемое»
- Синонимы к слову «слагаемое»
- Предложения со словом «слагаемое»
- Цитаты из русской классики со словом «слагаемое»
- Значение слова «слагаемое»
- Отправить комментарий
- Дополнительно
- Значение слова «слагаемое»
- Предложения со словом «слагаемое»
- Синонимы к слову «слагаемое»
- Ассоциации к слову «слагаемое»
- Морфология
- Карта слов и выражений русского языка
Как пишется «сложение» или «слажение». Почему?
Здесь не надо искать проверочных слов, так как перед нами корень с чередующейся гласной «лож»-«лаг». В качестве доказательства приведу однокоренные слова к слову «сложение»:
С помощью подбора однокоренных слов видно, что гласные в корне чередуются. Значит при написании слов с такими корнями надо отталкиваться от соответствующего правила:
Так как в слове «сложение» нет суффикса «а», то в корне правильно писать «о», т.е. «слОжение».
Вот и проверили и выяснили, что правильно это слово писать только через букву О.
Тут важно еще не перепутать с другими похожими по написанию, но совсем другими по смыслу словами, например, слаженный, что значит согласованно.
При написании слова «сл*жение» можно сделать ошибку, поскольку наша сомнительная гласная в корне безударная. Для того чтобы не ошибаться, нам нужно путем подбора проверочного слова уточнить корневую гласную.
Для проверки выбираем такое слово, в котором ударение выпадет на сомнительный гласный, тем самым усилив его звучание. Таким словом вполне может быть «слОжит», поскольку гласная «о» в нем звучит отчетливо. Из этого следует, что и в нашем слове «слОжение» нужно прописывать в корне гласную букву «о», а не «а».
Первоклассники на уроке математики повторили сложение чисел, а затем приступили к знакомству с вычитанием.
Источник
Значение слова «сложение»
1. Действие по глаг. сложить (во 2, 5 и 8 знач.). Сложение чисел. Сложение полномочий.
2. Обратное вычитанию математическое действие, посредством которого из двух или нескольких чисел (или величин) получают новое, содержащее столько единиц (или величин), сколько было во всех данных числах (величинах) вместе.
3. То же, что телосложение. Красота гребенской женщины особенно поразительна соединением самого чистого типа черкесского лица с широким и могучим сложением северной женщины. Л. Толстой, Казаки. Чепраков был не крепкого сложения: узкогрудый, сутулый, длинноногий. Чехов, Моя жизнь.
4. Спец. Строение, структура вещества. Пластинчатое сложение почвы.
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
является число, называемое суммой[стиль] чисел
(слагаемых) и обозначаемое
. Это одна из четырёх элементарных математических операций арифметики, вместе с вычитанием, умножением и делением. Сложение двух натуральных чисел есть общая сумма этих величин[стиль]. Например, комбинация из трёх и двух яблок[стиль] (на рисунке) в сумме даёт 5 яблок. Это наблюдение эквивалентно алгебраическому выражению «3 + 2 = 5», то есть «3 плюс 2 равно 5».
Помимо подсчёта фруктов, сложение можно представить, комбинируя другие физические объекты. Используя систематические обобщения, сложение можно определить для абстрактных величин, таких как целые числа, рациональные числа, вещественные числа и комплексные числа и для других абстрактных объектов, таких как векторы и матрицы.
В арифметике также разработаны специальные правила для сложения дробей и отрицательных чисел. В алгебре сложение изучается более абстрактно.
В общем виде сложение можно записать так:
. То есть каждой паре элементов
ставится в соответствие элемент
.Сложение возможно только, если оба аргумента принадлежат одному множеству элементов (имеют одинаковый тип).
У сложения есть несколько важных свойств (например, для A — множества вещественных чисел) (см. Сумма):
(нулевого элемента) даёт число, равное исходному:
Сложение также подчиняется правилам, касающимся операций вычитания и умножения.
Сложение — одна из простейших операций с числами. Сложение очень маленьких чисел понятно даже де
СЛОЖЕ’НИЕ, я, ср. 1. только ед. Действие по глаг. сложить во 2, 5 и 7 знач. — складывать — слагать. С. сил (замена нескольких сил одной, производящей равноценное действие; физ.). С. величин. С. обязанностей. 2. только ед. Одно из четырех арифметических действий, посредством к-рого из двух или нескольких чисел (слагаемых) получают новое (сумму), содержащее столько единиц, сколько было во всех данных числах вместе. Правило сложения. Задача на с. Произвести с. 3. То же, что телосложение; общее физическое состояние организма. Богатырского сложения, здоровенный был детинушка. Некрасов. Не хвастаюсь сложеньем, однако бодр и свеж, и дожил до седин. Грибоедов. || Строение вещества (спец.). Ноздреватое с.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
сложе́ние
1. действие по значению гл. слагать, сложить; составление ◆ «Славянский» язык сложился и окреп именно в христианской школе и под сильным влиянием греческого церковного языка, и это был не только словесный процесс, но именно сложение мысли. Георгий Флоровский, «Пути русского богословия», 1936 г. (цитата из НКРЯ)
2. матем. одна из основных операций в разных разделах математики, позволяющая объединить два объекта, добавив один к другому ◆ Поэтому у Явлинского осознают, что сложение вероятных 5 процентов избирателей «Яблока» с 5 процентами избирателей СПС в итоге даст не 10, а 6 процентов голосов на выборах. Геннадий Зюганов, «Неутешительный диагноз положения страны», 2003 г. (цитата из НКРЯ)
3. то же, что телосложение; строение, формы тела; фигура
4. спец. строение, структура вещества ◆ «Тёмные» части ― складываются, как сложение концентраций… простые (но, очевидно, не самые простые) «эфирные тела» ― электроны, протоны ― группируются и образуют атомы, атомы образуют молекулы, и так далее вплоть до галактик и их скоплений… «Форум о медицинской диагностике», 2010 г. (цитата из НКРЯ)
5. отказ от какой-то обязанности ◆ Политолог предлагает не роспуск, а самороспуск палаты, сложение депутатами полномочий. Михаил Виноградов, «Материал для скульптора. Политологи решили сохранить Госдуму», 2001 г. (цитата из НКРЯ)
Делаем Карту слов лучше вместе

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова жаровой (прилагательное):
Источник
Связанные словари
Сложение
Сложение
⇒ Гласные буквы в слове:
гласные выделены красным
гласными являются: о, е, и, е
общее количество гласных: 4 (четыре)
ударная гласная выделена знаком ударения « ́ »
ударение падает на букву: е
безударные гласные выделены пунктирным подчеркиванием « »
безударными гласными являются: о, и, е
общее количество безударных гласных: 3 (три)
⇒ Согласные буквы в слове:
согласные выделены зеленым
согласными являются: с, л, ж, н
общее количество согласных: 4 (четыре)
звонкие согласные выделены одинарным подчеркиванием « »
звонкими согласными являются: л, ж, н
общее количество звонких согласных: 3 (три)
глухие согласные выделены двойным подчеркиванием « »
глухими согласными являются: с
общее количество глухих согласных: 1 (одна)
Источник
Как правильно пишется слово «слагаемое»
Источник: Орфографический академический ресурс «Академос» Института русского языка им. В.В. Виноградова РАН (словарная база 2020)
Делаем Карту слов лучше вместе

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова ямс (существительное):
Ассоциации к слову «слагаемое»
Синонимы к слову «слагаемое»
Предложения со словом «слагаемое»
Цитаты из русской классики со словом «слагаемое»
Значение слова «слагаемое»
Отправить комментарий
Дополнительно
Значение слова «слагаемое»
Предложения со словом «слагаемое»
От перемены мест слагаемых сумма в лучшую сторону не меняется.
Это ведь только в арифметике от перемены мест слагаемых сумма не изменяется.
Второе слагаемое успеха – мотивация, желание человека стать успешным бегуном.
Синонимы к слову «слагаемое»
Ассоциации к слову «слагаемое»
Морфология
Карта слов и выражений русского языка
Онлайн-тезаурус с возможностью поиска ассоциаций, синонимов, контекстных связей и примеров предложений к словам и выражениям русского языка.
Справочная информация по склонению имён существительных и прилагательных, спряжению глаголов, а также морфемному строению слов.
Сайт оснащён мощной системой поиска с поддержкой русской морфологии.
Источник
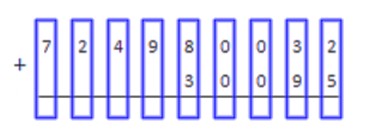
Сложение столбиком, или как еще говорят, сложение в столбик — это метод, широко используемый для сложения многозначных натуральных чисел. Суть этого метода в том, что сложение двух и более многозначных чисел сводится к нескольким простым операциям сложения однозначных чисел.
В статье подробно расписано, как выполнять сложение двух и большего количества многозначных натуральных чисел. Дано правило сложения чисел в столбик и примеры решения с разбором всех самых характерных ситуаций, возникающих при сложении чисел в столбик.
Сложение двух чисел в столбик: что нужно знать?
Прежде чем мы перейдем непосредственно к операции сложения в столбик, рассмотрим некоторые важные моменты. Для быстрого освоения материала желательно:
- Знать и хорошо ориентироваться в таблице сложения. Так, при проведении промежуточных вычислений, вам не придется тратить время и постоянно обращаться к таблице сложения.
- Помнить свойства сложения натуральных чисел. Особенно свойства, связанные со сложением нулей. Напомним их кратко. Если одно из двух слагаемых равно нулю, то сумма равна другому слагаемому. Сумма двух нулей есть нуль.
- Знать правила сравнения натуральных чисел.
- Знать, что такое разряд натурального числа. Напомним, что разряд — это позиция и значение цифры в записи числа. Разряд определяет значение цифры в числе — единицы, десятки, сотни, тысячи и т.д.
Сложение двух натуральных чисел в столбик
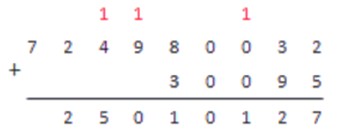
Опишем алгоритм сложения чисел столбиком с использованием конкретного примера. Пусть мы складываем числа 724980032 и 30095. Сначала следует записать эти числа по правилам записи сложения в столбик.
Числа записываются одно под другим, цифры каждого разряда располагаются, соответственно, одна под другой. Слева ставим знак «плюс», а под числами проводим горизонтальную линию.
Теперь мысленно разбиваем запись на столбики по разрядам.
Все, что остается сделать — сложить однозначные числа в каждом столбике.
Начинаем с крайнего правого столбика (разряд единиц). Складываем числа, и под чертой записываем значение единиц. Если при сложении значение десятков в результате получилось отличным от нуля, запоминаем это число.
Складываем цифры второго столбика. К результату прибавляем число десятков, которое мы запомнили на предыдущем шаге.
Повторяем весь процесс с каждым столбиком, вплоть до крайнего левого.
Данное изложение — упрощенная схема алгоритма сложения натуральных чисел столбиком. Теперь, когда мы разобрались с сутью метода, рассмотрим каждый шаг подробно.
Сначала складываем единицы, то есть числа в правом столбце. Если у нас получилось число, меньшее чем 10, записываем его в том же столбике и переходим к следующему. Если же результат сложения больше или равен 10, то под чертой в первом столбике записываем значение разряда единиц, а значение разряда десятков — запоминаем. Например, получилось число 17. Тогда записываем число 7 — значение единиц, а значение десятков — 1 — запоминаем. Обычно говорят: «семь пишем, один в уме».
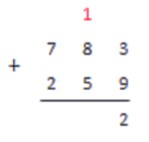
В нашем примере, при сложении чисел первого столбика, мы получаем число 7.
7<10, поэтому записываем это число в разряд единиц результата, а запоминать нам ничего не нужно.
Далее складываем числа в следующем столбце, то есть в разряде десятков. Проводим те же действия, только к сумме нужно прибавить число, которое мы держали в уме. Если сумма получилась меньше 10, просто записываем число под вторым столбиком. Если же результат больше или равен 10, записываем во втором столбике значение единиц этого числа, а цифру из разряда десятков запоминаем.
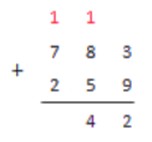
В нашем случае мы складываем числа 3 и 9, в результате имеем 3+9=12. На предыдущем шаге мы ничего не запоминали, поэтому к этому результату ничего прибавлять не нужно.
12>10, поэтому во втором столбике записываем цифру 2 из разряда единиц, а цифру 1 из разряда десятков держим в уме. Для удобства можно записать это число над следующим столбиком другим цветом.
Переходя к третьему, четвертому и так далее столбику повторяем действие, пока столбики не закончатся.
В третьем столбике сумма цифр равна нулю (0+0=0). К этой сумме прибавляем то число, которое ранее держали в уме, и получаем 0+1=1. записываем:
Переходя к следующему столбцу также складываем 0+0=0 и записываем в результате 0, так как на предыдущем шаге мы ничего не запоминали.
Следующий шаг дает 8+3=11. В столбике записываем цифру 1 из разряда единиц. Цифру 1 из разряда десятков держим в уме и переходим к следующему столбцу.
Этот столбик содержит только одно число 9. Если бы у нас не было в памяти числа 1, мы бы просто переписали число 9 под горизонтальную черту. Однако, учитывая, что не предыдущем шаге мы запомнили число 1, нужно сложить 9+1 и записать результат.
9+1=10
Поэтому, под горизонтальной чертой мы записываем 0, а единицу снова держим в уме.
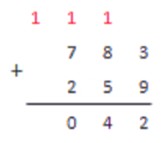
Переходя к следующему столбику складываем 4 и 1, результат пишем под чертой.
Следующий столбик содержит только число 2. Так на предыдущем шаге мы ничего не запоминали, просто переписываем это число под черту.
Также поступаем и с последним столбиком, содержащим число 7.
Столбцов более нет, и в памяти также ничего нет, поэтому можно сказать, что операция сложения в столбик окончена. Число, записанное под чертой — результат сложения двух верхних чисел.
Чтобы разобраться со всеми возможными нюансами, рассмотрим еще несколько примеров.
Сложим два натуральных числа: 21 и 36.
Сначала запишем эти числа по правилу записи при сложении столбиком:
Начав с правого столбика, приступаем к сложению чисел.
1+6=7
Так как 7<10, записываем 7 под чертой.
Складываем числа во втором столбике.
2+3=5
Так как 5<10, а в памяти с предыдущего шага ничего нет, записываем результат
В памяти и в следующем столбике чисел более нет, сложение закончено. 21+36=57
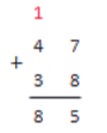
Сколько будет 47+38?
Запишем:
7+8=15, поэтому запишем 5 в первом столбике под чертой, а 1 будем держать в уме.
Теперь складываем значения из разряда десятков: 4+3=7. Не забываем о единице и прибавляем ее к результату:
7+1=8. Полученное число записываем под чертой.
Это и есть результат сложения.
47+38=85
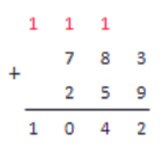
Теперь возьмем два трехзначных числа и выполним их сложение.
3+9=12; 12>10
Записываем 2 под чертой, 1 держим в уме.
8+5=13; 13>10
Складываем 13 и запомненную единицу, получаем:
13+1=14; 14>10
Записываем 4 под чертой, 1 держим в уме.
7+2=9
Не забываем, что на предыдущем шаге мы запомнили 1.
9+1=10
Записываем 0 под чертой, 1 держим в уме.
В последнем столбике переносим единицу, которую мы запомнили ранее, под черту, и получаем окончательный результат сложения.
783+259=1042
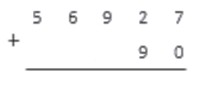
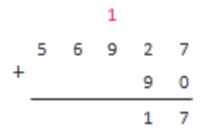
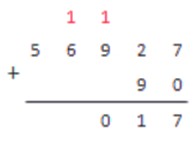
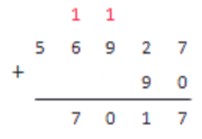
Найдем сумму чисел 56927 и 90.
Как всегда, сначала записываем условие:
7+0=7; 7<10
Записываем 7 под чертой и переходим к следующему столбику.
2+9=11; 11>10
Записываем 1 под чертой, 1 держим в уме и переходим к следующему столбику.
9+1=10
Записываем 0 под чертой, 1 держим в уме и переходим к следующему столбику.
Столбик содержит одно число 6. Складываем его с запомненной единицей.
6+1=7; 7<10
Записываем 7 под чертой и переходим к следующему столбику.
Столбик содержит одно число 5. Переносим его под черту и заканчиваем операцию сложения.
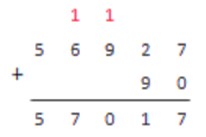
56927+90=57017
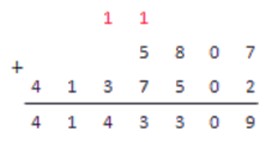
Следующий пример приведем без промежуточных результатов и пояснений, как образец записи сложения в столбик на практике.
5807+4137502=?
Ответ: 5807+4137502=4143309
Сложение столбиком трех и более чисел. Что нужно знать?
Во первых, нужно усвоить всю информацию, уже изложенную в этой статье. Во вторых, также помним, что нули не влияют на результат сложения, и сколько бы не было в выражении слагаемых нулей, их сумма будет равна нулю.
Этапы сложения в столбик трех и более чисел аналогичны этапам из уже рассмотренных примеров с двумя числами. Обратимся к практике и поясним ход решения.
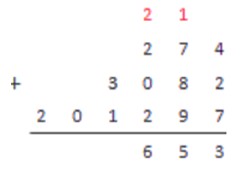
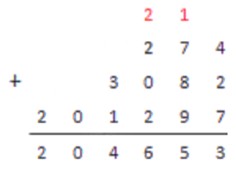
Сложим столбиком числа 274, 3082 и 201297.
Сначала делаем запись:
Начинаем с первого столбика, справа налево.
4+2+7=13; 13>10
3 пишем, 1 в уме. Переходим ко второму столбику.
7+8+9=24; 24+1=25; 25>10
5 пишем, 2 в уме. Переходим к третьему столбику.
2+0+2=4; 4+2=6; 6<10
6 пишем, и ничего не запоминаем. Переходим к четвертому столбику.
3+1=4; 4<10
4 пишем, и ничего не запоминаем. Переходим к пятому столбику. Пятый и шестой столбики содержат по одному числу, в уме с предыдущих шагов мы ничего не держим, поэтому просто переносим числа из последних двух столбиков под черту.
Ответ: 274+3082+201297=204653
Совет: при сложении трех и большего количества чисел в столбик, если вычисления выходят слишком громоздкими, бывает удобнее последовательно сложить два числа, затем еще два и так далее.
Сложение натуральных чисел
- Слагаемые и сумма
- Проверка сложения
Сложение чисел — это арифметическое действие, с помощью которого единицы двух чисел объединяются в одно новое число.
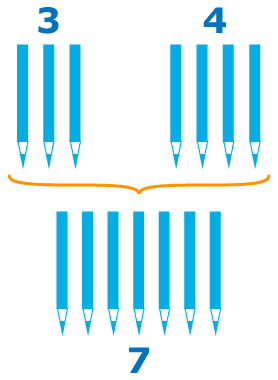
Пример. На столе лежало 3 карандаша, к ним положили ещё 4 карандаша. Сколько карандашей лежит на столе?
Чтобы ответить на этот вопрос, надо посчитать все карандаши, которые лежат на столе:
Считая карандаши, мы к карандашам, которые лежали на столе, прибавили карандаши, которые положили на стол, и получили общее число всех карандашей, то есть 7.
Для записи сложения используется знак +
(плюс), который ставится между складываемыми числами. Например:
3 + 4.
Эта запись означает, что складываются два числа: 3 и 4. Справа от записи сложения ставится знак =
(равно), после которого записывает полученный результат:
3 + 4 = 7.
Слагаемые и сумма
Слагаемые — это числа, единицы которых складываются. Например, в записи:
2 + 5,
2 — это первое слагаемое, 5 — второе слагаемое.
Сумма — это число, которое получается в результате сложения. Например, в записи:
2 + 5 = 7,
7 — это сумма. При этом сама запись 2 + 5 тоже называется суммой.
Эту запись можно прочитать так: сумма двух и пяти равна семи
, два плюс пять равно семи
или к двум прибавить пять, получится семь
.
Проверка сложения
Рассмотрим выражение
3 + 5 = 8,
где 3 — это первое слагаемое, 5 — это второе слагаемое, а 8 — сумма. Чтобы узнать правильно ли было выполнено сложение, можно:
- Вычесть из суммы первое слагаемое, если получится второе слагаемое, то сложение было выполнено верно:
8 — 3 = 5.
- Вычесть из суммы второе слагаемое, если получится первое слагаемое, то сложение было выполнено верно:
8 — 5 = 3.
Сложение двух чисел можно проверить вычитанием, для этого из суммы надо вычесть одно из слагаемых, если разность окажется равной другому слагаемому, то сложение выполнено верно.