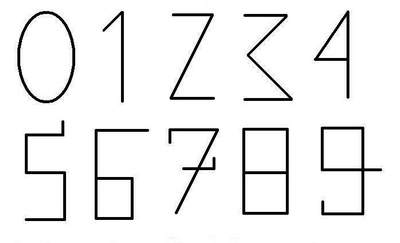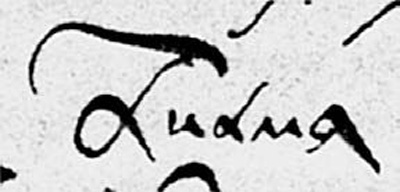Дети часто задают разные вопросы, в том числе откуда произошли цифры? Поможем вам ответить на этот непростой вопрос.
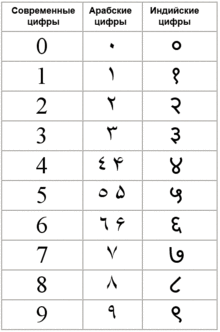
Современные цифры (1, 2, 3, 4, 5, 6, 7, 8, 9 и 0) были заимствованы арабами в Индии и принесены в Европу. Так как арабы их принесли в Европу, немного видоизменив их написание, то принято называть эти цифры «арабскими», хотя правильнее было бы их называть «индийскими».
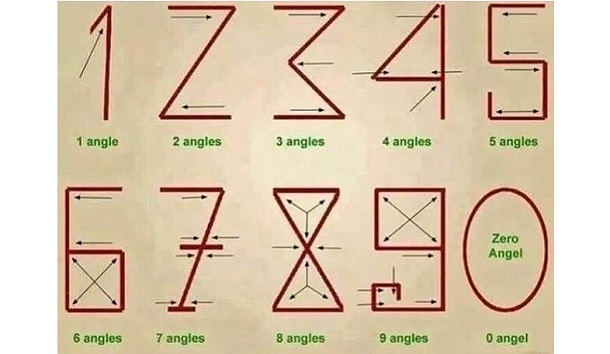
Существуют множество гипотез о происхождения начертания цифр. Одна из самых распространенных говорит о том, что количество углов соответствует числовому значению цифры. Так у цифры 1 в начертании один угол, у цифры 2 — два угла, у цифры 3 – три угла и т.д. У ноля углов нет, поэтому он круглый. Данная гипотеза ненаучная, но достаточно наглядная и понятная. Еще понятней для детей она становится, если вспомнить, что арабы – это народ кочевой и их главное богатство – это был скот. Вот так и обозначали одну голову быка — галочкой, похожей на V. То есть это не угол, а рога. Получается, что цифры изображали количество животных. Так у цифры 1 в начертании одни рога, у цифры 2 — две пары рогов, у цифры 3 – три пары рогов и т.д.
Вот так в старину люди рисовали картины-образы — пиктограммы. Со временем некоторые элементы цифр были упразднили при написании за ненадобностью, так как в них перестали видеть образы. Остались только цифры. И их волшебство в том, что всего десятью цифрами можно передать невообразимое количество всевозможных чисел.
Отгадайте, какую цифру больше всего любят в мире?
Оказывается, это цифра 7. Профессор Сюзан Краус Уитборн из Массачусетского университета в Амхерсте составила список причин, по которым мы так любим семерку.
7 — Религиозная цифра, отсылает к семи смертным грехам, седьмому небу и семи чудесам света.
7 — Окружает нас повсюду: семь континентов, семь дней в неделе, семь цветов радуги, семь нот.
7 — Число, на котором следует остановиться. Семь раз отмерь — один отрежь.
7 — Радует наш слух: «семь гномов» и «семья» звучат куда естественнее, чем «восемь карликов» или «ячейка общества». Поговорки бесконечно ссылаются на семерку — от «семь бед — один ответ» до «семи пядей во лбу».
7 — Частей какой-либо информации способна воспринять за один раз наша кратковременная память. Это доказал психолог Джордж Миллер. Его опыты убедительно доказали: человек может справиться с любым объемом информации, если поделит ее на семь.
7 — Любимое число нейронов. В 2008 году было проведено исследование, в ходе которого выяснилось, что нейроны, отвечающие за память, лучше всего воспроизводят информацию, когда у них семь дендритов — отростков, отвечающих за возбуждение и торможение.

Индийцы разработали позиционное счисление и объяснили смысл понятия «0» не позднее V столетия н. э. После этого стали появляться индоарабские и арабские цифры, из «индийских», как их во время становления и распространения называли арабы.
Доказательства того, что именно Индия является родиной арабских цифр
Во-первых, арабы пишут буквы, начиная с правой стороны строки, двигаясь налево, а цифры наоборот, что в корне не соответствует их технике письма.
Традиционные цифры, используемые во многих странах для записи чисел, на самом деле придумали индийцы. Миф об арабских корнях сформировался из-за того, что арабы активно способствовали распространению этой системы счисления, основанной на 10-ти численных знаках. Сегодня именно в арабских странах, занимающих территории Азии, и в Египте используют отличные от всего мира символы для записи чисел.
Индийцы разработали позиционное счисление и объяснили смысл понятия «0» не позднее V столетия н. э. После этого стали появляться индоарабские и арабские цифры, из «индийских», как их во время становления и распространения называли арабы.
Доказательства того, что именно Индия является родиной арабских цифр
Во-первых, арабы пишут буквы, начиная с правой стороны строки, двигаясь налево, а цифры наоборот, что в корне не соответствует их технике письма.
Происхождение знаков, обозначающих цифры
Существует 2 основные версии происхождения цифр. По первой, они появились в древнеиндийском языке деванагари, произошедшем от письменности брахми. Принципы построения графики в нем зависили от произношения слов. Числительные записывались той буквой, с которой начинается произношение слова, обозначающего ее.
По этой версии первые индийские цифры выглядели следующим образом:
Арабские цифры (шрифт без засечек)
| Системы счисления в культуре | |
|---|---|
| Индо-арабская система счисления | |
| Арабская Индийские Тамильская Бирманская |
Кхмерская Лаоская Монгольская Тайская |
| Восточноазиатские системы счисления | |
| Китайская Японская Сучжоу Корейская |
Вьетнамская Счётные палочки |
| Алфавитные системы счисления | |
| Абджадия Армянская Ариабхата Кириллическая |
Греческая Эфиопская Еврейская Катапаяди |
| Другие системы | |
| Вавилонская Египетская Этруская Римская |
Аттическая Кипу Майская |
| Позиционные системы счисления | |
| Десятичная система счисления (10) | |
| 2, 3, 4, 5, 6, 7, 8, 9, 12, 16, 20, 60 | |
| Нега-позиционная система счисления | |
| Симметричная система счисления | |
| Смешанные системы счисления | |
| Фибоначчиева система счисления | |
| Непозиционные системы счисления | |
| Единичная (унарная) система счисления | |
| Список систем счисления |
Арабские цифры — традиционное название набора из десяти знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9; ныне использующегося в большинстве стран для записи чисел в десятичной системе счисления.
История
Арабские цифры. Цифры 4, 5 и 6 существуют в двух вариантах, слева — арабский, справа — персидский.
Индийские цифры возникли в Индии не позднее V века. Тогда же было открыто и формализовано понятие нуля (шунья), которое позволило перейти к позиционной записи чисел.
Арабские и индо-арабские цифры являются видоизменёнными начертаниями индийских цифр, приспособленными к арабскому письму[1].
Индийскую систему записи широко популяризировал учёный ал-Хорезми, автор знаменитой работы «Китаб аль-джебр ва-ль-мукабала», от названия которой произошёл термин «алгебра».
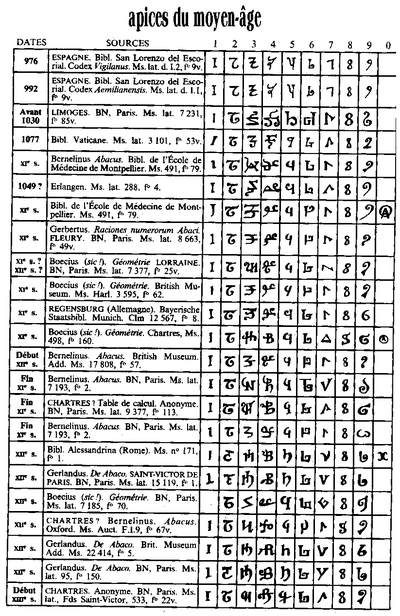
Арабские цифры стали известны европейцам в X веке. Благодаря тесным связям христианской Барселоны (Барселонское графство) и мусульманской Кордовы (Кордовский халифат), Сильвестр II (папа римский с 999 по 1003 годы) имел возможность доступа к научной информации, которой не имел никто в тогдашней Европе. В частности, он одним из первых среди европейцев познакомился с арабскими цифрами, понял удобство их употребления по сравнению с римскими цифрами и начал всячески пропагандировать их внедрение в европейскую науку.
| Арабские цифры, используемые в арабских странах Африки (кроме Египта) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Индо-арабские цифры, используемые в арабских странах Азии и в Египте | ٠ | ١ | ٢ | ٣ | ٤ | ٥ | ٦ | ٧ | ٨ | ٩ |
| Персидские цифры | ۰ | ۱ | ۲ | ۳ | ۴ | ۵ | ۶ | ۷ | ۸ | ۹ |
| Индийские цифры (в письме деванагари), используемые в Индии | ० | १ | २ | ३ | ४ | ५ | ६ | ७ | ८ | ९ |
| Цифры в письме гуджарати | ૦ | ૧ | ૨ | ૩ | ૪ | ૫ | ૬ | ૭ | ૮ | ૯ |
| Цифры в письме гурмукхи | ੦ | ੧ | ੨ | ੩ | ੪ | ੫ | ੬ | ੭ | ੮ | ੯ |
| Цифры в письме лимбу (Limbu) | ᥆ | ᥇ | ᥈ | ᥉ | ᥊ | ᥋ | ᥌ | ᥍ | ᥎ | ᥏ |
| Цифры в бенгальском письме | ০ | ১ | ২ | ৩ | ৪ | ৫ | ৬ | ৭ | ৮ | ৯ |
| Цифры в письме ория | ୦ | ୧ | ୨ | ୩ | ୪ | ୫ | ୬ | ୭ | ୮ | ୯ |
| Цифры в письме телугу | ౦ | ౧ | ౨ | ౩ | ౪ | ౫ | ౬ | ౭ | ౮ | ౯ |
| Цифры в письме каннада | ೦ | ೧ | ೨ | ೩ | ೪ | ೫ | ೬ | ೭ | ೮ | ೯ |
| Цифры в письме малаялам | ൦ | ൧ | ൨ | ൩ | ൪ | ൫ | ൬ | ൭ | ൮ | ൯ |
| Цифры в тамильском письме | ೦ | ௧ | ௨ | ௩ | ௪ | ௫ | ௬ | ௭ | ௮ | ௯ |
| Цифры в тибетском письме | ༠ | ༡ | ༢ | ༣ | ༤ | ༥ | ༦ | ༧ | ༨ | ༩ |
| Цифры в бирманском письме | ၀ | ၁ | ၂ | ၃ | ၄ | ၅ | ၆ | ၇ | ၈ | ၉ |
| Цифры в тайском письме | ๐ | ๑ | ๒ | ๓ | ๔ | ๕ | ๖ | ๗ | ๘ | ๙ |
| Цифры в кхмерском письме | ០ | ១ | ២ | ៣ | ៤ | ៥ | ៦ | ៧ | ៨ | ៩ |
| Цифры в лаосском письме | ໐ | ໑ | ໒ | ໓ | ໔ | ໕ | ໖ | ໗ | ໘ | ໙ |
Одна из легенд происхождения начертания современных арабских цифр[2]. Количество углов соответствует числовому значению цифры.
|
|
|
Название «арабские цифры» образовалось исторически, из-за того что именно арабы распространяли десятичную позиционную систему счисления. Цифры, которые используют в арабских странах, по начертанию сильно отличаются от используемых в европейских странах.
Примечания
- ↑ وجهات النظر حول أصل الأرقام ا&# … (ар.)
- ↑ Florian Cajori A History of Mathematical Notations. — Cosimo, Inc., 2007. — Vol. I. — P. 64-66. — ISBN 9781602066847
Ссылки
- Арабские цифры // Энциклопедический словарь Брокгауза и Ефрона: В 86 томах (82 т. и 4 доп.). — СПб., 1890—1907.
- «Арабские цифры» в Большой советской энциклопедии
- Титло — переводчик национальных начертаний арабских и других чисел
- Арабские цифры, использующиеся при датировке ковров
Время чтения 2 мин.Просмотры 8.2к.
Написание арабских цифр состояло из отрезков прямых линий, где количество углов соответствовало величине знака. Вероятно, кто-то из арабских математиков когда-то предложил идею — связать числовое значение цифры с количеством углов в ее начертании.
Как выглядели настоящие арабские цифры
Итак, смотрим на оригинальное изображение арабских цифр и видим, что:
0 — цифра без единого угла в начертании;
1 — содержит один острый угол;
2 — уже два острых угла;
3 — здесь три острых угла (правильное, арабское, начертание цифры получается при написании цифры 3 при заполнении почтового индекса на конверте);
4 — тут 4 прямых угла (именно этим объясняется наличие «хвостика» внизу цифры, никак не влияющего на ее узнаваемость и идентификацию);
5 — видим 5 прямых углов (назначение нижнего хвостика — то же самое, что у цифры 4 — достройка последнего угла);
6 — содержит 6 прямых углов;
7 — получается 7 прямых и острых углов (правильное, арабское, написание цифры 7 отличается от приведенного на рисунке наличием дефиса, пересекающего под прямым углом вертикальную линию посередине (вспомним, как мы пишем цифру 7), что дает 4 прямых угла и 3 угла дает еще верхняя ломаная линия);
8 — из 8 прямых углов;
9 — содержит 9 прямых углов (именно этим объясняется столь замысловатый нижний хвостик у девятки, который должен был достроить аж 3 угла, чтобы общее их число стало равно 9.
Время сгладило углы в арабских цифрах
Со временем углы сгладились, и цифры приобрели привычный нам вид. Вот уже много столетий весь мир пользуется арабской системой записи чисел. Этими десятью значками можно легко выразить огромные значения.
Кстати, слово «цифра» тоже арабское. Арабские математики перевели индийское слово «сунья» по смыслу на свой язык. Вместо «сунья» они стали говорить «сифр» или «цифр», а это уже знакомое нам слово. Так слово «цифра» по наследству от арабов досталось и нам.
Источник
Сегодняшний пост будет несколько отличаться от всего, что писал ранее. Один заголовок, уже может вызвать удивление, но давайте расскажу почему же эта тема вдруг появилась в блоге.
На днях меня попросили сделать арабскую версию одного сайта, материалы все предоставлял заказчик. Надо сказать, что с арабским то этого, я столкнулся лишь один раз, когда восстанавливал Asus All-in-one PC c флешки и получил Windows 8.1 на арабском.
Впечатления, надо сказать, непередаваемые — здесь дело даже не только в том, что весь интерфейс шиворот-навыворот, а сколько вскрывается тонкостей при разработке, о которых и не подозреваешь изначально. От того вдвойне интересней, плюс новый опыт. К делу я привык подходить основательно, но видя арабский текст, чувствуешь себя немного обезьяной, а потому следует хоть немного изучить предмет и понять суть. Постепенно вникая в тему, узнал об одной интересной особенности арабского языка, о которой ранее даже не подозревал. Далее текст не мой, позаимствовал его с https://rusdrus.livejournal.com/2585.html. Полагаю, будет весьма интересно почитать для общего развития.
Почему арабы пишут буквы справа налево, а цифры — наоборот
Один мой приятель после посещения Египта передал мне свой диалог с другим российским туристом во время экскурсии к пирамидам. Люди, бывавшие там, знают как это выглядит: арабы, бегающие со свистками и прогоняющие любителей полазить по пирамидам. После непродолжительного созерцания этого цирка попутчик спросил его «Ты веришь, что ЭТИ могли построить такое? Я — нет». Приятель с ним согласился.
Тем не менее каждый раз, когда я позволяю себе нелицеприятные высказывания об арабах, находится человек, который напоминает мне, что позиционную систему исчисления, которой мы пользуемся, придумали арабы и именно поэтому цифры называются «арабскими», в отличие от римских.
Однако арабскими эти числа назвали европейцы, которые позаимствовали их у арабов.
В XII веке книга Аль-Хорезми «Об индийском счёте» была переведена на латинский язык и сыграла очень большую роль в развитии европейской арифметики и внедрении индо-арабских цифр. (источник)
А вот на арабском они называются «ар ракм аль хинди», что означает «индийский счёт». Индийскими называют их и в Иране: «шумаре ха йе хенди» на фарси означает «индийские цифры». Мы не можем знать наверняка, построили ли арабы пирамиды, но то, что они не имеют никакого отношения к созданию так называемых «арабских» чисел — это достоверный и общепризнанный факт.
Индийские цифры возникли в Индии не позднее V века. Тогда же было открыто и формализовано понятие нуля (шунья), которое позволило перейти к позиционной записи чисел. Арабские и индо-арабские цифры являются видоизменёнными начертаниями индийских цифр, приспособленными к арабскому письму. Индийскую систему записи широко популяризировал учёный Аль-Хорезми, автор знаменитой работы «Китаб аль-джебр ва-ль-мукабала», от названия которой произошёл термин «алгебра». (источник)
Но представим, что у нас нет доступа к интернету и книгам или мы не верим написанному в википедии. О том, что арабы просто воспользовались результатом, можно легко догадаться даже не зная про «индийские цифры». Как известно, арабы пишут справа налево. Но при этом написание цифр происходит как у большинства белых народов, слева направо. Поэтому, если при письме арабу надо написать число, ему приходится отступать влево, прикидывая сколько места оно займёт, вписывать число слева направо и потом возвращаться обратно к письму справа налево. Возьмите лист бумаги и попытайтесь писать текст справа налево, а цифры — как обычно, и вы поймёте, что имеется в виду. Если писать приходится быстро, то можно второпях недооценить необходимое для числа место, и тогда оно будет сплющенное к концу.
Более образованный оппонент сразу скажет, что мол достижение арабов не столько в создании системы позиционного исчисления, сколько в создании алгебры, прародителем которой считают выдающегося арабского (об этом чуть ниже) математика Аль-Хорезми. Cоздателем алгебры его считают конечно же не за «арабские» числа, а за упомянутый выше труд, книгу «Китаб аль-джебр ва-ль-мукабала». Слово «аль-джебр» в названии означает «перенос», а слово «ва-ль-мукбала» означает «приведение». Перенос членов и приведение подобных — это одни из основных действий при решении уравнений. Кстати, слово «алгоритм» происходит как раз от имени Аль-Хорезми — латинский перевод его книги начинался словами «Dixit Algorizmi» (сказал Алгоризми).
Мухаммад Аль-Хорезми, (предположительно) персидский математик, трудившийся под арабской оккупацией. Реального изображения конечно же не сохранилось и автор по какой-то причине решил нарисовать учёному арабский клювообразный нос. (фото отсюда)
Википедия сообщает нам, что Аль-Хорезми ввёл некую классификацию для линейных и квадратных уравнений и описал правила их решения. Методы решения квадратных уравнений — это вне всякого сомнения достижение для того времени. Но только они были известны уже до него
Один из первых известных выводов формулы корней квадратного уравнения принадлежит индийскому учёному Брахмагупте (около 598 г.); Брахмагупта изложил универсальное правило решения квадратного уравнения, приведённого к каноническому виду (источник)
Как можно понять из имени, Брахмагупта принадлежал к индийской касте брахманов (то есть был арийцем, а не индусом; подробнее тут и тут ).
«Брахма-спхута-сиддханта» («Усовершенствованное учение Брахмы», или «Пересмотр системы Брахмы») — самый известный труд Брахмагупты, посвящённый математике и астрономии. Трактат написан стихами и содержит только результаты без доказательств. Труд состоит из 25 глав (в других источниках говорится о 24 главах и приложении с таблицами). 18-я глава, «Распылитель», имеет прямое отношение к алгебре, но поскольку такого термина ещё не существовало, названа по первой задаче, рассматриваемой в главе. (источник)
Может быть Аль-Хорезми не был знаком с трудами Брахмагупты и переоткрыл способы решения квадратных уравнений?
Во второй половине VIII века, когда багдадский халиф из династии Аббасидов Абу-ль-Аббас Абд-Аллах аль-Мамун (712—775) был с посольством в Индии, пригласил в Багдад учёного из Удджайна по имени Канках, который преподавал индийскую систему астрономии на основе «Брахма-спхута-сиддханта». Халиф заказал письменный перевод книги на арабский язык, который был осуществлён математиком и философом Ибрахимом аль-Фазари в 771 году. Перевод, выполненный в виде таблиц — зиджа — с необходимыми пояснениями и рекомендациями, получил название «Большой Синдхинд». Известно, что этой работой пользовался ал-Хорезми для написания своих трудов по астрономии («Зидж ал-Хорезми») и арифметике («Книга об индийском счёте»). (источник)
Как видим, Аль-Хорезми был хорошо знаком с книгой Брахмагупты. Да, он был несомненно крупным учёным своего времени, но никак не основоположником алгебры. И если бы европейская математика получала знания напрямую из Индии, а не через Багдад, то алгебра сейчас называлась бы какой-нибудь «брахмаспхутой».
Скорее всего не был Аль-Хорезми и арабом. Почему? Помните, мы упоминали о том, что в арабской системе письма (справа налево) запись цифр слева направо выглядит весьма неестественно? Неужели крупный математик своего времени не мог догадаться, что можно писать цифры и справа налево? Наверняка мог. Даже не с целью скрыть факт заимствования, а просто из соображений удобства. Но не сделал. Почему? Вполне возможно намеренно, чтобы оставить очевидным факт того, что это чужая система, не арабская. Это как послание из глубины веков, мол смотрите люди, арабы не имеют никакого отношения к числам. Нашу догадку частично подтверждает википедия
Сведений о жизни учёного сохранилось крайне мало. Родился предположительно в Хиве в 783 году. В некоторых источниках аль-Хорезми называют «аль-маджуси», то есть маг, из этого делается вывод, что он происходил из рода зороастрийских жрецов, позже принявших ислам. (источник)
Зороастризм, который упоминает википедия, — это не этническая принадлежность, а религиозная. Понятно, что если семья Аль-Хорезми исповедовала зороастризм, то арабом он быть никак не мог. Но кем тогда? Зороастризм исповедовали в основном персы, то есть скорее всего он был персом.
Ещё более искушённый оппонент возможно скажет, что мол выше упоминалось, что багдадский халиф аль-Мамун заказал перевод книги Брахмагупты, а значит поддерживал развитие науки. Чтобы у читателя не осталось ложных ощущений на этот счёт, посмотрим на историю Хорезма, родины Аль-Хорезми.
В 712 году происходит завоевание Хорезма арабским полководцем Кутейбой ибн Муслимом, учинившим жестокую расправу над хорезмийской аристократией. Особенно жестокие репрессии Кутейба обрушил на учёных Хорезма. Как пишет в «Хрониках минувших поколений» аль-Бируни, «и всеми способами рассеял и уничтожил Кутейба всех, кто знал письменность хорезмийцев, кто хранил их предания, всех учёных, что были среди них, так что покрылось всё это мраком и нет истинных знаний о том, что было известно из их истории во время пришествия к ним ислама». (источник)
Вот что представляло собой нашествие арабов на просвещенный мир — вырезать всех учёных, а для нескольких оставшихся построить библиотеку в Багдаде.
Аль-Хорезми родился предположительно в 783 году, то есть спустя примерно 60 лет после прихода арабов. Представьте, что вашу родину захватило племя кочевников и ваши деды вечерами рассказывают истории, как захватчики вырезали ваших родственников. Видимо тихо ненавидел Аль-Хорезми мусульманских оккупантов, вот и оставил направление записи чисел как у индусов. Мол пусть арабские животные хоть так помучаются, записывая тексты то справа налево, то слева направо.
Что имеем в сухом остатке? Арабские цифры — вовсе не арабские, а индийские, а гордость арабского мира, якобы основоположник алгебры математик Аль-Хорезми, алгебру не создавал и скорее всего даже не был арабом.
Подписывайтесь на канал
Яндекс.Дзен
и узнавайте первыми о новых материалах, опубликованных на сайте.
Если бы вас попросили назвать без раздумий несколько величайших изобретений или открытий, то большинство вспомнило бы, очевидно, об электричестве, радио, воздухоплавании, атомной энергии — и вряд ли назвало бы нашу цифровую систему. Десять знаков, меняющих свое значение от позиции, не связанных с определенным языком… Это просто, удобно. «Арабские» цифры так естественно вошли в нашу жизнь, что кажутся существующими вечно. Ну, по крайней мере, они выглядят как ровесники рычага или колеса. (А ведь помимо всего прочего появление арабских цифр имело и большое влияние в том числе, например, на развитие облика современных канцтоваров, которые сегодня можно приобрести на сайте https://nosorog.net.ua/738-kanctovary).
В действительности это не так. Точную дату назвать трудно, но можно уверенно утверждать, что арабским цифрам немногим больше тысячи лет, во всяком случае, не более полутора тысяч. Настоящую же оценку и широкое практическое применение это гениальное порождение человеческого разума нашло всего лишь пятьсот-четыреста лет назад.
Откуда же взялась эта система цифр? Считается, что она пришла в Европу (в Испанию) вместе с арабами-завоевателями. Те же, в свою очередь, заимствовали ее в Индии. В самом деле, до VII века, до появления ислама и начала завоеваний у арабов арабской цифири не было. Первые ее следы появляются в IX в. (874 и 878 гг.). А до тех пор, подобно грекам, евреям, грузинам и армянам, арабы для обозначения чисел пользовались алфавитом!
У южных арабов, кроме того, была своя, так называемая «сабейская» цифирь, построенная по другому принципу: единица в ней — вертикальная палочка, двойка — две палочки, тройка — три, четверка — четыре, десятка — кружочек, две десятки — два кружочка и т. д., и т. п. Мало общего с арабскими цифрами.
А с индийскими? Ведь считается, что изначально наша цифирь пошла оттуда. И вот оказывается: и в индийских рукописях в это время тоже нет ничего похожего!
Из 17 древнейших индийских записей, содержащих позиционную расстановку цифровых знаков, 15 оказались поддельными! Первая неподдельная запись датирована 876 годом: она содержит число 270, написанное арабскими цифрами с круглым нолем. Знак ноля в виде точки встречается в одной («Бакхшалинской») рукописи, которую различные исследователи датируют по-разному: от II до VIII и IX веков. На мой взгляд, датировки VIII и IX веками вернее.
Странная вещь. Если арабы заимствовали свои цифры у индийцев, то естественно ожидать большего сходства между «арабскими» цифрами индийцев и их соседей — восточных арабов. В действительности же индийские цифры гораздо более похожи на западно-арабские цифры «губар». Как могли индийские цифры попасть непосредственно в мавританские государства Испании и западной Африки, «перепрыгнув» страны Передней Азии?
А что, если мы беремся за проблему не с того конца? Между старыми арабской и греческой цифровыми системами и нашей «арабской» общего мало. Но оно все же есть! Так, единица обеих арабских систем похожа на нашу единицу, а облик некоторых греческих букв сходен с обликом соответствующих им «арабских» цифр 7, 8 и 9. Не здесь ли ключ к тайне? Правда, цифры от единицы до шести не похожи на обозначающие их греческие значки. С этим мы еще разберемся. А пока обратим внимание вот на что. Позиционный принцип расстановки цифр был известен грекам еще со времен античности: они использовали для вычисления счетную доску с графами — абаку. Цифры вырезались из чего-нибудь на манер нашей разрезной детской азбуки и помещались в соответствующие графы на таблице-абаке. Именно абаке мы обязаны нашей теперешней манерой изображения чисел. Вот, скажем, 15 — это же типичный пример позиционного размещения цифр.
Но у греков не было ноля. Для расчетов на абаке в нем не было нужды (оставалась пустая клетка), а для записи целых десятков существовали отдельные обозначения (20 обозначалось буквой к — каппа и т. п.). Зато в арабских системах мы видим ноль. Все эти рассуждения были нужны нам для главного вывода: новая цифровая система, существующая и в наше время, возникла благодаря изобретению ноля и введению его в греческую буквенную цифирь. Прежде чем это доказать, проследим, почему это могло произойти.
Завоевав южные и восточные побережья Средиземного моря, арабы в VII веке стали хозяевами обширных областей, где до того господствовала византийская культура. Заимствования молодой, развивающейся арабской культуры у высокоразвитой византийской — в богословии, философии, медицине, архитектуре и в других областях — общеизвестны. Они не были механическими; то, что воспринималось, всегда творчески перерабатывалось. Естественно, и появление ноля требовало смены способов обозначения цифр.
Но почему же арабы не применили новоизобретенный знак в своей алфавитной системе, а воспользовались греческой? Ответ напрашивается сам собой. Собственная система была для арабов настолько привычна, что казалась неприкосновенной. Поэтому эксперименты было гораздо удобнее провести на системе покоренной страны. К тому же население завоеванных арабами земель было хорошо знакомо именно с греческой цифровой системой.
Допустим, в греческую алфавитную цифирь введен арабский ноль. Теперь можно отказаться от прослужившей свое абаки. Но… как обозначать десятку? Возможны два варианта: приписать ноль к альфе-единице или приписать ноль к йоте-десятке. В последнем случае единицей становится йота.
Арабы вполне могли предпочесть второй вариант, потому что и в арабской алфавитной цифири, и в южно-арабской, сабейской, единица обозначается вертикальной палочкой, то есть так же, как йота. И вот йота поднимается с десятого места на первое, становится впереди альфы. Остальным буквам ничего не остается, как потесниться.
Но в таком случае знаков (греческих букв) оказывается больше, чем требуется: на девять «вакантных мест» (от единицы до девяти) десять знаков, считая с единицей-йотой. Каким-то знаком надо пожертвовать. Каким?
(Стигму), служившую у греков для обозначения цифры 6, в цифири удерживала лишь консервативная традиция. Из алфавита она давно уже выпала. Естественно, что под «нажимом» йоты наименьшие шансы уцелеть имела именно архаическая, непонятная стигма, и особенно — в глазах пришлых арабов, свободных от греческих привычек и традиций.
Итак, йота становится единицей. Значки, обозначавшие цифры от единицы до пяти сдвигаются на одно деление, причем последний из них, эпсилон, занимает освободившееся от стигмы место цифры шесть. Нетрудно заметить, что теперь к сходству дзеты, эты и теты с цифрами 7, 8 и 9 добавилось некоторое сходство альфы, беты, гаммы, дельты и эпсилона с цифрами 2, 3, 4, 5 и 6.
Хранимые в библиотеках средневековые рукописи позволяют проследить «судьбу» каждого из этих знаков от первоначального написания в виде буквы греческого алфавита до привычных нам цифр. Начнем с VII— XI веков и сразу заметим, что здесь нас должен интересовать не унициальный их вид (прямолинейный, геометрический), а скорописный, курсивный. Как раз в это время курсив получает у греков все более широкое распространение.
Мы уже упоминали счетную доску — абаку. Вырезанные цифры помещались при счете в соответствующие отделения. Естественно, что фигурка-цифра могла быть перевернута, положена «вверх ногами» или на другой бок. Например, некоторые варианты древнего изображения двойки, тройки похожи на перевернутую альфу, бету и гамму. В Европу греческие буквы, ставшие «арабскими» цифрами, возвращались, вероятнее всего, через Испанию, захваченную арабами.
Выдающимся деятелем культуры конца десятого века был Герберт, впоследствии возведенный на папский престол под именем Сильвестра II. О нем прямо говорили, что он научился у арабов в Испании колдовству. Он познакомил христианскую Европу с искусством вычисления на абаке, с таким астрономическим прибором, как астролябия, и т. д. И Герберт, и другие абацисты X и XI столетий употребляли для своих счетных операций девять начальных букв греческого алфавита или цифры, которые мы называем арабскими. Авторы того времени (в отличие от многих наших современников) не делали различия между греческими буквами и арабскими цифрами, даже называли их одинаково…
Арабские цифры пока еще не пишутся, а раскладываются на абаке. Поэтому и ноля еще нет: он попадается только в одной рукописи X века. Зато и Герберт, и другие математики X и XI веков довольно часто писали единицу как букву I, даже с точкой сверху; и это встречало удивление и непонимание их современников. Окончательный, канонический, современный вид «арабские» цифры получили в XV веке, в Европе.
В то же время история арабских цифр на мусульманском Востоке пошла несколько иным путем. Западноарабские цифры («губар») сохранили более древний, более близкий к древнегреческим буквам облик. Именно они, очевидно, и послужили «предками» индийских цифр, а не наоборот.
Арабские отряды проникли к границам Индии уже в середине VII в.; в начале VIII в. Синд, то есть область Нижнего Инда, был присоединен к халифату. В это же время мусульманские купцы становятся хозяевами — и хозяевами очень энергичными — восточных сухопутных и морских торговых путей вплоть до Китая. К началу IX века арабские поселения существовали уже по всему западному побережью Индии. Точно так же, как арабы познакомили со своей системой счета европейцев, они, я полагаю, познакомили с ней и индийцев. Впрочем, не исключено, что это был уже второй случай прихода греческих букв в качестве цифр к индийцам. Отчетливо видно некоторое сходство древнеиндийских знаков, обозначавших цифры «шесть», «семь», «восемь», и с арабскими, и с древнегреческими цифрами. Но вспомним о походах Александра Македонского и о последующем влиянии Бактрии на территорию современной Индии. Не восходят ли эти знаки к более древним образцам все тех же греческих букв-цифр — к стигме, дзете пэте?
Итак, древнегреческие буквы двумя путями — на Запад и на Восток — ушли в Европу и в Индию. Когда это произошло?
Наиболее тесные связи между Испанией и Ближним Востоком поддерживались до середины VIII века. В то время на территории современной Сирии существовал халифат династии Омейядов со столицей в Дамаске. Я далек от того, чтобы идеализировать это громадное, созданное завоеваниями государство. Но именно в это время, при Омейядах, в просвещенных столичных кругах религиозная вражда мусульман к христианам как бы отходит на второй план, уступая первое место уважению к уму и культуре иноверцев. Именно в это время финансовое ведомство арабского халифа возглавлял знаменитый Иоанн Дамаскин, впоследствии воспетый А. К. Толстым. Помните?
Любим калифом Иоанн.
Ему, что день, почет и ласка,
К делам правления призван
Лишь он один из христиан
Порабощенного Дамаска.
Что же, скажете вы, вот и имя названо? Нет, это была бы гипотеза, слишком далеко уходящая от строгих фактов, которых мы держались во время нашего разговора. Но так или иначе, нити наших поисков ведут в Дамаск первой половины VIII века. В середине VIII века халифат Омейядов прекратил свое существование, и его место занял халифат Аббасидов, утвердивших свою столицу в Багдаде. Последний уцелевший потомок Омейи и все, кому грозила расправа и кому удалось от нее уйти, бежали на Пиринейский полуостров, в созданное Омейядами арабское государство в Испании.
Приток в Испанию беглецов от Аббасидов усилил в ее культуре арабские черты. С этого времени начинается расхождение культур восточных и западных арабов. Вот почему разошлись западно- и восточно-арабские начертания цифр. Вот почему западно-арабские цифры, пришедшие позже в христианскую Европу, сохранили более архаический вид — тот вид, какой они имели при Омейядах в Сирии и который послужил образцом для индийцев.
Автор: Г. Прохоров.
Схожі статті:
5.2. Как появились арабские цифры для позиционной записи чисел
Д.Я. Стройк пишет: «Весьма разнообразны знаки, которые применялись для записи цифр в позиционной системе, но имеются два главных типа: индийские обозначения, которые применялись восточными арабами, и так называемые цифры „гобар“ (или „губар“), которые применялись западными арабами в Испании. Знаки первого типа и сейчас еще применяются в арабском мире, но наша современная система, по-видимому, произошла из системы „гобар“» [821], с. 89.
ВОПРОС О ПРОИСХОЖДЕНИИ «АРАБСКИХ ЦИФР» ОСТАЕТСЯ В СКАЛИГЕРОВСКОЙ ИСТОРИИ НАУКИ ДО СИХ ПОР ОТКРЫТЫМ. Существуют различные теории на сей счет. Например, теория Вепке. Согласно которой, эти знаки проникли на Запад якобы в V веке н. э. из Александрии через неопифагорейцев [821], с. 90. Есть и другая теория — Н.М. Бубнова. Согласно ей, знаки «гобар» произошли из давних римско-греческих символов [821], с. 90. Но ни в том, ни в другом случае, не приводятся РОДОНАЧАЛЬНИКИ хорошо всем знакомых арабских цифр. В качестве таких прародителей объявляются давние (в смысле ЗАБЫТЫЕ) римско-греческие символы. Или «александрийские символы». Тоже забытые. А потому сегодня неизвестные. Никому, даже историкам.
Известный русский историк математики В.В. Бобынин писал: «ИСТОРИЯ НАШИХ ЦИФР ПРЕДСТАВЛЯЕТ НЕ БОЛЕЕ КАК РЯД ПРЕДПОЛОЖЕНИЙ, ПЕРЕМЕЖАЮЩИХСЯ С ПРОИЗВОЛЬНЫМИ ДОПУЩЕНИЯМИ, производящими иногда, вследствие предшествующего употребления метода внушения, впечатление КАК БЫ ЧЕГО-ТО ДОКАЗАННОГО». Цит. по [989], с. 53. Авторы Энциклопедии [989], после изложения различных теорий происхождения арабских цифр, делают следующий многозначительный вывод. «Таким образом, МЫ ДО СИХ ПОР НЕ ИМЕЕМ ИСТОРИЧЕСКИ ОБОСНОВАННОЙ ГИПОТЕЗЫ, КОТОРАЯ ДОСТАТОЧНО УДОВЛЕТВОРИТЕЛЬНО ОБЪЯСНЯЛА БЫ ПРОИСХОЖДЕНИЕ НАШИХ ЦИФР» [989], с. 52.
Нам представляется, что дело намного проще. Стоит лишь задаться этим вопросом и отрешиться от неправильных скалигеровских датировок, как происхождение «арабских цифр» становится, в общем-то, очевидным. И весьма естественным. Как мы сейчас покажем, ВСЕ «АРАБСКИЕ ЦИФРЫ» ПРОИЗОШЛИ ИЗ ПРЕДШЕСТВУЮЩЕЙ ПОЛУ-ПОЗИЦИОННОЙ СЛАВЯНО-ГРЕЧЕСКОЙ СИСТЕМЫ СЧИСЛЕНИЯ. Причем, будет явно видно, что использовался именно СЛАВЯНСКИЙ ВАРИАНТ букв-символов. Источником послужила русская скоропись шестнадцатого века. ПРОИЗОШЛО ВСЕ ЭТО, СКОРЕЕ ВСЕГО, В XVI ВЕКЕ. То есть в эпоху изобретения позиционной системы, см. выше. Перейдем к подробностям.
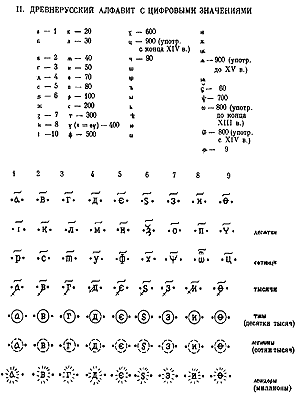
До позиционной системы счисления и арабских цифр на Руси использовалась полу-позиционная система, где для каждой десятичной цифры имелось три различных значка [782], вып. 1, с. 16. А именно, один значок для изображения цифры в разряде единиц. Другой — для изображения той же цифры, но в разряде десятков. И, наконец, третий — для изображения цифры в разряде сотен, рис. 1.36. Ноль отсутствовал. Но поскольку в разных разрядах обозначение цифры было разным, то само обозначение сразу указывало на разряд, в котором стояла данная цифра. С помощью такой системы можно было производить все обычные арифметические действия с целыми числами в пределах от единицы до тысячи. Для чисел, больших тысячи, приходилось применять специальные дополнительные значки, рис. 1.36. Для этого использовались буквы кириллицы.
Рис. 1.36. Старая славяно-греческая полу-позиционная система записи цифр. Взято из [782], выпуск 1, с. 16
Поясним таблицу на рис. 1.36. Например, цифра «один» изображалась тремя способами.
1) Буквой А, если единица стояла в разряде единиц, то есть в первом разряде.
2) Буквой I, если единица стояла в разряде десятков, то есть во втором разряде.
3) Буквой Р, если единица стояла в разряде сотен, то есть в третьем разряде.
Скажем, число РА означало 101. В нашей современной позиционной системе при записи числа 101 используется ноль, так как здесь отсутствует цифра во втором разряде. В старой же славянской полу-позиционной записи нуля не было. Но само обозначение единиц буквами указывало, что одна из них стоит в первом, а другая — в третьем разряде. То есть цифра во втором разряде здесь отсутствует.
Таким образом, для записи целых чисел от единицы до тысячи использовались не ДЕВЯТЬ символов, как сегодня (не считая нуля), а в ТРИ РАЗА БОЛЬШЕ. А именно, ДВАДЦАТЬ СЕМЬ букв кириллицы. НА КАЖДУЮ ЦИФРУ ПРИХОДИЛОСЬ ТЕМ САМЫМ ПО ТРИ БУКВЫ. В таблице на рис. 1.36 двадцать семь кириллических букв расположены в трех верхних строках. Под каждой арабской цифрой мы видим три различные буквы кириллицы. Остальные четыре строки таблицы на самом деле повторяют первую строку, но снабжены специальными дополнительными символами, чтобы обеспечить следующие разряды от тысячи до миллиона. Новых букв тут не появляется.
Зададимся вопросом. Что должно было произойти, когда решили заменить указанную систему обозначений на полностью позиционную? То есть с нулем. Для этого следовало оставить вместо двадцати семи цифр всего лишь девять. Требовалось каким-то образом выбрать девять цифр-букв из двадцати семи. Например, из трех обозначений-букв для единицы нужно было оставить только одну кириллическую букву. То же самое для двойки. И так далее до девятки.
Оказывается, именно эту простую процедуру и проделали. Как мы сейчас увидим, в результате получились привычные нам сегодня «арабские цифры», которыми все пользуются до сегодняшнего дня. Что сразу же делает очевидным тот факт, что люди, впервые придумавшие «арабские цифры», пользовались до этого именно славяно-греческой полу-позиционной системой счисления. Причем, для «арабских цифр» были использованы во многих случаях РУССКИЕ СКОРОПИСНЫЕ формы кириллических букв XVI века. Что может означать лишь одно. Люди, придумавшие «арабские цифры» хорошо читали и писали по-русски. Для них РУССКАЯ СКОРОПИСЬ XVI ВЕКА была хорошо знакомым, привычным почерком.
В частности, исчезает «великая загадка» скалигеровской истории — откуда же взялись «арабские цифры»? Наш ответ таков. Они произошли из славяно-греческих цифр-букв в русской скорописи XVI века. Кроме того, и другие детали, о которых мы ниже расскажем, однозначно показывают, что использовалась именно РУССКАЯ, А НЕ ГРЕЧЕСКАЯ азбука XVI века. Эти азбуки несколько отличаются.
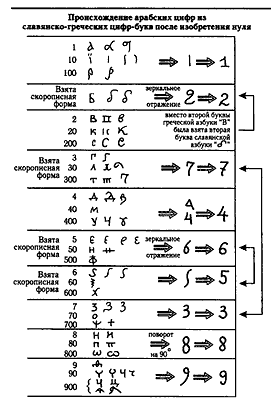
Обратимся теперь к таблице на рис. 1.37. Обсудим каждую цифру отдельно.
Рис. 1.37. Наша таблица происхождения арабских цифр из славянских цифр-букв предшествующей полу-позиционной системы счисления. Обратите внимание, что во многих случаях ДЛЯ АРАБСКИХ ЦИФР БЫЛИ ВЗЯТЫ РУССКИЕ СКОРОПИСНЫЕ ФОРМЫ КИРИЛЛИЧЕСКИХ БУКВ
1) ЕДИНИЦА. Из трех обозначений единицы выбрали букву «I» из второго разряда, как наиболее простую из трех. Получилась «индо-арабская» единица.
2) ДВОЙКА. Для двойки избрали не букву «В» (то есть вторую букву греческой азбуки), а букву «Б» — вторую букву славянской азбуки. При этом взяли скорописную форму этой буквы и зеркально отразили, рис. 1.37. Получилась привычная нам сегодня «индо-арабская» двойка. В данном случае автор новых обозначений явно показал свое предпочтение славянской азбуке перед греческой. В греческой азбуке буквы «Б» нет. Она пропущена, и сразу после «А» идет «В».
Тройку мы пока пропустим, так как ее обозначение переставлено с семеркой.
4) ЧЕТВЕРКА. У четверки есть две формы: открытая и закрытая. Закрытая форма «домиком» получается из славянской буквы «Д», обозначавшей четверку в первом разряде. Открытая же форма получается из славянской буквы «У», обозначавшей четверку в третьем разряде, рис. 1.37. Получилась «индо-арабская» четверка.
Пятерку, шестерку и семерку мы пока пропустим, так как их обозначения переставлены. Подробнее об этом — ниже.

9) ДЕВЯТКА. Здесь для «индо-арабской» цифры употребили нестандартную, ЧИСТО РУССКУЮ форму девятки в третьем разряде. Обычно в славяно-греческих обозначениях для этого использовалась буква «Ц». Однако, на Руси употребляли также букву «Я» для обозначения девятки в третьем разряде. Мы видим, что ее скорописная форма — это в точности «индо-арабская» девятка с приделанной палочкой. Палочку отбросили. Получилась хорошо знакомая нам сегодня «индо-арабская» цифра девять, рис. 1.37. Эта скорописная форма буквы «Я» была, с небольшими изменениями, канонизирована во время петровской реформы и используется до сих пор. На рис. 1.38 приведен образец русской скорописи начала XVII века [791], выпуск 19, форзац. Здесь написано русское слово «знамя». В его конце стоит буква «Я».
Рис. 1.38. Скорописная форма славянской буквы «Я» в конце слова «знамя». Ясно видно, что если отбросить верхнюю палочку, то получится «ИНДО-АРАБСКАЯ» ДЕВЯТКА. Взято из [791], выпуск 19
Перейдем теперь к «индо-арабским» цифрам: ТРОЙКА, ПЯТЕРКА, ШЕСТЕРКА И СЕМЕРКА.
3 и 7) ТРОЙКА и СЕМЕРКА. Для «индо-арабской» тройки была использована русская скорописная форма буквы 3, обозначавшая семерку в первом разряде, рис. 1.37. Формы русской скорописной буквы «3» и «индо-арабской» тройки полностью идентичны! И наоборот, для «индо-европейской» семерки взяли скорописную форму русской буквы «Т», обозначающую тройку в третьем разряде, рис. 1.39. Таким образом, обозначения для тройки и семерки были почему-то ПЕРЕСТАВЛЕНЫ местами.
Рис. 1.39. Скорописная форма славянской буквы «Т» в начале слова. Ясно видно, что это в точности «ИНДО-АРАБСКАЯ» СЕМЕРКА. Взято из [791], выпуск 19
5 и 6) ПЯТЕРКА и ШЕСТЕРКА. Для «индо-арабской» пятерки была использована скорописная форма русской буквы «зело», обозначавшая шестерку в первом разряде, рис. 1.37. И наоборот, для «индо-арабской» шестерки взяли скорописную форму славянской буквы «Е», обозначавшую пятерку в первом разряде. Эта форма, кстати, очень близка к современной форме рукописной буквы «Е». Создатели «индо-арабских» цифр просто зеркально отразили славянскую букву «Е» и получили шестерку На рис. 1.40 приведен образец русской скорописи начала XVII века, где буква «Е» в конце слова «великие» написана как зеркально отраженная шестерка [787], выпуск 7. Таким образом, обозначения для пятерки и шестерки почему-то ПЕРЕСТАВИЛИ местами. Как и в случае тройки и семерки.
Рис. 1.40. Скорописная форма славянской буквы «Е» в конце слова «великие». Ясно видно, что «ИНДО-АРАБСКАЯ» ШЕСТЕРКА получается из этой буквы «Е» зеркальным отражением. Взято из [787], выпуск 7
0) НОЛЬ. Вопрос о НУЛЕ особенно интересен. Поскольку именно изобретение нуля позволило ввести НОВУЮ СИСТЕМУ СЧИСЛЕНИЯ. В этой, общепринятой сегодня системе счисления, ноль обозначает ОТСУТСТВУЮЩУЮ ЦИФРУ. То есть говорит о том, что В ДАННОМ РАЗРЯДЕ ЦИФРЫ НЕТ. И ее пустое место обозначает 0 = ноль. Скорее всего, 0 = «ноль», это сокращение какого-то слова. Зададимся вопросом, какого именно? Оказывается, это очень легко объяснить в предположении, что слово было славянским. Как сообщает В. Даль, слово или предлог «О» в русском языке раньше могло употребляться вместо предлога ОТ [223], т. 2, столбец 1467. А предлог ОТ в русском языке означает ОТСУТСТВИЕ чего-либо. Этимологический словарь сообщает, что ОТ — это «глагольная приставка — обозначает прекращение, завершение действия; удаление, устранение чего-либо» [955], т. 1, с. 610. Таким образом, отсутствующую цифру вполне естественно было обозначить символом, похожим на букву «О». По-видимому, именно так и возник ноль = 0.
Возможно и другое объяснение. Слово НОЛЬ могло произойти от старого русского слова НОЛИ или НОЛЬНО. Сегодня оно уже забыто, но раньше, до XVII века, часто использовалось в русском языке. Об этом говорят многочисленные примеры его употребления в старых текстах, приведенные в Словаре Русского Языка XI–XVII веков [789], с. 420–421. Слово НОЛЬНО, или НОЛЬНЫ, НОЛЬНЕ, НОЛЬНА использовалось, в частности, как ограничительная частица, в смысле «не прежде чем, только когда» [789], с. 421. Но ведь и ноль в десятичной записи числа можно рассматривать, как ограничительный знак, «не пускающий» цифру соседнего разряда на место отсутствующей цифры данного разряда. Дело в том, что в предшествующей славяно-греческой полу-позиционной системе счисления если значащей цифры в том или ином разряде не было, то цифры соседних разрядов сдвигались друг к другу, занимая пустое место отсутствующей цифры. Именно поэтому и приходилось обозначать цифры разных разрядов по-разному, чтобы как-то различать их. В позиционной системе этого не происходит, потому что на «пустое» место цифры других разрядов «не пускает» ноль. Поэтому ноль могли первое время рассматривать как ограничительный знак, а значит и его название вполне могло произойти от ограничительной частицы НОЛЬНО в старом русском языке. Нольно — ноль.
Кроме того, слово НОЛИ в старом русском языке употреблялось также и для обозначения неосуществившейся возможности: «помышлялъ есмь въ себе:… ноли буду лучии тогда, но худъ есмь и боленъ» [789], с. 420. В современном переводе: «я думал про себя: может быть („ноли“) буду лучше тогда, но [это не осуществилось] я плох и болен». Этот смысл старого слова НОЛИ тоже, по-видимому, подходил для нового знака — нуля в позиционной системе. Ведь цифра ноль тоже как бы обозначает неосуществившуюся возможность — а именно, возможность поставить значащую цифру в данном разряде. Ноль говорит, что значащей цифры в данном разряде нет, хотя она МОГЛА БЫ здесь быть.
Возможно, конечно, попытаться произвести обозначение нуля = 0 из латинского слова ОВ, одним из значений которого было «в ОБМЕН на» [237], с. 684. Но не произошло ли само это «античное» латинское слово из славянской приставки ОБ в слове ОБМЕН? О том, что в фундаменте «древней латыни» лежит славянский язык, мы подробно говорим в книге «Русские корни „древней“ латыни».
Итак, название новой цифры НОЛЬ, позволившей ввести новую для того времени позиционную систему счисления, возникло, скорее всего, на основе именно русского языка. Так же как и новые обозначения «индо-арабских» цифр появились в результате легкого видоизменения старых русских цифр-букв. Все это происходило, как мы выяснили, не так уж давно — скорее всего, не ранее конца XVI века. А не в далеком средневековье, как это ошибочно утверждает скалигеровская хронология.
В заключение отметим, что в принципе можно пытаться искать буквы, похожие на «индо-арабские» цифры, и в других азбуках. Однако важно подчеркнуть, что для выяснения происхождения «индо-арабских» цифр подходит ДАЛЕКО НЕ ВСЯКАЯ АЗБУКА. Ведь требуется найти не просто какие-то буквы, «похожие на цифры», что иногда удается. Необходимо найти буквы-цифры, ДЕЙСТВИТЕЛЬНО ИСПОЛЬЗОВАВШИЕСЯ В СРЕДНИЕ ВЕКА В КАЧЕСТВЕ ОБОЗНАЧЕНИЙ ЦИФР. Причем, в силу естественной консервативности обозначений, цифровые значения старых цифр-букв должны в основном сохраняться и в новой системе счисления. Как это имеет место для славяно-греческой азбуки и «индо-арабских цифр». Азбуки же, не использовавшиеся для обозначения цифр, привлекать не имеет смысла.
С нашим выводом о том, что ноль изобретен только в конце XVI века, прекрасно согласуется и следующий известный в истории факт. Он поразителен с точки зрения скалигеровской хронологии. Нам предлагают считать, что ноль был известен еще в глубокой древности. Однако в то же время, отмечается, что математики, даже в XVI веке еще НЕ РАССМАТРИВАЛИ КОРНИ УРАВНЕНИЙ, РАВНЫЕ НУЛЮ [219], с. 153. Кроме того, как сообщают историки науки, естественная идея — оставить в правой части уравнения НОЛЬ, появилась лишь в конце XVI — начале XVII века [219], с. 153. Хотя ноль, как нас уверяют, к тому времени уже давным-давно известен, якобы несколько сотен лет. Цитируем: «Идея приравнивания уравнения нулю БЫЛА ЧУЖДА МАТЕМАТИКЕ ВОЗРОЖДЕНИЯ. ВПЕРВЫЕ КАНОНИЧЕСКУЮ ФОРМУ УРАВНЕНИЯ привел англичанин Т. Гэрриот (1580–1621) в книге „Применение аналитического искусства“» [219], с. 153. Но это, конечно же, означает, что обозначения для нуля не существовало вплоть до конца XVI века. Другое объяснение вряд ли возможно.
Данный текст является ознакомительным фрагментом.
Читайте также
Часть III Период от первых чисел января до первых чисел августа 1915 года: июльские бои, или Евфратская операция
Часть III
Период от первых чисел января до первых чисел августа 1915 года: июльские бои, или Евфратская операция
Крутясь по кривым и узким улицам Сарыкамыша, автомобиль, преодолев последний крутой подъем, остановился у здания бывшего лазарета 155-го пехотного Кубинского
25. Как и когда были придуманы арабские цифры
25. Как и когда были придуманы арабские цифры
Историк математики В.В. Бобынин писал: «ИСТОРИЯ НАШИХ ЦИФР ПРЕДСТАВЛЯЕТ НЕ БОЛЕЕ КАК РЯД ПРЕДПОЛОЖЕНИЙ, ПЕРЕМЕЖАЮЩИХСЯ С ПРОИЗВОЛЬНЫМИ ДОПУЩЕНИЯМИ, производящими иногда, вследствие предшествующего употребления метода
12. Кое-что о мистике, или символике цифр, чисел и дат
12. Кое-что о мистике, или символике цифр, чисел и дат
Итак, формально, мы завершили свое исследование, полностью ответив на вопросы о происхождении псевдонима «Сталин». На этом можно было бы и закончить, если бы не одно обстоятельство, которое во-первых, выяснилось в ходе
5.2. Как появились арабские цифры для позиционной записи чисел
5.2. Как появились арабские цифры для позиционной записи чисел
Д.Я. Стройк пишет: «Весьма разнообразны знаки, которые применялись для записи цифр в позиционной системе, но имеются два главных типа: индийские обозначения, которые применялись восточными арабами, и так
25. Как и когда были придуманы арабские цифры
25. Как и когда были придуманы арабские цифры
Историк математики В.В. Бобынин писал: «ИСТОРИЯ НАШИХ ЦИФР ПРЕДСТАВЛЯЕТ НЕ БОЛЕЕ КАК РЯД ПРЕДПОЛОЖЕНИЙ, ПЕРЕМЕЖАЮЩИХСЯ С ПРОИЗВОЛЬНЫМИ ДОПУЩЕНИЯМИ, производящими иногда, вследствие предшествующего употребления метода
Загадки пирамидионов и тайна чисел Тота
Загадки пирамидионов и тайна чисел Тота
Доподлинно неизвестно, откуда именно взялся таинственный камень: он исчез задолго до того, как Геродот посетил Египет. Но его название перешло на камни-пирамидионы (пирамидки), которые обычно ставились на вершины пирамид и, позднее,
Тайны сакральных чисел
Тайны сакральных чисел
В процессе этой работы я постоянно имел в виду числовую символику древних египтян как один из второстепенных вопросов и постепенно пришел к выводу, что она является ключевой для понимания мышления египтян, особенно — строителей загадочных
Часть 6 Поиск новых средств и способов прорыва позиционной обороны. Новые формы борьбы
Часть 6
Поиск новых средств и способов прорыва позиционной обороны. Новые формы борьбы
Ход этой войны оказался абсолютно непредсказуемым для политиков и военных. Перед войной среди военных специалистов считалось общепринятым и очевидным, что война должна быть закончена
Тирания чисел
Тирания чисел
Несмотря на все свои достижения и огромную пользу, наука, тем не менее, не в состоянии помочь человеку разобраться со всеми без исключения проблемами. Да, наука достигла головокружительных высот, но ее методы зачастую пытаются применить там, где она
6. Государственная тайна 13 чисел
6. Государственная тайна 13 чисел
Солнце не будет больше взирать ни на одну страну за пределами нашей… Все земли я превращу в одну.
Ксеркс 485 г. до Р.Хр., персидский царь
Если в зеркало смотрит обезьяна, из него не выглянет апостол.
Георг Кристоф Лихтенберг (1742–1799), немецкий
Глава I Смысл чисел
Глава I
Смысл чисел
1.Необходимо прежде всего определить некоторые основные понятия, употребляемые здесь в строгом и отчасти новом смысле; их метафизическое содержание само выяснится в ходе дальнейшего изложения, но уже с самого начала они должны быть ограждены от всякой