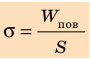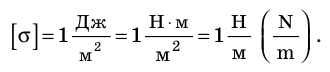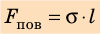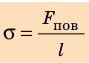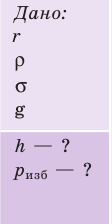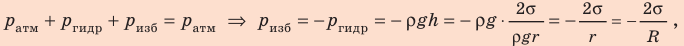Понятие и характеристики поверхностного натяжения
С явлением поверхностного натяжения жидкости мы сталкиваемся каждый день:
- капли воды стремятся принять форму, близкую к шарообразной (а в невесомости они совсем шарообразные);
- струя воды из-под крана стремится к цилиндрической форме;
- булавка не тонет на поверхности воды в стакане;
- многие насекомые могут скользить по поверхности воды.
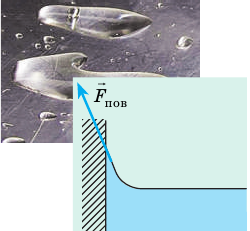
Силы поверхностного натяжения действуют вдоль поверхности жидкости, стремясь сократить ее площадь. Как будто жидкость заключена в упругую пленку, которая стремится сжать свое содержимое.
Потенциальная энергия взаимного притяжения молекул жидкости примерно равна их кинетической энергии. Это позволяет веществу сохранять объем (но не форму), и этот объем ограничивается поверхностью жидкости.
На молекулу жидкости, которая находится внутри, действуют силы притяжения со стороны других молекул, и они уравновешивают друг друга. А на ту молекулу, что находится на поверхности, действуют силы притяжения не только со стороны других молекул жидкости, но и со стороны газа (внешней среды). Эти вторые значительно меньше первых, поэтому равнодействующая сила притяжения направлена внутрь жидкости, что способствует удержанию молекулы на поверхности.
Поверхностное натяжение — это величина, которая показывает стремление жидкости сократить свою свободную поверхность, то есть уменьшить избыток своей потенциальной энергии на границе раздела с газообразной фазой.
Чем больше площадь поверхности жидкости, тем больше молекул, которые обладают избыточной потенциальной энергией, и тем больше поверхностная энергия. Этот факт можно записать в виде следующего соотношения:
Поверхностная энергия жидкости
W = σS
W — поверхностная энергия жидкости [Дж]
S — площадь свободной поверхности [м2]
σ — коэффициент поверхностного натяжения [Н/м]
Отсюда мы можем вывести формулу коэффициента поверхностного натяжения.
Коэффициент поверхностного натяжения — это физическая величина, которая характеризует данную жидкость и численно равна отношению поверхностной энергии к площади свободной поверхности жидкости.
Коэффициент поверхностного натяжения
σ = W/S
W — поверхностная энергия жидкости [Дж]
S — площадь свободной поверхности [м2]
σ — коэффициент поверхностного натяжения [Н/м]
Коэффициент поверхностного натяжения жидкости зависит:
- от природы жидкости;
- температуры жидкости;
- свойств газа, который граничит с данной жидкостью;
- наличия поверхностно-активных веществ (например, мыло или стиральный порошок), которые уменьшают поверхностное натяжение.
Коэффициент поверхностного натяжения не зависит от площади свободной поверхности жидкости, хотя может быть рассчитан с ее помощью.
Если на жидкость не действуют другие силы или их действие мало, жидкость будет стремиться принимать форму сферы, как капля воды или мыльный пузырь. Так же ведет себя вода в невесомости. Жидкость ведет себя так, как будто по касательной к ее поверхности действуют силы, стягивающие эту поверхность. Эти силы называются силами поверхностного натяжения.
Сила поверхностного натяжения
F = σl
F — сила поверхностного натяжения [Н]
l — длина контура, ограничивающего поверхность жидкости [м]
σ — коэффициент поверхностного натяжения [Н/м]
В химической промышленности в воду часто добавляют специальные реагенты-смачиватели, не дающие ей собираться в капли на какой-либо поверхности. Например, их добавляют в жидкие средства для посудомоечных машин. Попадая в поверхностный слой воды, молекулы таких реагентов заметно ослабляют силы поверхностного натяжения, вода не собирается в капли и не оставляет на поверхности пятен после высыхания.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Полезные подарки для родителей
В колесе фортуны — гарантированные призы, которые помогут наладить учебный процесс и выстроить отношения с ребёнком!
Поверхностное натяжение некоторых жидкостей на границе с воздухом
|
Вещество |
Температура, °C |
Поверхностное натяжение, 10−3 Н/м |
|
Хлорид натрия (водный раствор) |
20 |
82,55 |
|
Хлорид натрия |
801 |
115 |
|
Глицерин |
30 |
64,7 |
|
Олово |
400 |
518 |
|
Азотная кислота 70% |
20 |
59,4 |
|
Анилин |
20 |
42,9 |
|
Ацетон |
20 |
23,7 |
|
Бензол |
20 |
29,0 |
|
Вода |
20 |
72,86 |
|
Глицерин |
20 |
59,4 |
|
Нефть |
20 |
26 |
|
Ртуть |
20 |
486,5 |
|
Серная кислота 85% |
20 |
57,4 |
|
Спирт этиловый |
20 |
22,8 |
|
Уксусная кислота |
20 |
27,8 |
|
Этиловый эфир |
20 |
16,9 |
|
Раствор мыла |
20 |
43 |
Пример решения задачи
Тонкое алюминиевое кольцо радиусом 7,8 см соприкасается с мыльным раствором. Каким усилием можно оторвать кольцо от раствора? Температуру раствора считать комнатной. Масса кольца 7 г. Коэффициент поверхностного натяжения мыльного раствора при комнатной температуре равен 4 × 10-2 Н/м.
Решение
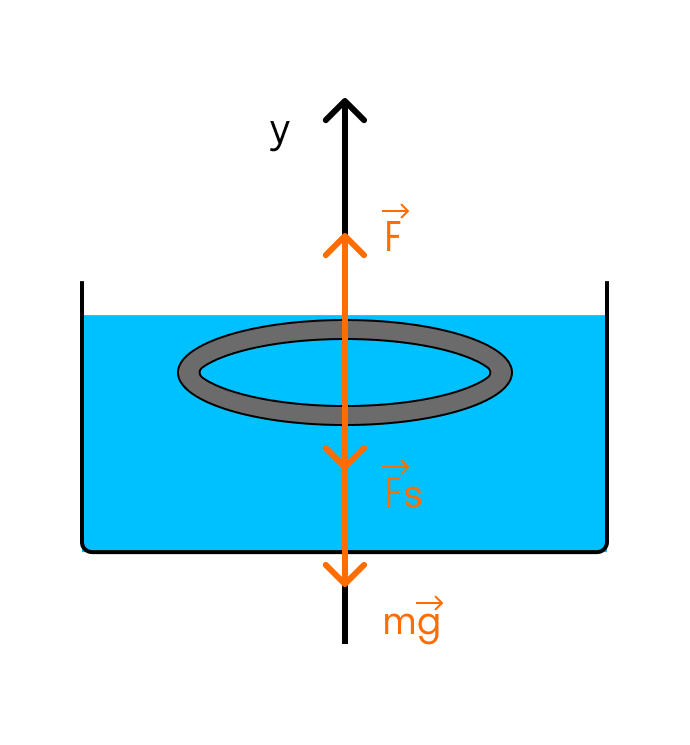
Выполним рисунок:
На кольцо действуют сила тяжести, сила поверхностного натяжения и внешняя сила, с которой отрывают кольцо от раствора.
Так как кольцо соприкасается с раствором и внешней и внутренней сторонами, то сила поверхностного натяжения удваивается:
Fs = 2σl
Контур, ограничивающий поверхность жидкости, имеет форму окружности. Значит, его длина будет равна:
l = 2πR
Подставляем в формулу силы поверхностного натяжения:
Fs = 4σπR
Условие отрыва кольца от поверхности раствора имеет вид второго закона Ньютона для инерциальных систем отсчета:
F = mg + Fs
Подставляем силу поверхностного натяжения:
F = mg + 4σπR
И вычисляем:
F = 0,007 × 10 + 4 × 4 × 10-2 × 3,14 × 7,8 × 10-2 = 0,11 Н
Ответ: Для того, чтобы оторвать кольцо от раствора, необходимо приложить силу в 0,11 Н.
Важность поверхностного натяжения
Выше мы уже показали, что поверхностное натяжение встречается в повседневной жизни достаточно часто. Но на самом деле оно встречается еще чаще!
В некоторых отраслях промышленности поверхностное натяжение используют как простой показатель загрязнения продуктов. Поскольку оно определяется на молекулярном уровне, любое изменение компонентов вещества может привести к изменению этого показателя. То есть если мы знаем, каким должно быть поверхностное натяжение совершенно чистого вещества, то по отклонению от этой нормы мы можем установить уровень его загрязнения.
Не только человек, но и представители живой природы используют физические явления в своих целях. Например, за счет поверхностного натяжения насекомые водомерки могут перемещаться по водной глади, не промочив лапки. Конечности водомерки отталкивают воду и захватывают воздух, что позволяет насекомым продавливать поверхность воды, не нарушая ее.
За счет поверхностного натяжения возникает такое любопытное явление, как ламинарное течение. Это упорядоченный режим течения вязкой жидкости или газа, при котором соседние слои жидкости не перемешиваются. Выглядит ламинарная струя так, как будто вода застыла.
И это еще не все: поверхностное натяжение позволяет предметам плавать, благодаря ему выживают и развиваются экосистемы, и даже состав воды стабилен только за счет этого явления. Без него вода бы постоянно находилась на границе двух агрегатных состояний: испарялась и вновь конденсировалась, так как молекулы легко выскакивали бы с ее поверхности.
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
Содержание:
Поверхностное натяжение жидкости:
В отличие от газов жидкости имеют свободную поверхность. Молекулы, расположенные на поверхности жидкости, и молекулы внутри жидкости находятся в разных условиях:
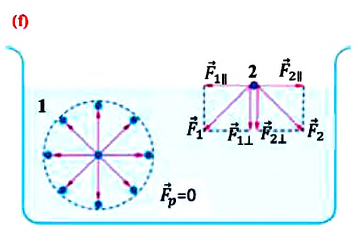
a) молекулы внутри жидкости окружены другими молекулами жидкости со всех сторон. Молекула 1 внутри жидкости испытывает действие соседних молекул со всех сторон, поэтому равнодействующая сил притяжения, действующих на нее, равна нулю (f; молекула 1);
b) молекулы на поверхности жидкости испытывают действие со стороны соседних молекул жидкости только сбоку и снизу. Притяжение со стороны молекул газа (пара жидкости или воздуха) над жидкостью во много раз слабее, чем со стороны молекул жидкости, поэтому не принимаются во внимание (f; молекула 2). В результате каждая из равнодействующих сил
Сила поверхностного натяжения
Сила поверхностного натяжения — это сила, направленная по касательной к поверхности жидкости, перпендикулярно к линии, ограничивающей поверхность жидкости, и стремящаяся сократить площадь поверхности жидкости. Сила поверхностного натяжения прямо пропорциональна длине границы соприкосновения свободной поверхности жидкости с твердым телом:
Здесь 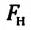
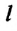
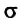
Коэффициент поверхностного натяжения
Коэффициент поверхностного натяжения — численно равен силе поверхностного натяжения, приходящейся на единицу длины линии, ограничивающей поверхность жидкости:
Значение коэффициента поверхностного натяжения зависит от вида жидкости и ее температуры, то есть с увеличением температуры жидкости коэффициент его поверхностного натяжения уменьшается и при критической температуре равен нулю. Единица коэффициента поверхностного натяжения в СИ:
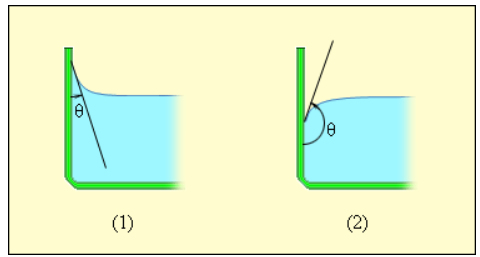
Смачивающая и несмачивающая жидкость. При внимательном рассмотрении можно увидеть искривление поверхности жидкости на границе между жидкостью и твердым телом.
Мениск — это искривление свободной поверхности жидкости в месте ее соприкосновении с поверхностью твердого тела (или другой жидкости). Угол между поверхностью мениска и поверхностью твердого тела называется краевым углом.
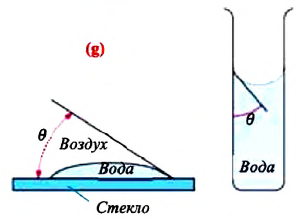
Значение краевого угла 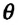
Смачивающая жидкость —это жидкость, у которой краевой угол острый. Сила взаимного притяжения между молекулами смачивающей жидкости и твердого тела больше, чем силы взаимного притяжения между молекулами самой жидкости. В результате свободная поверхность жидкости в сосуде становится вогнутой, например, вода в стеклянном сосуде — смачивающая жидкость (g).
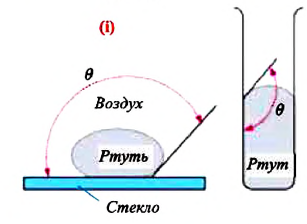
Несмачивающая жидкость — это жидкость, у которой краевой угол тупой. Сила взаимного притяжения между молекулами несмачивающей жидкости и твердого тела меньше, чем сила взаимного притяжения между молекулами самой жидкости. В результате свободная поверхность жидкости в сосуде бывает выпуклой, например, ртуть в стеклянном сосуде — несмачивающая жидкость (i).
Капиллярные явления
В повседневной жизни встречаются и используются тела, с легкостью впитывающие в себя воду, например, полотенце, промокательная бумага, сахар, кирпич, растения и др. Это свойство в телах объясняется существованием в них большого количества очень узких трубочек — капилляров.
Капилляр — это узкая трубка (канал) диаметром меньше 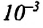
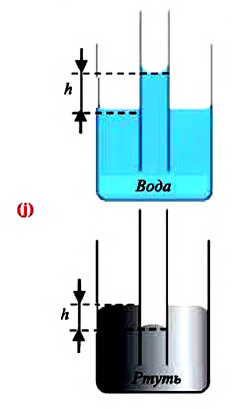
Капиллярными явлениями называют явления подъема смачивающей и опускания несмачивающей жидкости по капилляру относительно общего уровня жидкости под действием сил поверхностного натяжения (j).
В таблице 6.4 дана зависимость между величинами, характеризующими жидкость, поднимающуюся в капилляре.
Таблица 6.4
|
Характеристики жидкости, поднимающейся в капилляре |
Формула |
| Вес жидкости, поднимающейся в капилляре |
Где |
| Масса жидкости, поднимающейся в капилляре | 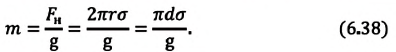 |
| Высота жидкости, поднимающейся в капилляре |
Если жидкость полностью смачиваемая, то получаем в Где |
| Давление жидкости, поднимающейся в капилляре | 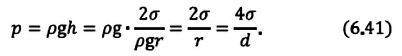 |
Поверхностное натяжение жидкости
Некоторые виды пауков могут передвигаться по поверхности воды не проваливаясь, как будто эта поверхность покрыта невидимой тонкой пленкой. такое же впечатление создается, если наблюдать за вытеканием воды из маленького отверстия — вода течет не тоненькой струйкой, а образует капли. Бумажная салфетка впитывает воду, едва коснувшись ее поверхности. какая сила является причиной всех этих явлений?
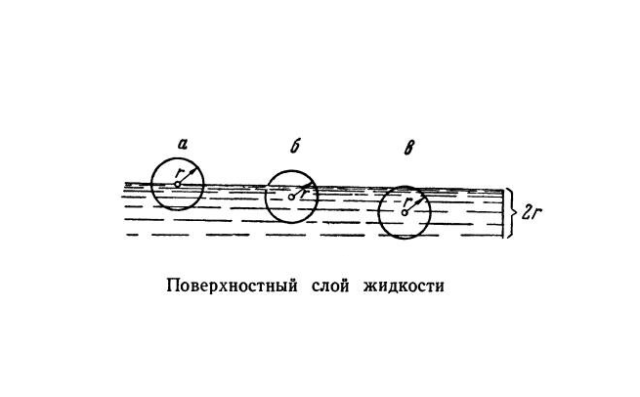
Каковы особенности поверхностного слоя жидкости
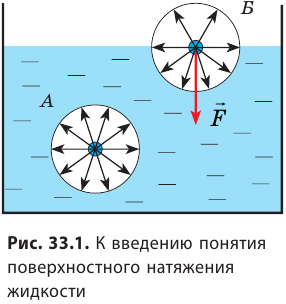
На свободной поверхности жидкости молекулы находятся в особых условиях, отличающихся от условий, в которых находятся молекулы внутри жидкости. Рассмотрим две молекулы — А и Б (рис. 33.1): молекула А находится внутри жидкости, а молекула Б — на ее поверхности. Молекула А окружена другими молекулами жидкости равномерно, поэтому силы, действующие на молекулу А со стороны молекул, попадающих в сферу межмолекулярного взаимодействия, скомпенсированы, то есть их равнодействующая равна нулю.
Молекула Б с одной стороны окружена молекулами жидкости, а с другой — молекулами газа. Со стороны жидкости на нее действует гораздо больше молекул, чем со стороны газа, поэтому равнодействующая F межмолекулярных сил направлена в глубь жидкости. Чтобы молекула из глубины попала в поверхностный слой, нужно совершить работу против межмолекулярных сил. Это означает, что молекулы поверхностного слоя жидкости (по сравнению с молекулами внутри жидкости) обладают избыточной потенциальной энергией. Эта избыточная энергия является частью внутренней энергии жидкости и называется поверхностной энергией (Wпов). Очевидно, что чем больше площадь S поверхности жидкости, тем больше поверхностная энергия: W S пов = σ , где σ (сигма) — коэффициент пропорциональности, который называют поверхностным натяжением жидкости.
Поверхностное натяжение жидкости — физическая величина, которая характеризует данную жидкость и равна отношению поверхностной энергии к площади поверхности жидкости:
Единица поверхностного натяжения в СИ — ньютон на метр:
Поверхностное натяжение жидкости определяется силами межмолекулярного взаимодействия, поэтому оно зависит:
- от природы жидкости: у летучих жидкостей (эфир, спирт, бензин) поверхностное натяжение меньше, чем у нелетучих (ртуть, жидкие металлы);
- температуры жидкости: чем выше температура жидкости, тем меньше поверхностное натяжение;
- присутствия в составе жидкости поверхностно активных веществ — их наличие уменьшает поверхностное натяжение;
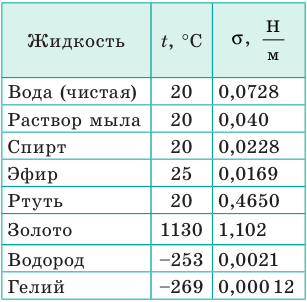
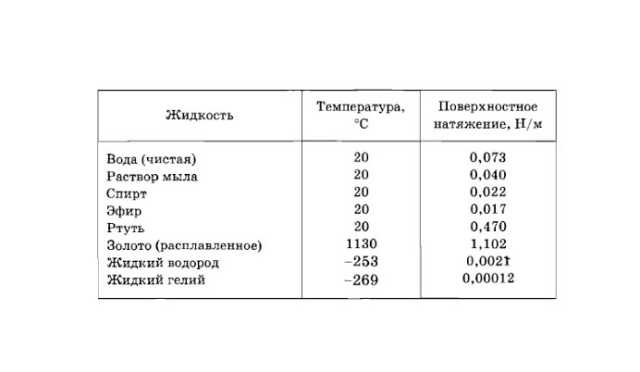
- свойств газа, с которым жидкость граничит. В таблицах обычно приводят значение поверхностного натяжения на границе жидкости и воздуха при определенной температуре (табл. 1).
Таблица 1
Поверхностное натяжение σ некоторых жидкостей
Что такое сила поверхностного натяжения
Поскольку поверхностный слой жидкости обладает избыточной потенциальной энергией (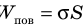
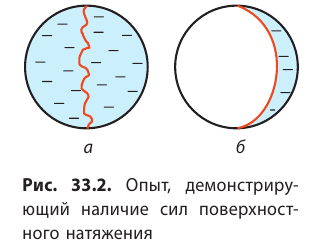
Наличие сил поверхностного натяжения делает поверхность жидкости похожей на натянутую резиновую пленку, однако упругие силы в резиновой пленке зависят от площади ее поверхности (от того, насколько пленка деформирована), а поверхность жидкости всегда «натянута» одинаково, то есть силы поверхностного натяжения не зависят от площади поверхности жидкости. Наличие сил поверхностного натяжения можно доказать с помощью такого опыта. Если проволочный каркас с закрепленной на нем нитью опустить в мыльный раствор, каркас затянется мыльной пленкой, а нить приобретет произвольную форму (рис. 33.2, а).
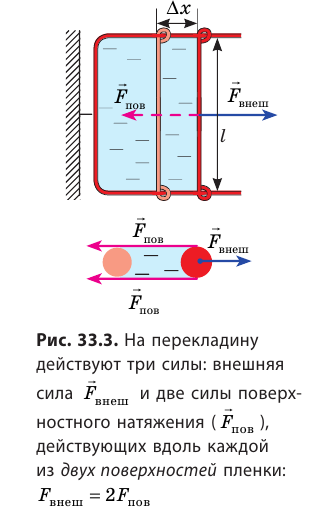
Если осторожно проткнуть иглой мыльную пленку по одну сторону от нити, сила поверхностного натяжения мыльного раствора, действующая с другой стороны, натянет нить (рис. 33.2, б). Опустим в мыльный раствор проволочную рамку, одна из сторон которой подвижна. На рамке образуется мыльная пленка (рис. 33.3). Будем растягивать эту пленку, действуя на перекладину (подвижную сторону рамки) с некоторой силой 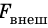
Если под действием этой силы перекладина переместится на ∆x , то внешние силы совершат работу: 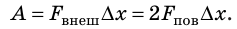
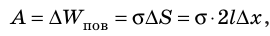
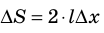
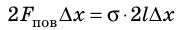
Таким образом, поверхностное натяжение σ численно равно силе поверхностного натяжения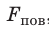
С одним из методов определения поверхностного натяжения жидкости вы ознакомитесь, выполняя лабораторную работу № 7.
- Заказать решение задач по физике
Где проявляется поверхностное натяжение
В жизни вы постоянно сталкиваетесь с проявлениями сил поверхностного натяжения. Так, благодаря ему на поверхности воды удерживаются легкие предметы (рис. 33.4) и некоторые насекомые.
Рис. 33.4. Монетка удерживается на поверхности воды благодаря силе поверхностного натяжения. (Чтобы провести такой опыт, монетку нужно потереть между пальцев и осторожно опустить на поверхность воды.)
Когда вы ныряете, ваши волосы расходятся во все стороны, но как только вы окажетесь над водой, волосы слипнутся, так как в этом случае площадь свободной поверхности воды намного меньше, чем при раздельном расположении прядей в воде. По этой же причине можно лепить фигуры из влажного песка: вода, обволакивая песчинки, прижимает их друг к другу.
Рис. 33.5. Капля удерживается около небольшого отверстия до тех пор, пока сила поверхностного натяжения уравновешивает силу тяжести
Стремлением жидкости уменьшить площадь поверхности объясняется и тот факт, что в условиях невесомости вода принимает форму шара, — при заданном объеме шарообразной форме соответствует наименьшая площадь поверхности. Форму шара приобретают тонкие мыльные пленки (мыльные пузыри). Поверхностным натяжением объясняется образование пены: пузырек газа, достигнув поверхности жидкости, имеет над собой тонкий слой жидкости; если пузырек мал, то архимедовой силы недостаточно, чтобы разорвать двойной поверхностный слой, и пузырек «застревает» вблизи поверхности. Благодаря поверхностному натяжению жидкость не выливается из маленького отверстия тоненькой струйкой, а капает (рис. 33.5), дождь не проливается через ткань зонта или палатки и т. д.
Почему одни жидкости собираются в капли, а другие растекаются
Наличие сил поверхностного натяжения проявляется в сферической форме мелких капелек росы, в каплях воды, разбегающихся по раскаленной плите, в капельках ртути на поверхности стекла. Однако при соприкосновении с твердым телом сферическая форма капли, как правило, не сохраняется. Форма свободной поверхности жидкости зависит также от сил взаимодействия молекул жидкости с молекулами твердого тела.
Если силы взаимодействия между молекулами жидкости больше, чем силы взаимодействия между молекулами жидкости и твердого тела, жидкость не смачивает поверхность твердого тела (рис. 33.6). Например, ртуть не смачивает стекло, а вода не смачивает покрытую сажей поверхность.
Рис. 33.6. Капля несмачивающей жидкости принимает форму, близкую к сферической, а поверхность жидкости вблизи стенки сосуда является выпуклой
Если же капельку ртути поместить на цинковую пластину, то капелька будет стремиться растечься по поверхности пластины; так же ведет себя и капелька воды на стекле (рис. 33.7). Если силы взаимодействия между молекулами жидкости меньше сил взаимодействия между молекулами жидкости и твердого тела, жидкость смачивает поверхность твердого тела.
Рис. 33.7. Капля смачивающей жидкости стремится растечься по поверхности твердого тела, а вблизи стенки сосуда поверхность жидкости принимает вогнутую форму
Почему жидкость поднимается в капиллярах
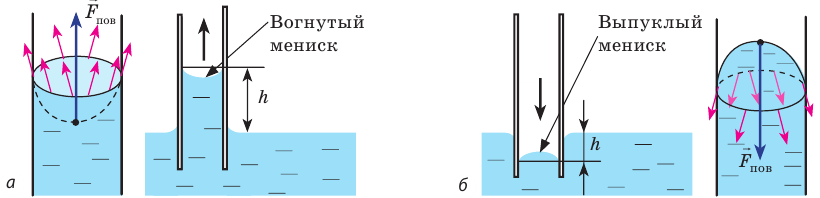
В природе часто встречаются тела, пронизанные многочисленными мелкими капиллярами (от лат. capillaris — волосяной) — узкими каналами произвольной формы. Такую структуру имеют бумага, дерево, почва, многие ткани и строительные материалы. В цилиндрических капиллярах искривленная поверхность жидкости представляет собой часть сферы, которую называют мениском. У смачивающей жидкости образуется вогнутый мениск (рис. 33.8, а), а у несмачивающей — выпуклый (рис. 33.8, б).
Рис. 33.8. капиллярные явления: а — смачивающая жидкость поднимается по капилляру; б — несмачивающая жидкость опускается в капилляре
Поверхность жидкости стремится к минимуму потенциальной энергии, а искривленная поверхность обладает большей площадью по сравнению с площадью сечения капилляра, поэтому поверхность жидкости стремится выровняться и под ней возникает избыточное (отрицательное или положительное) давление — лапласово давление (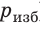
Под вогнутой поверхностью (жидкость смачивает капилляр) лапласово давление отрицательное и жидкость втягивается в капилляр. Так поднимаются влага и питательные вещества в стеблях растений, керосин по фитилю, влага в почве. Вследствие лапласового давления салфетки или ткань впитывают воду, брюки в дождливую погоду сильно намокают снизу и т. д. Под выпуклой поверхностью (жидкость не смачивает капилляр) лапласово давление положительное и жидкость в капилляре опускается. Чем меньше радиус капилляра, тем больше высота подъема (или опускания) жидкости (см. задачу ниже).
Пример решения задачи
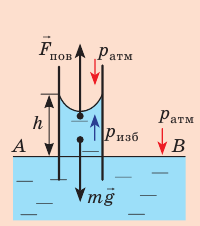
Капиллярную трубку радиусом r одним концом опустили в жидкость, смачивающую внутреннюю поверхность капилляра. На какую высоту поднимется жидкость в капилляре, если плотность жидкости ρ, а ее поверхностное натяжение σ ? Чему равно лапласово давление под вогнутой поверхностью капилляра? Смачивание считайте полным.
Решение:
На жидкость в капилляре действуют сила тяжести и сила поверхностного натяжения (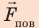
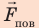
Поиск математической модели, решение
Поскольку m V = ρ , а объем воды в цилиндрическом капилляре 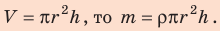
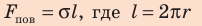
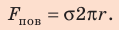
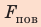

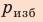
где R — радиус кривизны мениска (при полном смачивании r=R).
Ответ: (Данные выводы следует запомнить!)
Выводы:
- Свойства паров в физике
- Кипение жидкостей в физике
- Электромагнитные явления в физике
- Электромагнитные волны и их свойства
- Расчет количества теплоты при нагревании и охлаждении
- Удельная теплота сгорания топлива
- Плавление и кристаллизация в физике
- Испарение жидкостей в физике
Что такое поверхностное натяжение жидкости
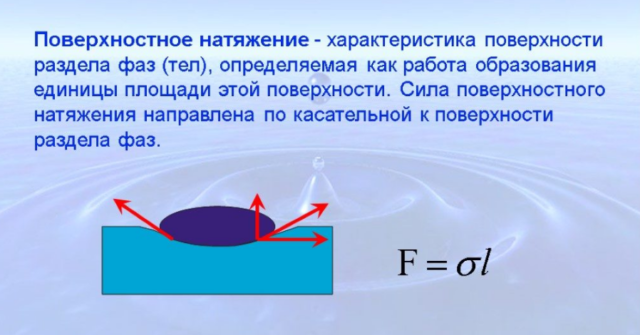
Поверхностное натяжение — характеристика поверхности раздела двух фаз, которые находятся в равновесии. Характеристика определяется работой образования единицы площади этой поверхности раздела.
Выражается произведением:
(mathcal F=sigmamathcal l), Н
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
(sigma) — коэффициент поверхностного натяжения, Н/м
(mathcal l) — длина, м
Направление силы: по касательной к поверхности.
Коэффициент поверхностного натяжения
Коэффициент поверхностного натяжения ((sigma)) — сила, которая действует на единицу длины линии, ограничивающей поверхность жидкости (Н/м).
Коэффициент поверхностного натяжения – коэффициент, равный работе, которую необходимо совершить для образования поверхности жидкости площадью (S) при постоянной температуре.
(sigma=frac{{mathcal F}_{пов}}{mathcal l} )
(sigma=frac{{mathcal F}_{пов}}{mathcal S})
(mathcal S) — площадь поверхности жидкости
Зависит от:
- Рода жидкости и ее свойств.
- Температуры (чем больше температура, тем меньше натяжение).
- Наличия ПАВ (поверхностно-активных веществ. Например, мыло).
- Присутствия каких-либо примесей.
- Свойств газа, контактирующего с жидкостью.
Чем вызвано поверхностное натяжение
Причина возникновения явления поверхностного напряжения: молекулы, которые составляют верхний слой жидкости. Они создают взаимодействие между собой, возникает натяжение.
Жидкости стремятся принять форму, которая требует минимальной площади поверхности.
Силы поверхностного натяжения
Силы поверхностного натяжения работают вдоль поверхности жидкости перпендикулярно контуру. Сокращают ее площадь. Это похоже на пленку, которая стягивает объем. На сам объем силы не оказывают влияние.
Примеры в окружающей среде
- движение водомерки по воде (ее лапки покрыты воскообразным веществом);
- капля росы, дождя, из пипетки;
- цилиндрическая форма струи воды;
- мыльный пузырь.
Расчет поверхностного натяжения в задачах
Задача 1
Дано
Имеется пипетка с диаметром отверстия (d=2) мм. В ходе опыта выяснилось, что (40) капель имеют массу равную (1,9) г. Вычислите коэффициент поверхностного натяжения.
Решение
Найдем массу одной капли и длину окружности.
(mathcal m=frac{{mathcal m}_{общ}}{mathcal n}\)
(mathcal l=mathrmpimathcal d\)
Напишем условие равновесия капли из пипетки.
({mathcal m}_0mathcal g=mathcal F\)
Подставим формулы.
(frac{mathcal m}{mathcal n}mathcal g=sigmamathrmpimathcal d\)
Выразим коэффициент поверхностного натяжения.
(sigma=frac{mathcal{mg}}{mathcal nmathrmpimathcal d}=frac{1,9ast10^{-3}ast10}{40ast3,14ast2ast10^{-3}}=75,6ast10^{-3};Н/м\)
Ответ: (75,6ast10^{-3};Н/м\)
Задача 2
Дано
Сосуд со ртутью имеет отверстие диаметром 70 мкм. Возможно ли без измерения определить максимальную высоту слоя ртути, при которой она не будет вытекать через отверстие?
Решение
Ртуть начнет вытекать тогда, когда произойдет увеличение силы ее давления относительно силы поверхностного натяжения.
(mathcal{pS}=mathcal F\rhomathcal{ghS}=sigmamathcal l\)
Выразим высоту.
(mathcal k=frac{sigmamathcal l}{rhomathcal{gS}}=frac{sigmamathrmpimathcal d}{rhomathcal g{displaystylefrac{mathrmpimathcal d^2}4}}=frac{4sigma}{rhomathcal{gd}}=frac{4ast472ast10^{-3}}{13600ast9,8ast70ast10^{-6}}=0,2;м\\)
Ответ: (0,2) м
Задача 3
Дано
Есть игла длиной (3,5) см и массой (0,3) г. Сможем ли мы произвести следующее действие: положить иголку на поверхность воды. Или же она утонет? Какие силы действуют на иголку?
Решение
На иглу действует сила тяжести. Если мы найдем ее и сравним с силой поверхностного натяжения, то узнаем ответ.
({mathcal F}_{тяж}=mathcal{mg}=0,3ast10^{-3}ast9,8=2,9ast10^{-3};Н\\\\)
({mathcal F}_{пн}=sigmamathcal l=73ast10^{-3}ast3,5ast10^{-2}=2,5ast10^{-3};Н\\\\\\\\)
Сравниваем силы и видим, что значение силы тяжести больше величины поверхностного натяжения.
Ответ: Игла утонет.
Задача 4
Почему возникают сложности с тем, чтобы снять мокрые перчатки с рук?
Ответ: Молекулы воды взаимодействуют с молекулами перчатки. По этой причине мы чувствуем сопротивление при стягивании перчаток с рук.
Задача 5
Дано
Есть капиллярная трубка ((R=0,5) мм). В ней столб жидкости высотой 11 мм. Определите плотность жидкости, если (sigma=22;мН/м.\\\\)
Решение
Воспользуемся формулой для капилляра.
(rho=frac{2sigmacosleft(alpharight)}{mathcal{hrg}}\\\\)
(alpha-угол;смачивания;жидкостью;стенки;капилляра.;Возьмем;за;90^circ\\\\)
(rho=frac{2,22ast10^{-3}ast1}{11ast10^{-3}ast0,5ast10^{-3}ast10}=800;кг/м^3\\\\)
Ответ: (800 кг/м^3\\\\)
Задача 6
Дано
Алюминиевое кольцо массой 7 г и радиусом 7,8 см соприкасается с мыльным раствором. Какую силу нужно приложить, чтобы оторвать кольцо от жидкости? Раствор имеет комнатную температуру.
Решение
Помимо натяжения на кольцо действует внешняя сила и сила тяжести.
Важно то, что кольцо соприкасается жидкости двумя сторонами. Умножаем на 2.
({mathcal F}_{пн}=2sigmamathcal l\mathcal l=2mathrm{πR}\{mathcal F}_{mathrm{пн}}=4mathrm{πσR}\\\\)
(mathcal F=mg+4mathrm{πσR}\mathcal F=7ast10^{-3}ast9,8+4mathrmpiast4ast10^{-2}ast7,8ast10^{-2}=0,11;mathrm Н\\\)
Ответ: 11 Н
Коэффициент поверхностного натяжения

4.3
Средняя оценка: 4.3
Всего получено оценок: 83.
4.3
Средняя оценка: 4.3
Всего получено оценок: 83.
В различных жидкостях силы притяжения молекул различны. Это приводит к тому, что и силы поверхностного натяжения также различаются. Для характеристики этих сил существует специальная величина — коэффициент поверхностного натяжения. Рассмотрим физический смысл коэффициента поверхностного натяжения.
Поверхностная энергия
В отличие от газов, молекулы жидкости не обладают достаточно высокой тепловой энергией, чтобы покидать жидкость. Поэтому молекулы в жидкости находятся на близких расстояниях друг от друга. Эти расстояния уменьшаются до тех пор, пока не начнут возникать деформации молекул, препятствующие дальнейшему сближению. На этом расстоянии силы притяжения и отталкивания уравновешиваются.
При этом молекулы вблизи поверхности и в глубине слоя жидкости находятся в различных условиях. На поверхности молекулы испытывают в основном силы притяжения. Эти силы передаются и молекулам нижележащих слоев, которые также добавляют к ним свои силы притяжения, и чем глубже находится молекула, тем большая сумма сил сжатия на нее действует.
В результате молекулы в глубине находятся в среднем на меньших расстояниях друг от друга. Получается, что молекулы на поверхности обладают некоторой избыточной потенциальной энергией по сравнению с ними.
Потенциальная энергия, которой обладают молекулы поверхностного слоя жидкости по сравнению с молекулами в глубине, называют поверхностной энергией.
Коэффициент поверхностного натяжения
Поскольку поверхностная энергия обуславливается взаимным притяжением молекул поверхностного слоя жидкости, то ее величина пропорциональна количеству молекул поверхностного слоя, которое пропорционально его площади. Таким образом, поверхностная энергия пропорциональна площади поверхностного слоя:
$$W_{пов}=sigma S$$
Коэффициент пропорциональности $sigma$ называется коэффициентом поверхностного натяжения. Этот коэффициент зависит от свойств молекул жидкости и от температуры. Поскольку энергия измеряется в джоулях, а площадь в квадратных метрах, то его размерность — джоуль на квадратный метр (или ньютон на метр).
Отсюда можно видеть физический смысл коэффициента поверхностного натяжения — это поверхностная энергия жидкости, имеющей единичную площадь поверхности.
Измерение силы поверхностного натяжения
Для определения силы и коэффициента поверхностного натяжения используют кольцо или рамку, помещенную в жидкость, связанную с чувствительным динамометром.
Если динамометр с рамкой медленно поднимать, то в момент отрыва рамки от жидкости динамометр начнет отмечать увеличение усилия. Самое большое значение силы $F_{max}$, зафиксированное динамометром в момент отрыва рамки длиной $l$ от поверхности жидкости, и позволит определить коэффициент поверхностного натяжения:
$$sigma = {F_{max} over 2l}$$
Таким образом, коэффициент поверхностного натяжения жидкости будет пропорционален максимальной силе, зафиксированной динамометром, и обратно пропорционален длине рамки. Двойка в знаменателе формулы появляется потому, что у пленки жидкости две внешние поверхности.
Если таким образом определить, например, коэффициент поверхностного натяжения воды, то для рамки длиной 10 см при 20 ⁰С максимальная сила при отрыве составит 14–15 мН. Подставив данные в формулу, получим значение 70–75 мН/м. Для других жидкостей коэффициенты при комнатной температуре приведены в таблице:
Ртуть имеет значительно больший коэффициент поверхностного натяжения, чем вода. Именно поэтому капельки ртути имеют почти шарообразную форму, хотя капельки воды того же объема растекаются.
Что мы узнали?
Поверхностная энергия жидкости характеризуется специальным параметром, который называется «коэффициент поверхностного натяжения». Его физический смысл в том, что это поверхностная энергия жидкости, имеющей единичную площадь поверхности.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.3
Средняя оценка: 4.3
Всего получено оценок: 83.
А какая ваша оценка?
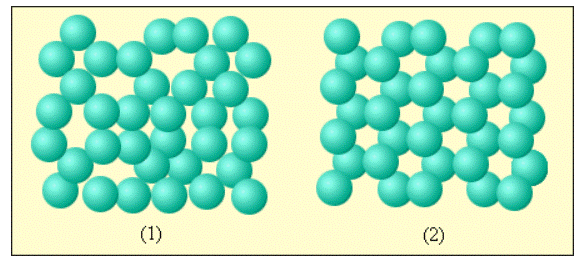
Вещество, находящееся в жидком состоянии, характеризуется крайне плотным расположением молекул друг относительно друга. Отличаясь от твердых кристаллических тел, чьи молекулы формируют упорядоченные структуры по всему объему кристалла и ограничены в своих тепловых колебаниях фиксированными центрами, молекулы жидкости обладают значительной степенью свободы. Любая конкретная молекула жидкого вещества, как это происходит и в твердых телах, «зажата» соседними молекулами и может совершать тепловые колебания поблизости с некоторым положением равновесия. Несмотря на это, в какой-то момент, любая молекула может переместиться на соседнее вакантное место. Подобные перемещения в жидкостях происходят довольно часто, благодаря чему молекулы не привязаны к конкретным центрам, как в кристаллах, а имеют возможность перемещаться по всему объему жидкости. Именно на этом факте основывается текучесть жидкостей.
По причине сильного взаимодействия между близко расположенными молекулами они могут образовывать локальные, то есть неустойчивые, упорядоченные группы, включающие в себя несколько молекул. Данное явление носит название ближнего порядка (рис. 3.5.1).
Рисунок 3.5.1. Пример ближнего порядка молекул жидкости и дальнего порядка молекул кристаллического вещества: 1 – вода; 2 – лед.
Свойства жидкостей
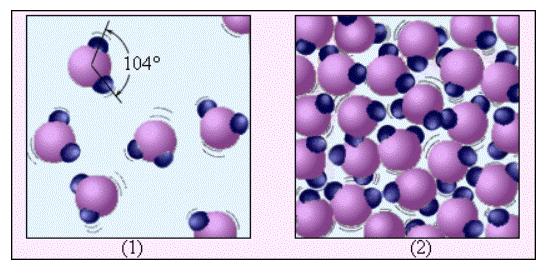
На рисунке 3.5.2, на примере воды, проиллюстрировано различие между газообразным веществом и жидкостью. Молекула воды H2O включает в свой состав один атом кислорода и два атома водорода, которые расположены под углом 104°. В среднем, расстояние между молекулами пара в десятки раз больше, чем между молекулами воды. На рисунке 3.5.2, в отличие от рисунка 3.5.1, на котором молекулы воды представляют из себя шарики, дается представление о структуре молекулы воды.
Рисунок 3.5.2. Водяной пар (1) и вода (2). Молекулы воды увеличены примерно в 5·107 раз.
Сжимаемость жидкостей, то есть изменение объема вещества при изменении давления, по причине плотности расположения молекул в десятки и сотни тысяч раз меньше, чем сжимаемость газов. К примеру, чтобы изменить объем воды всего на 1 % необходимо повысить значение давления примерно в 200 раз. Подобное увеличение давления по сравнению с атмосферным достигается на глубине близкой к 2 км.
Подобно твердым телам, жидкости имеют свойство менять свой объем при изменении температуры. В случае не самых больших интервалов температур относительное изменение объема ΔVV0 пропорционально изменению температуры ΔT, что может быть записано в виде следующего соотношения:
ΔVV0=β∆T.
В котором коэффициент β представляет собой температурный коэффициент объемного расширения. Данный коэффициент у жидкостей в десятки раз превышает значение такого же у твердых тел.
К примеру, у воды в случае, если температура равна 20 °С βв≈2·10–4 К–1, у стали βст≈3,6·10–5 К–1, у кварцевого стекла βкв≈9·10–6 К–1.
Тепловое расширение воды обладает важным для жизни на Земле эффектом. В условиях температуры ниже 4 °С вода начинает расширяется при снижении температуры β<0. Максимальную плотность ρв=103 кг/м3 вода приобретает при температуре 4 °С.
Замерзая, вода расширяется, из-за чего лед продолжает плавать на поверхности замерзающего водоема. Температура замерзающей воды подо льдом эквивалентна величине в 0 °С. У дна водоема, то есть слоях воды, обладающих большей плотностью, температура держится около 4 °С.
Поверхностное натяжение
Наличие свободной поверхности в жидкостях является одной из самых интересных ее особенностей. В отличие от газов, жидкость не заполняет весь объем сосуда, в котором она находится. Между жидкостью и газом, возможно паром, возникает граница раздела, находящаяся в особых условиях по сравнению с остальной массой жидкости. В отличие от молекул в глубине жидкости, молекулы, располагающиеся в пограничном ее слое, окружены другими молекулами этой же жидкости не со всех сторон. В среднем воздействующие на одну из молекул внутри жидкости со стороны соседних молекул силы межмолекулярного взаимодействия взаимно скомпенсированы. Каждая отдельно взятая молекула в пограничном слое притягивается находящимися внутри жидкости молекулами. При этом, силами, которые оказывают воздействие на такую молекулу жидкости со стороны молекул газа можно пренебречь. Вследствие этого возникает некая направленная вглубь жидкости равнодействующая сила. Поверхностные молекулы втягиваются внутрь жидкости, с помощью действия сил межмолекулярного притяжения. Однако все молекулы, в том числе и принадлежащие пограничному слою, должны находиться в состоянии равновесия. Оно достигается за счет сокращения расстояния между молекулами в пограничном слое и ближайшими их соседями в жидкости. Как проиллюстрировано на рисунке 3.1.2, в процессе уменьшения расстояния расстояния между молекулами появляются силы отталкивания. В случае, когда средняя величина расстояния между молекулами в жидкости равна r0, молекулы поверхностного слоя расположены плотнее, и по этой причине по сравнению с внутренними молекулами они имеют дополнительным запас потенциальной энергии, что можно увидеть на рисунке 3.1.2.
Стоит обратить внимание на то, что более плотного поверхностного слоя не приводит к сколь-нибудь заметному изменению объема жидкости по причине чрезвычайно низкой сжимаемости.
Силы межмолекулярного взаимодействия совершают положительную работу, в случае, когда молекула перемещается с поверхности внутрь жидкости. И наоборот, чтобы достать некоторое количество молекул на поверхность из глубины жидкости, то есть повысить площадь поверхности жидкости, внешним силам необходимо произвести пропорциональную изменению ΔS площади поверхности положительную работу ΔAвнеш:
ΔAвнеш=σ∆S,
где коэффициент σ носит название коэффициента поверхностного натяжения (σ>0).
Из всего вышесказанного следует, что коэффициент поверхностного натяжения — это величина равная работе, необходимой для увеличения площади поверхности жидкости при постоянной температуре на единицу.
В СИ коэффициент поверхностного натяжения измеряется в джоулях на метр квадратный (Дж/м2) или же в ньютонах на метр (1 Н/м=1 Дж/м2).
Таким образом, по сравнению с молекулами внутри жидкости молекулы поверхностного слоя жидкости обладают избыточной потенциальной энергией. Потенциальная энергия Eр поверхности жидкости пропорциональна ее площади и выражается в виде следующей формулы:
Eр=Aвнеш=σS.
Из раздела механики известно, что равновесным состояниям системы соответствует минимальное значение ее потенциальной энергии. Следовательно, свободная поверхность жидкости стремится уменьшить свою площадь. По данной причине свободная капля жидкости принимает шарообразную форму.
Жидкость ведет себя таким образом, будто по касательной к ее поверхности действуют сокращающие данную поверхность силы. Такие силы называются силами поверхностного натяжения.
Силы поверхностного натяжения влияют на поверхность жидкости таким образом, что она становится похожей на упругую растянутую пленку, с той лишь разницей, что упругие силы в пленке зависят от площади ее поверхности, то есть от степени деформированности пленки, а силы поверхностного натяжения, зависимости от площади поверхности жидкости не имеют.
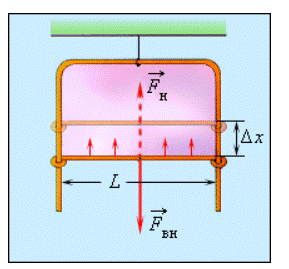
Некоторые жидкости, например, мыльная вода, имеют способность формировать тонкие пленки. Хорошо известные каждому человеку мыльные пузыри обладают правильной сферической формой, в чем также проявляется воздействие сил поверхностного натяжения. В случае, когда в мыльный раствор опускают проволочную рамку с одной подвижной стороной, вся она затягивается пленкой жидкости, как это показано на рисунке 3.5.3.
Рисунок 3.5.3. Подвижная сторона проволочной рамки в равновесии под действием внешней силы Fвн→ и результирующей сил поверхностного натяжения Fн→.
Силы поверхностного натяжения действуют на уменьшение поверхности пленки. Ради равновесия подвижной стороны рамки к ней необходимо приложить внешнюю силу
Fвн→=-Fн→. Если воздействие силы Fвн→ спровоцирует перемещение перекладины на некоторое Δx, то будет произведена работа ΔAвн=FвнΔx=ΔEp=σΔS, где ΔS=2LΔx является увеличением площади поверхности обеих сторон мыльной пленки. По той причине, что модули сил Fвн→ и Fн→ эквивалентны, справедливой будет запись:
Fн∆x=σ2L∆x или σ=Fн2L.
Исходя из этого, можно заявить, что коэффициент поверхностного натяжения σ может быть определен как модуль силы поверхностного натяжения, действующей на единицу длины линии, ограничивающей поверхность.
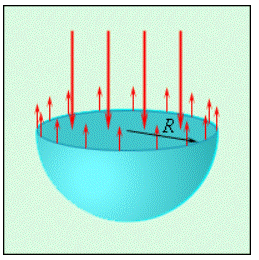
По причине воздействия сил поверхностного натяжения на капли жидкости и их действия внутри мыльных пузырей появляется некоторое избыточное давление Δp. При мысленном разрезании сферической капли с радиусом R на две равные части каждая из половин должна находиться в равновесии под действием приложенных к границе разреза длиной 2πR и сил избыточного давления, действующих на площадь πR2 сечения (рис. 3.5.4) сил поверхностного натяжения. Условие равновесия может быть записано в следующем виде:
σ2πR=∆pπR2.
Исходя из этого, можно заявить, что избыточное давление внутри капли эквивалентно:
∆p=2σR(капля жидкости).
Рисунок 3.5.4. Сечение сферической капли жидкости.
Из-за того, что пленка обладает двумя поверхностями, величина избыточного давления внутри мыльного пузыря в два раза выше, чем в капле:
∆p=4σR(мыльный пузырь).
Пренебрегая взаимодействием с молекулами газа, можно сказать, что поблизости с границей между твердым телом, жидкостью и газом форма свободной поверхности жидкости зависима от сил взаимодействия молекул жидкости с молекулами твердого тела.
В случае, когда данные силы превышают силы взаимодействия между молекулами жидкости, жидкость смачивает поверхность твердого тела. В таком случае жидкость подходит к поверхности твердого тела под некоторым характерным для данной пары жидкость – твердое тело острым углом θ. Такой угол носит название краевого угла.
Краевой угол θ является тупым (рисунок 3.5.5), в случае, если силы взаимодействия между молекулами жидкости превосходят силы их взаимодействия с молекулами твердого тела. В подобном случае можно сказать, что поверхность твердого тела не смачивается жидкостью. В условиях полного смачивания θ=0, полного несмачивания θ=180°.
Рисунок 3.5.5. Краевые углы смачивающей (1) и несмачивающей (2) жидкостей.
Капиллярные явления
Капиллярными явлениями называют процесс подъема или опускания жидкости в трубках малого диаметра, другими словами, в капиллярах.
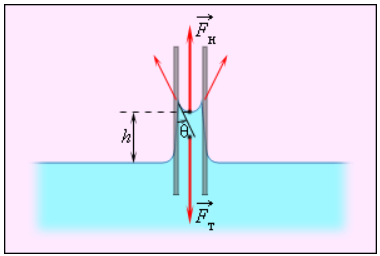
Смачивающие жидкости поднимаются по капиллярам, несмачивающие – опускаются. На рисунке 3.5.6 проиллюстрирована опущенная нижним концом в смачивающую жидкость плотности ρ капиллярная трубка, обладающая некоторым радиусом r. При этом верхний конец капилляра является открытым. Подъем жидкости в капилляре будет происходить до тех пор, пока сила тяжести Fт→, оказывающая воздействие на столб жидкости в капилляре, не станет эквивалентна по модулю результирующей Fн действующих вдоль границы соприкосновения жидкости с поверхностью капилляра сил поверхностного натяжения: Fт=Fн, где Fт=mg=ρhπr2g, Fн=σ2πr cos θ.
Из этого следует:
h=2σ cos θρgr.
Рисунок 3.5.6. Подъем смачивающей жидкости в капилляре.
При полном смачивании θ=0, cos θ=1. В таком случае:
h=2σρgr.
При полном несмачивании θ=180°, cos θ=–1 и, соответственно, h<0. Уровень несмачивающей жидкости в капилляре опускается ниже уровня жидкости в сосуде, в которую опущен капилляр.
Вода почти полностью смачивает чистую поверхность стекла. Ртуть же, строго наоборот, полностью не смачивает стеклянную поверхность. По этой причине уровень ртути в стеклянном капилляре опускается ниже, чем уровень в сосуде.



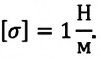
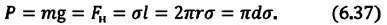
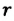 — радиус капилляра,
— радиус капилляра, 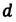 — диаметр капилляра.
— диаметр капилляра.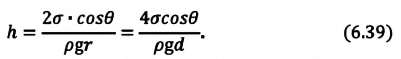
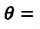
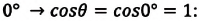

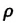 — плотность жидкости, поднимающейся в капилляре. Высота подъема жидкости в капилляре зависит от рода жидкости и обратно пропорциональна радиусу капилляра.
— плотность жидкости, поднимающейся в капилляре. Высота подъема жидкости в капилляре зависит от рода жидкости и обратно пропорциональна радиусу капилляра.