Коэффициент пуассона как пишется - Правописание и грамматика

Эта статья — о параметре, характеризующем упругие свойства материала. О понятии в термодинамике см. Показатель адиабаты.

Коэффициент Пуассона (обозначается как или ) — абсолютная величина отношения поперечной к продольной относительной деформации образца материала. Этот коэффициент зависит не от размеров тела, а от природы материала, из которого изготовлен образец. Коэффициент Пуассона и модуль Юнга полностью характеризуют упругие свойства изотропного материала.

При приложении к телу растягивающего усилия оно начинает удлиняться (то есть продольная длина увеличивается), а поперечное сечение уменьшается. Коэффициент Пуассона показывает, во сколько раз поперечная деформация деформируемого тела больше продольной деформации, при его растяжении или сжатии. Для абсолютно хрупкого материала коэффициент Пуассона равен 0, для абсолютно несжимаемого — 0,5. Для большинства сталей этот коэффициент лежит в районе 0,3, для резины он примерно равен 0,5.

Безразмерен, но может быть указан в относительных единицах: мм/мм, м/м.

Содержание

1 Ауксетики
2 Уравнение
3 Грунты
4 Значения коэффициента Пуассона для некоторых изотропных материалов
5 Примечания
6 См. также

Ауксетики

Существуют также материалы (преимущественно полимеры), у которых коэффициент Пуассона отрицателен, такие материалы называют ауксетиками. Это значит, что при приложении растягивающего усилия поперечное сечение тела увеличивается.

К примеру, бумага из однослойных нанотрубок имеет положительный коэффициент Пуассона, а по мере увеличения доли многослойных нанотрубок наблюдается резкий переход к отрицательному значению −0,20.

Отрицательным коэффициентом Пуассона обладают многие анизотропные кристаллы^[1], так как коэффициент Пуассона для таких материалов зависит от угла ориентации кристаллической структуры относительно оси растяжения. Отрицательный коэффициент обнаруживается у таких материалов, как литий (минимальное значение равно −0.54), натрий (−0.44), калий (−0.42), кальций (−0.27), медь (−0.13) и других. 67 % кубических кристаллов из таблицы Менделеева имеют отрицательный коэффициент Пуассона.

Уравнение

$mu = left|frac{varepsilon^prime}{varepsilon}right|$

где

— коэффициент Пуассона;

— деформация в поперечном направлении (отрицательна при осевом растяжении, положительна при осевом сжатии);

— продольная деформация (положительна при осевом растяжении, отрицательна при осевом сжатии).

Грунты

Коэффициент Пуассона для грунтов определяется по табл. 5.10 СП 22.13330.2011 Основания зданий и сооружений

Грунты	Коэффициент поперечной деформации ν
Крупнообломочные грунты	0,27
Пески и супеси	0,30 — 0,35
Суглинки	0,35 — 0,37
Глины при показателе текучести I_L
I_L < 0 0 < I_L <= 0,25 0,25 < I_L <= 1	0,20 — 0,30 0,30 — 0,38 0,38 — 0,45
Примечание. Меньшие значения ν применяют при большей плотности грунта.

Значения коэффициента Пуассона для некоторых изотропных материалов

Материал	Коэффициент Пуассона μ
Бетон	0,2 по СНиП, в расчётах возможно снижение до 0,15—0,17
Алюминий	0,34
Вольфрам	0,29
Германий	0,31
Дюралюминий	0,34
Иридий	0,26
Кварцевое стекло	0,17
Константан	0,33
Латунь	0,35
Манганин	0,33
Медь	0,35
Органическое стекло	0,35
Полистирол	0,35
Свинец	0,44
Олово	0,44
Серебро	0,37
Серый чугун	0,22
Сталь	0,28
Стекло	0,25
Фарфор	0,23

Примечания

↑ Гольдштейн Р. В., Городцов В. А., Лисовенко Д. С. Ауксетическая механика кристаллических материалов. Известия РАН, МТТ, 2010 г., № 4, стр.43-62.

См. также

Модули упругости для гомогенных изотропных материалов
Модуль объёмной упругости () \| Модуль Юнга () \| Параметры Ламе () \| Модуль сдвига () \| Коэффициент Пуассона () \| en:P-wave modulus ()

Источник

коэффициент Пуассона
Размерность	1
Единицы измерения
СИ	безразмерная
СГС	безразмерная

Коэффициент Пуассона (обозначается как [math]displaystyle{ nu }[/math], [math]displaystyle{ sigma }[/math] или [math]displaystyle{ mu }[/math]) — упругая константа^[1], величина отношения относительного поперечного сжатия к относительному продольному растяжению. Этот коэффициент зависит не от размеров тела, а от природы материала, из которого изготовлен образец. Коэффициент Пуассона и модуль Юнга полностью характеризуют упругие свойства изотропного материала^[2]. Безразмерен, но может быть указан в относительных единицах: мм/мм, м/м.

Детальное определение

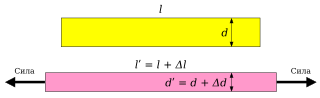
Однородный стержень до и после приложения к нему растягивающих сил.

Приложим к однородному стержню растягивающие его силы. В результате воздействия таких сил стержень в общем случае окажется деформирован как в продольном, так и в поперечном направлениях.

Пусть [math]displaystyle{ l }[/math] и [math]displaystyle{ d }[/math] длина и поперечный размер образца до деформации, а [math]displaystyle{ l^prime }[/math] и [math]displaystyle{ d^prime }[/math] — длина и поперечный размер образца после деформации. Тогда продольным удлинением называют величину, равную [math]displaystyle{ (l^prime — l) }[/math], а поперечным сжатием — величину, равную [math]displaystyle{ — (d^prime — d) }[/math]. Если [math]displaystyle{ (l^prime — l) }[/math] обозначить как [math]displaystyle{ Delta l }[/math], а [math]displaystyle{ ( d^prime — d) }[/math] как [math]displaystyle{ Delta d }[/math], то относительное продольное удлинение будет равно величине [math]displaystyle{ frac{Delta l}{l} }[/math], а относительное поперечное сжатие — величине [math]displaystyle{ — frac{Delta d}{d} }[/math]. Тогда в принятых обозначениях коэффициент Пуассона [math]displaystyle{ mu }[/math] имеет вид:[math]displaystyle{ mu = -frac{Delta d}{d} frac {l} {Delta l} }[/math]Обычно при приложении к стержню растягивающих усилий он удлиняется в продольном направлении и сокращается в поперечных направлениях. Таким образом, в подобных случаях выполнятся [math]displaystyle{ frac{Delta l}{l} gt 0 }[/math] и [math]displaystyle{ frac{Delta d}{d} lt 0 }[/math], так что коэффициент Пуассона положителен. Как показывает опыт, при сжатии коэффициент Пуассона имеет то же значение, что и при растяжении.

Для абсолютно хрупких материалов коэффициент Пуассона равен 0, для абсолютно несжимаемых — 0,5. Для большинства сталей этот коэффициент лежит в районе 0,3, для резины он равен приблизительно 0,5^[3]. Для большинства сплавов, металлов, горных пород значение коэффициента Пуассона лежит в пределах 0,25-0,35, в бетоне 0,16-0,18^[1].

Связь с другими упругими константами

1) Через модуль сдвига [math]displaystyle{ G }[/math] и модуль всестороннего сжатия [math]displaystyle{ K }[/math][math]displaystyle{ sigma = frac{1}{2}frac{3K-2G}{3K+G} }[/math]2) Через отношение скоростей продольных и поперечных упругих волн волн^[4]:

[math]displaystyle{ sigma = frac {gamma^2-2}{2(gamma^2-1)} }[/math][math]displaystyle{ frac = frac{V_P}{V_S} }[/math]

Ауксетики

Отрицательным коэффициентом Пуассона обладают многие анизотропные кристаллы^[5], так как коэффициент Пуассона для таких материалов зависит от угла ориентации кристаллической структуры относительно оси растяжения. Отрицательный коэффициент обнаруживается у таких материалов, как литий (минимальное значение равно −0,54), натрий (−0,44), калий (−0,42), кальций (−0,27), медь (−0,13) и других. 67 % кубических кристаллов из таблицы Менделеева имеют отрицательный коэффициент Пуассона.

Значения коэффициента Пуассона

Грунты

Коэффициент Пуассона (коэффицент бокового расширения) для грунтов^[6]:

Грунты	Коэффициент поперечной деформации ν
Крупнообломочные грунты	0,27
Пески и супеси	0,30 — 0,35
Суглинки	0,35 — 0,37
Глины при показателе текучести I_L
I_L < 0 0 < I_L <= 0,25 0,25 < I_L <= 1	0,20 — 0,30 0,30 — 0,38 0,38 — 0,45
Примечание. Меньшие значения ν применяют при большей плотности грунта.

В бентонитовом растворе Коэффициент Пуассона≈0,5 т.к. в жидкости жесткости E там нет.

Изотропные материалы

Материал	Коэффициент Пуассона μ
Бетон	0,2 по СНиП, в расчётах возможно снижение до 0,15—0,17
Алюминий	0,34
Вольфрам	0,29
Германий	0,31
Дюралюминий	0,34
Иридий	0,26
Кварцевое стекло	0,17
Константан	0,33
Латунь	0,35
Манганин	0,33
Медь	0,35
Органическое стекло	0,35
Полистирол	0,35
Свинец	0,44
Олово	0,44
Серебро	0,37
Серый чугун	0,22
Сталь	0,25
Стекло	0,25
Фарфор	0,23

Примечания

↑ ^1,0 ^1,1 Владимир Атапин, Александр Пель, Анатолий Темников. Сопротивление материалов. Базовый курс. Дополнительные главы. — Litres, 2021-03-16. — 507 с. — ISBN 978-5-04-112997-2. Архивная копия от 30 декабря 2021 на Wayback Machine
↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит, 2005. — Т. I. Механика. — С. 414. — 560 с. — ISBN 5-9221-0225-7.
↑ Владимир Черняк, Паригорий Суетин. Механика сплошных сред. — Litres, 2018-12-20. — 353 с. — ISBN 978-5-457-96786-1. Архивная копия от 30 декабря 2021 на Wayback Machine
↑ Виталий Щербинин, Анатолий Зацепин. Акустические измерения. Учебное пособие для вузов. — Litres, 2021-12-02. — 210 с. — ISBN 978-5-04-041588-5. Архивная копия от 30 декабря 2021 на Wayback Machine
↑ Гольдштейн Р. В., Городцов, В. А., Лисовенко Д. С. «Ауксетическая механика кристаллических материалов». Известия РАН, МТТ, 2010 г., № 4, С. 43—62.
↑ Таблица 5.10, СП 22.13330.2016 Основания зданий и сооружений.

См. также

Модуль упругости
Модуль Юнга

Источник

Коэффициент Пуассона материала определяет отношение поперечной деформации (направление x) к осевой деформации (направление y).

В материаловедения и механики деформируемого твердого тела , коэффициент Пуассона ( nu ) — мера эффекта Пуассона , деформации (расширения или сжатия) материала в направлениях, перпендикулярных определенному направлению нагрузки . Величина коэффициента Пуассона является отрицательной величиной отношения поперечной деформации к осевой деформации . При малых значениях этих измененийпредставляет собой величину поперечного удлинения, деленную на величину осевого сжатия . Для большинства материалов коэффициент Пуассона находится в диапазоне от 0,0 до 0,5. Для мягких материалов ^[1], таких как резина, у которых модуль объемной упругости намного выше модуля сдвига, коэффициент Пуассона составляет около 0,5. Для пенопластов с открытыми порами коэффициент Пуассона близок к нулю, поскольку ячейки имеют тенденцию разрушаться при сжатии. Многие типичные твердые тела имеют коэффициент Пуассона в диапазоне 0,2-0,3. Отношение названо в честь французского математика и физика Симеона Пуассона .

Происхождение

Коэффициент Пуассона является мерой эффекта Пуассона, явления, при котором материал имеет тенденцию расширяться в направлениях, перпендикулярных направлению сжатия. И наоборот, если материал растягивается, а не сжимается, он обычно имеет тенденцию сжиматься в направлениях, поперечных направлению растяжения. Обычное наблюдение, когда резинка растягивается, она становится заметно тоньше. Опять же, коэффициент Пуассона будет отношением относительного сжатия к относительному расширению и будет иметь то же значение, что и выше. В некоторых редких случаях ^[2] материал действительно сжимается в поперечном направлении при сжатии (или расширяется при растяжении), что дает отрицательное значение коэффициента Пуассона.

Коэффициент Пуассона стабильной, изотропной , линейной упругой материала должна быть в пределах от -1,0 и +0,5 из-за требования для модуля Юнга , с модулем сдвига и объемного модуля , чтобы иметь положительные значения. ^{[3] Для} большинства материалов коэффициент Пуассона находится в диапазоне от 0,0 до 0,5. Совершенно несжимаемый изотропный материал, упруго деформируемый при малых деформациях, имел бы коэффициент Пуассона точно 0,5. Большинство сталей и жестких полимеров при использовании в пределах их проектных ограничений (до текучести ) показывают значения около 0,3, увеличиваясь до 0,5 для деформации после выхода текучести, которая происходит в основном при постоянном объеме. ^[4]Резина имеет коэффициент Пуассона около 0,5. Коэффициент Пуассона Корка близок к 0, показывая очень небольшое поперечное расширение при сжатии, а стекло находится между 0,18 и 0,30. Некоторые материалы, например, полимерная пена, складки оригами, ^[5]^[6] и некоторые ячейки могут иметь отрицательный коэффициент Пуассона, и их называют ауксетическими материалами . Если эти ауксетические материалы растягиваются в одном направлении, они становятся толще в перпендикулярном направлении. Напротив, некоторые анизотропные материалы, такие как углеродные нанотрубки , зигзагообразные листовые материалы ^[7]^[8] и сотовые ауксетические метаматериалы ^[9] чтобы назвать несколько, может показывать один или несколько коэффициентов Пуассона выше 0,5 в определенных направлениях.

Предполагая, что материал растягивается или сжимается только в одном направлении ( ось x на диаграмме ниже):

куда

— результирующий коэффициент Пуассона,

— поперечная деформация (отрицательная для осевого растяжения (растяжения), положительная для осевого сжатия)

— осевая деформация (положительная для осевого растяжения, отрицательная для осевого сжатия).

Коэффициент Пуассона от изменений геометрии

Изменение длины

Рисунок 1: Куб со сторонами длиной L из изотропного линейно упругого материала, подверженного растяжению вдоль оси x, с коэффициентом Пуассона 0,5. Зеленый куб не деформирован, красный расширен в направлении x наиз-за напряжения и сжался в направлениях y и z на.

Для куба, вытянутого в направлении оси x (см. Рисунок 1) с увеличением длины нав направлении x , и уменьшение длины нав направлениях y и z бесконечно малые диагональные деформации равны

Если коэффициент Пуассона постоянен из-за деформации, интегрирование этих выражений и использование определения коэффициента Пуассона дает

Решая и возводя в степень, отношения между а также затем

Для очень малых значений а также , первое приближение дает:

Изменение объема

Теперь можно рассчитать относительное изменение объема ΔV / V куба из-за растяжения материала. С использованием а также :

Используя полученное выше отношение между а также :

и для очень малых значений а также , первое приближение дает:

Для изотропных материалов можно использовать соотношение Ламе ^[10]

куда это объемный модуль упругости и— модуль Юнга .

Изменение ширины

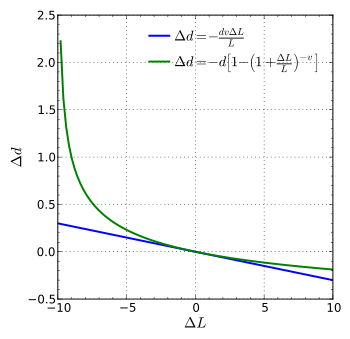
Рисунок 2: Сравнение двух формул, одна для малых деформаций, другая для больших деформаций

Если стержень диаметром (или шириной, или толщиной) d и длиной L подвергается растяжению, так что его длина изменится на ΔL, то его диаметр d изменится на:

Приведенная выше формула верна только в случае небольших деформаций; если деформации большие, то можно использовать следующую (более точную) формулу:

куда

оригинальный диаметр

изменение диаметра стержня

коэффициент Пуассона

оригинальная длина, до растяжки

изменение длины.

Значение отрицательное, потому что оно уменьшается с увеличением длины.

Характерные материалы

Изотропный

Для линейного изотропного материала, подверженного только сжимающим (то есть нормальным) силам, деформация материала в направлении одной оси вызовет деформацию материала вдоль другой оси в трех измерениях. Таким образом, можно обобщить закон Гука (для сжимающих сил) в трех измерениях:

куда:

, а также которые напрягают в направлении, а также ось

, а также это напряжение в направлении, а также ось

— модуль Юнга (одинаков во всех направлениях:, а также для изотропных материалов)

— коэффициент Пуассона (одинаков во всех направлениях: , а также для изотропных материалов)

все эти уравнения можно синтезировать следующим образом:

В самом общем случае будут сохраняться и касательные напряжения , и нормальные напряжения, и полное обобщение закона Гука дается выражением:

куда — дельта Кронекера . Обычно используются обозначения Эйнштейна :

написать уравнение просто как:

Анизотропный

Для анизотропных материалов коэффициент Пуассона зависит от направления растяжения и поперечной деформации.

Здесь коэффициент Пуассона, — модуль Юнга , — единичный вектор, направленный вдоль направления растяжения, — единичный вектор, направленный перпендикулярно направлению растяжения. Коэффициент Пуассона имеет разное количество специальных направлений в зависимости от типа анизотропии. ^[11]^[12]

Ортотропный

Ортотропные материалы имеют три взаимно перпендикулярные плоскости симметрии свойств материала. Примером может служить древесина, которая является наиболее жесткой (и прочной) вдоль волокон и менее — в других направлениях.

Тогда закон Гука можно выразить в матричной форме как ^[13]^[14]

куда

— модуль Юнга по оси

является модуль сдвига в направлении на плоскости, нормаль которой направлена

коэффициент Пуассона, соответствующий сжатию в направлении когда расширение применяется в направлении .

Коэффициент Пуассона ортотропного материала различен в каждом направлении (x, y и z). Однако симметрия тензоров напряжений и деформаций означает, что не все шесть коэффициентов Пуассона в уравнении являются независимыми. Есть только девять независимых свойств материала: три модуля упругости, три модуля сдвига и три коэффициента Пуассона. Остальные три коэффициента Пуассона можно получить из соотношений

Из приведенных выше соотношений видно, что если тогда . Чем больше коэффициент Пуассона (в данном случае) называется большим коэффициентом Пуассона, а меньший (в данном случае) называется минорным коэффициентом Пуассона . Мы можем найти аналогичные отношения между другими коэффициентами Пуассона.

Трансверсально изотропный

Трансверсально изотропные материалы имеют плоскость изотропии, в которой упругие свойства изотропны. Если предположить, что эта плоскость изотропии равна, то закон Гука принимает вид ^[15]

где мы использовали плоскость изотропии для уменьшения количества констант, т. е. .

Из симметрии тензоров напряжений и деформаций следует, что

Это оставляет нам шесть независимых констант . Однако поперечная изотропия приводит к дополнительному ограничению между а также который

Следовательно, существует пять независимых свойств упругого материала, два из которых являются коэффициентами Пуассона. Для предполагаемой плоскости симметрии большее из а также — главный коэффициент Пуассона. Остальные большие и второстепенные коэффициенты Пуассона равны.

Значения коэффициента Пуассона для разных материалов

Влияние добавок выбранных стеклянных компонентов на коэффициент Пуассона конкретного базового стекла. ^[16]

Материал	Коэффициент Пуассона
резина	0,4999 ^[17]
золото	0,42–0,44
насыщенная глина	0,40–0,49
магний	0,252–0,289
титан	0,265–0,34
медь	0,33
алюминий — сплав	0,32
глина	0,30–0,45
нержавеющая сталь	0,30–0,31
сталь	0,27–0,30
чугун	0,21–0,26
песок	0,20–0,455
конкретный	0,1–0,2
стакан	0,18–0,3
металлические очки	0,276–0,409 ^[18]
мыло	0,10–0,50
пробка	0,0

Материал	Плоскость симметрии
Ячеистая сердцевина Nomex	, лента в направление	0,49	0,69	0,01	2,75	3,88	0,01
стекловолокно — эпоксидная смола		0,29	0,32	0,06	0,06	0,32

Материалы с отрицательным коэффициентом Пуассона

Некоторые материалы, известные как ауксетические материалы, имеют отрицательный коэффициент Пуассона. Когда он подвергается положительной деформации по продольной оси, поперечная деформация в материале фактически будет положительной (т. Е. Увеличит площадь поперечного сечения). Для этих материалов это обычно связано с однозначно ориентированными шарнирными молекулярными связями. Чтобы эти скрепления растягивались в продольном направлении, петли должны «открываться» в поперечном направлении, эффективно демонстрируя положительную деформацию. ^[19]
Это также может быть сделано структурированным образом и приведет к новым аспектам в материальном дизайне, как и в отношении механических метаматериалов .

Исследования показали, что некоторые виды твердой древесины показывают отрицательный коэффициент Пуассона исключительно во время испытания на ползучесть при сжатии . ^[20]^[21] Первоначально испытание на ползучесть при сжатии показывает положительные коэффициенты Пуассона, но постепенно уменьшается, пока не достигнет отрицательных значений. Следовательно, это также показывает, что коэффициент Пуассона для древесины зависит от времени при постоянной нагрузке, а это означает, что деформации в осевом и поперечном направлениях не увеличиваются с одинаковой скоростью.

Среды с инженерной микроструктурой могут иметь отрицательный коэффициент Пуассона. В простом случае ауксетичность достигается удалением материала и созданием периодической пористой среды. ^[22] Решетки могут достигать более низких значений коэффициента Пуассона, ^[23] которые могут быть бесконечно близкими к предельному значению -1 в изотропном случае. ^[24]

Более трехсот кристаллических материалов имеют отрицательный коэффициент Пуассона. ^[25]^[26]^[27] Например, Li, Na, K, Cu, Rb, Ag, Fe, Ni, Co, Cs, Au, Be, Ca, Zn Sr, Sb, MoS и другие.

Функция Пуассона

При конечных деформациях соотношение поперечных и осевых деформаций а также обычно не очень хорошо описывается коэффициентом Пуассона. Фактически, коэффициент Пуассона часто считается функцией приложенной деформации в режиме большой деформации. В таких случаях коэффициент Пуассона заменяется функцией Пуассона, для которой существует несколько конкурирующих определений. ^[28] Определение поперечного растяжения и осевое растяжение , где поперечное растяжение является функцией осевого растяжения (т. е. ) наиболее распространены функции Генки, Био, Грина и Альманси.

Применение эффекта Пуассона

Одна область, в которой эффект Пуассона имеет значительное влияние, — это поток в трубе под давлением. Когда воздух или жидкость внутри трубы находятся под высоким давлением, они оказывают равномерное усилие на внутреннюю часть трубы, что приводит к кольцевому напряжению внутри материала трубы. Из-за эффекта Пуассона это кольцевое напряжение приведет к увеличению диаметра трубы и небольшому уменьшению ее длины. Уменьшение длины, в частности, может оказать заметное влияние на соединения труб, поскольку эффект будет накапливаться для каждой секции трубы, соединенной последовательно. Сдерживаемый сустав может быть разорван или иным образом подвержен поломке. ^{[ необходима цитата ]}

Еще одна область применения эффекта Пуассона — структурная геология . Камни, как и большинство материалов, подвержены эффекту Пуассона при напряжении. В геологическом масштабе времени чрезмерная эрозия или осаждение земной коры может создавать или снимать большие вертикальные напряжения на подстилающей породе. Эта порода будет расширяться или сжиматься в вертикальном направлении в результате приложенного напряжения, а также будет деформироваться в горизонтальном направлении в результате эффекта Пуассона. Это изменение деформации в горизонтальном направлении может повлиять на соединения и спящие напряжения в породе или образовать их. ^[29]

Хотя исторически пробка была выбрана для герметизации винных бутылок по другим причинам (включая ее инертную природу, непроницаемость, гибкость, герметичность и упругость) ^[30] , нулевой коэффициент Пуассона пробки дает еще одно преимущество. Когда пробка вставляется в бутылку, верхняя часть, которая еще не вставлена, не расширяется в диаметре, поскольку она сжимается в осевом направлении. Сила, необходимая для того, чтобы вставить пробку в бутылку, возникает только из-за трения между пробкой и бутылкой из-за радиального сжатия пробки. Если бы стопор был изготовлен, например, из резины (с коэффициентом Пуассона около 1/2), то для преодоления радиального расширения верхней части резинового стопора потребовалась бы относительно большая дополнительная сила.

Большинство автомехаников знают, что трудно снять резиновый шланг (например, шланг охлаждающей жидкости) с металлического патрубка, так как натяжение при растяжении приводит к уменьшению диаметра шланга, плотно сжимая патрубок. Шланги легче снимать с концов с помощью широкого плоского лезвия.

См. Также

Линейная эластичность
Закон Гука
Техника импульсного возбуждения
Ортотропный материал
Модуль сдвига
Модуль для младших
Коэффициент температурного расширения

Ссылки

^ Для мягких материалов объемный модуль (K) обычно больше по сравнению с модулем сдвига (G), поэтому их можно рассматривать как несжимаемые, поскольку легче изменить форму, чем сжать. Это приводит к тому, что модуль Юнга (E) равен и, следовательно . Ястшебский Д. (1959). Природа и свойства инженерных материалов (изд. Wiley International). John Wiley & Sons, Inc.
^ Лейкс, Р. и Войцеховски, К.В., 2008. Отрицательная сжимаемость, отрицательный коэффициент Пуассона и стабильность. Physica Status Solidi B, 245 (3), стр. 545-551.
^ Герчек, Х. (январь 2007 г.). «Значения коэффициента Пуассона для горных пород». Международный журнал механики горных пород и горных наук . 44 (1): 1–13. DOI : 10.1016 / j.ijrmms.2006.04.011 .
^ Парк, RJT. Сейсмические характеристики стальных бетонных свай
^ Марк, Шенк (2011). Складчатые конструкции оболочки, кандидатская диссертация (PDF) . Кембриджский университет, Клэр-колледж.
^ Вэй, З.Ы .; Guo, ZV; Dudte, L .; Liang, HY; Махадеван, Л. (21 мая 2013 г.). «Геометрическая механика периодического гофрированного оригами» (PDF) . Письма с физическим обзором . 110 (21): 215501. arXiv : 1211.6396 . Bibcode : 2013PhRvL.110u5501W . DOI : 10.1103 / PhysRevLett.110.215501 . PMID 23745895 . S2CID 9145953 .
^ Эйдини, Марьям; Паулино, Глаусио Х. (2015). «Раскрытие свойств метаматериалов в листах, сложенных зигзагообразно» . Наука продвигается . 1 (8): e1500224. arXiv : 1502.05977 . Bibcode : 2015SciA …. 1E0224E . DOI : 10.1126 / sciadv.1500224 . ISSN 2375-2548 . PMC 4643767 . PMID 26601253 .
^ Eidini, Марьям (2016). «Зигзагообразно-фальцованные листовые ячеистые механические метаматериалы». Письма об экстремальной механике . 6 : 96–102. arXiv : 1509.08104 . DOI : 10.1016 / j.eml.2015.12.006 . S2CID 118424595 .
^ Мусанежад, Давуд; Бабай, Сахаб; Эбрахими, Хамид; Гош, Ранаджай; Хамуда, Абдельмагид Салем; Бертольди, Катя; Вазири, Ашкан (16 декабря 2015 г.). «Иерархические сотовые ауксетические метаматериалы» . Научные отчеты . 5 : 18306. Bibcode : 2015NatSR … 518306M . DOI : 10.1038 / srep18306 . ISSN 2045-2322 . PMC 4680941 . PMID 26670417 .
^ https://arxiv.org/ftp/arxiv/papers/1204/1204.3859.pdf — Пределы коэффициента Пуассона в изотропных материалах — общий результат для произвольной деформации.
^ Епишин, AI; Лисовенко, Д.С. (2016). «Экстремальные значения коэффициента Пуассона кубических кристаллов». Техническая физика . 61 (10): 1516–1524. Bibcode : 2016JTePh..61.1516E . DOI : 10.1016 / j.mechmat.2019.03.017 .
^ Городцов, В.А.; Лисовенко Д.С. (2019). «Экстремальные значения модуля Юнга и коэффициента Пуассона гексагональных кристаллов». Механика материалов . 134 : 1–8. DOI : 10.1016 / j.mechmat.2019.03.017 .
^ Boresi, А. Р, Шмидт, RJ и Sidebottom О.М., 1993, Advanced механика материалов , Wiley.
^ Лехницкий, С.Г., (1963), Теория упругости анизотропного упругого тела , Holden-Day Inc.
^ Тан, SC, 1994, Концентрации напряжений в ламинированных композитах , Technomic Publishing Company, Ланкастер, Пенсильвания.
^ Флюгель, Александр. «Расчет коэффициента Пуассона для очков» . www.glassproperties.com . Архивировано 23 октября 2017 года . Проверено 28 апреля 2018 .
^ «Архивная копия» (PDF) . Архивировано (PDF) из оригинала 31.10.2014 . Проверено 24 сентября 2014 . CS1 maint: archived copy as title (link)
^ Журнал прикладной физики 110, 053521 (2011)
^ Лейкс, Род. «Отрицательный коэффициент Пуассона» . silver.neep.wisc.edu . Архивировано 16 февраля 2018 года . Проверено 28 апреля 2018 .
^ Озихар, Томаш; Геринг, Стефан; Немц, Питер (март 2013). «Вязкоупругие характеристики древесины: зависимость от времени ортотропной податливости при растяжении и сжатии». Журнал реологии . 57 (2): 699–717. Bibcode : 2013JRheo..57..699O . DOI : 10.1122 / 1.4790170 . ISSN 0148-6055 .
^ Цзян, Цзяли; Эрик Валентин, Бахтияр; Лу, Цзяньсюн; Немц, Питер (2016-11-01). «Временная зависимость модулей ортотропного сжатия Юнга и коэффициентов Пуассона древесины пихты китайской» (PDF) . Holzforschung . 70 (11): 1093–1101. DOI : 10,1515 / ВЧ-2016-0001 . ЛВП : 20.500.11850 / 122097 . ISSN 1437-434X . S2CID 137799672 .
^ Карта, Джорджио; Брун, Мишель; Бальди, Антонио (2016). «Конструкция пористого материала с изотропным отрицательным коэффициентом Пуассона». Механика материалов . 97 : 67–75. DOI : 10.1016 / j.mechmat.2016.02.012 .
^ Кабрас, Луиджи; Брун, Мишель (2016). «Класс ауксетических трехмерных решеток» . Журнал механики и физики твердого тела . 91 : 56–72. arXiv : 1506.04919 . Bibcode : 2016JMPSo..91 … 56C . DOI : 10.1016 / j.jmps.2016.02.010 . S2CID 85547530 .
^ Кабрас, Луиджи; Брун, Мишель (2014). «Ауксетические двумерные решетки с коэффициентом Пуассона, сколь угодно близким к -1». Труды Королевского общества А . 470 (2172): 20140538. arXiv : 1407.5679 . Bibcode : 2014RSPSA.47040538C . DOI : 10,1098 / rspa.2014.0538 . S2CID 119321604 .
^ Goldstein, RV; Городцов В.А.; Лисовенко, Д.С. (2013). «Классификация кубических ауксетиков». Physica Status Solidi B . 250 (10): 2038–2043. DOI : 10.1002 / pssb.201384233 .
^ Goldstein, RV; Городцов В.А.; Лисовенко, Д.С. (2011). «Изменчивость упругих свойств гексагональных ауксетиков». Доклады Физики . 56 (12): 602–605. DOI : 10.1134 / S1028335811120019 . S2CID 120998323 .
^ Goldstein, RV; Городцов В.А.; Лисовенко Д.С.; Волков, М.А. (2015). «Ауксетики среди 6-константных тетрагональных кристаллов» . Письма о материалах . 5 (4): 409–413. DOI : 10.22226 / 2410-3535-2015-4-409-413 .
^ Михай, Лос-Анджелес; Гориели, А. (03.11.2017). «Как охарактеризовать нелинейный упругий материал? Обзор нелинейных основных параметров в изотропной конечной упругости» . Труды Королевского общества А . 473 (2207): 20170607. Bibcode : 2017RSPSA.47370607M . DOI : 10,1098 / rspa.2017.0607 . PMC 5719638 . PMID 29225507 .
^ «Конспект лекций по структурной геологии — эффективное напряжение» . Проверено 3 июля 2019 .
^ Сильва и др. «Корк: свойства, возможности и приложения». Архивировано 9августа 2017 г.в Wayback Machine. Проверено 4 мая 2017 г.

Внешние ссылки

Значение коэффициента Пуассона
Материалы с отрицательным коэффициентом Пуассона
Подробнее о материалах с отрицательным коэффициентом Пуассона (ауксетические)

Формулы преобразования
Однородные изотропные линейные упругие материалы обладают своими упругими свойствами, однозначно определяемыми любыми двумя модулями из них; таким образом, для любых двух любых других модулей упругости можно рассчитать по этим формулам.
							Примечания








							Есть два верных решения. Знак плюс ведет к. Знак минус ведет к .

							Не может использоваться, когда

Источник

Коэффициент Пуассона (коэффициент поперечной деформации) одна из механических характеристик материалов, показывает зависимость между продольными и поперечными деформациями элемента, характеризует упругие свойства материала.

Обозначается строчными греческими буквами ν или μ и не имеет размерности.

Определяется отношением относительных поперечных ε_поп и продольных ε_пр деформаций бруса (элемента):

Порядок определения коэффициента поперечной деформации:

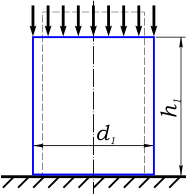
Рассмотрим деформацию элемента цилиндрической формы (рис. 1) который до нагружения имеет следующие размеры:

Рис. 1. Размеры бруса до нагружения

здесь
h₀ — начальный продольный размер;
d₀ — начальный поперечный размер (в данном случае — диаметр).

После нагружения некоторой продольной системой сил (например сжимающей) брус изменит свои размеры, продольный размер уменьшится (т.к. сжатие) а поперечный наоборот увеличится (рис. 2).

Рис. 2. Размеры бруса после деформации

Полученные в результате деформации размеры обозначим соответственно h₁ и d₁, где:

h₁=h₀ — Δh

d₁=d₀ + Δd

здесь Δh и Δd соответственно абсолютные продольные и поперечные деформации.

Отношение абсолютных деформаций к соответствующим начальным размерам покажет относительные деформации:

а их отношение в свою очередь определяет коэффициент Пуассона материала бруса.

Значение коэффициента принимается по модулю, т.к. продольная и поперечная деформации всегда имеют противоположные знаки (удлинение бруса приводит к его сужению и наоборот).

Лабораторная работа по определению коэффициента поперечной деформации.

В таблице 1 приведены сравнительные значения коэффициента для некоторых материалов.

Таблица 1

Материал	Коэффициент Пуассона, ν
Сталь	0,3
Чугун	0,25
Медь	0,32
Титан	0,3
Алюминий	0,3
Бетон	0,16

Для всех существующих материалов его значение находится в пределах от 0 до 0,5.

Минимальное значение коэффициента свойственно хрупким материалам, максимальное — эластичным.

Для сталей в зависимости от марки, коэффициент Пуассона принимает значения от 0,27 до 0,32.

Модуль упругости I рода (модуль Юнга) >
Лабораторные работы >
Примеры решения задач >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Источник

Коэффициент Пуассона (обозначается как или ) — величина отношения относительного поперечного сжатия к относительному продольному растяжению. Этот коэффициент зависит не от размеров тела, а от природы материала, из которого изготовлен образец. Коэффициент Пуассона и модуль Юнга полностью характеризуют упругие свойства изотропного материала^[1]. Безразмерен, но может быть указан в относительных единицах: мм/мм, м/м.

Содержание

1 Детальное определение
2 Ауксетики
3 Значения коэффициента Пуассона
- 3.1 Грунты
- 3.2 Изотропные материалы
4 Примечания
5 См. также

Детальное определение

Однородный стержень до и после приложения к нему растягивающих сил.

Пусть и длина и поперечный размер образца до деформации, а ${displaystyle l^{prime }}$ и ${displaystyle d^{prime }}$ — длина и поперечный размер образца после деформации. Тогда продольным удлинением называют величину, равную ${displaystyle (l^{prime }-l)}$ , а поперечным сжатием — величину, равную ${displaystyle -(d^{prime }-d)}$ . Если ${displaystyle (l^{prime }-l)}$ обозначить как Delta l , а ${displaystyle (d^{prime }-d)}$ как , то относительное продольное удлинение будет равно величине ${displaystyle {frac {Delta l}{l}}}$ , а относительное поперечное сжатие — величине ${displaystyle -{frac {Delta d}{d}}}$ . Тогда в принятых обозначениях коэффициент Пуассона имеет вид:

${displaystyle mu =-{frac {Delta d}{d}}{frac {l}{Delta l}}.}$

Обычно при приложении к стержню растягивающих усилий он удлиняется в продольном направлении и сокращается в поперечных направлениях. Таким образом, в подобных случаях выполнятся ${displaystyle {frac {Delta l}{l}}>0}$ и ${displaystyle {frac {Delta d}{d}}<0}$ , так что коэффициент Пуассона положителен. Как показывает опыт, при сжатии коэффициент Пуассона имеет то же значение, что и при растяжении.

Ауксетики

Отрицательным коэффициентом Пуассона обладают многие анизотропные кристаллы^[2], так как коэффициент Пуассона для таких материалов зависит от угла ориентации кристаллической структуры относительно оси растяжения. Отрицательный коэффициент обнаруживается у таких материалов, как литий (минимальное значение равно −0,54), натрий (−0,44), калий (−0,42), кальций (−0,27), медь (−0,13) и других. 67 % кубических кристаллов из таблицы Менделеева имеют отрицательный коэффициент Пуассона.

Значения коэффициента Пуассона

Грунты

Коэффициент Пуассона для грунтов^[3]:

Грунты	Коэффициент поперечной деформации ν
Крупнообломочные грунты	0,27
Пески и супеси	0,30 — 0,35
Суглинки	0,35 — 0,37
Глины при показателе текучести I_L
I_L < 0 0 < I_L <= 0,25 0,25 < I_L <= 1	0,20 — 0,30 0,30 — 0,38 0,38 — 0,45
Примечание. Меньшие значения ν применяют при большей плотности грунта.

Изотропные материалы

Материал	Коэффициент Пуассона μ
Бетон	0,2 по СНиП, в расчётах возможно снижение до 0,15—0,17
Алюминий	0,34
Вольфрам	0,29
Германий	0,31
Дюралюминий	0,34
Иридий	0,26
Кварцевое стекло	0,17
Константан	0,33
Латунь	0,35
Манганин	0,33
Медь	0,35
Органическое стекло	0,35
Полистирол	0,35
Свинец	0,44
Олово	0,44
Серебро	0,37
Серый чугун	0,22
Сталь	0,25
Стекло	0,25
Фарфор	0,23

Примечания

↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит, 2005. — Т. I. Механика. — С. 414. — 560 с. — ISBN 5-9221-0225-7.
↑ Гольдштейн Р. В., Городцов, В. А., Лисовенко Д. С. «Ауксетическая механика кристаллических материалов». Известия РАН, МТТ, 2010 г., № 4, С. 43—62.
↑ Таблица 5.10, СП 22.13330.2011 Основания зданий и сооружений.

См. также

Модуль упругости
Модуль Юнга

Источник

From Wikipedia, the free encyclopedia

Poisson’s ratio of a material defines the ratio of transverse strain (x direction) to the axial strain (y direction)

In materials science and solid mechanics, Poisson’s ratio (nu) is a measure of the Poisson effect, the deformation (expansion or contraction) of a material in directions perpendicular to the specific direction of loading. The value of Poisson’s ratio is the negative of the ratio of transverse strain to axial strain. For small values of these changes, is the amount of transversal elongation divided by the amount of axial compression. Most materials have Poisson’s ratio values ranging between 0.0 and 0.5. For soft materials,^[1] such as rubber, where the bulk modulus is much higher than the shear modulus, Poisson’s ratio is near 0.5. For open-cell polymer foams, Poisson’s ratio is near zero, since the cells tend to collapse in compression. Many typical solids have Poisson’s ratios in the range of 0.2–0.3. The ratio is named after the French mathematician and physicist Siméon Poisson.

Origin[edit]

Poisson’s ratio is a measure of the Poisson effect, the phenomenon in which a material tends to expand in directions perpendicular to the direction of compression. Conversely, if the material is stretched rather than compressed, it usually tends to contract in the directions transverse to the direction of stretching. It is a common observation when a rubber band is stretched, it becomes noticeably thinner. Again, the Poisson ratio will be the ratio of relative contraction to relative expansion and will have the same value as above. In certain rare cases,^[2] a material will actually shrink in the transverse direction when compressed (or expand when stretched) which will yield a negative value of the Poisson ratio.

The Poisson’s ratio of a stable, isotropic, linear elastic material must be between −1.0 and +0.5 because of the requirement for Young’s modulus, the shear modulus and bulk modulus to have positive values.^[3] Most materials have Poisson’s ratio values ranging between 0.0 and 0.5. A perfectly incompressible isotropic material deformed elastically at small strains would have a Poisson’s ratio of exactly 0.5. Most steels and rigid polymers when used within their design limits (before yield) exhibit values of about 0.3, increasing to 0.5 for post-yield deformation which occurs largely at constant volume.^[4] Rubber has a Poisson ratio of nearly 0.5. Cork’s Poisson ratio is close to 0, showing very little lateral expansion when compressed and glass is between 0.18 and 0.30. Some materials, e.g. some polymer foams, origami folds,^[5]^[6] and certain cells can exhibit negative Poisson’s ratio, and are referred to as auxetic materials. If these auxetic materials are stretched in one direction, they become thicker in the perpendicular direction. In contrast, some anisotropic materials, such as carbon nanotubes, zigzag-based folded sheet materials,^[7]^[8] and honeycomb auxetic metamaterials^[9] to name a few, can exhibit one or more Poisson’s ratios above 0.5 in certain directions.

Assuming that the material is stretched or compressed in only one direction (the x axis in the diagram below):

$nu =-{frac {dvarepsilon _{{mathrm {trans}}}}{dvarepsilon _{{mathrm {axial}}}}}=-{frac {dvarepsilon _{{mathrm {y}}}}{dvarepsilon _{{mathrm {x}}}}}=-{frac {dvarepsilon _{{mathrm {z}}}}{dvarepsilon _{{mathrm {x}}}}}$

where

and positive strain indicates extension and negative strain indicates contraction.

Poisson’s ratio from geometry changes[edit]

Length change[edit]

Figure 1: A cube with sides of length L of an isotropic linearly elastic material subject to tension along the x axis, with a Poisson’s ratio of 0.5. The green cube is unstrained, the red is expanded in the x direction by ΔL due to tension, and contracted in the y and z directions by Δ’L.

For a cube stretched in the x-direction (see Figure 1) with a length increase of Delta L in the x direction, and a length decrease of in the y and z directions, the infinitesimal diagonal strains are given by

${displaystyle dvarepsilon _{x}={frac {dx}{x}}qquad dvarepsilon _{y}={frac {dy}{y}}qquad dvarepsilon _{z}={frac {dz}{z}}.}$

If Poisson’s ratio is constant through deformation, integrating these expressions and using the definition of Poisson’s ratio gives

${displaystyle -nu int _{L}^{L+Delta L}{frac {dx}{x}}=int _{L}^{L+Delta L'}{frac {dy}{y}}=int _{L}^{L+Delta L'}{frac {dz}{z}}.}$

Solving and exponentiating, the relationship between Delta L and is then

${displaystyle left(1+{frac {Delta L}{L}}right)^{-nu }=1+{frac {Delta L'}{L}}.}$

For very small values of Delta L and , the first-order approximation yields:

${displaystyle nu approx -{frac {Delta L'}{Delta L}}.}$

Volumetric change[edit]

The relative change of volume ΔV/V of a cube due to the stretch of the material can now be calculated. Using ${displaystyle V=L^{3}}$ and ${displaystyle V+Delta V=(L+Delta L)left(L+Delta L'right)^{2}}$ :

${displaystyle {frac {Delta V}{V}}=left(1+{frac {Delta L}{L}}right)left(1+{frac {Delta L'}{L}}right)^{2}-1}$

Using the above derived relationship between Delta L and :

${displaystyle {frac {Delta V}{V}}=left(1+{frac {Delta L}{L}}right)^{1-2nu }-1}$

and for very small values of Delta L and , the first-order approximation yields:

${frac {Delta V}{V}}approx (1-2nu ){frac {Delta L}{L}}$

For isotropic materials we can use Lamé’s relation^[10]

$nu approx {frac {1}{2}}-{frac {E}{6K}}$

where is bulk modulus and is Young’s modulus.

Width change[edit]

Figure 2: Comparison between the two formulas, one for small deformations, another for large deformations

If a rod with diameter (or width, or thickness) d and length L is subject to tension so that its length will change by ΔL then its diameter d will change by:

${displaystyle {Delta d over d}=-nu {frac {Delta L}{L}}}$

The above formula is true only in the case of small deformations; if deformations are large then the following (more precise) formula can be used:

${displaystyle Delta d=-dleft(1-{left(1+{frac {Delta L}{L}}right)}^{-nu }right)}$

where

The value is negative because it decreases with increase of length

Characteristic materials[edit]

Isotropic[edit]

For a linear isotropic material subjected only to compressive (i.e. normal) forces, the deformation of a material in the direction of one axis will produce a deformation of the material along the other axis in three dimensions. Thus it is possible to generalize Hooke’s Law (for compressive forces) into three dimensions:

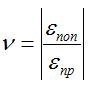
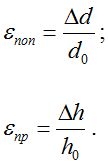
${displaystyle varepsilon _{xx}={frac {1}{E}}left[sigma _{xx}-nu left(sigma _{yy}+sigma _{zz}right)right]}$

${displaystyle varepsilon _{yy}={frac {1}{E}}left[sigma _{yy}-nu left(sigma _{xx}+sigma _{zz}right)right]}$

${displaystyle varepsilon _{zz}={frac {1}{E}}left[sigma _{zz}-nu left(sigma _{xx}+sigma _{yy}right)right]}$

where:

these equations can be all synthesized in the following:

${displaystyle varepsilon _{ii}={frac {1}{E}}left[sigma _{ii}(1+nu )-nu sum _{k}sigma _{kk}right]}$

In the most general case, also shear stresses will hold as well as normal stresses, and the full generalization of Hooke’s law is given by:

${displaystyle varepsilon _{ij}={frac {1}{E}}left[sigma _{ij}(1+nu )-nu delta _{ij}sum _{k}sigma _{kk}right]}$

where $delta _{ij}$ is the Kronecker delta. The Einstein notation is usually adopted:

${displaystyle sigma _{kk}equiv sum _{l}delta _{kl}sigma _{kl}}$

to write the equation simply as:

${displaystyle varepsilon _{ij}={frac {1}{E}}left[sigma _{ij}(1+nu )-nu delta _{ij}sigma _{kk}right]}$

Anisotropic[edit]

For anisotropic materials, the Poisson ratio depends on the direction of extension and transverse deformation

${displaystyle nu (mathbf {n} ,mathbf {m} )=-Eleft(mathbf {n} right)s_{ijalpha beta }n_{i}n_{j}m_{alpha }m_{beta }}$

${displaystyle E^{-1}(mathbf {n} )=s_{ijalpha beta }n_{i}n_{j}n_{alpha }n_{beta }}$

Here is Poisson’s ratio, is Young’s modulus, is unit vector directed along the direction of extension, is unit vector directed perpendicular to the direction of extension. Poisson’s ratio has a different number of special directions depending on the type of anisotropy.^[11]^[12]

Orthotropic[edit]

Orthotropic materials have three mutually perpendicular planes of symmetry in their material properties. An example is wood, which is most stiff (and strong) along the grain, and less so in the other directions.

Then Hooke’s law can be expressed in matrix form as^[13]^[14]

${displaystyle {begin{bmatrix}epsilon _{xx}\epsilon _{yy}\epsilon _{zz}\2epsilon _{yz}\2epsilon _{zx}\2epsilon _{xy}end{bmatrix}}={begin{bmatrix}{tfrac {1}{E_{x}}}&-{tfrac {nu _{yx}}{E_{y}}}&-{tfrac {nu _{zx}}{E_{z}}}&0&0&0\-{tfrac {nu _{xy}}{E_{x}}}&{tfrac {1}{E_{y}}}&-{tfrac {nu _{zy}}{E_{z}}}&0&0&0\-{tfrac {nu _{xz}}{E_{x}}}&-{tfrac {nu _{yz}}{E_{y}}}&{tfrac {1}{E_{z}}}&0&0&0\0&0&0&{tfrac {1}{G_{yz}}}&0&0\0&0&0&0&{tfrac {1}{G_{zx}}}&0\0&0&0&0&0&{tfrac {1}{G_{xy}}}\end{bmatrix}}{begin{bmatrix}sigma _{xx}\sigma _{yy}\sigma _{zz}\sigma _{yz}\sigma _{zx}\sigma _{xy}end{bmatrix}}}$

where

The Poisson ratio of an orthotropic material is different in each direction (x, y and z). However, the symmetry of the stress and strain tensors implies that not all the six Poisson’s ratios in the equation are independent. There are only nine independent material properties: three elastic moduli, three shear moduli, and three Poisson’s ratios. The remaining three Poisson’s ratios can be obtained from the relations

${displaystyle {frac {nu _{yx}}{E_{y}}}={frac {nu _{xy}}{E_{x}}}~,qquad {frac {nu _{zx}}{E_{z}}}={frac {nu _{xz}}{E_{x}}}~,qquad {frac {nu _{yz}}{E_{y}}}={frac {nu _{zy}}{E_{z}}}}$

From the above relations we can see that if ${displaystyle E_{x}>E_{y}}$ then ${displaystyle nu _{xy}>nu _{yx}}$ . The larger Poisson’s ratio (in this case $nu_{xy}$ ) is called the major Poisson’s ratio while the smaller one (in this case ${displaystyle nu _{yx}}$ ) is called the minor Poisson’s ratio. We can find similar relations between the other Poisson’s ratios.

Transversely isotropic[edit]

Transversely isotropic materials have a plane of isotropy in which the elastic properties are isotropic. If we assume that this plane of isotropy is y-z , then Hooke’s law takes the form^[15]

${displaystyle {begin{bmatrix}epsilon _{xx}\epsilon _{yy}\epsilon _{zz}\2epsilon _{yz}\2epsilon _{zx}\2epsilon _{xy}end{bmatrix}}={begin{bmatrix}{tfrac {1}{E_{x}}}&-{tfrac {nu _{yx}}{E_{y}}}&-{tfrac {nu _{zx}}{E_{z}}}&0&0&0\-{tfrac {nu _{xy}}{E_{x}}}&{tfrac {1}{E_{y}}}&-{tfrac {nu _{zy}}{E_{z}}}&0&0&0\-{tfrac {nu _{xz}}{E_{x}}}&-{tfrac {nu _{yz}}{E_{y}}}&{tfrac {1}{E_{z}}}&0&0&0\0&0&0&{tfrac {1}{G_{rm {yz}}}}&0&0\0&0&0&0&{tfrac {1}{G_{rm {zx}}}}&0\0&0&0&0&0&{tfrac {1}{G_{rm {xy}}}}\end{bmatrix}}{begin{bmatrix}sigma _{xx}\sigma _{yy}\sigma _{zz}\sigma _{yz}\sigma _{zx}\sigma _{xy}end{bmatrix}}}$

where we have used the plane of isotropy y-z to reduce the number of constants, i.e., $E_{y}=E_{z},~nu _{{xy}}=nu _{{xz}},~nu _{{yx}}=nu _{{zx}}$ .

The symmetry of the stress and strain tensors implies that

${displaystyle {frac {nu _{xy}}{E_{x}}}={frac {nu _{yx}}{E_{y}}}~,~~nu _{yz}=nu _{zy}~.}$

This leaves us with six independent constants ${displaystyle E_{x},E_{y},G_{xy},G_{yz},nu _{xy},nu _{yz}}$ . However, transverse isotropy gives rise to a further constraint between ${displaystyle G_{yz}}$ and ${displaystyle E_{y},nu _{yz}}$ which is

${displaystyle G_{yz}={frac {E_{y}}{2(1+nu _{yz})}}~.}$

Therefore, there are five independent elastic material properties two of which are Poisson’s ratios. For the assumed plane of symmetry, the larger of $nu_{xy}$ and ${displaystyle nu _{yx}}$ is the major Poisson’s ratio. The other major and minor Poisson’s ratios are equal.

Poisson’s ratio values for different materials[edit]

Influences of selected glass component additions on Poisson’s ratio of a specific base glass.^[16]

Material	Poisson’s ratio
rubber	0.4999^[17]
gold	0.42–0.44
saturated clay	0.40–0.49
magnesium	0.252–0.289
titanium	0.265–0.34
copper	0.33
aluminium-alloy	0.32
clay	0.30–0.45
stainless steel	0.30–0.31
steel	0.27–0.30
cast iron	0.21–0.26
sand	0.20–0.455
concrete	0.1–0.2
glass	0.18–0.3
metallic glasses	0.276–0.409^[18]
foam	0.10–0.50
cork	0.0

Material	Plane of symmetry	$nu _{{{rm {xy}}}}$	$nu _{{{rm {yx}}}}$	$nu _{{{rm {yz}}}}$	$nu _{{{rm {zy}}}}$	$nu _{{{rm {zx}}}}$	$nu _{{{rm {xz}}}}$
Nomex honeycomb core	, ribbon in direction	0.49	0.69	0.01	2.75	3.88	0.01
glass fiber-epoxy resin		0.29	0.32	0.06	0.06	0.32

Negative Poisson’s ratio materials[edit]

Some materials known as auxetic materials display a negative Poisson’s ratio. When subjected to positive strain in a longitudinal axis, the transverse strain in the material will actually be positive (i.e. it would increase the cross sectional area). For these materials, it is usually due to uniquely oriented, hinged molecular bonds. In order for these bonds to stretch in the longitudinal direction, the hinges must ‘open’ in the transverse direction, effectively exhibiting a positive strain.^[19]
This can also be done in a structured way and lead to new aspects in material design as for mechanical metamaterials.

Studies have shown that certain solid wood types display negative Poisson’s ratio exclusively during a compression creep test.^[20]^[21] Initially, the compression creep test shows positive Poisson’s ratios, but gradually decreases until it reaches negative values. Consequently, this also shows that Poisson’s ratio for wood is time-dependent during constant loading, meaning that the strain in the axial and transverse direction do not increase in the same rate.

Media with engineered microstructure may exhibit negative Poisson’s ratio. In a simple case auxeticity is obtained removing material and creating a periodic porous media.^[22] Lattices can reach lower values of Poisson’s ratio,^[23] which can be indefinitely close to the limiting value −1 in the isotropic case.^[24]

More than three hundred crystalline materials have negative Poisson’s ratio.^[25]^[26]^[27] For example, Li, Na, K, Cu, Rb, Ag, Fe, Ni, Co, Cs, Au, Be, Ca, Zn Sr, Sb, MoS $_{2}$ and other.

Poisson function[edit]

At finite strains, the relationship between the transverse and axial strains ${displaystyle varepsilon _{text{trans}}}$ and ${displaystyle varepsilon _{text{axial}}}$ is typically not well described by the Poisson ratio. In fact, the Poisson ratio is often considered a function of the applied strain in the large strain regime. In such instances, the Poisson ratio is replaced by the Poisson function, for which there are several competing definitions.^[28] Defining the transverse stretch ${displaystyle lambda _{text{trans}}=varepsilon _{text{trans}}+1}$ and axial stretch ${displaystyle lambda _{text{axial}}=varepsilon _{text{axial}}+1}$ , where the transverse stretch is a function of the axial stretch (i.e., ${displaystyle lambda _{text{trans}}=lambda _{text{trans}}(lambda _{text{axial}})}$ ) the most common are the Hencky, Biot, Green, and Almansi functions

${displaystyle {begin{aligned}nu ^{text{Hencky}}&=-{frac {ln lambda _{text{trans}}}{ln lambda _{text{axial}}}}\[6pt]nu ^{text{Biot}}&={frac {1-lambda _{text{trans}}}{lambda _{text{axial}}-1}}\[6pt]nu ^{text{Green}}&={frac {1-lambda _{text{trans}}^{2}}{lambda _{text{axial}}^{2}-1}}\[6pt]nu ^{text{Almansi}}&={frac {lambda _{text{trans}}^{-2}-1}{1-lambda _{text{axial}}^{-2}}}end{aligned}}}$

Applications of Poisson’s effect[edit]

One area in which Poisson’s effect has a considerable influence is in pressurized pipe flow. When the air or liquid inside a pipe is highly pressurized it exerts a uniform force on the inside of the pipe, resulting in a hoop stress within the pipe material. Due to Poisson’s effect, this hoop stress will cause the pipe to increase in diameter and slightly decrease in length. The decrease in length, in particular, can have a noticeable effect upon the pipe joints, as the effect will accumulate for each section of pipe joined in series. A restrained joint may be pulled apart or otherwise prone to failure.^{[citation needed]}

Another area of application for Poisson’s effect is in the realm of structural geology. Rocks, like most materials, are subject to Poisson’s effect while under stress. In a geological timescale, excessive erosion or sedimentation of Earth’s crust can either create or remove large vertical stresses upon the underlying rock. This rock will expand or contract in the vertical direction as a direct result of the applied stress, and it will also deform in the horizontal direction as a result of Poisson’s effect. This change in strain in the horizontal direction can affect or form joints and dormant stresses in the rock.^[29]

Although cork was historically chosen to seal wine bottle for other reasons (including its inert nature, impermeability, flexibility, sealing ability, and resilience),^[30] cork’s Poisson’s ratio of zero provides another advantage. As the cork is inserted into the bottle, the upper part which is not yet inserted does not expand in diameter as it is compressed axially. The force needed to insert a cork into a bottle arises only from the friction between the cork and the bottle due to the radial compression of the cork. If the stopper were made of rubber, for example, (with a Poisson’s ratio of about 1/2), there would be a relatively large additional force required to overcome the radial expansion of the upper part of the rubber stopper.

Most car mechanics are aware that it is hard to pull a rubber hose (e.g. a coolant hose) off a metal pipe stub, as the tension of pulling causes the diameter of the hose to shrink, gripping the stub tightly. Hoses can more easily be pushed off stubs instead using a wide flat blade.

References[edit]

^ For soft materials, the bulk modulus (K) is typically large compared to the shear modulus (G) so that they can be regarded as incompressible, since it is easier to change shape than to compress. This results in the Young’s modulus (E) being and hence .Jastrzebski, D. (1959). Nature and Properties of Engineering Materials (Wiley International ed.). John Wiley & Sons, Inc.
^ Lakes, R. and Wojciechowski, K.W., 2008. Negative compressibility, negative Poisson’s ratio, and stability. Physica Status Solidi B, 245(3), pp.545-551.
^ Gercek, H. (January 2007). «Poisson’s ratio values for rocks». International Journal of Rock Mechanics and Mining Sciences. 44 (1): 1–13. doi:10.1016/j.ijrmms.2006.04.011.
^ Park, RJT. Seismic Performance of Steel-Encased Concrete Piles
^ Mark, Schenk (2011). Folded Shell Structures, PhD Thesis (PDF). University of Cambridge, Clare College.
^ Wei, Z. Y.; Guo, Z. V.; Dudte, L.; Liang, H. Y.; Mahadevan, L. (2013-05-21). «Geometric Mechanics of Periodic Pleated Origami» (PDF). Physical Review Letters. 110 (21): 215501. arXiv:1211.6396. Bibcode:2013PhRvL.110u5501W. doi:10.1103/PhysRevLett.110.215501. PMID 23745895. S2CID 9145953.
^ Eidini, Maryam; Paulino, Glaucio H. (2015). «Unraveling metamaterial properties in zigzag-base folded sheets». Science Advances. 1 (8): e1500224. arXiv:1502.05977. Bibcode:2015SciA….1E0224E. doi:10.1126/sciadv.1500224. ISSN 2375-2548. PMC 4643767. PMID 26601253.
^ Eidini, Maryam (2016). «Zigzag-base folded sheet cellular mechanical metamaterials». Extreme Mechanics Letters. 6: 96–102. arXiv:1509.08104. doi:10.1016/j.eml.2015.12.006. S2CID 118424595.
^ Mousanezhad, Davood; Babaee, Sahab; Ebrahimi, Hamid; Ghosh, Ranajay; Hamouda, Abdelmagid Salem; Bertoldi, Katia; Vaziri, Ashkan (2015-12-16). «Hierarchical honeycomb auxetic metamaterials». Scientific Reports. 5: 18306. Bibcode:2015NatSR…518306M. doi:10.1038/srep18306. ISSN 2045-2322. PMC 4680941. PMID 26670417.
^ Mott, P. H.; Roland, C. M. (3 April 2012). «Limits to Poisson’s ratio in isotropic materials—general result for arbitrary deformation». Physica Scripta. Chemistry Division, Naval Research Laboratory. 87 (5): 055404. arXiv:1204.3859. doi:10.1088/0031-8949/87/05/055404. S2CID 55920779.
^ Epishin, A.I.; Lisovenko, D.S. (2016). «Extreme values of Poisson’s ratio of cubic crystals». Technical Physics. 61 (10): 1516–1524. Bibcode:2016JTePh..61.1516E. doi:10.1016/j.mechmat.2019.03.017. S2CID 140493258.
^ Gorodtsov, V.A.; Lisovenko, D.S. (2019). «Extreme values of Young’s modulus and Poisson’s ratio of hexagonal crystals». Mechanics of Materials. 134: 1–8. doi:10.1016/j.mechmat.2019.03.017. S2CID 140493258.
^ Boresi, A. P, Schmidt, R. J. and Sidebottom, O. M., 1993, Advanced Mechanics of Materials, Wiley.
^ Lekhnitskii, S. G. (1981). Theory of elasticity of an anisotropic elastic body. Mir Publishing. p. 36.
^ Tan, S. C., 1994, Stress Concentrations in Laminated Composites, Technomic Publishing Company, Lancaster, PA.
^ Fluegel, Alexander. «Poisson’s Ratio Calculation for Glasses». www.glassproperties.com. Archived from the original on 23 October 2017. Retrieved 28 April 2018.
^ P. H. Mott; C. M. Roland (20 October 2009). «Limits to Poisson’s ratio in isotropic materials» (PDF). Physical Review B. 80 (13): 132104. arXiv:0909.4697. Bibcode:2009PhRvB..80m2104M. doi:10.1103/PhysRevB.80.132104. Archived (PDF) from the original on 2014-10-31. Retrieved 2014-09-24.{{cite journal}}: CS1 maint: multiple names: authors list (link)
^ Journal of Applied Physics 110, 053521 (2011)
^ Lakes, Rod. «Negative Poisson’s ratio». silver.neep.wisc.edu. Archived from the original on 16 February 2018. Retrieved 28 April 2018.
^ Ozyhar, Tomasz; Hering, Stefan; Niemz, Peter (March 2013). «Viscoelastic characterization of wood: Time dependence of the orthotropic compliance in tension and compression». Journal of Rheology. 57 (2): 699–717. Bibcode:2013JRheo..57..699O. doi:10.1122/1.4790170. ISSN 0148-6055.
^ Jiang, Jiali; Erik Valentine, Bachtiar; Lu, Jianxiong; Niemz, Peter (2016-11-01). «Time dependence of the orthotropic compression Young’s moduli and Poisson’s ratios of Chinese fir wood» (PDF). Holzforschung. 70 (11): 1093–1101. doi:10.1515/hf-2016-0001. hdl:20.500.11850/122097. ISSN 1437-434X. S2CID 137799672.
^ Carta, Giorgio; Brun, Michele; Baldi, Antonio (2016). «Design of a porous material with isotropic negative Poisson’s ratio». Mechanics of Materials. 97: 67–75. doi:10.1016/j.mechmat.2016.02.012.
^ Cabras, Luigi; Brun, Michele (2016). «A class of auxetic three-dimensional lattices». Journal of the Mechanics and Physics of Solids. 91: 56–72. arXiv:1506.04919. Bibcode:2016JMPSo..91…56C. doi:10.1016/j.jmps.2016.02.010. S2CID 85547530.
^ Cabras, Luigi; Brun, Michele (2014). «Auxetic two-dimensional lattices with Poisson’s ratio arbitrarily close to -1». Proceedings of the Royal Society A. 470 (2172): 20140538. arXiv:1407.5679. Bibcode:2014RSPSA.47040538C. doi:10.1098/rspa.2014.0538. S2CID 119321604.
^ Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S. (2013). «Classification of cubic auxetics». Physica Status Solidi B. 250 (10): 2038–2043. doi:10.1002/pssb.201384233. S2CID 117802510.
^ Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S. (2011). «Variability of elastic properties of hexagonal auxetics». Doklady Physics. 56 (12): 602–605. doi:10.1134/S1028335811120019. S2CID 120998323.
^ Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S.; Volkov, M.A. (2015). «Auxetics among 6-constant tetragonal crystals». Letters on Materials. 5 (4): 409–413. doi:10.22226/2410-3535-2015-4-409-413.
^ Mihai, L. A.; Goriely, A. (2017-11-03). «How to characterize a nonlinear elastic material? A review on nonlinear constitutive parameters in isotropic finite elasticity». Proceedings of the Royal Society A. 473 (2207): 20170607. Bibcode:2017RSPSA.47370607M. doi:10.1098/rspa.2017.0607. PMC 5719638. PMID 29225507.
^ «Lecture Notes in Structural Geology – Effective Stress». Retrieved 2019-07-03.
^ Silva, et al. «Cork: properties, capabilities and applications» Archived 2017-08-09 at the Wayback Machine, Retrieved May 4, 2017

External links[edit]

Meaning of Poisson’s ratio
Negative Poisson’s ratio materials
More on negative Poisson’s ratio materials (auxetic) Archived 2018-02-08 at the Wayback Machine

Conversion formulae
Homogeneous isotropic linear elastic materials have their elastic properties uniquely determined by any two moduli among these; thus, given any two, any other of the elastic moduli can be calculated according to these formulas, provided both for 3D materials (first part of the table) and for 2D materials (second part).
3D formulae							Notes
			${tfrac {3K(3K-E)}{9K-E}}$	${tfrac {3KE}{9K-E}}$	${tfrac {3K-E}{6K}}$	${tfrac {3K(3K+E)}{9K-E}}$
		${tfrac {9K(K-lambda )}{3K-lambda }}$		${tfrac {3(K-lambda )}{2}}$	${tfrac {lambda }{3K-lambda }}$
		${tfrac {9KG}{3K+G}}$	$K-{tfrac {2G}{3}}$		${tfrac {3K-2G}{2(3K+G)}}$	$K+{tfrac {4G}{3}}$
			${tfrac {3Knu }{1+nu }}$	${tfrac {3K(1-2nu )}{2(1+nu )}}$		${tfrac {3K(1-nu )}{1+nu }}$
		${tfrac {9K(M-K)}{3K+M}}$	${tfrac {3K-M}{2}}$	${tfrac {3(M-K)}{4}}$	${tfrac {3K-M}{3K+M}}$
	${tfrac {E+3lambda +R}{6}}$			${tfrac {E-3lambda +R}{4}}$	${tfrac {2lambda }{E+lambda +R}}$	${tfrac {E-lambda +R}{2}}$	$R={sqrt {E^{2}+9lambda ^{2}+2Elambda }}$
	${tfrac {EG}{3(3G-E)}}$		${tfrac {G(E-2G)}{3G-E}}$		${tfrac {E}{2G}}-1$	${tfrac {G(4G-E)}{3G-E}}$
	${tfrac {E}{3(1-2nu )}}$		${tfrac {Enu }{(1+nu )(1-2nu )}}$	${tfrac {E}{2(1+nu )}}$		${tfrac {E(1-nu )}{(1+nu )(1-2nu )}}$
	${tfrac {3M-E+S}{6}}$		${tfrac {M-E+S}{4}}$	${tfrac {3M+E-S}{8}}$	${tfrac {E-M+S}{4M}}$		$S=pm {sqrt {E^{2}+9M^{2}-10EM}}$ There are two valid solutions. The plus sign leads to . The minus sign leads to .
	$lambda +{tfrac {2G}{3}}$	${tfrac {G(3lambda +2G)}{lambda +G}}$			${tfrac {lambda }{2(lambda +G)}}$
	${tfrac {lambda (1+nu )}{3nu }}$	${tfrac {lambda (1+nu )(1-2nu )}{nu }}$		${tfrac {lambda (1-2nu )}{2nu }}$		${tfrac {lambda (1-nu )}{nu }}$	Cannot be used when
	${tfrac {M+2lambda }{3}}$	${tfrac {(M-lambda )(M+2lambda )}{M+lambda }}$		${tfrac {M-lambda }{2}}$	${tfrac {lambda }{M+lambda }}$
	${tfrac {2G(1+nu )}{3(1-2nu )}}$		${tfrac {2Gnu }{1-2nu }}$			${tfrac {2G(1-nu )}{1-2nu }}$
	$M-{tfrac {4G}{3}}$	${tfrac {G(3M-4G)}{M-G}}$			${tfrac {M-2G}{2M-2G}}$
	${tfrac {M(1+nu )}{3(1-nu )}}$	${tfrac {M(1+nu )(1-2nu )}{1-nu }}$	${tfrac {Mnu }{1-nu }}$	${tfrac {M(1-2nu )}{2(1-nu )}}$
2D formulae	${displaystyle K_{mathrm {2D} }=,}$	${displaystyle E_{mathrm {2D} }=,}$	${displaystyle lambda _{mathrm {2D} }=,}$	${displaystyle G_{mathrm {2D} }=,}$	${displaystyle nu _{mathrm {2D} }=,}$	${displaystyle M_{mathrm {2D} }=,}$	Notes
${displaystyle (K_{mathrm {2D} },,E_{mathrm {2D} })}$			${displaystyle {tfrac {2K_{mathrm {2D} }(2K_{mathrm {2D} }-E_{mathrm {2D} })}{4K_{mathrm {2D} }-E_{mathrm {2D} }}}}$	${displaystyle {tfrac {K_{mathrm {2D} }E_{mathrm {2D} }}{4K_{mathrm {2D} }-E_{mathrm {2D} }}}}$	${displaystyle {tfrac {2K_{mathrm {2D} }-E_{mathrm {2D} }}{2K_{mathrm {2D} }}}}$	${displaystyle {tfrac {4K_{mathrm {2D} }^{2}}{4K_{mathrm {2D} }-E_{mathrm {2D} }}}}$
${displaystyle (K_{mathrm {2D} },,lambda _{mathrm {2D} })}$		${displaystyle {tfrac {4K_{mathrm {2D} }(K_{mathrm {2D} }-lambda _{mathrm {2D} })}{2K_{mathrm {2D} }-lambda _{mathrm {2D} }}}}$		${displaystyle K_{mathrm {2D} }-lambda _{mathrm {2D} }}$	${displaystyle {tfrac {lambda _{mathrm {2D} }}{2K_{mathrm {2D} }-lambda _{mathrm {2D} }}}}$	${displaystyle 2K_{mathrm {2D} }-lambda _{mathrm {2D} }}$
${displaystyle (K_{mathrm {2D} },,G_{mathrm {2D} })}$		${displaystyle {tfrac {4K_{mathrm {2D} }G_{mathrm {2D} }}{K_{mathrm {2D} }+G_{mathrm {2D} }}}}$	${displaystyle K_{mathrm {2D} }-G_{mathrm {2D} }}$		${displaystyle {tfrac {K_{mathrm {2D} }-G_{mathrm {2D} }}{K_{mathrm {2D} }+G_{mathrm {2D} }}}}$	${displaystyle K_{mathrm {2D} }+G_{mathrm {2D} }}$
${displaystyle (K_{mathrm {2D} },,nu _{mathrm {2D} })}$		${displaystyle 2K_{mathrm {2D} }(1-nu _{mathrm {2D} }),}$	${displaystyle {tfrac {2K_{mathrm {2D} }nu _{mathrm {2D} }}{1+nu _{mathrm {2D} }}}}$	${displaystyle {tfrac {K_{mathrm {2D} }(1-nu _{mathrm {2D} })}{1+nu _{mathrm {2D} }}}}$		${displaystyle {tfrac {2K_{mathrm {2D} }}{1+nu _{mathrm {2D} }}}}$
${displaystyle (E_{mathrm {2D} },,G_{mathrm {2D} })}$	${displaystyle {tfrac {E_{mathrm {2D} }G_{mathrm {2D} }}{4G_{mathrm {2D} }-E_{mathrm {2D} }}}}$		${displaystyle {tfrac {2G_{mathrm {2D} }(E_{mathrm {2D} }-2G_{mathrm {2D} })}{4G_{mathrm {2D} }-E_{mathrm {2D} }}}}$		${displaystyle {tfrac {E_{mathrm {2D} }}{2G_{mathrm {2D} }}}-1}$	${displaystyle {tfrac {4G_{mathrm {2D} }^{2}}{4G_{mathrm {2D} }-E_{mathrm {2D} }}}}$
${displaystyle (E_{mathrm {2D} },,nu _{mathrm {2D} })}$	${displaystyle {tfrac {E_{mathrm {2D} }}{2(1-nu _{mathrm {2D} })}}}$		${displaystyle {tfrac {E_{mathrm {2D} }nu _{mathrm {2D} }}{(1+nu _{mathrm {2D} })(1-nu _{mathrm {2D} })}}}$	${displaystyle {tfrac {E_{mathrm {2D} }}{2(1+nu _{mathrm {2D} })}}}$		${displaystyle {tfrac {E_{mathrm {2D} }}{(1+nu _{mathrm {2D} })(1-nu _{mathrm {2D} })}}}$
${displaystyle (lambda _{mathrm {2D} },,G_{mathrm {2D} })}$	${displaystyle lambda _{mathrm {2D} }+G_{mathrm {2D} }}$	${displaystyle {tfrac {4G_{mathrm {2D} }(lambda _{mathrm {2D} }+G_{mathrm {2D} })}{lambda _{mathrm {2D} }+2G_{mathrm {2D} }}}}$			${displaystyle {tfrac {lambda _{mathrm {2D} }}{lambda _{mathrm {2D} }+2G_{mathrm {2D} }}}}$	${displaystyle lambda _{mathrm {2D} }+2G_{mathrm {2D} },}$
${displaystyle (lambda _{mathrm {2D} },,nu _{mathrm {2D} })}$	${displaystyle {tfrac {lambda _{mathrm {2D} }(1+nu _{mathrm {2D} })}{2nu _{mathrm {2D} }}}}$	${displaystyle {tfrac {lambda _{mathrm {2D} }(1+nu _{mathrm {2D} })(1-nu _{mathrm {2D} })}{nu _{mathrm {2D} }}}}$		${displaystyle {tfrac {lambda _{mathrm {2D} }(1-nu _{mathrm {2D} })}{2nu _{mathrm {2D} }}}}$		${displaystyle {tfrac {lambda _{mathrm {2D} }}{nu _{mathrm {2D} }}}}$	Cannot be used when ${displaystyle nu _{mathrm {2D} }=0Leftrightarrow lambda _{mathrm {2D} }=0}$
${displaystyle (G_{mathrm {2D} },,nu _{mathrm {2D} })}$	${displaystyle {tfrac {G_{mathrm {2D} }(1+nu _{mathrm {2D} })}{1-nu _{mathrm {2D} }}}}$	${displaystyle 2G_{mathrm {2D} }(1+nu _{mathrm {2D} }),}$	${displaystyle {tfrac {2G_{mathrm {2D} }nu _{mathrm {2D} }}{1-nu _{mathrm {2D} }}}}$			${displaystyle {tfrac {2G_{mathrm {2D} }}{1-nu _{mathrm {2D} }}}}$
${displaystyle (G_{mathrm {2D} },,M_{mathrm {2D} })}$	${displaystyle M_{mathrm {2D} }-G_{mathrm {2D} }}$	${displaystyle {tfrac {4G_{mathrm {2D} }(M_{mathrm {2D} }-G_{mathrm {2D} })}{M_{mathrm {2D} }}}}$	${displaystyle M_{mathrm {2D} }-2G_{mathrm {2D} },}$		${displaystyle {tfrac {M_{mathrm {2D} }-2G_{mathrm {2D} }}{M_{mathrm {2D} }}}}$

Источник

From Wikipedia, the free encyclopedia

Poisson’s ratio of a material defines the ratio of transverse strain (x direction) to the axial strain (y direction)

Origin[edit]

Assuming that the material is stretched or compressed in only one direction (the x axis in the diagram below):

where

and positive strain indicates extension and negative strain indicates contraction.

Poisson’s ratio from geometry changes[edit]

Length change[edit]

${displaystyle dvarepsilon _{x}={frac {dx}{x}}qquad dvarepsilon _{y}={frac {dy}{y}}qquad dvarepsilon _{z}={frac {dz}{z}}.}$

If Poisson’s ratio is constant through deformation, integrating these expressions and using the definition of Poisson’s ratio gives

${displaystyle -nu int _{L}^{L+Delta L}{frac {dx}{x}}=int _{L}^{L+Delta L'}{frac {dy}{y}}=int _{L}^{L+Delta L'}{frac {dz}{z}}.}$

Solving and exponentiating, the relationship between Delta L and is then

${displaystyle left(1+{frac {Delta L}{L}}right)^{-nu }=1+{frac {Delta L'}{L}}.}$

For very small values of Delta L and , the first-order approximation yields:

${displaystyle nu approx -{frac {Delta L'}{Delta L}}.}$

Volumetric change[edit]

${displaystyle {frac {Delta V}{V}}=left(1+{frac {Delta L}{L}}right)left(1+{frac {Delta L'}{L}}right)^{2}-1}$

Using the above derived relationship between Delta L and :

${displaystyle {frac {Delta V}{V}}=left(1+{frac {Delta L}{L}}right)^{1-2nu }-1}$

and for very small values of Delta L and , the first-order approximation yields:

${frac {Delta V}{V}}approx (1-2nu ){frac {Delta L}{L}}$

For isotropic materials we can use Lamé’s relation^[10]

$nu approx {frac {1}{2}}-{frac {E}{6K}}$

where is bulk modulus and is Young’s modulus.

Width change[edit]

Figure 2: Comparison between the two formulas, one for small deformations, another for large deformations

If a rod with diameter (or width, or thickness) d and length L is subject to tension so that its length will change by ΔL then its diameter d will change by:

${displaystyle {Delta d over d}=-nu {frac {Delta L}{L}}}$

The above formula is true only in the case of small deformations; if deformations are large then the following (more precise) formula can be used:

${displaystyle Delta d=-dleft(1-{left(1+{frac {Delta L}{L}}right)}^{-nu }right)}$

where

The value is negative because it decreases with increase of length

Characteristic materials[edit]

Isotropic[edit]

${displaystyle varepsilon _{xx}={frac {1}{E}}left[sigma _{xx}-nu left(sigma _{yy}+sigma _{zz}right)right]}$

${displaystyle varepsilon _{yy}={frac {1}{E}}left[sigma _{yy}-nu left(sigma _{xx}+sigma _{zz}right)right]}$

${displaystyle varepsilon _{zz}={frac {1}{E}}left[sigma _{zz}-nu left(sigma _{xx}+sigma _{yy}right)right]}$

where:

these equations can be all synthesized in the following:

${displaystyle varepsilon _{ii}={frac {1}{E}}left[sigma _{ii}(1+nu )-nu sum _{k}sigma _{kk}right]}$

In the most general case, also shear stresses will hold as well as normal stresses, and the full generalization of Hooke’s law is given by:

${displaystyle varepsilon _{ij}={frac {1}{E}}left[sigma _{ij}(1+nu )-nu delta _{ij}sum _{k}sigma _{kk}right]}$

where $delta _{ij}$ is the Kronecker delta. The Einstein notation is usually adopted:

${displaystyle sigma _{kk}equiv sum _{l}delta _{kl}sigma _{kl}}$

to write the equation simply as:

${displaystyle varepsilon _{ij}={frac {1}{E}}left[sigma _{ij}(1+nu )-nu delta _{ij}sigma _{kk}right]}$

Anisotropic[edit]

For anisotropic materials, the Poisson ratio depends on the direction of extension and transverse deformation

${displaystyle nu (mathbf {n} ,mathbf {m} )=-Eleft(mathbf {n} right)s_{ijalpha beta }n_{i}n_{j}m_{alpha }m_{beta }}$

${displaystyle E^{-1}(mathbf {n} )=s_{ijalpha beta }n_{i}n_{j}n_{alpha }n_{beta }}$

Orthotropic[edit]

Then Hooke’s law can be expressed in matrix form as^[13]^[14]

where

${displaystyle {frac {nu _{yx}}{E_{y}}}={frac {nu _{xy}}{E_{x}}}~,qquad {frac {nu _{zx}}{E_{z}}}={frac {nu _{xz}}{E_{x}}}~,qquad {frac {nu _{yz}}{E_{y}}}={frac {nu _{zy}}{E_{z}}}}$

Transversely isotropic[edit]

Transversely isotropic materials have a plane of isotropy in which the elastic properties are isotropic. If we assume that this plane of isotropy is y-z , then Hooke’s law takes the form^[15]

${displaystyle {begin{bmatrix}epsilon _{xx}\epsilon _{yy}\epsilon _{zz}\2epsilon _{yz}\2epsilon _{zx}\2epsilon _{xy}end{bmatrix}}={begin{bmatrix}{tfrac {1}{E_{x}}}&-{tfrac {nu _{yx}}{E_{y}}}&-{tfrac {nu _{zx}}{E_{z}}}&0&0&0\-{tfrac {nu _{xy}}{E_{x}}}&{tfrac {1}{E_{y}}}&-{tfrac {nu _{zy}}{E_{z}}}&0&0&0\-{tfrac {nu _{xz}}{E_{x}}}&-{tfrac {nu _{yz}}{E_{y}}}&{tfrac {1}{E_{z}}}&0&0&0\0&0&0&{tfrac {1}{G_{rm {yz}}}}&0&0\0&0&0&0&{tfrac {1}{G_{rm {zx}}}}&0\0&0&0&0&0&{tfrac {1}{G_{rm {xy}}}}\end{bmatrix}}{begin{bmatrix}sigma _{xx}\sigma _{yy}\sigma _{zz}\sigma _{yz}\sigma _{zx}\sigma _{xy}end{bmatrix}}}$

where we have used the plane of isotropy y-z to reduce the number of constants, i.e., $E_{y}=E_{z},~nu _{{xy}}=nu _{{xz}},~nu _{{yx}}=nu _{{zx}}$ .

The symmetry of the stress and strain tensors implies that

${displaystyle {frac {nu _{xy}}{E_{x}}}={frac {nu _{yx}}{E_{y}}}~,~~nu _{yz}=nu _{zy}~.}$

${displaystyle G_{yz}={frac {E_{y}}{2(1+nu _{yz})}}~.}$

Poisson’s ratio values for different materials[edit]

Influences of selected glass component additions on Poisson’s ratio of a specific base glass.^[16]

Material	Poisson’s ratio
rubber	0.4999^[17]
gold	0.42–0.44
saturated clay	0.40–0.49
magnesium	0.252–0.289
titanium	0.265–0.34
copper	0.33
aluminium-alloy	0.32
clay	0.30–0.45
stainless steel	0.30–0.31
steel	0.27–0.30
cast iron	0.21–0.26
sand	0.20–0.455
concrete	0.1–0.2
glass	0.18–0.3
metallic glasses	0.276–0.409^[18]
foam	0.10–0.50
cork	0.0

Material	Plane of symmetry	$nu _{{{rm {xy}}}}$	$nu _{{{rm {yx}}}}$	$nu _{{{rm {yz}}}}$	$nu _{{{rm {zy}}}}$	$nu _{{{rm {zx}}}}$	$nu _{{{rm {xz}}}}$
Nomex honeycomb core	, ribbon in direction	0.49	0.69	0.01	2.75	3.88	0.01
glass fiber-epoxy resin		0.29	0.32	0.06	0.06	0.32

Negative Poisson’s ratio materials[edit]

More than three hundred crystalline materials have negative Poisson’s ratio.^[25]^[26]^[27] For example, Li, Na, K, Cu, Rb, Ag, Fe, Ni, Co, Cs, Au, Be, Ca, Zn Sr, Sb, MoS $_{2}$ and other.

Poisson function[edit]

Applications of Poisson’s effect[edit]

References[edit]

^ For soft materials, the bulk modulus (K) is typically large compared to the shear modulus (G) so that they can be regarded as incompressible, since it is easier to change shape than to compress. This results in the Young’s modulus (E) being and hence .Jastrzebski, D. (1959). Nature and Properties of Engineering Materials (Wiley International ed.). John Wiley & Sons, Inc.
^ Lakes, R. and Wojciechowski, K.W., 2008. Negative compressibility, negative Poisson’s ratio, and stability. Physica Status Solidi B, 245(3), pp.545-551.
^ Gercek, H. (January 2007). «Poisson’s ratio values for rocks». International Journal of Rock Mechanics and Mining Sciences. 44 (1): 1–13. doi:10.1016/j.ijrmms.2006.04.011.
^ Park, RJT. Seismic Performance of Steel-Encased Concrete Piles
^ Mark, Schenk (2011). Folded Shell Structures, PhD Thesis (PDF). University of Cambridge, Clare College.
^ Wei, Z. Y.; Guo, Z. V.; Dudte, L.; Liang, H. Y.; Mahadevan, L. (2013-05-21). «Geometric Mechanics of Periodic Pleated Origami» (PDF). Physical Review Letters. 110 (21): 215501. arXiv:1211.6396. Bibcode:2013PhRvL.110u5501W. doi:10.1103/PhysRevLett.110.215501. PMID 23745895. S2CID 9145953.
^ Eidini, Maryam; Paulino, Glaucio H. (2015). «Unraveling metamaterial properties in zigzag-base folded sheets». Science Advances. 1 (8): e1500224. arXiv:1502.05977. Bibcode:2015SciA….1E0224E. doi:10.1126/sciadv.1500224. ISSN 2375-2548. PMC 4643767. PMID 26601253.
^ Eidini, Maryam (2016). «Zigzag-base folded sheet cellular mechanical metamaterials». Extreme Mechanics Letters. 6: 96–102. arXiv:1509.08104. doi:10.1016/j.eml.2015.12.006. S2CID 118424595.
^ Mousanezhad, Davood; Babaee, Sahab; Ebrahimi, Hamid; Ghosh, Ranajay; Hamouda, Abdelmagid Salem; Bertoldi, Katia; Vaziri, Ashkan (2015-12-16). «Hierarchical honeycomb auxetic metamaterials». Scientific Reports. 5: 18306. Bibcode:2015NatSR…518306M. doi:10.1038/srep18306. ISSN 2045-2322. PMC 4680941. PMID 26670417.
^ Mott, P. H.; Roland, C. M. (3 April 2012). «Limits to Poisson’s ratio in isotropic materials—general result for arbitrary deformation». Physica Scripta. Chemistry Division, Naval Research Laboratory. 87 (5): 055404. arXiv:1204.3859. doi:10.1088/0031-8949/87/05/055404. S2CID 55920779.
^ Epishin, A.I.; Lisovenko, D.S. (2016). «Extreme values of Poisson’s ratio of cubic crystals». Technical Physics. 61 (10): 1516–1524. Bibcode:2016JTePh..61.1516E. doi:10.1016/j.mechmat.2019.03.017. S2CID 140493258.
^ Gorodtsov, V.A.; Lisovenko, D.S. (2019). «Extreme values of Young’s modulus and Poisson’s ratio of hexagonal crystals». Mechanics of Materials. 134: 1–8. doi:10.1016/j.mechmat.2019.03.017. S2CID 140493258.
^ Boresi, A. P, Schmidt, R. J. and Sidebottom, O. M., 1993, Advanced Mechanics of Materials, Wiley.
^ Lekhnitskii, S. G. (1981). Theory of elasticity of an anisotropic elastic body. Mir Publishing. p. 36.
^ Tan, S. C., 1994, Stress Concentrations in Laminated Composites, Technomic Publishing Company, Lancaster, PA.
^ Fluegel, Alexander. «Poisson’s Ratio Calculation for Glasses». www.glassproperties.com. Archived from the original on 23 October 2017. Retrieved 28 April 2018.
^ P. H. Mott; C. M. Roland (20 October 2009). «Limits to Poisson’s ratio in isotropic materials» (PDF). Physical Review B. 80 (13): 132104. arXiv:0909.4697. Bibcode:2009PhRvB..80m2104M. doi:10.1103/PhysRevB.80.132104. Archived (PDF) from the original on 2014-10-31. Retrieved 2014-09-24.{{cite journal}}: CS1 maint: multiple names: authors list (link)
^ Journal of Applied Physics 110, 053521 (2011)
^ Lakes, Rod. «Negative Poisson’s ratio». silver.neep.wisc.edu. Archived from the original on 16 February 2018. Retrieved 28 April 2018.
^ Ozyhar, Tomasz; Hering, Stefan; Niemz, Peter (March 2013). «Viscoelastic characterization of wood: Time dependence of the orthotropic compliance in tension and compression». Journal of Rheology. 57 (2): 699–717. Bibcode:2013JRheo..57..699O. doi:10.1122/1.4790170. ISSN 0148-6055.
^ Jiang, Jiali; Erik Valentine, Bachtiar; Lu, Jianxiong; Niemz, Peter (2016-11-01). «Time dependence of the orthotropic compression Young’s moduli and Poisson’s ratios of Chinese fir wood» (PDF). Holzforschung. 70 (11): 1093–1101. doi:10.1515/hf-2016-0001. hdl:20.500.11850/122097. ISSN 1437-434X. S2CID 137799672.
^ Carta, Giorgio; Brun, Michele; Baldi, Antonio (2016). «Design of a porous material with isotropic negative Poisson’s ratio». Mechanics of Materials. 97: 67–75. doi:10.1016/j.mechmat.2016.02.012.
^ Cabras, Luigi; Brun, Michele (2016). «A class of auxetic three-dimensional lattices». Journal of the Mechanics and Physics of Solids. 91: 56–72. arXiv:1506.04919. Bibcode:2016JMPSo..91…56C. doi:10.1016/j.jmps.2016.02.010. S2CID 85547530.
^ Cabras, Luigi; Brun, Michele (2014). «Auxetic two-dimensional lattices with Poisson’s ratio arbitrarily close to -1». Proceedings of the Royal Society A. 470 (2172): 20140538. arXiv:1407.5679. Bibcode:2014RSPSA.47040538C. doi:10.1098/rspa.2014.0538. S2CID 119321604.
^ Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S. (2013). «Classification of cubic auxetics». Physica Status Solidi B. 250 (10): 2038–2043. doi:10.1002/pssb.201384233. S2CID 117802510.
^ Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S. (2011). «Variability of elastic properties of hexagonal auxetics». Doklady Physics. 56 (12): 602–605. doi:10.1134/S1028335811120019. S2CID 120998323.
^ Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S.; Volkov, M.A. (2015). «Auxetics among 6-constant tetragonal crystals». Letters on Materials. 5 (4): 409–413. doi:10.22226/2410-3535-2015-4-409-413.
^ Mihai, L. A.; Goriely, A. (2017-11-03). «How to characterize a nonlinear elastic material? A review on nonlinear constitutive parameters in isotropic finite elasticity». Proceedings of the Royal Society A. 473 (2207): 20170607. Bibcode:2017RSPSA.47370607M. doi:10.1098/rspa.2017.0607. PMC 5719638. PMID 29225507.
^ «Lecture Notes in Structural Geology – Effective Stress». Retrieved 2019-07-03.
^ Silva, et al. «Cork: properties, capabilities and applications» Archived 2017-08-09 at the Wayback Machine, Retrieved May 4, 2017

External links[edit]

Meaning of Poisson’s ratio
Negative Poisson’s ratio materials
More on negative Poisson’s ratio materials (auxetic) Archived 2018-02-08 at the Wayback Machine

Conversion formulae
Homogeneous isotropic linear elastic materials have their elastic properties uniquely determined by any two moduli among these; thus, given any two, any other of the elastic moduli can be calculated according to these formulas, provided both for 3D materials (first part of the table) and for 2D materials (second part).
3D formulae							Notes
			${tfrac {3K(3K-E)}{9K-E}}$	${tfrac {3KE}{9K-E}}$	${tfrac {3K-E}{6K}}$	${tfrac {3K(3K+E)}{9K-E}}$
		${tfrac {9K(K-lambda )}{3K-lambda }}$		${tfrac {3(K-lambda )}{2}}$	${tfrac {lambda }{3K-lambda }}$
		${tfrac {9KG}{3K+G}}$	$K-{tfrac {2G}{3}}$		${tfrac {3K-2G}{2(3K+G)}}$	$K+{tfrac {4G}{3}}$
			${tfrac {3Knu }{1+nu }}$	${tfrac {3K(1-2nu )}{2(1+nu )}}$		${tfrac {3K(1-nu )}{1+nu }}$
		${tfrac {9K(M-K)}{3K+M}}$	${tfrac {3K-M}{2}}$	${tfrac {3(M-K)}{4}}$	${tfrac {3K-M}{3K+M}}$
	${tfrac {E+3lambda +R}{6}}$			${tfrac {E-3lambda +R}{4}}$	${tfrac {2lambda }{E+lambda +R}}$	${tfrac {E-lambda +R}{2}}$	$R={sqrt {E^{2}+9lambda ^{2}+2Elambda }}$
	${tfrac {EG}{3(3G-E)}}$		${tfrac {G(E-2G)}{3G-E}}$		${tfrac {E}{2G}}-1$	${tfrac {G(4G-E)}{3G-E}}$
	${tfrac {E}{3(1-2nu )}}$		${tfrac {Enu }{(1+nu )(1-2nu )}}$	${tfrac {E}{2(1+nu )}}$		${tfrac {E(1-nu )}{(1+nu )(1-2nu )}}$
	${tfrac {3M-E+S}{6}}$		${tfrac {M-E+S}{4}}$	${tfrac {3M+E-S}{8}}$	${tfrac {E-M+S}{4M}}$		$S=pm {sqrt {E^{2}+9M^{2}-10EM}}$ There are two valid solutions. The plus sign leads to . The minus sign leads to .
	$lambda +{tfrac {2G}{3}}$	${tfrac {G(3lambda +2G)}{lambda +G}}$			${tfrac {lambda }{2(lambda +G)}}$
	${tfrac {lambda (1+nu )}{3nu }}$	${tfrac {lambda (1+nu )(1-2nu )}{nu }}$		${tfrac {lambda (1-2nu )}{2nu }}$		${tfrac {lambda (1-nu )}{nu }}$	Cannot be used when
	${tfrac {M+2lambda }{3}}$	${tfrac {(M-lambda )(M+2lambda )}{M+lambda }}$		${tfrac {M-lambda }{2}}$	${tfrac {lambda }{M+lambda }}$
	${tfrac {2G(1+nu )}{3(1-2nu )}}$		${tfrac {2Gnu }{1-2nu }}$			${tfrac {2G(1-nu )}{1-2nu }}$
	$M-{tfrac {4G}{3}}$	${tfrac {G(3M-4G)}{M-G}}$			${tfrac {M-2G}{2M-2G}}$
	${tfrac {M(1+nu )}{3(1-nu )}}$	${tfrac {M(1+nu )(1-2nu )}{1-nu }}$	${tfrac {Mnu }{1-nu }}$	${tfrac {M(1-2nu )}{2(1-nu )}}$
2D formulae	${displaystyle K_{mathrm {2D} }=,}$	${displaystyle E_{mathrm {2D} }=,}$	${displaystyle lambda _{mathrm {2D} }=,}$	${displaystyle G_{mathrm {2D} }=,}$	${displaystyle nu _{mathrm {2D} }=,}$	${displaystyle M_{mathrm {2D} }=,}$	Notes
${displaystyle (K_{mathrm {2D} },,E_{mathrm {2D} })}$			${displaystyle {tfrac {2K_{mathrm {2D} }(2K_{mathrm {2D} }-E_{mathrm {2D} })}{4K_{mathrm {2D} }-E_{mathrm {2D} }}}}$	${displaystyle {tfrac {K_{mathrm {2D} }E_{mathrm {2D} }}{4K_{mathrm {2D} }-E_{mathrm {2D} }}}}$	${displaystyle {tfrac {2K_{mathrm {2D} }-E_{mathrm {2D} }}{2K_{mathrm {2D} }}}}$	${displaystyle {tfrac {4K_{mathrm {2D} }^{2}}{4K_{mathrm {2D} }-E_{mathrm {2D} }}}}$
${displaystyle (K_{mathrm {2D} },,lambda _{mathrm {2D} })}$		${displaystyle {tfrac {4K_{mathrm {2D} }(K_{mathrm {2D} }-lambda _{mathrm {2D} })}{2K_{mathrm {2D} }-lambda _{mathrm {2D} }}}}$		${displaystyle K_{mathrm {2D} }-lambda _{mathrm {2D} }}$	${displaystyle {tfrac {lambda _{mathrm {2D} }}{2K_{mathrm {2D} }-lambda _{mathrm {2D} }}}}$	${displaystyle 2K_{mathrm {2D} }-lambda _{mathrm {2D} }}$
${displaystyle (K_{mathrm {2D} },,G_{mathrm {2D} })}$		${displaystyle {tfrac {4K_{mathrm {2D} }G_{mathrm {2D} }}{K_{mathrm {2D} }+G_{mathrm {2D} }}}}$	${displaystyle K_{mathrm {2D} }-G_{mathrm {2D} }}$		${displaystyle {tfrac {K_{mathrm {2D} }-G_{mathrm {2D} }}{K_{mathrm {2D} }+G_{mathrm {2D} }}}}$	${displaystyle K_{mathrm {2D} }+G_{mathrm {2D} }}$
${displaystyle (K_{mathrm {2D} },,nu _{mathrm {2D} })}$		${displaystyle 2K_{mathrm {2D} }(1-nu _{mathrm {2D} }),}$	${displaystyle {tfrac {2K_{mathrm {2D} }nu _{mathrm {2D} }}{1+nu _{mathrm {2D} }}}}$	${displaystyle {tfrac {K_{mathrm {2D} }(1-nu _{mathrm {2D} })}{1+nu _{mathrm {2D} }}}}$		${displaystyle {tfrac {2K_{mathrm {2D} }}{1+nu _{mathrm {2D} }}}}$
${displaystyle (E_{mathrm {2D} },,G_{mathrm {2D} })}$	${displaystyle {tfrac {E_{mathrm {2D} }G_{mathrm {2D} }}{4G_{mathrm {2D} }-E_{mathrm {2D} }}}}$		${displaystyle {tfrac {2G_{mathrm {2D} }(E_{mathrm {2D} }-2G_{mathrm {2D} })}{4G_{mathrm {2D} }-E_{mathrm {2D} }}}}$		${displaystyle {tfrac {E_{mathrm {2D} }}{2G_{mathrm {2D} }}}-1}$	${displaystyle {tfrac {4G_{mathrm {2D} }^{2}}{4G_{mathrm {2D} }-E_{mathrm {2D} }}}}$
${displaystyle (E_{mathrm {2D} },,nu _{mathrm {2D} })}$	${displaystyle {tfrac {E_{mathrm {2D} }}{2(1-nu _{mathrm {2D} })}}}$		${displaystyle {tfrac {E_{mathrm {2D} }nu _{mathrm {2D} }}{(1+nu _{mathrm {2D} })(1-nu _{mathrm {2D} })}}}$	${displaystyle {tfrac {E_{mathrm {2D} }}{2(1+nu _{mathrm {2D} })}}}$		${displaystyle {tfrac {E_{mathrm {2D} }}{(1+nu _{mathrm {2D} })(1-nu _{mathrm {2D} })}}}$
${displaystyle (lambda _{mathrm {2D} },,G_{mathrm {2D} })}$	${displaystyle lambda _{mathrm {2D} }+G_{mathrm {2D} }}$	${displaystyle {tfrac {4G_{mathrm {2D} }(lambda _{mathrm {2D} }+G_{mathrm {2D} })}{lambda _{mathrm {2D} }+2G_{mathrm {2D} }}}}$			${displaystyle {tfrac {lambda _{mathrm {2D} }}{lambda _{mathrm {2D} }+2G_{mathrm {2D} }}}}$	${displaystyle lambda _{mathrm {2D} }+2G_{mathrm {2D} },}$
${displaystyle (lambda _{mathrm {2D} },,nu _{mathrm {2D} })}$	${displaystyle {tfrac {lambda _{mathrm {2D} }(1+nu _{mathrm {2D} })}{2nu _{mathrm {2D} }}}}$	${displaystyle {tfrac {lambda _{mathrm {2D} }(1+nu _{mathrm {2D} })(1-nu _{mathrm {2D} })}{nu _{mathrm {2D} }}}}$		${displaystyle {tfrac {lambda _{mathrm {2D} }(1-nu _{mathrm {2D} })}{2nu _{mathrm {2D} }}}}$		${displaystyle {tfrac {lambda _{mathrm {2D} }}{nu _{mathrm {2D} }}}}$	Cannot be used when ${displaystyle nu _{mathrm {2D} }=0Leftrightarrow lambda _{mathrm {2D} }=0}$
${displaystyle (G_{mathrm {2D} },,nu _{mathrm {2D} })}$	${displaystyle {tfrac {G_{mathrm {2D} }(1+nu _{mathrm {2D} })}{1-nu _{mathrm {2D} }}}}$	${displaystyle 2G_{mathrm {2D} }(1+nu _{mathrm {2D} }),}$	${displaystyle {tfrac {2G_{mathrm {2D} }nu _{mathrm {2D} }}{1-nu _{mathrm {2D} }}}}$			${displaystyle {tfrac {2G_{mathrm {2D} }}{1-nu _{mathrm {2D} }}}}$
${displaystyle (G_{mathrm {2D} },,M_{mathrm {2D} })}$	${displaystyle M_{mathrm {2D} }-G_{mathrm {2D} }}$	${displaystyle {tfrac {4G_{mathrm {2D} }(M_{mathrm {2D} }-G_{mathrm {2D} })}{M_{mathrm {2D} }}}}$	${displaystyle M_{mathrm {2D} }-2G_{mathrm {2D} },}$		${displaystyle {tfrac {M_{mathrm {2D} }-2G_{mathrm {2D} }}{M_{mathrm {2D} }}}}$

Источник

Содержание

Ауксетики

Уравнение

Грунты

Значения коэффициента Пуассона для некоторых изотропных материалов

Примечания

См. также

Детальное определение

Связь с другими упругими константами

Ауксетики

Значения коэффициента Пуассона

Грунты

Изотропные материалы

Примечания

См. также

Происхождение

Коэффициент Пуассона от изменений геометрии

Изменение длины

Изменение объема

Изменение ширины

Характерные материалы

Изотропный

Анизотропный

Ортотропный

Трансверсально изотропный

Значения коэффициента Пуассона для разных материалов

Материалы с отрицательным коэффициентом Пуассона

Функция Пуассона

Применение эффекта Пуассона

См. Также

Ссылки

Внешние ссылки

Содержание

Детальное определение

Ауксетики

Значения коэффициента Пуассона

Грунты

Изотропные материалы

Примечания

См. также

Origin[edit]

Poisson’s ratio from geometry changes[edit]

Length change[edit]

Volumetric change[edit]

Width change[edit]

Characteristic materials[edit]

Isotropic[edit]

Anisotropic[edit]

Orthotropic[edit]

Transversely isotropic[edit]

Poisson’s ratio values for different materials[edit]

Negative Poisson’s ratio materials[edit]

Poisson function[edit]

Applications of Poisson’s effect[edit]

See also[edit]

References[edit]

External links[edit]

Origin[edit]

Poisson’s ratio from geometry changes[edit]

Length change[edit]

Volumetric change[edit]

Width change[edit]

Characteristic materials[edit]

Isotropic[edit]

Anisotropic[edit]

Orthotropic[edit]

Transversely isotropic[edit]

Poisson’s ratio values for different materials[edit]

Negative Poisson’s ratio materials[edit]

Poisson function[edit]

Applications of Poisson’s effect[edit]

See also[edit]

References[edit]

External links[edit]