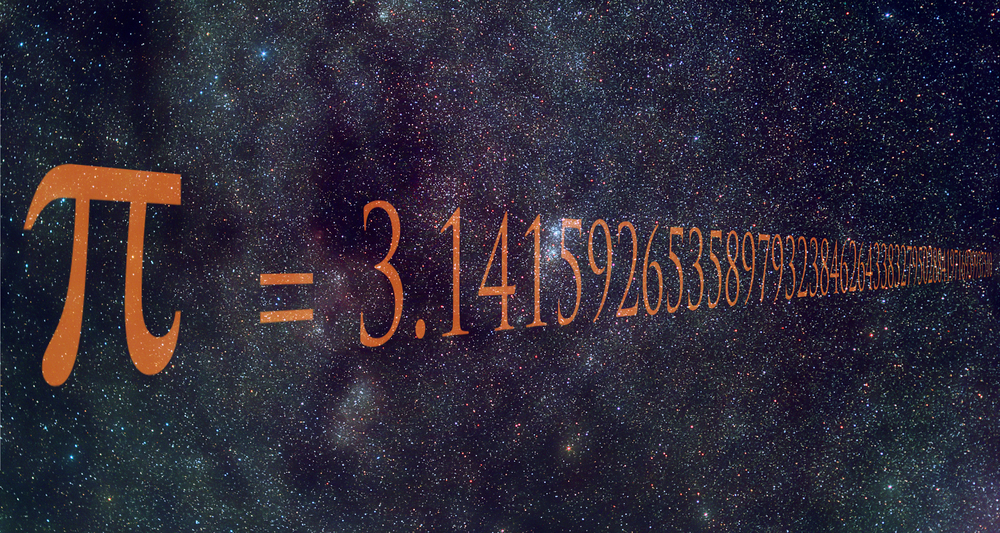У этого термина существуют и другие значения, см. Константа.
Математическая константа — величина, значение которой не меняется; в этом она противоположна переменной. В отличие от физических констант, математические константы определены независимо от каких бы то ни было физических измерений.
Некоторые избранные константы
Использованные сокращения: И — иррациональное число, А — алгебраическое число, Т — трансцендентное число, ? — неизвестно; мат — обычная математика, ТЧ — теория чисел, ТХ — теория хаоса, комб — комбинаторика, АИТ — Алгоритмическая теория информации.
| Символ | Приближенное значение | Название | Область | Значение | Впервые описана | Число известных знаков |
|---|---|---|---|---|---|---|
 |
≈ 3,141 592 653 589 793 238 462 643 383 279 502 88 | пи, архимедова константа | мат | Т | ? | 10 000 000 000 000[1] |
| e | ≈ 2,718 281 828 459 045 235 360 287 471 352 662 50 | константа Непера, основание натурального логарифма | мат | Т | 12 884 901 000 | |
 |
≈ 1,414 213 562 373 095 048 801 688 724 209 698 08 | константа Пифагора, квадратный корень из 2 | мат | А, но И | 137 438 953 444 | |
 |
≈ 1,732 050 807 568 877 293 527 446 341 505 872 37 | константа Теодоруса, квадратный корень из 3 | мат | А, но И | ||
| γ | ≈ 0,577 215 664 901 532 860 606 512 090 082 402 43 | постоянная Эйлера — Маскерони | мат, ТЧ | ? | 108 000 000 | |
| φ | ≈ 1,618 033 988 749 894 848 204 586 834 365 638 12 | золотое сечение | мат | А, но И | 3 141 000 000 | |
| β* | ≈ 0,702 58 | константа Эмбри — Трефтена | ТЧ | |||
| δ | ≈ 4,669 201 609 102 990 671 853 203 820 466 201 61 | постоянная Фейгенбаума | ТХ | |||
| α | ≈ 2,502 907 875 095 892 822 283 902 873 218 215 78 | константа Фейгенбаума | ТХ | |||
| C2 | ≈ 0,660 161 815 846 869 573 927 812 110 014 555 77 | константа простых близнецов | ТЧ | 5 020 | ||
| M1 | ≈ 0,261 497 212 847 642 783 755 426 838 608 695 85 | константа Мейсселя — Мертенса | ТЧ | 1866; 1874 | 8010 | |
| B2 | ≈ 1,902 160 583 104[2] | константа Бруна для простых близнецов | ТЧ | 1919 | 10 | |
| B4 | ≈ 0,870 588 380 0 | константа Бруна для простых четвёрок | ТЧ | |||
| Λ | ≈ -2,7 · 10−9 | константа де Брюйна — Ньюмана | ТЧ | 1950? | ||
| K | ≈ 0,915 965 594 177 219 015 054 603 514 932 384 11 | постоянная Каталана | комб | 31 026 000 000 | ||
| K | ≈ 0,764 223 653 589 220 66 | константа Ландау — Рамануджана | ТЧ | И (?) | 30 010 | |
| K | ≈ 1,131 988 24 | константа Висваната 1 | ТЧ | 8 | ||
| J | ≈ 3,058 198 247 456 354 132 564 564 787 888 767… | константа Поля-Гаусса | ТЧ | 10343 | ||
| B´L | 1 или 1,08366[3] | константа Лежандра (англ.) | ТЧ | |||
| μ | ≈ 1,451 369 234 883 381 050 283 968 485 892 027 | константа Рамануджана — Солднера | ТЧ | 75 500 | ||
| E’B | ≈ 1,606 695 152 415 291 763 | константа Эрдёша — Борвейна | ТЧ | И | ||
| Ω | ≈ 0,007 874 996 997 812 384 4 | константа Хайтина | АИТ | Т | ||
| ζ(3) | ≈ 1,202 056 903 159 594 285 399 738 161 511 449 99 | постоянная Апери | ТЧ | И | 1735 | 100 000 001 000 |
| ɯ | ≈ 0,739 085 133 215 160 641 655 312 087 673 873 40 | число Дотти[4], притягивающая неподвижная точка функции cos(x) | ТХ | |||
| A | ≈ 1,282 427 129 100 622 636 875 342 568 869 791 73 | постоянная Глейшера — Кинкелина | ТЧ | 1860 |
Литература
- Steven R. Finch, Mathematical Constants. Cambridge, 2003 (ISBN 0-521-81805-2)
См. также
- Постоянная
Примечания
- ↑ Определено 10 триллионов цифр десятичного разложения для π
- ↑ последовательность A065421 в OEIS
- ↑ Weisstein, Eric W. Legendre’s Constant (англ.) на сайте Wolfram MathWorld.
- ↑ последовательность A003957 в OEIS
Ссылки
- Mathematical Constants — страница Стивена Финча
A mathematical constant is a key number whose value is fixed by an unambiguous definition, often referred to by a special symbol (e.g., an alphabet letter), or by mathematicians’ names to facilitate using it across multiple mathematical problems.[1] Constants arise in many areas of mathematics, with constants such as e and π occurring in such diverse contexts as geometry, number theory, statistics, and calculus.
Some constants arise naturally by a fundamental principle or intrinsic property, such as the ratio between the circumference and diameter of a circle (π). Other constants are notable more for historical reasons than for their mathematical properties. The more popular constants have been studied throughout the ages and computed to many decimal places.
All named mathematical constants are definable numbers, and usually are also computable numbers (Chaitin’s constant being a significant exception).
Basic mathematical constants[edit]
These are constants which one is likely to encounter during pre-college education in many countries.
Archimedes’ constant π[edit]
Main article: Pi
The circumference of a circle with diameter 1 is π.
The constant π (pi) has a natural definition in Euclidean geometry as the ratio between the circumference and diameter of a circle. It may be found in many other places in mathematics: for example, the Gaussian integral, the complex roots of unity, and Cauchy distributions in probability. However, its ubiquity is not limited to pure mathematics. It appears in many formulas in physics, and several physical constants are most naturally defined with π or its reciprocal factored out. For example, the ground state wave function of the hydrogen atom is
where 
π is an irrational number and a transcendental number.
The numeric value of π is approximately 3.1415926536 (sequence A000796 in the OEIS). Memorizing increasingly precise digits of π is a world record pursuit.
The imaginary unit i[edit]
The imaginary unit i in the complex plane. Real numbers lie on the horizontal axis, and imaginary numbers lie on the vertical axis
The imaginary unit or unit imaginary number, denoted as i, is a mathematical concept which extends the real number system 

There are in fact two complex square roots of −1, namely i and −i, just as there are two complex square roots of every other real number (except zero, which has one double square root).
In contexts where the symbol i is ambiguous or problematic, j or the Greek iota (ι) is sometimes used. This is in particular the case in electrical engineering and control systems engineering, where the imaginary unit is often denoted by j, because i is commonly used to denote electric current.
Euler’s number e[edit]
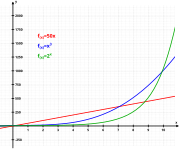
Exponential growth (green) describes many physical phenomena.
Euler’s number e, also known as the exponential growth constant, appears in many areas of mathematics, and one possible definition of it is the value of the following expression:
The constant e is intrinsically related to the exponential function 
The Swiss mathematician Jacob Bernoulli discovered that e arises in compound interest: If an account starts at $1, and yields interest at annual rate R, then as the number of compounding periods per year tends to infinity (a situation known as continuous compounding), the amount of money at the end of the year will approach eR dollars.
The constant e also has applications to probability theory, where it arises in a way not obviously related to exponential growth. As an example, suppose that a slot machine with a one in n probability of winning is played n times, then for large n (e.g., one million), the probability that nothing will be won will tend to 1/e as n tends to infinity.
Another application of e, discovered in part by Jacob Bernoulli along with French mathematician Pierre Raymond de Montmort, is in the problem of derangements, also known as the hat check problem.[2] Here, n guests are invited to a party, and at the door each guest checks his hat with the butler, who then places them into labelled boxes. The butler does not know the name of the guests, and hence must put them into boxes selected at random. The problem of de Montmort is: what is the probability that none of the hats gets put into the right box. The answer is
which, as n tends to infinity, approaches 1/e.
e is an irrational number.
The numeric value of e is approximately 2.7182818284 (sequence A001113 in the OEIS).
Pythagoras’ constant √2[edit]
The square root of 2, often known as root 2, radical 2, or Pythagoras’ constant, and written as √2, is the positive algebraic number that, when multiplied by itself, gives the number 2. It is more precisely called the principal square root of 2, to distinguish it from the negative number with the same property.
Geometrically the square root of 2 is the length of a diagonal across a square with sides of one unit of length; this follows from the Pythagorean theorem. It was probably the first number known to be irrational. Its numerical value truncated to 65 decimal places is:
- 1.41421356237309504880168872420969807856967187537694807317667973799… (sequence A002193 in the OEIS).
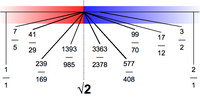
Alternatively, the quick approximation 99/70 (≈ 1.41429) for the square root of two was frequently used before the common use of electronic calculators and computers. Despite having a denominator of only 70, it differs from the correct value by less than 1/10,000 (approx. 7.2 × 10 −5).
Theodorus’ constant √3[edit]
The numeric value of √3 is approximately 1.7320508075 (sequence A002194 in the OEIS).
Constants in advanced mathematics[edit]
These are constants which are encountered frequently in higher mathematics.
The Feigenbaum constants α and δ[edit]
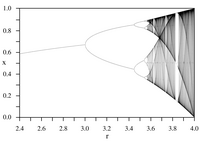
Bifurcation diagram of the logistic map.
Iterations of continuous maps serve as the simplest examples of models for dynamical systems.[3] Named after mathematical physicist Mitchell Feigenbaum, the two Feigenbaum constants appear in such iterative processes: they are mathematical invariants of logistic maps with quadratic maximum points[4] and their bifurcation diagrams. Specifically, the constant α is the ratio between the width of a tine and the width of one of its two subtines, and the constant δ is the limiting ratio of each bifurcation interval to the next between every period-doubling bifurcation.
The logistic map is a polynomial mapping, often cited as an archetypal example of how chaotic behaviour can arise from very simple non-linear dynamical equations. The map was popularized in a seminal 1976 paper by the Australian biologist Robert May,[5] in part as a discrete-time demographic model analogous to the logistic equation first created by Pierre François Verhulst. The difference equation is intended to capture the two effects of reproduction and starvation.
The numeric value of α is approximately 2.5029. The numeric value of δ is approximately 4.6692.
Apéry’s constant ζ(3)[edit]
Apery’s constant is the sum of the series
Apéry’s constant is an irrational number and its numeric value is approximately 1.2020569.
Despite being a special value of the Riemann zeta function, Apéry’s constant arises naturally in a number of physical problems, including in the second- and third-order terms of the electron’s gyromagnetic ratio, computed using quantum electrodynamics.[6]
The golden ratio φ[edit]
The number φ, also called the golden ratio, turns up frequently in geometry, particularly in figures with pentagonal symmetry. Indeed, the length of a regular pentagon’s diagonal is φ times its side. The vertices of a regular icosahedron are those of three mutually orthogonal golden rectangles. Also, it appears in the Fibonacci sequence, related to growth by recursion.[7] Kepler proved that it is the limit of the ratio of consecutive Fibonacci numbers.[8] The golden ratio has the slowest convergence of any irrational number.[9] It is, for that reason, one of the worst cases of Lagrange’s approximation theorem and it is an extremal case of the Hurwitz inequality for Diophantine approximations. This may be why angles close to the golden ratio often show up in phyllotaxis (the growth of plants).[10] It is approximately equal to 1.6180339887498948482, or, more precisely 2⋅sin(54°) = 
The Euler–Mascheroni constant γ[edit]
The area between the two curves (red) tends to a limit, namely the Euler-Mascheroni constant.
The Euler–Mascheroni constant is defined as the following limit:
The Euler–Mascheroni constant appears in Mertens’ third theorem and has relations to the gamma function, the zeta function and many different integrals and series.
It is yet unknown whether 
The numeric value of 
Conway’s constant λ[edit]
Conway’s constant is the invariant growth rate of all derived strings similar to the look-and-say sequence (except for one trivial one).[11]
It is given by the unique positive real root of a polynomial of degree 71 with integer coefficients.[11]
The value of λ is approximately 1.30357.
Khinchin’s constant K[edit]
If a real number r is written as a simple continued fraction:
where ak are natural numbers for all k, then, as the Russian mathematician Aleksandr Khinchin proved in 1934, the limit as n tends to infinity of the geometric mean: (a1a2…an)1/n exists and is a constant, Khinchin’s constant, except for a set of measure 0.[12]
The numeric value of K is approximately 2.6854520010.
The Glaisher–Kinkelin constant A[edit]
The Glaisher–Kinkelin constant is defined as the limit:
It appears in some expressions of the derivative of the Riemann zeta function. It has a numerical value of approximately 1.2824271291.
Mathematical curiosities and unspecified constants[edit]
Simple representatives of sets of numbers[edit]
This Babylonian clay tablet gives an approximation of the square root of 2 in four sexagesimal figures: 1; 24, 51, 10, which is accurate to about six decimal figures.[13]
Some constants, such as the square root of 2, Liouville’s constant and Champernowne constant:
are not important mathematical invariants but retain interest being simple representatives of special sets of numbers, the irrational numbers,[14] the transcendental numbers[15] and the normal numbers (in base 10)[16] respectively. The discovery of the irrational numbers is usually attributed to the Pythagorean Hippasus of Metapontum who proved, most likely geometrically, the irrationality of the square root of 2. As for Liouville’s constant, named after French mathematician Joseph Liouville, it was the first number to be proven transcendental.[17]
Chaitin’s constant Ω[edit]
In the computer science subfield of algorithmic information theory, Chaitin’s constant is the real number representing the probability that a randomly chosen Turing machine will halt, formed from a construction due to Argentine-American mathematician and computer scientist Gregory Chaitin. Chaitin’s constant, though not being computable, has been proven to be transcendental and normal. Chaitin’s constant is not universal, depending heavily on the numerical encoding used for Turing machines; however, its interesting properties are independent of the encoding.
Unspecified constants[edit]
When unspecified, constants indicate classes of similar objects, commonly functions, all equal up to a constant—technically speaking, this may be viewed as ‘similarity up to a constant’. Such constants appear frequently when dealing with integrals and differential equations. Though unspecified, they have a specific value, which often is not important.
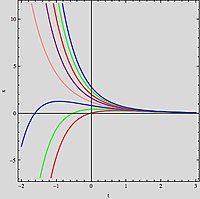
Solutions with different constants of integration of 
In integrals[edit]
Indefinite integrals are called indefinite because their solutions are only unique up to a constant. For example, when working over the field of real numbers
where C, the constant of integration, is an arbitrary fixed real number.[18] In other words, whatever the value of C, differentiating sin x + C with respect to x always yields cos x.
In differential equations[edit]
In a similar fashion, constants appear in the solutions to differential equations where not enough initial values or boundary conditions are given. For example, the ordinary differential equation y‘ = y(x) has solution Cex where C is an arbitrary constant.
When dealing with partial differential equations, the constants may be functions, constant with respect to some variables (but not necessarily all of them). For example, the PDE
has solutions f(x,y) = C(y), where C(y) is an arbitrary function in the variable y.
Notation[edit]
Representing constants[edit]
It is common to express the numerical value of a constant by giving its decimal representation (or just the first few digits of it). For two reasons this representation may cause problems. First, even though rational numbers all have a finite or ever-repeating decimal expansion, irrational numbers don’t have such an expression making them impossible to completely describe in this manner. Also, the decimal expansion of a number is not necessarily unique. For example, the two representations 0.999… and 1 are equivalent[19][20] in the sense that they represent the same number.
Calculating digits of the decimal expansion of constants has been a common enterprise for many centuries. For example, German mathematician Ludolph van Ceulen of the 16th century spent a major part of his life calculating the first 35 digits of pi.[21] Using computers and supercomputers, some of the mathematical constants, including π, e, and the square root of 2, have been computed to more than one hundred billion digits. Fast algorithms have been developed, some of which — as for Apéry’s constant — are unexpectedly fast.
Some constants differ so much from the usual kind that a new notation has been invented to represent them reasonably. Graham’s number illustrates this as Knuth’s up-arrow notation is used.[22][23]
It may be of interest to represent them using continued fractions to perform various studies, including statistical analysis. Many mathematical constants have an analytic form, that is they can be constructed using well-known operations that lend themselves readily to calculation. Not all constants have known analytic forms, though; Grossman’s constant[24] and Foias’ constant[25] are examples.
Symbolizing and naming of constants[edit]
Symbolizing constants with letters is a frequent means of making the notation more concise. A common convention, instigated by René Descartes in the 17th century and Leonhard Euler in the 18th century, is to use lower case letters from the beginning of the Latin alphabet 

However, for more important constants, the symbols may be more complex and have an extra letter, an asterisk, a number, a lemniscate or use different alphabets such as Hebrew, Cyrillic or Gothic.[23]
Sometimes, the symbol representing a constant is a whole word. For example, American mathematician Edward Kasner’s 9-year-old nephew coined the names googol and googolplex.[23][26]
Other names are either related to the meaning of the constant (universal parabolic constant, twin prime constant, …) or to a specific person (Sierpiński’s constant, Josephson constant, and so on).
Selected mathematical constants[edit]
Abbreviations used:
- R – Rational number, I – Irrational number (may be algebraic or transcendental), A – Algebraic number (irrational), T – Transcendental number
- Gen – General, NuT – Number theory, ChT – Chaos theory, Com – Combinatorics, Inf – Information theory, Ana – Mathematical analysis
| Symbol | Value | Name | Field | N | First described | Number of known decimal digits |
|---|---|---|---|---|---|---|
|
0 |
= 0 | Zero | Gen | R | by c. 500 BC | all |
|
1 |
= 1 | One, Unity | Gen | R | all | |
|
i |
= √–1 | Imaginary unit, unit imaginary number | Gen, Ana | A | by c. 1500 | all |
|
π |
≈ 3.14159 26535 89793 23846 26433 83279 50288 | Pi, Archimedes’ constant or Ludolph’s number | Gen, Ana | T | by c. 2600 BC | 62,831,853,071,796[27] |
|
e |
≈ 2.71828 18284 59045 23536 02874 71352 66249 | e, Napier’s constant, or Euler’s number | Gen, Ana | T | 1618 | 31,415,926,535,897[27] |
|
√2 |
≈ 1.41421 35623 73095 04880 16887 24209 69807 | Pythagoras’ constant, square root of 2 | Gen | A | by c. 800 BC | 10,000,000,000,000[27] |
|
√3 |
≈ 1.73205 08075 68877 29352 74463 41505 87236 | Theodorus’ constant, square root of 3 | Gen | A | by c. 800 BC | 2,199,023,255,552[28] |
|
√5 |
≈ 2.23606 79774 99789 69640 91736 68731 27623 | Square root of 5 | Gen | A | by c. 800 BC | 2,199,023,255,552[28] |
|
|
≈ 0.57721 56649 01532 86060 65120 90082 40243 | Euler–Mascheroni constant | Gen, NuT | 1735 | 600,000,000,100[28] | |
|
|
≈ 1.61803 39887 49894 84820 45868 34365 63811 | Golden ratio | Gen | A | by c. 200 BC | 10,000,000,000,000[28] |
|
|
 [29][30][31][32] [29][30][31][32]
|
de Bruijn–Newman constant | NuT, Ana | 1950 | none | |
|
M1 |
≈ 0.26149 72128 47642 78375 54268 38608 69585 | Meissel–Mertens constant | NuT | 1866 1874 |
8,010 | |
|
|
≈ 0.28016 94990 23869 13303 | Bernstein’s constant[33] | Ana | |||
|
|
≈ 0.30366 30028 98732 65859 74481 21901 55623 | Gauss–Kuzmin–Wirsing constant | Com | 1974 | 385 | |
|
|
≈ 0.35323 63718 54995 98454 35165 50432 68201 | Hafner–Sarnak–McCurley constant | NuT | 1993 | ||
|
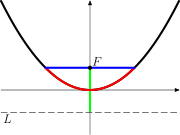
L |
≈ 0.5 | Landau’s constant | Ana | 1 | ||
|
Ω |
≈ 0.56714 32904 09783 87299 99686 62210 35554 | Omega constant | Ana | T | ||
|
|
≈ 0.62432 99885 43550 87099 29363 83100 83724 | Golomb–Dickman constant | Com, NuT | 1930 1964 |
||
| ≈ 0.64341 05462 | Cahen’s constant | T | 1891 | 4000 | ||
|
C2 |
≈ 0.66016 18158 46869 57392 78121 10014 55577 | Twin prime constant | NuT | 5,020 | ||
| ≈ 0.66274 34193 49181 58097 47420 97109 25290 | Laplace limit | |||||
|
|
≈ 0.70258 | Embree–Trefethen constant | NuT | |||
|
K |
≈ 0.76422 36535 89220 66299 06987 31250 09232 | Landau–Ramanujan constant | NuT | 30,010 | ||
|
B4 |
≈ 0.87058 838 | Brun’s constant for prime quadruplets | NuT | 8 | ||
|
G |
≈ 0.91596 55941 77219 01505 46035 14932 38411 | Catalan’s constant | Com | 1,000,000,001,337[28] | ||
|
B´L |
= 1 | Legendre’s constant | NuT | R | all | |
|
K |
≈ 1.13198 824 | Viswanath’s constant | NuT | 8 | ||
|
|
≈ 1.20205 69031 59594 28539 97381 61511 44999 | Apéry’s constant | I | 1979 | 1,200,000,000,100[28] | |
|
|
≈ 1.30357 72690 34296 39125 70991 12152 55189 | Conway’s constant | NuT | A | ||
|
|
≈ 1.30637 78838 63080 69046 86144 92602 60571 | Mills’ constant | NuT | 1947 | 6850 | |
|
|
≈ 1.32471 79572 44746 02596 09088 54478 09734 | Plastic constant | NuT | A | 1928 | |
|
|
≈ 1.45136 92348 83381 05028 39684 85892 02744 | Ramanujan–Soldner constant | NuT | I | 75,500 | |
| ≈ 1.45607 49485 82689 67139 95953 51116 54356 | Backhouse’s constant[34] | |||||
| ≈ 1.46707 80794 | Porter’s constant[35] | NuT | 1975 | |||
| ≈ 1.53960 07178 | Lieb’s square ice constant[36] | Com | A | 1967 | ||
|
EB |
≈ 1.60669 51524 15291 76378 33015 23190 92458 | Erdős–Borwein constant | NuT | I | ||
| ≈ 1.70521 11401 05367 76428 85514 53434 50816 | Niven’s constant | NuT | 1969 | |||
|
B2 |
≈ 1.90216 05831 04 | Brun’s constant for twin primes | NuT | 1919 | 12 | |
|
P2 |
≈ 2.29558 71493 92638 07403 42980 49189 49039 | Universal parabolic constant | Gen | T | ||
|
|
≈ 2.50290 78750 95892 82228 39028 73218 21578 | Feigenbaum constant | ChT | |||
|
K |
≈ 2.58498 17595 79253 21706 58935 87383 17116 | Sierpiński’s constant | ||||
| ≈ 2.68545 20010 65306 44530 97148 35481 79569 | Khinchin’s constant | NuT | 1934 | 7350 | ||
|
F |
≈ 2.80777 02420 28519 36522 15011 86557 77293 | Fransén–Robinson constant | Ana | |||
| ≈ 3.27582 29187 21811 15978 76818 82453 84386 | Lévy’s constant | NuT | ||||
|
|
≈ 3.35988 56662 43177 55317 20113 02918 92717 | Reciprocal Fibonacci constant[37] | I | |||
|
|
≈ 4.66920 16091 02990 67185 32038 20466 20161 | Feigenbaum constant | ChT | 1975 |
See also[edit]
- Invariant (mathematics)
- List of mathematical symbols
- List of numbers
- Physical constant
Notes[edit]
- ^ Weisstein, Eric W. «Constant». mathworld.wolfram.com. Retrieved 2020-08-08.
- ^ Grinstead, C.M.; Snell, J.L. «Introduction to probability theory». p. 85. Retrieved 2007-12-09.
- ^ Collet & Eckmann (1980). Iterated maps on the inerval as dynamical systems. Birkhauser. ISBN 3-7643-3026-0.
- ^ Finch, Steven (2003). Mathematical constants. Cambridge University Press. p. 67. ISBN 0-521-81805-2.
- ^ May, Robert (1976). Theoretical Ecology: Principles and Applications. Blackwell Scientific Publishers. ISBN 0-632-00768-0.
- ^ Steven Finch. «Apéry’s constant». MathWorld.
- ^ Livio, Mario (2002). The Golden Ratio: The Story of Phi, The World’s Most Astonishing Number. New York: Broadway Books. ISBN 0-7679-0815-5.
- ^ Tatersall, James (2005). Elementary number theory in nine chapters (2nd ed.
- ^ «The Secret Life of Continued Fractions»
- ^ Fibonacci Numbers and Nature — Part 2 : Why is the Golden section the «best» arrangement?, from Dr. Ron Knott’s Fibonacci Numbers and the Golden Section, retrieved 2012-11-29.
- ^ a b Steven Finch. «Conway’s Constant». MathWorld.
- ^ Steven Finch. «Khinchin’s Constant». MathWorld.
- ^ Fowler, David; Eleanor Robson (November 1998). «Square Root Approximations in Old Babylonian Mathematics: YBC 7289 in Context». Historia Mathematica. 25 (4): 368. doi:10.1006/hmat.1998.2209.
Photograph, illustration, and description of the root(2) tablet from the Yale Babylonian Collection
High resolution photographs, descriptions, and analysis of the root(2) tablet (YBC 7289) from the Yale Babylonian Collection - ^ Bogomolny, Alexander. «Square root of 2 is irrational».
- ^ Aubrey J. Kempner (Oct 1916). «On Transcendental Numbers». Transactions of the American Mathematical Society. Transactions of the American Mathematical Society, Vol. 17, No. 4. 17 (4): 476–482. doi:10.2307/1988833. JSTOR 1988833.
- ^ Champernowne, David (1933). «The Construction of Decimals Normal in the Scale of Ten». Journal of the London Mathematical Society. 8 (4): 254–260. doi:10.1112/jlms/s1-8.4.254.
- ^ Weisstein, Eric W. «Liouville’s Constant». MathWorld.
- ^ Edwards, Henry; David Penney (1994). Calculus with analytic geometry (4e ed.). Prentice Hall. p. 269. ISBN 0-13-300575-5.
- ^ Rudin, Walter (1976) [1953]. Principles of mathematical analysis (3e ed.). McGraw-Hill. p.61 theorem 3.26. ISBN 0-07-054235-X.
- ^ Stewart, James (1999). Calculus: Early transcendentals (4e ed.). Brooks/Cole. p. 706. ISBN 0-534-36298-2.
- ^ Ludolph van Ceulen Archived 2015-07-07 at the Wayback Machine – biography at the MacTutor History of Mathematics archive.
- ^ Knuth, Donald (1976). «Mathematics and Computer Science: Coping with Finiteness. Advances in Our Ability to Compute are Bringing Us Substantially Closer to Ultimate Limitations». Science. 194 (4271): 1235–1242. doi:10.1126/science.194.4271.1235. PMID 17797067. S2CID 1690489.
- ^ a b c «mathematical constants». Archived from the original on 2012-09-07. Retrieved 2007-11-27.
- ^ Weisstein, Eric W. «Grossman’s constant». MathWorld.
- ^ Weisstein, Eric W. «Foias’ constant». MathWorld.
- ^ Edward Kasner and James R. Newman (1989). Mathematics and the Imagination. Microsoft Press. p. 23.
- ^ a b c Alexander J. Yee. «y-cruncher – A Multi-Threaded Pi Program». numberworld.org. Retrieved 14 March 2020.
- ^ a b c d e f Alexander J. Yee. «Records Set by y-cruncher». numberworld.org. Retrieved 14 March 2020.
- ^ Rodgers, Brad; Tao, Terence (2018). «The De Bruijn–Newman constant is non-negative». arXiv:1801.05914 [math.NT]. (preprint)
- ^ «The De Bruijn-Newman constant is non-negative». 19 January 2018. Retrieved 2018-01-19. (announcement post)
- ^ Polymath, D.H.J. (2019), «Effective approximation of heat flow evolution of the Riemann ξ function, and a new upper bound for the de Bruijn-Newman constant», Research in the Mathematical Sciences, 6 (3), arXiv:1904.12438, Bibcode:2019arXiv190412438P, doi:10.1007/s40687-019-0193-1, S2CID 139107960
- ^
Platt, Dave; Trudgian, Tim (2021). «The Riemann hypothesis is true up to 3·1012». Bulletin of the London Mathematical Society. 53 (3): 792–797. arXiv:2004.09765. doi:10.1112/blms.12460. S2CID 234355998.(preprint) - ^ Weisstein, Eric W. «Bernstein’s Constant». MathWorld.
- ^ Weisstein, Eric W. «Backhouse’s Constant». MathWorld.
- ^ Weisstein, Eric W. «Porter’s Constant». MathWorld.
- ^ Weisstein, Eric W. «Lieb’s Square Ice Constant». MathWorld.
- ^ Weisstein, Eric W. «Reciprocal Fibonacci Constant». MathWorld.
External links[edit]
- Constants – from Wolfram MathWorld
- Inverse symbolic calculator (CECM, ISC) (tells you how a given number can be constructed from mathematical constants)
- On-Line Encyclopedia of Integer Sequences (OEIS)
- Simon Plouffe’s inverter
- Steven Finch’s page of mathematical constants (BROKEN LINK)
- Steven R. Finch, «Mathematical Constants,» Encyclopedia of mathematics and its applications, Cambridge University Press (2003).
- Xavier Gourdon and Pascal Sebah’s page of numbers, mathematical constants and algorithms
A mathematical constant is a key number whose value is fixed by an unambiguous definition, often referred to by a special symbol (e.g., an alphabet letter), or by mathematicians’ names to facilitate using it across multiple mathematical problems.[1] Constants arise in many areas of mathematics, with constants such as e and π occurring in such diverse contexts as geometry, number theory, statistics, and calculus.
Some constants arise naturally by a fundamental principle or intrinsic property, such as the ratio between the circumference and diameter of a circle (π). Other constants are notable more for historical reasons than for their mathematical properties. The more popular constants have been studied throughout the ages and computed to many decimal places.
All named mathematical constants are definable numbers, and usually are also computable numbers (Chaitin’s constant being a significant exception).
Basic mathematical constants[edit]
These are constants which one is likely to encounter during pre-college education in many countries.
Archimedes’ constant π[edit]
Main article: Pi
The circumference of a circle with diameter 1 is π.
The constant π (pi) has a natural definition in Euclidean geometry as the ratio between the circumference and diameter of a circle. It may be found in many other places in mathematics: for example, the Gaussian integral, the complex roots of unity, and Cauchy distributions in probability. However, its ubiquity is not limited to pure mathematics. It appears in many formulas in physics, and several physical constants are most naturally defined with π or its reciprocal factored out. For example, the ground state wave function of the hydrogen atom is
where 
π is an irrational number and a transcendental number.
The numeric value of π is approximately 3.1415926536 (sequence A000796 in the OEIS). Memorizing increasingly precise digits of π is a world record pursuit.
The imaginary unit i[edit]
The imaginary unit i in the complex plane. Real numbers lie on the horizontal axis, and imaginary numbers lie on the vertical axis
The imaginary unit or unit imaginary number, denoted as i, is a mathematical concept which extends the real number system 

There are in fact two complex square roots of −1, namely i and −i, just as there are two complex square roots of every other real number (except zero, which has one double square root).
In contexts where the symbol i is ambiguous or problematic, j or the Greek iota (ι) is sometimes used. This is in particular the case in electrical engineering and control systems engineering, where the imaginary unit is often denoted by j, because i is commonly used to denote electric current.
Euler’s number e[edit]
Exponential growth (green) describes many physical phenomena.
Euler’s number e, also known as the exponential growth constant, appears in many areas of mathematics, and one possible definition of it is the value of the following expression:
The constant e is intrinsically related to the exponential function 
The Swiss mathematician Jacob Bernoulli discovered that e arises in compound interest: If an account starts at $1, and yields interest at annual rate R, then as the number of compounding periods per year tends to infinity (a situation known as continuous compounding), the amount of money at the end of the year will approach eR dollars.
The constant e also has applications to probability theory, where it arises in a way not obviously related to exponential growth. As an example, suppose that a slot machine with a one in n probability of winning is played n times, then for large n (e.g., one million), the probability that nothing will be won will tend to 1/e as n tends to infinity.
Another application of e, discovered in part by Jacob Bernoulli along with French mathematician Pierre Raymond de Montmort, is in the problem of derangements, also known as the hat check problem.[2] Here, n guests are invited to a party, and at the door each guest checks his hat with the butler, who then places them into labelled boxes. The butler does not know the name of the guests, and hence must put them into boxes selected at random. The problem of de Montmort is: what is the probability that none of the hats gets put into the right box. The answer is
which, as n tends to infinity, approaches 1/e.
e is an irrational number.
The numeric value of e is approximately 2.7182818284 (sequence A001113 in the OEIS).
Pythagoras’ constant √2[edit]
The square root of 2, often known as root 2, radical 2, or Pythagoras’ constant, and written as √2, is the positive algebraic number that, when multiplied by itself, gives the number 2. It is more precisely called the principal square root of 2, to distinguish it from the negative number with the same property.
Geometrically the square root of 2 is the length of a diagonal across a square with sides of one unit of length; this follows from the Pythagorean theorem. It was probably the first number known to be irrational. Its numerical value truncated to 65 decimal places is:
- 1.41421356237309504880168872420969807856967187537694807317667973799… (sequence A002193 in the OEIS).
Alternatively, the quick approximation 99/70 (≈ 1.41429) for the square root of two was frequently used before the common use of electronic calculators and computers. Despite having a denominator of only 70, it differs from the correct value by less than 1/10,000 (approx. 7.2 × 10 −5).
Theodorus’ constant √3[edit]
The numeric value of √3 is approximately 1.7320508075 (sequence A002194 in the OEIS).
Constants in advanced mathematics[edit]
These are constants which are encountered frequently in higher mathematics.
The Feigenbaum constants α and δ[edit]
Bifurcation diagram of the logistic map.
Iterations of continuous maps serve as the simplest examples of models for dynamical systems.[3] Named after mathematical physicist Mitchell Feigenbaum, the two Feigenbaum constants appear in such iterative processes: they are mathematical invariants of logistic maps with quadratic maximum points[4] and their bifurcation diagrams. Specifically, the constant α is the ratio between the width of a tine and the width of one of its two subtines, and the constant δ is the limiting ratio of each bifurcation interval to the next between every period-doubling bifurcation.
The logistic map is a polynomial mapping, often cited as an archetypal example of how chaotic behaviour can arise from very simple non-linear dynamical equations. The map was popularized in a seminal 1976 paper by the Australian biologist Robert May,[5] in part as a discrete-time demographic model analogous to the logistic equation first created by Pierre François Verhulst. The difference equation is intended to capture the two effects of reproduction and starvation.
The numeric value of α is approximately 2.5029. The numeric value of δ is approximately 4.6692.
Apéry’s constant ζ(3)[edit]
Apery’s constant is the sum of the series
Apéry’s constant is an irrational number and its numeric value is approximately 1.2020569.
Despite being a special value of the Riemann zeta function, Apéry’s constant arises naturally in a number of physical problems, including in the second- and third-order terms of the electron’s gyromagnetic ratio, computed using quantum electrodynamics.[6]
The golden ratio φ[edit]
The number φ, also called the golden ratio, turns up frequently in geometry, particularly in figures with pentagonal symmetry. Indeed, the length of a regular pentagon’s diagonal is φ times its side. The vertices of a regular icosahedron are those of three mutually orthogonal golden rectangles. Also, it appears in the Fibonacci sequence, related to growth by recursion.[7] Kepler proved that it is the limit of the ratio of consecutive Fibonacci numbers.[8] The golden ratio has the slowest convergence of any irrational number.[9] It is, for that reason, one of the worst cases of Lagrange’s approximation theorem and it is an extremal case of the Hurwitz inequality for Diophantine approximations. This may be why angles close to the golden ratio often show up in phyllotaxis (the growth of plants).[10] It is approximately equal to 1.6180339887498948482, or, more precisely 2⋅sin(54°) = 
The Euler–Mascheroni constant γ[edit]
The area between the two curves (red) tends to a limit, namely the Euler-Mascheroni constant.
The Euler–Mascheroni constant is defined as the following limit:
The Euler–Mascheroni constant appears in Mertens’ third theorem and has relations to the gamma function, the zeta function and many different integrals and series.
It is yet unknown whether 
The numeric value of 
Conway’s constant λ[edit]
Conway’s constant is the invariant growth rate of all derived strings similar to the look-and-say sequence (except for one trivial one).[11]
It is given by the unique positive real root of a polynomial of degree 71 with integer coefficients.[11]
The value of λ is approximately 1.30357.
Khinchin’s constant K[edit]
If a real number r is written as a simple continued fraction:
where ak are natural numbers for all k, then, as the Russian mathematician Aleksandr Khinchin proved in 1934, the limit as n tends to infinity of the geometric mean: (a1a2…an)1/n exists and is a constant, Khinchin’s constant, except for a set of measure 0.[12]
The numeric value of K is approximately 2.6854520010.
The Glaisher–Kinkelin constant A[edit]
The Glaisher–Kinkelin constant is defined as the limit:
It appears in some expressions of the derivative of the Riemann zeta function. It has a numerical value of approximately 1.2824271291.
Mathematical curiosities and unspecified constants[edit]
Simple representatives of sets of numbers[edit]
This Babylonian clay tablet gives an approximation of the square root of 2 in four sexagesimal figures: 1; 24, 51, 10, which is accurate to about six decimal figures.[13]
Some constants, such as the square root of 2, Liouville’s constant and Champernowne constant:
are not important mathematical invariants but retain interest being simple representatives of special sets of numbers, the irrational numbers,[14] the transcendental numbers[15] and the normal numbers (in base 10)[16] respectively. The discovery of the irrational numbers is usually attributed to the Pythagorean Hippasus of Metapontum who proved, most likely geometrically, the irrationality of the square root of 2. As for Liouville’s constant, named after French mathematician Joseph Liouville, it was the first number to be proven transcendental.[17]
Chaitin’s constant Ω[edit]
In the computer science subfield of algorithmic information theory, Chaitin’s constant is the real number representing the probability that a randomly chosen Turing machine will halt, formed from a construction due to Argentine-American mathematician and computer scientist Gregory Chaitin. Chaitin’s constant, though not being computable, has been proven to be transcendental and normal. Chaitin’s constant is not universal, depending heavily on the numerical encoding used for Turing machines; however, its interesting properties are independent of the encoding.
Unspecified constants[edit]
When unspecified, constants indicate classes of similar objects, commonly functions, all equal up to a constant—technically speaking, this may be viewed as ‘similarity up to a constant’. Such constants appear frequently when dealing with integrals and differential equations. Though unspecified, they have a specific value, which often is not important.
Solutions with different constants of integration of 
In integrals[edit]
Indefinite integrals are called indefinite because their solutions are only unique up to a constant. For example, when working over the field of real numbers
where C, the constant of integration, is an arbitrary fixed real number.[18] In other words, whatever the value of C, differentiating sin x + C with respect to x always yields cos x.
In differential equations[edit]
In a similar fashion, constants appear in the solutions to differential equations where not enough initial values or boundary conditions are given. For example, the ordinary differential equation y‘ = y(x) has solution Cex where C is an arbitrary constant.
When dealing with partial differential equations, the constants may be functions, constant with respect to some variables (but not necessarily all of them). For example, the PDE
has solutions f(x,y) = C(y), where C(y) is an arbitrary function in the variable y.
Notation[edit]
Representing constants[edit]
It is common to express the numerical value of a constant by giving its decimal representation (or just the first few digits of it). For two reasons this representation may cause problems. First, even though rational numbers all have a finite or ever-repeating decimal expansion, irrational numbers don’t have such an expression making them impossible to completely describe in this manner. Also, the decimal expansion of a number is not necessarily unique. For example, the two representations 0.999… and 1 are equivalent[19][20] in the sense that they represent the same number.
Calculating digits of the decimal expansion of constants has been a common enterprise for many centuries. For example, German mathematician Ludolph van Ceulen of the 16th century spent a major part of his life calculating the first 35 digits of pi.[21] Using computers and supercomputers, some of the mathematical constants, including π, e, and the square root of 2, have been computed to more than one hundred billion digits. Fast algorithms have been developed, some of which — as for Apéry’s constant — are unexpectedly fast.
Some constants differ so much from the usual kind that a new notation has been invented to represent them reasonably. Graham’s number illustrates this as Knuth’s up-arrow notation is used.[22][23]
It may be of interest to represent them using continued fractions to perform various studies, including statistical analysis. Many mathematical constants have an analytic form, that is they can be constructed using well-known operations that lend themselves readily to calculation. Not all constants have known analytic forms, though; Grossman’s constant[24] and Foias’ constant[25] are examples.
Symbolizing and naming of constants[edit]
Symbolizing constants with letters is a frequent means of making the notation more concise. A common convention, instigated by René Descartes in the 17th century and Leonhard Euler in the 18th century, is to use lower case letters from the beginning of the Latin alphabet 

However, for more important constants, the symbols may be more complex and have an extra letter, an asterisk, a number, a lemniscate or use different alphabets such as Hebrew, Cyrillic or Gothic.[23]
Sometimes, the symbol representing a constant is a whole word. For example, American mathematician Edward Kasner’s 9-year-old nephew coined the names googol and googolplex.[23][26]
Other names are either related to the meaning of the constant (universal parabolic constant, twin prime constant, …) or to a specific person (Sierpiński’s constant, Josephson constant, and so on).
Selected mathematical constants[edit]
Abbreviations used:
- R – Rational number, I – Irrational number (may be algebraic or transcendental), A – Algebraic number (irrational), T – Transcendental number
- Gen – General, NuT – Number theory, ChT – Chaos theory, Com – Combinatorics, Inf – Information theory, Ana – Mathematical analysis
| Symbol | Value | Name | Field | N | First described | Number of known decimal digits |
|---|---|---|---|---|---|---|
|
0 |
= 0 | Zero | Gen | R | by c. 500 BC | all |
|
1 |
= 1 | One, Unity | Gen | R | all | |
|
i |
= √–1 | Imaginary unit, unit imaginary number | Gen, Ana | A | by c. 1500 | all |
|
π |
≈ 3.14159 26535 89793 23846 26433 83279 50288 | Pi, Archimedes’ constant or Ludolph’s number | Gen, Ana | T | by c. 2600 BC | 62,831,853,071,796[27] |
|
e |
≈ 2.71828 18284 59045 23536 02874 71352 66249 | e, Napier’s constant, or Euler’s number | Gen, Ana | T | 1618 | 31,415,926,535,897[27] |
|
√2 |
≈ 1.41421 35623 73095 04880 16887 24209 69807 | Pythagoras’ constant, square root of 2 | Gen | A | by c. 800 BC | 10,000,000,000,000[27] |
|
√3 |
≈ 1.73205 08075 68877 29352 74463 41505 87236 | Theodorus’ constant, square root of 3 | Gen | A | by c. 800 BC | 2,199,023,255,552[28] |
|
√5 |
≈ 2.23606 79774 99789 69640 91736 68731 27623 | Square root of 5 | Gen | A | by c. 800 BC | 2,199,023,255,552[28] |
|
|
≈ 0.57721 56649 01532 86060 65120 90082 40243 | Euler–Mascheroni constant | Gen, NuT | 1735 | 600,000,000,100[28] | |
|
|
≈ 1.61803 39887 49894 84820 45868 34365 63811 | Golden ratio | Gen | A | by c. 200 BC | 10,000,000,000,000[28] |
|
|
 [29][30][31][32] [29][30][31][32]
|
de Bruijn–Newman constant | NuT, Ana | 1950 | none | |
|
M1 |
≈ 0.26149 72128 47642 78375 54268 38608 69585 | Meissel–Mertens constant | NuT | 1866 1874 |
8,010 | |
|
|
≈ 0.28016 94990 23869 13303 | Bernstein’s constant[33] | Ana | |||
|
|
≈ 0.30366 30028 98732 65859 74481 21901 55623 | Gauss–Kuzmin–Wirsing constant | Com | 1974 | 385 | |
|
|
≈ 0.35323 63718 54995 98454 35165 50432 68201 | Hafner–Sarnak–McCurley constant | NuT | 1993 | ||
|
L |
≈ 0.5 | Landau’s constant | Ana | 1 | ||
|
Ω |
≈ 0.56714 32904 09783 87299 99686 62210 35554 | Omega constant | Ana | T | ||
|
|
≈ 0.62432 99885 43550 87099 29363 83100 83724 | Golomb–Dickman constant | Com, NuT | 1930 1964 |
||
| ≈ 0.64341 05462 | Cahen’s constant | T | 1891 | 4000 | ||
|
C2 |
≈ 0.66016 18158 46869 57392 78121 10014 55577 | Twin prime constant | NuT | 5,020 | ||
| ≈ 0.66274 34193 49181 58097 47420 97109 25290 | Laplace limit | |||||
|
|
≈ 0.70258 | Embree–Trefethen constant | NuT | |||
|
K |
≈ 0.76422 36535 89220 66299 06987 31250 09232 | Landau–Ramanujan constant | NuT | 30,010 | ||
|
B4 |
≈ 0.87058 838 | Brun’s constant for prime quadruplets | NuT | 8 | ||
|
G |
≈ 0.91596 55941 77219 01505 46035 14932 38411 | Catalan’s constant | Com | 1,000,000,001,337[28] | ||
|
B´L |
= 1 | Legendre’s constant | NuT | R | all | |
|
K |
≈ 1.13198 824 | Viswanath’s constant | NuT | 8 | ||
|
|
≈ 1.20205 69031 59594 28539 97381 61511 44999 | Apéry’s constant | I | 1979 | 1,200,000,000,100[28] | |
|
|
≈ 1.30357 72690 34296 39125 70991 12152 55189 | Conway’s constant | NuT | A | ||
|
|
≈ 1.30637 78838 63080 69046 86144 92602 60571 | Mills’ constant | NuT | 1947 | 6850 | |
|
|
≈ 1.32471 79572 44746 02596 09088 54478 09734 | Plastic constant | NuT | A | 1928 | |
|
|
≈ 1.45136 92348 83381 05028 39684 85892 02744 | Ramanujan–Soldner constant | NuT | I | 75,500 | |
| ≈ 1.45607 49485 82689 67139 95953 51116 54356 | Backhouse’s constant[34] | |||||
| ≈ 1.46707 80794 | Porter’s constant[35] | NuT | 1975 | |||
| ≈ 1.53960 07178 | Lieb’s square ice constant[36] | Com | A | 1967 | ||
|
EB |
≈ 1.60669 51524 15291 76378 33015 23190 92458 | Erdős–Borwein constant | NuT | I | ||
| ≈ 1.70521 11401 05367 76428 85514 53434 50816 | Niven’s constant | NuT | 1969 | |||
|
B2 |
≈ 1.90216 05831 04 | Brun’s constant for twin primes | NuT | 1919 | 12 | |
|
P2 |
≈ 2.29558 71493 92638 07403 42980 49189 49039 | Universal parabolic constant | Gen | T | ||
|
|
≈ 2.50290 78750 95892 82228 39028 73218 21578 | Feigenbaum constant | ChT | |||
|
K |
≈ 2.58498 17595 79253 21706 58935 87383 17116 | Sierpiński’s constant | ||||
| ≈ 2.68545 20010 65306 44530 97148 35481 79569 | Khinchin’s constant | NuT | 1934 | 7350 | ||
|
F |
≈ 2.80777 02420 28519 36522 15011 86557 77293 | Fransén–Robinson constant | Ana | |||
| ≈ 3.27582 29187 21811 15978 76818 82453 84386 | Lévy’s constant | NuT | ||||
|
|
≈ 3.35988 56662 43177 55317 20113 02918 92717 | Reciprocal Fibonacci constant[37] | I | |||
|
|
≈ 4.66920 16091 02990 67185 32038 20466 20161 | Feigenbaum constant | ChT | 1975 |
See also[edit]
- Invariant (mathematics)
- List of mathematical symbols
- List of numbers
- Physical constant
Notes[edit]
- ^ Weisstein, Eric W. «Constant». mathworld.wolfram.com. Retrieved 2020-08-08.
- ^ Grinstead, C.M.; Snell, J.L. «Introduction to probability theory». p. 85. Retrieved 2007-12-09.
- ^ Collet & Eckmann (1980). Iterated maps on the inerval as dynamical systems. Birkhauser. ISBN 3-7643-3026-0.
- ^ Finch, Steven (2003). Mathematical constants. Cambridge University Press. p. 67. ISBN 0-521-81805-2.
- ^ May, Robert (1976). Theoretical Ecology: Principles and Applications. Blackwell Scientific Publishers. ISBN 0-632-00768-0.
- ^ Steven Finch. «Apéry’s constant». MathWorld.
- ^ Livio, Mario (2002). The Golden Ratio: The Story of Phi, The World’s Most Astonishing Number. New York: Broadway Books. ISBN 0-7679-0815-5.
- ^ Tatersall, James (2005). Elementary number theory in nine chapters (2nd ed.
- ^ «The Secret Life of Continued Fractions»
- ^ Fibonacci Numbers and Nature — Part 2 : Why is the Golden section the «best» arrangement?, from Dr. Ron Knott’s Fibonacci Numbers and the Golden Section, retrieved 2012-11-29.
- ^ a b Steven Finch. «Conway’s Constant». MathWorld.
- ^ Steven Finch. «Khinchin’s Constant». MathWorld.
- ^ Fowler, David; Eleanor Robson (November 1998). «Square Root Approximations in Old Babylonian Mathematics: YBC 7289 in Context». Historia Mathematica. 25 (4): 368. doi:10.1006/hmat.1998.2209.
Photograph, illustration, and description of the root(2) tablet from the Yale Babylonian Collection
High resolution photographs, descriptions, and analysis of the root(2) tablet (YBC 7289) from the Yale Babylonian Collection - ^ Bogomolny, Alexander. «Square root of 2 is irrational».
- ^ Aubrey J. Kempner (Oct 1916). «On Transcendental Numbers». Transactions of the American Mathematical Society. Transactions of the American Mathematical Society, Vol. 17, No. 4. 17 (4): 476–482. doi:10.2307/1988833. JSTOR 1988833.
- ^ Champernowne, David (1933). «The Construction of Decimals Normal in the Scale of Ten». Journal of the London Mathematical Society. 8 (4): 254–260. doi:10.1112/jlms/s1-8.4.254.
- ^ Weisstein, Eric W. «Liouville’s Constant». MathWorld.
- ^ Edwards, Henry; David Penney (1994). Calculus with analytic geometry (4e ed.). Prentice Hall. p. 269. ISBN 0-13-300575-5.
- ^ Rudin, Walter (1976) [1953]. Principles of mathematical analysis (3e ed.). McGraw-Hill. p.61 theorem 3.26. ISBN 0-07-054235-X.
- ^ Stewart, James (1999). Calculus: Early transcendentals (4e ed.). Brooks/Cole. p. 706. ISBN 0-534-36298-2.
- ^ Ludolph van Ceulen Archived 2015-07-07 at the Wayback Machine – biography at the MacTutor History of Mathematics archive.
- ^ Knuth, Donald (1976). «Mathematics and Computer Science: Coping with Finiteness. Advances in Our Ability to Compute are Bringing Us Substantially Closer to Ultimate Limitations». Science. 194 (4271): 1235–1242. doi:10.1126/science.194.4271.1235. PMID 17797067. S2CID 1690489.
- ^ a b c «mathematical constants». Archived from the original on 2012-09-07. Retrieved 2007-11-27.
- ^ Weisstein, Eric W. «Grossman’s constant». MathWorld.
- ^ Weisstein, Eric W. «Foias’ constant». MathWorld.
- ^ Edward Kasner and James R. Newman (1989). Mathematics and the Imagination. Microsoft Press. p. 23.
- ^ a b c Alexander J. Yee. «y-cruncher – A Multi-Threaded Pi Program». numberworld.org. Retrieved 14 March 2020.
- ^ a b c d e f Alexander J. Yee. «Records Set by y-cruncher». numberworld.org. Retrieved 14 March 2020.
- ^ Rodgers, Brad; Tao, Terence (2018). «The De Bruijn–Newman constant is non-negative». arXiv:1801.05914 [math.NT]. (preprint)
- ^ «The De Bruijn-Newman constant is non-negative». 19 January 2018. Retrieved 2018-01-19. (announcement post)
- ^ Polymath, D.H.J. (2019), «Effective approximation of heat flow evolution of the Riemann ξ function, and a new upper bound for the de Bruijn-Newman constant», Research in the Mathematical Sciences, 6 (3), arXiv:1904.12438, Bibcode:2019arXiv190412438P, doi:10.1007/s40687-019-0193-1, S2CID 139107960
- ^
Platt, Dave; Trudgian, Tim (2021). «The Riemann hypothesis is true up to 3·1012». Bulletin of the London Mathematical Society. 53 (3): 792–797. arXiv:2004.09765. doi:10.1112/blms.12460. S2CID 234355998.(preprint) - ^ Weisstein, Eric W. «Bernstein’s Constant». MathWorld.
- ^ Weisstein, Eric W. «Backhouse’s Constant». MathWorld.
- ^ Weisstein, Eric W. «Porter’s Constant». MathWorld.
- ^ Weisstein, Eric W. «Lieb’s Square Ice Constant». MathWorld.
- ^ Weisstein, Eric W. «Reciprocal Fibonacci Constant». MathWorld.
External links[edit]
- Constants – from Wolfram MathWorld
- Inverse symbolic calculator (CECM, ISC) (tells you how a given number can be constructed from mathematical constants)
- On-Line Encyclopedia of Integer Sequences (OEIS)
- Simon Plouffe’s inverter
- Steven Finch’s page of mathematical constants (BROKEN LINK)
- Steven R. Finch, «Mathematical Constants,» Encyclopedia of mathematics and its applications, Cambridge University Press (2003).
- Xavier Gourdon and Pascal Sebah’s page of numbers, mathematical constants and algorithms
Функция или значение, которое не изменяется в процессе
В математике, t Слово константа может иметь несколько значений. Как прилагательное, оно относится к отсутствию дисперсии (т. Е. Неизменность по отношению к некоторому другому значению ); как существительное, оно имеет два различных значения:
- фиксированное и четко определенное число или другой неизменяющийся математический объект. Термины математическая константа или физическая константа иногда используются для различения этого значения.
- A функция, значение которой остается неизменным (т. Е. постоянная функция ). Такая константа обычно представлена переменной, которая не зависит от основной рассматриваемой переменной (ов). Это имеет место, например, для константы интегрирования , которая представляет собой произвольную постоянную функцию (т. Е. Не зависящую от переменной интегрирования), добавленную к конкретной первообразной , чтобы получить все первообразные данной функции.
Например, общая квадратичная функция обычно записывается как:
- ax 2 + bx + c, { displaystyle ax ^ {2} + bx + c ,,}
где a, b и c — константы (или параметры), а xa переменная — заполнитель для аргумента изучаемой функции. Более явный способ обозначить эту функцию:
- x ↦ ax 2 + bx + c, { displaystyle x mapsto ax ^ {2} + bx + c ,,}
, который делает статус аргумента функции x (и, следовательно, постоянство a, b и c) ясно. В этом примере a, b и c — коэффициенты полинома . Поскольку c встречается в члене, который не включает x, он называется постоянным членом полинома и может рассматриваться как коэффициент при x. В более общем смысле, любой полиномиальный член или выражение степени нуля является константой.
Содержание
- 1 Постоянная функция
- 2 Контекстная зависимость
- 3 Известные математические константы
- 4 Константы в исчислении
- 4.1 Примеры
- 5 См. также
- 6 Ссылки
- 7 Внешние ссылки
Постоянная функция
Константа может использоваться для определения постоянной функции который игнорирует свои аргументы и всегда дает одно и то же значение. Постоянная функция одной переменной, например f (x) = 5 { displaystyle f (x) = 5}
Контекстная зависимость
Контекстно-зависимый характер понятия «константа» можно увидеть в этом примере из элементарного исчисления:
- ddx 2 x = lim h → 0 2 x + h — 2 xh = lim h → 0 2 x 2 h — 1 h = 2 x lim h → 0 2 h — 1 h, поскольку x постоянно (т.е. не зависит от h) = 2 x ⋅ constant, где константа означает не зависит от х. { displaystyle { begin {align} { frac {d} {dx}} 2 ^ {x} = lim _ {h to 0} { frac {2 ^ {x + h} -2 ^ { x}} {h}} = lim _ {h to 0} 2 ^ {x} { frac {2 ^ {h} -1} {h}} \ [8pt] = 2 ^ {x} lim _ {h to 0} { frac {2 ^ {h} -1} {h}} { text {, поскольку}} x { text {является постоянным (т.е. не зависит от}} h { text {)}} \ [8pt] = 2 ^ {x} cdot mathbf {constant,} { text {where}} mathbf {constant} { text {означает не зависит от}} x. end {align}}}
«Константа» означает независимость от какой-либо переменной; не меняется при изменении этой переменной. В первом случае это означает, что не зависит от h; во втором — не зависит от x. Константа в более узком контексте может рассматриваться как переменная в более широком контексте.
Известные математические константы
Некоторые значения часто встречаются в математике и обычно обозначаются специальным символом. Эти стандартные символы и их значения называются математическими константами. Примеры включают:
- 0 (ноль ).
- 1 (один ), натуральное число после нуля.
- π (pi ), константа, представляющая отношение длины окружности круга к его диаметру, приблизительно равное 3,141592653589793238462643.
- e, приблизительно равное 2,718281828459045235360287.
- i, мнимая единица такая, что я = -1.
- 2 { displaystyle { sqrt {2}}}
(квадратный корень из 2 ), длина диагонали квадрата со сторонами, равными единице, приблизительно равно 1,414213562373095048801688.
- φ (золотое сечение ), приблизительно равно 1,618033988749894848204586, или алгебраически 1 + 5 2 { displaystyle 1 + { sqrt {5} } over 2}
.
Константы в исчислении
В исчислении константы обрабатываются несколькими способами в зависимости от операции. Например, производная постоянной функции равна нулю. Это связано с тем, что производная измеряет скорость изменения функции по отношению к переменной, а поскольку константы по определению не изменяются, их производная, следовательно, равна нулю.
И наоборот, при интегрировании постоянной функции, постоянная умножается на переменную интегрирования. Во время оценки предела константа остается такой же, как была до и после оценки.
Интегрирование функции одной переменной часто включает константу интегрирования. Это возникает из-за того, что интегральный оператор является обратным к дифференциальному оператору, что означает, что цель интегрирования — восстановить исходную функцию до дифференцирования.. Дифференциал постоянной функции равен нулю, как отмечалось выше, а дифференциальный оператор является линейным оператором, поэтому функции, которые отличаются только постоянным членом, имеют одинаковую производную. Чтобы подтвердить это, к неопределенному интегралу добавляется постоянная интегрирования; это гарантирует включение всех возможных решений. Константа интегрирования обычно обозначается как «c» и представляет собой константу с фиксированным, но неопределенным значением.
Примеры
Если f — постоянная функция, такая что f (x) = 72 { displaystyle f (x) = 72}
- е ‘(Икс) знак равно 0 ∫ е (Икс) dx = 72 Икс + с { Displaystyle { begin {Выровнено} f’ (х) = 0 \ int f (x) , dx = 72x + c end {align}}}
См. Также
- Константа (значения)
- Выражение
- Список математических констант
- Физическая константа
Ссылки
Внешние ссылки
Носители, относящиеся к Константам на Викискладе
Математические постоянные
В противоположность переменным величинам существуют математические постоянные. Математическая постоянная или константа — это величина, значение которой неизменно. Главной отличительной чертой математических констант является их независимость от физических измерений.
Если принять диаметр окружности за единицу, то длина окружности — это число «пи».
Все математические константы имеют буквенный символ.
| Символ | Приближенное значение | Название | Область | Значение | Число известных знаков |
|---|---|---|---|---|---|
| π | ≈ 3,141 592 653 589 793 238 462 643 383 279 502 88 | число Пи, Архимедова константа | мат | Трансцендентное число | 1 241 100 000 000 |
| e | ≈ 2,718 281 828 459 045 235 360 287 471 352 662 50 | константа Непера, основание натурального логарифма | мат | Трансцендентное число | 12 884 901 000 |
| ≈ | 1,414 213 562 373 095 048 801 688 724 209 698 08 | константа Пифагора, квадратный корень из 2 | мат | Иррациональное число | 137 438 953 444 |
| ≈ | 1,732 050 807 568 877 293 527 446 341 505 872 37 | константа Теодоруса, квадратный корень из 3 | мат | Иррациональное число | |
| γ | ≈ 0,577 215 664 901 532 860 606 512 090 082 402 43 | постоянная Эйлера — Маскерони | мат, Теория Чисел | ? | 108 000 000 |
| φ | ≈ 1,618 033 988 749 894 848 204 586 834 365 638 12 | золотое сечение | мат | Алгебраическое | 3 141 000 000 |
| β* | ≈ 0,702 58 | константа Эмбри — Трефтена | Теория Чисел | ||
| δ | ≈ 4,669 201 609 102 990 671 853 203 820 466 201 61 | константа Фейгенбаума | Теория Хаоса | ||
| α | ≈ 2,502 907 875 095 892 822 283 902 873 218 215 78 | константа Фейгенбаума | Теория Хаоса | ||
| C2 | ≈ 0,660 161 815 846 869 573 927 812 110 014 555 77 | константа простых близнецов | Теория Чисел | 5 020 | |
| M1 | ≈ 0,261 497 212 847 642 783 755 426 838 608 695 85 | константа Мейсселя — Мертенса | Теория Чисел | 8010 | |
| B2 | ≈ 1,902 160 582 3 | константа Бруна для простых близнецов | Теория Чисел | 10 | |
| B4 | ≈ 0,870 588 380 0 | константа Бруна для простых четвёрок | Теория Чисел | ||
| Λ | ≈ -2,7 ? 10−9 | константа де Брюйна — Ньюмана | Теория Чисел | ||
| K | ≈ 0,915 965 594 177 219 015 054 603 514 932 384 11 | константа Каталана | Комбинаторика | 201 000 000 | |
| K | ≈ 0,764 223 653 589 220 66 | константа Ландау — Рамануджана | Теория Чисел | Иррациональное число | 30 010 |
| K | ≈ 1,131 988 24 | константа Висваната 1 | Теория Чисел | 8 | |
| B´L | ≈ 1,083 66 | константа Лежандра | Теория Чисел | ||
| μ | ≈ 1,451 369 234 883 381 050 283 968 485 892 027 | константа Рамануджана — Солднера | Теория Чисел | 75 500 | |
| E’B | ≈ 1,606 695 152 415 291 763 | константа Эрдёша — Борвейна | Теория Чисел | Иррациональное число | |
| Ω | ≈ 0,0078749969978123844 | Константа Хайтина | Алгоритмическая Теория информации | Трансцендентное число |
Поделиться ссылкой
Константа (математика)
Из Википедии, бесплатной энциклопедии
Перейти к навигации
Перейти к поиску
В математике слово константа может иметь несколько значений. Как прилагательное, оно относится к неизменности (т.е. неизменности по отношению к некоторому другому значению ); как существительное оно имеет два разных значения:
- Фиксированное и четко определенное число или другой неизменный математический объект . Иногда для обозначения этого значения используются термины математическая константа или физическая константа .
- Функция , значение которой остается неизменным (т.е. функция , постоянная ). [1] Такая константа обычно представлена переменной, которая не зависит от основной рассматриваемой переменной (ов). Это имеет место, например, для константы интегрирования , которая представляет собой произвольную постоянную функцию (т. Е. Ту, которая не зависит от переменной интегрирования), добавляемую к конкретной первообразной, чтобы получить все первообразные данной функции.
Например, общая квадратичная функция обычно записывается как:
где a , b и c — константы (или параметры), а x — переменная — заполнитель для аргумента изучаемой функции. Более явный способ обозначить эту функцию —
что делает ясным статус функции-аргумента x (и, как следствие, постоянство a , b и c ). В этом примере а , б и с являются коэффициентами этого полинома . Поскольку c встречается в члене, который не включает x , он называется постоянным членом многочлена и может рассматриваться как коэффициент при x 0 . В более общем смысле, любой полиномиальный член или выражение нулевой степени является константой. [2] : 18
Постоянная функция
Константа может использоваться для определения постоянной функции, которая игнорирует свои аргументы и всегда дает одно и то же значение. Постоянная функция одной переменной, например, имеет график горизонтальной прямой, параллельной оси x . Такая функция всегда принимает одно и то же значение (в данном случае 5), потому что ее аргумент не появляется в выражении, определяющем функцию.
Контекстная зависимость
Контекстно-зависимый характер понятия «константа» можно увидеть в этом примере из элементарного исчисления:
«Константа» означает отсутствие зависимости от какой-либо переменной; не меняется при изменении этой переменной. В первом случае это означает, что не зависит от h ; во втором — не зависит от x . Константу в более узком контексте можно рассматривать как переменную в более широком контексте.
Известные математические константы
Некоторые значения часто встречаются в математике и условно обозначаются специальным символом. Эти стандартные символы и их значения называются математическими константами. Примеры включают:
- 0 ( ноль ).
- 1 ( один ), натуральное число после нуля.
- π ( пи ), константа, представляющая отношение длины окружности к ее диаметру, приблизительно равная 3,141592653589793238462643. [3]
- е , примерно равно 2,718281828459045235360287.
- i , мнимая единица такая, что i 2 = −1 .
- ( корень квадратный из 2 ), длина диагонали квадрата со сторонами, равными единице, примерно равна 1,414213562373095048801688.
- φ ( золотое сечение ), приблизительно равное 1,618033988749894848204586, или алгебраически,.
Константы в исчислении
В исчислении константы обрабатываются по-разному в зависимости от операции. Например, производная постоянной функции равна нулю. Это связано с тем, что производная измеряет скорость изменения функции по отношению к переменной, а поскольку константы по определению не меняются, их производная, следовательно, равна нулю.
И наоборот, при интегрировании постоянной функции постоянная умножается на переменную интегрирования. Во время оценки предела константа остается такой же, как была до и после оценки.
Интегрирование функции одной переменной часто включает постоянную интегрирования . Это возникает из — за того , что интегральный оператор является обратным от дифференциального оператора , а это означает , что цель интеграции восстановить исходную функцию , прежде чем дифференциации. Дифференциал постоянной функции равен нулю, как отмечалось выше, а дифференциальный оператор является линейным оператором, поэтому функции, которые отличаются только постоянным членом, имеют одинаковую производную. Чтобы признать это, к неопределенному интегралу добавляется постоянная интегрирования.; это гарантирует включение всех возможных решений. Константа интегрирования обычно обозначается как «c» и представляет собой константу с фиксированным, но неопределенным значением.
Примеры
Если f — постоянная функция такая, чтодля каждого x тогда
См. Также
- Константа (значения)
- Выражение
- Уровень установлен
- Список математических констант
- Физическая постоянная
Ссылки
- ^ Вайсштейн, Эрик В. «Константа» . mathworld.wolfram.com . Проверено 8 августа 2020 .
- Перейти ↑ Foerster, Paul A. (2006). Алгебра и тригонометрия: функции и приложения, Издание для учителей (Классический ред.). Река Аппер Сэдл, штат Нью-Джерси: Prentice Hall . ISBN 0-13-165711-9.
- ^ Арндт, Йорг; Хенель, Кристоф (2001). Пи — развязанный . Springer. п. 240 . ISBN 978-3540665724.
Внешние ссылки
СМИ, связанные с константами, на Викискладе?
В основе нашей Вселенной стоят числа, также известные как фундаментальные константы. Они показывают, как движутся галактики, как расширяется Вселенная, как вообще работает пространство и время. Рассказываем, кто их открыл и за что отвечает каждое число.
Читайте «Хайтек» в
Что такое математическая константа?
В противоположность переменным величинам существуют математические постоянные. Математическая постоянная, или константа — это величина, значение которой неизменно. Главной отличительной чертой математических констант является их независимость от физических измерений. Все математические константы имеют буквенный символ.
Число Пи
Число Пи (π) — это математическая константа, равная отношению длины окружности к ее диаметру. Десятичное представление числа никогда не заканчивается и является эталоном для высокопроизводительных вычислений.
Чему равно: 3,1415926535…
На сегодняшний день число Пи рассчитали с точностью до 62,8 трлн знаков после запятой — с помощью 32-ядерных процессоров AMD.
Если измерить веревкой длину окружности, получится, что она равна приблизительно трем ее диаметрам. Человечество выяснило это еще в древности. Кстати, это соотношение подходит для любой окружности — неважно, речь о часах или колесе обозрения. Иными словами, все окружности в мире связаны этой математической константой. Еще до нашей эры люди знали, что это число чуть больше трех. Вопрос в том, насколько. Столетия эта загадка не давала покоя мыслителям, поскольку имела большое значение и была почти высчитана. Но это «почти» растянулось на несколько тысяч лет.
Точное авторство числа Пи неизвестно. Вообще, открытие приписывается древним индийцам, грекам, китайцам и прочим хорошим людям. Впервые обозначил его греческой буквой π в начале XVIII века английский математик Уильям Джонс.
Числу π столько же лет, сколько всей математике: около 4 тыс. Старейшие шумерские таблички приводят для него цифру 25/8, или 3,125. Ошибка — меньше процента. Вавилоняне абстрактной математикой особо не увлекались, так что π вывели опытным путем, просто измеряя длину окружностей. Кстати, это первый эксперимент по численному моделированию мира.
Число Бога
Число Фи (φ) — число Бога, Золотое Сечение, Золотая Пропорция — у него много названий. Сам по себе это отношение одной части чего-либо к другой с коэффициентом 1,618 (это 61,8%), или 62% на 38%.
Чему равно: 1,6180339887…
Классическое определение Золотой Пропорции: меньшее относится к большему так, как большее относится к целому, с коэффициентом 1,618.
Принято считать, что впервые закономерности соотношения размеров тела человека и отдельных его частей обобщил и сформулировал в 1855 году немецкий исследователь Цейзинг в своем научном труде «Эстетические исследования». За основу своей теории он взял учение о Золотом Сечении.
Еще в VI веке до н. э. древнегреческий философ и математик Пифагор ввел в научный обиход понятие «золотое деление». «Золотое деление» — это пропорциональное деление отрезка на неравные части. При этом меньший отрезок так относится к большему, как больший отрезок относится ко всему отрезку. a : b = b : c или с : b = b : а.
История Золотого Сечения связана еще с одним известным итальянским математиком Фибоначчи. До наших времен дошел ряд чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т. д., известный как ряд Фибоначчи.
Особенность последовательности данных чисел заключается в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих (2+3=5, 3+5=8), а отношение смежных чисел ряда приближается к отношению Золотого Сечения (21:34=0,617, а 34:55=0,618). Впоследствии все исследователи Золотого Сечения в растительном и животном мире, искусстве и анатомии приходили к этому ряду как арифметическому выражению закона золотого деления. Интересно, что свой закон Фибоначчи вывел, подсчитывая количество рожденных кроликов от пары кроликов за год.
Так в чем же ореол таинственности Золотого сечения?
Все, что растет и приобретает какую-либо форму в живом мире нашей планеты ,— растет вверх или закручивается по спирали. Спираль (например, морская раковина) — пример соотношения в пропорциях Золотого Сечения. Спирали прослеживаются в расположении семян в шишках хвойных деревьев, в семенах подсолнечника и др.
Число Непера
Число е — своего рода двойник π. Если π отвечает за пространство, то е — за время, и тоже проявляет себя почти всюду. Скажем, радиоактивность полония-210 уменьшается в е раз за средний срок жизни одного атома, а раковина моллюска Nautilus — это график степеней е, обернутый вокруг оси.
Чему равно: 2,718281828…
е — основание натурального логарифма, математическая константа, иррациональное и трансцендентное число. Приблизительно равно 2,71828. Иногда его называют числом Эйлера или числом Непера. Обозначается строчной латинской буквой «e».
Иными словами, число е является базовым соотношением роста для всех непрерывно растущих процессов. Оно участвует как в системах с экспоненциальным, так и постоянным ростом: население, радиоактивный распад, подсчет процентов и других. Даже ступенчатые системы, которые не растут равномерно, можно аппроксимировать с помощью числа е.
Также, как любое число можно рассматривать в виде «масштабированной» версии 1 (базовой единицы), любую окружность можно рассматривать в виде «масштабированной» версии единичной окружности (с радиусом 1). И любой коэффициент роста может быть рассмотрен в виде «масштабированной» версии е («единичного» коэффициента роста).
Так что число е — это не случайное, взятое наугад число. Число е воплощает в себе идею, что все непрерывно растущие системы являются масштабированными версиями одного и того же показателя.
Число открыл Джон Непер, шотландский математик, в 1618 году. Самого числа он не упоминал, зато выстроил на его основе свои таблицы логарифмов. Одновременно кандидатами в авторы константы считаются Якоб Бернулли, Лейбниц, Гюйгенс и Эйлер. Достоверно известно только то, что символ е взялся из фамилии последнего.
Как и π, е — трансцендентное число. Говоря проще, его нельзя выразить через дроби и корни. Есть гипотеза, что у таких чисел в бесконечном «хвосте» после запятой встречаются все комбинации цифр, какие только возможны.
Читать далее
Гигантский айсберг A74 столкнулся с побережьем Антарктиды
В США обнаружили рыбу с человеческими зубами
В России специально выпустят диких клещей для борьбы с вредителями










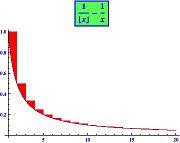
![{displaystyle {begin{aligned}gamma &=lim _{nto infty }left(left(sum _{k=1}^{n}{frac {1}{k}}right)-ln nright)\[5px]end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d88eb872b328b49bf0e02f930ab8e9298e8b79a)
























![{ displaystyle { begin {align} { frac {d} {dx}} 2 ^ {x} = lim _ {h to 0} { frac {2 ^ {x + h} -2 ^ {x} } {h}} = lim _ {h to 0} 2 ^ {x} { frac {2 ^ {h} -1} {h}} \ [8pt] = 2 ^ {x} lim _ {h to 0} { frac {2 ^ {h} -1} {h}} { text {Since}} x { text {является постоянным (т.е. не зависит от}} h { text {)}} \ [8pt] = 2 ^ {x} cdot mathbf {constant,} { text {where}} mathbf {c onstant} { text {означает](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed672b9951131405250911742302ee75b18048f8)
 (квадратный корень из 2 ), длина диагонали квадрата со сторонами, равными единице, приблизительно равно 1,414213562373095048801688.
(квадратный корень из 2 ), длина диагонали квадрата со сторонами, равными единице, приблизительно равно 1,414213562373095048801688. .
.