Рады помочь вам узнать, как пишется слово «косинус».
Пишите и говорите правильно.
О словаре
Сайт создан на основе «Русского орфографического словаря», составленного Институтом русского языка имени В. В. Виноградова РАН. Объем второго издания, исправленного и дополненного, составляет около 180 тысяч слов, и существенно превосходит все предшествующие орфографические словари. Он является нормативным справочником, отражающим с возможной полнотой лексику русского языка начала 21 века и регламентирующим ее правописание.

Слова русского языка,
поиск и разбор слов онлайн
- Слова русского языка
- К
- косинус
Правильно слово пишется: ко́синус
Ударение падает на 1-й слог с буквой о.
Всего в слове 7 букв, 3 гласных, 4 согласных, 3 слога.
Гласные: о, и, у;
Согласные: к, с, н, с.
Номера букв в слове
Номера букв в слове «косинус» в прямом и обратном порядке:
- 7
к
1 - 6
о
2 - 5
с
3 - 4
и
4 - 3
н
5 - 2
у
6 - 1
с
7
Разбор по составу
Разбор по составу (морфемный разбор) слова косинус делается следующим образом:
косинус
Морфемы слова: ко —приставка, синус — корень, нулевое окончание, косинус — основа слова.
- Слова русского языка
- Русский язык
- О сайте
- Подборки слов
- Поиск слов по маске
- Составление словосочетаний
- Словосочетаний из предложений
- Деление слов на слоги
- Словари
- Орфографический словарь
- Словарь устаревших слов
- Словарь новых слов
- Орфография
- Орфограммы
- Проверка ошибок в словах
- Исправление ошибок
- Лексика
- Омонимы
- Устаревшие слова
- Заимствованные слова
- Новые слова
- Диалекты
- Слова-паразиты
- Сленговые слова
- Профессиональные слова
- Интересные слова
А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я
ко́синус, -а
Рядом по алфавиту:
Коса́я Гора́ , (поселок)
ко́свенно , нареч.
ко́свенно-паде́жный
ко́свенность , -и
ко́свенный , кр. ф. -вен, -венна
косе́канс , -а
косёнка , -и, р. мн. -нок
ко́сенький
косе́ть , -е́ю, -е́ет
косе́ц , косца́, тв. косцо́м, р. мн. косцо́в
коси́ки-карате́ , нескл., с.
коси́лка , -и, р. мн. -лок
коси́лка-измельчи́тель , коси́лки-измельчи́теля, ж.
косина́ , -ы́
коси́нка , -и
ко́синус , -а
косинусо́ида , -ы
косисе́но , -а (насекомое)
коси́ть , кошу́, ко́сит (от чего и под кого; сниж.)
коси́ть(ся) , кошу́, ко́сит(ся) (среза́ть(ся) косой)
коси́ть(ся) , кошу́(сь), коси́т(ся) (к косо́й)
коси́ца , -ы, тв. -ей
коси́чка , -и, р. мн. -чек
косма́тевший , (от косма́теть)
косма́теть , -ею, -еет (становиться косматым)
косма́тивший(ся) , (от косма́тить(ся)
косма́тить , -а́чу, -а́тит (кого, что)
косма́титься , -а́чусь, -а́тится
косма́тость , -и
косма́тый
косма́тящий(ся)
Ответ:
Правильное написание слова — косинус
Ударение и произношение — к`осинус
Значение слова -тригонометрическая функция угла, в прямоуголном треугольнике равная отношению к гипотенузе катета, прилежащего к данному острому углу
Выберите, на какой слог падает ударение в слове — НОВОРОЖДЁННЫЙ ?
или
Слово состоит из букв:
К,
О,
С,
И,
Н,
У,
С,
Похожие слова:
арккосинус
Рифма к слову косинус
гервинус, градус, корпус, каптенармус, вкус, иисус, трус, пус, соус, глобус, страус
Толкование слова. Правильное произношение слова. Значение слова.
→
косинусов — существительное, родительный п., мн. ч.
Часть речи: существительное
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Основные формулы тригонометрии — это формулы, устанавливающие связи между основными тригонометрическими функциями. Синус, косинус, тангенс и котангенс связаны между собой множеством соотношений. Ниже приведем основные тригонометрические формулы, а для удобства сгруппируем их по назначению. С использованием данных тригонометрических формул можно находить и решать практически любую задачу из стандартного курса тригонометрии. Сразу отметим, что ниже приведены лишь все тригонометрические формулы, а не их вывод, которому будут посвящены отдельные статьи.
Основные тождества тригонометрии
Тригонометрические тождества дают связь между синусом, косинусом, тангенсом и котангенсом одного угла, позволяя выразить одну функцию через другую (посредством преобразования).
sin2a+cos2a=1tgα=sinαcosα, ctgα=cosαsinαtgα·ctgα=1tg2α+1=1cos2α, ctg2α+1=1sin2α
Эти тождества напрямую вытекают из определений единичной окружности, синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg) и их свойств.
Основные формулы приведения в тригонометрии
Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов, то есть, преобразовывать их.
sinα+2πz=sinα, cosα+2πz=cosαtgα+2πz=tgα, ctgα+2πz=ctgαsin-α+2πz=-sinα, cos-α+2πz=cosαtg-α+2πz=-tgα, ctg-α+2πz=-ctgαsinπ2+α+2πz=cosα, cosπ2+α+2πz=-sinαtgπ2+α+2πz=-ctgα, ctgπ2+α+2πz=-tgαsinπ2-α+2πz=cosα, cosπ2-α+2πz=sinαtgπ2-α+2πz=ctgα, ctgπ2-α+2πz=tgαsinπ+α+2πz=-sinα, cosπ+α+2πz=-cosαtgπ+α+2πz=tgα, ctgπ+α+2πz=ctgαsinπ-α+2πz=sinα, cosπ-α+2πz=-cosαtgπ-α+2πz=-tgα, ctgπ-α+2πz=-ctgαsin3π2+α+2πz=-cosα, cos3π2+α+2πz=sinαtg3π2+α+2πz=-ctgα, ctg3π2+α+2πz=-tgαsin3π2-α+2πz=-cosα, cos3π2-α+2πz=-sinαtg3π2-α+2πz=ctgα, ctg3π2-α+2πz=tgα
Формулы приведения являются следствием периодичности тригонометрических функций.
Все формулы сложения в тригонометрии
Формулы сложения в тригонометрии позволяют выразить тригонометрическую функцию суммы или разности углов через тригонометрические функции этих углов.
sinα±β=sinα·cosβ±cosα·sinβcosα+β=cosα·cosβ-sinα·sinβcosα-β=cosα·cosβ+sinα·sinβtgα±β=tgα±tgβ1±tgα·tgβctgα±β=-1±ctgα·ctgβctgα±ctgβ
На основе формул сложения выводятся тригонометрические формулы кратного угла.
Формулы кратного угла: двойного, тройного и т.д.
sin2α=2·sinα·cosαcos2α=cos2α-sin2α, cos2α=1-2sin2α, cos2α=2cos2α-1tg2α=2·tgα1-tg2α сtg2α=сtg2α-12·сtgα sin3α=3sinα·cos2α-sin3α, sin3α=3sinα-4sin3αcos3α=cos3α-3sin2α·cosα, cos3α=-3cosα+4cos3αtg3α=3tgα-tg3α1-3tg2αctg3α=ctg3α-3ctgα3ctg2α-1
Формулы половинного угла
Формулы половинного угла в тригонометрии являются следствием формул двойного угла и выражают соотношения между основными функциями половинного угла и косинусом целого угла.
sin2α2=1-cosα2cos2α2=1+cosα2tg2α2=1-cosα1+cosαctg2α2=1+cosα1-cosα
Формулы понижения степени
sin2α=1-cos2α2cos2α=1+cos2α2sin3α=3sinα-sin3α4cos3α=3cosα+cos3α4sin4α=3-4cos2α+cos4α8cos4α=3+4cos2α+cos4α8
Часто при расчетах действовать с громоздкими степенями неудобно. Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:
для четных n решение
sinnα=Cn2n2n+12n-1∑k=0n2-1(-1)n2-k·Ckn·cos((n-2k)α)cosnα=Cn2n2n+12n-1∑k=0n2-1Ckn·cos((n-2k)α)
для нечетных n
sinnα=12n-1∑k=0n-12(-1)n-12-k·Ckn·sin((n-2k)α)cosnα=12n-1∑k=0n-12Ckn·cos((n-2k)α)
Сумма и разность тригонометрических функций
Разность и сумму тригонометрических функций можно представить в виде произведения. Разложение на множители разностей синусов и косинусов очень удобно для применения при решении тригонометрических уравнений и упрощении выражений.
sinα+sinβ=2sinα+β2·cosα-β2sinα-sinβ=2sinα-β2·cosα+β2cosα+cosβ=2cosα+β2·cosα-β2cosα-cosβ=-2sinα+β2·sinα-β2, cosα-cosβ=2sinα+β2·sinβ-α2
Произведение тригонометрических функций
Если формулы суммы и разности функций позволяют перейти к их произведению или умножению, то формулы произведения (здесь нужно умножать) тригонометрических функций осуществляют обратный переход — от произведения к сумме. Рассматриваются формулы произведения синусов, косинусов и синуса на косинус.
sinα·sinβ=12·(cos(α-β)-cos(α+β))cosα·cosβ=12·(cos(α-β)+cos(α+β))sinα·cosβ=12·(sin(α-β)+sin(α+β))
Универсальная тригонометрическая подстановка
Все основные тригонометрические функции — тангенс, котангенс, синус, косинус — могут быть выражены через тангенс половинного угла.
sinα=2tgα21+tg2α2cosα=1-tg2α21+tg2α2tgα=2tgα21-tg2α2ctgα=1-tg2α22tgα2
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Запрос «sin» перенаправляется сюда; см. также другие значения.
Запрос «sec» перенаправляется сюда; см. также другие значения.
Запрос «Синус» перенаправляется сюда; см. также другие значения.
Рис. 1
Графики тригонометрических функций: синуса косинуса тангенса котангенса секанса косеканса
Тригонометри́ческие фу́нкции — элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости сторон этих треугольников от острых углов при гипотенузе (или, что эквивалентно, зависимость хорд и высот от центрального угла в круге). Эти функции нашли широчайшее применение в самых разных областях науки. Впоследствии определение тригонометрических функций было расширено, их аргументом теперь может быть произвольное вещественное или даже комплексное число. Наука, изучающая свойства тригонометрических функций, называется тригонометрией.
К тригонометрическим функциям относятся:
- прямые тригонометрические функции
- синус (sin x)
- косинус (cos x)
- производные тригонометрические функции
- тангенс (tg x)
- котангенс (ctg x)
- другие тригонометрические функции
- секанс (sec x)
- косеканс (cosec x)
В западной литературе тангенс, котангенс и косеканс обозначаются tan x, cot x, csc x.
Кроме этих шести, существуют также некоторые редко используемые тригонометрические функции (версинус и т.д.), а также обратные тригонометрические функции (арксинус, арккосинус и т. д.), рассматриваемые в отдельных статьях.
Синус и косинус вещественного аргумента являются периодическими непрерывными и неограниченно дифференцируемыми вещественнозначными функциями. Остальные четыре функции на вещественной оси также вещественнозначные, периодические и неограниченно дифференцируемые на области определения, но не непрерывные. Тангенс и секанс имеют разрывы второго рода в точках ±πn + π/2, а котангенс и косеканс — в точках ±πn.
Содержание
- 1 Способы определения
- 1.1 Геометрическое определение
- 1.1.1 Определение тригонометрических функций для острых углов
- 1.2 Определение тригонометрических функций как решений дифференциальных уравнений
- 1.3 Определение тригонометрических функций как решений функциональных уравнений
- 1.4 Определение тригонометрических функций через ряды
- 1.1 Геометрическое определение
- 2 Значения тригонометрических функций для некоторых углов
- 2.1 Значения тригонометрических функций нестандартных углов
- 3 Свойства тригонометрических функций
- 3.1 Простейшие тождества
- 3.2 Непрерывность
- 3.3 Чётность
- 3.4 Периодичность
- 3.5 Формулы приведения
- 3.6 Формулы сложения
- 3.7 Формулы для кратных углов
- 3.8 Произведения
- 3.9 Степени
- 3.10 Суммы
- 3.11 Однопараметрическое представление
- 4 Производные и интегралы
- 5 Тригонометрические функции комплексного аргумента
- 5.1 Определение
- 5.2 Комплексные графики
- 6 История названий
- 7 См. также
- 8 Литература
- 9 Ссылки
Способы определения
Геометрическое определение
Рис. 2
Определение тригонометрических функций
Обычно тригонометрические функции определяются геометрически. Пусть нам дана декартова система координат на плоскости, и построена окружность радиуса R с центром в начале координат O. Измерим углы как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки В обозначим xB, ординату обозначим yB (см. рисунок).
Рис. 3
Численные значения тригонометрических функций угла 
Ясно, что значения тригонометрических функций не зависят от величины радиуса окружности R в силу свойств подобных фигур. Часто этот радиус принимают равным величине единичного отрезка, тогда синус равен просто ординате yB, а косинус — абсциссе xB. На рисунке 3 показаны величины тригонометрических функций для единичной окружности.
Если α — вещественное число, то синусом α в математическом анализе называется синус угла, радианная мера которого равна α, аналогично для прочих тригонометрических функций.
Определение тригонометрических функций для острых углов
Рис. 4
Тригонометрические функции острого угла
Во многих учебниках элементарной геометрии до настоящего времени тригонометрические функции острого угла определяются как отношения сторон прямоугольного треугольника. Пусть OAB — треугольник с углом α. Тогда:
- Синусом угла α называется отношение AB/OB (отношение противолежащего катета к гипотенузе).
- Косинусом угла α называется отношение ОА/OB (отношение прилежащего катета к гипотенузе).
- Тангенсом угла α называется отношение AB/OA (отношение противолежащего катета к прилежащему).
- Котангенсом угла α называется отношение ОА/AB (отношение прилежащего катета к противолежащему).
- Секансом угла α называется отношение ОB/OA (отношение гипотенузы к прилежащему катету).
- Косекансом угла α называется отношение ОB/AB (отношение гипотенузы к противолежащему катету).
Построив систему координат с началом в точке O, направлением оси абсцисс вдоль OA и в случае необходимости изменив ориентацию (перевернув) треугольник так, чтобы он находился в первой четверти системы координат, и затем, построив окружность с радиусом, равным гипотенузе, сразу находим, что такое определение функций приводит к тому же результату, что и предыдущее.
Данное определение имеет некоторое педагогическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач про тупоугольные треугольники (см.: Теорема синусов, Теорема косинусов).
Определение тригонометрических функций как решений дифференциальных уравнений
Функции косинус и синус можно определить как чётное (косинус) и нечётное (синус) решение дифференциального уравнения
с начальными условиями 
Определение тригонометрических функций как решений функциональных уравнений
Функции косинус и синус можно определить как непрерывные решения (f и g соответственно) системы функциональных уравнений:
Определение тригонометрических функций через ряды
Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу и что производная косинуса равна минус синусу. Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде степенны́х рядов:
Пользуясь этими формулами, а также уравнениями 



где
— числа Бернулли,
— числа Эйлера.
Значения тригонометрических функций для некоторых углов
Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице. («∞» означает, что функция в указанной точке не определена, а в её окрестности стремится к бесконечности).
 |
0°(0 рад) | 30° (π/6) | 45° (π/4) | 60° (π/3) | 90° (π/2) | 180° (π) | 270° (3π/2) | 360° (2π) |
|---|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Значения косинуса и синуса на окружности.
Значения тригонометрических функций нестандартных углов
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Значения тригонометрических функций прочих углов
Свойства тригонометрических функций
Простейшие тождества
Поскольку синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α, то, согласно уравнению единичной окружности или теореме Пифагора, имеем:
Это соотношение называется основным тригонометрическим тождеством.
Деля это уравнение на квадрат косинуса и синуса соответственно имеем далее:
Непрерывность
Синус и косинус — непрерывные функции. Тангенс и секанс имеют точки разрыва 
Чётность
Косинус и секанс — чётные. Остальные четыре функции — нечётные, то есть:
Периодичность
Функции 


Формулы приведения
Формулами приведения называются формулы следующего вида:
Здесь f — любая тригонометрическая функция, g — соответствующая ей кофункция (то есть косинус для синуса, синус для косинуса, тангенс для котангенса, котангенс для тангенса, секанс для косеканса и косеканс для секанса), n — целое число. Перед полученной функцией ставится тот знак, который имеет исходная функция в заданной координатной четверти при условии, что угол α острый, например:
Некоторые формулы приведения:
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Формулы сложения
Значения тригонометрических функций суммы и разности двух углов:
Аналогичные формулы для суммы трёх углов:
Формулы для кратных углов
Формулы двойного угла:
Формулы тройного угла:
Прочие формулы для кратных углов:
следует из формулы дополнения и формулы Гаусса для Гамма-функции
Формулы половинного угла:
Произведения
Формулы для произведений функций двух углов:
Аналогичные формулы для произведений синусов и косинусов трёх углов:
Формулы для произведений тангенсов и котангенсов трёх углов можно получить, поделив правые и левые части соответствующих равенств, представленных выше.
Степени
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Суммы
Для функций от аргумента 
где угол 
Однопараметрическое представление
Все тригонометрические функции можно выразить через тангенс половинного угла.
Производные и интегралы
Все тригонометрические функции непрерывно и неограниченно дифференцируемы на всей области определения:
Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом:
Тригонометрические функции комплексного аргумента
Определение
Формула Эйлера:
позволяет определить тригонометрические функции от комплексных аргументов через экспоненту или (с помощью рядов) как аналитическое продолжение их вещественных аналогов:
где
Соответственно, для вещественного x,
Комплексные синус и косинус тесно связаны с гиперболическими функциями:
Большинство перечисленных выше свойств тригонометрических функций сохраняются и в комплексном случае. Некоторые дополнительные свойства:
- комплексные синус и косинус, в отличие от вещественных, могут принимать сколь угодно большие по модулю значения;
- все нули комплексных синуса и косинуса лежат на вещественной оси.
Комплексные графики
На следующих графиках изображена комплексная плоскость, а значения функций выделены цветом. Яркость отражает абсолютное значение (чёрный — ноль). Цвет изменяется от аргумента и угла согласно карте.
|
|
|
|
|
|
|
 |
 |
 |
 |
 |
 |
История названий
Линия синуса у индийских математиков первоначально называлась «арха-джива» («полутетива», то есть половина хорды), затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские переводчики не перевели слово «джива» арабским словом «ватар», обозначающим тетиву и хорду, а транскрибировали арабскими буквами и стали называть линию синуса «джиба». Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса «джайб», что буквально обозначает «впадина», «пазуха». При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.
Современные краткие обозначения sin и cos введены Уильямом Отредом и закреплены в трудах Эйлера.
Термины «тангенс» (от лат. tangens — касающийся) и «секанс» (лат. secans — секущий) были введены датским математиком Томасом Финке (1561—1656) в его книге «Геометрия круглого» (Geometria rotundi, 1583).
Сам термин тригонометрические функции введён Клюгелем в 1770 году.
См. также
- Гиперболические функции
- Интегральный синус
- Интегральный косинус
- Обратные тригонометрические функции
- Решение треугольников
- Синус-верзус
- Сферическая тригонометрия
- Функция Гудермана
- Четырёхзначные математические таблицы (Таблицы Брадиса)
- Эллиптические функции
Литература
- Бронштейн И. Н., Семендяев К. А. Прямолинейная тригонометрия // Справочник по математике. — Изд. 7-е, стереотипное. — М.: Государственное издательство технико-теоретической литературы, 1967. — С. 179—184.
- Г. Б. Двайт Тригонометрические функции // Таблицы интегралов и другие математические формулы. — 4-е изд. — М.: Наука, 1973. — С. 70—102.
Ссылки
- GonioLab — прояснённая единичная окружность, тригонометрические и гиперболические функции (Java Web Start)
- Weisstein, Eric W. Тригонометрические функции (англ.) на сайте Wolfram MathWorld.
- Онлайн калькулятор: вычисление значений тригонометрических функций
- Интерактивная карта значений тригонометрических функций
Хотя, положа руку на сердце, я скажу тебе, что знание последней не так уж и обязательно (хотя желательно!), поскольку она легко выражается через тангенс.
Да и сам тангенс, по сути – тоже лишь тригонометрическое выражение, зависящее от синуса и косинуса.
Таким образом, у нас есть две основные тригонометрические функции – синус и косинус и две «второстепенные» – тангенс и котангенс.
Я не буду сейчас определять, что такое синус и косинус, ты и так это уже знаешь из предыдущих разделов. Я лишь скажу пару слов про важность этих понятий.
Итак, пара слов: первые зачатки тригонометрии возникли более 3 тысяч лет назад. Я думаю, что тебе очевидно, что тогда люди не занимались «формулами ради формул».
Так что тригонометрические функции имеют полезные практические свойства. Я не буду их перечислять. Если тебе интересно, ты всегда можешь найти море информации в интернете.
Если все, что я сказал выше, звучало для тебя древним эльфийским языком, то посмотри статью о тригонометрической окружности.
А сейчас я приведу тебе некоторые основные соотношения между тригонометрическими величинами, которые оказываются полезными при решении задач.
Уже получилось 7 формул! К сожалению, это еще далеко не предел. Совсем не предел.
Тем не менее последние 4 формулы есть ни что иное, как простое следствие первой. В самом деле, ты заметил, почему это так?
Формула 4 получается делением обеих частей формулы 1 на ( displaystyle co{{s}^{2}}alpha ) и применением формулы 2.
Формула 5 получается аналогично: разделим обе части формулы 1 на ( displaystyle si{{n}^{2}}alpha ) и вместо выражения ( displaystyle frac{co{{s}^{2}}alpha }{si{{n}^{2}}alpha }) запишем ( displaystyle ct{{g}^{2}}alpha ), исходя из определения 3.
Формулы 1 – 5 мы трактуем вполне однозначно. Чего нельзя сказать про формулы 6 и 7. В чем «фишка» формул 6 и 7?
Их особенность заключается в знаке ( displaystyle pm ), который стоит перед корнем.
Как это понимать? А понимать надо так: в некоторых случаях мы ставим плюс, а в некоторых – минус.
Теперь у тебя должен возникнуть вопрос: в каких-таких «некоторых случаях»? Туманность этой формулировки снимается следующим правилом:
Если в формуле
( displaystyle sin alpha =pm sqrt{1-co{{s}^{2}}alpha })
угол ( displaystyle alpha ) таков, что ( displaystyle text{sin} text{ }!!alpha!!text{ }<0), то ставим знак «минус», иначе – «плюс».
Если в формуле
( displaystyle cos alpha =pm sqrt{1-si{{n}^{2}}alpha })
угол ( displaystyle alpha ) таков, что ( displaystyle text{cos} text{ }!!alpha!!text{ }<0), то ставим знак «минус», иначе – «плюс».
Есть опять некий «запутанный» момент в правиле, не так ли? В чем осталось разобраться?
Осталось понять, как связан угол со знаком тригонометрической функции. Ответом на этот вопрос (если ты, конечно, забыл) служат следующие картинки:
Они подскажут тебе, какой нужно выбирать знак для той или иной функции, так что ты не допустишь досадной ошибки.
К тому же это избавит тебя от мучительных размышлений по поводу того «а зачем в этом примере нужен этот угол?!».
Решения:
1. Так как ( displaystyle cosalpha =pm sqrt{1-si{{n}^{2}}alpha }), то подставим сюда значение( displaystyle sinalpha =-frac{2sqrt{2}}{3}), тогда ( displaystyle cosalpha =pm sqrt{1-{{left( -frac{2sqrt{2}}{3} right)}^{2}}}=pm sqrt{1-frac{4cdot 2}{9}}=pm sqrt{1-frac{8}{9}}=)
( displaystyle=pm sqrt{frac{1}{9}}=pm frac{1}{3}.)
Теперь дело за малым: разобраться со знаком. Что нам для этого нужно? Знать, в какой четверти находится наш угол.
По условию задачи: ( displaystyle alpha in left( frac{3pi }{2};2pi right)). Смотри на картинку. Какая это четверть? Четвертая.
Каков знак косинуса в четвертой четверти? На картинке стоит знак «плюс», значит косинус в четвертой четверти положительный.
Тогда нам остается выбрать знак «плюс» перед ( displaystyle frac{1}{3}). ( displaystyle text{cos} text{ }!!alpha!!text{ }=frac{1}{3}), тогда ( displaystyle 3cosalpha =3cdot frac{1}{3}=1).
Ответ: ( displaystyle 1).
Ну вот видишь, ничего сложного. Абсолютно ничего. Нужно лишь запомнить знаки синуса, косинуса и тангенса (котангенса) по четвертям. Ну а как это делать автоматически описано в статье, посвященной тригонометрической окружности.
Давай разберем оставшиеся примеры.
2. Так как ( displaystyle sin alpha =pm sqrt{1-co{{s}^{2}}alpha }), то все, что нам нужно – это подставить ( displaystyle cosalpha =frac{2sqrt{6}}{5}) в нашу формулу. Что мы с тобой и сделаем:
( displaystyle sinalpha =pm sqrt{1-{{left( frac{2sqrt{6}}{5} right)}^{2}}}=pm sqrt{1-left( frac{4cdot 6}{25} right)}=pm sqrt{frac{1}{25}}=pm frac{1}{5}).
Опять нужно определиться со знаком. Смотрим на рисунок. Четверть – снова четвертая. Знак синуса четвертой четверти – отрицательный. Ставим знак «минус». ( displaystyle sinalpha =-frac{1}{5}), тогда ( displaystyle 5sinalpha =-5cdot frac{1}{5}=-1).
Ответ: ( displaystyle -1).
3. Ничего нового. Скорее для закрепления. Снова подставляем в формулу ( displaystyle cos alpha =pm sqrt{1-si{{n}^{2}}alpha }) значение ( displaystyle sinalpha =frac{2sqrt{6}}{5}):
( displaystyle cosalpha =pm sqrt{1-{{left( frac{2sqrt{6}}{5} right)}^{2}}}=pm sqrt{1-left( frac{4cdot 6}{25} right)}=pm sqrt{frac{1}{25}}=pm frac{1}{5}).
Смотрим на знак косинуса при ( displaystyle alpha in left( frac{pi }{2};pi right)). Какая это четверть? Вторая. Косинус второй четверти отрицательный. Тогда выбираем знак «минус».
Ответ: ( displaystyle -0,2).
4. Здесь перед нами стоит задачка чуть сложнее. Однако, не стоит огорчаться. Давай вспомним, что такое тангенс. Это ведь отношение синуса к косинусу. Синус нам уже дан.
Давай вначале найдем косинус. Как это сделать, ты уже знаешь. ( displaystyle cosalpha =pm sqrt{1-{{left( -frac{5}{sqrt{26}} right)}^{2}}}=pm sqrt{1-frac{25}{26}}=pm sqrt{frac{1}{26}}=pm frac{1}{sqrt{26}}).
Так как ( displaystyle alpha in left( pi ;frac{3pi }{2} right)) (это угол в третьей четверти, а косинус в третьей четверти имеет знак «минус»), то ( displaystyle cosalpha =-frac{1}{sqrt{26}}).
Теперь все, что нам осталось, это воспользоваться определением тангенса:
( displaystyle tgalpha =frac{sinalpha }{cosalpha }=frac{-frac{5}{sqrt{26}}}{-frac{1}{sqrt{26}}}=5.)
Ответ: ( displaystyle 5).
Уф, выдохнули! Ну вот мы с тобой решили некоторые (довольно типичные и распространенные) примеры. Ты спросишь: «И что, это все?». Я отвечу, что, увы нет. Это далеко не все.
Далее нам потребуются более сложные формулы тригонометрии.
Разбор 3 примеров
1. Доказать тождество: ( displaystyle frac{3-4cos2alpha +cos4alpha }{3+4cos2alpha +cos4alpha }=t{{g}^{4}}alpha )
С виду тождество угрожающе! Но разберёмся по порядку. Формулы понижения степени, конечно, если их прочитать задом наперёд повышают степень!
И вообще, приглядись внимательно: первые две формулы есть ничто иное, как косинус двойного угла, записанный в несколько странной форме!
Вот и распишем по правилам:
( displaystyle begin{array}{l}frac{3-4cos2alpha +cos4alpha }{3+4cos2alpha +cos4alpha }=frac{3-4cos2alpha +left( 2{cos^{2}}2alpha -1 right)}{3+4cos2alpha +left( 2{cos^{2}}2alpha -1 right)}=\=frac{2-4cos2alpha +2{cos^{2}}2alpha }{2+4cos2alpha +2{cos^{2}}2alpha }=frac{1-2cos2alpha +{cos^{2}}2alpha }{1+2cos2alpha +{cos^{2}}2alpha }end{array})
Тебе ничего по форме не напоминают числитель и знаменатель дроби? Приглядись внимательно, здесь «зарыта» хорошо известная тебе формула. Увидел её? Это же квадрат разности и квадрат суммы! (Подробнее об этом читай в статье о формулах сокращенного умножения)
( displaystyle frac{1-2cos2alpha +{cos^{2}}2alpha }{1+2cos2alpha +{cos^{2}}2alpha }=frac{{{left( 1-cos2alpha right)}^{2}}}{{{left( 1+cos2alpha right)}^{2}}}={{left( frac{1-cos2alpha }{1+cos2alpha } right)}^{2}})
А выражение в скобках есть ничто иное, как ( displaystyle t{{g}^{2}}alpha ), окончательно получим:
( displaystyle {{left( frac{1-cos2alpha }{1+cos2alpha } right)}^{2}}={{left( t{{g}^{2}}alpha right)}^{2}}=t{{g}^{4}}alpha )
Тождество доказано!
Следующий пример очень схож с предыдущим, постарайся решить его самостоятельно.
2. Доказать тождество: ( displaystyle frac{1+sin2alpha +cos2alpha }{1+sin2alpha -cos2alpha }=ctgalpha )
Решение (хотя может и отличаться от твоего):
Опять «повысим степень» у косинуса: ( displaystyle cos2alpha =2{cos^{2}}alpha -1)
( displaystyle frac{1+sin2alpha +cos2alpha }{1+sin2alpha -cos2alpha }=frac{1+sin2alpha +2{cos^{2}}alpha -1}{1+sin2alpha -2{cos^{2}}alpha +1}=frac{sin2alpha +2{cos^{2}}alpha }{2+sin2alpha -2{cos^{2}}alpha })
Надо сокращать дальше! Что делать? Ясно, что надо избавляться от двойных углов у синуса. Действуем по формуле синуса двойного угла и сокращаем двойки:
( displaystyle frac{sin2alpha +2{cos^{2}}alpha }{2+sin2alpha -2{cos^{2}}alpha }=frac{2sin{alpha} cos{alpha} +2{cos^{2}}alpha }{2+2sin{alpha} cos{alpha}-2{cos^{2}}alpha }=frac{sinalpha cosalpha +{cos^{2}}alpha }{1+sinalpha cos{alpha}-{cos^{2}}alpha })
Числитель раскладывается на множители. Знаменатель –пока нет. До тех пор, пока мы не применим основное тригонометрическое тождество:
( displaystyle 1-{cos^{2}}alpha ={sin^{2}}alpha )
( displaystyle frac{sinalpha cosalpha +{cos^{2}}alpha }{1+sinalpha cosalpha -{cos^{2}}alpha }=frac{sinalpha cosalpha +{cos^{2}}alpha }{{sin^{2}}alpha +sinalpha cosalpha }=frac{cosalpha left( sinalpha +cosalpha right)}{sinalpha left( sinalpha +cosalpha right)}=ctgalpha )
Вот ещё один пример, но не такой простой.
3. Доказать, что если ( displaystyle 0<alpha <frac{pi }{2}), то ( displaystyle sqrt{1+sinalpha }-sqrt{1-sinalpha }=2sinfrac{alpha }{2})
Зачем нам дан угол? Наверное, чтобы оценить выражения: синус ( displaystyle alpha )будет положительным, ( displaystyle sinfrac{alpha }{2}>0,~1+sinalpha >1,~0<1-sinalpha <1)
Тогда и левая, и правая части тождества больше нуля. Это даёт мне право без задней мысли возвести их в квадрат:
( displaystyle {{left( sqrt{1+sinalpha }-sqrt{1-sinalpha } right)}^{2}}=4{sin^{2}}frac{alpha }{2}) – вот такое тождество нам нужно теперь доказать.
Раскроем скобки в левой части по формуле квадрата разности!
( displaystyle begin{array}{l}{{left( sqrt{1+sin alpha }-sqrt{1-sin alpha } right)}^{2}}=1+sin alpha -2sqrt{1+sin alpha }cdot sqrt{1-sin alpha }+1-\-sin alpha =2-2sqrt{1+sin alpha }cdot sqrt{1-sin alpha }=2left( 1-sqrt{1+sin alpha }cdot sqrt{1-sin alpha } right)=\2left( 1-sqrt{1+{{sin }^{2}}alpha } right)=2left( 1-sqrt{{cos^{2}}}alpha right)end{array})
Я не сомневаюсь в твоей грамотности и поэтому даже не упоминаю про использованные мною формулы в выкладках.
Теперь надо бы убрать корень из косинуса. Но мы знаем, что просто так это делать нельзя, ибо ( displaystyle sqrt{{{a}^{2}}}=left| a right|).
В то же время вспоминаем про четверть: наш угол лежит в первой четверти, тогда косинус имеет знак «плюс» и мы просто убираем корень:
( displaystyle 2left( 1-sqrt{{cos^{2}}}alpha right)=2left( 1-cosalpha right))
Тогда нам надо доказать, что
( displaystyle 2left( 1-cosalpha right)=4{sin^{2}}frac{alpha }{2})
( displaystyle left( 1-cosalpha right)=2{sin^{2}}frac{alpha }{2})
Справа применим формулу понижения степени:
( displaystyle {sin^{2}}frac{alpha }{2}=frac{1-cosalpha }{2}), тогда ( displaystyle 2{sin^{2}}frac{alpha }{2}=1-cosalpha )
Тождество доказано!
Конечно, можно привести ещё массу примеров, где применяются формулы понижения степени, ты их и сам без труда отыщешь.
Теперь вторая (и заключительная в этом обзоре) группа формул – формулы преобразования произведения в сумму и суммы в произведение.
Решение 5 примеров
1. Доказать тождество: ( displaystyle frac{sinalpha +sin3alpha }{cosalpha +cos3alpha }=tg2alpha )
Давай не будем долго думать, а, как говорится, пойдём в лобовую атаку: в числителе и знаменателе перейдём от суммы к произведению:
( displaystyle begin{array}{l}~frac{sinalpha+sin3alpha}{cosalpha+cos3alpha}=frac{2sinfrac{alpha+3alpha}{2}cosfrac{alpha-3alpha}{2}}{2cosfrac{alpha+3alpha}{2}cosfrac{alpha-3alpha}{2}}=frac{2cdot sin2alphacdot cosleft( -alpha right)}{2cdot cos2alphacdot cosleft( -alpha right)}=\=frac{sin2alpha}{cos2alpha}=tg2alphaend{array})
И минуты не прошло, а пример уже решён!
Теперь попробуй сам.
2. Доказать тождество: ( displaystyle frac{sin2alpha +sin4alpha }{cos2alpha -cos4alpha }=ctgalpha )
Решение – опять лобовая атака:
( displaystyle begin{array}{l}frac{sin2alpha+sin4alpha}{cos2alpha-cos4alpha}=frac{2sinfrac{2alpha+4alpha}{2}cosfrac{2alpha-4alpha}{2}}{-2sinfrac{2alpha+4alpha}{2}sinfrac{2alpha-4alpha}{2}}=frac{2sin3alphacdot cosleft( -alpha right)}{-2sin3alphacdot sinleft( -alpha right)}=frac{cosleft( -alpha right)}{-sinleft( -alpha right)}end{array})
Так как синус – функция нечётная, а косинус – чётная, то:
( displaystyle frac{cosleft( -alpha right)}{-sinleft( -alpha right)}=frac{cosalpha }{-left( -sinalpha right)}=frac{cosalpha }{sinalpha }=ctgalpha )
Этот пример чуть похитрее, будь внимателен!
3. Доказать тождество: ( displaystyle frac{sin2alpha +sin5alpha -sin3alpha }{cosalpha +1-2{sin^{2}}2alpha }=2sinalpha )
Я не хочу трогать синус двойного угла. Уж больно он удобно раскладывается на множители, чего не скажешь о синусе тройного и тем более пятикратного угла.
Поэтому я сверну в произведение последние 2 слагаемых в числителе:
( displaystyle begin{array}{l}frac{sin2alpha +sin5alpha -sin3alpha }{cosalpha +1-2{sin^{2}}2alpha }=frac{sin2alpha +2sinfrac{5alpha -3alpha }{2}cosfrac{5alpha +3alpha }{2}}{cosalpha +1-2{sin^{2}}2alpha }=\=frac{2sinalpha cosalpha +2sinalpha cos4alpha }{cosalpha +1-2{sin^{2}}2alpha }=frac{2sinalpha left( cosalpha +cos4alpha right)}{cosalpha +1-2{sin^{2}}2alpha }end{array})
Конечно, теперь можно было бы и свернуть числитель ещё раз, но я пойду иным путём. В знаменателе у меня тоже спрятана формула, вот она:
( displaystyle 1-2{sin^{2}}2alpha ).
Что это за формула? Это косинус двойного угла!
( displaystyle 1-2{sin^{2}}2alpha =cosleft( 2cdot 2alpha right)=cos4alpha )
( displaystyle frac{2sinalpha left( cosalpha +cos4alpha right)}{cosalpha +1-2{sin^{2}}2alpha }=frac{2sinalpha left( cosalpha +cos4alpha right)}{cosalpha +cos4alpha }=2sinalpha )
Тождество доказано!
Теперь попробуй решить вот этот пример для закрепления пройденного материала.
4. Доказать тождество: ( displaystyle {cos^{4}}alpha -{sin^{4}}alpha +sin2alpha =sqrt{2}cosleft( 2alpha -frac{pi }{4} right))
Проверяем!
( displaystyle begin{array}{l}{cos^{4}}alpha -{sin^{4}}alpha +sin2alpha =left( {cos^{2}}alpha -{sin^{2}}alpha right)left( {cos^{2}}alpha +{sin^{2}}alpha right)+sin2alpha =\=cos2alpha +sin2alpha end{array})
C другой стороны:
( displaystyle begin{array}{l}sqrt{2}cos left( 2alpha-frac{pi }{4} right)=sqrt{2}left( cos{2alpha}cos{frac{pi }{4}}+sin{2alpha}sin{frac{pi }{4}} right)=\=sqrt{2}left( frac{sqrt{2}}{2}cos2alpha+frac{sqrt{2}}{2}sin2alpha right)=sqrt{2}cdot frac{sqrt{2}}{2}left( cos2alpha+sin2alpha right)=\=cos2alpha+sin2alphaend{array})
Тождество доказано!
На этом примере я буду закругляться потихоньку.
Сразу оговорюсь: не переживай и не волнуйся, если у тебя что-то сразу не выходит. Тригонометрия – сложная и очень обширная тема. Здесь все зависит не только от знания формул, но и от мастерства и смекалки. На их выработку тебе понадобится время и усердие.
Более того, скажу тебе вот что: изначально я хотел вставить другой пример в качестве заключительного. Однако на его решение мне понадобилось около 20 минут, причём я использовал ещё более сложную методику его решения. Так что не только ты сталкиваешься с трудностями при решении примеров, трудности бывают у всех!
Все-таки я приведу здесь этот трудный пример, вдруг да и получится у тебя решить его, может, я что-то упустил. Вот он:
5. Упростить: ( displaystyle frac{1+sinalpha -cos2alpha -sin3alpha }{2{sin^{2}}alpha +sinalpha -1})
А вот какой у меня получился в итоге ответ: ( displaystyle 2sinalpha.)
Дерзай!
В следующей части статьи я рассмотрю его решение, но прибегну к ещё более изощрённой технике нежели та, что рассматривалась здесь! Удачи!
Формулы понижения 3-й степени
- ( displaystyle si{{n}^{3}}alpha =frac{3sinalpha -sin3alpha }{4})
- ( displaystyle co{{s}^{3}}a=frac{3cosa+cos3a}{4})
Из данных формул можно вывести формулы тройного угла.
Формулы тройного угла
- ( displaystyle sin3alpha =3sinalpha -4si{{n}^{3}}alpha )
- ( displaystyle cos3a=4co{{s}^{3}}a-3cosa)
- ( displaystyle tg3alpha =frac{3tgalpha -t{{g}^{3}}alpha }{1-3t{{g}^{2}}alpha })
- ( displaystyle ctg3alpha =frac{3ctgalpha -ct{{g}^{3}}alpha }{1-3ct{{g}^{2}}alpha })
Ты мне можешь задать резонный вопрос: как часто эти формулы используются? Я отвечу: постарайся избегать прибегать к ним. Они нужны на тот случай, когда ничего другого уже не можешь придумать.
В частности, они могут быть полезными при решении сложных уравнений, которые встречаются во вступительных экзаменах на математические специальности.
Однако уравнениям у нас будет посвящена отдельная статья, так что здесь я рассмотрю случаи, когда данные формулы позволяют упрощать тригонометрические выражения.
Пример 1
Упростить: ( displaystyle A=frac{1}{3}co{{s}^{3}}alpha cdot sin3alpha +frac{1}{3}si{{n}^{3}}alpha cdot cos3alpha )
Решение:
Подставим вместо ( displaystyle sin3alpha ) и ( displaystyle cos3alpha ) их представления согласно формулам тройного угла, тогда:
( displaystyle begin{array}{l}A=frac{1}{3}co{{s}^{3}}alpha left( 3sinalpha -4si{{n}^{3}}alpha right)+frac{1}{3}si{{n}^{3}}alpha left( 4co{{s}^{3}}alpha -3cosalpha right)=\=co{{s}^{3}}alpha cdot sinalpha -frac{4}{3}co{{s}^{3}}alpha cdot si{{n}^{3}}alpha +frac{4}{3}co{{s}^{3}}alpha cdot si{{n}^{3}}alpha -si{{n}^{3}}alpha cdot cosalpha =\=co{{s}^{3}}alpha cdot sinalpha -si{{n}^{3}}alpha cdot cosalpha end{array})
Теперь вынесем в оставшемся выражении общий множитель за скобки:
( displaystyle co{{s}^{3}}alpha cdot sinalpha -si{{n}^{3}}alpha cdot cosalpha =sinalpha cdot cosalpha left( co{{s}^{2}}alpha -si{{n}^{2}}alpha right))
По формулам двойного угла: ( displaystyle sinalpha cdot cosalpha =frac{1}{2}sin2alpha ), ( displaystyle co{{s}^{2}}alpha -si{{n}^{2}}alpha =cos2alpha ):
( displaystyle sinalpha cdot cosalpha left( co{{s}^{2}}alpha -si{{n}^{2}}alpha right)=frac{1}{2}sin2alpha cdot cos2alpha )
Ну а здесь снова спрятан синус двойного угла:
( displaystyle frac{1}{2}sin2alpha cdot cos2alpha =frac{1}{4}sin4alpha )
Ответ: ( displaystyle A=frac{1}{4}sin4alpha )
Следующий пример попробуй решить самостоятельно. Не уверен, что в нем обязательно использовать формулу тройного угла, но можно сделать и с ее помощью.
Пример 2
Упростить: ( displaystyle frac{1+sinalpha -cos^2{alpha}-cos2alpha -sin3alpha }{2si{{n}^{2}}alpha +sinalpha -1})
Решение:
Моя цель – свести числитель дроби к выражению, зависящему только от синусов одиночного угла. Для этого я преобразую
( displaystyle cos^2 {alpha} =1-si{{n}^{2}}alpha )
( displaystyle cos2alpha =1-2si{{n}^{2}}alpha )
( displaystyle sin3alpha =3sinalpha -4si{{n}^{3}}alpha )
Имеем:
( displaystyle begin{array}{l}frac{1+sinalpha -cos2alpha -sin3alpha }{2si{{n}^{2}}alpha +sinalpha -1}=frac{1+sinalpha -left( 1-si{{n}^{2}}alpha right) -left( 1-2si{{n}^{2}}alpha right)-left( 3sinalpha -4si{{n}^{3}}alpha right)}{2si{{n}^{2}}alpha +sinalpha -1}=\=frac{4si{{n}^{3}}alpha +3si{{n}^{2}}alpha -2sinalpha -1}{2si{{n}^{2}}alpha +sinalpha -1}end{array})
Казалось бы, стало еще хуже. Но это так кажется. Давай для удобства вычислений заменим ( displaystyle sinalpha =t), тогда мне надо упростить дробь
( displaystyle frac{4{{t}^{3}}+3{{t}^{2}}-2t-1}{2{{t}^{2}}+t-1})
Нижнее выражение разложим на множители:
( displaystyle 2{{t}^{2}}+t-1=left( t+1 right)left( 2t-1 right))
С верхним фокус сложнее. Мы не умеем с тобой решать кубические уравнения. Но мы хорошо играем в «угадайку».
Угадай-ка один корень уравнения ( displaystyle 4{{t}^{3}}+3{{t}^{2}}-2t-1=0). Угадал? Я угадал ( displaystyle -1).
Тогда по теореме Безу (которую ты, быть может, знаешь, а если не знаешь, то без проблем отыщешь сам) выражение ( displaystyle 4{{t}^{3}}+3{{t}^{2}}-2t-1) делится без остатка на ( displaystyle t+1)
Разделим столбиком ( displaystyle 4{{t}^{3}}+3{{t}^{2}}-2t-1) на ( displaystyle t+1). Я получу:
( displaystyle 4{{t}^{3}}+3{{t}^{2}}-2t-1=left( t+1 right)left( 4{{t}^{2}}-t-1 right))
В свою очередь ( displaystyle 4{{t}^{2}}-t-1=4left( t-frac{1}{2} right)left( t+frac{1}{4} right))
Окончательно получим:
( displaystyle begin{array}{l}frac{4{{t}^{3}}+3{{t}^{2}}-2t-1}{2{{t}^{2}}+t-1}=frac{4left( t+1 right)left( t-frac{1}{2} right)left( t+frac{1}{4} right)}{left( t+1 right)left( 2t-1 right)}=frac{left( t+1 right)left( 2t-1 right)left( 2t+0,5 right)}{left( t+1 right)left( 2t-1 right)}=\=2t+0,5end{array})
Тогда исходное выражение можно упростить до: ( displaystyle 2sinx+0,5)
В завершение я приведу тебе пример одного уравнения, которое было предложено на психологический (???!!!) факультет одного из ВУЗов в 1990 году. Такие задачи называются задачи-гробы (никакая смекалка без знания конкретной формулы не позволит их решить):
Решить уравнение: ( displaystyle sqrt{3}co{{s}^{3}}x-3co{{s}^{2}}x-3sqrt{3}cosx+1=0)
Не сделав вот такую странную замену: ( displaystyle cosx=tgalpha ) решить его очень сложно. А с такой заменой у нас получится вот что:
( displaystyle sqrt{3}t{{g}^{3}}alpha -3t{{g}^{2}}alpha -3sqrt{3}tgalpha +1=0)
( displaystyle sqrt{3}t{{g}^{3}}alpha -3sqrt{3}tgalpha =3t{{g}^{2}}alpha -1)
( displaystyle sqrt{3}(t{{g}^{3}}alpha -3tgalpha )=3t{{g}^{2}}alpha -1)
( displaystyle -sqrt{3}left( 3tgalpha -t{{g}^{3}}alpha right)=-left( 1-3t{{g}^{2}}alpha right))
( displaystyle frac{left( 3tgalpha -t{{g}^{3}}alpha right)}{left( 1-3t{{g}^{2}}alpha right)}=frac{1}{sqrt{3}})
А вот ради чего весь этот сыр-бор: ( displaystyle frac{left( 3tgalpha -t{{g}^{3}}alpha right)}{left( 1-3t{{g}^{2}}alpha right)}=tg3alpha )
( displaystyle tg3alpha =frac{1}{sqrt{3}})
Это уравнение уже несказанно легче решается. Скоро мы вместе в этом убедимся. Но тут проблема в обратной замене… Тем не менее, эта задача почти нерешаема без знания формулы тангенса тройного угла. Вот так вот.
Бонусы: Вебинары из нашего курса подготовки к ЕГЭ по математике
ЕГЭ 9. Тригонометрическая окружность, табличные значения
На этом уроке мы узнаем, что такое тригонометрическая окружность и насколько она важна для тригонометрии. М
ы увидим, что она – основной инструмент в тригонометрии: с её помощью можно вывести любую формулу и найти любые значения.
Мы поймем, как “работает” окружность – а значит, поймём тригонометрию в целом.
ЕГЭ 13б. Тригонометрическая окружность
Тригонометрическая окружность – это очень простой и эффективный инструмент для решения любой тригонометрической задачи. На этом уроке вы узнаете как пользоваться тригонометрической окружностью для решения пункта “б” из задачи №13 профильного ЕГЭ.
Пункт “б” задачи №13 ЕГЭ 2020 В 2020 году на ЕГЭ в пункте “б” необходимо было указать корни тригонометрического уравнения принадлежащие отрезку.
Вообще-то решать пункт “б” можно двумя способами: – отметить корни уравнения на единичной окружности (способ разобранный в этом видео); – через двойное неравенство.
И вы должны знать, что второй способ чуть дольше, чем первый, но зато вы сможете проще описать все ваши рассуждения и вам будет сложнее ошибиться.
И еще один плюс второго способа – его проще оформить, так, чтобы к вам не придрались на ЕГЭ.
Мы считаем второй способ (через двойное неравенство) более предпочтительным на ЕГЭ по математике, но теме не менее для глубокого понимания темы (что может выручить на ЕГЭ) необходимо разобраться и с первым способом
Уравнения разложения тригонометрических функций:квадрат синус альфа, косинус альфа, тангенс альфа, котангенс альфа.
Формулы преобразования функций двойного угла (2α) в выражение через одинарный угол (α)
sin(2α)- через sin и cos:
sin(2α)- через tg и ctg:
cos(2α)- через sin и cos:
cos(2α)- через tg и ctg:
tg(2α) и сtg(2α):
Формулы преобразования функций (синус, косинус, тангенс, котангенс), тройного угла (3α) в выражение через одинарный угол (α):
Тригонометрические формулы преобразования разности аргументов
sin(α)=OA
cos(α)=OC
tg(α)=DE
ctg(α)=MK
R=OB=1
Значения функций для некоторых углов, α
В таблице показаны формулы приведения для тригонометрических функций (sin, cos, tg, ctg).
Функции угла 
В математике, тригонометрические функции (также называемые круговые функции, угловыми функциями или гониометрическими функциями ) являются действительными функциями, которые связывают угол прямоугольный треугольник в использовании двух сторон. Они широко используются во всех науках, связанных с геометрией, таких как навигация, механика твердого тела, небесная механика, геодезия и многие другие. Они также используются для изучения периодических явлений посредством анализа периода Фурье.
. Наиболее широко используемыми тригонометрическими используемыми функциями являются синус, косинус и тангенс . Их обратные величины представляют собой соответственно косеканс, секанс и котангенс, которые менее используются в современной математике. Из этих тригонометрических функций имеет соответствующую обратную функцию (называемую обратную тригонометрическую функцию ), эквивалентную в гиперболических функциях.
Самые старые определения тригонометрические функции, относящиеся к прямоугольным треугольникам, определяют их только для острых углов. Чтобы распространить определение этих функций, область, которая представляет собой проективно расширенную вещественную линию, геометрические определения с использованием стандартной единичной окружности (т. Е. Окружности с радиус 1 ед.). Современные определения тригонометрических функций как бесконечный ряд или как решения дифференциальных уравнений. Это позволяет определить некоторые синусоидальные и косинусные функции на всей комплексной плоскости , а также в области других тригонометрических функций на комплексной плоскости (из которых удалены изолированные точки).
Содержание
- 1 Определения прямоугольного треугольника
- 2 Радианы в зависимости от градусов
- 3 Определения единичного круга
- 4 Алгебраические значения
- 4.1 Простые алгебраические значения
- 5 В исчислении
- 5.1 Определение с помощью дифференциальных уравнений
- 5.2 Расширение степенной ряд
- 5.3 Разложение на частичную дробь
- 5.4 Разложение на бесконечное произведение
- 5.5 Связь с экспоненциальной функцией (формула Эйлера)
- 5.6 Определения с использованием функциональных уравнений
- 5.7 В комплексной плоскости
- 6 Основные тождества
- 6.1 Четкость
- 6.2 Периоды
- 6.3 Пифагорова идентичность
- 6.4 Формулы суммы и разности
- 6.5 Производные и первообразные
- 7 Обратные функции
- 8 Применение
- 8.1 Углы и стороны треугольника
- 8.1.1 Закон синусов
- 8.1.2 Закон косинусов
- 8.1.3 Закон касательных
- 8.1.4 Закон котангенсов
- 8.2 Периодические функции
- 8.1 Углы и стороны треугольника
- 9 История
- 10 Этимология
- 11 См. Также
- 12 Примечания
- 13 Ссылки
- 14 Внешние ссылки
Определения прямоугольного треугольника

В этом разделе одна и та же заглавная буква обозначает вершину треугольника и меру соответствующего угла; та же строчная буква обозначает край треугольника и его длину.
Учитывая острый угол A = θ прямоугольного треугольника, гипотенуза h — это, соединяющая два острых угла. Сторона b, связная с θ, — это сторона треугольника, соединяющего θ с прямым углом. Говорят, что третья сторона противоположна θ.
Если задан угол θ, то все стороны прямоугольного треугольника четко с точным до коэффициента масштабирования. Это означает, что соотношение любых двух длин сторон зависит только от θ. Таким образом, эти шесть шести определяют шесть функций от θ, которые являются тригонометрическими функциями. Точнее, шесть тригонометрических функций:
- синус
- грех θ = ah = противогипотенуза { displaystyle sin theta = { frac {a} {h}} = { frac { mathrm {напротив}} { mathrm {гипотенуза}}
- косинус
- cos θ = bh = bh = гипотенуза { displaystyle cos theta = { frac {b} {h}} = { frac { mathrm {смежная}} { mathrm {гипотенуза}}}
- касательная
- загар θ = ab = противоположный аналогичный { displaystyle tan theta = { frac {a} {b}} = { frac { mathrm {напротив }} { mathrm {другой}}}}
- косеканс
- csc θ = ha = гипотенуза напротив { displaystyle csc theta = { frac {h} {a}} = { гидроразрыв { mathrm {гипотенуза}} { mathrm {напротив}}}}
- секанс
- сек θ = hb = гипотенуза, вспомогательная { displaystyle sec theta = { frac {h} {b}} = { frac { mathrm {hypotenuse}} { mathrm {материальный}}}
- котангенс
- кроватка θ = ba = противоположная противоположная { displaystyle cot theta = { frac {b} {a} знак р авно frac { mathrm {djacent}} { mathrm {Against}}}
В прямоугольном треугольнике сумма двух острых углов является прямым углом, то есть 90 ° или π 2 { textstyle { frac { pi } {2}}}
| Функция | Аббревиатура | Описание | Связь | |
|---|---|---|---|---|
| с использованием радианы | с использованием градусов | |||
| синуса | sin | противоположного направления / гипотенузы | sin θ = cos (π 2 — θ) = 1 csc θ { displaystyle sin theta = cos left ({ frac { pi} {2}} — theta right) = { frac {1} { csc theta}}} |
грех Икс знак равно соз (90 ∘ — Икс) знак равно 1 csc Икс { Displaystyle х грех = соз влево (90 ^ { circ} -x вправо) = { гидроразрыва {1} { csc х }}} |
| косинус | cos | конструктивный / гипотенуза | cos θ = грех (π 2 — θ) = 1 секунда θ { displaystyle cos theta = sin left ({ frac { pi} {2}} — theta right) = { frac {1} { sec th eta}} ,} |
cos x = sin (90 ∘ — х) знак равно 1 сек Икс { Displaystyle соз х = влево (90 ^ {грех} -x вправо) = { гидроразрыва {1} { sec x}} ,} |
| касательная | загар (или tg) | напротив / рядом | загар θ = грех θ θ = детская кроватка (π 2 — θ) = 1 детская кроватка θ { displaystyle tan theta = { frac { sin theta } { cos theta}} = cot left ({ frac { pi} {2}} — theta right) = { frac {1} { cot theta}}} |
загар x = sin x cos x = кроватка (90 ∘ — x) = 1 детская кроватка x { displaystyle tan x = { frac { sin x} { cos x}} = cot left (90 ^ { circ} -x right) = { frac {1} { cot x}} |
| котангенс | детская кроватка (или котан, или cotg, или ctg, или ctn) | родственная / противоположная | детская кроватка θ знак равно соз θ грех θ = загар (π 2 — θ) = 1 загар θ { Displaystyle cot theta = { frac { cos theta} { sin theta}} = tan слева ({ frac { pi} {2}} — theta right) = { frac {1} { tan theta}}} |
детская кроватка x = cos Икс грех Икс = загар (90 ∘ — x) = 1 загар Икс { Displaystyle кроватка x = { frac { cos x} { sin x}} = tan left (90 ^ { circ} -x right) = { frac {1} { tan x}}} |
| секущая | сек | гипотенуза / вспомогательная | сек θ знак равно csc (π 2 — θ) знак равно 1 соз θ { displa ystyle sec theta = csc left ({ frac { pi} {2}} — theta right) = { frac {1} { cos theta}}} |
сек x = csc (90 ∘ — x) = 1 соз x { displaystyle sec x = csc left (90 ^ { circ} — x right) = { frac {1} { cos x}}} |
| косеканс | csc (или cosec) | гипотенуза / противоположность | csc θ = sec (π 2 — θ) знак равно 1 грех θ { displaystyle csc theta = sec left ({ frac { pi} {2}} — theta right) = { frac {1} { sin theta}}} |
csc x = sec (90 ∘ — Икс) = 1 грех Икс { Displ aystyle csc x = сек left (90 ^ { circ} -x right) = { frac {1} { sin x}}} |

Радианы в сравнении с градусами
В геометрических приложениях аргумент тригонометрической функции обычно является мерой угла. Для этой цели удобна любая угловая единица, а углы обычно измеряются в градусах (особенно в элементарной математике ).
При использовании тригонометрической функции в исчислении их аргументом обычно является не угол, а действительное число . В этом случае более целесообразно выразить аргумент тригонометрии как дуги дуги единичной окружности , ограниченный угол с окружности в качестве вершины.. Следовательно, в качестве угловой единицы используется радиан : радиан — это угол, ограничивающий дугу длины 1 на единичной окружности. Таким образом, полный поворот на равным образом 2π радиан.
Большим преимуществом является упрощенная формула многих формул, как правило, всех производных и интегралов.
Из-за этого часто понимают что, когда угловая единица не указана явно, аргументы тригонометрических функций всегда выражаются в радианах.
Определения единичной окружности


Шесть тригонометрических функций могут быть как значения координат точек на евклидовой плоскости, которые связаны с единичной окружностью, которая является окружностью радиуса один с центром в начале этой системы. В то время как определения прямоугольного треугольника допускают определение тригонометрических функций для углов между 0 и π 2 { textstyle { frac { pi} {2}}}
Вращение луча от направления положительной половины оси x на угол θ (против часовой стрелки для θ>0, { displaystyle theta>0,}и clockwis e для θ < 0 {displaystyle theta <0}






Тригонометрические функции cos и sin соответственно как координаты x и y точки A. То есть
- cos θ = x A { displaystyle cos theta = x _ { mathrm {A}} quad }
и грех θ = Y A. { displaystyle quad sin theta = y _ { mathrm {A}}.}
В диапазоне 0 ≤ θ ≤ π / 2 { displaystyle 0 leq theta leq pi / 2}


- cos 2 θ + sin 2 θ = 1. { displaystyle cos ^ {2} theta + sin ^ {2} theta = 1.}
Другие тригонометрические функции можно найти вдоль единичной окружности как
- tan θ знак равно YB { displaystyle tan theta = y _ { mathrm {B}} quad}
и детская кроватка θ = x C, { displaystyle quad cot theta = x _ { mathrm {C}},}
- csc θ = y D { displaystyle csc theta = y _ { mathrm {D}} quad}
и сек. θ = х E. { displaystyle quad sec theta = x _ { mathrm {E}}.}
Применяя методы пифагорова тождества и геометрического доказательства, можно легко показать, что эти определения совпадают с определениями касательной, котангенса, секанса и косеканс в терминах синуса и косинуса, то есть
- tan θ = sin θ cos θ, cot θ = cos θ sin θ, sec θ = 1 cos θ, csc θ = 1 грех θ. { displaystyle tan theta = { frac { sin theta} { cos theta}}, quad cot theta = { frac { cos theta} { sin theta}}, quad sec theta = { frac {1} { cos theta}}, quad csc theta = { frac {1} { sin theta}}.}

Так как поворот на угол ± 2 π { displaystyle pm 2 pi}


- грех θ = грех (θ + 2 к π) { displaystyle sin theta = sin left ( theta + 2k pi right) quad}
и соз θ = соз (θ + 2 к π) { displaystyle quad cos theta = cos left ( theta + 2k pi right)}
для любого угла θ и любое целое число k. То же самое и с четырьмя другими тригонометрическими функциями. Наблюдая за знаком и монотонностью функций синуса, косинуса, косеканса и секанса в четырех квадрантах, можно показать, что 2π — наименьшее значение, для которого они периодичны (т. Е. 2π — это основной период этих функций). После поворота на угол π { displaystyle pi}
- загар θ = загар (θ + к π) { displaystyle tan theta = tan ( theta + k pi) quad}
и детская кроватка θ = детская кроватка (θ + k π) { displaystyle quad cot theta = cot ( theta + k pi)}
удерживается для любого угла θ и любого целого числа k.
Алгебраические значения

608>алгебраические выражения для наиболее важных углов:
- грех 0 = грех 0 ∘ = 0 2 = 0 { displaystyle sin 0 = sin 0 ^ { circ} quad = { frac { sqrt {0}} {2}} = 0}
(прямой угол )
- грех π 6 = грех 30 ∘ = 1 2 = 1 2 { displaystyle sin { frac { pi } {6}} = sin 30 ^ { circ} = { frac { sqrt {1}} {2}} = { frac {1} {2}}}
- sin π 4 = грех 45 ∘ знак равно 2 2 { displaystyle sin { frac { pi} {4}} = sin 45 ^ { circ} = { frac { sqrt {2}} {2}}}
- π 3 = грех 60 ∘ = 3 2 { displaystyle sin { frac { pi} {3}} = sin 60 ^ { circ} = { frac { sqrt {3}} {2 }}}
- грех π 2 = грех 90 ∘ = 4 2 = 1 { displaystyle sin { frac { pi} {2}} = sin 90 ^ { circ} = { frac { sqrt {4}} {2}} = 1}
(прямой угол )
Запись числителей в виде последовательных неотрицательных целых со знаменателем 2 простой способ запомнить значения.
Такие простые выражения обычно не существуют для других углов, которые используют рациональные прямые прямые границы. Для угла, который измеряется в градусах и кратен трем, синус и косинус могут быть выражены в виде квадратных корней, см. Тригонометрические константы, выраженные в действительных радикалах. Таким образом, эти значения синуса и косинуса могут быть построены с помощью линейки и компаса.
. Для угла в целое число градусов синус и косинус могут быть выражены в виде квадратных корней и кубический корень из не действительного комплексного числа. Теория Галуа позволяет доказать, что, если угол не кратен 3 °, нереальные кубические корни неизбежны.
Для угла, который измеряется в градусах, является рациональным числом, синус и косинус являются алгебраическими числами, которые могут быть выражены в терминах корни n-й степени. Это является следствием того факта, что группы Галуа из циклотомических многочленов являются циклическими.
. Для угла, который измеряется в градусах, не является рациональным числом, либо угол или оба синуса, и косинуса являются трансцендентными числами. Это следствие теоремы Бейкера, доказанной в 1966 году.
Простые алгебраические значения
В приведенной таблице представлены простейшие алгебраические значения тригонометрических функций. Символ ∞ представляет собой бесконечно удаленную точку на проективно удлиненной вещественной прямой ; он не подписан, потому что, когда он указывает в таблице, соответствующая тригонометая функция стремится к + ∞ с одной стороны и к –∞ с другой стороны, когда он указывает в таблице значению.
- Радианная степень 0 0 ∘ π 12 15 ∘ π 8 22,5 ∘ π 6 30 ∘ π 4 45 ∘ π 3 60 ∘ 3 π 8 67,5 ∘ 5 π 12 75 ∘ π 2 90 ∘ sin 0 6 — 2 4 2 — 2 2 1 2 2 2 3 2 2 + 2 2 6 + 2 4 1 cos 1 6 + 2 4 2 + 2 2 3 2 2 2 1 2 2 — 2 2 6-2 4 0 tan 0 2 — 3 2 — 1 3 3 1 3 2 + 1 2 + 3 ∞ детская кроватка ∞ 2 + 3 2 + 1 3 1 3 3 2 — 1 2 — 3 0 сек 1 6 — 2 2 2 — 2 2 3 3 2 2 2 2 + 2 6 + 2 ∞ csc ∞ 6 + 2 2 2 + 2 2 2 2 3 3 2 2 — 2 6 — 2 1 { displaystyle { begin {array} {| c | ccccccccc |} hline { begin {matrix} { text {Radian}} \ { text {Degree}} end {matrix}} { begin {matrix} 0 \ 0 ^ { circ} end {matrix}} { begin {matrix} { frac { pi} {12}} \ 15 ^ { circ} end {matrix}} { begin {matrix} { frac { pi } {8}} \ 22.5 ^ { circ} end {matrix}} { begin {matrix} { frac { pi} {6}} \ 30 ^ { circ} end {matrix} } { begin {matrix} { frac { pi} {4}} \ 45 ^ { circ} end {matrix}} { begin {matrix} { frac { pi} {3} } \ 60 ^ { circ} end {матрица}} { begin {matrix} { frac {3 pi} {8}} \ 67.5 ^ { circ} end {matrix}} { begin {matrix} { frac {5 pi} {12}} \ 75 ^ { circ} end {matrix}} { begin {matrix} { frac { pi} {2}} 90 ^ { cir c} end {matrix}} \ hline sin 0 { frac {{ sqrt {6}} — { sqrt {2}}} {4}} и { frac { sqrt {2- { sqrt {2}}}} {2}} и { frac {1} {2}} и { frac { sqrt {2}} {2}} и { frac { sqrt {3}} {2}} и { frac { sqrt {2 + { sqrt {2}}}} {2}} и { frac {{ sqrt {6}} + { sqrt {2}}} {4}} 1 \ cos 1 { frac {{ sqrt {6}} + { sqrt {2}}} {4}} и { frac { sqrt {2 + { sqrt {2}}}} {2}} и { frac { sqrt {3}} {2}} и { frac { sqrt {2}} {2}} и { frac {1} {2}} и { frac { sqrt {2 — { sqrt {2}}}} {2}} и { frac {{ sqrt {6}} — { sqrt {2 }}} {4}} 0 \ tan 0 2- { sqrt {3}} { sqrt {2}} — 1 { frac { sqrt {3}} {3}} 1 { sqrt {3}} { sqrt {2}} + 1 и 2 + { sqrt {3}} infty \ cot infty 2 + { sqrt {3}} { sqrt {2}} + 1 { sqrt {3}} 1 { frac { sqrt {3}} {3}} { sqrt {2}} — 1 и 2 — { sqrt {3}} 0 \ sec 1 { sqrt {6}} — { sqrt {2}} и { sqrt {2}} { sqrt {2 — { sqrt {2}} }} и { frac {2 { sqrt {3}}} {3}} и { sqrt {2}} и 2 и { sqrt {2}} { sqrt {2 + { sqrt {2} }}} и { sqrt {6}} + { sqrt {2}} infty \ csc infty { sqrt {6}} + { sqrt {2}} и { sqrt { 2}} { sqrt {2 + { sqrt {2}}}} и 2 и { sqrt {2}} и { frac {2 { sqrt {3}}} {3}} и { sqrt {2}} { sqrt {2 — { sqrt {2}}}} и { sqrt { 6}} — { sqrt {2}} 1 \ hline end {array}}}
В исчислении


cos (x) { displaystyle cos (x)}

pn (x) = ∑ k = 0 n (- 1) kx 2 k (2 л)! { displaystyle p_ {n} (x) = sum _ {k = 0} ^ {n} (- 1) ^ {k} { frac {x ^ {2k}} {(2k)!}}}
Тригонометрические функции дифференцируемы. Это не сразу видно из приведенных выше геометрических определений. Более того, современная математическая тенденция состоит в том, чтобы строить геометрию на основе исчисления, а не наоборот. Поэтому, за исключением очень элементарного уровня, тригонометрические функции с использованием методов исчисления.
Для определения тригонометрических функций внутри исчисления есть две эквивалентные возможности: либо с использованием степенного ряда, либо дифференциальных уравнений. Эти определения эквивалентны, поскольку, начиная с одного из них, легко получить другое как свойство. Использование уравнения в чем-то более естественное, поскольку, например, коэффициенты степенного ряда может показаться совершенно произвольным, а тождество Пифагора проще вывести из дифференциальных уравнений.
Определение с помощью различных вариантов
Синус и косинус уникальными дифференцируемыми функциями такими, что
- ddx sin x = cos x, ddx cos x = — Икс, грех 0 знак равно 0, соз 0 знак равно 1. { Displaystyle { begin {align} { frac {d} {dx}} sin x = cos x, \ { frac {d} {dx}} cos x = — sin x, \ sin 0 = 0, \ cos 0 = 1. end {align}}}
Дифференцируя эти уравнения, получаем, что и синус, и косинус решения являются дифференциальными уравнениями
- y ″ + y = 0. { displaystyle y » + y = 0.}
Применение правила частного к определению касательная как отношение синуса к косинусу, получается, что функция касательной проверяет
- ddx tan x = 1 + tan 2 x. { displaystyle { frac {d} {dx}} tan x = 1 + tan ^ {2} x.}
Разложение в степенной ряду
Применение дифференциальных уравнений к степенному ряду с неопределенными коэффициентами, можно вывести рекуррентные соотношения для коэффициентов ряда Тейлора функций синуса и косинуса. Эти рекуррентные соотношения легко решить и дать разложения в ряд
- sin x = x — x 3 3! + х 5 5! — х 7 7! + ⋯ знак равно ∑ N знак равно 0 ∞ (- 1) N Икс 2 N + 1 (2 N + 1)! соз х знак равно 1 — х 2 2! + х 4 4! — х 6 6! + ⋯ знак равно ∑ N знак равно 0 ∞ (- 1) N Икс 2 N (2 N)!. { displaystyle { begin {align} sin x = x — { frac {x ^ {3}} {3!}} + { frac {x ^ {5}} {5!}} — { frac {x ^ {7}} {7!}} + cdots \ [8pt] = sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n} x ^ {2n + 1}} {(2n + 1)!}} \ [8pt] cos x = 1 — { frac {x ^ {2}} {2!}} + { Frac {x ^ { 4}} {4!}} — { frac {x ^ {6}} {6!}} + Cdots \ [8pt] = sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n} x ^ {2n}} {(2n)!}}. End {align}}}
радиус сходимости этих рядов бесконечен. Следовательно, синус и косинус могут быть расширены до целых функций (также называемых «синусом» и «косинусом»), которые (по определению) являются комплексными функциями, которые и голоморфные на всей комплексной плоскости.
Будучи определенными как совокупные функции, другие тригонометрические функции могут быть расширены до мероморфных функций, то есть функции, которые являются голоморфными во всей комплексной плоскости, за исключением некоторых полученных точек, называемых полюсами. Здесь полюсы — это число в форме (2 k + 1) π 2 { textstyle (2k + 1) { frac { pi} {2}}}

Отношения повторений также могут быть вычислены для коэффициентов ряда Тейлора других тригонометрических функций. Эти серии имеют конечный радиус сходимости. Их коэффициенты имеют комбинаторную интерпретацию: они перечисляют чередующиеся перестановки конечных множеств.
Точнее, определяя
- Un, н-е число вверх / вниз,
- Bn, н-е число Бернулли, и
- En, это н-е число Эйлера,
, которое имеет следующие разложения в ряд:
- tan x = ∑ n = 0 ∞ U 2 N + 1 Икс 2 N + 1 (2 N + 1)! Знак равно ∑ N знак равно 1 ∞ (- 1) N — 1 2 2 N (2 2 N — 1) B 2 N Икс 2 N — 1 (2 N)! = x + 1 3 x 3 + 2 15 x 5 + 17 315 x 7 + ⋯, для | х | < π 2. {displaystyle {begin{aligned}tan x{}=sum _{n=0}^{infty }{frac {U_{2n+1}x^{2n+1}}{(2n+1)!}}\{}=sum _{n=1}^{infty }{frac {(-1)^{n-1}2^{2n}left(2^{2n}-1right)B_{2n}x^{2n-1}}{(2n)!}}\{}=x+{frac {1}{3}}x^{3}+{frac {2}{15}}x^{5}+{frac {17}{315}}x^{7}+cdots,qquad {text{for }}|x|<{frac {pi }{2}}.end{aligned}}}
- csc x знак равно ∑ n знак равно 0 ∞ (- 1) n + 1 2 (2 2 n — 1 — 1) B 2 n x 2 n — 1 (2 n)! = x — 1 + 1 6 x + 7 360 x 3 + 31 15120 x 5 +, для 0 < | x | < π. {displaystyle {begin{aligned}csc x{}=sum _{n=0}^{infty }{frac {(-1)^{n+1}2left(2^{2n-1}-1right)B_{2n}x^{2n-1}}{(2n)!}}\{}=x^{-1}+{frac {1}{6}}x+{frac {7}{360}}x^{3}+{frac {31}{15120}}x^{5}+cdots,qquad {text{for }}0<|x|<pi.end{aligned}}}
- секунд x = ∑ n = 0 ∞ U 2 n x 2 n (2 n)! Знак равно ∑ N знак равно 0 ∞ (- 1) N… 2 N Икс 2 N (2 N)! = 1 + 1 2 x 2 + 5 24 x 4 + 61 720 x 6 + ⋯, для | х | < π 2. {displaystyle {begin{aligned}sec x{}=sum _{n=0}^{infty }{frac {U_{2n}x^{2n}}{(2n)!}}=sum _{n=0}^{infty }{frac {(-1)^{n}E_{2n}x^{2n}}{(2n)!}}\{}=1+{frac {1}{2}}x^{2}+{frac {5}{24}}x^{4}+{frac {61}{720}}x^{6}+cdots,qquad {text{for }}|x|<{frac {pi }{2}}.end{aligned}}}
- детская кроватка x = ∑ n = 0 ∞ (- 1) n 2 2 n B 2 n x 2 n — 1 (2 n)! = x — 1 — 1 3 x — 1 45 x 3 — 2 945 x 5 — ⋯, для 0 < | x | < π. {displaystyle {begin{aligned}cot x{}=sum _{n=0}^{infty }{frac {(-1)^{n}2^{2n}B_{2n}x^{2n-1}}{(2n)!}}\{}=x^{-1}-{frac {1}{3}}x-{frac {1}{45}}x^{3}-{frac {2}{945}}x^{5}-cdots,qquad {text{for }}0<|x|<pi.end{aligned}}}
Расширение частичной дроби
Существует представление ряда расширение частичной дроби где только что переведенные обратные функции суммируются, так что полюса функции котангенса и обратных соглашений совпадают:
- π cot π x = lim N → ∞ ∑ n = — NN 1 х + п. { displaystyle pi cot pi x = lim _ {N to infty} sum _ {n = -N} ^ {N} { frac {1} {x + n}}.}
Эту идентичность можно доказать с помощью трюка Herglotz. Объединение (–n) -го с n-м слагаемыми приводит к абсолютно сходящемуся ряду :
- π cot π x = 1 x + 2 x ∑ n = 1 ∞ 1 x 2 — n 2. { displaystyle pi cot pi x = { frac {1} {x}} + 2x sum _ {n = 1} ^ { infty} { frac {1} {x ^ {2} -n ^ {2}}}.}
Аналогичным образом можно найти частичное дробное разложение для функций секущей, косеканса и касательной:
- π sin π x = 1 x + 2 x ∑ n = 1 ∞ (- 1) nx 2 — n 2, { displaystyle { frac { pi} { sin pi x}} = { frac {1} {x}} + 2x sum _ {n = 1} ^ { infty} { frac {(-1) ^ {n}} {x ^ {2} -n ^ {2}}},}
- π cos π x = ∑ n = 0 ∞ (- 1) n (2 n + 1) (N + 1 2) 2 — Икс 2, { Displaystyle { frac { pi} { cos pi x}} = sum _ {n = 0} ^ { infty} (-1) ^ {n} { frac {(2n + 1)} {(n + { tfrac {1} {2}}) ^ {2} -x ^ {2}}},}
- π загар π Икс знак равно 2 Икс ∑ N знак равно 0 ∞ 1 (N + 1 2) 2 — Икс 2. { displaystyle pi tan pi x = 2x sum _ {n = 0} ^ { infty} { frac {1} {(n + { tfrac {1} {2}}) ^ {2} — x ^ {2}}}.}
Ра зложение бесконечного произведения
Следующее бесконечное произведение для синуса имеет большое значение в комплексном анализе:
- sin z = z ∏ n = 1 ∞ (1 — z 2 n 2 π 2), z ∈ C. { displaystyle sin z = z displaystyle prod _ {n = 1} ^ { infty} left (1 — { frac {z ^ {2}} {n ^ {2} pi ^ {2}) }} right), quad z in mathbb {C}.}
Для доказательства этого разложения см. Синус. Отсюда можно вывести, что
- cos z = ∏ n = 1 ∞ (1 — z 2 (n — 1 2) 2 π 2), z ∈ C. { displaystyle cos z = displaystyle prod _ { n = 1} ^ { infty} left (1 — { frac {z ^ {2}} { left (n — { frac {1} {2}} right) ^ {2} pi ^ {2}}} right), quad z in mathbb {C}.}
Связь с экспоненциальной функцией (формула Эйлера)
cos (θ) { displaystyle cos ( theta)}

грех (θ) { displaystyle sin ( theta)}

ei θ { displaystyle e ^ {i theta}}

Формула Эйлера связывает синус и косинус с экспоненциальной функцией :
- eix = cos х + я грех х. { displaystyle e ^ {ix} = cos x + i sin x.}
Эта формула обычно используется для реальных значений x, но остается верной для всех комплексных значений.
Доказательство: Пусть f 1 (x) = cos x + i sin x, { displaystyle f_ {1} (x) = cos x + i sin x,}





Имеется
- e i x = cos x + i sin x e — i x = cos x — i sin x. { displaystyle { begin {align} e ^ {ix} = cos x + i sin x \ [5pt] e ^ {- ix} = cos xi sin x. end {выравнивается}}}
Решая эту линейную систему в синусе и косинусе, можно выразить их через экспоненциальную функцию:
- sin x = eix — e — ix 2 i cos x = eix + д — ix 2. { displaystyle { begin {align} sin x = { frac {e ^ {ix} -e ^ {- ix}} {2i}} \ [5pt] cos x = { frac {e ^ {ix} + e ^ {- ix}} {2}}. end {align}}}
Когда x является вещественным, это можно переписать как
- cos x = Re (eix), sin х = Im (eix). { displaystyle cos x = operatorname {Re} left (e ^ {ix} right), qquad sin x = operatorname {Im} left (e ^ {ix} right).}
Большинство тригонометрических тождеств можно продемонстрировать, выразить тригонометрические функции в терминах комплексной экспоненциальной функции, используя приведенные выше формулы, а используя тождество ea + b = eaeb { displaystyle e ^ {a + b} = e ^ {a} e ^ {b}}
Определить использование различных функций
Можно также определить тригонометрические функции с помощью различных функциональных функций.
Например, синус и косинус образуют уникальную пару непрерывных функций, удовлетворяющие формуле разности
- cos (x — y) = cos x cos y + sin x sin y { displaystyle cos (xy) = cos x cos y + sin x sin y ,}
и добавленное условие
- 0 < x cos x < sin x < x for 0 < x < 1. {displaystyle 0
В комплексной плоскости
Синус и косинус комплексного числа z = x + iy { displaystyle z = x + iy}
- sin z = sin x cosh y + я соз Икс зп Y соз Z знак равно соз Икс сш Y — я грех Икс зп Y { Displaystyle { begin {выровнено} грех г = грех х сш у + я соз х sinh y \ [5pt] cos z = cos x cosh yi sin x sinh y end {align}}}
Воспользовавшись преимуществом раскраски домена, можно построить график тригонометрических функций как комплексных значений функций. На графике можно увидеть различные особенности, уникальные для сложных функций; например, функции синуса и косинуса можно рассматривать как неограниченные, поскольку мнимая часть z { displaystyle z}
 |
 |
 |
 |
 |
 |
sin z { displaystyle sin z ,} |
cos z { displaystyle cos z ,} |
tan z { displaystyle tan z ,} |
детская кроватка z { displaystyle cot z ,} |
sec z { displaystyle sec z ,} |
csc z { displaystyle csc z ,} |
Основные тождества
Многие тождества связывают тригонометрические функции. В этом разделе собраны самые основные; для получения дополнительных сведений см. Список тригонометрических идентификаторов. Эти тождества могут быть доказаны геометрически из определений единичного круга или определений прямоугольного треугольника (хотя для последних определений необходимо учитывать углы, которые не находятся в интервале [0, π / 2], см. Доказательства тригонометрических тождеств ). Для негеометрических доказательств, использующих только инструменты исчисления, можно напрямую использовать дифференциальные уравнения таким же образом, как и в вышеупомянутом доказательстве тождества Эйлера. Можно также использовать тождество Эйлера для выражения всех тригонометрических функций в терминах комплексных экспонент и с использованием свойств экспоненциальной функции.
Четность
Косинус и секанс являются четными функциями ; другие тригонометрические функции — это нечетные функции. То есть:
- sin (- x) = — sin x cos (- x) = cos x tan (- x) = — tan x cot (- x) = — cot x csc (- x) = — csc x sec (- x) = sec x. { Displaystyle { begin {align} sin (-x) = — sin x \ cos (-x) = cos x \ tan (-x) = — tan x \ cot (-x) = — cot x \ csc (-x) = — csc x \ sec (-x) = sec x. end {align}}}
Периоды
Все тригонометрические функции являются периодическими функциями периода 2π. Это наименьший период, за исключением тангенса и котангенса, у которых π является наименьшим периодом. Это означает, что для каждого целого числа k выполняется
- sin (x + 2 k π) = sin x cos (x + 2 k π) = cos x tan (x + k π) = tan x детская кроватка (x + k π) = детская кроватка x csc (x + 2 k π) = csc x sec (x + 2 k π) = sec x. { Displaystyle { begin {align} sin (x + 2k pi) = sin x \ cos (x + 2k pi) = cos x \ tan (x + k pi) = tan x \ кроватка (x + k pi) = cot x \ csc (x + 2k pi) = csc x \ sec (x + 2k pi) = sec x. end {align}}}
Пифагорейская идентичность
Пифагорейская идентичность — это выражение теоремы Пифагора в терминах тригонометрических функций. Это
- sin 2 x + cos 2 x = 1. { displaystyle sin ^ {2} x + cos ^ {2} x = 1.}
Формулы суммы и разности
Формулы суммы и разности позволяют разложить синус, косинус и тангенс суммы или разности двух углов на синусы, косинусы и тангенсы самих углов. Их можно получить геометрически, используя аргументы, относящиеся к Птолемею. Их также можно получить алгебраически, используя формулу Эйлера.
- Sum
- sin (x + y) = sin x cos y + cos x sin y, cos (x + y) = cos x cos y — грех x sin y, tan (x + y) = tan x + tan y 1 — tan x tan y. { Displaystyle { begin {align} sin left (x + y right) = sin x cos y + cos x sin y, \ cos left (x + y right) = cos x cos y- sin x sin y, \ tan (x + y) = { frac { tan x + tan y} {1- tan x tan y}}. end {выровнено}}}
- Разница
- sin (x — y) = sin x cos y — cos x sin y, cos (x — y) = cos x cos y + sin x sin y, tan (x — y) = tan x — tan y 1 + tan x tan y. { Displaystyle { begin {align} sin left (xy right) = sin x cos y- cos x sin y, \ cos left (xy right) = cos x cos y + sin x sin y, \ tan (xy) = { frac { tan x- tan y} {1+ tan x tan y}}. end {выравнивается}}}
Когда два угла равны, формулы суммы сводятся к более простым уравнениям, известным как формулы двойного угла .
- sin 2 x = 2 sin x cos x = 2 tan x 1 + tan 2 x, cos 2 x = cos 2 x — sin 2 x = 2 cos 2 x — 1 = 1-2 sin 2 x = 1 — tan 2 x 1 + tan 2 x, tan 2 х знак равно 2 загар х 1 — загар 2 х. { displaystyle { begin {align} sin 2x = 2 sin x cos x = { frac {2 tan x} {1+ tan ^ {2} x}}, \ cos 2x = cos ^ {2} x- sin ^ {2} x = 2 cos ^ {2} x-1 = 1-2 sin ^ {2} x = { frac {1- tan ^ {2} x } {1+ tan ^ {2} x}}, \ tan 2x = { frac {2 tan x} {1- tan ^ {2} x}}. End {align}}}
Эти обозначения обозначения вакансии идентичности продукта к сумме.
По установке θ = 2 x { displaystyle theta = 2x}



- грех θ = 2 t 1 + t 2, cos θ знак равно 1 — T 2 1 + T 2, загар θ = 2 t 1 — t 2. { displaystyle { begin {align} sin theta = { frac {2t} {1 + t ^ { 2}}}, \ cos theta = { frac {1-t ^ {2}} {1 + t ^ {2}}}, \ tan theta = { frac {2t} {1-t ^ {2}}}. End {align}}}
Вместе с
- d θ = 2 1 + t 2 dt, { displaystyle d theta = { frac {2} {1 + t ^ {2}}} , dt,}
это подстановка касательных полууглов, которое позволяет сократить вычисление интегралов и первообразных тригонометрических функций до вычислений дробей.
Производные и первообразные
производные тригонометрические функции получаются из производных синуса и косинуса с применением правила частных. Значения, приведенные для первообразных в следующей таблице, можно проверить путем их дифференциации. Число C является константой интегрирования.
- f (x) f ′ (x) ∫ f (x) dx sin x cos x — cos x + C cos x — sin x sin x + C tan x sec 2 x = 1 + tan 2 x — ln (| cos x |) + C детская кроватка x — csc 2 x = — (1 + кроватка 2 x) ln (| sin x |) + C sec x sec x tan x ln (| sec x + tan x |) + C csc x — csc x детская кроватка x — ln (| csc x + детская кроватка Икс |) + С { Displaystyle { begin {array} {| c | c | c |} hline f (x) f ‘(x) int f (x) , dx \ hline sin x cos x — cos x + C \ cos x — sin x sin x + C \ tan x sec ^ {2} x = 1 + tan ^ {2} x — ln left (| cos x | right) + C \ cot x — csc ^ {2} x = — (1+ cot ^ {2} x) ln left (| sin x | right) + C \ sec x sec x tan x ln left (| sec x + tan x | right) + C \ csc x — csc x cot x — ln left (| csc x + cot x | right) + C \ hline end {array}}}
Обратные функции
Тригонометрические функции являются периодическими и, следовательно, не инъективными, поэтому, строго говоря, у них нет обратной функции . Однако на каждом интервале, на котором тригонометрическая функция монотонна, можно определить обратную функцию, и это определить обратные тригонометрические функции как многозначные функции. Чтобы определить истинную обратную функцию, необходимо ограничить область действия интервалом, в которой функция является монотонной, и, в которой эта функция является монотонной, биективно от этого интервала до своего изображения функцию. Общий выбор для этого интервала, называемый набором основных значений, приведен в следующей таблице. Как правило, обратные тригонометрические функции обозначаются префиксом «дуга» перед названием или его сокращением.
- Область определения функций Набор главных значений y = arcsin x sin y = x — 1 ≤ x ≤ 1 — π 2 ≤ y ≤ π 2 y = arccos x cos y = x — 1 ≤ x ≤ 1 0 ≤ y ≤ π y = arctan x tan y = x — ∞ ≤ x ≤ ∞ — π 2 < y < π 2 y = arccot x cot y = x − ∞ ≤ x ≤ ∞ 0 < y < π y = arcsec x sec y = x x < − 1 or x>1 0 ≤ y ≤ π, y ≠ π 2 y = arccsc x csc y = xx < − 1 or x>1 — π 2 ≤ y ≤ π 2, y ≠ 0 { displaystyle { begin {array} {| c | c | c | c |} hline { text {Function}} { text {Definition}} { text {Домен}} { text {Набор основных значений}} \ hline y = arcsin x sin y = x -1 leq x leq 1 — { frac { pi} {2}} leq y leq { frac { pi} {2}} \ y = arccos x cos y = x -1 leq x leq 1 0 leq y leq pi \ y = arctan x tan y = x — infty leq x leq infty — { frac { pi} {2}} 1 0 leq y leq pi, ; y neq { frac { pi} {2}} \ y = operatorname {arccsc} x csc y = x x <-1{text{ or }}x>1 — { frac { pi} {2} } leq y leq { frac { pi} {2}}, ; y neq 0 \ hline end {array}}}
Обозначение sin cos и т. д. часто используются для arcsin и arccos и т. д. При использовании этого обозначения обратные функции можно спутать с мультипликативными обратными функциями. путаницы, хотя «arcsec» для arcsecant можно спутать с «arcsecond «.
Так же, как синус и косинус, обратные тригонометрические функции также могут быть выражены в виде бесконечных рядов. выразить с помощью комплексных логарифмов. Подробнее см. Обратные тригонометрические функции.
Приложения
Углы и стороны треугольника
В этих Соответствующие противоположные краевы, обозначенные различными формулами A, B, C, обозначают три (внутренние) треугольника, а a, b, c. анными по тригонометрическим функциям, которые они включают.
Закон синусов
Закон синусов гласит, что для произвольного треугольника со сторонами a, b и c и углами, противоположными сторонами A, B и C:
- грех A a = B b = грех C c = 2 Δ abc, { displaystyle { frac { sin A} {a}} = { frac { sin B} { b}} = { frac { sin C} {c}} = { frac {2 Delta} {abc}},}
где Δ — площадь треугольника, или, что то же самое,
- A = б грех B = c C = 2 R, { displaystyle { frac {a} { sin A}} = { frac {b} { sin B}} = { frac { c} { sin C}} = 2R,}
где R — описанный радиус.
треугольника. Это можно доказать, разделив треугольник на два прямоугольных и используя приведенное выше определение синуса.. Закон синусов полезен для вычислений длин неизвестных сторон треугольника, если известны два угла и одна сторона. Это обычная ситуация, развивающая в триангуляции, методы определения неизвестных расстояний путем измерения двух углов и доступного замкнутого расстояния.
Закон косинусов
Закон косинусов (также известный как формула косинусов или правило косинусов) является расширением Теорема Пифагора :
- c 2 = a 2 + b 2 — 2 ab cos C, { displaystyle c ^ {2} = a ^ {2} + b ^ {2} -2ab cos C, ,}
или, что эквивалентно,
- cos C = a 2 + b 2 — c 2 2 ab. { displaystyle cos C = { frac {a ^ {2} + b ^ {2} -c ^ {2}} {2ab}}.}
В этой формуле угла при C противоположен стороне c. Эту теорему можно доказать, разделив треугольник на два прямоугольных и используя теорему Пифагора.
Закон косинусов можно использовать для определения стороны треугольника, если известны две стороны и угол между ними. Его можно использовать для нахождения косинусов угла (и, соответственно, всех углов), если известны длины сторон.
Закон касательных
Все нижеприведенные примеры образуют закон касательных
- tan A — B 2 tan A + B 2 = a — b a + b; tan A — C 2 tan A + C 2 = a — c a + c; tan B — C 2 tan B + C 2 = b — c b + c. { displaystyle { frac { tan { frac {AB} {2}}} { tan { frac {A + B} {2}}}} = { frac {ab} {a + b}} ,; qquad { frac { tan { frac {AC} {2}}} { tan { frac {A + C} {2}}}} = { frac {ac} {a + c}} ,; qquad { frac { tan { frac {BC} {2}}} { tan { frac {B + C} {2}}}} = { frac {bc} {b + c}}. }
Объяснение формул на словах было бы громоздким, но схемы сумм и разностей для длин и противоположных углов очевидны в теореме.
Закон котангенсов
Если
- ζ = 1 s (s — a) (s — b) (s — c) { displaystyle zeta = { sqrt {{ frac {1} {s}} (sa) (sb) (sc)}} ~}
(радиус вписанной окружности для треугольника)
и
- s = a + b + c 2 { displaystyle s = { frac {a + b + c} {2}} ~}
(полупериметр треугольника),
тогда все следующие образуют закон котангенсов
- кроватка A 2 = s — а ζ; кроватка B 2 = s — b ζ; кроватка C 2 = s — c ζ. { displaystyle cot { frac {A} {2}} = { frac {sa} { zeta}} ~; qquad cot { frac {B} {2}} = { frac {sb} { zeta}} ~; qquad cot { frac {C} {2}} = { frac {sc} { zeta}} ~.}
Отсюда следует, что
- кроватка A 2 s — a = детская кроватка B 2 s — b = детская кроватка C 2 s — c = 1 ζ. { displaystyle { frac { cot { dfrac {A} {2}}} {sa}} = { frac { cot { dfrac {B} {2}}} {sb}} = { frac { cot { dfrac {C} {2}}} {sc}} = { frac {1} { zeta}} ~.}
На словах теорема такова: котангенс полуугла равенство полупериметра минус сторона, противоположная указанному углу, к внутреннему радиусу треугольника.

Периодические функции


. Тригонометрические функции также важны в физике. Функции синуса и косинуса, например, используются для описания простое гармоническое движение, которое моделирует многие природные явления, такие как движение массы, прикрепленной к пружине, и для малых углов, маятниковое движение. массы, висящей на веревке. Функции синуса и косинуса являются одномерными проекциями равномерного кругового движения.
Тригонометрические функции также оказываются полезными при изучении общих периодических функций. Характерные волновые структуры периодических функций полезны для повторяющихся явлений, таких как звуковые или световые волны.
В общих условиях периодическая функция f (x) может быть выражена как сумма синусоидальных или косинусоидальных волн в ряд Фурье. Обозначая синус или косинус базисных функций через φ k, разложение периодической функции f (t) принимает вид:
- f (t) = ∑ k = 1 ∞ ck φ k (t). { displaystyle f (t) = sum _ {k = 1} ^ { infty} c_ {k} varphi _ {k} (t).}
Например, прямоугольная волна может быть записан как ряд Фурье
- f квадрат (t) = 4 π ∑ k = 1 ∞ sin ((2 k — 1) t) 2 k — 1. { displaystyle f _ { text {square }} (t) = { frac {4} { pi}} sum _ {k = 1} ^ { infty} { sin { big (} (2k — 1) t { big)} over 2k-1}.}
На анимации прямоугольной волны в верхнем углу видно, что всего несколько элементов уже дают довольно хорошее приближение. Суперпозиция нескольких членов в разложении пилообразной волны на ниже.
История
В то время как раннее изучение тригонометрии можно проследить до глубокой древности, тригонометрические функции в том виде, в котором они используются сегодня, были разработаны в средневековый период. Функция хорды была обнаружена Гиппархом в Никее (180–125 до н.э.) и Птолемеем в Римском Египте (90–165 гг. Н. Э.). Функции синуса и версина (1 — косинус) можно проследить до функций джья и коти-джья, использовал в период Гупта индийская астрономия ( Арьябхатия, Сурья Сиддханта ), посредством перевода с санскрита на арабский, а с арабского на латинский. (См. таблицу синусов Арьябхаты.)
Все шесть тригонометрических функций, используемых в настоящее время, были известны в исламской математике к 9 веку, как и закон синусы, используемое в решение треугольников. За исключением синуса (был заимствован из индийской математики), персидскими математиками были открыты другие пять современных тригонометрических функций, включая косинус, тангенс, котангенс, секанс и косеканс. Аль-Хваризми (c 780–850) составили таблицы синусов, косинусов и тангенсов. Около 830 г., Хабаш аль-Хасиб аль-Марвази открыл котангенс и составил таблицы касательных и котангенсов. Мухаммад ибн Джабир аль-Харрани аль-Баттани (853–929) открыл взаимные функции секанса и косеканса, и была произведена первая таблица косекансов для каждой степени от 1 ° до 90 °. Позднее тригонометрические функции изучались математиками, в том числе Омаром Хайямом, Бхаскарой II, Насиром ад-Дином ат-Туси, Джамшидом аль-Каши (14 век), Улугбек (14 век), Региомонтан (1464), Ретикус и ученик Ретикуса Валентин Отон.
Мадхава из Сангамаграмы (ок. 1400) сделал первые шаги в анализ тригонометрических функций в терминах бесконечных рядов. (См. серию Мадхавы и таблицу синусов Мадхавы.)
Термины тангенс и секанс впервые были введены датским математиком Томасом. Финке в своей книге Geometria rotundi (1583 г.).
16 век Французский математик Альбер Жирар впервые опубликовал свое сокращение sin, cos, и tan в книге Trigonométrie.
В статье опубликованной в 1682 году, Лейбниц доказал, что sin x не является алгебраической функцией от x. Хотя они представлены как отношения прямоугольного треугольника и таким образом, выглядят как рациональные функции, результат Лейбница установил, что они на самом деле являются трансцендентными функциями своего аргумента. Задача ассимиляции круговых функций в алгебраических выражениях была решена Эйлером в его Введение в анализ бесконечного (1748). Его метод заключен в том, чтобы показать, что функции синуса и косинуса являются чередующимися рядами, образованными из четных и нечетных членов соответственно экспоненциального ряда. Он представил «формулу Эйлера », а также почти современные сокращения (sin., Cos., Tang., Cot., Sec. И cosec.).
Несколько функций были обычным явлением исторически, но сейчас используются редко, например, аккорд, версин (который появился в самых ранних таблицах), покрывающий синус, гаверсинус, экзосеканс и экзосеканс. Список тригонометрических отождествлений показывает взаимосвязей между используемыми функциями.
- crd (θ) = 2 sin (θ / 2)
- versin (θ) = 1 — cos (θ) = 2 sin (θ / 2)
- охватывает (θ) = 1 — sin (θ) = versin (π / 2 — θ))
- haversin (θ) = 1 / 2versin (θ) = sin (θ / 2)
- exsec (θ) = sec (θ) — 1
- excsc (θ) = exsec (π / 2 — θ) = csc (θ) — 1
Этимология
Слово синус происходит от латинское sinus, что означает «изгиб; залив », а точнее« свисающая складка верхней части тоги »,« пазухи одежды », который был выбран в качестве перевода того, что интерпретировалось как арабское слово jaib, означающее« карман »или« складка »в переводе XII века произведений аль-Баттани и аль-Хваризми на средневековую латынь. Выбор был основан на неправильном прочтении арабской письменной формы jyb (جيب ), которая сама возникла как транслитерация санскритского дживы, который вместе со своим синонимом jyā (стандартный санскритский термин для синуса) переводится как « тетива », что в свою очередь заимствовано из древнегреческого χορδή « струна ».
Слово тангенс происходит от латинского tangens, означающего «касаться», поскольку касается окружности единичного радиуса, тогда как секанс происходит от латинского secans — «разрезание» — линия пересекает окружность.
Префикс » co- «(в« косинус »,« котангенс »,« косеканс ») можно найти в каноне triangulorum Эдмунда Гюнтера (1620), в котором косинус определяется как сокращение синусового комплемента (синуса дополнительный угол ) и аналогичным образом переходит к определению котангенов.
См. Также
- Все студенты принимают исчисление — мнемоника для вызова знаков тригонометрических функций в определенном квадранте декартовой системы координат. плоскость
- Формула синусоидальной аппроксимации Бхаскары I
- Дифференциация тригонометрических функций
- Обобщенная тригонометрия
- Создание тригонометрических таблиц
- Гиперболическая функция
- Список интегралов тригонометрических функций
- Список интегралов тригонометрических функций
- периодических функций
- Список тригонометрических тождеств
- Полярный синус — обобщение для вершинных углов
- Доказательства тригонометрических тождеств
- Версин — для нескольких менее используемых тригонометрических функций
Примечания
Ссылки
Внешние ссылки
- , Энциклопедия математики, EMS Press, 2001 [1994]
- Visionlearning Module по волновой математике
- GonioLab Визуализация единичной окружности, тригонометрических и гиперболических функций
- q-Sine Статья о q-аналоге греха на MathWorld
- q-Cosine Статья о q-аналоге cos в MathWorld



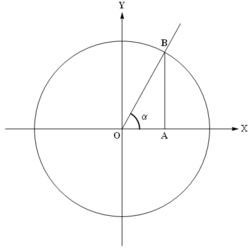












 — числа Бернулли,
— числа Бернулли, — числа Эйлера.
— числа Эйлера.






































 следует из формулы дополнения и формулы Гаусса для Гамма-функции
следует из формулы дополнения и формулы Гаусса для Гамма-функции














































 где
где 





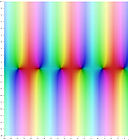
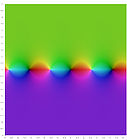


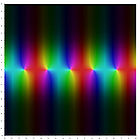
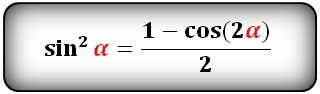
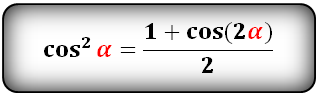
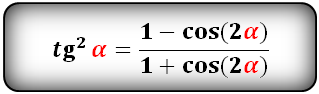
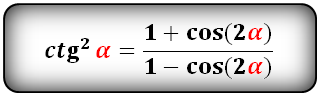
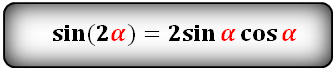
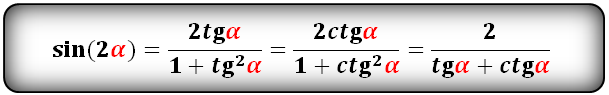
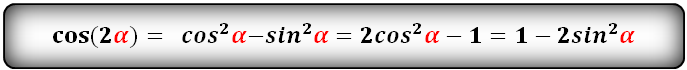
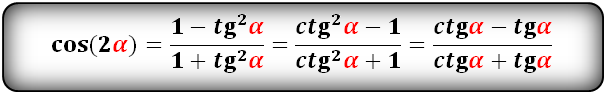
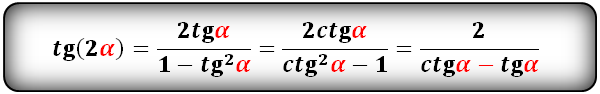
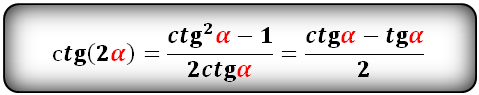


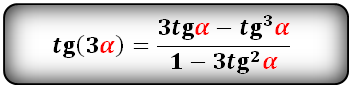
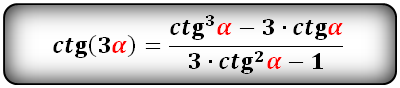


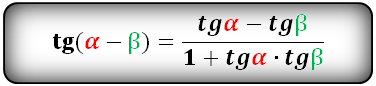
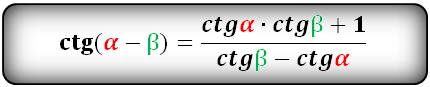
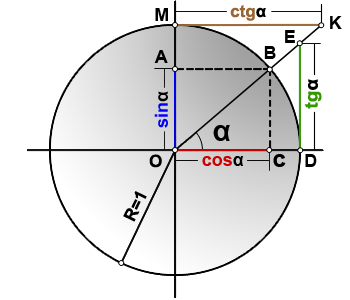
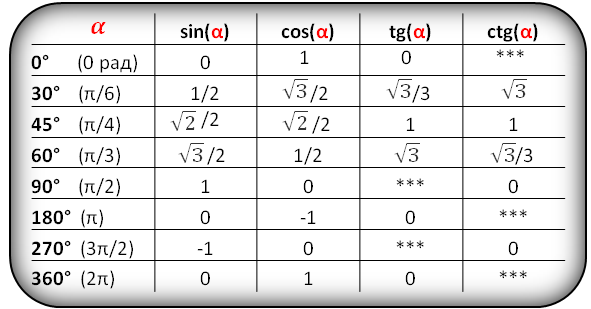
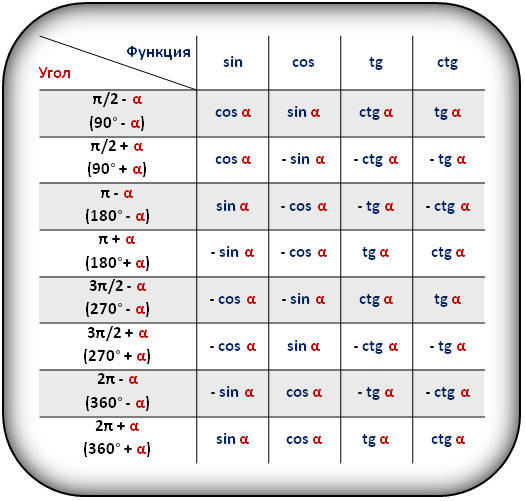
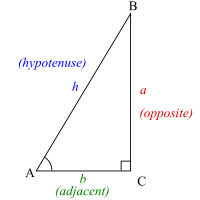






 и грех θ = Y A. { displaystyle quad sin theta = y _ { mathrm {A}}.}
и грех θ = Y A. { displaystyle quad sin theta = y _ { mathrm {A}}.}

 и детская кроватка θ = x C, { displaystyle quad cot theta = x _ { mathrm {C}},}
и детская кроватка θ = x C, { displaystyle quad cot theta = x _ { mathrm {C}},}
 и сек. θ = х E. { displaystyle quad sec theta = x _ { mathrm {E}}.}
и сек. θ = х E. { displaystyle quad sec theta = x _ { mathrm {E}}.}

 и соз θ = соз (θ + 2 к π) { displaystyle quad cos theta = cos left ( theta + 2k pi right)}
и соз θ = соз (θ + 2 к π) { displaystyle quad cos theta = cos left ( theta + 2k pi right)}
 и детская кроватка θ = детская кроватка (θ + k π) { displaystyle quad cot theta = cot ( theta + k pi)}
и детская кроватка θ = детская кроватка (θ + k π) { displaystyle quad cot theta = cot ( theta + k pi)}
 (прямой угол )
(прямой угол )


 (прямой угол )
(прямой угол )





![{ displaystyle { begin {align} sin x = x - { frac {x ^ {3}} {3!}} + { Frac {x ^ {5}} {5!}} - { frac {x ^ {7}} {7!}} + Cdots \ [8pt] = sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n} x ^ {2n + 1}} {(2n + 1)!}} \ [8pt] cos x = 1 - { frac {x ^ {2}} {2! }} + { frac {x ^ {4}} {4!}} - { frac {x ^ {6}} {6!}} + cdots \ [8pt] = sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n} x ^ {2n}} {(2n)!}}. end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b96cbd9a749c461b481fbd08d70ed37ebb8efd1)













![{ displaystyle { begin {align} e ^ {ix} = соз х + я грех х \ [5pt] е ^ {- ix} = соз хи грех х. конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d374fafbe34908c7766b67e4c51797589906940)
![{ Displaystyle { begin {align} sin x = { fr ac {e ^ {ix} -e ^ {- ix}} {2i}} \ [5pt] cos x = { frac {e ^ {ix } + e ^ {- ix}} {2}}. end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/590e4a1bbe3ccdb7521fe06a6e5b56e538d4e729)



![{ displaystyle { begin {align} sin z = sin x cosh y + i cos x sinh y [5pt] cos z = cos x cosh yi sin x sinh y end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1646655eab602e234f42df85cae241ffbb867cf)















 (радиус вписанной окружности для треугольника)
(радиус вписанной окружности для треугольника) (полупериметр треугольника),
(полупериметр треугольника),


