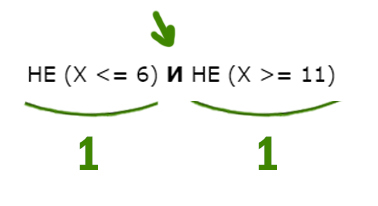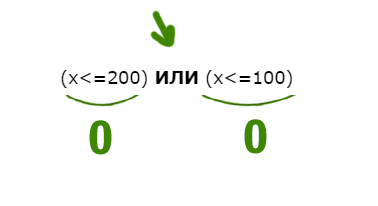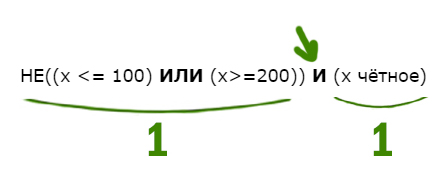Привет! Продолжаем разбирать ОГЭ по информатике 2023. Сегодня посмотрим 3 задание.
Третье задание из ОГЭ по информатике проверяет умение работать с логическим выражением.
В логическом выражении могут использоваться союз И и союз ИЛИ.
Пусть 0 — это ложь, 1 — Истина. Тогда напишем таблицу истинности для союза И и для союза ИЛИ.
Таблица истинности для союза И
| Выражение | Результат |
| 0 И 0 | 0 |
| 0 И 1 | 0 |
| 1 И 0 | 0 |
| 1 И 1 | 1 |
Союз И похож на умножение в математике. Если в логическом выражении присутствует 0 (ложь), то в итоге тоже получается 0 (ложь). Лишь две единицы дают тоже единицу.
Таблица истинности для союза ИЛИ
| Выражение | Результат |
| 0 ИЛИ 0 | 0 |
| 0 ИЛИ 1 | 1 |
| 1 ИЛИ 0 | 1 |
| 1 ИЛИ 1 | 1 |
Эта операция похоже на суммирование в математике. Лишь 1 или 1 даёт не 2, как в математике, а 1.
Перейдём к решению примерных задач из ОГЭ по информатике 2023.
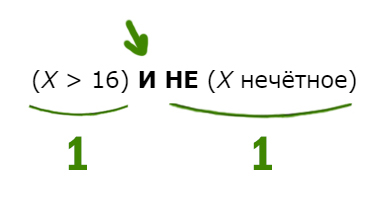
Задача (Классическая)
Напишите наименьшее число X, для которого истинно высказывание:
(X > 16) И НЕ (X нечётное)
Решение:
Нужно, чтобы высказывание было истинным. Посмотрим, когда единица (истина) получается для союза И. Такое происходит только когда слева и справа стоят 1 (единицы).
Получается наш X должен быть больше 16, и число должно быть не нечётное, т.е. чётное! Наименьшее чётное число большее 16 будет 18.
Ответ: 18
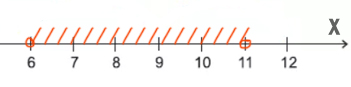
Задача (Закрепление)
Напишите наибольшее целое число x, для которого истинно высказывание:
НЕ (X <= 6) И НЕ (X >= 11)
Решение:
Опять высказывание должно быть истинным.
С одной стороны X должен быть НЕ меньше или равно 6, т.е значит, X нужно взять больше 6 (X > 6). Причём само число 6 не входит в этот диапазон.
С другой стороны X НЕ больше или равно 11, т.е. X должен быть меньше 11 (X < 11).
Наибольшее целое число будет 10.
Ответ: 10
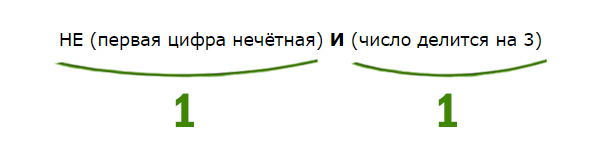
Задача (Союз И)
Напишите наименьшее натуральное двузначное число, для которого истинно высказывание:
НЕ (первая цифра нечётная) И (число делится на 3)
Решение:
Высказывание должно быть истинным.
Первая цифра должна быть НЕ нечётная. Значит, она должна быть чётная. Число должно делится на 3. Найдём наименьшее двухзначное число, у которого первая цифра чётная, и оно делится на 3. Это будет 21.
Ответ: 21
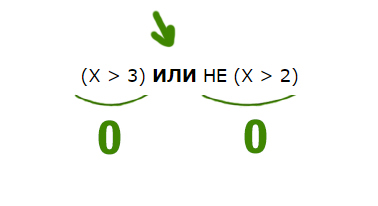
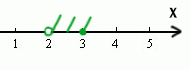
Задача (Союз ИЛИ)
Для какого целого числа X ЛОЖНО высказывание:
(X > 3) ИЛИ НЕ (X > 2)
Решение:
В этой задаче используется союз ИЛИ. Нужно, чтобы высказывание было ложным. Ложь при союзе ИЛИ получается только в одном случае, когда слева и справа стоят нули.
Утверждение, что X > 3 должно быть ложно, значит, если его перевернуть, получится X <= 3. Второе утверждение НЕ (X > 2) тоже должно быть ложно. Значит, если перевернём это утверждение, частицу НЕ нужно убрать. Получается просто X > 2.
Получается, что только одно целое число входит в допустимый диапазон. Это тройка.
Ответ: 3
Задача (Частица НЕ над всем выражением)
Напишите наименьшее натуральное число x, для которого истинно высказывание:
НЕ((x<=200) ИЛИ (x<=100))
Решение:
Нам нужно сделать выражение истинным. Но всё выражение находится под влиянием частицы НЕ. Можно эту частицу полностью убрать, но воспринимать, как будто нужно сделать выражение ложным. А дальше всё как обычно.
Ложь у союза ИЛИ получается в одном случае.
Первое выражение выдаёт ноль, когда x>200 (равно 200 не входит). Второе выражение выдаёт ноль, когда x>100. Объединив эти два условия получаем:
x > 200
Наименьшее число получается 201.
Ответ: 201
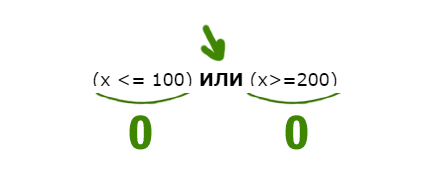
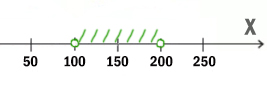
Задача (Крепкий орешек)
Напишите наименьшее натуральное число x, для которого истинно высказывание:
НЕ((x <= 100) ИЛИ (x>=200)) И (x чётное)
Решение:
В этой примерной задаче из ОГЭ по информатике применим все приёмы, которые мы разбирали до этого.
Когда союз И выдаёт единицу ?
Посмотрим, когда левое выражение выдаёт 1. Уберём частицу НЕ, но тогда будем смотреть, когда левое выражение выдаёт 0.
Перевернём оба выражения, которые находятся по обе стороны от союза ИЛИ. С одной стороны X>100, с другой X<200.
Учтём правое от союза И выражение. Наименьшее чётное число получается 102.
Ответ: 102
Всего: 182 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Напишите наименьшее целое число x, для которого истинно высказывание:
НЕ (X < 2) И (X < 5).
Напишите наименьшее целое число x, для которого истинно высказывание:
НЕ (X < 2) И (X чётное).
Напишите наименьшее целое число x, для которого истинно высказывание:
НЕ (X < 7) И (X чётное).
Напишите наименьшее целое число x, для которого истинно высказывание:
НЕ (X < 6) И (X нечётное).
Напишите наименьшее целое число x, для которого истинно высказывание:
НЕ (X < 9) И НЕ (X нечётное).
Напишите наименьшее целое число x, для которого истинно высказывание:
НЕ (X <= 7) И (X < 20).
Напишите наибольшее целое число x, для которого истинно высказывание:
НЕ (X <= 15) И (X < 20).
Напишите наибольшее целое число x, для которого истинно высказывание:
НЕ (X <= 14) И (X <= 18).
Напишите наибольшее целое число x, для которого истинно высказывание:
НЕ (X <= 10) И НЕ (X > 16).
Напишите наибольшее целое число x, для которого истинно высказывание:
НЕ (X <= 6) И НЕ (X >= 11).
Напишите наибольшее целое число x, для которого истинно высказывание:
НЕ (X <= 3) И НЕ (X >= 7).
Напишите наибольшее целое число x, для которого истинно высказывание:
НЕ (X чётное) И НЕ (X >= 7).
Напишите наибольшее целое число x, для которого истинно высказывание:
НЕ (X чётное) И НЕ (X >= 11).
Напишите наибольшее целое число x, для которого истинно высказывание:
НЕ (X нечётное) И НЕ (X >= 10).
Напишите наибольшее целое число x, для которого истинно высказывание:
НЕ (X нечётное) И НЕ (X >= 6).
Напишите наибольшее целое число x, для которого истинно высказывание:
(X >= 6) И НЕ (X > 12).
Напишите наибольшее целое число x, для которого истинно высказывание:
(X > 5) И НЕ (X > 15).
Напишите наименьшее целое число x, для которого истинно высказывание:
(X > 2) И НЕ (X > 13).
Напишите наименьшее целое число x, для которого истинно высказывание:
НЕ (X < 2) И НЕ (X > 10).
Напишите наименьшее целое число x, для которого истинно высказывание:
НЕ (X < 5) И НЕ (X > 9).
Всего: 182 1–20 | 21–40 | 41–60 | 61–80 …
Задание №3. Определение истинности составного высказывания.
Уровень сложности: базовый; макс. балл за задание: 1; примерное время выполнения: 3 минуты.
Знать: логические значения, операции, выражения.
Уметь: определять истинность составного высказывания.
Пример задания.
Напишите наименьшее число x, для которого истинно высказывание:
(x > 16) И НЕ (x нечётное).
Разбор задания.
Мы имеем составное высказывания из двух простых связанных между собой конъюнкцией (операцией логического умножения). Конъюнкция истинна только в одном случае, когда оба простых высказывания истинны. Следовательно требуемое число должно быть больше 16 и не нечётное (т.е. чётное). Наименьшее такое число — 18.
Ответ: 18.
Пример задания.
Напишите наибольшее число x, для которого ложно высказывание:
НЕ ((x < 54) И (x простое число)) ИЛИ НЕ (x <= 16)
Разбор задания.
Это задание гораздо сложнее предыдущего. Для решения таких логических примеров не мешало бы знать законы алгебры логики для того, чтобы можно было упростить выражение.
Сначала «избавимся» от отрицания:
(x >= 54) ИЛИ (x не простое число) ИЛИ (x > 16)
В данном примере трудно сообразить, для какого наибольшего числа x это высказывание будет ложно. Но можно ко всему выражению применить «отрицание» и найти для какого наибольшего числа x это высказывание будет истинным!
(x < 54) И (x простое число) И (x <= 16)
Глядя на это выражение можно понять, что наибольшее простое число х , которое меньше 54, меньше либо равно 16 — это число 13, что и будет ответом к нашему заданию.
Ответ: 13.
Проводя анализ результатов пробного ОГЭ по информатике в нашем районе и увидев процент решаемости заданий на логику (задание №3), я пришел к такому выводу, что просто необходимо разобрать побольше типичных задач. Предлагаю Вам решить некоторые такие задания.
Задание №1. Напишите наибольшее число x, для которого ложно высказывание:
(x > 72) ИЛИ НЕ (x чётное).
Задание №2. Напишите наибольшее число x, для которого ложно высказывание:
НЕ (x ≤ 26) ИЛИ (x нечётное).
Задание №3. Напишите наименьшее число x, для которого истинно высказывание:
НЕ (x ≤ 25) И (x кратное 5) И (x ≠ 30).
Задание №4. Напишите наибольшее число x, для которого ложно высказывание:
(x ≥ 90) ИЛИ НЕ (x кратное 3) ИЛИ (x ≠ 87).
Задание №5. Напишите наибольшее число x, для которого истинно высказывание:
НЕ ((x ≥ 23) ИЛИ НЕ (x нечётное)) И НЕ (x > 25).
Задание №6. Напишите наименьшее число x, для которого ложно высказывание:
НЕ ((x ≥ 100) И НЕ (x кратно 4)) ИЛИ НЕ (x > 125).
Задание №7. Напишите наибольшее число x, для которого ложно высказывание:
НЕ ((x < 54) И (x простое число)) ИЛИ НЕ (x ≤ 16).
Дальше разберём каждое задание по отдельности, и вы сможете сравнить свои ответы с правильными.
Задание №1. Напишите наибольшее число x, для которого ложно высказывание:
(x > 72) ИЛИ НЕ (x чётное).
Разбор задания №1. Для успешного решения заданий такого типа необходимо знать, что такое конъюнкция, дизъюнкция, отрицание и законы Де Моргана. Также, необходимо для конъюнкции и дизъюнкции уметь строить таблицы истинности.
Итак, перед нами сложное высказывание, состоящее из двух простых:
(x > 72) ИЛИ НЕ (x чётное).
Для удобства я выделил высказывания разным цветом. Необходимо помнить, что связками между простыми высказываниями будут конъюнкция (логическое И), дизъюнкция (логическое ИЛИ), а также и другие логические операции, но их изучают в старших классах и в заданиях ОГЭ они не встречаются.
Когда же это сложное высказывание будет ложным? А ложным оно будет тогда и только тогда, когда оба простых высказывания будут ложными. Следовательно (x > 72) должно давать ложь и НЕ (x чётное) тоже должно давать ложь.
Теперь всё делаем по порядку.
- Все числа x, которые меньше или равны 72, нам подойдут. Из условия знаем, что число должно быть наибольшим. Следовательно, возьмём число 72. Проверяем условие 72 > 72 – нет, это ложь.
- Разберём второе высказывание НЕ (x чётное). Сначала «избавимся» от отрицания. НЕ (x чётное) — это тоже самое, что (x нечётное). При проверке первого высказывания мы выяснили, что число не может быть больше 72. Подставим его во вторую часть высказывания. (72 нечётное) – нет, это ложь, следовательно, нам вполне подходит.
Ответ: 72.
Задание №2. Напишите наибольшее число x, для которого ложно высказывание:
НЕ (x ≤ 26) ИЛИ (x нечётное).
Разбор задания №2. По аналогии с первым заданием выполняем и это. Мы имеем сложное высказывание. Связаны высказывания между собой дизъюнкцией, а дизъюнкция ложна тогда и только тогда, когда ложны все её составляющие!
- Разберём первую часть — НЕ (x ≤ 26). По законам Де Моргана «избавляемся» от отрицания. НЕ (x ≤ 26) = (x > 26). Чтобы эта часть высказывания была ложной нам подойдут все числа, которые меньше, чем 26 и само число 26, т.к. (26 > 26) – это ложь.
- По условию нам нужно наибольшее число x. Подставим во вторую часть высказывания (x нечётное) число 26. (26 нечётное) – нет, это ложь. Нам подходит, следовательно, оно и будет ответом.
Ответ: 26.
Это были задачи попроще. Теперь разберём немного потруднее.
Задание №3. Напишите наименьшее число x, для которого истинно высказывание:
НЕ (x ≤ 25) И (x кратное 5) И (x ≠ 30).
Разбор задания №3. Мы имеем сложное высказывание, но только оно состоит из трёх простых высказываний, связанных между собой конъюнкцией (логической операцией И). Конъюнкция истинна тогда и только тогда, когда все части составного высказывания будут истинны!
- Рассмотрим первую часть НЕ (x ≤ 25). По закону Де Моргана «избавимся» от отрицания. НЕ (x ≤ 25) = (x > 25). Нам подойдёт любое число больше, чем 25, т.е. от 26 до бесконечности. Из условия мы знаем, что нам нужно наименьшее из таких чисел – это 26.
- Рассмотрим вторую часть составного высказывания — (x кратное 5). Число 26 нам не подходит, т.к. оно не кратно пяти. Все числа кратные пяти заканчиваются на пять или на ноль. Нам бы подошло число 30. Оно больше, чем 25 и оно кратно 5.
- Рассмотрим третью часть составного высказывания, она то и даст верный ответ на нашу задачу. Число x не должно равняться 30, следовательно, наш x – это число больше 25, кратное 5, но не равняется 30. Такое ближайшее число – это 35. Оно полностью подходит всем условиям и является ответом к нашему заданию.
Ответ: 35.
Задание №4. Напишите наибольшее число x, для которого ложно высказывание:
(x ≥ 90) ИЛИ НЕ (x кратное 3) ИЛИ (x ≠ 87).
Разбор задания №4. Как и в предыдущем задании, мы имеем сложное, которое состоит из трёх простых, высказывание, только все они связаны дизъюнкцией (логической операцией ИЛИ). А ложно составное высказывание будет ложно только в том случае, когда будут ложны все его части!
- Рассмотрим первую часть (x ≥ 90). Она будет ложной в том случае, когда x будет строго меньше 90, т.е. от 89 до минус бесконечность. Так как от нас требуется найти наибольшее из этих чисел, то пока остановимся на числе 89.
- Далее рассмотрим второе высказывание НЕ (x кратное 3). Если «избавится» от отрицания, то мы имеем выражение (x не кратно 3). Это высказывание будет ложным в тех случаях, когда число на три делится! Ближайшее наибольшее число из диапазона от минус бесконечность до 89 будет число 87. Остановимся пока на нём и перейдем к третьему высказыванию.
- Из высказывания (x ≠ 87) становится ясным, что число 87 нам вполне подходит, т.к. выражение (87 ≠ 87) ложно.
Ответ: 87.
Задание №5. Напишите наибольшее число x, для которого истинно высказывание:
НЕ ((x ≥ 23) ИЛИ НЕ (x нечётное)) И НЕ (x > 25).
Разбор задания №5. Обратите внимание, что всё наше сложное высказывание включает в себя одно сложное высказывание (выделено красными скобками) НЕ ((x ≥ 23) ИЛИ НЕ (x нечётное)) и одно простое высказывание НЕ (x > 25), это всё связано конъюнкцией (логической операцией И). Всё выражение будет истинным только в том случае, когда обе его части будут истинны!
- В данном примере сразу применим закон Де Моргана. Когда мы отрицаем всё то, что заключено в скобках, то все знаки внутри скобок «переворачиваем».
НЕ ((x ≥ 23) ИЛИ НЕ (x нечётное)) = ((x < 23) И (x нечётное))
Следовательно, наше число x должно быть меньше, чем 23 и нечётное. Подойдёт число 21. Проверим его в следующей части выражения.
- Имеем высказывание НЕ (x > 25). «Избавимся» от отрицания и подставим в него для проверки число 21. Проверяем: (21 ≤ 25) – это истина.
Ответ: 21.
Задание №6. Напишите наименьшее число x, для которого ложно высказывание:
НЕ ((x ≥ 100) И НЕ (x кратно 4)) ИЛИ НЕ (x > 125).
Разбор задания №6. По структуре задание напоминает предыдущее. Оно также включает в себя одно сложное высказывание (выделено красными скобками) НЕ ((x ≥ 100) И НЕ (x кратно 4)) и одно простое высказывание НЕ (x > 125), это всё связано дизъюнкцией (логической операцией ИЛИ). И это всё должно быть ложно.
- «Избавляемся» от отрицания – все знаки внутри скобок «переворачиваем»:
НЕ ((x ≥ 100) И НЕ (x кратно 4)) = ((x < 100) ИЛИ (x кратно 4))
Мы имеем вот такое выражение ((x < 100) ИЛИ (x кратно 4)), осталось понять, когда же оно ложно. А ложно оно будет тогда и только тогда, когда ложны его обе части, т.е. x – это число от 100 до плюс бесконечности и оно не должно делиться нацело на 4. Такое наименьшее число – 101.
- Подставим для проверки это число во вторую часть выражения. НЕ (101 > 125). К сожалению, это выражение истинно, а из условия мы знаем, что всё выражение должно быть ложно. Значит, число x должно быть строго больше 125 и не должно делится на 4. Такое минимальное число — 126.
Ответ: 126.
На уроке рассмотрен материал для подготовки к огэ по информатике, решение задания 3
3-е задание: «Значение логического выражения»
Уровень сложности — базовый,
Максимальный балл — 1,
Примерное время выполнения — 3 минуты.
* до 2020 г — это задание № 2 ОГЭ
- Для подготовки к решению 3 задания ОГЭ по информатике следует вспомнить знаки сравнения. В логических выражениях используются следующие знаки сравнения:
- В логических выражениях участвуют всего два значения выражений: ИСТИНА и ЛОЖЬ.
- Рассмотрим результат выполнения логических выражений для двух высказываний — А и Б:
- Если отрицание НЕ стоит перед скобкой с выражением, то НЕ ставится перед каждой частью выражения в скобках и при этом операция внутри скобок меняется:
|
> |
больше |
|
< |
меньше |
|
= |
равно |
|
≥ |
больше или равно |
|
≤ |
меньше или равно |
| 1 | А ИЛИ Б = ИСТИНА → | если А=истина И Б=истина |
| 2 | если А=истина И Б=ложь | |
| 3 | если А=ложь И Б=истина | |
| 4 | А ИЛИ Б = ЛОЖЬ → | если А=ложь И Б=ложь |
Вывод: логическое выражение с операцией ИЛИ легче проверить «на ложь»:
с операцией ИЛИ результатом будет ЛОЖЬ только в одном единственном случае, — когда оба выражения — А и Б — ложны
| 1 | А И Б = ИСТИНА → | если А=истина И Б=истина |
| 2 | А И Б = ЛОЖЬ → | если А=истина И Б=ложь |
| 3 | если А=ложь И Б=истина | |
| 4 | если А=ложь И Б=ложь |
Вывод: логическое выражение с операцией И легче проверить «на истинность»:
с операцией И результатом будет ИСТИНА только в одном единственном случае, — когда оба выражения — А и Б — истинны
| Исходные значения | Результат | |
|---|---|---|
| 1 | НЕ А если А=истина |
А = ЛОЖЬ |
| НЕ(5 > 0) | 5 ≤ 0 | |
| 2 | НЕ А если А=ложь |
А = ИСТИНА |
| НЕ(-2 > 0) | -2 ≤ 0 | |
| 3 | НЕ (НЕ А) | = А |
| 1 | НЕ |
| 2 | выражение в скобках |
| 3 | И |
| 4 | ИЛИ |
| 1 | НЕ (А ИЛИ Б) | НЕ А И НЕ Б |
| 2 | НЕ (А И Б) | НЕ А ИЛИ НЕ Б |
ОГЭ информатика разбор задания 3
Подробный видеоразбор по ОГЭ 3 задания:
📹 Видеорешение на RuTube здесь
Актуальное
Значение логического выражения
Разбор задания 3.7. Демонстрационный вариант ОГЭ 2022 г ФИПИ:
Напишите наименьшее число x, для которого истинно высказывание:
(x > 16) И НЕ (x нечётное)
✍ Решение:
- Выполним первую по приоритету операцию — операцию НЕ:
НЕ (x нечётное) результат: x чётное
(x > 16) И (x чётное)
(x > 16) И (x чётное) = ИСТИНА истина истина
Ответ: 18
Разбор задания 3.12:
Напишите наименьшее число x, для которого ложно высказывание:
(x ≤ 15) ИЛИ НЕ (x нечётное)
✍ Решение:
- Выполним первую по приоритету операцию — операцию НЕ:
НЕ (x нечётное) результат: x чётное
(x ≤ 15) ИЛИ (x чётное) = 0 (ложь)
(x ≤ 15) ИЛИ (x чётное) = ЛОЖЬ ложь ложь
Ответ: 17
Тренировочные
Разбор задания 3.1:
Для какого из приведённых значений числа X ложно высказывание:
НЕ (X < 6) ИЛИ (X < 5) ?
1) 7
2) 6
3) 5
4) 4
Подобные задания для тренировки
✍ Решение:
- Выполним первую по приоритету операцию — операцию НЕ:
НЕ (X < 6) (X < 6) - ложь, значит результат: X ≥ 6
(X ≥ 6) ИЛИ (X < 5)
(X ≥ 6) ИЛИ (X < 5) = ЛОЖЬ ложь ложь
1. (X ≥ 6) = ЛОЖЬ => X < 6 2. (X < 5) = ЛОЖЬ => X ≥ 5
5 < 6 и 5 ≥ 5
Ответ: 3
Разбор задания 3.2:
Для какого из приведённых значений числа X истинно высказывание:
(X < 8) И НЕ (X < 7) ?
1) 9
2) 8
3) 7
4) 6
Подобные задания для тренировки
✍ Решение:
- Выполним первую по приоритету операцию — операцию НЕ:
НЕ (X < 7) (X < 7) - ложь, значит результат: X ≥ 7
(X < 8) И (X ≥ 7)
(X < 8) И (X ≥ 7) = ИСТИНА истина истина
1. (X < 8) = ИСТИНА => X < 8 2. (X ≥ 7) = ИСТИНА => X ≥ 7
7 < 8 и 7 ≥ 7
Ответ: 3
Разбор задания 3.3:
Для какого из приведённых имён ЛОЖНО высказывание:
НЕ ((Третья буква согласная) И (Последняя буква гласная)) ?
1) Анна
2) Елена
3) Павел
4) Егор
Подобные задания для тренировки
✍ Решение:
- Обратим внимание на то, что в заданном выражении операция НЕ относится ко всей общей скобке.
- Выполним первую по приоритету операцию — операцию НЕ, по таблице 6 для НЕ перед скобкой с выражением имеем:
НЕ ((Третья буква согласная) И (Последняя буква гласная)) = = (НЕ(Третья буква согласная) ИЛИ НЕ(Последняя буква гласная))
1. НЕ(Третья буква согласная) => Третья буква НЕ согласная 2. НЕ(Последняя буква гласная) => Последняя буква НЕ гласная
(Третья буква не согласная) ИЛИ (Последняя буква не гласная)
(Третья буква не согласная) ИЛИ (Последняя буква не гласная) = ЛОЖЬ
ложь ложь
1. (Третья буква не согласная) = ЛОЖЬ => Третья буква согласная 2. (Последняя буква не гласная) = ЛОЖЬ => Последняя буква гласная
Третья буква "н" согласная и Последняя буква "а" гласная
Ответ: 1
Разбор задания 3.4:
Для какого из приведённых имён ИСТИННО высказывание:
НЕ ((число > 50) ИЛИ НЕ(число четное)) ?
1) 43
2) 50
3) 61
4) 72
Подобные задания для тренировки
✍ Решение:
- Обратим внимание на то, что в заданном выражении операция НЕ относится ко всей общей скобке.
- Выполним первую по приоритету операцию — операцию НЕ в малых скобках:
НЕ(число четное) => число нечетное
НЕ ((число > 50) ИЛИ (число нечетное)) = = (НЕ(число > 50) И НЕ(число нечетное))
1. НЕ(число > 50) => число <= 50 2. НЕ(число нечетное) => число четное
(число <= 50) И (число четное)
(число <= 50) И (число нечетное) = ИСТИНА
истина истина
Ответ: 2
Разбор задания 3.5.:
Для какого из приведённых слов ЛОЖНО высказывание:
(последняя буква согласная) ИЛИ НЕ ((первая буква согласная) И (вторая буква гласная)) ?
1) Тигр
2) Выдра
3) Енот
4) Краб
✍ Решение:
- Обратим внимание на то, что в заданном выражении операция НЕ относится ко всей общей скобке.
- Выполним первую по приоритету операцию — операцию НЕ, по таблице 6 для НЕ перед скобкой с выражением имеем:
НЕ ((первая буква согласная) И (вторая буква гласная)) = = (НЕ(первая буква гласная) ИЛИ НЕ(вторая буква гласная))
1. НЕ(первая буква согласная) => первая буква гласная 2. НЕ(вторая буква гласная) => вторая буква согласная
(первая буква гласная) ИЛИ (вторая буква согласная)
(последняя буква согласная) ИЛИ (первая буква гласная) ИЛИ (вторая буква согласная)
(последняя буква согласная) ИЛИ (первая буква согласная) ИЛИ
ложь ложь
(вторая буква согласная) = ЛОЖЬ
ложь
1. (последняя буква согласная) = ЛОЖЬ => последняя буква гласная 2. (первая буква гласная) = ЛОЖЬ => первая буква согласная 3. (вторая буква согласная) = ЛОЖЬ => вторая буква гласная
Ответ: 2
Разбор задания 3.6:
Для какого из приведённых слов верно высказывание:
(первая буква гласная) И ((последняя буква согласная) ИЛИ (вторая буква согласная)) ?
1) АИДА
2) СЕРГЕЙ
3) СТЕПАН
4) АРТЕМ
Подобные задания для тренировки
✍ Решение:
- Обратим внимание на то, что в заданном выражении находятся большие скобки, с которых необходимо начать решение.
- Внешняя операция, т.е. последняя по приоритету — это операция И. Рассмотрим ее подробней, разделив общее высказывание на две части относительно этой операции:
(первая буква гласная) И ((последняя буква согласная) ИЛИ (вторая буква согласная))
(первая буква гласная) И ((последняя буква согласная) ИЛИ (вторая буква согласная)) истина истина
((последняя буква согласная) ИЛИ (вторая буква согласная))
истина ИЛИ истина
(первая буква гласная) И (или первая или вторая буква в слове согласная) истина истина
Ответ: 4
Осуществление поиска в готовой базе данных по сформулированному условию
* до 2020 г — это задание № 12 ОГЭ
Разбор задания 3.8:
Ниже в табличной форме представлен фрагмент базы данных «Отправление поездов дальнего следования»:
| Пункт назначения | Категория поезда | Время в пути | Вокзал |
|---|---|---|---|
| Рига | скорый | 15:45 | Рижский |
| Ростов | фирменный | 17:36 | Казанский |
| Самара | фирменный | 14:20 | Казанский |
| Самара | скорый | 17:40 | Казанский |
| Самара | скорый | 15:56 | Казанский |
| Самара | скорый | 15:56 | Павелецкий |
| Самара | фирменный | 23:14 | Курский |
| Санкт-Петербург | скорый | 8:00 | Ленинградский |
| Санкт-Петербург | скорый | 4:00 | Ленинградский |
| Саратов | скорый | 14:57 | Павелецкий |
| Саратов | пассажирский | 15:58 | Павелецкий |
| Саратов | скорый | 15:30 | Павелецкий |
Сколько записей в данном фрагменте удовлетворяют условию:
(Категория поезда = «скорый») ИЛИ (Вокзал = «Павелецкий»)?
✍ Решение:
- В условии находится логическая операция ИЛИ, которая истинна тогда, кода хоть одно из логических выражений истинно. Для нашего случая это говорит о том, что нужно посчитать те строки, в которых:
1. Категория поезда = «скорый» и Вокзал = любой 2. Категория поезда = «скорый» и Вокзал = «Павелецкий» 3. Категория поезда = любой и Вокзал = «Павелецкий»
Ответ: 9
Разбор задания 3.9:
Ниже в табличной форме представлен фрагмент базы данных «Отправление поездов дальнего следования»:
| Пункт назначения | Категория поезда | Время в пути | Вокзал |
|---|---|---|---|
| Балаково | скорый | 20:22 | Павелецкий |
| Бийск | скорый | 61:11 | Казанский |
| Бишкек | скорый | 121:20 | Казанский |
| Благовещенск | пассажирский | 142:06 | Ярославский |
| Брест | скорый | 14:19 | Белорусский |
| Валуйки | фирменный | 14:57 | Курский |
| Варна | скорый | 47:54 | Киевский |
| Волгоград | скорый | 18:50 | Павелецкий |
| Волгоград | скорый | 24:50 | Курский |
| Воркута | пассажирский | 48:19 | Ярославский |
| Воркута | пассажирский | 48:19 | Ярославский |
| Гродно | скорый | 16:34 | Белорусский |
Сколько записей в данном фрагменте удовлетворяют условию:
(Категория поезда = «скорый») И (Время в пути > 40:00)?
✍ Решение:
- В условии находится логическая операция И, которая истинна только тогда, кода оба (все) выражения истинны. Для нашего случая это говорит о том, что нужно посчитать те строки, в которых:
Категория поезда = «скорый» и Время в пути > 40:00 одновременно
Ответ: 3
Разбор задания 3.10:
Ниже в табличной форме представлен фрагмент базы данных «Отправление поездов дальнего следования»:
| Пункт назначения | Категория поезда | Время в пути | Вокзал |
|---|---|---|---|
| Балаково | скорый | 20:22 | Павелецкий |
| Бийск | скорый | 61:11 | Казанский |
| Бишкек | скорый | 121:20 | Казанский |
| Благовещенск | пассажирский | 142:06 | Ярославский |
| Брест | скорый | 14:19 | Белорусский |
| Валуйки | фирменный | 14:57 | Курский |
| Варна | скорый | 47:54 | Киевский |
| Волгоград | скорый | 18:50 | Павелецкий |
| Волгоград | скорый | 24:50 | Курский |
| Воркута | пассажирский | 48:19 | Ярославский |
| Воркута | пассажирский | 48:19 | Ярославский |
| Гродно | скорый | 16:34 | Белорусский |
Сколько записей в данном фрагменте удовлетворяют условию:
(Пункт назначения = «Волгоград») ИЛИ (Категория поезда = «пассажирский») И (Время в пути < 50:00)?
В ответе укажите одно число — искомое количество записей.
✍ Решение:
- В условии находятся две логических операции: И и ИЛИ. Первой всегда выполняется операция И, затем добавляются записи для операции ИЛИ.
- Операция И истинна только тогда, кода оба (все) выражения истинны.
(Категория поезда = «пассажирский») И (Время в пути < 50:00) одновременно
(Пункт назначения = «Волгоград») добавить к предыдущему результату
Ответ: 4
Разбор задания 3.11:
Ниже в табличной форме представлен фрагмент базы данных «Отправление поездов дальнего следования»:
| Пункт назначения | Категория поезда | Время в пути | Вокзал |
|---|---|---|---|
| Махачкала | скорый | 39.25 | Павелецкий |
| Махачкала | скорый | 53.53 | Курский |
| Мурманск | скорый | 35.32 | Ленинградский |
| Мурманск | скорый | 32.50 | Ленинградский |
| Мурманск | пассажирский | 37.52 | Ленинградский |
| Мурманск | пассажирский | 37.16 | Ленинградский |
| Назрань | пассажирский | 40.23 | Павелецкий |
| Нальчик | скорый | 34.55 | Казанский |
| Нерюигри | скорый | 125.41 | Казанский |
| Новосибирск | скорый | 47.30 | Ярославский |
| Нижневартовск | скорый | 52.33 | Казанский |
| Нижний Тагил | фирменный | 31.36 | Ярославский |
Сколько записей в данном фрагменте удовлетворяют условию:
НЕ (Вокзал = «Ленинградский») И (Время в пути > 50.00)?
✍ Решение:
- В условии находятся две логических операции: НЕ и И.
- Первой всегда выполняется операция НЕ, затем добавляются записи для операции И.
- Операция НЕ обозначает обратное высказывание:
НЕ(Вокзал = «Ленинградский»)
то же самое, что
(Вокзал ≠ «Ленинградский»)
(Вокзал ≠ «Ленинградский») И (Время в пути > 50.00) одновременно
Ответ: 3