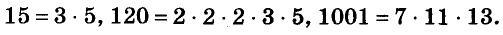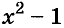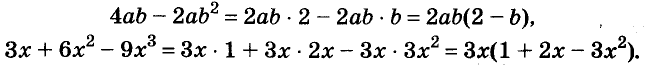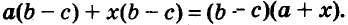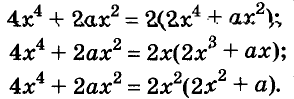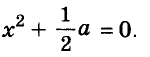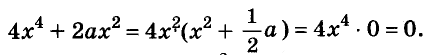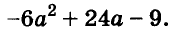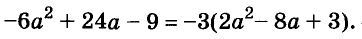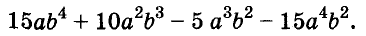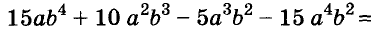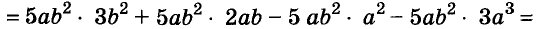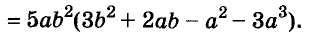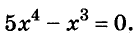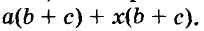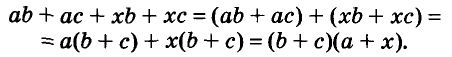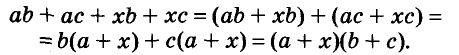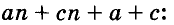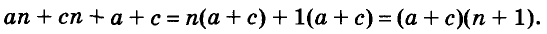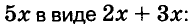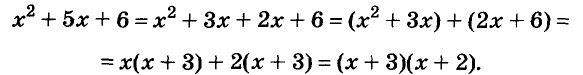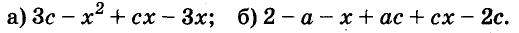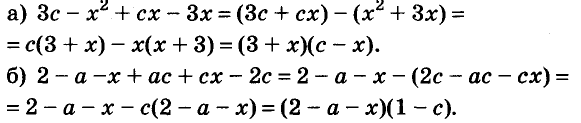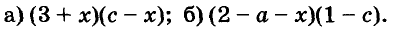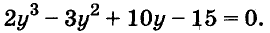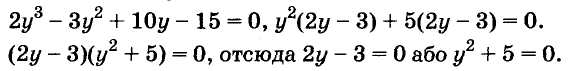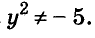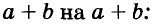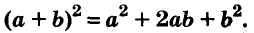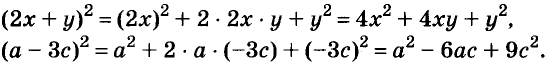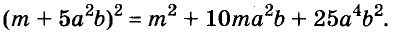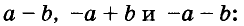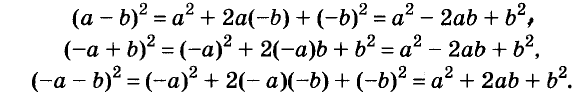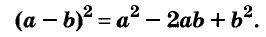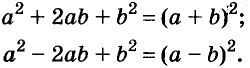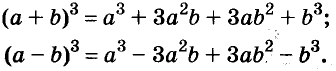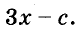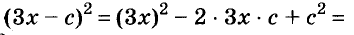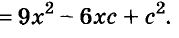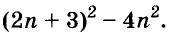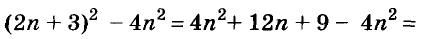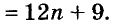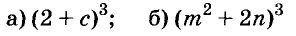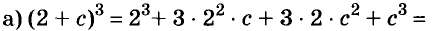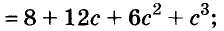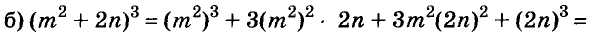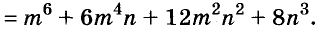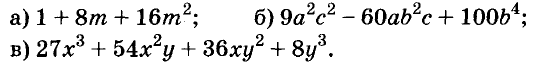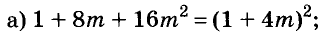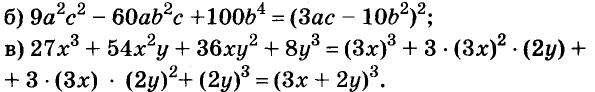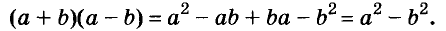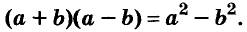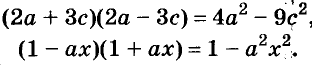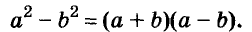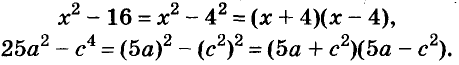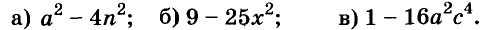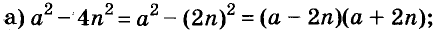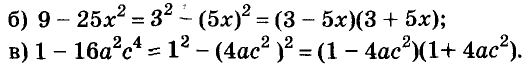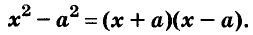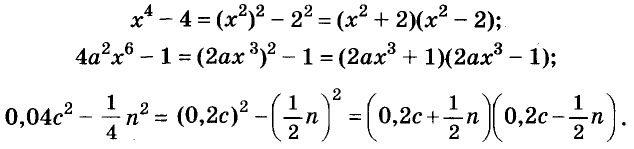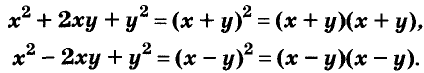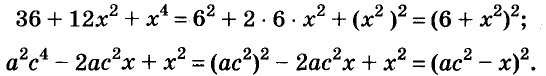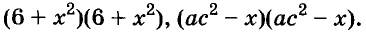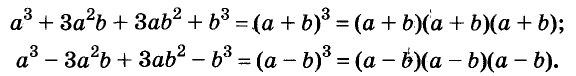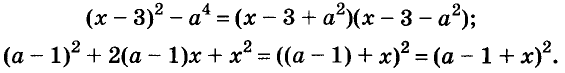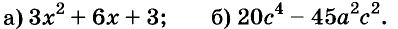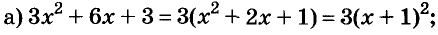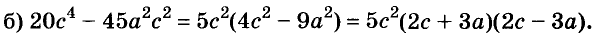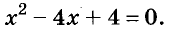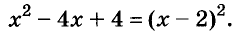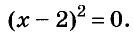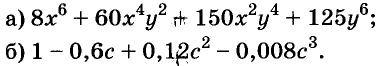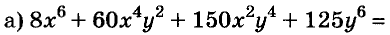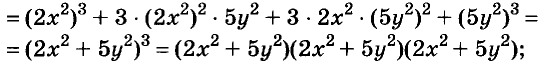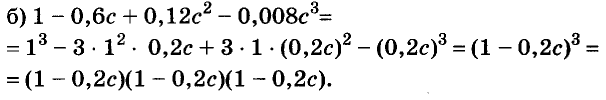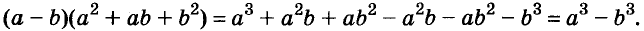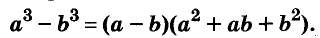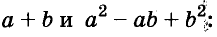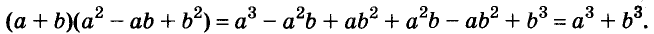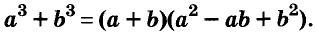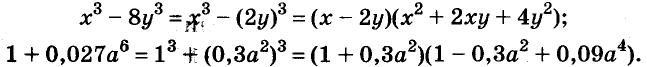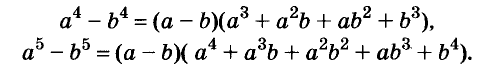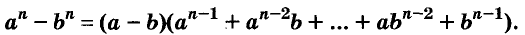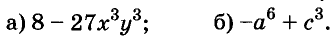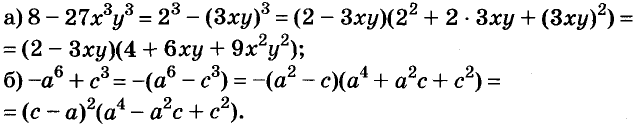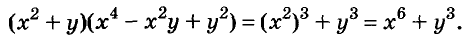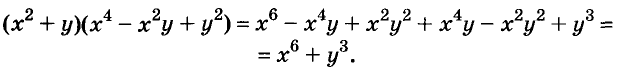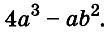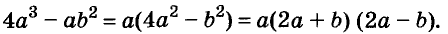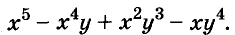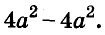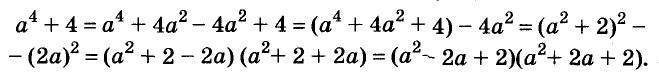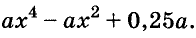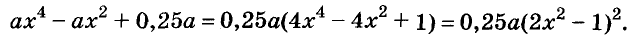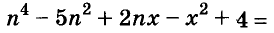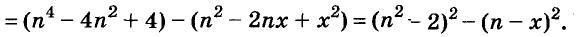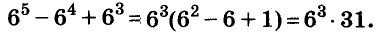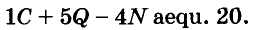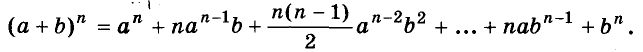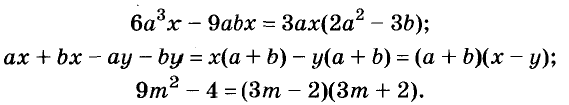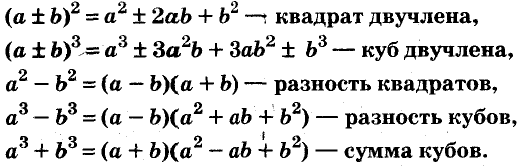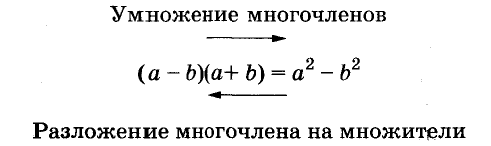В современном русском языке есть немало выражений, написание которых вызывает трудности. Одно из таких − выражение для повышения эффекта ожидания «жду не дождусь». Многие допускают ошибку в этом сочетании, используя дефис между частями выражения. Чтобы раз и навсегда запомнить, как писать: «жду не дождусь» или «жду − не дождусь», рассмотрим, каким правилом можно воспользоваться в этом случае.
Как правильно пишется?
«Жду не дождусь» необходимо писать отдельно, без дефиса. Это единственный вариант, который является правильным в современном русском языке.
Данное требование объясняется тем, что сочетание «жду не дождусь» представляет собой неразложимое выражение, повышающее эмоциональность от ожидания.
То есть, замена хотя бы одного слова из данного выражения или изменение порядка слов приведет к нарушению всего смысла. Поэтому необходимо запомнить, что это сочетание нужно писать в три слова, без использования дефиса и каких-либо знаков препинания.
Этот же принцип характерен и остальным формам глагола «жду», если образовывать от него по аналогии сочетания: «ждут не дождутся», «ждет не дождется», «ждем не дождемся», «ждете не дождетесь» и т.д.
Примеры предложений
- Жду не дождусь, когда вновь смогу вернуться к привычным обязанностям.
- Надеюсь, когда-нибудь он съедет из нашей квартиры – жду не дождусь этого момента!
- Жду не дождусь, когда мы все вместе соберемся и, наконец, поговорим по душам, расскажем друг другу о наболевшем.
- Ты знаешь, я жду не дождусь, когда придет приказ о моем увольнении.
- Очень хочу, чтобы Новый год поскорее наступил, жду не дождусь!
Синонимы выражения «жду не дождусь»
К неразложимому сочетанию «жду не дождусь» можно подобрать следующие синонимичные сочетания слов:
- жду с нетерпением, места себе не нахожу, очень надеюсь, сижу как на иголках, горю нетерпением, жду как манны небесной, мне не терпится, считаю минуты, предвкушаю.
Ошибочное написание «жду не дождусь»
Это выражение нельзя писать через дефис: «жду – не дождусь», а также писать частицу «не» слитно с глаголом: «жду недождусь».
Заключение
Выбрать правильный способ написания сочетания слов «жду не дождусь» несложно. Для этого достаточно запомнить, что это выражение относится к неразложимым словосочетаниям, которые в русском языке всегда нужно писать раздельно, без использования дефиса и каких-либо знаков препинания.
Исходить мы будем из того, что в русском языке существуют имена прилагательные «неразложимый» и «разложимый». Вот они показаны на двух изображениях-скриншотах ниже:
_
Фактически, этого знания уже достаточно для того, чтобы уверенно предполагать возможность обоих вариантов написания слова «не(?)разложимый»: и слитного, и раздельного.
А далее можно рассуждать, вспоминая общие правила, касающиеся не только слова-сочетания «не(?)разложимый». Покажем это на примерах предложений:
«Неразложимый — это тот, который разложить невозможно». В предложении слово «неразложимый» находится под знаком утвердительной семантики, поэтому и написано слитно.
«Мы имеем в виду не разложимый на некоторые составляющие процесс, а единую, то есть неразложимую, цель». Присутствие в предложении союза «а», являющегося сигналом противопоставления, указывает на написание » не разложимый» (раздельно) в первой части данного противопоставления.
«Системность лексики опирается на так называемые неразложимые смысловые компоненты». Понятие неразложимости (видите, мы и существительное это слитно написали) в данном предложении утверждается с помощью формы «неразложимые». Отрицания нет, поэтому напишем слитно.
Ответ:
Правильное написание слова — неразложимый
Ударение и произношение — неразлож`имый
Значение слова -такой, что нельзя разложить, разделить на части
Выберите, на какой слог падает ударение в слове — МЫТАРСТВО?
Слово состоит из букв:
Н,
Е,
Р,
А,
З,
Л,
О,
Ж,
И,
М,
Ы,
Й,
Похожие слова:
нераздражительный
нераздробленный
неразличимость
неразличимый
неразложимость
неразлучен
неразлучна
неразлучная
неразлучник
неразлучно
Рифма к слову неразложимый
неудержимый, движимый, независимый, ненавидимый, непреодолимый, любимый, неразрешимый, подсудимый, необходимый, разносимый, относимый, руководимый, невидимый, поддерживаемый, допускаемый, называемый, сопутствуемый, отбиваемый, прерываемый, обвиняемый, подаваемый, пригреваемый, покрываемый, отдаваемый, вызываемый, предлагаемый, напутствуемый, застилаемый, требуемый, многоуважаемый, оглушаемый, откладываемый, занимаемый, заглушаемый, провожаемый, повторяемый, ожидаемый, управляемый, наказываемый, перебиваемый, самый, обожаемый, предшествуемый, нескончаемый, пересыпаемый, скрываемый, примериваемый, ощущаемый, делаемый, замечаемый, неумолкаемый, чувствуемый, посещаемый, неподражаемый, резвый, моложавый, березовый, шутливый, здравый, находчивый, красивый, фланговый, отчетливый, левый, дождливый, слабый, учтивый, грубый, курчавый, уродливый, плешивый, хвастливый, правдивый, насмешливый, целковый, задумчивый, медовый, забывчивый, юродивый, правый, ленивый, лукавый, ворчливый, мозаиковый, худощавый, шелковый, коричневый, розовый, милостивый, трезвый, особый, торопливый, молчаливый, кровавый, вый, бравый, фальшивый, заботливый, шаловливый, счастливый, поворотливый, фризовый, словоохотливый, вспыльчивый
Толкование слова. Правильное произношение слова. Значение слова.
Проверьте, пожалуйста, мое написание слов с НЕ и НИ ⇐ Высшее образование
Информация
Уважаемые студенты!
Вместе с заданиями размещайте и свои варианты решения. В противном случае ваше сообщение будет проигнорировано.
-
Автор темы
statina.93
- помощник писаря
- Всего сообщений: 4
- Зарегистрирован: 29.10.2012
- Образование: студент
- Откуда: Новокузнецк
- Возраст: 29
Проверьте, пожалуйста, мое написание слов с НЕ и НИ
1. Независимое от материальных условий положение. Слово, не склоняемое в русском языке. Неизменяемая форма глагола. Ни в какой мере не зависимое мнение. Не проходимый судами пролив. Совершенно непроходимая грязь. Не проходимая в весеннюю пору грязь. Нестерпимая для меня боль. Абсолютно нестерпимая при операции боль. Не терпимый в нашем обществе субъект. Никем не терпимый человек. Далеко не терпимое неудобство. Совершенно не терпимое поведение.
2. Не разложимое на данные множители и неделимое на три число. Ни в чем неразложимое вещество. Неделимая непроизводная основа. Неумолкаемый днем и ночью городской шум. Вовсе неумолкаемый морской прибой. Нисколько неумолкаемый вой ветра. Непроницаемая для воды оболочка. Не сгибаемая в колене нога. Совершенно не сгибаемая нога. Ничем несгибаемая воля. Неподражаемый в исполнении этой роли актер. Не различимые в тумане предметы. Почти не различимые оттенки цветов. Ни в чем не различимые изделия.
3. Ничем не заменимая утрата. Не заменимый в путешествии предмет. Совершенно не заменимый работник. Не выполнимая для путешественника задача. Множитель, не выносимый за скобку. Его не выносимый для всех эгоизм. Никакими средствами не излечимая болезнь. Еще не излечимая болезнь. Почти неизлечимая болезнь. Не мыслимый для меня вывод. Не мыслимый мною случай. Незабываемое по силе впечатление.
-
Марго
- Гениалиссимус
- Всего сообщений: 13772
- Зарегистрирован: 11.11.2009
-
Лучшие Ответы: 2
- Образование: высшее гуманитарное
- Откуда: Моcква
Re: Помогите проверить правильное написание Не НИ со словами
Сообщение
Марго » 29 окт 2012, 08:39
statina.93, посмотрите вверх:
Информация
Уважаемые студенты!
Вместе с заданиями размещайте и свои варианты решения. В противном случае ваше сообщение будет проигнорировано.
-
Автор темы
statina.93
- помощник писаря
- Всего сообщений: 4
- Зарегистрирован: 29.10.2012
- Образование: студент
- Откуда: Новокузнецк
- Возраст: 29
Re: Проверти пожалуйста мое написание слов с НЕ и НИ
Сообщение
statina.93 » 29 окт 2012, 08:44
Я написала свой вариант
-
Марго
- Гениалиссимус
- Всего сообщений: 13772
- Зарегистрирован: 11.11.2009
-
Лучшие Ответы: 2
- Образование: высшее гуманитарное
- Откуда: Моcква
Re: Проверти пожалуйста мое написание слов с НЕ и НИ
Сообщение
Марго » 29 окт 2012, 08:49
А что означает «проверти» в заголовке? Провертеть?
-
Автор темы
statina.93
- помощник писаря
- Всего сообщений: 4
- Зарегистрирован: 29.10.2012
- Образование: студент
- Откуда: Новокузнецк
- Возраст: 29
Re: Проверти пожалуйста мое написание слов с НЕ и НИ
Сообщение
statina.93 » 02 ноя 2012, 13:42
Нужно проверить правильность(Слитного,раздельного) написания НЕ и НИ со словами.
-
vadim_i_z
- Гениалиссимус
- Всего сообщений: 7814
- Зарегистрирован: 27.09.2006
- Образование: высшее естественно-научное
- Откуда: Минск, Беларусь
- Возраст: 66
Re: Проверти пожалуйста мое написание слов с НЕ и НИ
Сообщение
vadim_i_z » 02 ноя 2012, 14:35
Все-таки исправьте, пожалуйста. заголовок. Глаз спотыкается.
-
alex-ter
- ВПЗР
- Всего сообщений: 2490
- Зарегистрирован: 26.01.2012
- Образование: высшее техническое
- Профессия: программист
- Откуда: Санкт-Петербург
- Возраст: 65
Re: Проверьте, пожалуйста, мое написание слов с НЕ и НИ
Сообщение
alex-ter » 02 ноя 2012, 21:15
1. Независимое от материальных условий положение. Слово, не склоняемое в русском языке. Неизменяемая форма глагола. Ни в какой мере не зависимое мнение. Не проходимый судами пролив. Совершенно непроходимая грязь. Не проходимая в весеннюю пору грязь. Нестерпимая для меня боль. Абсолютно нестерпимая при операции боль. Нетерпимый в нашем обществе субъект. Никем не терпимый человек. Далеко не терпимое неудобство. Совершенно нетерпимое поведение.
2. Неразложимое на данные множители и неделимое на три число. Ни в чем не разложимое вещество. Неделимая непроизводная основа. Неумолкаемый днем и ночью городской шум. Вовсе не умолкаемый морской прибой. Нисколько не умолкаемый вой ветра. Непроницаемая для воды оболочка. Не сгибаемая в колене нога. Совершенно не сгибаемая нога. Ничем не сгибаемая воля. Неподражаемый в исполнении этой роли актер. Неразличимые в тумане предметы. Почти неразличимые оттенки цветов. Ни в чем не различимые изделия.
3. Ничем не заменимая утрата. Незаменимый в путешествии предмет. Совершенно незаменимый работник. Невыполнимая для путешественника задача. Множитель, не выносимый за скобку. Его невыносимый для всех эгоизм. Никакими средствами не излечимая болезнь. Еще не излечимая болезнь. Почти неизлечимая болезнь. Немыслимый для меня вывод. Не мыслимый мною случай. Незабываемое по силе впечатление.
Уж простите… Красным я выделил сочетания, которые, на мой взгляд, в живом языке совершенно не употребляются. Они только для диктантов — чтоб школьников запутать.
Для отправки ответа, комментария или отзыва вам необходимо авторизоваться
-
- 4 Ответы
- 651 Просмотры
-
Последнее сообщение Наташа240190
14 янв 2013, 18:44
-
- 10 Ответы
- 1542 Просмотры
-
Последнее сообщение Саид
28 сен 2010, 21:29
-
- 26 Ответы
- 3708 Просмотры
-
Последнее сообщение Завада
06 июн 2014, 10:49
-
- 26 Ответы
- 16228 Просмотры
-
Последнее сообщение Darina
16 окт 2012, 09:49
-
- 2 Ответы
- 1062 Просмотры
-
Последнее сообщение Донни
18 ноя 2008, 20:28
неразложимый
- неразложимый
-
неразложимый
Слитно или раздельно? Орфографический словарь-справочник. — М.: Русский язык.
.
1998.
Синонимы:
Антонимы:
Смотреть что такое «неразложимый» в других словарях:
-
неразложимый — единый, целый, цельный, целостный, неделимый, неразделимый, монолитный; неразлагаемый. Ant. разложимый, приводимый Словарь русских синонимов. неразложимый неделимый Словарь синонимов русского языка. Практический справочник. М.: Русский язык. З. Е … Словарь синонимов
-
НЕРАЗЛОЖИМЫЙ — НЕРАЗЛОЖИМЫЙ, неразложимая, неразложимое; неразложим, неразложима, неразложимо (книжн.). Такой, что нельзя разложить, разделить на части. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
-
НЕРАЗЛОЖИМЫЙ — НЕРАЗЛОЖИМЫЙ, ая, ое; им. Такой, что нельзя разложить, разделить на части. | сущ. неразложимость, и, жен. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
-
неразложимый — неразрешимый — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность Синонимы неразрешимый EN irresoluble … Справочник технического переводчика
-
Неразложимый класс — Определение Пусть однородная цепь Маркова с дискретным временем. Состояние j называется достижимым из состояния i, если существует n = n(i,j) такое, что . Пишут … Википедия
-
Неразложимый элемент — Неприводимый элемент (неразложимый элемент) одно из основных понятий теории колец. Пусть R область целостности, т.е. коммутативное кольцо без делителей нуля. Элемент p≠0 называется неприводимым, если он не является единицей, а из равенства p=bc,… … Википедия
-
Неразложимый — прил. Такой, который трудно или невозможно разложить на составные части. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
-
неразложимый — неразложимый, неразложимая, неразложимое, неразложимые, неразложимого, неразложимой, неразложимого, неразложимых, неразложимому, неразложимой, неразложимому, неразложимым, неразложимый, неразложимую, неразложимое, неразложимые, неразложимого,… … Формы слов
-
неразложимый — отделимый … Словарь антонимов
-
неразложимый — неразлож имый … Русский орфографический словарь
Основные определения (разбираемся со “сложными” словами)
Одночлены
Одночленами могут быть числа, переменные, произведения чисел и переменных, а так же переменные в степени (если забыл, что такое степень, посмотри тему «Степень и ее свойства»)
Например:
- ( 4)
- ( x)
- ( 4x)
- ( 4{{x}^{2}})
- ( 4{{x}^{2}}y)
Все это – одночлены. Видишь у них нет знаков “+” или “-“, как бы нет других членов.
Многочлены
Многочлен – это выражение, состоящее из суммы (или разности) нескольких одночленов различного вида:
- ( 4{{x}^{2}}+9x)
- ( 2{{x}^{3}}-16{{x}^{2}}+4x)
- ( 8xcdot 4{{y}^{2}}-12+4{{x}^{2}}y-3{{y}^{2}}cdot {{x}^{4}}+6-5{{y}^{2}}{{x}^{4}})
Множители
Так, ну давай по порядку. Как нетрудно догадаться, слово «множитель» происходит от слова «умножать».
Возьмем, например, число ( 12), разложить его на множители означает расписать его в виде «умножения» или, как принято говорить в математике «произведения» множителей.
Так ( 12) мы можем получить, умножив ( 2) на ( 6).
А ( 6), в свою очередь, можно представить как произведение ( 2) и ( 3).
Чтоб было более наглядно, обратимся к картинке:
На картинке мы видим пошаговое разложение на множители, те которые подчеркнуты – это множители, которые дальше разложить уже нельзя.
То есть их нельзя уже представить в виде произведения (можно конечно представить каждое из них как единица, умноженная на само число, но это нам ничего не дает).
Я обещал, что картинка все разъяснит, ну разве из нее не понятно, что, ( 12=2cdot 6), а ( 6=2cdot 3)?
Вот и я говорю, что элементарно!
Иными словами, ( 2cdot 2cdot 3=12).
Тут ( 2), еще раз ( 2) и ( 3) – это и есть множители, на которые мы раскладываем.
Зачем нужно раскладывать многочлен на множители?
Это самый главный вопрос. Я уже говорил – чтобы облегчить тебе жизнь.
Раскладывая многочлен на множители, ты упрощаешь выражение! Ты как бы делишь одну большую и сложную проблему, на несколько маленьких и простых и потом разбираешься с каждой маленькой проблемой по отдельности.
А теперь “официальное” определение.
Разложение многочлена на множители – тождественное преобразование, превращающее сумму в произведение нескольких множителей. При этом каждый множитель может быть как многочленом, так и одночленом.
Для чего нужно знать все пять способов?
Потому что нет универсального способа, подходящего для всех многочленов.
Давай посмотрим на каждый из них…
5 способов разложения многочлена на множители
1. Вынесение общего множителя за скобки
( displaystyle ac+bc=c(a+b))
2. Формулы сокращенного умножения
( begin{array}{l}left[ 1 right] {{left( a+b right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}\left[ 2 right] {{left( a-b right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}\left[ 3 right] {{a}^{2}}-{{b}^{2}}=left( a-b right)left( a+b right)\left[ 4 right] {{left( a+b right)}^{3}}={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}}\left[ 5 right] {{left( a-b right)}^{3}}={{a}^{3}}-3{{a}^{2}}b+3a{{b}^{2}}-{{b}^{3}}\left[ 6 right] {{a}^{3}}+{{b}^{3}}=left( a+b right)left( {{a}^{2}}-ab+{{b}^{2}} right)\left[ 7 right] {{a}^{3}}-{{b}^{3}}=left( a-b right)left( {{a}^{2}}+ab+{{b}^{2}} right)end{array})
3. Метод группировки
Применяется если преобразование не очевидно. Здесь, например, можно переставить второй член на другое место:
( {{x}^{3}}-5{{x}^{2}}y-3xy+15{{y}^{2}})
Группируем члены парами, получаем:
( ({{x}^{3}}-5{{x}^{2}}y)-(3xy-15{{y}^{2}}))
( {{x}^{2}}(x-5y)-3y(x-5y))
( ({{x}^{2}}-3y)(x-5y))
4. Выделение полного квадрата
Можно преобразовать многочлен и привести к виду разности квадратов, например и применить формулу сокращенного умножения
( {{x}^{4}}-4{{x}^{2}}-1=underbrace{{{x}^{4}}-2cdot 2cdot {{x}^{2}}+4}_{text{ }{{left( {{x}^{2}}-2 right)}^{2}}}-4-1={{left( {{x}^{2}}-2 right)}^{2}}-5=left( {{x}^{2}}-2+sqrt{5} right)left( {{x}^{2}}-2-sqrt{5} right))
5. Разложение квадратного трехчлена на множители
Квадратный трехчлен – многочлен вида
( a{{x}^{2}}+bx+c=0)
Теорема. Если квадратное уравнение ( a{{x}^{2}}+bx+c=0) имеет корни ( {{x}_{1}},text{ }{{x}_{2}}), то его можно записать в виде:
( a{{x}^{2}}+bx+c=aleft( x-{{x}_{1}} right)left( x-{{x}_{2}} right)).
Подробнее о каждом из 5-ти способов разложения на множители
1. Вынесение общего множителя за скобки
Это один из самых элементарных способов упростить выражение. Для применения этого метода давай вспомним распределительный закон умножения относительно сложения (не пугайся этих слов, ты обязательно знаешь этот закон, просто мог забыть его название).
Закон гласит:
Чтобы сумму двух чисел умножить на третье число, нужно каждое слагаемое умножить на это число и полученные результаты сложить.
Иначе говоря, ( aleft( btext{ }+text{ }c right)text{ }=text{ }abtext{ }+text{ }ac).
Так же можно проделать и обратную операцию, ( abtext{ }+text{ }actext{ }=text{ }aleft( btext{ }+text{ }c right)).
Вот именно эта обратная операция нас и интересует. Как видно из образца, общий множитель а, можно вынести за скобку.
Подобную операцию можно проделывать как с переменными, такими как ( x) и ( y), например, так и с числами: ( 6text{ }+text{ }8text{ }=text{ }2left( 3text{ }+text{ }4 right)).
Да, это слишком элементарный пример, так же, как и приведенный ранее пример, с разложением числа ( 12), ведь все знают, что числа ( 6), ( 
А как быть, если вам досталось выражение посложнее:
( 3xy+123y)?
Как узнать на что, например, делится число ( 123).
Нееет! С калькулятором-то любой сможет, а без него слабо?
А для этого существуют признаки делимости, эти признаки действительно стоит знать, они помогут быстро понять, можно ли вынести за скобку общий множитель.
Что ж, вернемся к выражению ( 3xy+123y), может вынести за скобку ( y) да и хватит с него?
Нет, у математиков принято упрощать, так по полной, выносить ВСЕ, что выносится!
И так, с игреком все понятно, а что с числовой частью выражения? Оба числа нечетные, так что на ( 2) разделить не удастся.
Можно воспользоваться признаком делимости на ( 3), сумма цифр ( 1), ( 2) и ( 3), из которых состоит число ( 123), равна ( 6), а ( 6) делится на ( 3), значит и ( 123) делится на ( 3).
Зная это, можно смело делить в столбик, в результате деления ( 123) на ( 3) получаем ( 41) (признаки делимости пригодились!).
Таким образом, число ( 3) мы можем вынести за скобку, так же, как y и в результате имеем:
( 3xytext{ }+text{ }123ytext{ }=text{ }3ycdot left( xtext{ }+text{ }41 right)).
Чтобы удостовериться, что разложили все верно, можно проверить разложение, умножением!
Также общий множитель можно выносить и в степенных выражениях.
Вот тут, например, ( 2{{x}^{3}}-16{{x}^{2}}+4x), видишь общий множитель?
У всех членов этого выражения есть иксы – выносим, все делятся на ( 2) – снова выносим, смотрим что получилось: ( 2{{x}^{3}}-16{{x}^{2}}+4x=2x({{x}^{2}}-8x+2)).
2. Формулы сокращенного умножения
Формулы сокращенного умножения уже упоминались в теории, если ты с трудом помнишь что это, то тебе стоит освежить их в памяти «Формулы сокращенного умножения».
А вот здесь можно решить вместе с нашим репетитором Алексеем Шевчуком 119 задач на формулы сокращенного умножения!
А вот здесь наше видео о том, какой навык, относящийся к формулам сокращенного умножения является самым сложным и самым важным – выделение полного кавдрата!
Справка.
Эти видео – часть нашего курса подготовки к ЕГЭ по математике. Можно провести бесплатный “тест-драйв” этого курса. Например, посетить наши пробные вебинары.
В чем суть разложения на множители с помощью формул сокращенного умножения?
Суть этого разложения в том, что бы заметить в имеющемся перед тобой выражении какую-то определенную формулу, применить ее и получить, таким образом, произведение чего-то и чего-то, вот и все разложение.
Формулы сокращенного умножения (таблица)
( displaystyle begin{array}{l}left[ 1 right] {{left( a+b right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}\left[ 2 right] {{left( a-b right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}\left[ 3 right] {{a}^{2}}-{{b}^{2}}=left( a-b right)left( a+b right)\left[ 4 right] {{left( a+b right)}^{3}}={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}}\left[ 5 right] {{left( a-b right)}^{3}}={{a}^{3}}-3{{a}^{2}}b+3a{{b}^{2}}-{{b}^{3}}\left[ 6 right] {{a}^{3}}+{{b}^{3}}=left( a+b right)left( {{a}^{2}}-ab+{{b}^{2}} right)\left[ 7 right] {{a}^{3}}-{{b}^{3}}=left( a-b right)left( {{a}^{2}}+ab+{{b}^{2}} right)end{array})
А теперь попробуй, разложи на множители следующие выражения, используя приведенные выше формулы:
- ( displaystyle 16{{b}^{2}}-8b+1)
- ( displaystyle -42c+9{{c}^{2}}+49)
- ( displaystyle {{left( 5text{a} right)}^{2}}-3)
- ( displaystyle frac{left( 4text{a}+2text{b} right)cdot left( 4text{a}-2text{b} right)}{16{{text{a}}^{2}}+4{{text{b}}^{2}}-16text{ab}})
- ( displaystyle {{left( 3text{a} right)}^{3}}-1)
Вот что должно было получиться:
3. Метод группировки
А вот тебе еще примерчик:
( displaystyle {{x}^{3}}-3xy-5{{x}^{2}}y+15{{y}^{2}})
Ну и что с ним делать будешь? Вроде бы и на ( displaystyle 3) что-то делится и на ( displaystyle 5), а что-то на ( displaystyle x) и на ( displaystyle y)
Но все вместе на что-то одно не разделишь, ну нет тут общего множителя, как не ищи, что, так и оставить, не раскладывая на множители?
Тут надо смекалку проявить, а имя этой смекалке – группировка!
Применяется она как раз, когда общие делители есть не у всех членов. Для группировки необходимо найти группки слагаемых, имеющих общие делители и переставить их так, чтобы из каждой группы можно было получить один и тот же множитель.
Переставлять местами конечно не обязательно, но это дает наглядность, для наглядности же можно взять отдельные части выражения в скобки, их ставить не запрещается сколько угодно, главное со знаками не напутать.
Не очень понятно все это? Объясню на примере:
В многочлене ( displaystyle {{x}^{3}}-3xy-5{{x}^{2}}y+15{{y}^{2}}) ставим член – ( displaystyle 3xy) после члена – ( displaystyle 5x2y) получаем:
( displaystyle {{x}^{3}}-5{{x}^{2}}y-3xy+15{{y}^{2}})
Группируем первые два члена вместе в отдельной скобке и так же группируем третий и четвертый члены, вынеся за скобку знак «минус», получаем:
( displaystyle ({{x}^{3}}-5{{x}^{2}}y)-(3xy-15{{y}^{2}}))
А теперь смотрим по отдельности на каждую из двух “кучек”, на которые мы разбили выражение скобками.
Хитрость в том, чтоб разбить на такие кучки, из которых можно будет вынести максимально большой множитель, либо, как в этом примере, постараться сгруппировать члены так, чтобы после вынесения из кучек множителей за скобку у нас внутри скобок оставались одинаковые выражения.
Из обеих скобок выносим за скобки общие множители членов, из первой скобки ( displaystyle {{x}^{2}}), а из второй ( displaystyle 3y), получаем:
( displaystyle {{x}^{2}}(x-5y)-3y(x-5y))
Но это же не разложение!
После разложения должно остаться только умножение, а пока у нас многочлен просто поделен на две части…
НО! Этот многочлен имеет общий множитель. Это ( displaystyle (x-5y))
( displaystyle (x-5y))за скобку и получаем финальное произведение ( displaystyle ({{x}^{2}}-3y)(x-5y))
Бинго! Как видишь, тут уже произведение и вне скобок нет ни сложения, ни вычитания, разложение завершено, т.к. вынести за скобки нам больше нечего.
Может показаться чудом, что после вынесения множителей за скобки у нас в скобках остались одинаковые выражения ( displaystyle (x-5y)), которые опять же мы и вынесли за скобку.
И вовсе это не чудо, дело в том, что примеры в учебниках и в ЕГЭ специально сделаны так, что большинство выражений в заданиях на упрощение или разложение на множители при правильном к ним подходе легко упрощаются и резко схлопываются как зонтик при нажатии на кнопку, вот и ищи в каждом выражении ту самую кнопку.
Что-то я отвлекся, что у нас там с упрощением? Замысловатый многочлен принял более простой вид: ( displaystyle {{x}^{3}}-3xy-5{{x}^{2}}y+15{{y}^{2}}=({{x}^{2}}-3y)(x-5y)).
Согласись, уже не такой громоздкий, как был?
4. Выделение полного квадрата
Иногда для применения формул сокращенного умножения (повтори тему «Формулы сокращенного умножения») необходимо преобразовать имеющийся многочлен, представив одно из его слагаемых в виде суммы или разности двух членов.
В каком случае приходится это делать, узнаешь из примера:
Многочлен ( displaystyle {{x}^{2}}-4x+2) в таком виде не может быть разложен при помощи формул сокращенного умножения, поэтому его необходимо преобразовать.
Возможно, поначалу тебе будет не очевидно какой член на какие разбивать, но со временем ты научишься сразу видеть формулы сокращенного умножения, даже если они не присутствуют не целиком, и будешь довольно быстро определять, чего здесь не хватает до полной формулы, а пока – учись, студент, точнее школьник.
Для полной формулы квадрата разности здесь нужно ( displaystyle 4) вместо ( displaystyle 2).
Представим третий член ( displaystyle 2) как разность ( displaystyle 4-2), получим: ( displaystyle {{x}^{2}}-4x+4-2=({{x}^{2}}-4x+4)-2)
К выражению в скобках можно применить формулу квадрата разности (не путать с разностью квадратов!!!), имеем: ( displaystyle {{left( x-2 right)}^{2}}-2), к данному выражению можно применить формулу разности квадратов (не путать с квадратом разности!!!), представив ( displaystyle 2), как ( displaystyle sqrt{2}), получим: ( displaystyle (x-2-sqrt{2})(x-2+sqrt{2})).
Не всегда разложенное на множители выражение выглядит проще и меньше, чем было до разложения, но в таком виде оно становится более подвижным, в том плане, что можно не париться про смену знаков и прочую математическую ерунду.
Ну а вот тебе для самостоятельного решения, следующие выражения нужно разложить на множители.
Примеры:
- ( displaystyle 25{{m}^{2}}-49{{n}^{2}};)
- ( displaystyle {{b}^{2}}-{{(a+1)}^{2}};)
- ( displaystyle {{(x-y)}^{2}}-{{(x+y+1)}^{2}};)
- ( displaystyle {{x}^{2}}+2{x}-3)
- ( displaystyle {{x}^{2}}+6x+5;)
Решения:
5. Разложение квадратного трехчлена на множители. Пример
Квадратный трехчлен – многочлен вида ( displaystyle a{{x}^{2}}+bx+c=0), где ( displaystyle x) – неизвестное, ( displaystyle a), ( displaystyle b), ( displaystyle c) – некоторые числа, причем ( displaystyle ane 0).
Значения переменной ( displaystyle x), которые обращают квадратный трехчлен в ноль, называются корнями трехчлена. Следовательно, корни трехчлена – это корни квадратного уравнения ( displaystyle a{{x}^{2}}+bx+c=0).
Если не помнишь, как находить эти корни, читай тему «Квадратные уравнения».
Теорема.
Если квадратное уравнение ( displaystyle a{{x}^{2}}+bx+c=0) имеет корни ( displaystyle {{x}_{1}},text{ }{{x}_{2}}), то его можно записать в виде: ( displaystyle a{{x}^{2}}+bx+c=aleft( x-{{x}_{1}} right)left( x-{{x}_{2}} right)).
Пример:
Разложим на множители квадратный трехчлен: ( displaystyle 2{{x}^{2}}+5x-3).
Сначала решим квадратное уравнение: Теперь можно записать разложение данного квадратного трехчлена на множители:
( displaystyle begin{array}{l}2{{x}^{2}}+5x-3=0.\{{x}_{1,2}}=frac{-5pm sqrt{{{5}^{2}}-4cdot 2cdot left( -3 right)}}{2cdot 2}=frac{-5pm sqrt{25+24}}{4}=frac{-5pm 7}{4};\{{x}_{1}}=frac{1}{2};text{ }{{x}_{2}}=-3.end{array})
( displaystyle 2{{x}^{2}}+5x-3=2left( x-frac{1}{2} right)left( x+3 right)).
Как пишется?
Формы слов русского языка онлайн
Введите слово:
Неразложимого как пишется?
неразложимый
→
неразложимого — прилагательное, родительный п., муж. p., ед. ч.
↳
неразложимого — прилагательное, винительный п., муж. p., од., ед. ч.
↳
неразложимого — прилагательное, родительный п., ср. p., од., ед. ч.
Часть речи: прилагательное
Положительная степень:
| Единственное число | Множественное число | |||
|---|---|---|---|---|
| Мужской род | Женский род | Средний род | ||
| Им. |
неразложимый |
неразложимая |
неразложимое |
неразложимые |
| Рд. |
неразложимого |
неразложимой |
неразложимого |
неразложимых |
| Дт. |
неразложимому |
неразложимой |
неразложимому |
неразложимым |
| Вн. |
неразложимого неразложимый |
неразложимую |
неразложимое |
неразложимые неразложимых |
| Тв. |
неразложимым |
неразложимою неразложимой |
неразложимым |
неразложимыми |
| Пр. |
неразложимом |
неразложимой |
неразложимом |
неразложимых |
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Содержание:
Разложение многочленов на множители
Разложение многочленов на множители — операция, об-I ратная умножению многочленов. Как вы уже знаете, решая разные задачи, иногда умножают два или более чисел, а иногда — раскладывают данное число на множители. Подобные задачи возникают и при преобразовании целых алгебраических выражений. В этой главе вы узнаете о:
- вынесении общего множителя за скобки;
- способе группировки;
- формулах сокращённого умножения;
- применении разных способов разложения многочленов на множители.
Вынесение общего множителя за скобки
Вы уже умеете раскладывать на множители натуральные числа. Например,
На множители раскладывают и многочлены. Разложить многочлен на множители — это означает заменить его произведением нескольких многочленов, тождественным данному многочлену. Например, многочлен
Один из способов разложения многочленов на множители — вынесение общего множителя за скобки. Рассмотрим его.
Каждый член многочлена ах + ау имеет общий множитель а. На основании распределительного закона умножения 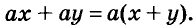
Другие примеры:
Чтобы убедиться, правильно ли разложен многочлен на множители, нужно выполнить умножение полученных множителей. Если всё верно, то в результате должен получиться данный многочлен.
Иногда приходится раскладывать на множители и выражения, имеющие общий многочленный множитель. Например, в выражении 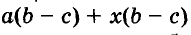
Один и тот же многочлен можно разложить на множители по-разному. Например,
Как правило, стараются вынести за скобки такой общий множитель, чтобы в скобках осталось простейшее выражение. Поэтому чаще всего в качестве коэффициента общего множителя берут наибольший общий делитель (НОД) коэффициентов всех членов данного многочлена или их модулей. Но не всегда. Все зависит от того, с какой целью раскладывают на множители многочлен.
Пусть, например, надо найти значение выражения 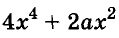
Чтобы использовать условие, это упражнение можно решить так:
Здесь вынесено за скобки не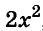
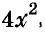
Пример:
Разложите на множители многочлен
Решение:
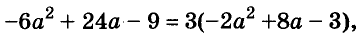
Пример:
Разложите на множители многочлен
Решение:
Пример:
Докажите, что число 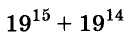
Доказательство:
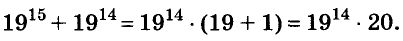
Пример:
Решите уравнение
Решение:
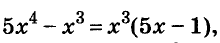
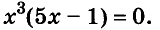
Значит, 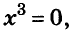
Ответ. Уравнение имеет два корня: 0 и 0,2.
Способ группировки
Разложим на множители многочлен 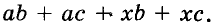
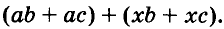
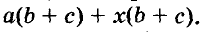
Указанные преобразования можно записать цепочкой:
Такой способ разложения многочленов на множители называют способом группировки.
Замечание. Раскладывая на множители представленный выше многочлен, можно сгруппировать его члены иначе:
Получили такой же результат.
Разложим на множители многочлен
Записывать сумму а + с в виде 1 (а + с) необязательно, но сначала, чтобы не допускать ошибок, можно писать и так.
Чтобы воспользоваться способом группировки, иногда приходится один член данного многочлена представлять в виде суммы или разности одночленов. Чтобы разложить на множители трёхчлен 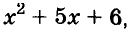
Подобные преобразования также можно выполнять, используя тождества.
Пример:
Разложите на множители многочлен:
Решение:
Ответ.
Пример:
Решите уравнение:
Решение:
Разложим левую часть уравнения на множители:
Корнем первого уравнения является у = 1,5, а второе уравнение корней не имеет, так как
Ответ. у = 1,5.
Квадрат двучлена
Решая различные задачи, часто приходится умножать двучлены вида 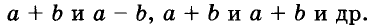
Умножим двучлен
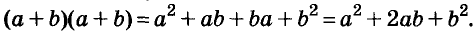
Квадрат двучлена равен квадрату первого его члена плюс удвоенное произведение первого на второй плюс квадрат второго члена.
Доказанное равенство — тождество, его называют формулой квадрата двучлена. Пользуясь ею, можно сразу записать:
Промежуточные преобразования желательно выполнять устно, тем самым сокращается запись:
По формуле квадрата двучлена можно возводить в квадрат любые двучлены, в том числе
Запомните формулу
Формулы квадрата двучлена используют и в «обратном направлении»:
Формулу 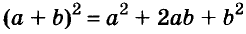
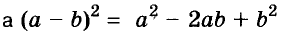
Для положительных чисел а и b формулу
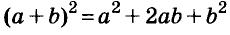
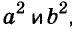
Существуют и другие формулы сокращённого умножения:
Пример:
Возведите в квадрат двучлен
Решение:
Пример:
Упростите выражение
Решение:
Пример:
Представьте в виде многочлена выражение:
Решение:
Пример:
Представьте выражение в виде степени двучлена:
Решение:
- Заказать решение задач по высшей математике
Разность квадратов
Умножим сумму переменных а и b на их разность.
Значит,
Это равенство — тождество. Словами его читают так:
Произведение суммы двух выражений и их разности равно разности квадратов этих выражений.
Пользуясь доказанной формулой, можно сразу записать:
Левую и правую части доказанной формулы можно поменять местами. Получим формулу разности квадратов двух выражений:
Разность квадратов двух выражений равна произведению их суммы и разности.
Пример:
Формула разности квадратов очень удобна для разложения многочленов на множители.
Для положительных чисел а и b формулу 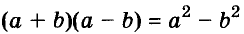
Истинность формулы разности квадратов следует из правила умножения многочленов, а это правило — из законов действий сложения и умножения. Законы сложения и умножения чисел — это своеобразные аксиомы, следствиями которых являются алгебраические тождества.
Пример:
Напишите разность квадратов и квадрат разности выражений
Решение:
Пример:
Запишите в виде произведения двух двучленов выражение:
Решение:
Пример:
Представьте в виде двучлена выражение:
Решение:
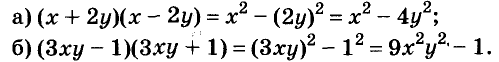
Используя формулу разности квадратов, промежуточные вычисления и преобразования можно выполнять устно, а записывать лишь конечный результат.
Использование формул сокращённого умножения
С помощью формул сокращённого умножения некоторые многочлены можно разложить на множители. Например, двучлен 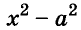
Примеры:
Трёхчлены 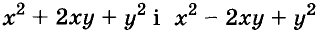
Примеры:
Полученные, выражения можно разложить на множители и записать так:
Многочлен 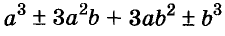
Раскладывать на множители можно не только многочлены, но и некоторые другие целые выражения.
Например, 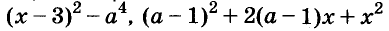
Пример:
Разложите на множители многочлен:
Решение:
Пример:
Решите уравнение
Решение:
Значит, данное уравнение равносильно такому:
Квадрат числа равен нулю только тогда, когда это число равно 0. А х — 2 = 0, когда х = 2.
Ответ. х = 2.
Пример:
Разложите на множители многочлен:
Решение:
Разность и сумма кубов
Выполним умножение многочленов 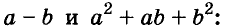
Следовательно, при любых значениях а и b
Трёхчлен 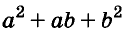
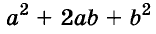
разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.
Выполним умножение многочленов
Следовательно,
Трёхчлен 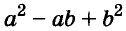
сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.
С помощью доказанных формул можно раскладывать на множители многочлены, являющиеся разностями или суммами кубов.
Примеры:
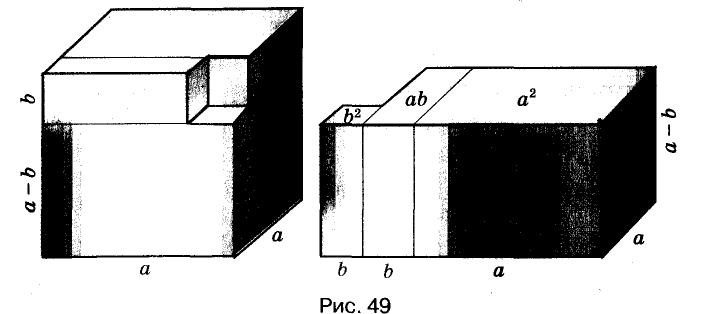
Формулу «разность кубов» для положительных значений а и b можно проиллюстрировать геометрически, как показано на рисунке 49.
Можно доказать, что для каждого натурального значения n истинна формула:
Формулы «разность квадратов» и «разность кубов» — простейшие случаи этой общей формулы.
Пример:
Разложите на множители двучлен:
Решение:
Пример:
Найдите произведение многочленов: 
Решение:
Первый способ. По формуле суммы кубов:
Второй способ. По правилу умножения многочленов:
Применение разных способов разложения многочленов на множители
Чтобы разложить многочлен на множители, иногда приходится применять несколько способов.
Пример:
Разложите на множители многочлен
Решение:
Сначала за скобки вынесен общий множитель а, потом выражение в скобках разложено на множители по формуле разности квадратов.
Пример:
Разложите на множители выражение
Решение:
Здесь применены способ группировки, вынесение общего множителя за скобки и формула суммы кубов.
Чтобы разложить на множители более сложные многочлены, приходится применять несколько известных способов или искусственные приёмы.
В этом случае можно использовать такое правило-ориентир:
- Вынести общий множитель (если он есть) за скобки.
- Проверить, не является ли выражение в скобках разностью квадратов, разностью или суммой кубов.
- Если это трёхчлен, то проверить, не является ли он квадратом двучлена.
- Если многочлен содержит больше трёх членов, то надо попробовать группировать их и к каждой группе применить п. 1—3.
Иногда удаётся разложить многочлен на множители, прибавляя и вычитая из него одно и то же выражение.
Пример:
Разложите на множители двучлен
Решение:
Прибавим к данному двучлену выражение
Пример:
Разложите на множители выражение
Решение:
Пример:
Представьте многочлен 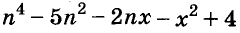
Решение:
Пример:
Докажите, что число 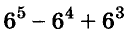
Доказательство:
Последнее произведение делится на 31, поэтому делится на 31 и равное ему данное числовое выражение.
Исторические сведения:
Наибольший вклад в развитие алгебраической символики внёс известный французский математик Ф. Виет, которого называли «отцом алгебры ». Он часто использовал буквенные обозначения. Вместо
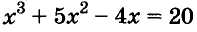
Степени чисел продолжительное время не имели специальных обозначений, четвёртую степень числа а записывали в виде произведения аааа. Позднее такое произведение начали записывать 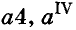
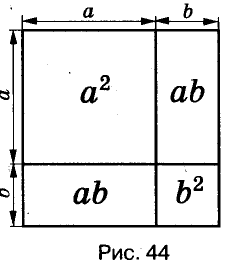
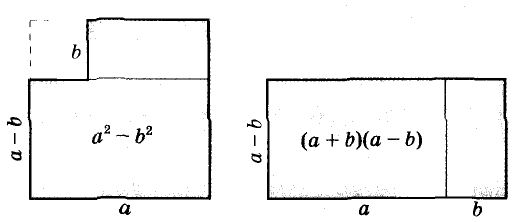
Формулы сокращённого умножения древним китайским и греческим математикам были известны за много веков до начала нашей эры. Записывали их тогда не с помощью букв, а словами и доказывали геометрически (только для положительных чисел). Пользуясь рисунком, объясняли, что для любых чисел а и b площадь квадрата со стороной а + b равна сумме площадей двух квадратов со сторонами а и b к двух прямоугольников со сторонами а, b. Итак, 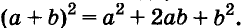
В учебнике рассмотрены простейшие формулы сокращённого умножения.
Формулы квадрата и куба двучлена — простейшие случаи общей формулы бинома Ньютона:
Напомню:
Разложить многочлен на множители — это означает заменить его произведением нескольких многочленов, тождественным данному многочлену.
Простейшие способы разложения многочленов на множители:
- вынесение общего множителя за скобки;
- способ группировки;
- использование формул сокращённого умножения.
Примеры:
Формулы сокращённого умножения
Разложение многочленов на множители — это преобразование, обратное умножению многочленов. Схематично эти две операции можно изобразить, например, так.
- Системы линейных уравнений с двумя переменными
- Рациональные выражения
- Квадратные корни
- Квадратные уравнения
- Целые выражения
- Одночлены
- Многочлены
- Формулы сокращенного умножения