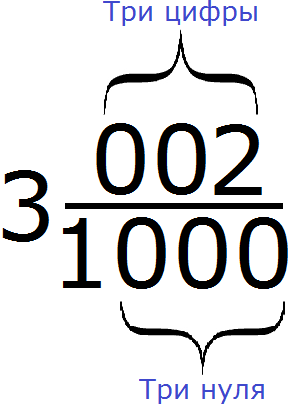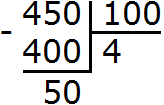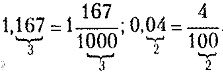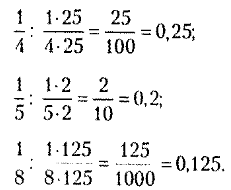Например: 101 – 3.14 – 0,5 – 1/4 – 1 2/3.
Число 0.3 прописью: ноль целых три десятых.
Является десятичной дробью с 1-м знаком после запятой, разряд — десятые.
| Падеж | Вопрос | 0.3 |
|---|---|---|
| Именительный | есть что? | ноль целых три десятых |
| Родительный | нет чего? | ноля целых трёх десятых |
| Дательный | рад чему? | нолю целых трём десятым |
| Винительный | вижу что? | ноль целых три десятых |
| Творительный | оплачу чем? | нолём целых тремя десятыми |
| Предложный | думаю о чём? | ноле целых трёх десятых |
Всего найдено: 94
Добрый день!
Как лучше писать:
1) «В середине тридцатых годов…» или «В середине 30-х годов…»?
2) «В двадцатом столетии…» или «В ХХ столетии…»?
3) «в сто раз больше…» или «в 100 раз больше…»?
Есть ли разница между художественными и научными текстами?
Спасибо за ответ
Ответ справочной службы русского языка
Написание числительного в цифровой или словесной форме зависит от типа текста. Приводим основные рекомендации.
В изданиях художественной и близкой ей литератур рекомендуется все числительные писать прописью, поскольку цифры придают тексту деловой вид.
Как исключение цифровая форма предпочтительна в следующих случаях:
1. Когда требуется имитировать документы, письма, вывески, поскольку пропись в них маловероятна и будет нарушать их «подлинность».
2. Когда в авторском тексте (не в прямой речи) приводятся номера домов, учреждений и т. п. и необходимо передать их в том виде, в каком они предстают на бланке, вывеске и т. п.
3. Когда в прямой речи встречается сложный номер и стремятся упростить его чтение.
4. Когда стремятся подчеркнуть (иногда иронически) особую точность чисел.
В изданиях деловой и научной литератур цифровая форма более уместна, особенно в следующих случаях:
1) если однозначные числа (даже в косвенных падежах) стоят в одном ряду с дву- и многозначными: серии из 3, 5, 12 упражнений;
2) когда однозначные целые числа образуют сочетания с единицами физических величин, денежными единицами: 7 кг., 7 руб.;
3) для многозначных целых чисел цифровая форма в подавляющем большинстве случаев является предпочтительной.
Словесная форма чисел рекомендуется в изданиях деловой и научной литератур, если однозначные числа стоят в косвенных падежах (не при единицах величин, денежных единицах), напр.: оборудовать лабораторию четырьмя мойками (не 4 мойками) или если количественное числительное начинает собой предложение: Пять станков размещают (не 5 станков размещают).
См.: Мильчин А. Э., Чельцова Л. К. Справочник издателя и автора. М., 2003.
Как правильно пишется: Средний возраст жителей составил 38,1 лет или года?
Ответ справочной службы русского языка
Правильно: _Средний возраст жителей составил 38,1 года_ (читается: составил тридцать восемь целых и одну десятую года).
Спасибо за своевременный ответ. Еще один мой вопрос, наверное, затерялся. Фын (фамилия) Ли-да (имя) — верно? И дополнительно: 11,862, 164,79 года(лет)? Ваша помощь нужна,как всегда, очень срочно.
Ответ справочной службы русского языка
Что касается имени и фамилии, то точно ответить нельзя, лучше спросить у носителя.
Если эти числа — десятичные дроби (11 целых 862 тысячных и 164 целых 79 сотых), то верно: _года_.
Скажите, пожалуйста, нужно ли ставить в род.п. проценты, если число с половиной: 6,5 процентОВ? Или шесть и пять десятых процентА?
Ответ справочной службы русского языка
Правильно: _шесть целых пять десятых процента, шесть с половиной процентов_.
Добрый день! Прошу помочь. Какое окончание должно быть у словосочетания «квадратные метры» во фразе «общей площадью 129,2 (сто двадцать девять целых и два десятых) квадратных метров (?)». Предложенный вариант правильный? Если нет, то как правильно? Спасибо.
Ответ справочной службы русского языка
Верно: _квадратного метра_.
Добрый день! Скажите пожалуйста, когда в тексте пишем цифры с рублями, то рубли согласуем с целой или дробной частью? Например: 2033,33 рубля или 2033,33 рублей. Спасибо!
Ответ справочной службы русского языка
Правильно: _2033,33 рубля_ (читаем: две тысячи тридцать три целых тридцать три сотых рубля).
является ли употребление слова «прозвонить» в значении «позвонить по телефону кому-либо» грамотным? Насколько мне известно слово «прозвонить» является скорее техническим, чем общеупотребительным словом. Какие вообще значения может принимать это слово?
Ответ справочной службы русского языка
_Прозвонить_. 1. Издать непродолжительный звон. _Прозвонил звонок_. 2. Звоном возвестить, объявить о чем-то. _Прозвонить перемену_. 3. Проверить правильность монтажа с помощью электроприбора. _Прозвонить электрическую схему_. 4. Звонить в течение какого-то времени. _Прозвонить целых двадцать минут_. 5. _Разг. Истратить на телефонные разговоры. _Прозвонить двадцать рублей_.
Употребление слова _прозвонить_ в значении ‘обзвонить’ — просторечие.
как правильно писать: 2,32 кв.м. (две целых тридцать две сотых или сотые)
Ответ справочной службы русского языка
Возможны оба варианта, предпочтительно: _сотые_.
Здравствуйте! Подскажите, как согласно актуальным нормам современного русского языка правильно пишется, риэлтОр или риэлтЕр. Академический словарь трудностей рекомендуют писать через Е, а интернет (Яндекс) рекомендует через О. Понятно, что интернет показывает только количественный перевес, но как может быть, чтобы 1 мнл. ссылок было на Е и целых 4 млн. на О. Получается, что это такая распространённая ошибка, или за последнее время в русском языке относительно этого слова произошли изменения? Как быть? Заранее благодарю!
Ответ справочной службы русского языка
См. ответ № 189997 .
Правильно ли написана цифра прописью: Сегодняшний курс составил 25,4144 рубля за доллар — двадцать пять (целых) четыре тысячи сто сорок четыре рубля. Спасибо.
Ответ справочной службы русского языка
Верно: _двадцать пять целых четыре тысячи сто сорок четыре десятитысячных рубля._
равный нулю целых (целым) одной десятой?
Ответ справочной службы русского языка
Правильно: равный нулю целым и одной десятой. Однако обычно слова «ноль целых» при прочтении опускают.
Подскажите пожайлуста как правильно написать «доля в размере 0,022% (Ноль целых двадцать двЕ тысячных процента или Ноль целых двадцать двА тысячных процента ) С уважением, Екатерина
Ответ справочной службы русского языка
Верно: _двадцать две тысячных_.
как правильно написать словами «1001,44 евро»: 1) «одна тысяча один целых сорок четыре сотых евро» или 2) «одна тысяча одна целая сорок четыре сотых евро»?
Ответ справочной службы русского языка
Верен второй вариант.
«… по ставке 2,5 % (Два целых и пять десятых)процента Как правильно указать в скобках «Две целых и пять десятых» процента или «Два целых и пять десятых» процента. Спасибо.
Ответ справочной службы русского языка
Верно: _Две целых и пять десятых процента_.
Подскажите,пожалуйста,как правильно написать прописью и полностью:32,4 кв.м. С уважением,Масленников Андрей.
Ответ справочной службы русского языка
_Тридцать две целых четыре десятых квадратного метра_. Страницы: первая 1 2 3 4 6 7 последняя
Десятичная дробь отличается от обыкновенной дроби тем, что знаменатель у нее — это разрядная единица.
Например: 
Десятичные дроби выделены из обыкновенных дробей в отдельный вид, что привело к собственным правилам сравнения, сложения, вычитания, умножения и деления этих дробей. В принципе, с десятичными дробями можно работать и по правилам обыкновенных дробей. Собственные правила преобразования десятичных дробей упрощают вычисления, а правила преобразования обыкновенных дробей в десятичные, и наоборот, служат связкой между этими видами дроби.
Запись и чтение десятичных дробей позволяет их записывать, сравнивать и производить действия над ними по правилам, очень похожим на правила действий с натуральными числами.
Впервые система десятичных дробей и действий над ними была изложена в XV в. самаркандским математиком и астрономом Джемшид ибн-Масудаль-Каши в книге «Ключ к искусству счета».
Целая часть десятичной дроби отделена от дробной части запятой, в некоторых странах (США) ставят точку. Если в десятичной дроби нет целой части, то перед запятой ставят число 0.
К дробной части десятичной дроби справа можно дописывать любое количество нулей, это величину дроби не изменяет. Дробная часть десятичной дроби читается по последнему значащему разряду.
Например:
0,3 — три десятых
0,75 — семьдесят пять сотых
0,000005 — пять миллионных.
Чтение целой части десятичной дроби такое же, как и натуральных чисел.
Например:
27,5 — двадцать семь…;
1,57 — одна…
После целой части десятичной дроби произносится слово «целых».
Например:
10.7 — десять целых семь десятых
0,67 — ноль целых шестьдесят семь сотых.
Десятичные знаки — это цифры дробной части. Дробная часть читается не по разрядам (в отличие от натуральных чисел), а целиком, поэтому дробная часть десятичной дроби определяется последним справа значащим разрядом. Разрядная система дробной части десятичной дроби несколько иная, чем у натуральных чисел.
- 1-й разряд после занятой — разряд десятых
- 2-й разряд после запятой — разряд сотых
- 3-й разряд после запятой — разряд тысячных
- 4-й разряд после запятой — разряд десятитысячных
- 5-й разряд после запятой — разряд стотысячных
- 6-й разряд после запятой — разряд миллионных
- 7-й разряд после запятой — разряд десятимиллионных
- 8-й разряд после запятой — разряд стомиллионных
В вычислениях чаще всего используются первые три разряда. Большая разрядность дробной части десятичных дробей используется только в специфических отраслях знаний, где вычисляются бесконечно малые величины.
Перевод десятичной дроби в смешанную дробь состоит н следующем: число, стоящее до запятой записать целой частью смешанной дроби; число, стоящее после запятой — числителем ее дробной части, а в знаменателе дробной части записать единицу со столькими нулями, сколько цифр стоит после запятой.
Например:
Перевод обыкновенной дроби в десятичную дробь — это вычисление частного отделения числителя дроби на знаменатель по правилам действий с десятичными дробями:
Но не все обыкновенные дроби можно перевести в десятичную дробь. Например: — нет такого множителя, который с множителем 3 даст в произведении разрядную единицу.
1 января 2017
Вот, казалось бы, перевод десятичной дроби в обычную — элементарная тема, но многие ученики её не понимают! Поэтому сегодня мы подробно рассмотрим сразу несколько алгоритмов, с помощью которых вы разберётесь с любыми дробями буквально за секунду.
Напомню, что существует как минимум две формы записи одной и той же дроби: обыкновенная и десятичная. Десятичные дроби — это всевозможные конструкции вида 0,75; 1,33; и даже −7,41. А вот примеры обыкновенных дробей, которые выражают те же самые числа:
Сейчас разберёмся: как от десятичной записи перейти к обычной? И самое главное: как сделать это максимально быстро?
Основной алгоритм
На самом деле существует как минимум два алгоритма. И мы сейчас рассмотрим оба. Начнём с первого — самого простого и понятного.
Чтобы перевести десятичную дробь в обыкновенную, необходимо выполнить три шага:
Важное замечание по поводу отрицательных чисел. Если в исходном примере перед десятичной дробью стоит знак «минус», то и на выходе перед обыкновенной дробью тоже должен стоять «минус». Вот ещё несколько примеров:

Особое внимание хотелось бы обратить на последний пример. Как видим, в дроби 0,0025 присутствует много нулей после запятой. Из-за этого приходится аж целых четыре раза умножать числитель и знаменатель на 10. Можно ли как-то упростить алгоритм в этом случае?
Конечно, можно. И сейчас мы рассмотрим альтернативный алгоритм — он чуть более сложен для восприятия, но после небольшой практики работает намного быстрее стандартного.
Более быстрый способ
В данном алгоритме также 3 шага. Чтобы получить обычную дробь из десятичной, нужно выполнить следующее:
Вот и всё! На первый взгляд, эта схема сложнее предыдущей. Но на самом деле он и проще, и быстрее. Судите сами:
Ещё один пример:
Наконец, последний пример:
Особенность этой дроби — наличие целой части. Поэтому на выходе у нас получается неправильная дробь 47/25. Можно, конечно, попытаться разделить 47 на 25 с остатком и таким образом вновь выделить целую часть. Но зачем усложнять себе жизнь, если это можно сделать ещё на этапе преобразований? Что ж, разберёмся.
Что делать с целой частью
На самом деле всё очень просто: если мы хотим получить правильную дробь, то необходимо убрать из неё целую часть на время преобразований, а затем, когда получим результат, вновь дописать её справа перед дробной чертой.
Например, рассмотрим то же самое число: 1,88. Забьём на единицу (целую часть) и посмотрим на дробь 0,88. Она легко преобразуется:
Затем вспоминаем про «утерянную» единицу и дописываем её спереди:
Вот и всё! Ответ получился тем же самым, что и после выделения целой части в прошлый раз. Ещё парочка примеров:
В этом и состоит прелесть математики: каким бы путём вы не пошли, если все вычисления выполнены правильно, ответ всегда будет одним и тем же.:)
В заключение хотел бы рассмотреть ещё один приём, который многим помогает.
Преобразования «на слух»
Давайте задумаемся о том, что вообще такое десятичная дробь. Точнее, как мы её читаем. Например, число 0,64 — мы читаем его как «ноль целых, 64 сотых», правильно? Ну, или просто «64 сотых». Ключевое слово здесь — «сотых», т.е. число 100.
А что насчёт 0,004? Это же «ноль целых, 4 тысячных» или просто «четыре тысячных». Так или иначе, ключевое слово — «тысячных», т.е. 1000.
Ну и что в этом такого? А то, что именно эти числа в итоге «всплывают» в знаменателях на втором этапе алгоритма. Т.е. 0,004 — это «четыре тысячных» или «4 разделить на 1000»:
Попробуйте потренироваться сами — это очень просто. Главное — правильно прочесть исходную дробь. Например, 2,5 — это «2 целых, 5 десятых», поэтому
А какое-нибудь 1,125 — это «1 целая, 125 тысячных», поэтому
В последнем примере, конечно, кто-то возразит, мол, не всякому ученику очевидно, что 1000 делится на 125. Но здесь нужно помнить, что 1000 = 103, а 10 = 2 ∙ 5, поэтому
Таким образом, любая степень десятки раскладывается лишь на множители 2 и 5 — именно эти множители нужно искать и в числителе, чтобы в итоге всё сократилось.
На этом урок окончен. Переходим к более сложной обратной операции — см. «Переход от обыкновенной дроби к десятичной».
Опубликовано 3 года назад по предмету
Математика
от Dem333
Плиз, помогите
Найдите:
1. Ноль целых три десятых от тридцати.
2. Десять процентов от шести.
3. Четыре девятых от восемнадцати.
4. Квадрат трех восьмых.
5. Сумму одной третьей и одной седьмой умножьте на двадцать один.
6. Две целых одну пятую умножьте на три.
Верно ли высказывание (ответьте «да» или «нет»):
7. Произведение пяти и трех целых четырех пятых равно девятнадцати.
-
Ответ
Ответ дан
tana19900428вот так получилось решение………..
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.
Калькулятор «Калькулятор десятичных дробей»
Какая десятичная дробь 3/10?
Ответ: Дробь 3/10 в десятичном виде это 0.3
Объяснение конвертации дроби 3/10 в десятичную
Для того, чтобы перевести дробь 3/10 в десятичный формат необходимо разделить числитель 3 на знаменатель 10:
3 ÷ 10 = 0.3
Смотрите также: Сократить дробь 3/10
Поделитесь текущим расчетом
https://calculat.io/ru/number/fraction-as-a-decimal/0—3—10
<a href=»https://calculat.io/ru/number/fraction-as-a-decimal/0—3—10″>Перевести дробь 3/10 в десятичную — Calculatio</a>
О калькуляторе «Калькулятор десятичных дробей»
Данный калькулятор поможет конвертировать обыкновенную дробь в десятичную. Например, Какая десятичная дробь 3/10? Введите дробь (целую часть, числитель и знаменатель) (например ‘3/10’) и нажмите кнопку ‘Конвертировать’.
Калькулятор «Калькулятор десятичных дробей»
Таблица конвертации обыкновенных дробей в десятичные
Мы уже говорили, что дроби бывают обыкновенные и десятичные. На данный момент мы немного изучили обыкновенные дроби. Мы узнали, что обыкновенные дроби бывают правильными и неправильными. Также мы узнали что обыкновенные дроби можно сокращать, складывать, вычитать умножать и делить. И ещё мы узнали, что бывают так называемые смешанные числа, которые состоят из целой и дробной части.
Мы ещё не полностью изучили обыкновенные дроби. Есть немало тонкостей и деталей, о которых следует поговорить, но уже сегодня мы начнём изучать десятичные дроби, поскольку обыкновенные и десятичные дроби достаточно часто приходиться сочетать. То есть, при решении задач приходиться работать с обоими видов дробей.
Этот урок возможно покажется сложным и непонятным. Это вполне нормально. Такого рода уроки требуют, чтобы их именно изучали, а не просматривали поверхностно.
Выражение величин в дробном виде
Иногда удобно бывает показать что-либо в дробном виде. Например, одна десятая часть дециметра записывается так:
Это выражение означает, что один дециметр был разделён на десять равных частей, и от этих десяти частей была взята одна часть. А одна часть из десяти в данном случае равна одному сантиметру:
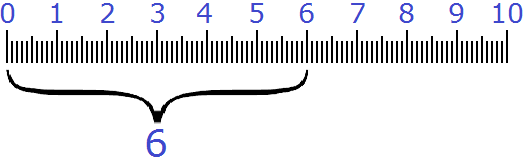
Рассмотрим следующий пример. Пусть требуется показать 6 см и ещё 3 мм в сантиметрах в дробном виде.
Итак, 6 целых сантиметров у нас уже есть:
Но осталось еще 3 миллиметра. Как показать эти 3 миллиметра, при этом в сантиметрах?
На помощь приходят дроби. Один сантиметр это десять миллиметров. Три миллиметра это три части из десяти. А три части из десяти записываются как см
Выражение см означает, что один сантиметр был разделён на десять равных частей, и от этих десяти частей взяли три части.
В результате имеем шесть целых сантиметров и три десятых сантиметра:
Цифра 6 показывает число целых сантиметров, а дробь — число дробных. Эта дробь читается как «шесть целых и три десятых сантиметра».
Дроби, в знаменателе которых присутствуют числа 10, 100, 1000 можно записывать без знаменателя. Сначала пишут цéлую часть, а потом числитель дробной части. Целая часть отделяется от числителя дробной части запятой.
Например, запишем без знаменателя. Сначала записываем целую часть. Целая часть это 6
6
Целая часть записана. Сразу же после написания целой части ставим запятую:
6,
И теперь записываем числитель дробной части. В смешанном числе числитель дробной части это число 3. Записываем после запятой тройку:
6,3
Любое число, которое представляется в таком виде, называется десятичной дробью.
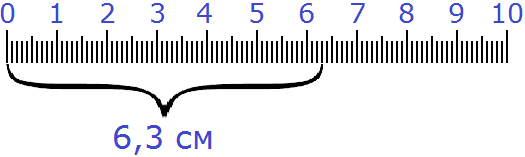
Поэтому показать 6 см и ещё 3 мм в сантиметрах можно с помощью десятичной дроби:
6,3 см
На рисунке выглядеть это будет так:
На самом деле десятичные дроби это те же самые обыкновенные дроби и смешанные числа. Особенность таких дробей заключается в том, что в знаменателе их дробной части содержатся числа 10, 100, 1 000 или 10 000.
Как и смешанное число, десятичная дробь имеет цéлую часть и дробную.
Например, в смешанном числе целая часть это 6, а дробная часть это
.
В десятичной дроби 6,3 целая часть это число 6, а дробная часть это числитель дроби , то есть число 3.
Бывает и так, что обыкновенные дроби в знаменателе которых числа 10, 100, 1000 даны без целой части. Например, дробь дана без целой части. Чтобы записать такую дробь как десятичную, сначала записывают 0, затем ставят запятую и записывают числитель дробной части.
Так, дробь без знаменателя будет записана так:
0,5
Читается как «ноль целых, пять десятых».
Перевод смешанных чисел в десятичные дроби
Когда мы записываем смешанные числа без знаменателя, мы тем самым перевóдим их в десятичные дроби. При переводе обыкновенных дробей в десятичные дроби нужно знать несколько моментов, о которых мы сейчас поговорим.
После того как записана целая часть, обязательно нужно посчитать количество нулей в знаменателе дробной части, поскольку количество нулей в знаменателе дробной части и количество цифр после запятой в десятичной дроби должно быть одинаковым. Что это значит?
Рассмотрим следующий пример: перевести смешанное число в десятичную дробь.
Сначала записываем цéлую часть и ставим запятую:
3,
И можно бы сразу записать числитель дробной части и десятичная дробь готова, но обязательно нужно посчитать сколько нулей содержится в знаменателе дробной части.
Итак, посчитаем количество нулей в дробной части смешанного числа . Видим, что в знаменателе дробной части один ноль. Значит в десятичной дроби после запятой будет одна цифра и это цифра будет числитель дробной части смешанного числа
, то есть число 2
3,2
Таким образом, смешанное число при переводе в десятичную дробь обращается в 3,2. Эта десятичная дробь читается так:
«Три целых, две десятых»
«Десятых» потому что в дробной части смешанного числа содержится число 10.
Пример 2. Перевести смешанное число в десятичную дробь.
Записываем цéлую часть и ставим запятую:
5,
И можно бы сразу записать числитель дробной части и получить десятичную дробь 5,3 но правило говорит, что после запятой должно быть столько цифр сколько нулей в знаменателе дробной части смешанного числа . А мы видим что в знаменателе дробной части
два нуля. Значит в нашей десятичной дроби после запятой должно быть две цифры, а не одна.
В таких случаях числитель дробной части нужно немного видоизменить: добавить ноль перед числителем, то есть перед числом 3
Теперь можно довести дело до конца. Записываем после запятой числитель дробной части:
5,03
Видим, что количество цифр после запятой и количество нулей в знаменателе дробной части смешанного числа одинаково.
Десятичная дробь 5,03 читается так:
«Пять целых, три сотых»
«Сотых» потому что в знаменателе дробной части смешанного числа содержится число 100.
Пример 3. Перевести смешанное число в десятичную дробь.
Из предыдущих примеров мы узнали, что для успешного перевода смешанного числа в десятичную дробь, количество цифр в числителе дробной части и количество нулей в знаменателе дробной части должно быть одинаковым.
Перед переводом смешанного числа в десятичную дробь, его дробную часть нужно немного видоизменить, а именно сделать так чтобы количество цифр в числителе дробной части и количество нулей в знаменателе дробной части было одинаковым.
В первую очередь смóтрим на количество нулей в знаменателе дробной части. Видим, что там три нуля:
Наша задача организовать в числителе дробной части три цифры. Одна цифра у нас уже есть — это цифра 2. Осталось добавить ещё две цифры. Ими будут два нуля. Добавим их перед цифрой 2. В результате количество нулей в знаменателе и количество цифр в числителе станет одинаковым:
Теперь можно заняться переводом этого смешанного числа в десятичную дробь. Записываем сначала цéлую часть и ставим запятую:
3,
и сразу записываем числитель дробной части
3,002
Видим, что количество цифр после запятой и количество нулей в знаменателе дробной части смешанного числа одинаково.
Десятичная дробь 3,002 читается так:
«Три целых, две тысячных»
«Тысячных» потому что в знаменателе дробной части смешанного числа содержится число 1000.
Перевод обыкновенных дробей в десятичные дроби
Обыкновенные дроби, у которых в знаменателе числа 10, 100, 1000 или 10000, тоже можно перевести в десятичные дроби. Поскольку у обыкновенной дроби целая часть отсутствует, сначала записывают 0, затем ставят запятую и записывают числитель дробной части.
Здесь также количество нулей в знаменателе и количество цифр в числителе должно быть одинаковым. Поэтому следует быть внимательным.
Пример 1. Перевести обыкновенную дробь в десятичную дробь.
Целая часть отсутствует, значит сначала записываем 0 и ставим запятую:
0,
Теперь смóтрим на количество нулей в знаменателе. Видим, что там один ноль. И в числителе одна цифра. Значит можно спокойно продолжить десятичную дробь, записав после запятой цифру 5
0,5
В полученной десятичной дроби 0,5 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена правильно.
Десятичная дробь 0,5 читается так:
«Ноль целых, пять десятых»
Пример 2. Перевести обыкновенную дробь в десятичную дробь.
Целая часть отсутствует. Записываем сначала 0 и стáвим запятую:
0,
Теперь смóтрим на количество нулей в знаменателе. Видим, что там два нуля. А в числителе только одна цифра. Чтобы сделать количество цифр и количество нулей одинаковым, добавим в числителе перед цифрой 2 один ноль. Тогда дробь примет вид . Теперь количество нулей в знаменателе и количество цифр в числителе одинаково. Значит можно продолжить десятичную дробь:
0,02
В полученной десятичной дроби 0,02 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена правильно.
Десятичная дробь 0,02 читается так:
«Ноль целых, две сотых».
Пример 3. Перевести обыкновенную дробь в десятичную дробь.
Записываем 0 и стáвим запятую:
0,
Теперь посчитаем количество нулей в знаменателе дроби . Видим, что там пять нулей, а в числителе только одна цифра. Чтобы сделать количество нулей в знаменателе и количество цифр в числителе одинаковым, нужно в числителе перед цифрой 5 дописать четыре нуля:
Теперь можно продолжить десятичную дробь. Записываем после запятой числитель дроби
0,00005
В полученной десятичной дроби 0,00005 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена правильно.
Десятичная дробь 0,00005 читается так:
«Ноль целых, пять стотысячных».
Перевод неправильных дробей в десятичную дробь
Неправильная дробь это дробь, у которой числитель больше знаменателя.
Бывают неправильные дроби, у которых в знаменателе содержатся числа 10, 100, 1000 или 10000. Такие дроби можно переводить в десятичные. Но перед переводом в десятичную дробь, у таких дробей необходимо выделять цéлую часть.
Пример 1. Перевести неправильную дробь в десятичную.
Дробь является неправильной. Чтобы перевести такую дробь в десятичную, нужно в первую очередь выделить у нее цéлую часть. Вспоминаем, как выделять целую часть у неправильных дробей. Если забыли, советуем вернуться к этой теме и хорошенько изучить её.
Итак, выделим целую часть в неправильной дроби . Напомним, что дробь означает деление — в данном случае деление числа 112 на число 10. Деление нужно выполнить с остатком:
Посмóтрим на этот рисунок и соберём новое смешанное число, подобно детскому конструктору. Частное 11 будет целой частью, остаток 2 — числителем дробной части, делитель 10 — знаменателем дробной части:
Мы получили смешанное число . Его и переведём в десятичную дробь. А как переводить такие числа в десятичные дроби мы уже знаем. Сначала записываем целую часть и ставим запятую:
11,
Теперь посчитаем количество нулей в знаменателе дробной части. Видим, что там один ноль. И в числителе дробной части одна цифра. Значит количество нулей в знаменателе дробной части и количество цифр в числителе дробной части одинаково. Это даёт нам возможность сразу записать после запятой числитель дробной части:
11,2
Значит, неправильная дробь при переводе в десятичную обращается в 11,2
Десятичная дробь 11,2 читается так:
«Одиннадцать целых, две десятых».
Пример 2. Перевести неправильную дробь в десятичную дробь.
Это неправильная дробь, поскольку числитель больше знаменателя. Но её можно перевести в десятичную дробь, поскольку в знаменателе содержится число 100.
В первую очередь выделим целую часть этой дроби. Для этого разделим уголком 450 на 100:
Соберём новое смешанное число — получим . Теперь переведём его в десятичную дробь. Записываем целую часть и ставим запятую:
4,
Теперь посчитаем количество нулей в знаменателе дробной части и количество цифр в числителе дробной части. Видим, что количество нулей в знаменателе и количество цифр в числителе одинаково. Это даёт нам возможность сразу записать числитель дробной части после запятой:
4,50
Значит неправильная дробь при переводе в десятичную обращается в 4,50
При решении задач, если в конце десятичной дроби оказываются нули, их можно отбросить. Давайте и мы отбросим ноль в нашем ответе. Тогда мы получим 4,5
Это одна из интересных особенностей десятичных дробей. Она заключается в том, что нули которые стоят в конце дроби, не придают этой дроби никакого веса. Другими словами, десятичные дроби 4,50 и 4,5 равны и между ними можно поставить знак равенства:
4,50 = 4,5
Возникает вопрос «а почему так происходит?» Ведь на вид 4,50 и 4,5 разные дроби. Весь секрет кроется в основном свойстве дроби, котором мы изучали ранее. Мы попробуем доказать, почему равны десятичные дроби 4,50 и 4,5, но после изучения следующей темы, которая называется «перевод десятичной дроби в смешанное число».
Перевод десятичной дроби в смешанное число
Любая десятичная дробь может быть обратно переведена в смешанное число. Для этого достаточно уметь читать десятичные дроби.
Например, переведём 6,3 в смешанное число. 6,3 это шесть целых и три десятых. Записываем сначала шесть целых:
6
и рядом три десятых:
Пример 2. Перевести десятичную дробь 3,002 в смешанное число
3,002 это три целых и две тысячных. Записываем сначала три целых
3
и рядом записываем две тысячных:
3
Пример 3. Перевести десятичную дробь 4,50 в смешанное число
4,50 это четыре целых и пятьдесят сотых. Записываем четыре целых
4
и рядом пятьдесят сотых:
Кстати, давайте вспомним последний пример из предыдущей темы. Мы сказали, что десятичные дроби 4,50 и 4,5 равны. Также мы сказали, что ноль можно отбросить. Докажем, что десятичные 4,50 и 4,5 равны. Для этого переведем обе десятичные дроби в смешанные числа.
После перевода в смешанное число десятичная дробь 4,50 обращается в , а десятичная дробь 4,5 обращается в
Имеем два смешанных числа и
. Переведём эти смешанные числа в неправильные дроби:
Теперь имеем две дроби и
. Теперь вспоминаем основное свойство дроби, которое говорит о том, что при умножении (или делении) числителя и знаменателя дроби на одно и то же число, значение дроби не меняется.
Давайте разделим числитель и знаменатель первой дроби на число 10
Получили , а это есть вторая дробь. Значит
и
равны между собой и равны одному и тому же значению:
=
Попробуйте на калькуляторе разделить сначала 450 на 100, а затем 45 на 10. Забавная штука получится.
Перевод десятичной дроби в обыкновенную дробь
Любая десятичная дробь может быть обратно переведена в обыкновенную дробь. Для этого опять же достаточно уметь читать десятичные дроби. Например, переведём 0,3 в обыкновенную дробь. 0,3 это ноль целых и три десятых. Записываем сначала ноль целых:
0
и рядом три десятых 0 . Ноль по традиции не записывают, поэтому окончательный ответ будет не 0
, а просто
.
Пример 2. Перевести десятичную дробь 0,02 в обыкновенную дробь.
0,02 это ноль целых и две сотых. Ноль не записываем, поэтому сразу записываем две сотых
Пример 3. Перевести 0,00005 в обыкновенную дробь
0,00005 это ноль целых и пять сто тысячных. Ноль не записываем, поэтому сразу записываем пять сто тысячных
Пример 4. Перевести 3,5 в обыкновенную дробь
Сначала переведём данную десятичную дробь в смешанное число:
Теперь смешанное число переведём в неправильную (обыкновенную) дробь:
Пример 5. Перевести 1,25 в обыкновенную дробь
Сначала переведём данную десятичную дробь в смешанное число:
Теперь смешанное число переведём в неправильную (обыкновенную) дробь:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

Запись и чтение десятичных дробей
Десятичная дробь отличается от обыкновенной дроби тем, что знаменатель у нее — это разрядная единица.
Например: 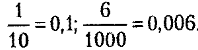
Десятичные дроби выделены из обыкновенных дробей в отдельный вид, что привело к собственным правилам сравнения, сложения, вычитания, умножения и деления этих дробей. В принципе, с десятичными дробями можно работать и по правилам обыкновенных дробей. Собственные правила преобразования десятичных дробей упрощают вычисления, а правила преобразования обыкновенных дробей в десятичные, и наоборот, служат связкой между этими видами дроби.
Запись и чтение десятичных дробей позволяет их записывать, сравнивать и производить действия над ними по правилам, очень похожим на правила действий с натуральными числами.
Впервые система десятичных дробей и действий над ними была изложена в XV в. самаркандским математиком и астрономом Джемшид ибн-Масудаль-Каши в книге «Ключ к искусству счета».
Целая часть десятичной дроби отделена от дробной части запятой, в некоторых странах (США) ставят точку. Если в десятичной дроби нет целой части, то перед запятой ставят число 0.
К дробной части десятичной дроби справа можно дописывать любое количество нулей, это величину дроби не изменяет. Дробная часть десятичной дроби читается по последнему значащему разряду.
Например:
0,3 — три десятых
0,75 — семьдесят пять сотых
0,000005 — пять миллионных.
Чтение целой части десятичной дроби такое же, как и натуральных чисел.
Например:
27,5 — двадцать семь…;
1,57 — одна…
После целой части десятичной дроби произносится слово «целых».
Например:
10.7 — десять целых семь десятых
0,67 — ноль целых шестьдесят семь сотых.
Десятичные знаки — это цифры дробной части. Дробная часть читается не по разрядам (в отличие от натуральных чисел), а целиком, поэтому дробная часть десятичной дроби определяется последним справа значащим разрядом. Разрядная система дробной части десятичной дроби несколько иная, чем у натуральных чисел.
- 1-й разряд после занятой — разряд десятых
- 2-й разряд после запятой — разряд сотых
- 3-й разряд после запятой — разряд тысячных
- 4-й разряд после запятой — разряд десятитысячных
- 5-й разряд после запятой — разряд стотысячных
- 6-й разряд после запятой — разряд миллионных
- 7-й разряд после запятой — разряд десятимиллионных
- 8-й разряд после запятой — разряд стомиллионных
В вычислениях чаще всего используются первые три разряда. Большая разрядность дробной части десятичных дробей используется только в специфических отраслях знаний, где вычисляются бесконечно малые величины.
Перевод десятичной дроби в смешанную дробь состоит н следующем: число, стоящее до запятой записать целой частью смешанной дроби; число, стоящее после запятой — числителем ее дробной части, а в знаменателе дробной части записать единицу со столькими нулями, сколько цифр стоит после запятой.
Например:
Перевод обыкновенной дроби в десятичную дробь — это вычисление частного отделения числителя дроби на знаменатель по правилам действий с десятичными дробями:
Но не все обыкновенные дроби можно перевести в десятичную дробь. Например: — нет такого множителя, который с множителем 3 даст в произведении разрядную единицу.