А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я
нулево́й
Рядом по алфавиту:
нуклеокапси́д , -а
нуклеолоне́ма , -ы
нуклео́ль , -и
нуклеопротеи́ды , -ов, ед. -еи́д, -а
нуклеоти́дный
нуклеоти́ды , -ов, ед. -ти́д, -а
нуклеофи́льный
ну́клеус , -а
нукли́дный
нукли́ды , -ов, ед. -и́д, -а
нукло́н , -а
нуку́сский , (от Нуку́с)
нуку́сцы , -ев, ед. -сец, -сца, тв. -сцем
нулеви́к , -ика́
нулёвка , -и, р. мн. -вок (сниж.)
нулево́й
ну́лик , -а и но́лик, -а
нуллисо́мики , -ов, ед. -мик, -а
нуллисоми́ческий
нуллисо́мия , -и
нуллифика́ция , -и
нуллифици́рованный , кр. ф. -ан, -ана
нуллифици́ровать(ся) , -рую, -рует(ся)
нуль , нуля́ и ноль, ноля́
нуль-дие́та , -ы и ноль-дие́та, -ы
нуль-индика́тор , -а
нуль-о́рган , -а
нуль-пу́нкт , -а
нуль-транспортиро́вка , -и
нуль-указа́тель , -я
нумеи́т , -а (минерал)
Определение вектора
Определение. Вектор — это направленный отрезок, то есть отрезок, имеющий длину и определенное направление. Графически вектора изображаются в виде направленных отрезков прямой определенной длины. (рис.1)
 |
| рис. 1 |
Обозначение вектора
Вектор началом которого есть точка А, а концом — точка В, обозначается AB (рис.1). Также вектора обозначают одной маленькой буквой, например a.
Длина вектора
Для обозначения длины вектора используются две вертикальные линии слева и справа |AB|.
Нулевой вектор
Определение. Нулевым вектором называется вектор, у которого начальная и конечная точка совпадают.
Нулевой вектор обычно обозначается как 0.
Длина нулевого вектора равна нулю.
Коллинеарные вектора
Определение. Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 2).
 |
| рис. 2 |
Сонаправленные вектора
Определение. Два коллинеарных вектора a и b называются сонаправленными векторами, если их направления совпадают: a↑↑b (рис. 3).
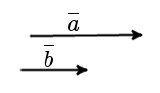 |
| рис. 3 |
Противоположно направленные вектора
Определение. Два коллинеарных вектора a и b называются противоположно направленными векторами, если их направления противоположны: a↑↓b (рис. 4).
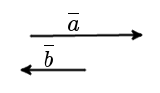 |
| рис. 4 |
Компланарные вектора
Определение. Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами. (рис. 5).
 |
| рис. 5 |
Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные.
Равные вектора
Определение. Вектора a и b называются равными, если они лежат на одной или параллельных прямых, их направления совпадают, а длины равны (рис. 6).
 |
| рис. 6 |
То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:
a = b, если a↑↑b и |a| = |b|.
Единичный вектор
Определение. Единичным вектором или ортом — называется вектор, длина которого равна единице.
- Главная
- Справочник
- Геометрия
- Вектора
- Вектор. Определение и основные понятия
Вектор — это направленный отрезок, то есть отрезок, имеющий длину и определенное направление. Графически вектора изображаются в виде направленных отрезков прямой определенной длины.
Обозначение вектора
Вектор началом которого есть точка ( A ), а концом — точка ( B ), обозначается ( vec{AB} ) . Также вектора обозначают одной маленькой буквой, например ( vec{a} )
Направление вектора (от начала к концу) на рисунках отмечается стрелкой.
Длина вектора
Для обозначения длины вектора используются две вертикальные линии слева и справа ( left| vec{AB} right| ).
Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора ( left| vec{AB} right| ).
Нулевой вектор
Нулевой вектор обычно обозначается как ( vec{0} ).
Длина нулевого вектора равна нулю.
Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают, и он не имеет какого-либо определенного направления.
Нулевым вектором называется вектор, у которого начальная и конечная точка совпадают.
Длина вектора на плоскости
[ d=sqrt{x^2+y^2} ]
Длина вектора в трехмерном пространстве
[ d=sqrt{x^2+y^2+z^2} ]
Длина вектора в n-мерном пространстве
[ d=sqrt{sumlimits_{i=0}^{n}{x_{i}^{2}} } ]
Коллинеарные вектора
Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами
Сонаправленные вектора
Два коллинеарных вектора ( vec{a} ) и ( vec{b} ) называются сонаправленными векторами, если их направления совпадают: ( vec{a} upuparrows vec{b} )
Противоположно направленные вектора
Два коллинеарных вектора ( vec{a} ) и ( vec{b} ) называются противоположно направленными векторами, если их направления совпадают: ( vec{a} uparrow downarrow vec{b} )
Компланарные вектора
Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами.
Равные вектора
Вектора ( vec{a} ) и ( vec{b} ) называются равными, если они лежат на одной или параллельных прямых, их направления совпадают, а длины равны.
То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:
( vec{a} = vec{b} ), если ( vec{a} upuparrows vec{b} ) и ( left|aright| = left|bright| ).
Больше интересного в телеграм @calcsbox
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
-
Координатами вектора называются проекции вектора на оси координат
-
Суммой двух векторов a и b называется третий вектор c, проведенный из начала a к концу b, если начало вектора b совпадает с концом вектора a. Разностью двух векторов a и b называется вектор c при условии: c = a − b, если c + b =a.
-
Декартовы координаты — система координат, состоящая из двух перпендикулярных осей.
-
Произведением вектора u≠0 на число λ≠0 называется вектор w, модуль которого равен |λ||u|, направление которого совпадает с вектором u при λ>0 и противоположно ему при λ
-
Скалярным произведением векторов u и v называется произведение их модулей на косинус угла между ними.
-
Векторным произведением векторов u и v называется третий вектор w, модуль которого равен произведению модулей векторов u и v на синус угла θ между ними и перпендикулярен им.
-
Смешанным произведением трех векторов u, v и w называется скалярное произведение вектора u на векторное произведение векторов v и w
-
Воздух – это смесь газов, и которых состоит атмосфера нашей планеты Земля. Воздух состоит из азота (около 80% объема) , кислорода, благородных газов, даже углекислого газа.
-
Периметр трапеции равен сумме длин всех четырех сторон
-
Вес — это физическая величина, а именно сила, воздействующая на горизонтальную поверхность или вертикальную подвеску.
-
Массой тела называется физическая величина, характеризующая его инерционные и гравитационные свойства.
-
В «современном» латинском алфавите 26 букв.
-
Bitcoin, Биткойн, часто Биткоин (от англ. bit — единица информации «бит», англ. coin — «монета») — пиринговая (как торрент или e-mule) электронная платёжная система, использующая одноимённую виртуальную валюту.
→
вектора — существительное, родительный п., муж. p., ед. ч.
Часть речи: существительное
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Ответ:
Правильное написание слова — вектор
Ударение и произношение — в`ектор
Значение слова -изображаемая отрезком прямой математическая величина, характеризующаяся численным значением и направлением
Выберите, на какой слог падает ударение в слове — ФАКСИМИЛЕ?
Слово состоит из букв:
В,
Е,
К,
Т,
О,
Р,
Похожие слова:
вектор-кардиография
векторе
векториальность
векториальный
векторный
конвектор
многовекторность
многовекторный
невекторный
псевдовектор
Рифма к слову вектор
архитектор, доктор, оратор, ритор, оператор, простор, император, аудитор, ефрейтор, берейтор, губернатор, сенатор, администратор, форейтор, импэратор, договор, собор, подбор, говор, напор, купор, коридор, колидор, упор, перебор, заговор, сговор, азор, майор, раздор, укор, тенор, вздор, гор, позор, топор, вор, сбор, свор, набор, узор, профессор, пор, рессор, выговор, двор, спор, разговор, бугор, выбор, приговор, шпор, дюпор, федор, уговор, обзор, кор, отпор, капор, прибор, забор, хведор
Толкование слова. Правильное произношение слова. Значение слова.
Вектор: определение и основные понятия
Определение вектора
Определение. Вектор — это направленный отрезок, то есть отрезок, имеющий длину и определенное направление. Графически вектора изображаются в виде направленных отрезков прямой определенной длины. (рис.1)
 |
| рис. 1 |
Обозначение вектора
Вектор началом которого есть точка А, а концом — точка В, обозначается AB (рис.1). Также вектора обозначают одной маленькой буквой, например a.
Длина вектора
Для обозначения длины вектора используются две вертикальные линии слева и справа |AB|.
Нулевой вектор
Определение. Нулевым вектором называется вектор, у которого начальная и конечная точка совпадают.
Нулевой вектор обычно обозначается как 0.
Длина нулевого вектора равна нулю.
Коллинеарные вектора
Определение. Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 2).
 |
| рис. 2 |
Сонаправленные вектора
Определение. Два коллинеарных вектора a и b называются сонаправленными векторами, если их направления совпадают: a↑↑b (рис. 3).
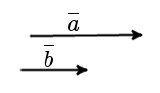 |
| рис. 3 |
Противоположно направленные вектора
Определение. Два коллинеарных вектора a и b называются противоположно направленными векторами, если их направления противоположны: a↑↓b (рис. 4).
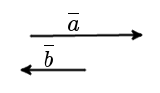 |
| рис. 4 |
Компланарные вектора
Определение. Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами. (рис. 5).
 |
| рис. 5 |
Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные.
Равные вектора
Определение. Вектора a и b называются равными, если они лежат на одной или параллельных прямых, их направления совпадают, а длины равны (рис. 6).
 |
| рис. 6 |
То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:
a = b, если a↑↑b и |a| = |b|.
Единичный вектор
Определение. Единичным вектором или ортом — называется вектор, длина которого равна единице.
Определение и обозначение вектора
Вектор в геометрии — это отрезок, для которого указано, какая из его граничных точек считается началом, а какая — концом. В некоторых учебниках вектор могут называть направленным отрезком.
Вектор обозначается одной строчной буквой латинского алфавита или двумя заглавными со стрелкой (в некоторых случаях — прямой линией) сверху.
Интересно, что порядок букв в названии вектора имеет значение! Первая буква отвечает за начало вектора, а последняя — за его конец. Поэтому
и
— абсолютно разные векторы.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Виды векторов
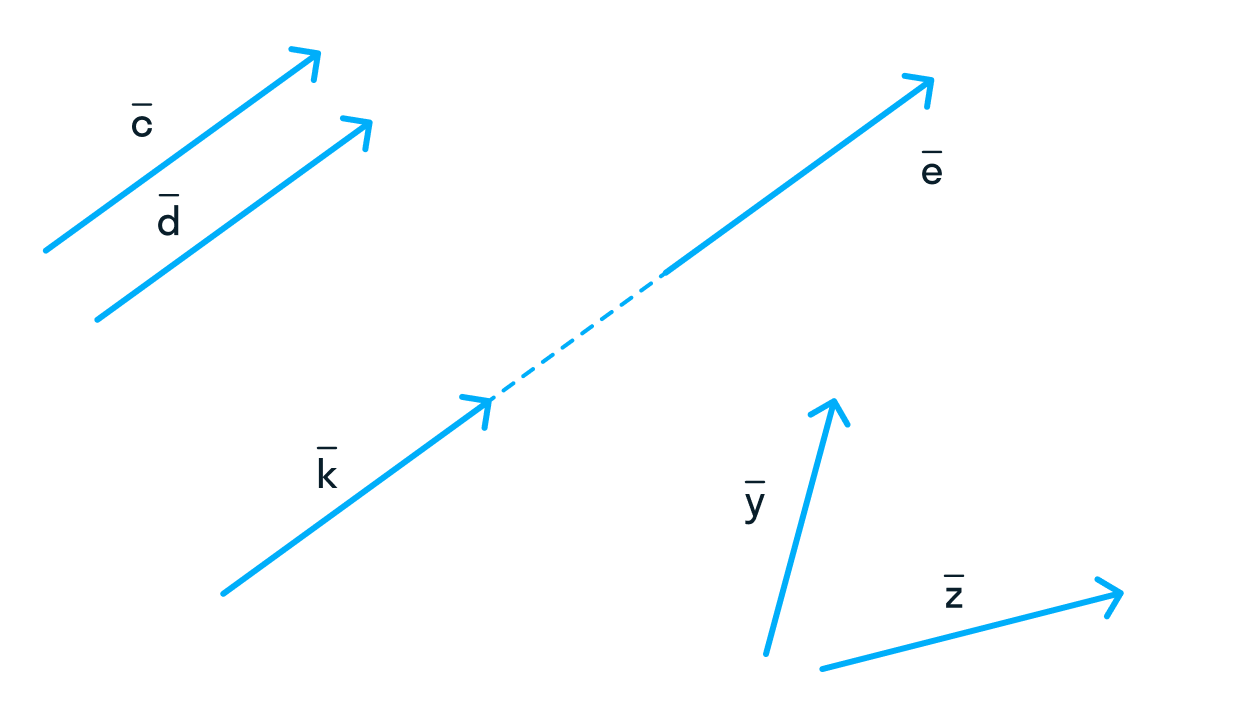
Во-первых, векторы бывают коллинеарными и неколлинеарными.
Коллинеарными называют те векторы, которые лежат на одной прямой или параллельных прямых. На рисунке
и
и
являются коллинеарными, а
и
относительно друг друга — нет.
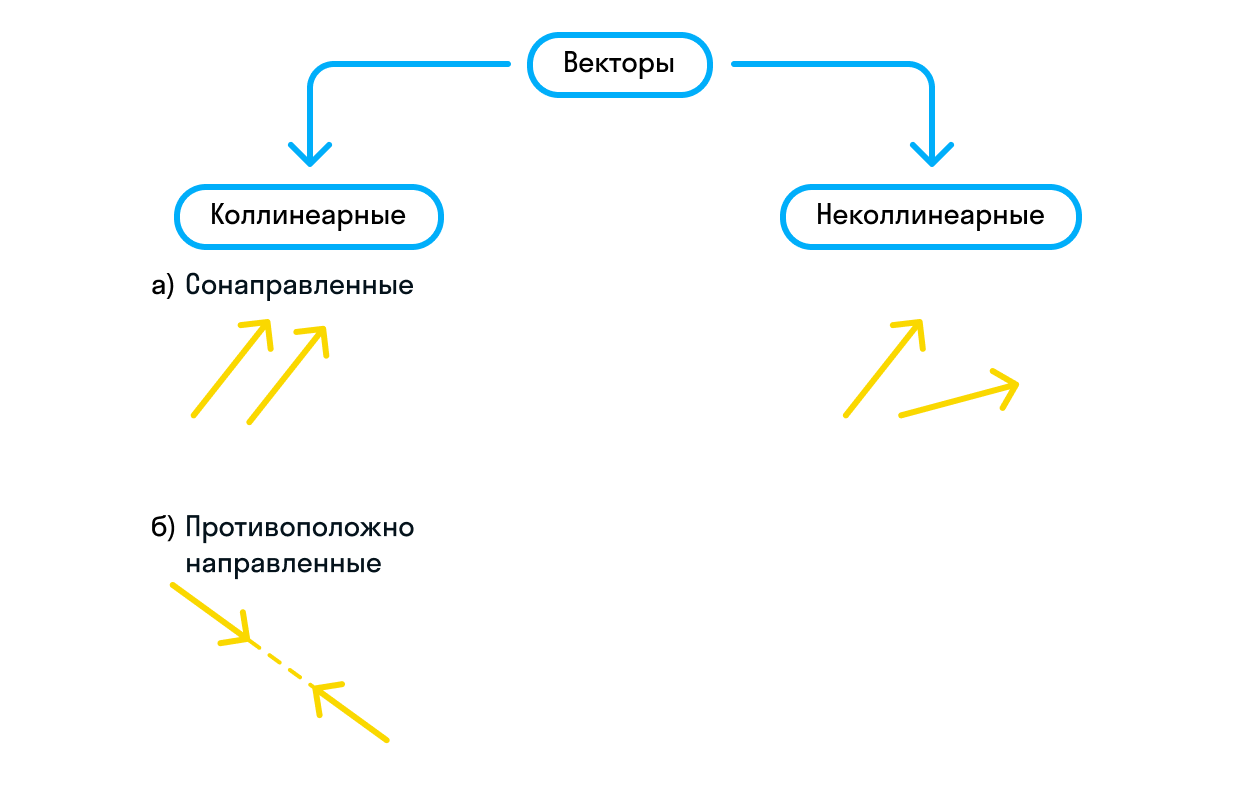
Векторы различаются и по направлению. Если векторы уже являются коллинеарными, они могут быть сонаправленными или противоположно направленными. Сонаправленные векторы обозначаются так:
Если же они противоположно направлены, мы можем записать это следующим образом:
Равными являются те векторы, которые одновременно и коллинеарны, и сонаправлены, а также имеют одинаковую длину.
Нулевой вектор — вектор, длина которого равна нулю. Чаще всего его обозначают так:
Он считается коллинеарным любому вектору.
Иногда в геометрии вводят дополнительные понятия, рассмотрим и их:
-
Закреплённый вектор — отрезок с упорядоченными концами: если С — точка начала вектора, а Е — точка конца, тогда
(это то, что мы понимаем под обычным вектором в школьной геометрии).
-
Свободный вектор — вектор, начало и конец которого не закреплены. Его можно перемещать как вдоль прямой, на которой он находится, так и параллельно этой прямой. По сути под свободным вектором понимают множество закреплённых векторов.
Сложение и вычитание векторов
Действия с векторами описываются и в алгебре, и в геометрии. Сегодня мы рассмотрим способы, благодаря которым можно сложить и вычесть векторы, не зная их координат.
Сложение: метод треугольника
Представим, что в пространстве заданы векторы
и
которые нам необходимо сложить. Эта задача особенно актуальна для физиков, поскольку такие векторные величины, как сила, часто приложены к одному и тому же телу. В таком случае возникает вопрос: а как же рассчитать результирующее действие всех этих сил?
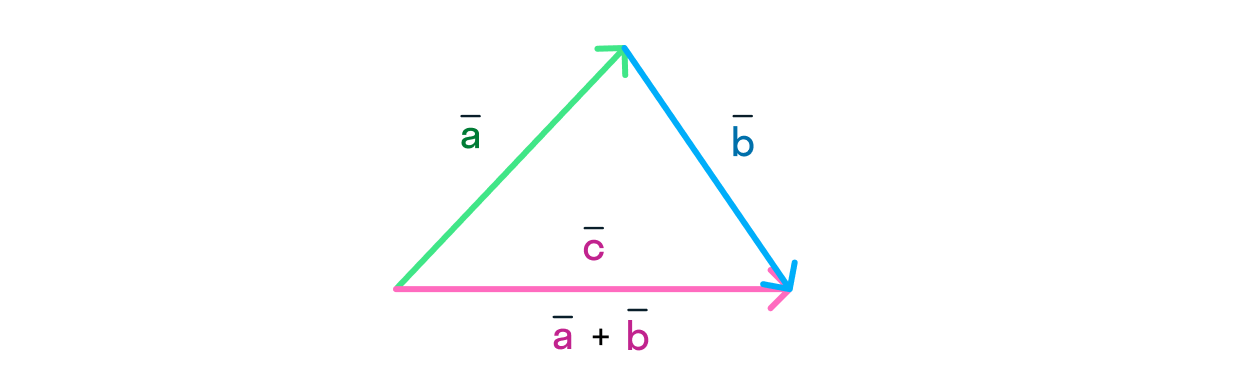
В этом на помощь физикам приходит математика — царица наук! Чтобы сложить два вектора, необходимо:
-
Отложить начало одного вектора от конца другого.
-
Вектор их суммы будет совпадать с вектором
, который соединяет начало вектора
с концом вектора
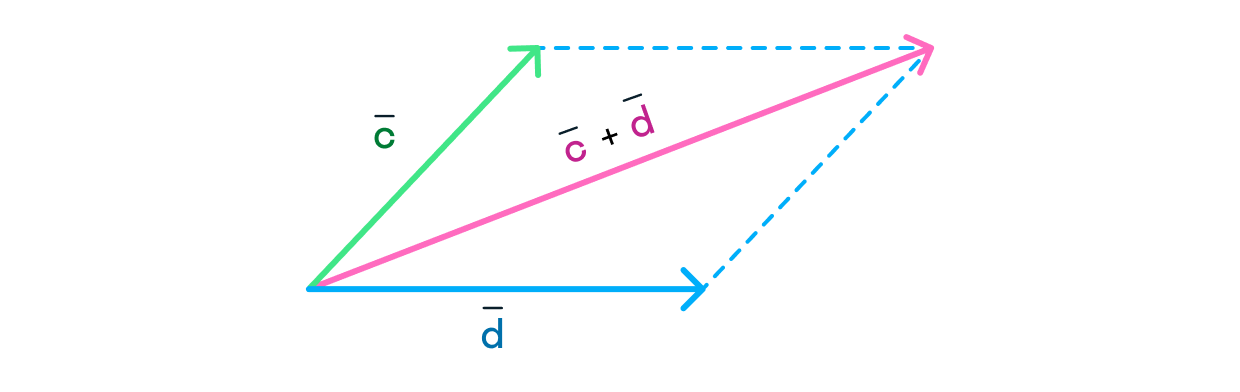
Сложение: метод параллелограмма
Сложить векторы можно и по-другому, используя метод параллелограмма:
-
Совместим между собой концы
и
-
Отложим от конца
вектор, равный
-
Отложим от конца
вектор, равный
-
Благодаря пунктам 2 и 3 мы получили параллелограмм (четырёхугольник, противоположные стороны которого параллельны и равны).
-
Проведём диагональ параллелограмма между
и
на которой будет лежать вектор, равный сумме
и
Задача решена, вы великолепны!
Обратите внимание
Как метод параллелограмма, так и метод треугольника подразумевает перемещение векторов в пространстве: мы или совмещаем их концы, или откладываем от конца одного вектора начало другого. Получить сумму векторов, не имеющих общей точки, с этими методами не представляется возможным.
Сложение: метод многоугольника
А что если векторов больше, чем два? На эту проблему математика уже подготовила решение: воспользуемся расширенным методом треугольника, который получил название «метод многоугольника».
Согласно этому методу мы последовательно совмещаем конец и начало векторов, а после изображаем суммирующий вектор, начало которого совпадает с началом первого вектора, а конец — с концом последнего. Лучше всего рассмотреть это на чертеже:
Вычитание векторов
Продолжаем проделывать с векторами всевозможные действия, на этот раз вычитание. Математики знают, что вычитание — это по своей сути то же сложение, но с обратным числом.
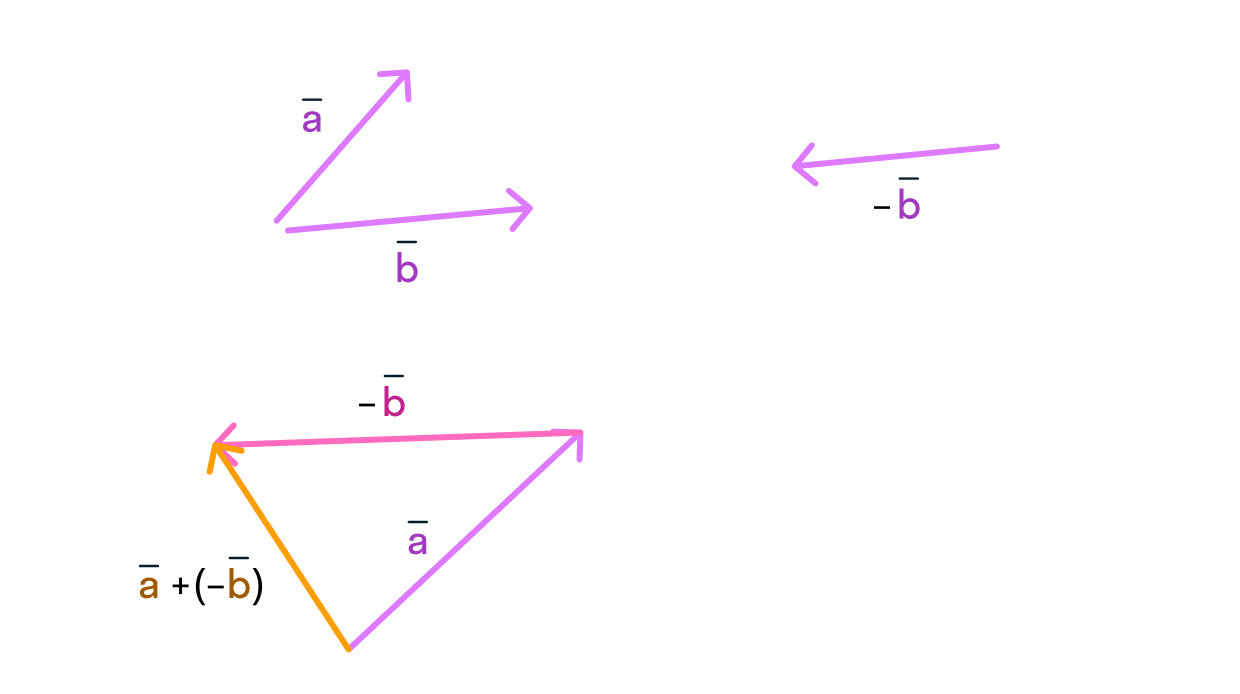
С векторами работает та же штука: вместо вычитания попробуем прибавить вектор, противоположно направленный исходному:
Изобразим разность векторов с помощью уже знакомого нам правила треугольника:
Боитесь запутаться в векторах сонаправленных и противоположно направленных?
Существует отдельное правило для их вычитания:
-
Отложим один вектор от начала другого.
-
Тогда вектор их разности совпадает с вектором, начало которого совмещено с концом вычитаемого вектора, а
начало — с концом уменьшаемого.
Этот метод схож и с методом параллелограмма, но в этом случае мы берём другую диагональ.
Координаты вектора на плоскости и в пространстве
Для выполнения остальных действий с векторами нам необходимо поместить их в такую систему координат, чтобы можно было
определить их положение относительно друг друга. Для этого используют декартову систему координат, которой можно
пользоваться как на плоскости с осями X и Y, так и в пространстве с осями
X, Y, Z.
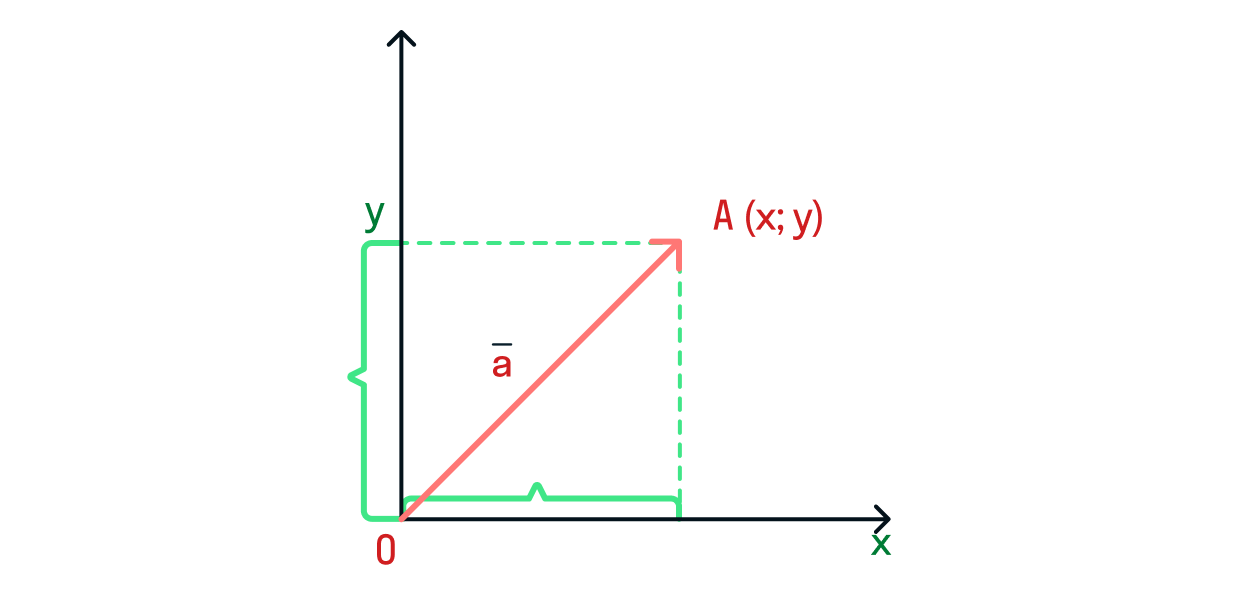
Тогда, если
находится на плоскости, его координаты можно выразить как
если в пространстве
—
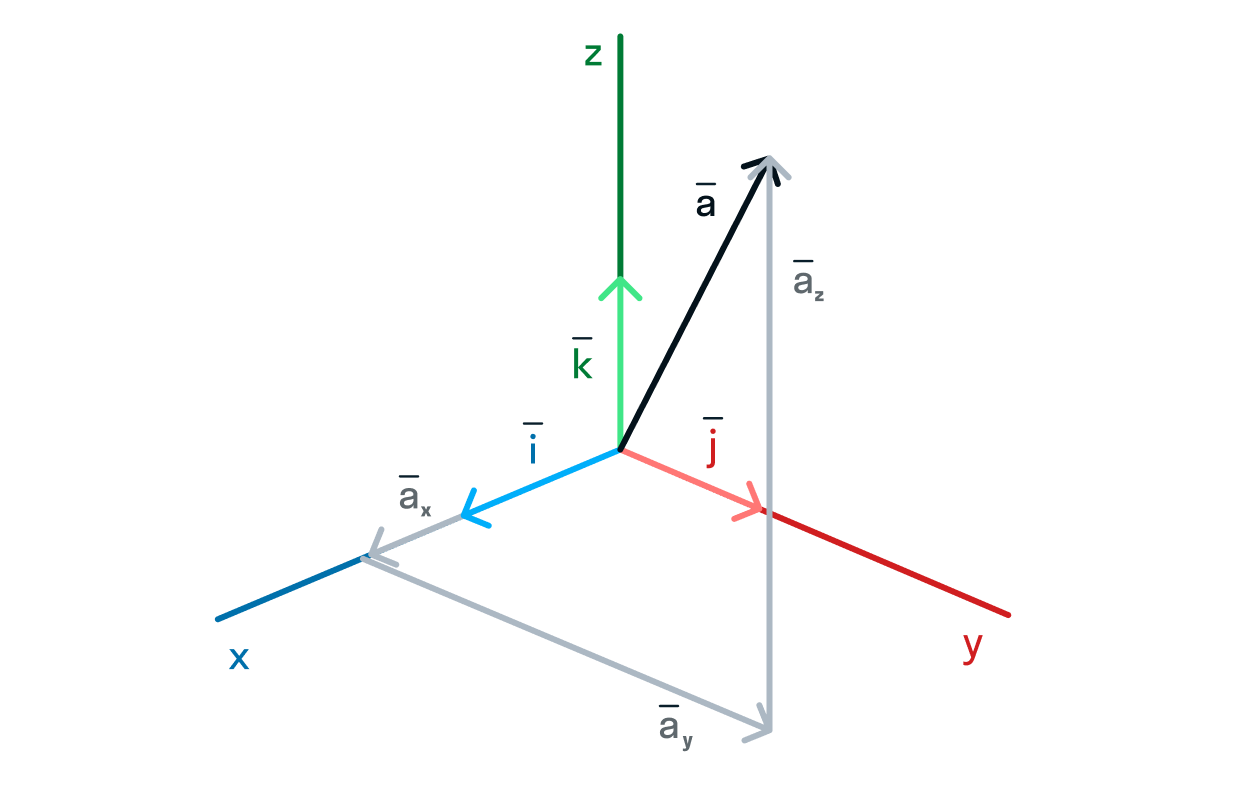
Базисные векторы — это векторы, каждый из которых направлен вдоль своей оси координат, в трёхмерном пространстве их обозначают
Любой вектор в трёхмерном пространстве можно разложить по трём базисным векторам.
с координатами
можно записать так:
Умножение вектора на число
Представьте, что нам необходимо растянуть вектор в два раза или же сжать, но уже в три. За все эти действия отвечает
одна простая задача: умножение вектора на число.
Для того чтобы увеличить или уменьшить вектор в некоторое количество раз, необходимо умножить все координаты вектора
на это число.
Таким образом, если
задан координатами
то
—
Кстати, подобным образом можно перевернуть вектор, направив его в противоположную сторону:
Длина вектора
Длина вектора — одно из основных понятий в этом разделе. И неудивительно, ведь она характеризует его протяженность в
пространстве и выражается числом.
Итак, длина вектора — это расстояние между его началом и концом. Её часто называют модулем, что
отражается и в обозначении. Если нам необходимо найти длину
мы так и запишем:
Длину вектора можно найти разными способами, вот основные:
-
через координаты вектора;
-
через координаты точек начала и конца вектора;
-
через теорему косинусов.
Давайте вместе разберём все методы!
Длина вектора через его координаты
Если
задан через координаты
то его длину можно найти как
Почему мы можем быть уверены, что эта формула правильная? Рассмотрим вектор
в декартовой системе координат.
Отложим вектор
от точки
с координатами
Тогда этот вектор можно назвать
, и так как мы строили его из
начала координат, координаты вектора могут быть найдены как
Рассчитаем длину
через теорему Пифагора:
Задача 1
Посчитайте, чему равен модуль
, если его координаты
Решение:
Модуль вектора — это его длина, а значит,
Задача 2
Длина
Чему равна координата по оси
, если координата по оси
Решение:
Длина вектора через координаты точек начала и конца
Для начала давайте вспомним, как задать координаты вектора через координаты его начала и конца.
Рассмотрим
где
и
Тогда координаты вектора можно выразить так:
Мы уже знаем, как найти длину вектора через его координаты, поэтому подставим полученное выражение в формулу:
Задача 3
Найдите длину
если
и
Решение:
Задача 4
Рассчитайте координату по
точки
вектора
, если его длина равна
а
Решение:
Остановимся здесь и подставим известные числа в формулу:
или
Длина вектора через теорему косинуса
К сожалению, в задачах не всегда даны координаты точек вектора или его самого. В таком случае мы воспользуемся
теоремой косинуса.
Давайте вспомним её формулировку.
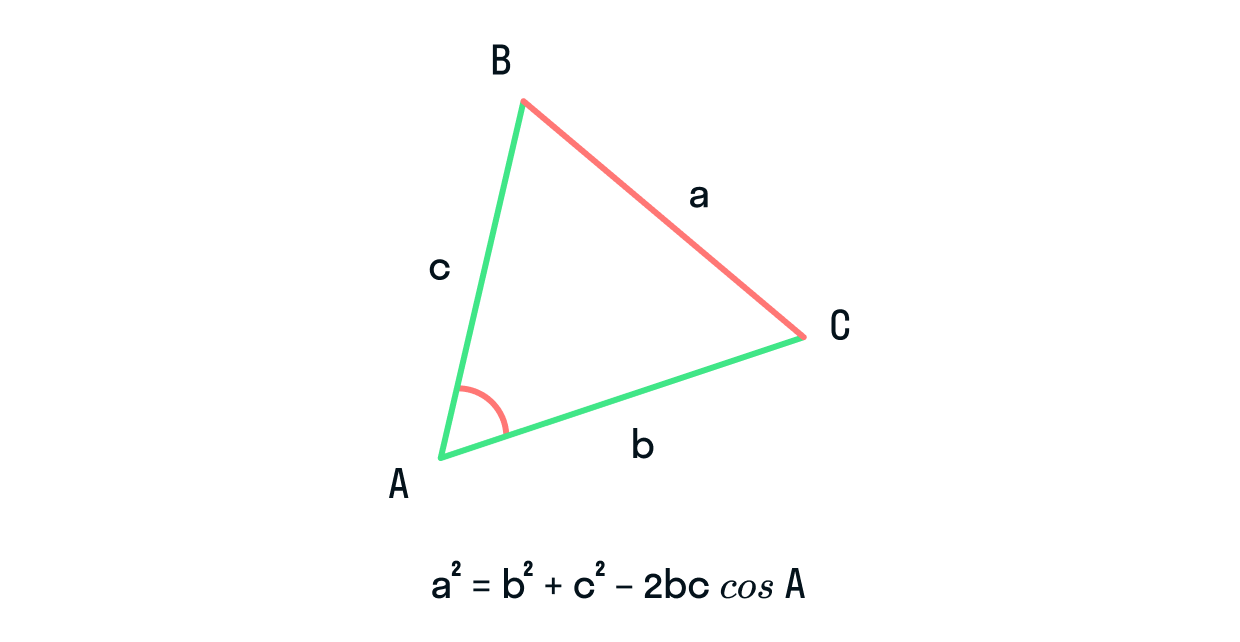
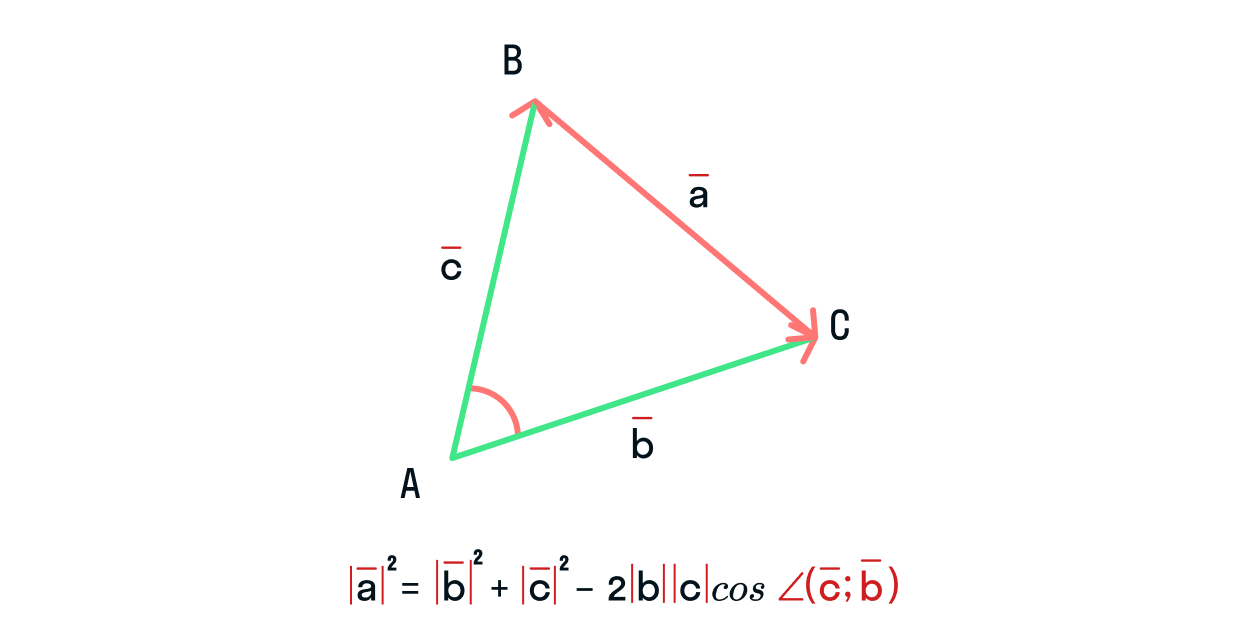
Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус
удвоенное произведение этих сторон на косинус угла между ними.
Формула теоремы косинусов:
Эту теорему можно применить и в векторной форме. Немного изменим рисунок:
Тогда, чтобы найти длину
, необходимо знать (или иметь возможность вычислить) длины
и
, знать угол между ними, а также уметь рассчитать произведение длин этих векторов.
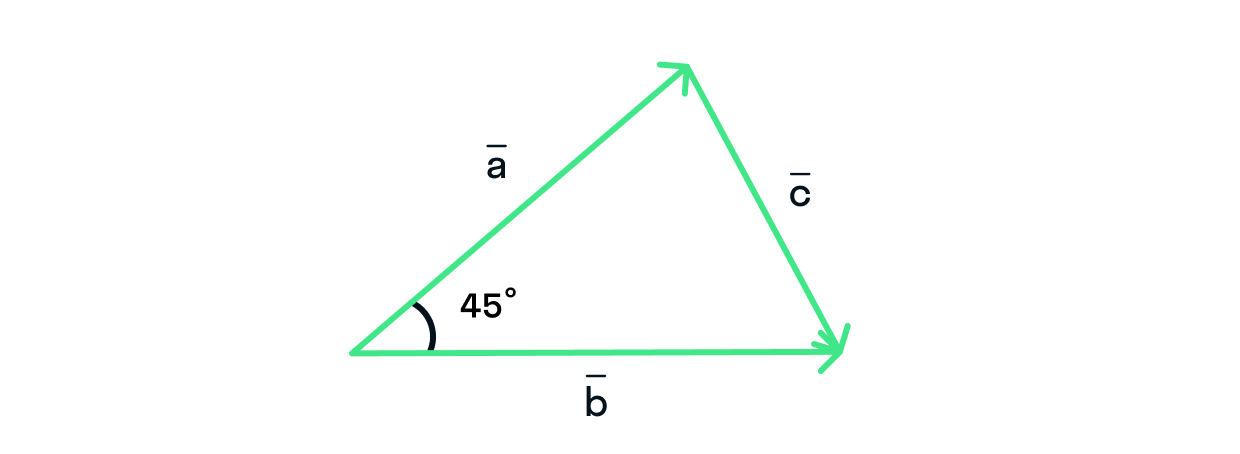
Задача 5
Длины
и
равны 4 и 6 соответственно, а угол между ними равен
Вычислите длину
Решение:
Задача 6
Рассчитайте модуль вектора
в треугольнике, если длина
= 8, длина
= 10, а угол между ними равен
Решение:
Скалярное произведение векторов
Мы практически дошли до финала нашего путешествия по царству векторов. 👑 Нам осталось изучить только скалярное
произведение векторов. Что это?
Скалярное произведение — это операция над двумя векторами, результатом которой является скаляр, то
есть число,
которое не зависит от выбора системы координат.
Скалярным произведением
и
будет скалярная величина, равная произведению модулей этих векторов, умноженная на
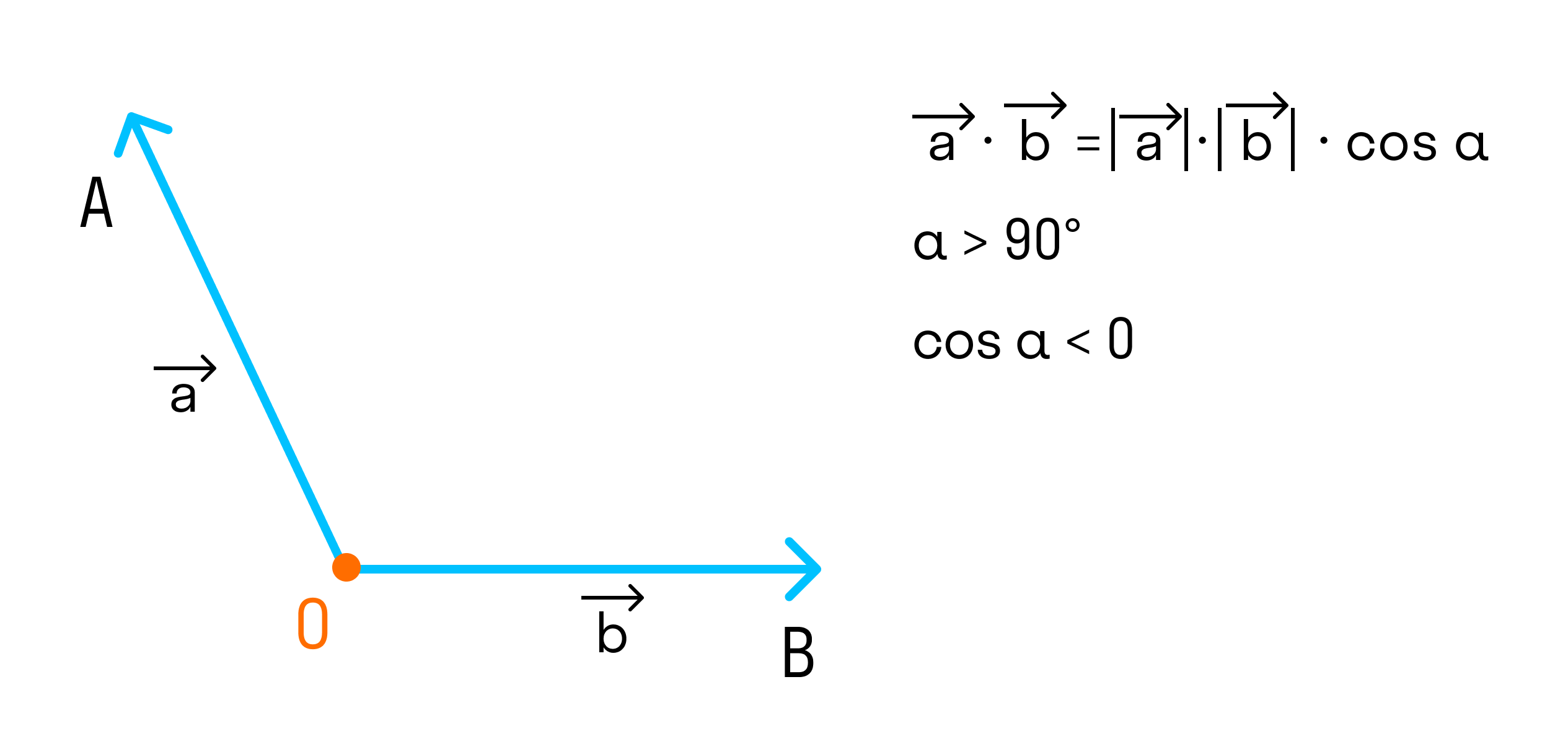
косинус угла между ними:
Вспомним, что в той же физике величины делятся на скалярные (не имеющие направления, например, масса) и векторные
(имеющие направление, например, сила, ускорение, скорость). В математике под вектором подразумевают направленный
отрезок, а понятие скаляра хоть и не равно, но очень близко к понятию числа.
Скалярное произведение показывает, насколько синхронизированы, скоординированы направления векторов. Так, чем больше
угол между векторами, тем меньше согласованности, а значит, скалярное произведение будет уменьшаться с ростом угла:
-
Скалярное произведение вектора на само себя равно квадрату его модуля:
В данном случае значение скалярного произведения является наибольшим из
возможных. -
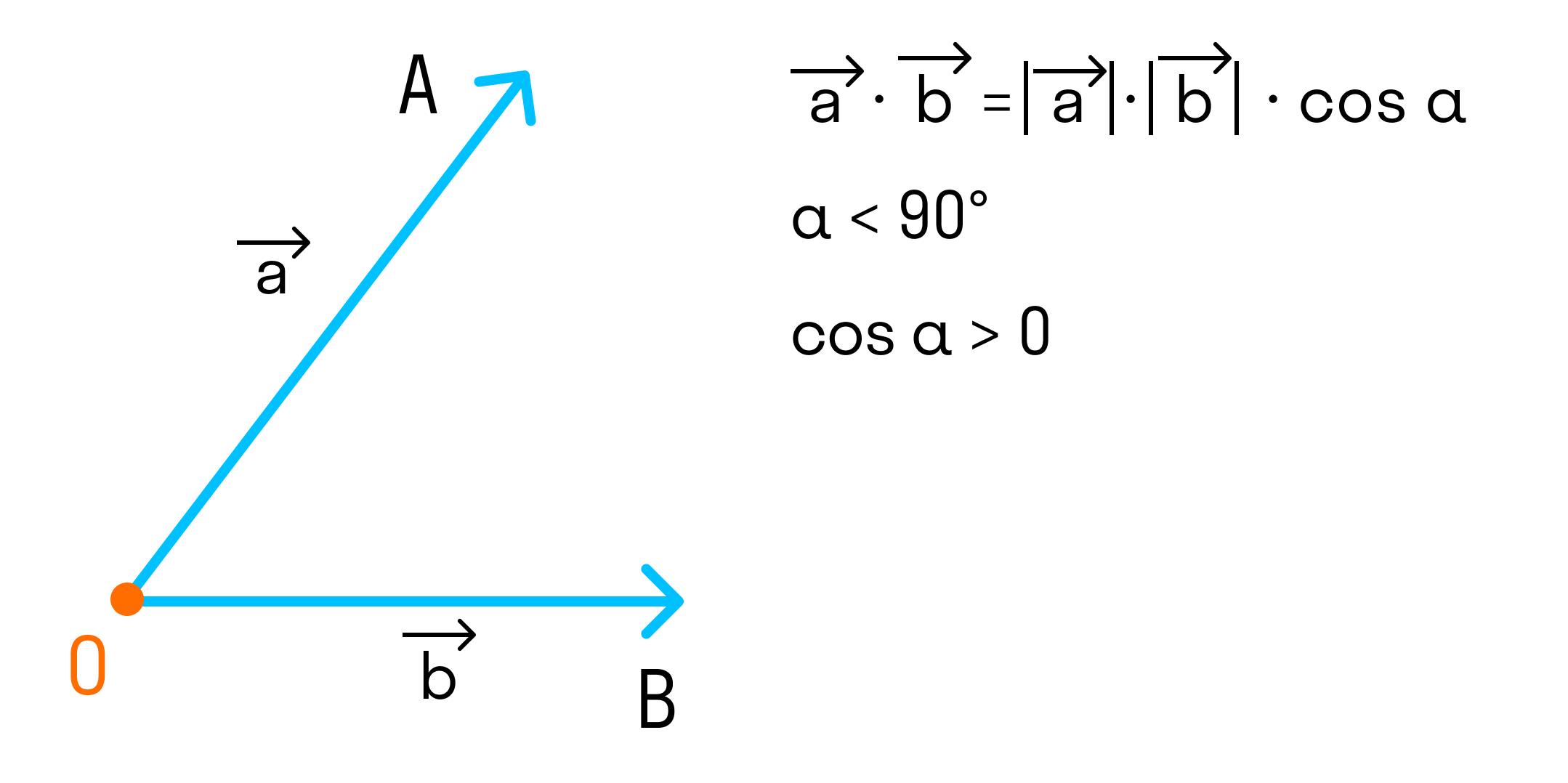
Если угол между векторами острый и векторы ненулевые, то скалярное произведение положительно, так как
-
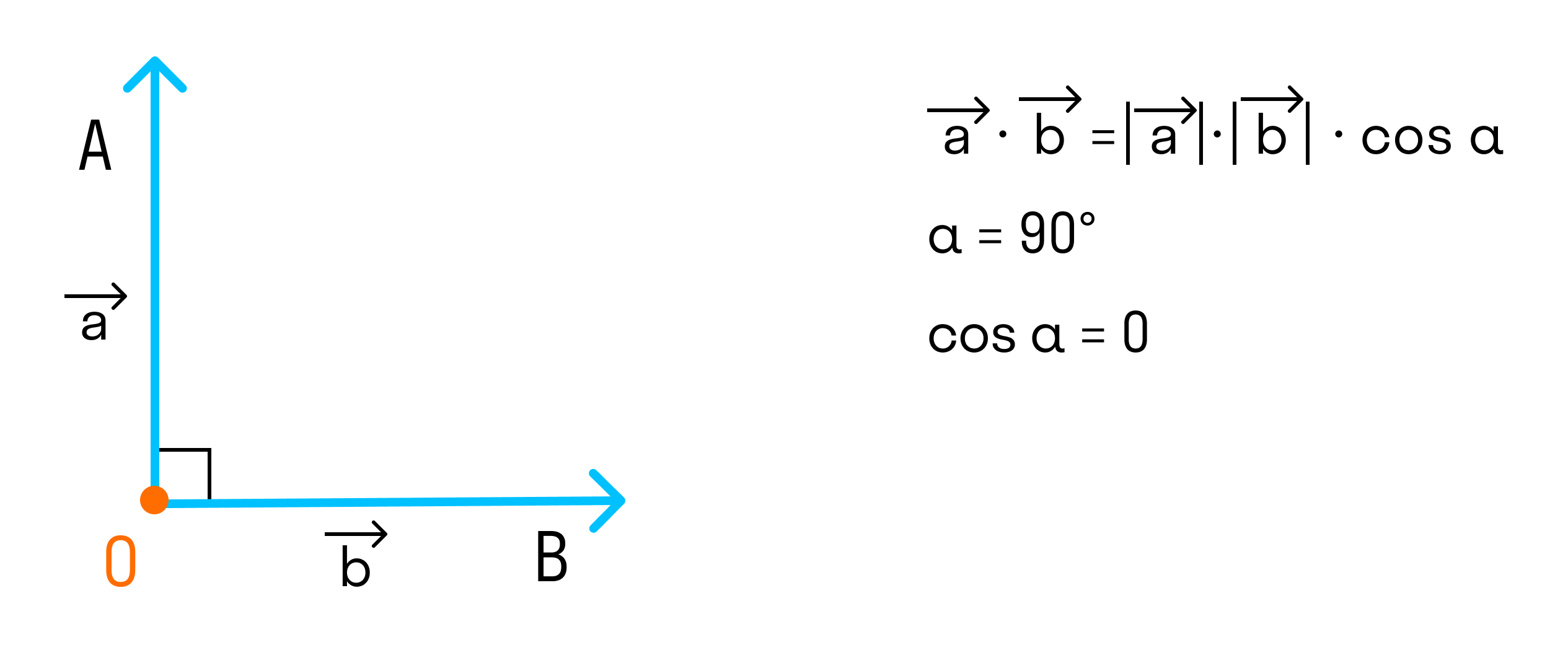
Если угол между векторами прямой, то скалярное произведение равно 0, так как
-
Если угол между векторами тупой и векторы ненулевые, то скалярное произведение отрицательно, так как
-
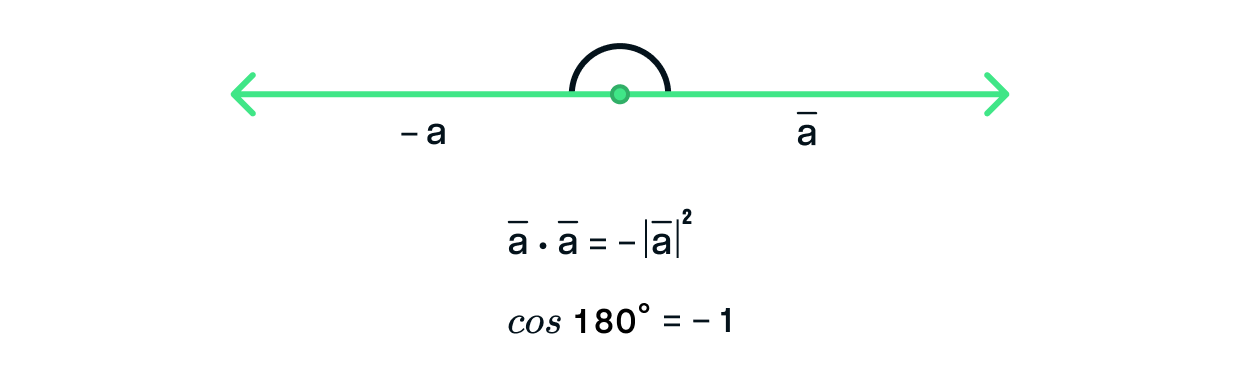
Cкалярное произведение вектора на противоположно направленный ему вектор равно отрицательному произведению их
длин . В данном случае значение скалярного произведения является наименьшим из возможных.
Конечно, вы можете возразить: «Согласованность направлений отлично показывает угол, для чего нам эти сложные
вычисления?». А всё дело в том, что в пространстве порой очень сложно измерить угол, а вот посчитать скалярное
произведение — просто, особенно если рассмотреть его через координаты.
Если
выражен координатами
а
то скалярное произведение этих векторов описывается формулой:
В пространстве скалярное произведение через координаты векторов будет задаваться так:
Где применяется скалярное произведение? Благодаря ему выполняется большое количество математических операций, таких
как нахождение угла между векторами и любых расстояний, если они заданы через координаты. Благодаря скалярному
произведению можно описать даже характеристику криволинейных поверхностей, но это мы обсудим как-нибудь в другой
раз. 🙂
Чтобы закрепить пройденный материал, нужно больше, чем пара заданий. Поэтом приглашаем на онлайн-уроки математики в
школу Skysmart. За короткое время благодаря особенной платформе и учителям-профессионалам вы сможете улучшить
школьные отметки, подготовиться к экзаменам и олимпиадам, и самое главное — понять и полюбить математику.
Вектор. Определение и основные понятия
Вектор — это направленный отрезок, то есть отрезок, имеющий длину и определенное направление. Графически вектора изображаются в виде направленных отрезков прямой определенной длины.
Обозначение вектора
Вектор началом которого есть точка ( A ) , а концом — точка ( B ) , обозначается ( vec ) . Также вектора обозначают одной маленькой буквой, например ( vec )
Направление вектора (от начала к концу) на рисунках отмечается стрелкой.
Длина вектора
Для обозначения длины вектора используются две вертикальные линии слева и справа ( left| vec right| ) .
Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора ( left| vec right| ) .
Нулевой вектор
Нулевой вектор обычно обозначается как ( vec <0>) .
Длина нулевого вектора равна нулю.
Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают, и он не имеет какого-либо определенного направления.
Нулевым вектором называется вектор, у которого начальная и конечная точка совпадают.
Длина вектора на плоскости
Длина вектора в трехмерном пространстве
Длина вектора в n-мерном пространстве
Коллинеарные вектора
Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами
Сонаправленные вектора
Противоположно направленные вектора
Компланарные вектора
Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами.
Равные вектора
То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
О сайте
На нашем сайте вы найдете множество полезных калькуляторов, конвертеров, таблиц, а также справочных материалов по основным дисциплинам.
Самый простой способ сделать расчеты в сети — это использовать подходящие онлайн инструменты. Воспользуйтесь поиском, чтобы найти подходящий инструмент на нашем сайте.
calcsbox.com
На сайте используется технология LaTeX.
Поэтому для корректного отображения формул и выражений
пожалуйста дождитесь полной загрузки страницы.
© 2022 Все калькуляторы online
Копирование материалов запрещено
Вектор: определение и основные понятия
Определение вектора
 |
| рис. 1 |
Обозначение вектора
Вектор началом которого есть точка А, а концом — точка В, обозначается AB (рис.1). Также вектора обозначают одной маленькой буквой, например a .
Длина вектора
Для обозначения длины вектора используются две вертикальные линии слева и справа | AB |.
Нулевой вектор
Нулевой вектор обычно обозначается как 0 .
Длина нулевого вектора равна нулю.
Коллинеарные вектора
 |
| рис. 2 |
Сонаправленные вектора
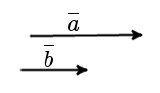 |
| рис. 3 |
Противоположно направленные вектора
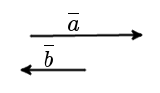 |
| рис. 4 |
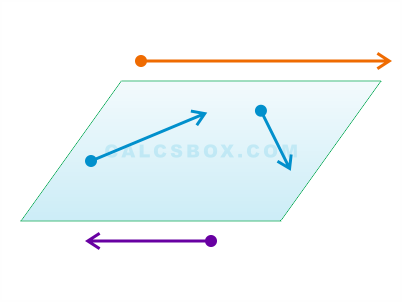
Компланарные вектора
 |
| рис. 5 |
Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные.
Равные вектора
 |
| рис. 6 |
То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:
a = b , если a ↑↑ b и | a | = | b |.
Единичный вектор
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Векторы на плоскости и в пространстве — основные определения
Определение вектора
В статье пойдет речь о том, что такое вектор, что он из себя представляет в геометрическом смысле, введем вытекающие понятия.
Для начала дадим определение:
Вектор – это направленный отрезок прямой.
Исходя из определения, под вектором в геометрии отрезок на плоскости или в пространстве, который имеет направление, и это направление задается началом и концом.
В математике для обозначения вектора обычно используют строчные латинские буквы, однако над вектором всегда ставится небольшая стрелочка, например a → . Если известны граничные точки вектора – его начало и конец, к примеру A и B , то вектор обозначается так A B → .
Нулевой вектор
Под нулевым вектором 0 → будем понимать любую точку плоскости или пространства.
Из определения становится очевидным, что нулевой вектор может иметь любое направление на плоскости и в пространстве.
Длина вектора
Под длиной вектора A B → понимается число, большее либо равное 0, и равное длине отрезка АВ.
Длину вектора A B → принято обозначать так A B → .
Понятия модуль вектора и длина вектора равносильны, потому что его обозначение совпадает со знаком модуля. Поэтому длину вектора также называют его модулем. Однако грамотнее использовать термин «длина вектора». Очевидно, что длина нулевого вектора принимает значение ноль.
Коллинеарность векторов
Два вектора лежащие на одной прямой или на параллельных прямых называются коллинеарными.
Два вектора не лежащие на одной прямой или на параллельных прямых называются неколлинеарными.
Следует запомнить, что Нулевой вектор всегда коллинеарен любому другому вектору, так как он может принимать любое направление.
Коллиниарные векторы в свою очередь тоже можно разделить на два класса: сонаправленные и противоположно направленные.
Направление векторов
Сонаправленными векторами называют два коллинеарных вектора a → и b → , у которых направления совпадают, такие векторы обозначаются так a → ↑ ↑ b → .
Противоположно направленными векторами называются два коллинеарных вектора a → и b → , у которых направления не совпадают, т.е. являются противоположными, такие векторы обозначаются следующим образом a → ↑ ↓ b → .
Считается, что нулевой вектор является сонаправленым к любым другим векторам.
Равные и противоположные векторы
Равными называются сонаправленные вектора, у которых длины равны.
Противопожными называются противоположно направленные вектора, у которых их длины равны.
Введенные выше понятия позволяют нам рассматривать векторы без привязки к конкретным точкам. Иначе говоря, можно заменить вектор равным ему вектором, отложенным от любой точки.
Пусть заданы два произвольных вектора на плоскости или в пространстве a → и b → . Отложим от некоторой точки O плоскости или пространства векторы O A → = a → и O B → = b → . Лучи OA и OB образуют угол ∠ A O B = φ .
Углы между векторами
Угол φ = ∠ A O B называется углом между векторами a → = O A → и b → = O B → .
Очевидно, что угол между сонаправленными векторами равен нулю градусам (или нулю радиан), так как сонаправленные векторы лежат на одной или на параллельных прямых и имеют одинаковое направление, а угол между противоположно направленными векторами равен 180 градусам (или π радиан), так как противоположно направленные векторы лежат на одной или на параллельных прямых, но имеют противоположные направления.
Перпендикулярными называются два вектора, угол между которыми равен 90 градусам (или π 2 радиан).
источники:
http://ru.onlinemschool.com/math/library/vector/vector-definition/
http://zaochnik.com/spravochnik/matematika/vektory/vectory_na_ploskosti_i_v_prostranstve/
Нуль-вектор
- Нуль-вектор
-
Нулевой вектор (нуль-вектор) — вектор, начало которого совпадает с его концом. Нулевой вектор имеет норму 0 и обозначается
или
.
Нулевой вектор определяет такое перемещением пространства, при котором каждая точка пространства переходит в себя, другими словами: нулевой вектор — тождественное преобразование пространства.
С нулевым вектором не связывают никакого направления в пространстве (т.е. его можно считать направленным во все стороны). Нулевой вектор принято считать сонаправленным любому вектору. Считается, что нулевой вектор одновременно параллелен и перпендикулярен любому вектору пространства.
Все координаты нулевого вектора в любой аффинной системе координат равны нулю.
Для любого вектора
Для любого числа c
Нулевой вектор равен сумме любых двух противоположных векторов:
.
См. также
Ссылки
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое «Нуль-вектор» в других словарях:
-
нуль-вектор — нуль вектор, нуль вектора … Орфографический словарь-справочник
-
нуль-вектор — nulinis vektorius statusas T sritis fizika atitikmenys: angl. null vector; zero vector vok. Nullvektor, m rus. нулевой вектор, m; нуль вектор, m pranc. vecteur nul, m; vecteur zéro, m … Fizikos terminų žodynas
-
нуль-вектор — (2 м), Р. нуль ве/ктора … Орфографический словарь русского языка
-
нуль-вектор — а, ч., мат. Вектор, що є тотожним перетворенням простору … Український тлумачний словник
-
Вектор (математика) — Вектор У этого термина существуют и другие значения, см. Вектор … Википедия
-
Нуль — Нуль: В Викисловаре есть статья «нуль» Нуль, 0 (число) целое число, разделяющее на числовой прямой положительные и отрицательные числа … Википедия
-
Вектор-функция — Вектор функция функция, значениями которой являются векторы в векторном пространстве двух, трёх или более измерений. Аргументами функции могут быть: одна скалярная переменная тогда значения вектор функции определяют в некоторую… … Википедия
-
ВЕКТОР — В физике и математике вектор это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент,… … Энциклопедия Кольера
-
Вектор Киллинга — Поле Киллинга векторное поле скоростей (локальной) однопараметрической группы движений риманова или псевдориманова многообразия. Другими словами, поток, который генерируется векторным полем Киллинга, задает непрерывное однопараметрическое… … Википедия
-
Нулевой вектор — (нуль вектор) вектор, начало которого совпадает с его концом. Нулевой вектор имеет норму 0 и обозначается или . Нулевой вектор определяет тождественное движение пространства, при котором каждая точка пространства переходит в себя. С нулевым… … Википедия
Нулевой вектор (нуль-вектор)
Предмет
Высшая математика
Разместил
🤓 MarlGrul
👍 Проверено Автор24
вектор, длина которого равна нулю, а направление не определено; нулевой элемент θ векторного пространства
Научные статьи на тему «Нулевой вектор (нуль-вектор)»
Скалярное произведение векторов
них является нулевым вектором, тогда угол между векторами равен $0^0$….
в двух случаях:
Если один из векторов будет нулевым вектором (Так как тогда его длина равна нулю)….
Отметим также, что скалярное произведение больше нуля, если угол между этими векторами острый (так как…
Пусть один из векторов будет нулевым вектором. К примеру, $overrightarrow{a}=(0,0)$….
не будут нулевыми векторами.

Статья от экспертов
Операторы типа набла: поверхностный, нулевой и мнимый нулевой
Вводится понятие о слагаемых векторных произведений, которыми являются первая или ортоположительная часть и вторая или ортоотрицательная часть; дальнейшим развитием этого понятия является представление о сопряженных векторах, векторном дифференциальном поверхностном операторе, поверхностном градиенте, производной по поверхности, поверхностных дивергенции и роторе. Рассматриваются поверхностные функции, их поверхностное дифференцирование и интегрирование. Показаны особенности поверхностных функций, для которых все слагаемые являются функциями не менее чем двух переменных, кроме того, поверхностные функции имеют смешанные частные производные второго порядка, при этом, по крайней мере, одна из смешанных частных производных второго порядка от любого слагаемого не обращается в нуль. Доказывается теорема о восстановлении поверхностной функции по ее поверхностному градиенту. Вводится понятие о линейной комбинации координат и ее делении на вектор, нулевом и мнимом нулевом векторных оператор…
Алгоритмы вычислительной геометрии
Каждую точку в пространстве тоже можно рассматривать как вектор, но подобный вектор считается нулевым…
Начало и конец нулевого вектора являются совпадающими, и такой вектор не обладает каким-либо определенным…
Автор24 — интернет-биржа студенческих работ
Соответственно, длина нулевого вектора равняется нулю….
Нулевой вектор может считаться сонаправленным с любым из векторов….
Когда оно равняется нулю, то это означает, что векторы являются коллинеарными, что означает, что все

Статья от экспертов
Поверхностные градиент, дивергенция и ротор
Вводится понятие о слагаемых векторных произведений, которыми являются первая, или ортоположительная часть и вторая, или ортоотрицательная часть; дальнейшим развитием этого понятия является представление о сопряженных векторах, векторном дифференциальном поверхностном операторе, поверхностном градиенте, производной по поверхности, поверхностных дивергенции и роторе. Рассматриваются поверхностные функции, их поверхностное дифференцирование и интегрирование. Показаны особенности поверхностных функций, для которых все слагаемые являются функциями не менее чем двух переменных, кроме того, поверхностные функции имеют смешанные частные производные второго порядка, при этом, по крайней мере, одна из смешанных частных производных второго порядка от любого слагаемого не обращается в нуль. Доказывается теорема о восстановлении поверхностной функции по ее поверхностному градиенту. Вводится понятие о линейной комбинации координат и ее делении на вектор, нулевом и мнимом нулевом векторных операт…
Повышай знания с онлайн-тренажером от Автор24!
- Напиши термин
- Выбери определение из предложенных или загрузи свое
-
Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных
карточек
- Главная
- Справочник
- Геометрия
- Вектора
- Вектор. Определение и основные понятия
Вектор. Определение и основные понятия
- Обозначение вектора
- Длина вектора
- Нулевой вектор
- Длина вектора на плоскости
- Длина вектора в трехмерном пространстве
- Длина вектора в n-мерном пространстве
- Коллинеарные вектора
- Сонаправленные вектора
- Противоположно направленные вектора
- Компланарные вектора
- Равные вектора
Вектор — это направленный отрезок, то есть отрезок, имеющий длину и определенное направление. Графически вектора изображаются в виде направленных отрезков прямой определенной длины.
Обозначение вектора
Вектор началом которого есть точка , а концом — точка , обозначается . Также вектора обозначают одной маленькой буквой, например
Направление вектора (от начала к концу) на рисунках отмечается стрелкой.
Длина вектора
Для обозначения длины вектора используются две вертикальные линии слева и справа .
Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора .
Нулевой вектор
Нулевой вектор обычно обозначается как .
Длина нулевого вектора равна нулю.
Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают, и он не имеет какого-либо определенного направления.
Нулевым вектором называется вектор, у которого начальная и конечная точка совпадают.
Длина вектора на плоскости
Длина вектора в трехмерном пространстве
Длина вектора в n-мерном пространстве
Коллинеарные вектора
Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами
Сонаправленные вектора
Два коллинеарных вектора и называются сонаправленными векторами, если их направления совпадают:
Противоположно направленные вектора
Два коллинеарных вектора и называются противоположно направленными векторами, если их направления совпадают:
Компланарные вектора
Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами.
Равные вектора
Вектора и называются равными, если они лежат на одной или параллельных прямых, их направления совпадают, а длины равны.
То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:
, если и .
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
-
Координатами вектора называются проекции вектора на оси координат
-
Суммой двух векторов a и b называется третий вектор c, проведенный из начала a к концу b, если начало вектора b совпадает с концом вектора a. Разностью двух векторов a и b называется вектор c при условии: c = a − b, если c + b =a.
-
Декартовы координаты — система координат, состоящая из двух перпендикулярных осей.
-
Произведением вектора u≠0 на число λ≠0 называется вектор w, модуль которого равен |λ||u|, направление которого совпадает с вектором u при λ>0 и противоположно ему при λ<0.
-
Скалярным произведением векторов u и v называется произведение их модулей на косинус угла между ними.
-
Векторным произведением векторов u и v называется третий вектор w, модуль которого равен произведению модулей векторов u и v на синус угла θ между ними и перпендикулярен им.
-
Смешанным произведением трех векторов u, v и w называется скалярное произведение вектора u на векторное произведение векторов v и w
-
Вес одного литра воды примерно 998,5 грамм.
-
1 ом представляет собой электрическое сопротивление между двумя точками проводника, когда постоянная разность потенциалов 1 вольт, приложенная к этим точкам, создаёт в проводнике ток 1 ампер, а в проводнике не действует какая-либо электродвижущая сила.
-
В «современном» латинском алфавите 26 букв.
-
В равных объемах газов (V) при одинаковых условиях (температуре Т и давлении Р) содержится одинаковое число молекул.
-
1 чайная ложка, 5 мл жидкости это приблизительно 5 грамм
-
Создать бесплатно пароль любой длины и уровня сложности для ваших приложений, аккаунтов, соц. сетей, паролей к Windows, зашифрованным архивам и т.д.







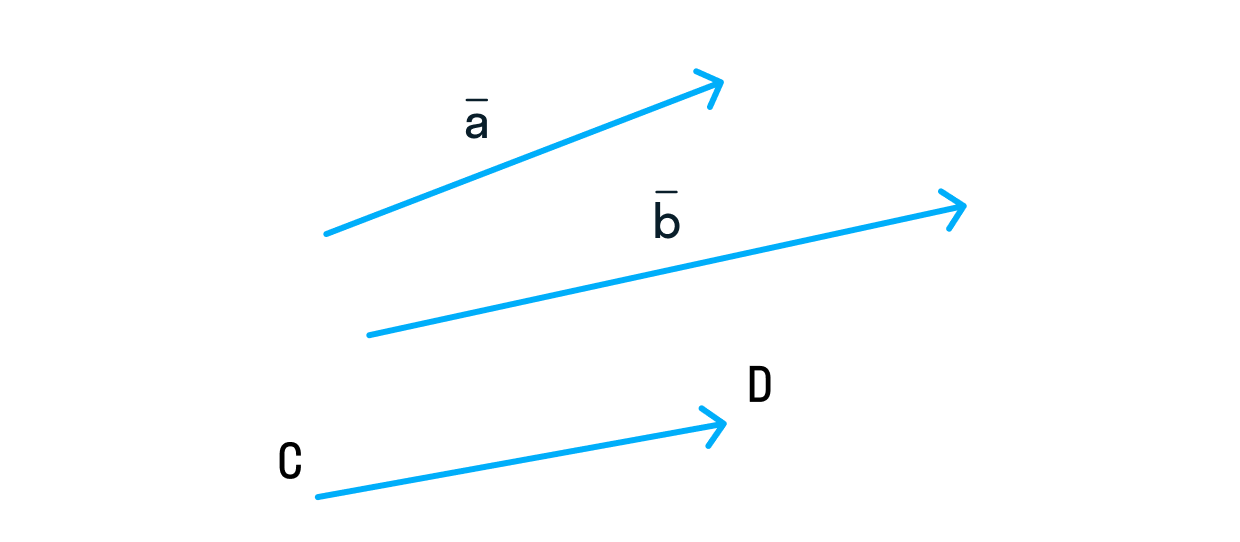









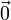 или
или 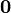 .
.
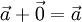
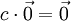
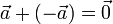 .
.