Плотность воздуха как пишется - Правописание и грамматика

Плотность воздуха — масса газа атмосферы Земли на единицу объема или удельная масса воздуха при естественных условиях. Величина плотности воздуха является функцией от высоты производимых измерений, от его температуры и влажности. Обычно стандартной величиной считается значение 1,225 ^кг⁄_м³, которая соответствует плотности сухого воздуха при 15°С на уровне моря.

Содержание

1 Взаимосвязи в пределах модели идеального газа
- 1.1 Температура, давление и плотность
- 1.2 Влияние влажности воздуха
- 1.3 Влияние высоты над уровнем моря в тропосфере
2 См. также
3 Примечания
4 Ссылки

Взаимосвязи в пределах модели идеального газа

Влияние температуры на свойства воздуха на ур. моря
Температура	Скорость звука	Плотность воздуха (из ур. Клапейрона)	Акустическое сопротивление
, С	c, м·сек⁻¹	ρ, кг·м⁻³	Z, Н·сек·м⁻³
+35	351,96	1,1455	403,2
+30	349,08	1,1644	406,5
+25	346,18	1,1839	409,4
+20	343,26	1,2041	413,3
+15	340,31	1,2250	416,9
+10	337,33	1,2466	420,5
+5	334,33	1,2690	424,3
±0	331,30	1,2920	428,0
-5	328,24	1,3163	432,1
-10	325,16	1,3413	436,1
-15	322,04	1,3673	440,3
-20	318,89	1,3943	444,6
-25	315,72	1,4224	449,1

Температура, давление и плотность

Плотность сухого воздуха может быть вычислена с использованием уравнения Менделеева-Клайперона для идеального газа при заданных температуре и давлении:

$rho = frac{p cdot M}{R cdot T} ,$

Здесь ρ — плотность воздуха, M — молярная масса (29-для сухого воздуха),p — абсолютное давление, R — универсальная газовая постоянная, T — абсолютная температура в Кельвинах. Таким образом подстановкой получаем:

при стандартной атмосфере Международного союза теоретической и прикладной химии (температуре 0 °С, давлении 100 кПа, нулевой влажности) плотность воздуха 1,2754 ^кг⁄_м³;
при 20 °C, 101,325 кПа и сухом воздухе плотность атмосферы составляет 1,2041 ^кг⁄_м³.

В приведенной таблице даны различные параметры воздуха, вычисленные на основании соответствующих элементарных формул, в зависимости от температуры (давление взято за 101,325 кПа )

Влияние влажности воздуха

Под влажностью понимается наличие в воздухе газообразного водяного пара, парциальное давление которого не превосходит давления насыщенного пара для данных атмосферных условий. Добавление водяного пара в воздух приводит к уменьшению его плотности, что объясняется более низкой молярной массой воды (18 ^гр⁄_мол) по сравнению с молярной массой сухого воздуха (29 ^гр⁄_мол).^[1] Влажный воздух может рассматриваться как смесь идеальных газов, комбинация плотностей каждого из которых позволяет получить требуемое значение для их смеси.^[2] Подобная интерпретация позволяет определение значения плотности с уровнем ошибки менее 0,2% в диапазоне температур от −10 °C до 50 °C и может быть выражена следующим образом:^[2]

$rho_{,mathrm{humid~air}} = frac{p_{d}}{R_{d} cdot T} + frac{p_{v}}{R_{v} cdot T} ,$

где $rho_{,mathrm{humid~air}}$ — плотность влажного воздуха (^кг⁄_м³); $p_{d}$ — парциальное давление сухого воздуха (Па); $R_{d}$ — газовая постоянная для сухого воздуха (287,058 ^Дж⁄_(кг·К)); — температура (K); $p_{v}$ — давление водяного пара (Па) и $R_{v}$ — постоянная для пара (461,495 ^Дж⁄_(кг·К)). Давление водяного пара может быть определено исходя из относительной влажности:

$p_{v} = phi cdot p_{mathrm{sat}} ,$

где $p_{v}$ — давление водяного пара; phi — относительная влажность и $p_{mathrm{sat}}$ — парциальное давление насыщенного пара, последнее может быть представлено в виде следующего упрощенного выражения:^[2]

$p(mb)_{mathrm{sat}} = 6.1078 cdot 10^{frac{7.5 cdot T-2048.625}{T-35.85}}$

которое дает результат в миллибарах. Давление сухого воздуха $p_{d}$ определяется простой разницей:

$p_{d} = p-p_{v} ,$

где обозначает абсолютное давление рассматриваемой системы.

Влияние высоты над уровнем моря в тропосфере

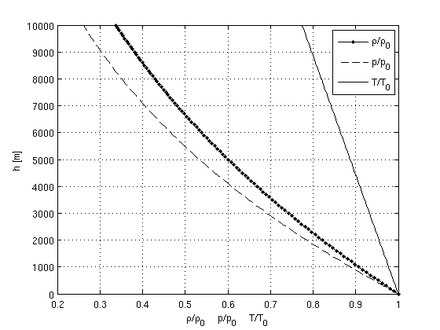
Зависимость давления, температуры и плотности воздуха от высоты по сравнению со стандартной атмосферой (p₀=101325 Па, T₀=288,15 K, rho_0 =1,225 кг/м³).

Для вычисления плотности воздуха на определенной высоте в тропосфере могут использоваться следующие параметры (в параметрах атмосферы указано значение для стандартной атмосферы):

стандартное атмосферное давление на уровне моря — p₀ = 101325 Па;
стандартная температура на уровне моря — T₀ = 288,15 K;
ускорение свободного падения над поверхностью Земли — g = 9,80665 ^м⁄_сек² (при данных вычислениях считается независимой от высоты величиной);
скорость падения температуры (англ.)русск. с высотой, в пределах тропосферы — L = 0,0065 ^K⁄_м;
универсальная газовая постоянная — R = 8,31447 ^Дж⁄_(Мол·K);
молярная масса сухого воздуха — M = 0,0289644 ^кг⁄_Мол.

Для тропосферы (то есть области линейного убывания температуры — это единственное свойство тропосферы, используемое здесь) температура на высоте h над уровнем моря может быть задана формулой:

Давление на высоте h:

$p = p_0 cdot left(1 - frac{L cdot h}{T_0} right)^frac{g cdot M}{R cdot L}$

Тогда плотность может быть вычислена подстановкой соответствующих данной высоте h температуры T и давления P в формулу:

$rho = frac{p cdot M}{R cdot T} ,$

Эти три формулы (зависимость температуры, давления и плотности от высоты) и использованы для построения графиков, приведенных справа. Графики нормализованы — показывают общий вид поведения параметров. «Нулевые» значения для верных вычислений нужно каждый раз подставлять в соответствии с показаниями соответствующих приборов (термометра и барометра) на данный момент на уровне моря.

См. также

Стандартная атмосфера
Модели атмосферы (англ.)русск.

Примечания

↑ Так как для любого газа, в соответствии с законом Авогадро, при постоянных температуре, давлении и объеме количество молекул остается неизменным, то добавление молекул воды приводит к снижению плотности воздуха.
↑ ¹ ² ³ (англ.) Equations — Air Density and Density Altitude

Ссылки

(англ.) Conversions of density units ρ
(англ.) Air density and density altitude calculations
(англ.) Reference manual for air density, density altitude, and grains of water
(англ.) Air density, density altitude, grains of water calculator by region

Источник

From Wikipedia, the free encyclopedia

The density of air or atmospheric density, denoted ρ, is the mass per unit volume of Earth’s atmosphere. Air density, like air pressure, decreases with increasing altitude. It also changes with variation in atmospheric pressure, temperature and humidity. At 101.325 kPa (abs) and 20 °C (68 °F), air has a density of approximately 1.204 kg/m³ (0.0752 lb/cu ft), according to the International Standard Atmosphere (ISA). At 101.325 kPa (abs) and 15 °C (59 °F), air has a density of approximately 1.225 kg/m³ (0.0765 lb/cu ft), which is about 1⁄800 that of water, according to the International Standard Atmosphere (ISA).^{[citation needed]} Pure liquid water is 1,000 kg/m³ (62 lb/cu ft).

Air density is a property used in many branches of science, engineering, and industry, including aeronautics;^[1]^[2]^[3] gravimetric analysis;^[4] the air-conditioning^[5] industry; atmospheric research and meteorology;^[6]^[7]^[8] agricultural engineering (modeling and tracking of Soil-Vegetation-Atmosphere-Transfer (SVAT) models);^[9]^[10]^[11] and the engineering community that deals with compressed air.^[12]

Depending on the measuring instruments used, different sets of equations for the calculation of the density of air can be applied. Air is a mixture of gases and the calculations always simplify, to a greater or lesser extent, the properties of the mixture.

Temperature[edit]

Other things being equal, hotter air is less dense than cooler air and will thus rise through cooler air. This can be seen by using the ideal gas law as an approximation.

Dry air[edit]

The density of dry air can be calculated using the ideal gas law, expressed as a function of temperature and pressure:^{[citation needed]}

${displaystyle {begin{aligned}rho &={frac {p}{R_{text{specific}}T}}\R_{text{specific}}&={frac {R}{M}}={frac {k_{rm {B}}}{m}}\rho &={frac {pM}{RT}}={frac {pm}{k_{rm {B}}T}}\end{aligned}}}$

where:^{[citation needed]}

, air density (kg/m³)^{[note 1]}

, absolute pressure (Pa)^{[note 1]}

, absolute temperature (K)^{[note 1]}

is the gas constant, 8.31446261815324 in J⋅K⁻¹⋅mol⁻¹ ^{[note 1]}

is the molar mass of dry air, approximately 0.0289652 in kg⋅mol⁻¹.^{[note 1]}

$k_{rm B}$

is the Boltzmann constant, 1.380649×10⁻²³ in J⋅K⁻¹^{[note 1]}

is the molecular mass of dry air, approximately 4.81×10⁻²⁶ in kg.^{[note 1]}

${displaystyle R_{text{specific}}}$

, the specific gas constant for dry air, which using the values presented above would be approximately 287.0500676 in J⋅kg⁻¹⋅K⁻¹^{[note 1]}.

Therefore:

At IUPAC standard temperature and pressure (0 °C and 100 kPa), dry air has a density of approximately 1.2754 kg/m³.^{[citation needed]}
At 20 °C and 101.325 kPa, dry air has a density of 1.2041 kg/m³.^{[citation needed]}
At 70 °F and 14.696 psi, dry air has a density of 0.074887 lb/ft³.^{[citation needed]}

The following table illustrates the air density–temperature relationship at 1 atm or 101.325 kPa:^{[citation needed]}^{[citation needed]}

Effect of temperature on properties of air

Celsius temperature θ (°C)	Speed of sound c (m/s)	Density of air ρ (kg/m³)	Characteristic specific acoustic impedance z₀ (Pa·s/m)
35	351.88	1.1455	403.2
30	349.02	1.1644	406.5
25	346.13	1.1839	409.4
20	343.21	1.2041	413.3
15	340.27	1.2250	416.9
10	337.31	1.2466	420.5
5	334.32	1.2690	424.3
0	331.30	1.2922	428.0
−5	328.25	1.3163	432.1
−10	325.18	1.3413	436.1
−15	322.07	1.3673	440.3
−20	318.94	1.3943	444.6
−25	315.77	1.4224	449.1

Humid air[edit]

Effect of temperature and relative humidity on air density

The addition of water vapor to air (making the air humid) reduces the density of the air, which may at first appear counter-intuitive. This occurs because the molar mass of water vapor (18 g/mol) is less than the molar mass of dry air^{[note 2]} (around 29 g/mol). For any ideal gas, at a given temperature and pressure, the number of molecules is constant for a particular volume (see Avogadro’s Law). So when water molecules (water vapor) are added to a given volume of air, the dry air molecules must decrease by the same number, to keep the pressure or temperature from increasing. Hence the mass per unit volume of the gas (its density) decreases.

The density of humid air may be calculated by treating it as a mixture of ideal gases. In this case, the partial pressure of water vapor is known as the vapor pressure. Using this method, error in the density calculation is less than 0.2% in the range of −10 °C to 50 °C. The density of humid air is found by:

${displaystyle rho _{text{humid air}}={frac {p_{text{d}}}{R_{text{d}}T}}+{frac {p_{text{v}}}{R_{text{v}}T}}={frac {p_{text{d}}M_{text{d}}+p_{text{v}}M_{text{v}}}{RT}}}$

^[13]

where:

${displaystyle rho _{text{humid air}}}$

, density of the humid air (kg/m³)

${displaystyle p_{text{d}}}$

, partial pressure of dry air (Pa)

${displaystyle R_{text{d}}}$

, specific gas constant for dry air, 287.058 J/(kg·K)

, temperature (K)

${displaystyle p_{text{v}}}$

, pressure of water vapor (Pa)

${displaystyle R_{text{v}}}$

, specific gas constant for water vapor, 461.495 J/(kg·K)

${displaystyle M_{text{d}}}$

, molar mass of dry air, 0.0289652 kg/mol

${displaystyle M_{text{v}}}$

, molar mass of water vapor, 0.018016 kg/mol

, universal gas constant, 8.31446 J/(K·mol)

The vapor pressure of water may be calculated from the saturation vapor pressure and relative humidity. It is found by:

${displaystyle p_{text{v}}=phi p_{text{sat}}}$

where:

${displaystyle p_{text{v}}}$

, vapor pressure of water

, relative humidity (0.0–1.0)

$p_{{text{sat}}}$

, saturation vapor pressure

The saturation vapor pressure of water at any given temperature is the vapor pressure when relative humidity is 100%. One formula is Tetens’ equation from^[14] used to find the saturation vapor pressure is:

${displaystyle p_{text{sat}}=6.1078times 10^{frac {7.5T}{T+237.3}}}$

where:

$p_{{text{sat}}}$

, saturation vapor pressure (hPa)

, temperature (°C)

See vapor pressure of water for other equations.

The partial pressure of dry air ${displaystyle p_{text{d}}}$ is found considering partial pressure, resulting in:

${displaystyle p_{text{d}}=p-p_{text{v}}}$

Where simply denotes the observed absolute pressure.

Variation with altitude[edit]

Standard atmosphere: p₀ = 101.325 kPa, T₀ = 288.15 K, ρ₀ = 1.225 kg/m³

Troposphere[edit]

To calculate the density of air as a function of altitude, one requires additional parameters. For the troposphere, the lowest part (~10 km) of the atmosphere, they are listed below, along with their values according to the International Standard Atmosphere, using for calculation the universal gas constant instead of the air specific constant:

$p_{0}$

, sea level standard atmospheric pressure, 101325 Pa

$T_{0}$

, sea level standard temperature, 288.15 K

, earth-surface gravitational acceleration, 9.80665 m/s²

, temperature lapse rate, 0.0065 K/m

, ideal (universal) gas constant, 8.31446 J/(mol·K)

, molar mass of dry air, 0.0289652 kg/mol

Temperature at altitude meters above sea level is approximated by the following formula (only valid inside the troposphere, no more than ~18 km above Earth’s surface (and lower away from Equator)):

${displaystyle T=T_{0}-Lh}$

The pressure at altitude is given by:

${displaystyle p=p_{0}left(1-{frac {Lh}{T_{0}}}right)^{frac {gM}{RL}}}$

Density can then be calculated according to a molar form of the ideal gas law:

${displaystyle rho ={frac {pM}{RT}}={frac {pM}{RT_{0}left(1-{frac {Lh}{T_{0}}}right)}}={frac {p_{0}M}{RT_{0}}}left(1-{frac {Lh}{T_{0}}}right)^{{frac {gM}{RL}}-1}}$

where:

, molar mass

, ideal gas constant

, absolute temperature

, absolute pressure

Note that the density close to the ground is ${textstyle rho _{0}={frac {p_{0}M}{RT_{0}}}}$

It can be easily verified that the hydrostatic equation holds:

${displaystyle {frac {dp}{dh}}=-grho .}$

Exponential approximation[edit]

As the temperature varies with height inside the troposphere by less than 25%, ${textstyle {frac {Lh}{T_{0}}}<0.25}$ and one may approximate:

${displaystyle rho =rho _{0}e^{left({frac {gM}{RL}}-1right)ln left(1-{frac {Lh}{T_{0}}}right)}approx rho _{0}e^{-left({frac {gM}{RL}}-1right){frac {Lh}{T_{0}}}}=rho _{0}e^{-left({frac {gMh}{RT_{0}}}-{frac {Lh}{T_{0}}}right)}}$

Thus:

${displaystyle rho approx rho _{0}e^{-h/H_{n}}}$

Which is identical to the isothermal solution, except that H_n, the height scale of the exponential fall for density (as well as for number density n), is not equal to RT₀/gM as one would expect for an isothermal atmosphere, but rather:

${displaystyle {frac {1}{H_{n}}}={frac {gM}{RT_{0}}}-{frac {L}{T_{0}}}}$

Which gives H_n = 10.4 km.

Note that for different gasses, the value of H_n differs, according to the molar mass M: It is 10.9 for nitrogen, 9.2 for oxygen and 6.3 for carbon dioxide. The theoretical value for water vapor is 19.6, but due to vapor condensation the water vapor density dependence is highly variable and is not well approximated by this formula.

The pressure can be approximated by another exponent:

${displaystyle p=p_{0}e^{left({frac {gM}{RL}}right)ln left(1-{frac {Lh}{T_{0}}}right)}approx p_{0}e^{-{frac {gM}{RL}}{frac {Lh}{T_{0}}}}=p_{0}e^{-{frac {gMh}{RT_{0}}}}}$

Which is identical to the isothermal solution, with the same height scale H_p = RT₀/gM. Note that the hydrostatic equation no longer holds for the exponential approximation (unless L is neglected).

H_p is 8.4 km, but for different gasses (measuring their partial pressure), it is again different and depends upon molar mass, giving 8.7 for nitrogen, 7.6 for oxygen and 5.6 for carbon dioxide.

Total content[edit]

Further note that since g, Earth’s gravitational acceleration, is approximately constant with altitude in the atmosphere, the pressure at height h is proportional to the integral of the density in the column above h, and therefore to the mass in the atmosphere above height h. Therefore the mass fraction of the troposphere out of all the atmosphere is given using the approximated formula for p:

${displaystyle 1-{frac {p(h=11{text{ km}})}{p_{0}}}=1-left({frac {T(11{text{ km}})}{T_{0}}}right)^{frac {gM}{RL}}approx 76%}$

For nitrogen, it is 75%, while for oxygen this is 79%, and for carbon dioxide, 88%.

Tropopause[edit]

Higher than the troposphere, at the tropopause, the temperature is approximately constant with altitude (up to ~20 km) and is 220 K. This means that at this layer L = 0 and T = 220 K, so that the exponential drop is faster, with H_TP = 6.3 km for air (6.5 for nitrogen, 5.7 for oxygen and 4.2 for carbon dioxide). Both the pressure and density obey this law, so, denoting the height of the border between the troposphere and the tropopause as U:

${displaystyle {begin{aligned}p&=p(U)e^{-{frac {h-U}{H_{text{TP}}}}}=p_{0}left(1-{frac {LU}{T_{0}}}right)^{frac {gM}{RL}}e^{-{frac {h-U}{H_{text{TP}}}}}\rho &=rho (U)e^{-{frac {h-U}{H_{text{TP}}}}}=rho _{0}left(1-{frac {LU}{T_{0}}}right)^{{frac {gM}{RL}}-1}e^{-{frac {h-U}{H_{text{TP}}}}}end{aligned}}}$

Composition[edit]

Composition of dry atmosphere, by volume^{[▽ note 1]}^{[▽ note 2]}

Gas (and others)	Various^[15]	CIPM-2007^[16]	ASHRAE^[17]	Schlatter^[18]	ICAO^[19]	US StdAtm76^[20]	▼ Tap to expand or collapse table ▲
ppmv ^{[▽ note 3]}	percentage	ppmv	percentage	ppmv	percentage	ppmv	percentage	ppmv	percentage	ppmv	percentage
Nitrogen	N₂	780,800	78.080%	780,848	78.0848%	780,818	78.0818%	780,840	78.084%	780,840	78.084%	780,840	78.084%
Oxygen	O₂	209,500	20.950%	209,390	20.9390%	209,435	20.9435%	209,460	20.946%	209,476	20.9476%	209,476	20.9476%
Argon	Ar	9,340	0.9340%	9,332	0.9332%	9,332	0.9332%	9,340	0.9340%	9,340	0.9340%	9,340	0.9340%
Carbon dioxide	CO₂	397.8	0.03978%	400	0.0400%	385	0.0385%	384	0.0384%	314	0.0314%	314	0.0314%
Neon	Ne	18.18	0.001818%	18.2	0.00182%	18.2	0.00182%	18.18	0.001818%	18.18	0.001818%	18.18	0.001818%
Helium	He	5.24	0.000524%	5.2	0.00052%	5.2	0.00052%	5.24	0.000524%	5.24	0.000524%	5.24	0.000524%
Methane	CH₄	1.81	0.000181%	1.5	0.00015%	1.5	0.00015%	1.774	0.0001774%	2	0.0002%	2	0.0002%
Krypton	Kr	1.14	0.000114%	1.1	0.00011%	1.1	0.00011%	1.14	0.000114%	1.14	0.000114%	1.14	0.000114%
Hydrogen	H₂	0.55	0.000055%	0.5	0.00005%	0.5	0.00005%	0.56	0.000056%	0.5	0.00005%	0.5	0.00005%
Nitrous oxide	N₂O	0.325	0.0000325%	0.3	0.00003%	0.3	0.00003%	0.320	0.0000320%	0.5	0.00005%	—	—
Carbon monoxide	CO	0.1	0.00001%	0.2	0.00002%	0.2	0.00002%	—	—	—	—	—	—
Xenon	Xe	0.09	0.000009%	0.1	0.00001%	0.1	0.00001%	0.09	0.000009%	0.087	0.0000087%	0.087	0.0000087%
Nitrogen dioxide	NO₂	0.02	0.000002%	—	—	—	—	—	—	Up to 0.02	Up to 0.000002%	—	—
Iodine	I₂	0.01	0.000001%	—	—	—	—	—	—	Up to 0.01	Up to 0.000001%	—	—
Ammonia	NH₃	trace	trace	—	—	—	—	—	—			—	—
Sulfur dioxide	SO₂	trace	trace	—	—	—	—	—	—	Up to 1.00	Up to 0.0001%	—	—
Ozone	O₃	0.02 to 0.07	2 to 7×10⁻⁶%	—	—	—	—	0.01 to 0.10	1 to 10×10⁻⁶%	Up to 0.02 to 0.07 ^{[▽ note 4]}	Up to 2 to 7×10⁻⁶% ^{[▽ note 4]}	—	—
Trace to 30 ppm ^{[▽ note 5]}	—	—	—	—	—	2.9	0.00029%	—	—	—	—	—	—
Dry air total	air	1,000,000	100.00%	1,000,000	100.00%	1,000,000	100.00%	1,000,000	100.00%	1,000,000	100.00%	1,000,080	100.00%
Not included in above dry atmosphere
Water vapor	H₂O	~0.25% by mass over full atmosphere, locally 0.001–5% by volume.^[21]	~0.25% by mass over full atmosphere, locally 0.001–5% by volume.^[21]
▽ notes ^ Concentration pertains to the troposphere ^ Total values may not add up to exactly 100% due to roundoff and uncertainty. ^ ppmv: parts per million by volume. Volume fraction is equal to mole fraction for ideal gas only, see volume (thermodynamics). ^ ^a ^b O₃ concentration up to 0.07 ppmv (7×10⁻⁶%) in summer and up to 0.02 ppmv (2×10⁻⁶%) in winter. ^ Volumetric composition value adjustment factor (sum of all trace gases, below the CO₂, and adjusts for 30 ppmv)

Notes[edit]

^ ^a ^b ^c ^d ^e ^f ^g ^h In the SI unit system. However, other units can be used.
^ as dry air is a mixture of gases, its molar mass is the weighted average of the molar masses of its components

References[edit]

^ Olson, Wayne M. (2000) AFFTC-TIH-99-01, Aircraft Performance Flight
^ ICAO, Manual of the ICAO Standard Atmosphere (extended to 80 kilometres (262 500 feet)), Doc 7488-CD, Third Edition, 1993, ISBN 92-9194-004-6.
^ Grigorie, T.L., Dinca, L., Corcau J-I. and Grigorie, O. (2010) Aircrafts’ [sic] Altitude Measurement Using Pressure Information:Barometric Altitude and Density Altitude
^ A., Picard, R.S., Davis, M., Gläser and K., Fujii (CIPM-2007) Revised formula for the density of moist air
^ S. Herrmann, H.-J. Kretzschmar, and D.P. Gatley (2009), ASHRAE RP-1485 Final Report
^ F.R. Martins, R.A. Guarnieri e E.B. Pereira, (2007) O aproveitamento da energia eólica (The wind energy resource).
^ Andrade, R.G., Sediyama, G.C., Batistella, M., Victoria, D.C., da Paz, A.R., Lima, E.P., Nogueira, S.F. (2009) Mapeamento de parâmetros biofísicos e da evapotranspiração no Pantanal usando técnicas de sensoriamento remoto
^ Marshall, John and Plumb, R. Alan (2008), Atmosphere, ocean, and climate dynamics: an introductory text ISBN 978-0-12-558691-7.
^ Pollacco, J. A., and B. P. Mohanty (2012), Uncertainties of Water Fluxes in Soil-Vegetation-Atmosphere Transfer Models: Inverting Surface Soil Moisture and Evapotranspiration Retrieved from Remote Sensing, Vadose Zone Journal, 11(3), doi:10.2136/vzj2011.0167.
^ Shin, Y., B. P. Mohanty, and A.V.M. Ines (2013), Estimating Effective Soil Hydraulic Properties Using Spatially Distributed Soil Moisture and Evapotranspiration, Vadose Zone Journal, 12(3), doi:10.2136/vzj2012.0094.
^ Saito, H., J. Simunek, and B. P. Mohanty (2006), Numerical Analysis of Coupled Water, Vapor, and Heat Transport in the Vadose Zone, Vadose Zone J. 5: 784-800.
^ Perry, R.H. and Chilton, C.H., eds., Chemical Engineers’ Handbook, 5th ed., McGraw-Hill, 1973.
^ Shelquist, R (2009) Equations — Air Density and Density Altitude
^ Shelquist, R (2009) Algorithms — Schlatter and Baker
^ Partial sources for figures: Base constituents, Nasa earth factsheet, (updated 2014-03). Carbon dioxide, NOAA Earth System Research Laboratory, (updated 2014-03). Methane and Nitrous Oxide, The NOAA Annual greenhouse gas index(AGGI) Greenhouse gas-Figure 2, (updated 2014-03).
^ A., Picard, R.S., Davis, M., Gläser and K., Fujii (2008), Revised formula for the density of moist air (CIPM-2007), Metrologia 45 (2008) 149–155 doi:10.1088/0026-1394/45/2/004, pg 151 Table 1
^ S. Herrmann, H.-J. Kretzschmar, and D.P. Gatley (2009), ASHRAE RP-1485 Final Report Thermodynamic Properties of Real Moist Air,Dry Air, Steam, Water, and Ice pg 16 Table 2.1 and 2.2
^ Thomas W. Schlatter (2009), Atmospheric Composition and Vertical Structure pg 15 Table 2
^ ICAO, Manual of the ICAO Standard Atmosphere (extended to 80 kilometres (262 500 feet)), Doc 7488-CD, Third Edition, (1993), ISBN 92-9194-004-6. pg E-x Table B
^ U.S. Committee on Extension to the Standard Atmosphere (COESA) (1976) U.S. Standard Atmosphere, 1976 pg 03 Table 3
^ ^a ^b Wallace, John M. and Peter V. Hobbs. Atmospheric Science; An Introductory Survey. Elsevier. Second Edition, 2006. ISBN 978-0-12-732951-2. Chapter 1

External links[edit]

Conversions of density units ρ by Sengpielaudio
Air density and density altitude calculations and by Richard Shelquist
Air density calculations by Sengpielaudio (section under Speed of sound in humid air)
Air density calculator by Engineering design encyclopedia
Atmospheric pressure calculator by wolfdynamics
Air iTools — Air density calculator for mobile by JSyA

Источник

From Wikipedia, the free encyclopedia

Temperature[edit]

Other things being equal, hotter air is less dense than cooler air and will thus rise through cooler air. This can be seen by using the ideal gas law as an approximation.

Dry air[edit]

The density of dry air can be calculated using the ideal gas law, expressed as a function of temperature and pressure:^{[citation needed]}

${displaystyle {begin{aligned}rho &={frac {p}{R_{text{specific}}T}}\R_{text{specific}}&={frac {R}{M}}={frac {k_{rm {B}}}{m}}\rho &={frac {pM}{RT}}={frac {pm}{k_{rm {B}}T}}\end{aligned}}}$

where:^{[citation needed]}

, air density (kg/m³)^{[note 1]}

, absolute pressure (Pa)^{[note 1]}

, absolute temperature (K)^{[note 1]}

is the gas constant, 8.31446261815324 in J⋅K⁻¹⋅mol⁻¹ ^{[note 1]}

is the molar mass of dry air, approximately 0.0289652 in kg⋅mol⁻¹.^{[note 1]}

$k_{rm B}$

is the Boltzmann constant, 1.380649×10⁻²³ in J⋅K⁻¹^{[note 1]}

is the molecular mass of dry air, approximately 4.81×10⁻²⁶ in kg.^{[note 1]}

${displaystyle R_{text{specific}}}$

, the specific gas constant for dry air, which using the values presented above would be approximately 287.0500676 in J⋅kg⁻¹⋅K⁻¹^{[note 1]}.

Therefore:

At IUPAC standard temperature and pressure (0 °C and 100 kPa), dry air has a density of approximately 1.2754 kg/m³.^{[citation needed]}
At 20 °C and 101.325 kPa, dry air has a density of 1.2041 kg/m³.^{[citation needed]}
At 70 °F and 14.696 psi, dry air has a density of 0.074887 lb/ft³.^{[citation needed]}

The following table illustrates the air density–temperature relationship at 1 atm or 101.325 kPa:^{[citation needed]}^{[citation needed]}

Effect of temperature on properties of air

Celsius temperature θ (°C)	Speed of sound c (m/s)	Density of air ρ (kg/m³)	Characteristic specific acoustic impedance z₀ (Pa·s/m)
35	351.88	1.1455	403.2
30	349.02	1.1644	406.5
25	346.13	1.1839	409.4
20	343.21	1.2041	413.3
15	340.27	1.2250	416.9
10	337.31	1.2466	420.5
5	334.32	1.2690	424.3
0	331.30	1.2922	428.0
−5	328.25	1.3163	432.1
−10	325.18	1.3413	436.1
−15	322.07	1.3673	440.3
−20	318.94	1.3943	444.6
−25	315.77	1.4224	449.1

Humid air[edit]

Effect of temperature and relative humidity on air density

${displaystyle rho _{text{humid air}}={frac {p_{text{d}}}{R_{text{d}}T}}+{frac {p_{text{v}}}{R_{text{v}}T}}={frac {p_{text{d}}M_{text{d}}+p_{text{v}}M_{text{v}}}{RT}}}$

^[13]

where:

${displaystyle rho _{text{humid air}}}$

, density of the humid air (kg/m³)

${displaystyle p_{text{d}}}$

, partial pressure of dry air (Pa)

${displaystyle R_{text{d}}}$

, specific gas constant for dry air, 287.058 J/(kg·K)

, temperature (K)

${displaystyle p_{text{v}}}$

, pressure of water vapor (Pa)

${displaystyle R_{text{v}}}$

, specific gas constant for water vapor, 461.495 J/(kg·K)

${displaystyle M_{text{d}}}$

, molar mass of dry air, 0.0289652 kg/mol

${displaystyle M_{text{v}}}$

, molar mass of water vapor, 0.018016 kg/mol

, universal gas constant, 8.31446 J/(K·mol)

The vapor pressure of water may be calculated from the saturation vapor pressure and relative humidity. It is found by:

${displaystyle p_{text{v}}=phi p_{text{sat}}}$

where:

${displaystyle p_{text{v}}}$

, vapor pressure of water

, relative humidity (0.0–1.0)

$p_{{text{sat}}}$

, saturation vapor pressure

${displaystyle p_{text{sat}}=6.1078times 10^{frac {7.5T}{T+237.3}}}$

where:

$p_{{text{sat}}}$

, saturation vapor pressure (hPa)

, temperature (°C)

See vapor pressure of water for other equations.

The partial pressure of dry air ${displaystyle p_{text{d}}}$ is found considering partial pressure, resulting in:

${displaystyle p_{text{d}}=p-p_{text{v}}}$

Where simply denotes the observed absolute pressure.

Variation with altitude[edit]

Standard atmosphere: p₀ = 101.325 kPa, T₀ = 288.15 K, ρ₀ = 1.225 kg/m³

Troposphere[edit]

$p_{0}$

, sea level standard atmospheric pressure, 101325 Pa

$T_{0}$

, sea level standard temperature, 288.15 K

, earth-surface gravitational acceleration, 9.80665 m/s²

, temperature lapse rate, 0.0065 K/m

, ideal (universal) gas constant, 8.31446 J/(mol·K)

, molar mass of dry air, 0.0289652 kg/mol

Temperature at altitude meters above sea level is approximated by the following formula (only valid inside the troposphere, no more than ~18 km above Earth’s surface (and lower away from Equator)):

${displaystyle T=T_{0}-Lh}$

The pressure at altitude is given by:

${displaystyle p=p_{0}left(1-{frac {Lh}{T_{0}}}right)^{frac {gM}{RL}}}$

Density can then be calculated according to a molar form of the ideal gas law:

${displaystyle rho ={frac {pM}{RT}}={frac {pM}{RT_{0}left(1-{frac {Lh}{T_{0}}}right)}}={frac {p_{0}M}{RT_{0}}}left(1-{frac {Lh}{T_{0}}}right)^{{frac {gM}{RL}}-1}}$

where:

, molar mass

, ideal gas constant

, absolute temperature

, absolute pressure

Note that the density close to the ground is ${textstyle rho _{0}={frac {p_{0}M}{RT_{0}}}}$

It can be easily verified that the hydrostatic equation holds:

${displaystyle {frac {dp}{dh}}=-grho .}$

Exponential approximation[edit]

As the temperature varies with height inside the troposphere by less than 25%, ${textstyle {frac {Lh}{T_{0}}}<0.25}$ and one may approximate:

Thus:

${displaystyle rho approx rho _{0}e^{-h/H_{n}}}$

${displaystyle {frac {1}{H_{n}}}={frac {gM}{RT_{0}}}-{frac {L}{T_{0}}}}$

Which gives H_n = 10.4 km.

The pressure can be approximated by another exponent:

${displaystyle p=p_{0}e^{left({frac {gM}{RL}}right)ln left(1-{frac {Lh}{T_{0}}}right)}approx p_{0}e^{-{frac {gM}{RL}}{frac {Lh}{T_{0}}}}=p_{0}e^{-{frac {gMh}{RT_{0}}}}}$

Which is identical to the isothermal solution, with the same height scale H_p = RT₀/gM. Note that the hydrostatic equation no longer holds for the exponential approximation (unless L is neglected).

H_p is 8.4 km, but for different gasses (measuring their partial pressure), it is again different and depends upon molar mass, giving 8.7 for nitrogen, 7.6 for oxygen and 5.6 for carbon dioxide.

Total content[edit]

${displaystyle 1-{frac {p(h=11{text{ km}})}{p_{0}}}=1-left({frac {T(11{text{ km}})}{T_{0}}}right)^{frac {gM}{RL}}approx 76%}$

For nitrogen, it is 75%, while for oxygen this is 79%, and for carbon dioxide, 88%.

Tropopause[edit]

Composition[edit]

Composition of dry atmosphere, by volume^{[▽ note 1]}^{[▽ note 2]}

Gas (and others)	Various^[15]	CIPM-2007^[16]	ASHRAE^[17]	Schlatter^[18]	ICAO^[19]	US StdAtm76^[20]	▼ Tap to expand or collapse table ▲
ppmv ^{[▽ note 3]}	percentage	ppmv	percentage	ppmv	percentage	ppmv	percentage	ppmv	percentage	ppmv	percentage
Nitrogen	N₂	780,800	78.080%	780,848	78.0848%	780,818	78.0818%	780,840	78.084%	780,840	78.084%	780,840	78.084%
Oxygen	O₂	209,500	20.950%	209,390	20.9390%	209,435	20.9435%	209,460	20.946%	209,476	20.9476%	209,476	20.9476%
Argon	Ar	9,340	0.9340%	9,332	0.9332%	9,332	0.9332%	9,340	0.9340%	9,340	0.9340%	9,340	0.9340%
Carbon dioxide	CO₂	397.8	0.03978%	400	0.0400%	385	0.0385%	384	0.0384%	314	0.0314%	314	0.0314%
Neon	Ne	18.18	0.001818%	18.2	0.00182%	18.2	0.00182%	18.18	0.001818%	18.18	0.001818%	18.18	0.001818%
Helium	He	5.24	0.000524%	5.2	0.00052%	5.2	0.00052%	5.24	0.000524%	5.24	0.000524%	5.24	0.000524%
Methane	CH₄	1.81	0.000181%	1.5	0.00015%	1.5	0.00015%	1.774	0.0001774%	2	0.0002%	2	0.0002%
Krypton	Kr	1.14	0.000114%	1.1	0.00011%	1.1	0.00011%	1.14	0.000114%	1.14	0.000114%	1.14	0.000114%
Hydrogen	H₂	0.55	0.000055%	0.5	0.00005%	0.5	0.00005%	0.56	0.000056%	0.5	0.00005%	0.5	0.00005%
Nitrous oxide	N₂O	0.325	0.0000325%	0.3	0.00003%	0.3	0.00003%	0.320	0.0000320%	0.5	0.00005%	—	—
Carbon monoxide	CO	0.1	0.00001%	0.2	0.00002%	0.2	0.00002%	—	—	—	—	—	—
Xenon	Xe	0.09	0.000009%	0.1	0.00001%	0.1	0.00001%	0.09	0.000009%	0.087	0.0000087%	0.087	0.0000087%
Nitrogen dioxide	NO₂	0.02	0.000002%	—	—	—	—	—	—	Up to 0.02	Up to 0.000002%	—	—
Iodine	I₂	0.01	0.000001%	—	—	—	—	—	—	Up to 0.01	Up to 0.000001%	—	—
Ammonia	NH₃	trace	trace	—	—	—	—	—	—			—	—
Sulfur dioxide	SO₂	trace	trace	—	—	—	—	—	—	Up to 1.00	Up to 0.0001%	—	—
Ozone	O₃	0.02 to 0.07	2 to 7×10⁻⁶%	—	—	—	—	0.01 to 0.10	1 to 10×10⁻⁶%	Up to 0.02 to 0.07 ^{[▽ note 4]}	Up to 2 to 7×10⁻⁶% ^{[▽ note 4]}	—	—
Trace to 30 ppm ^{[▽ note 5]}	—	—	—	—	—	2.9	0.00029%	—	—	—	—	—	—
Dry air total	air	1,000,000	100.00%	1,000,000	100.00%	1,000,000	100.00%	1,000,000	100.00%	1,000,000	100.00%	1,000,080	100.00%
Not included in above dry atmosphere
Water vapor	H₂O	~0.25% by mass over full atmosphere, locally 0.001–5% by volume.^[21]	~0.25% by mass over full atmosphere, locally 0.001–5% by volume.^[21]
▽ notes ^ Concentration pertains to the troposphere ^ Total values may not add up to exactly 100% due to roundoff and uncertainty. ^ ppmv: parts per million by volume. Volume fraction is equal to mole fraction for ideal gas only, see volume (thermodynamics). ^ ^a ^b O₃ concentration up to 0.07 ppmv (7×10⁻⁶%) in summer and up to 0.02 ppmv (2×10⁻⁶%) in winter. ^ Volumetric composition value adjustment factor (sum of all trace gases, below the CO₂, and adjusts for 30 ppmv)

Notes[edit]

^ ^a ^b ^c ^d ^e ^f ^g ^h In the SI unit system. However, other units can be used.
^ as dry air is a mixture of gases, its molar mass is the weighted average of the molar masses of its components

References[edit]

^ Olson, Wayne M. (2000) AFFTC-TIH-99-01, Aircraft Performance Flight
^ ICAO, Manual of the ICAO Standard Atmosphere (extended to 80 kilometres (262 500 feet)), Doc 7488-CD, Third Edition, 1993, ISBN 92-9194-004-6.
^ Grigorie, T.L., Dinca, L., Corcau J-I. and Grigorie, O. (2010) Aircrafts’ [sic] Altitude Measurement Using Pressure Information:Barometric Altitude and Density Altitude
^ A., Picard, R.S., Davis, M., Gläser and K., Fujii (CIPM-2007) Revised formula for the density of moist air
^ S. Herrmann, H.-J. Kretzschmar, and D.P. Gatley (2009), ASHRAE RP-1485 Final Report
^ F.R. Martins, R.A. Guarnieri e E.B. Pereira, (2007) O aproveitamento da energia eólica (The wind energy resource).
^ Andrade, R.G., Sediyama, G.C., Batistella, M., Victoria, D.C., da Paz, A.R., Lima, E.P., Nogueira, S.F. (2009) Mapeamento de parâmetros biofísicos e da evapotranspiração no Pantanal usando técnicas de sensoriamento remoto
^ Marshall, John and Plumb, R. Alan (2008), Atmosphere, ocean, and climate dynamics: an introductory text ISBN 978-0-12-558691-7.
^ Pollacco, J. A., and B. P. Mohanty (2012), Uncertainties of Water Fluxes in Soil-Vegetation-Atmosphere Transfer Models: Inverting Surface Soil Moisture and Evapotranspiration Retrieved from Remote Sensing, Vadose Zone Journal, 11(3), doi:10.2136/vzj2011.0167.
^ Shin, Y., B. P. Mohanty, and A.V.M. Ines (2013), Estimating Effective Soil Hydraulic Properties Using Spatially Distributed Soil Moisture and Evapotranspiration, Vadose Zone Journal, 12(3), doi:10.2136/vzj2012.0094.
^ Saito, H., J. Simunek, and B. P. Mohanty (2006), Numerical Analysis of Coupled Water, Vapor, and Heat Transport in the Vadose Zone, Vadose Zone J. 5: 784-800.
^ Perry, R.H. and Chilton, C.H., eds., Chemical Engineers’ Handbook, 5th ed., McGraw-Hill, 1973.
^ Shelquist, R (2009) Equations — Air Density and Density Altitude
^ Shelquist, R (2009) Algorithms — Schlatter and Baker
^ Partial sources for figures: Base constituents, Nasa earth factsheet, (updated 2014-03). Carbon dioxide, NOAA Earth System Research Laboratory, (updated 2014-03). Methane and Nitrous Oxide, The NOAA Annual greenhouse gas index(AGGI) Greenhouse gas-Figure 2, (updated 2014-03).
^ A., Picard, R.S., Davis, M., Gläser and K., Fujii (2008), Revised formula for the density of moist air (CIPM-2007), Metrologia 45 (2008) 149–155 doi:10.1088/0026-1394/45/2/004, pg 151 Table 1
^ S. Herrmann, H.-J. Kretzschmar, and D.P. Gatley (2009), ASHRAE RP-1485 Final Report Thermodynamic Properties of Real Moist Air,Dry Air, Steam, Water, and Ice pg 16 Table 2.1 and 2.2
^ Thomas W. Schlatter (2009), Atmospheric Composition and Vertical Structure pg 15 Table 2
^ ICAO, Manual of the ICAO Standard Atmosphere (extended to 80 kilometres (262 500 feet)), Doc 7488-CD, Third Edition, (1993), ISBN 92-9194-004-6. pg E-x Table B
^ U.S. Committee on Extension to the Standard Atmosphere (COESA) (1976) U.S. Standard Atmosphere, 1976 pg 03 Table 3
^ ^a ^b Wallace, John M. and Peter V. Hobbs. Atmospheric Science; An Introductory Survey. Elsevier. Second Edition, 2006. ISBN 978-0-12-732951-2. Chapter 1

External links[edit]

Conversions of density units ρ by Sengpielaudio
Air density and density altitude calculations and by Richard Shelquist
Air density calculations by Sengpielaudio (section under Speed of sound in humid air)
Air density calculator by Engineering design encyclopedia
Atmospheric pressure calculator by wolfdynamics
Air iTools — Air density calculator for mobile by JSyA

Источник

Единицы измерения
Плотность воздуха
$rho ={frac {m}{V}}$
Размерность	L⁻³ M
СИ	кг/м³
СГС	г/см³
Примечания
скалярная величина

Пло́тность во́здуха — масса газа атмосферы Земли на единицу объема или удельная масса воздуха при естественных условиях. Плотность воздуха является функцией от давления, температуры и влажности. Обычно, стандартной величиной плотности воздуха на уровне моря в соответствии с Международной стандартной атмосферой принимается значение 1,2250 кг/м³, которая соответствует плотности сухого воздуха при 15 °С и давлении 101330 Па.

Содержание

1 Взаимосвязи в пределах модели идеального газа
- 1.1 Температура, давление и плотность
- 1.2 Влияние влажности воздуха
- 1.3 Влияние высоты над уровнем моря в тропосфере
2 См. также
3 Примечания
4 Ссылки

Взаимосвязи в пределах модели идеального газа

Влияние температуры на свойства воздуха на уровне моря
Температура	Скорость звука	Плотность воздуха из уравнения Клапейрона	Акустическое сопротивление
, °С	c , м/с	ρ , кг/м³	Z , Н·с/м³
+35	351,96	1,1455	403,2
+30	349,08	1,1644	406,5
+25	346,18	1,1839	409,4
+20	343,26	1,2041	413,3
+15	340,31	1,2250	416,9
+10	337,33	1,2466	420,5
+5	334,33	1,2690	424,3
0	331,30	1,2920	428,0
−5	328,24	1,3163	432,1
−10	325,16	1,3413	436,1
−15	322,04	1,3673	440,3
−20	318,89	1,3943	444,6
−25	315,72	1,4224	449,1

Температура, давление и плотность

Плотность сухого воздуха может быть вычислена с использованием уравнения Менделеева-Клапейрона для идеального газа при заданных температуре и давлении:

${displaystyle rho ={frac {pcdot M}{Rcdot T}}.}$

Здесь rho — плотность воздуха, — молярная масса (29 г/моль для сухого воздуха), — абсолютное давление, — универсальная газовая постоянная, — абсолютная температура в Кельвинах. Таким образом, подстановкой получаем:

при стандартной атмосфере Международного союза теоретической и прикладной химии (температуре 0 °С, давлении 100 кПа, нулевой влажности) плотность воздуха 1,2754 кг/м³;
при 20 °C, 101,325 кПа и сухом воздухе плотность атмосферы составляет 1,2041 кг/м³.

В приведенной таблице даны различные параметры воздуха, вычисленные на основании соответствующих элементарных формул, в зависимости от температуры (давление взято равным 101,325 кПа).

Влияние влажности воздуха

Под влажностью понимается наличие в воздухе газообразного водяного пара, парциальное давление которого не превосходит давления насыщенного пара для данных атмосферных условий. Добавление водяного пара в воздух приводит к уменьшению его плотности, что объясняется более низкой молярной массой воды (18 г/моль) по сравнению с молярной массой сухого воздуха (~29 г/моль).^[1] Влажный воздух может рассматриваться как смесь идеальных газов, комбинация плотностей каждого из которых позволяет получить требуемое значение для их смеси.^[2] Подобная интерпретация позволяет определение значения плотности с уровнем ошибки менее 0,2 % в диапазоне температур от −10 до +50 °C и может быть выражена следующим образом:^[2]

${displaystyle rho _{,mathrm {humid~air} }={frac {p_{d}}{R_{d}cdot T}}+{frac {p_{v}}{R_{v}cdot T}},}$

где $rho _{{,{mathrm {humid~air}}}}$ — плотность влажного воздуха (кг/м³); $p_{{d}}$ — парциальное давление сухого воздуха (Па); $R_{{d}}$ — газовая постоянная для сухого воздуха (287,058 Дж/кг·К); — температура (K); $p_{{v}}$ — давление водяного пара (Па) и $R_{{v}}$ — постоянная для пара (461,495 Дж/кг·К).

Давление водяного пара может быть определено исходя из относительной влажности:

${displaystyle p_{v}=phi cdot p_{mathrm {sat} },}$

где $p_{{v}}$ — давление водяного пара; phi — относительная влажность и $p_{{{mathrm {sat}}}}$ — парциальное давление насыщенного пара, последнее может быть представлено в виде следующего упрощенного выражения:^[2]

${displaystyle p(mb)_{mathrm {sat} }=6.1078cdot 10^{frac {7.5cdot T-2048.625}{T-35.85}},}$

которое дает результат в миллибарах.

Давление сухого воздуха $p_{{d}}$ определяется разностью:

${displaystyle p_{d}=p-p_{v},}$

где обозначает абсолютное давление рассматриваемой системы.

Влияние высоты над уровнем моря в тропосфере

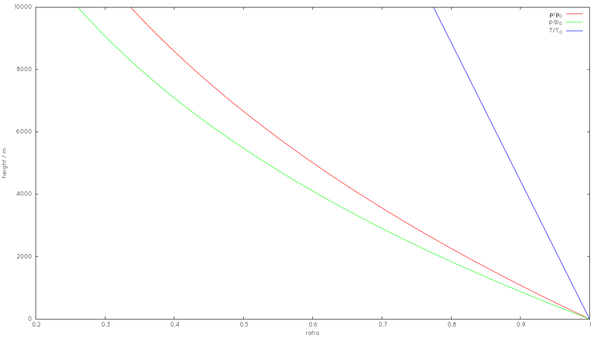
Зависимость давления, температуры и плотности воздуха от высоты по отношению к значениям этих величин на уровне моря ( ${displaystyle p_{0}=101,325}$ Па, ${displaystyle T_{0}=288,15}$ K, ${displaystyle rho _{0}=1,225}$ кг/м³) для «стандартной атмосферы».

Для вычисления плотности воздуха на определенной высоте в тропосфере (формула справедлива для высот менее 20 км) могут использоваться следующие параметры (в параметрах атмосферы указано значение для стандартной атмосферы):

Для тропосферы (то есть области линейного убывания температуры — это единственное свойство тропосферы, используемое здесь) температура на высоте над уровнем моря может быть задана формулой:

${displaystyle T=T_{0}+Lcdot h.}$

Давление на высоте :

${displaystyle p=p_{0}cdot left(1+{frac {Lcdot h}{T_{0}}}right)^{frac {-gcdot M}{Rcdot L}}.}$

Тогда плотность может быть вычислена подстановкой соответствующих данной высоте температуры и давления в формулу:

${displaystyle rho ={frac {pcdot M}{Rcdot T}}.}$

Эти три формулы (зависимость температуры, давления и плотности от высоты) и использованы для построения графиков, приведенных справа.
Графики нормализованы — показывают общий вид поведения параметров. «Нулевые» значения для верных вычислений нужно каждый раз подставлять в соответствии с показаниями соответствующих приборов (термометра и барометра) на данный момент на уровне моря.

См. также

Видеоурок: плотность воздуха

Стандартная атмосфера
Модели атмосферы (англ.)русск.

Примечания

↑ Для любого газа в соответствии с законом Авогадро при постоянных температуре, давлении и объеме количество молекул остается неизменным, поэтому добавление молекул воды приводит к снижению плотности воздуха.
↑ ¹ ² ³ Equations — Air Density and Density Altitude (англ.)

Ссылки

Conversions of density units ρ (англ.)
Air density and density altitude calculations (англ.)
Reference manual for air density, density altitude, and grains of water (англ.)
Air density, density altitude, grains of water calculator by region (англ.)

Источник

Плотность воздуха
[math]displaystyle{ rho = frac{m}{V} }[/math]
Размерность	L⁻³ M
Единицы измерения
СИ	кг/м³
СГС	г/см³
Примечания
скалярная величина

Пло́тность во́здуха — масса газа атмосферы Земли на единицу объема или удельная масса воздуха при естественных условиях. Плотность воздуха является функцией от давления, температуры и влажности. Обычно стандартной величиной плотности воздуха на уровне моря в соответствии с Международной стандартной атмосферой принимается значение 1,225 кг/м³, которая соответствует плотности сухого воздуха при 15 °С и давлении 101 330 Па.

Взаимосвязи в пределах модели идеального газа

Влияние температуры на свойства воздуха на уровне моря
Температура	Скорость звука	Плотность воздуха из уравнения Клапейрона	Акустическое сопротивление
[math]displaystyle{ vartheta }[/math], °С	c , м/с	ρ , кг/м³	Z , Н·с/м³
+35	351,96	1,1455	403,2
+30	349,08	1,1644	406,5
+25	346,18	1,1839	409,4
+20	343,26	1,2041	413,3
+15	340,31	1,2250	416,9
+10	337,33	1,2466	420,5
+5	334,33	1,2690	424,3
0	331,30	1,2920	428,0
−5	328,24	1,3163	432,1
−10	325,16	1,3413	436,1
−15	322,04	1,3673	440,3
−20	318,89	1,3943	444,6
−25	315,72	1,4224	449,1

Температура, давление и плотность

Плотность сухого воздуха может быть вычислена с использованием уравнения Менделеева — Клапейрона для идеального газа при заданных температуре и давлении:

[math]displaystyle{ rho = frac{p cdot M}{R cdot T}. }[/math]

Здесь [math]displaystyle{ rho }[/math] — плотность воздуха, [math]displaystyle{ M }[/math] — молярная масса (29 г/моль для сухого воздуха), [math]displaystyle{ p }[/math] — абсолютное давление, [math]displaystyle{ R }[/math] — универсальная газовая постоянная, [math]displaystyle{ T }[/math] — абсолютная температура в кельвинах. Таким образом, подстановкой получаем:

при стандартной атмосфере Международного союза теоретической и прикладной химии (температуре 0 °С, давлении 100 кПа, нулевой влажности) плотность воздуха 1,2754 кг/м³;
при 20 °C, 101,325 кПа и сухом воздухе плотность атмосферы составляет 1,2041 кг/м³.

Влияние влажности воздуха

Под влажностью понимается наличие в воздухе газообразного водяного пара, парциальное давление которого не превосходит давления насыщенного пара для данных атмосферных условий. Добавление водяного пара в воздух приводит к уменьшению его плотности, что объясняется более низкой молярной массой воды (18 г/моль) по сравнению с молярной массой сухого воздуха (~29 г/моль)^[1]. Влажный воздух может рассматриваться как смесь идеальных газов, комбинация плотностей каждого из которых позволяет получить требуемое значение для их смеси^[2]. Подобная интерпретация позволяет определять значение плотности с относительной погрешностью менее 0,2 % в диапазоне температур от −10 до +50 °C и может быть выражена следующим образом^[2]:

[math]displaystyle{ rho_{,mathrm{humid~air}} = frac{p_{d}}{R_{d} cdot T} + frac{p_{v}}{R_{v} cdot T}, }[/math]

где [math]displaystyle{ rho_{,mathrm{humid~air}} }[/math] — плотность влажного воздуха (кг/м³);

[math]displaystyle{ p_{d} }[/math] — парциальное давление сухого воздуха (Па);

[math]displaystyle{ R_{d} }[/math] — газовая постоянная для сухого воздуха (287,058 Дж/кг·К);

[math]displaystyle{ T }[/math] — температура (K); [math]displaystyle{ p_{v} }[/math] — давление водяного пара (Па) и [math]displaystyle{ R_{v} }[/math] — постоянная для пара (461,495 Дж/кг·К).

Давление водяного пара может быть определено исходя из относительной влажности:

[math]displaystyle{ p_{v} = phi cdot p_{mathrm{sat}}, }[/math]

где [math]displaystyle{ p_{v} }[/math] — давление водяного пара;

[math]displaystyle{ phi }[/math] — относительная влажность;

[math]displaystyle{ p_{mathrm{sat}} }[/math] — парциальное давление насыщенного пара.

Парциальное давление насыщенного пара может быть представлено в виде следующего упрощенного выражения^[2]:

[math]displaystyle{ p(mb)_{mathrm{sat}} = 6{,}1078 cdot 10^{frac{7{,}5 cdot T-2048{,}625}{T-35{,}85}}, }[/math]

которое дает результат в миллибарах.

Давление сухого воздуха [math]displaystyle{ p_{d} }[/math] определяется разностью:

[math]displaystyle{ p_{d} = p-p_{v}, }[/math]

где [math]displaystyle{ p }[/math] обозначает абсолютное давление рассматриваемой системы.

Влияние высоты над уровнем моря в тропосфере

Зависимость давления, температуры и плотности воздуха от высоты по отношению к значениям этих величин на уровне моря ([math]displaystyle{ p_0 = 101, 325 }[/math] Па, [math]displaystyle{ T_0 = 288{,}15 }[/math] K, [math]displaystyle{ rho_0= 1{,}225 }[/math] кг/м³) для «стандартной атмосферы»

Для вычисления плотности воздуха на определённой высоте в тропосфере (формула справедлива для высот менее 20 км) могут использоваться следующие параметры (в параметрах атмосферы указано значение для стандартной атмосферы):

стандартное атмосферное давление на уровне моря — [math]displaystyle{ p_0 }[/math] = 101 325 Па;
стандартная температура на уровне моря — [math]displaystyle{ T_0 }[/math] = 288,15 K;
ускорение свободного падения над поверхностью Земли — [math]displaystyle{ g }[/math] = 9,80665 м/с² (при данных вычислениях считается независимой от высоты величиной);
среднее значение вертикальной компоненты градиента температуры в тропосфере (см. Стандартная атмосфера) — [math]displaystyle{ L }[/math] = -0,0065 К/м (знак минус перед градиентом означает, что температура с высотой падает. Однако в атмосфере есть области с положительными значениями градиента температуры: на высотах с 35 до 53 км, а также выше 80 км);
универсальная газовая постоянная — [math]displaystyle{ R }[/math] = 8,31447 Дж/моль·K;
молярная масса сухого воздуха — [math]displaystyle{ M }[/math] = 0,0289644 кг/моль.

Для тропосферы (то есть области линейного убывания температуры — это единственное свойство тропосферы, используемое здесь) температура на высоте [math]displaystyle{ h }[/math] над уровнем моря может быть задана формулой:

[math]displaystyle{ T = T_0 + L cdot h. }[/math]

Давление на высоте [math]displaystyle{ h }[/math]:

[math]displaystyle{ p = p_0 cdot left(1 + frac{L cdot h}{T_0} right)^frac{ — g cdot M}{R cdot L}. }[/math]

Тогда плотность может быть вычислена подстановкой соответствующих данной высоте [math]displaystyle{ h }[/math] температуры [math]displaystyle{ T }[/math] и давления [math]displaystyle{ p }[/math] в формулу:

[math]displaystyle{ rho = frac{p cdot M}{R cdot T}. }[/math]

Эти три формулы (зависимость температуры, давления и плотности от высоты) и использованы для построения графиков, приведенных справа.
Графики нормализованы — показывают общий вид поведения параметров. «Нулевые» значения для верных вычислений нужно каждый раз подставлять в соответствии с показаниями соответствующих приборов (термометра и барометра) на данный момент на уровне моря.

См. также

Видеоурок: плотность воздуха

Стандартная атмосфера
Модели атмосферы (англ.) (рус.

Примечания

↑ Для любого газа в соответствии с законом Авогадро при постоянных температуре, давлении и объёме количество молекул остается неизменным, поэтому добавление молекул воды приводит к снижению плотности воздуха.
↑ ^2,0 ^2,1 ^2,2 Equations — Air Density and Density Altitude Архивная копия от 30 ноября 2010 на Wayback Machine (англ.)

Ссылки

Conversions of density units ρ Архивная копия от 29 ноября 2010 на Wayback Machine (англ.)
Air density and density altitude calculations Архивная копия от 30 ноября 2010 на Wayback Machine (англ.)
Reference manual for air density, density altitude, and grains of water Архивная копия от 23 октября 2014 на Wayback Machine (англ.)
Air density, density altitude, grains of water calculator by region Архивная копия от 3 марта 2022 на Wayback Machine (англ.)

Источник

Калькулятор определяет плотность воздуха в зависимости от:

- давления воздуха;
- температуры воздуха;
- относительной влажности воздуха.

Определение плотности воздуха.

Примечание.

Расчеты №1 и №2 составлены на основании уравнения идеального газа. Формулы не учитывают влажность воздуха и коэффициент сжимаемости воздуха. В связи с этим в реальных условиях эти формулы применимы для воздуха низкого давления близкого к атмосферному (атмосферный воздух, воздух в системах вентиляции и кондиционирования). Учитывая, что количество водяных паров в воздухе относительно невелико, уменьшением плотности в практических расчетах система вентиляции и кондиционирования можно смело пренебречь. При проведении метрологических расчетов данные формулы не используются.

Расчет №3 составлен на основании формулы Е.3-1 из ГОСТ OIML R 111-1-2009 . Формула позволяет учесть влажность воздуха. При области применения формулы 900 мбар≤P≤1100 мбар, 15ºC≤t≤25ºC и ≤80% относительная неопределенность определения плотности воздуха, вычисленная по формуле (Е.3-1), не превышает 2·10%.

Расчеты №1, №2, №3 не предназначен для определения плотности сжатого воздуха.

В комментарии приветствуются пожелания, замечания и рекомендации по улучшению программы.

Поделиться ссылкой:

Источник

Плотность воздуха — это физическая величина, характеризующая удельную массу воздуха при естественных условиях или массу газа атмосферы Земли на единицу объема. Величина плотности воздуха представляет собой функцию от высоты производимых измерений, от его влажности и температуры.

Плотность воздуха равна…
Определение плотности воздуха
Формула плотности воздуха
Что такое относительная плотность по воздуху?
Как плотность воздуха зависит от температуры?
Как измеряется плотность паров по воздуху?

Плотность воздуха равна… ^

За стандарт плотности воздуха принята величина, равная 1,29 кг/м3, которая вычисляется как отношение его молярной массы (29 г/моль) к молярному объему, одинаковому для всех газов (22,413996 дм3), соответствующая плотности сухого воздуха при 0°С (273,15°К) и давлении 760 мм ртутного столба (101325 Па) на уровне моря (то есть при нормальных условиях).

Определение плотности воздуха ^

Не так давно сведения о плотности воздуха получали косвенно за счет наблюдений за полярными сияниями, распространением радиоволн, метеорами. С момента появления искусственных спутников Земли плотность воздуха начали вычислять благодаря данным, полученным от их торможения.

Еще один метод заключается в наблюдениях за расплыванием искусственных облаков из паров натрия, создаваемых метеорологическими ракетами. В Европе плотность воздуха у поверхности Земли составляет 1,258 кг/м3, на высоте пяти км — 0,735, на высоте двадцати км — 0,087, на высоте сорока км — 0,004 кг/м3.

Различают два вида плотности воздуха: массовая и весовая (удельный вес).

Как выбрать освежители воздуха для комнаты, какие они бывают?

Если вам стало тяжело дышать, какие могут быть причины этого явления? Об этом можно прочитать здесь. Бережем свое здоровье!

Формула плотности воздуха ^

Весовая плотность определяет вес 1 м3 воздуха и вычисляется по формуле γ = G/V, где γ – весовая плотность, кгс/м3; G — вес воздуха, измеряемый в кгс; V – объем воздуха, измеряемый в м3. Установлено, что 1 м3 воздуха при стандартных условиях (барометрическое давление 760 мм ртутного столба, t=15°С) весит 1,225 кгс, исходя из этого, весовая плотность (удельный вес) 1 м3 воздуха равна γ =1,225 кгс/м3.

Что такое относительная плотность по воздуху? ^

Следует принять во внимание, что вес воздуха – это величина изменчивая и меняется в зависимости от различных условий, таких как географическая широта и сила инерции, которая возникает при вращении Земли вокруг своей оси. На полюсах вес воздуха на 5% больше, чем в зоне экватора.

Массовая плотность воздуха – это масса 1 м3 воздуха, обозначаемая греческой буквой ρ. Как известно, масса тела – величина постоянная. За единицу массы принято считать массу гири из иридистой платины, которая находится в Международной палате мер и весов в Париже.

Массовая плотность воздуха ρ вычисляется по следующей формуле: ρ = m / v. Здесь m – масса воздуха, измеряемая в кг×с2/м; ρ – его массовая плотность, измеряемая в кгс×с2/м4.

Массовая и весовая плотности воздуха находятся в зависимости: ρ = γ / g, где g – коэффициент ускорения свободного падения, равный 9,8 м/с². Откуда следует, что массовая плотность воздуха при стандартных условиях равна 0,1250 кг×с2/м4.

Как плотность воздуха зависит от температуры? ^

При изменении барометрического давления и температуры плотность воздуха изменяется. Исходя из закона Бойля-Мариотта, чем больше давление, тем больше будет плотность воздуха. Однако с уменьшением давления с высотой, уменьшается и плотности воздуха, что привносит свои коррективы, в результате чего закон изменения давления по вертикали становится сложнее.

Уравнение, которое выражает данный закон изменения давления с высотой в атмосфере, находящейся в покое, называется основным уравнением статики.

Оно гласит, что с увеличением высоты давление изменяется в меньшую сторону и при подъеме на одну и ту же высоту уменьшение давления тем больше, чем больше сила тяжести и плотность воздуха.

Важная роль в этом уравнении принадлежит изменениям плотности воздуха. В итоге можно сказать, что чем выше подниматься, тем меньше будет падать давление при подъеме на одинаковую высоту. Плотность воздуха от температуры зависит следующим образом: в теплом воздухе давление уменьшается менее интенсивно, чем в холодном, следовательно, на одинаково равной высоте в теплой воздушной массе давление более высокое, чем в холодной.

При изменяющихся значениях температуры и давления массовая плотность воздуха вычисляется по формуле: ρ = 0,0473хВ / Т. Здесь В – это барометрическое давление, измеряемое в мм ртутного столба, Т — температура воздуха, измеряемая в Кельвинах.

Как выбирают газовые обогреватели для дачи, по каким характеристикам, параметрам?

Что такое промышленный осушитель сжатого воздуха? Читайте про это здесь, наиболее интересная и актуальная информация.

Какие сейчас цены на озонотерапию? Вы узнаете об этом в данной статье:
http://about-air.ru/sostav-vozduha/ozon/ozonoterapiya-otzyvy.html. Отзывы, показания и противопоказания при озонотерапии.

Как измеряется плотность паров по воздуху? ^

Также плотность определяется и влажностью воздуха. Наличие водяных поров приводит к уменьшению плотности воздуха, что объясняется низкой молярной массой воды (18 г/моль) на фоне молярной массы сухого воздуха (29 г/моль). Влажный воздух можно рассмотреть как смесь идеальных газов, в каждом из которых комбинация плотностей позволяет получить требуемое значение плотности для их смеси.

Такая, своего рода, интерпретация позволяет определять значения плотности с уровнем погрешности менее 0,2% в диапазоне температур от −10 °C до 50 °C. Плотность воздуха позволяет получить величину его влагосодержания, которая вычисляется путем деления плотности водяного пара (в граммах), который содержится в воздухе, на показатель плотности сухого воздуха в килограммах.

Основное уравнение статики не позволяет решать постоянно возникающие практические задачи в реальных условиях изменяющейся атмосферы. Поэтому его решают при различных упрощенных предположениях, которые соответствуют фактическим реальным условиям, за счет выдвижения ряда частных предположений.

Основное уравнение статики дает возможность получить значение вертикального градиента давления, который выражает изменение давления при подъеме или спуске на единицу высоты, т. е. изменение давления на единицу расстояния по вертикали.

Вместо вертикального градиента нередко используют обратную ему величину — барическую ступень в метрах на миллибар (иногда еще встречается устаревший вариант термина «градиент давления» — барометрический градиент).

Низкая плотность воздуха определяет незначительное сопротивление передвижению. Многими наземными животными, в ходе эволюции, использовались экологические выгоды этого свойства воздушной среды, за счет чего они приобрели способность к полету. 75% всех видов наземных животных способны к активному полету. По большей части это насекомые и птицы, но встречаются млекопитающие и рептилии.

Видео на тему «Определение плотности воздуха»

Источник

Содержание

Взаимосвязи в пределах модели идеального газа

Температура, давление и плотность

Влияние влажности воздуха

Влияние высоты над уровнем моря в тропосфере

См. также

Примечания

Ссылки

Temperature[edit]

Dry air[edit]

Humid air[edit]

Variation with altitude[edit]

Troposphere[edit]

Exponential approximation[edit]

Total content[edit]

Tropopause[edit]

Composition[edit]

See also[edit]

Notes[edit]

References[edit]

External links[edit]

Temperature[edit]

Dry air[edit]

Humid air[edit]

Variation with altitude[edit]

Troposphere[edit]

Exponential approximation[edit]

Total content[edit]

Tropopause[edit]

Composition[edit]

See also[edit]

Notes[edit]

References[edit]

External links[edit]

Содержание

Взаимосвязи в пределах модели идеального газа

Температура, давление и плотность

Влияние влажности воздуха

Влияние высоты над уровнем моря в тропосфере

См. также

Примечания

Ссылки

Взаимосвязи в пределах модели идеального газа

Температура, давление и плотность

Влияние влажности воздуха

Влияние высоты над уровнем моря в тропосфере

См. также

Примечания

Ссылки

Определение плотности воздуха.

Примечание.

Поделиться ссылкой:

Плотность воздуха равна… ^

Определение плотности воздуха ^

Формула плотности воздуха ^

Что такое относительная плотность по воздуху? ^

Как плотность воздуха зависит от температуры? ^

Как измеряется плотность паров по воздуху? ^