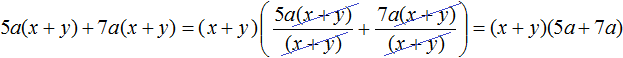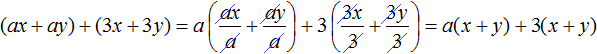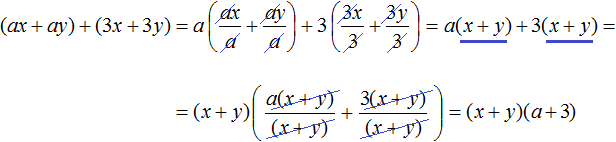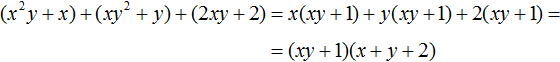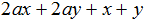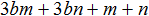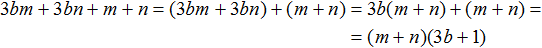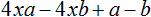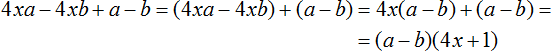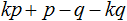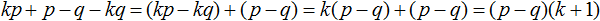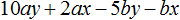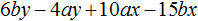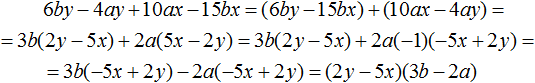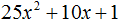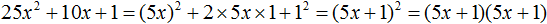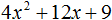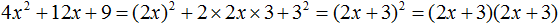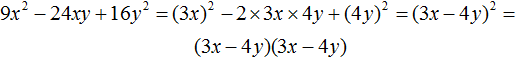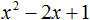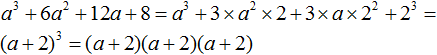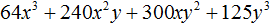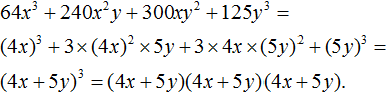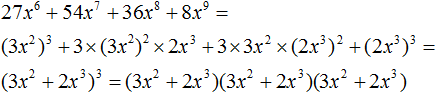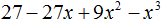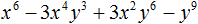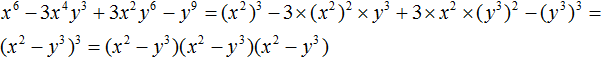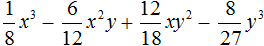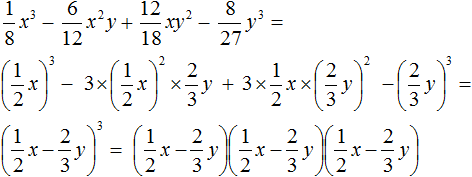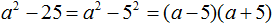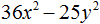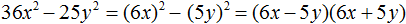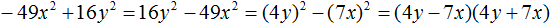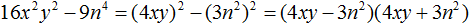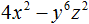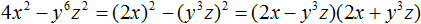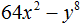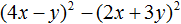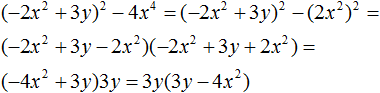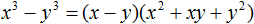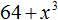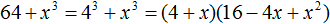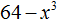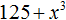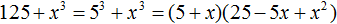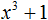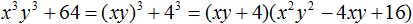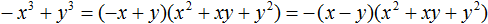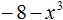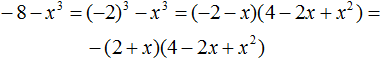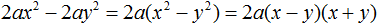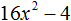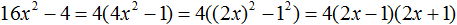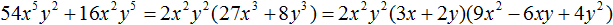Не нашли ответа?
Если вы не нашли ответа на свой вопрос, или сомневаетесь в его правильности, то можете воспользоваться формой ниже и уточнить решение. Или воспользуйтесь формой поиска и найдите похожие ответы по предмету Математика.
-
1
разлагать составное число на множители
Русско-английский словарь нормативно-технической терминологии > разлагать составное число на множители
-
2
factor a composite number
разлагать составное число на множители.
English-Russian cryptological dictionary > factor a composite number
См. также в других словарях:
-
разлагать составное число на множители — — [http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23] Тематики защита информации EN factor a composite number … Справочник технического переводчика
-
ЧИСЕЛ ТЕОРИЯ — раздел чистой математики, занимающийся изучением целых чисел 0, ±1, ±2,… и соотношений между ними. Иногда теорию чисел называют высшей арифметикой. Отдельные вычисления, производимые над конкретными числами, например, 9 + 16 = 25, не… … Энциклопедия Кольера
- разлагать на множители
- factor
Большой англо-русский и русско-английский словарь.
2001.
Смотреть что такое «разлагать на множители» в других словарях:
-
разлагать на множители — — [http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23] Тематики защита информации EN factor … Справочник технического переводчика
-
разлагать составное число на множители — — [http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23] Тематики защита информации EN factor a composite number … Справочник технического переводчика
-
ЧИСЕЛ ТЕОРИЯ — раздел чистой математики, занимающийся изучением целых чисел 0, ±1, ±2,… и соотношений между ними. Иногда теорию чисел называют высшей арифметикой. Отдельные вычисления, производимые над конкретными числами, например, 9 + 16 = 25, не… … Энциклопедия Кольера
-
Метод Кронекера — Метод Кронекера метод разложения многочлена с целыми коэффициентами на неприводимые множители над кольцом целых чисел; предложен в 1882 Кронекером. Алгоритм Кронекера находит для данного многочлена многочлен , такой, что делится на , или… … Википедия
-
Идеал — I Идеал (франц. idéal, от греч. idéa идея, первообраз) идеальный образ, определяющий способ мышления и деятельности человека или общественного класса. Формирование природы сообразно И. представляет собой специфически человеческую форму… … Большая советская энциклопедия
-
фактор — коэффициент разлагать на множители множитель сомножитель Например, prime factors простые сомножители, common factor общий множитель. Для любого целого числа n фактором является число, на которое n делится без остатка. Например, 7 фактор числа 91 … Справочник технического переводчика
-
Идеал (алгебраич. понятие) — Идеал (математический), одно из основных алгебраических понятий. Возникнув первоначально в связи с изучением алгебраических иррациональных чисел, И. нашли впоследствии многочисленные применения в других отделах математики. Известно, что всякое… … Большая советская энциклопедия
-
Алгоритм Берлекампа — Алгоритм Берлекампа данный алгоритм предназначен для факторизации полиномов, позволяет разлагать полиномы на неприводимые сомножители. Алгоритм был разработан Элвином Берлекэмпом в 1967 году. Следует различать алгоритм Берлекэмпа и алгоритм … Википедия
-
разложи́ть — ложу, ложишь; прич. страд. прош. разложенный, жен, а, о; сов., перех. 1. (несов. раскладывать). Положить, поставить отдельно одно от другого; разместить. Разложив все принесенное по столам и стульям, камердинер отправился выпить водки в буфет.… … Малый академический словарь
-
РАЗЛОЖИТЬ — РАЗЛОЖИТЬ, разложу, разложишь, совер. 1. (несовер. раскладывать) кого что. Положить отдельно по разным местам, разместить по какой нибудь поверхности. Разложить вещи. «Все товары разложу.» Некрасов. Разложить книги по всему столу. 2. (несовер.… … Толковый словарь Ушакова
-
РАЗЛОЖЕНИЕ — РАСПАД И РАЗЛОЖЕНИЕ В словарь общерусского литературного языка впиталось много научных и специальных терминов. Выйдя за пределы профессиональной речи, эти термины расширяют свои значения и вовлекаются в новые фразеологические контексты.… … История слов
Автор Amina задал вопрос в разделе Другое
как разлагать на множители и получил лучший ответ
Ответ от Lisa Ist.[гуру]
посмотри здесь. Вообще очень полезная страничка
Ответ от Ёали-Мали[гуру]
Искомое число дели на простое, результат опять дели на простое число и т. д. пока не получишь в результате простое число.
Произведение этих простых чисел даст искомое число разложенное на множители.
Например: 36 : 2=18, 18 : 2=9, 9 : 3=3;
результат: 36 = 2*2*3*3
Ответ от 3 ответа[гуру]
Привет! Вот подборка тем с похожими вопросами и ответами на Ваш вопрос: как разлагать на множители
SM
Знаток
(271),
на голосовании
11 лет назад
Голосование за лучший ответ
Сали-Мали
Просветленный
(29239)
11 лет назад
Искомое число дели на простое, результат опять дели на простое число и т. д. пока не получишь в результате простое число.
Произведение этих простых чисел даст искомое число разложенное на множители.
Например: 36 : 2=18, 18 : 2=9, 9 : 3=3;
результат: 36 = 2*2*3*3
Значение слова «РАЗЛАГАТЬ НА МНОЖИТЕЛИ» найдено в 8 источниках
РАЗЛАГАТЬ НА МНОЖИТЕЛИ
найдено в «Русско-английском политехническом словаре»
factor, factorize
* * *
1) present in factor form; 2) factored; 3) factor
найдено в «Русско-английском научно-техническом словаре»
•
To expand the number into factors …
найдено в «Русско-английском техническом словаре»
<math.> to factor
найдено в «Русско-английском словаре по физике»
expand into factors
найдено в «Русско-английском словаре по машиностроению»
factor
найдено в «Русско-английском словаре по электронике»
factor, factorize
найдено в «Русско-английском морском словаре»
factor
найдено в «Русско-английском толковом словаре терминов по информатике»
factor
АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ
ABCDEFGHIJKLMNOPQRSTUVWXYZ
Разлагать на множители: определение, значение, предложения
Предложения с «разлагать на множители»
| Другие результаты |
| Примеров к «разлагать на множители» не найдено. |
На данной странице приводится толкование (значение) фразы / выражения «разлагать на множители», а также синонимы, антонимы и предложения, при наличии их в нашей базе данных.
Мы стремимся сделать толковый словарь English-Grammar.Biz, в том числе и толкование фразы / выражения «разлагать на множители», максимально корректным и информативным. Если у вас есть предложения или замечания по поводу корректности определения «разлагать на множители», просим написать нам в разделе «Обратная связь».
Основные определения (разбираемся со “сложными” словами)
Одночлены
Одночленами могут быть числа, переменные, произведения чисел и переменных, а так же переменные в степени (если забыл, что такое степень, посмотри тему «Степень и ее свойства»)
Например:
- ( 4)
- ( x)
- ( 4x)
- ( 4{{x}^{2}})
- ( 4{{x}^{2}}y)
Все это – одночлены. Видишь у них нет знаков “+” или “-“, как бы нет других членов.
Многочлены
Многочлен – это выражение, состоящее из суммы (или разности) нескольких одночленов различного вида:
- ( 4{{x}^{2}}+9x)
- ( 2{{x}^{3}}-16{{x}^{2}}+4x)
- ( 8xcdot 4{{y}^{2}}-12+4{{x}^{2}}y-3{{y}^{2}}cdot {{x}^{4}}+6-5{{y}^{2}}{{x}^{4}})
Множители
Так, ну давай по порядку. Как нетрудно догадаться, слово «множитель» происходит от слова «умножать».
Возьмем, например, число ( 12), разложить его на множители означает расписать его в виде «умножения» или, как принято говорить в математике «произведения» множителей.
Так ( 12) мы можем получить, умножив ( 2) на ( 6).
А ( 6), в свою очередь, можно представить как произведение ( 2) и ( 3).
Чтоб было более наглядно, обратимся к картинке:
На картинке мы видим пошаговое разложение на множители, те которые подчеркнуты – это множители, которые дальше разложить уже нельзя.
То есть их нельзя уже представить в виде произведения (можно конечно представить каждое из них как единица, умноженная на само число, но это нам ничего не дает).
Я обещал, что картинка все разъяснит, ну разве из нее не понятно, что, ( 12=2cdot 6), а ( 6=2cdot 3)?
Вот и я говорю, что элементарно!
Иными словами, ( 2cdot 2cdot 3=12).
Тут ( 2), еще раз ( 2) и ( 3) – это и есть множители, на которые мы раскладываем.
Зачем нужно раскладывать многочлен на множители?
Это самый главный вопрос. Я уже говорил – чтобы облегчить тебе жизнь.
Раскладывая многочлен на множители, ты упрощаешь выражение! Ты как бы делишь одну большую и сложную проблему, на несколько маленьких и простых и потом разбираешься с каждой маленькой проблемой по отдельности.
А теперь “официальное” определение.
Разложение многочлена на множители – тождественное преобразование, превращающее сумму в произведение нескольких множителей. При этом каждый множитель может быть как многочленом, так и одночленом.
Для чего нужно знать все пять способов?
Потому что нет универсального способа, подходящего для всех многочленов.
Давай посмотрим на каждый из них…
5 способов разложения многочлена на множители
1. Вынесение общего множителя за скобки
( displaystyle ac+bc=c(a+b))
2. Формулы сокращенного умножения
( begin{array}{l}left[ 1 right] {{left( a+b right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}\left[ 2 right] {{left( a-b right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}\left[ 3 right] {{a}^{2}}-{{b}^{2}}=left( a-b right)left( a+b right)\left[ 4 right] {{left( a+b right)}^{3}}={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}}\left[ 5 right] {{left( a-b right)}^{3}}={{a}^{3}}-3{{a}^{2}}b+3a{{b}^{2}}-{{b}^{3}}\left[ 6 right] {{a}^{3}}+{{b}^{3}}=left( a+b right)left( {{a}^{2}}-ab+{{b}^{2}} right)\left[ 7 right] {{a}^{3}}-{{b}^{3}}=left( a-b right)left( {{a}^{2}}+ab+{{b}^{2}} right)end{array})
3. Метод группировки
Применяется если преобразование не очевидно. Здесь, например, можно переставить второй член на другое место:
( {{x}^{3}}-5{{x}^{2}}y-3xy+15{{y}^{2}})
Группируем члены парами, получаем:
( ({{x}^{3}}-5{{x}^{2}}y)-(3xy-15{{y}^{2}}))
( {{x}^{2}}(x-5y)-3y(x-5y))
( ({{x}^{2}}-3y)(x-5y))
4. Выделение полного квадрата
Можно преобразовать многочлен и привести к виду разности квадратов, например и применить формулу сокращенного умножения
( {{x}^{4}}-4{{x}^{2}}-1=underbrace{{{x}^{4}}-2cdot 2cdot {{x}^{2}}+4}_{text{ }{{left( {{x}^{2}}-2 right)}^{2}}}-4-1={{left( {{x}^{2}}-2 right)}^{2}}-5=left( {{x}^{2}}-2+sqrt{5} right)left( {{x}^{2}}-2-sqrt{5} right))
5. Разложение квадратного трехчлена на множители
Квадратный трехчлен – многочлен вида
( a{{x}^{2}}+bx+c=0)
Теорема. Если квадратное уравнение ( a{{x}^{2}}+bx+c=0) имеет корни ( {{x}_{1}},text{ }{{x}_{2}}), то его можно записать в виде:
( a{{x}^{2}}+bx+c=aleft( x-{{x}_{1}} right)left( x-{{x}_{2}} right)).
Подробнее о каждом из 5-ти способов разложения на множители
1. Вынесение общего множителя за скобки
Это один из самых элементарных способов упростить выражение. Для применения этого метода давай вспомним распределительный закон умножения относительно сложения (не пугайся этих слов, ты обязательно знаешь этот закон, просто мог забыть его название).
Закон гласит:
Чтобы сумму двух чисел умножить на третье число, нужно каждое слагаемое умножить на это число и полученные результаты сложить.
Иначе говоря, ( aleft( btext{ }+text{ }c right)text{ }=text{ }abtext{ }+text{ }ac).
Так же можно проделать и обратную операцию, ( abtext{ }+text{ }actext{ }=text{ }aleft( btext{ }+text{ }c right)).
Вот именно эта обратная операция нас и интересует. Как видно из образца, общий множитель а, можно вынести за скобку.
Подобную операцию можно проделывать как с переменными, такими как ( x) и ( y), например, так и с числами: ( 6text{ }+text{ }8text{ }=text{ }2left( 3text{ }+text{ }4 right)).
Да, это слишком элементарный пример, так же, как и приведенный ранее пример, с разложением числа ( 12), ведь все знают, что числа ( 6), ( 
А как быть, если вам досталось выражение посложнее:
( 3xy+123y)?
Как узнать на что, например, делится число ( 123).
Нееет! С калькулятором-то любой сможет, а без него слабо?
А для этого существуют признаки делимости, эти признаки действительно стоит знать, они помогут быстро понять, можно ли вынести за скобку общий множитель.
Что ж, вернемся к выражению ( 3xy+123y), может вынести за скобку ( y) да и хватит с него?
Нет, у математиков принято упрощать, так по полной, выносить ВСЕ, что выносится!
И так, с игреком все понятно, а что с числовой частью выражения? Оба числа нечетные, так что на ( 2) разделить не удастся.
Можно воспользоваться признаком делимости на ( 3), сумма цифр ( 1), ( 2) и ( 3), из которых состоит число ( 123), равна ( 6), а ( 6) делится на ( 3), значит и ( 123) делится на ( 3).
Зная это, можно смело делить в столбик, в результате деления ( 123) на ( 3) получаем ( 41) (признаки делимости пригодились!).
Таким образом, число ( 3) мы можем вынести за скобку, так же, как y и в результате имеем:
( 3xytext{ }+text{ }123ytext{ }=text{ }3ycdot left( xtext{ }+text{ }41 right)).
Чтобы удостовериться, что разложили все верно, можно проверить разложение, умножением!
Также общий множитель можно выносить и в степенных выражениях.
Вот тут, например, ( 2{{x}^{3}}-16{{x}^{2}}+4x), видишь общий множитель?
У всех членов этого выражения есть иксы – выносим, все делятся на ( 2) – снова выносим, смотрим что получилось: ( 2{{x}^{3}}-16{{x}^{2}}+4x=2x({{x}^{2}}-8x+2)).
2. Формулы сокращенного умножения
Формулы сокращенного умножения уже упоминались в теории, если ты с трудом помнишь что это, то тебе стоит освежить их в памяти «Формулы сокращенного умножения».
А вот здесь можно решить вместе с нашим репетитором Алексеем Шевчуком 119 задач на формулы сокращенного умножения!
А вот здесь наше видео о том, какой навык, относящийся к формулам сокращенного умножения является самым сложным и самым важным – выделение полного кавдрата!
Справка.
Эти видео – часть нашего курса подготовки к ЕГЭ по математике. Можно провести бесплатный “тест-драйв” этого курса. Например, посетить наши пробные вебинары.
В чем суть разложения на множители с помощью формул сокращенного умножения?
Суть этого разложения в том, что бы заметить в имеющемся перед тобой выражении какую-то определенную формулу, применить ее и получить, таким образом, произведение чего-то и чего-то, вот и все разложение.
Формулы сокращенного умножения (таблица)
( displaystyle begin{array}{l}left[ 1 right] {{left( a+b right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}\left[ 2 right] {{left( a-b right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}\left[ 3 right] {{a}^{2}}-{{b}^{2}}=left( a-b right)left( a+b right)\left[ 4 right] {{left( a+b right)}^{3}}={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}}\left[ 5 right] {{left( a-b right)}^{3}}={{a}^{3}}-3{{a}^{2}}b+3a{{b}^{2}}-{{b}^{3}}\left[ 6 right] {{a}^{3}}+{{b}^{3}}=left( a+b right)left( {{a}^{2}}-ab+{{b}^{2}} right)\left[ 7 right] {{a}^{3}}-{{b}^{3}}=left( a-b right)left( {{a}^{2}}+ab+{{b}^{2}} right)end{array})
А теперь попробуй, разложи на множители следующие выражения, используя приведенные выше формулы:
- ( displaystyle 16{{b}^{2}}-8b+1)
- ( displaystyle -42c+9{{c}^{2}}+49)
- ( displaystyle {{left( 5text{a} right)}^{2}}-3)
- ( displaystyle frac{left( 4text{a}+2text{b} right)cdot left( 4text{a}-2text{b} right)}{16{{text{a}}^{2}}+4{{text{b}}^{2}}-16text{ab}})
- ( displaystyle {{left( 3text{a} right)}^{3}}-1)
Вот что должно было получиться:
3. Метод группировки
А вот тебе еще примерчик:
( displaystyle {{x}^{3}}-3xy-5{{x}^{2}}y+15{{y}^{2}})
Ну и что с ним делать будешь? Вроде бы и на ( displaystyle 3) что-то делится и на ( displaystyle 5), а что-то на ( displaystyle x) и на ( displaystyle y)
Но все вместе на что-то одно не разделишь, ну нет тут общего множителя, как не ищи, что, так и оставить, не раскладывая на множители?
Тут надо смекалку проявить, а имя этой смекалке – группировка!
Применяется она как раз, когда общие делители есть не у всех членов. Для группировки необходимо найти группки слагаемых, имеющих общие делители и переставить их так, чтобы из каждой группы можно было получить один и тот же множитель.
Переставлять местами конечно не обязательно, но это дает наглядность, для наглядности же можно взять отдельные части выражения в скобки, их ставить не запрещается сколько угодно, главное со знаками не напутать.
Не очень понятно все это? Объясню на примере:
В многочлене ( displaystyle {{x}^{3}}-3xy-5{{x}^{2}}y+15{{y}^{2}}) ставим член – ( displaystyle 3xy) после члена – ( displaystyle 5x2y) получаем:
( displaystyle {{x}^{3}}-5{{x}^{2}}y-3xy+15{{y}^{2}})
Группируем первые два члена вместе в отдельной скобке и так же группируем третий и четвертый члены, вынеся за скобку знак «минус», получаем:
( displaystyle ({{x}^{3}}-5{{x}^{2}}y)-(3xy-15{{y}^{2}}))
А теперь смотрим по отдельности на каждую из двух “кучек”, на которые мы разбили выражение скобками.
Хитрость в том, чтоб разбить на такие кучки, из которых можно будет вынести максимально большой множитель, либо, как в этом примере, постараться сгруппировать члены так, чтобы после вынесения из кучек множителей за скобку у нас внутри скобок оставались одинаковые выражения.
Из обеих скобок выносим за скобки общие множители членов, из первой скобки ( displaystyle {{x}^{2}}), а из второй ( displaystyle 3y), получаем:
( displaystyle {{x}^{2}}(x-5y)-3y(x-5y))
Но это же не разложение!
После разложения должно остаться только умножение, а пока у нас многочлен просто поделен на две части…
НО! Этот многочлен имеет общий множитель. Это ( displaystyle (x-5y))
( displaystyle (x-5y))за скобку и получаем финальное произведение ( displaystyle ({{x}^{2}}-3y)(x-5y))
Бинго! Как видишь, тут уже произведение и вне скобок нет ни сложения, ни вычитания, разложение завершено, т.к. вынести за скобки нам больше нечего.
Может показаться чудом, что после вынесения множителей за скобки у нас в скобках остались одинаковые выражения ( displaystyle (x-5y)), которые опять же мы и вынесли за скобку.
И вовсе это не чудо, дело в том, что примеры в учебниках и в ЕГЭ специально сделаны так, что большинство выражений в заданиях на упрощение или разложение на множители при правильном к ним подходе легко упрощаются и резко схлопываются как зонтик при нажатии на кнопку, вот и ищи в каждом выражении ту самую кнопку.
Что-то я отвлекся, что у нас там с упрощением? Замысловатый многочлен принял более простой вид: ( displaystyle {{x}^{3}}-3xy-5{{x}^{2}}y+15{{y}^{2}}=({{x}^{2}}-3y)(x-5y)).
Согласись, уже не такой громоздкий, как был?
4. Выделение полного квадрата
Иногда для применения формул сокращенного умножения (повтори тему «Формулы сокращенного умножения») необходимо преобразовать имеющийся многочлен, представив одно из его слагаемых в виде суммы или разности двух членов.
В каком случае приходится это делать, узнаешь из примера:
Многочлен ( displaystyle {{x}^{2}}-4x+2) в таком виде не может быть разложен при помощи формул сокращенного умножения, поэтому его необходимо преобразовать.
Возможно, поначалу тебе будет не очевидно какой член на какие разбивать, но со временем ты научишься сразу видеть формулы сокращенного умножения, даже если они не присутствуют не целиком, и будешь довольно быстро определять, чего здесь не хватает до полной формулы, а пока – учись, студент, точнее школьник.
Для полной формулы квадрата разности здесь нужно ( displaystyle 4) вместо ( displaystyle 2).
Представим третий член ( displaystyle 2) как разность ( displaystyle 4-2), получим: ( displaystyle {{x}^{2}}-4x+4-2=({{x}^{2}}-4x+4)-2)
К выражению в скобках можно применить формулу квадрата разности (не путать с разностью квадратов!!!), имеем: ( displaystyle {{left( x-2 right)}^{2}}-2), к данному выражению можно применить формулу разности квадратов (не путать с квадратом разности!!!), представив ( displaystyle 2), как ( displaystyle sqrt{2}), получим: ( displaystyle (x-2-sqrt{2})(x-2+sqrt{2})).
Не всегда разложенное на множители выражение выглядит проще и меньше, чем было до разложения, но в таком виде оно становится более подвижным, в том плане, что можно не париться про смену знаков и прочую математическую ерунду.
Ну а вот тебе для самостоятельного решения, следующие выражения нужно разложить на множители.
Примеры:
- ( displaystyle 25{{m}^{2}}-49{{n}^{2}};)
- ( displaystyle {{b}^{2}}-{{(a+1)}^{2}};)
- ( displaystyle {{(x-y)}^{2}}-{{(x+y+1)}^{2}};)
- ( displaystyle {{x}^{2}}+2{x}-3)
- ( displaystyle {{x}^{2}}+6x+5;)
Решения:
5. Разложение квадратного трехчлена на множители. Пример
Квадратный трехчлен – многочлен вида ( displaystyle a{{x}^{2}}+bx+c=0), где ( displaystyle x) – неизвестное, ( displaystyle a), ( displaystyle b), ( displaystyle c) – некоторые числа, причем ( displaystyle ane 0).
Значения переменной ( displaystyle x), которые обращают квадратный трехчлен в ноль, называются корнями трехчлена. Следовательно, корни трехчлена – это корни квадратного уравнения ( displaystyle a{{x}^{2}}+bx+c=0).
Если не помнишь, как находить эти корни, читай тему «Квадратные уравнения».
Теорема.
Если квадратное уравнение ( displaystyle a{{x}^{2}}+bx+c=0) имеет корни ( displaystyle {{x}_{1}},text{ }{{x}_{2}}), то его можно записать в виде: ( displaystyle a{{x}^{2}}+bx+c=aleft( x-{{x}_{1}} right)left( x-{{x}_{2}} right)).
Пример:
Разложим на множители квадратный трехчлен: ( displaystyle 2{{x}^{2}}+5x-3).
Сначала решим квадратное уравнение: Теперь можно записать разложение данного квадратного трехчлена на множители:
( displaystyle begin{array}{l}2{{x}^{2}}+5x-3=0.\{{x}_{1,2}}=frac{-5pm sqrt{{{5}^{2}}-4cdot 2cdot left( -3 right)}}{2cdot 2}=frac{-5pm sqrt{25+24}}{4}=frac{-5pm 7}{4};\{{x}_{1}}=frac{1}{2};text{ }{{x}_{2}}=-3.end{array})
( displaystyle 2{{x}^{2}}+5x-3=2left( x-frac{1}{2} right)left( x+3 right)).
I ср.
1. процесс действия по гл. разложить II, разложиться II
2. Результат такого действия.
II ср.
1. процесс действия по гл. разложить V, разлагать I, разложиться III, разлагаться I 1., 2.
2. Результат такого действия; разлагание I 2..
III ср.
1. процесс действия по гл. разложить VI, разлагать II, разложиться IV, разлагаться II 1.
2. Результат такого действия; разлагание II 2..
IV ср.
1. процесс действия по гл. разложить VII, разлагать III
2. Результат такого действия.
РАЗЛОЖЕ́НИЕ, разложения, мн. нет, ср. (книжн.).
1. Действие по гл. разложить в 6, 7 и 8 знач. — разлагать. Разложение воды на составные части. Разложение множителя. Разложение окиси на ртуть и кислород. Разложение армии врага.
2. Состояние по гл. разложиться в 4, 5 и 6 знач. — разлагаться. Разложение трупа. Разложение капиталистического общества.
3. перен. Дезорганизованность, внутренний распад, упадок. «Оппозиционеры рассчитывали внести разложение в ряды большевистской партии после смерти Ленина…» История ВКП(б). В армии врага полное разложение. Дошел до окончательного разложения.
РАЗЛОЖИ́ТЬ 2, -ожу́, -о́жишь; -о́женный; сов.
РАЗЛОЖЕ́НИЕ -я; ср. к Разложи́ть (5-7 зн.) и Разложи́ться (2-4 зн.). Р. химических соединений. Р. числа на множители. Р. опавших листьев. Р. монархии.
-я, ср.
Действие по глаг. разложить (в 5, 6 и 7 знач.)
и состояние по глаг. разложиться (во 2, 3 и 4 знач.).
Разложение химических соединений. Разложение числа на множители. Разложение опавших листьев. Разложение монархии.
◊
Чем ближе подъезжал Григорий к фронту, тем шире открывалась перед его глазами отвратительная картина разложения Донской армии. Шолохов, Тихий Дон.
разложе́ние, разложе́ния, разложе́ний, разложе́нию, разложе́ниям, разложе́нием, разложе́ниями, разложе́нии, разложе́ниях
сущ., кол-во синонимов: 47
сущ.
1.
гниение
тление
тлен
распад
разрушение органического вещества)
2.
развращение
растление
доведение до морального падения)
1.
Syn: см. распад
1.
Syn: диссоциация, разбиение, расщепление, декомпозиция, распад
Ant: соединение, ассоциирование
2.
‘моральная деградация’
Syn: развращенность, аморальность
3.
‘характеристика нестабильности в государстве’
Syn: упадок, спад, загнивание
Ant: подъем
4.
Syn: гниение, порча
РАСПАД И РАЗЛОЖЕНИЕ
В словарь общерусского литературного языка впиталось много научных и специальных терминов. Выйдя за пределы профессиональной речи, эти термины расширяют свои значения и вовлекаются в новые фразеологические контексты. Внедрившись в литературную лексику, соотносительные термины из разных научных дисциплин становятся здесь синонимами.
Слово распад не зарегистрировано ни одним словарем русского литературного языка вплоть до словаря В. И. Даля. Оно не свойственно языку русской художественно-повествовательной прозы XIX в. Еще в самом конце XIX в. адвокат, поэт и литературный критик С. А. Андреевский, употребив это слово в своей статье «Вырождение рифмы», предупреждает читателя, что это, в сущности, специальный научный, в частности, медицинский термин: «…антитеза — Случевский и Ростан — всего лучше доказывает вырождение рифмы. Если содержание искренно и современно — зато форма плоха, когда форма превосходна — содержание фальшиво. «Распад», как выразился бы медик, установлен вполне» (Андреевский, с. 457).
Слово распад явилось семантическим восполнением более старого слова распадение и было вызвано к жизни теми смысловыми осложнениями, которые обозначились в истории глагола распадаться — распасться. В русском литературном языке до XIX в. слово распадаться — распасться выражало прямое конкретное значение: `разваливаться, разрушаться’ (см. сл. АР 1822, ч. 5, с. 963), `падая, приходить в разрушение’ (сл. 1867-1868, ч. 4, с. 94). То же значение отражалось и в производном существительном распадение. К этому основному значению глагола распадаться — распасться в русском литературном языке около середины XIX в. присоединился оттенок: `приходить в полное расстройство, разлаживаться’.
Кроме значений по глаголу распадаться — распасться, слово распадение в философском языке русских интеллигентов 30-40-х годов обозначало также отсутствие внутренней гармонии, мучительную борьбу духа (ср. немецк. Zerfall). Например, у М. А. Бакунина в статье «Гимназические речи Гегеля. Предисловие переводчика» (1837): «…жизнь его [призрачного человека] есть ряд беспрестанных мучений, беспрестанных разочарований, борьба без выхода и без конца — и это внутреннее распадение, эта внутренняя разорванность есть необходимое следствие отвлеченности и призрачности конечного рассудка, для которого нет ничего конкретного…».
В письме В. Г. Белинского к М. А. Бакунину от 12-24 октября 1838 г. читаем: «Но это распадение и эта отвлеченность были ужасным злом и страшною мукою для меня только в настоящем…».
В русском научном языке первой половины XIX в. глагол распадаться приобретает новое значение: «разделяться на составные элементы». Например, ткань распадается; молекула распалась на атомы.
Из языка естественных наук этот термин затем переходит и в область общественных наук, выражая близкое значение: `разъединяться, разбиваться на отдельные части, утратив цельность’. Например, общество распалось на обособленные группы.
Именно в связи с этими новыми значениями является потребность в термине распад.
Показательно, что даже В. И. Даль, обычно производящий все возможные типы отглагольных существительных со значением процесса, для глагола распадаться — распасться указывает лишь распаданье, распаденье. Только проф. И. А. Бодуэн де Куртенэ внес в словарь В. И. Даля слово распад с таким примером: «Он убеждается в страшной картине своего наступающего распада» (сл. Даля 1913, 4, с. 1607). У М. Горького в статье «О том, как я учился писать»: «В то время как в Европе идет процесс внутреннего распада человека, у нас, в трудовой массе, развивается крепкая уверенность в своей силе и в силе коллектива». Слово распад входит в широкий литературный оборот не ранее последних десятилетий XIX в. — начала XX в. Например, в книге А. А. Измайлова «Помрачение божков и новые кумиры»: «Людей психического распада беллетристы фотографировали в момент начинающегося перехода их за грань нормальности и подробно следили за ростом их навязчивой идеи, вплоть до разрешения ее в крови или смерти» (Измайлов, с. 168). В повести М. Пантюхова «Тишина и старик» (1907): «Женя в бреду ушла из дома, простудилась и умерла. Юрий оставляет ее в своем доме. Его влечет к ее трупу, несмотря на невыносимый запах разложения. Его собственный распад идет уже не по дням, а по часам» (Пантюхов, с. 204). У В. В. Вересаева в «Воспоминаниях» «…уже намечался и в самом народническом течении некоторый идейный распад (Вересаев, с. 279).
Слово распад, включившись в систему русской литературной лексики, вступило в синонимическое соотношение с книжным словом разложение, которое гораздо раньше укрепилось в русском общенациональном языке.
Глаголов разлагать или разложиться — разлагаться не найдем в словарях Академии Российской. А слово разложение здесь определяется как `раскладывание’ (сл. АР 1822, ч. 5, с. 963) соответственно конкретно-бытовым значениям глагола разложить. Но уже в словаре 1847 г. помещен глагол разлагать, в котором отмечается химическое значение: `разделять на составные части’. Разложить соль, селитру (сл. 1867-1868, 4, с. 37). Слово жеразложение рассматривается не только в связи с бытовыми значениями глагола разложить — раскладывать, но и как математический и химический термин (`изображение количества в каком-либо виде’): Разложение числа на множители. Разложение многоугольника на треугольники (сл. 1967-1968, 4, с. 39).Ср. франц. décomposition и в математике développement, немецк. Zerlegung и Zerfall.
В русском литературном языке 30-х годов, когда в разных его стилях намечается сильное стремление к сближению с научной терминологией и фразеологией, слова разложить и разложение в новых значениях из области химии переносятся на почву публицистической и повествовательной речи. По-видимому, раньше и ярче всего новое употребление этих слов выступает в языке О. И. Сенковского. Во всяком случае, в анонимной повести «Авторский вечер», направленной против «Библиотеки для чтения», нашел место такой пародический выпад: «Любовь разложила меня в стихии всех возможных чувствований, и если б она… меня… поцеловала, я бы в один миг испарился… я показываю, что я учился Физике и Химии, знаю, что можно разлагать всякую вещь на стихии; любовь разложила меня! Знаю, что все разложенное на стихии может испариться» (Авторский вечер, с. 119).
А. И. Герцен наряду с другими естественно-научными терминами вводит в широкий литературно-публицистический оборот и слова разложение, разложиться в их химическом значении, например, в отрывке «О себе»: « — Гемфри Деви умер, — отвечал магистр, весь занятый своим спором. — И, я думаю, рад от души, — продолжал оратор, — что, наконец, химически разложился и на себе может испытывать соединение и разложение».
В письме Н. Огарева и А. И. Герцена Н. Н. Обручеву (1861): «…как будто, историческая смерть есть вымирание людей, а не разложение общественных химических соединений известного порядка!». Сравните у Тургенева в «Казни Тропмана» (1854): «Замечено, что осужденные на казнь по объявлении им приговора либо впадают в совершенную бесчувственность и как бы заранее умирают и разлагаются…»
В воспоминаниях Д. В. Григоровича: «Если бы гр. Фредро можно было бы разложить химически, разлить его выжимку в склянки и дать выпить одну десяти французам, другую десяти англичанам, каждый из них непременно бы заявил себя чем-нибудь в том или другом роде; из гр. Фредро ничего не вышло…». Вместе с тем, термин разложение был тесно связан с философской гегельянской терминологией 30-40-х годов. Тургенев писал Некрасову (в письме от 10-го июля 1855 г.): «Я действительно, как ты говоришь, находился — и отчасти нахожусь — в моменте если не разложения, то сомнения в себе» (Голос минувшего, 1916, № 5-6, с. 33).
У К. Пруткова в пародическом стихотворении «Безвыходное положение», направленном против Ап. А. Григорьева и его критических статей («Русская литература в 1851 г.» и «Русская изящная литература в 1852 году»):
…Но разложенья вдруг нечаянный момент
Настиг мой славный план, и я вотще стараюсь
Хоть точку в сей беде исходную найти!
Получив такое широкое философское значение и применение, слово разложение стало одним из общепризнанных выражений публицистического языка 50-60-х годов. У Тургенева в «Воспоминаниях о Белинском» читаем: «Белинский еще потому благоговел перед памятью Петра Великого и, не обинуясь, признавал его нашим спасителем, что уже при Алексее Михайловиче он в нашем старом общественном и гражданском строе находил несомненные признаки разложения…». В письме К. Д. Кавелина к А. И. Герцену (май 1862): «…я счел бы себя бесчестным человеком, если б советовал барину, попу, мужику, офицеру, студенту ускоривать процесс разложения обветшалых исторических общественных форм».
У Аполлона Григорьева в «Моих литературных и нравственных скитальчествах»: «…так как процесс литературных стремлений есть процесс органический, то поприсмотритесь еще к данной минуте и посмотрим, нет ли уже в ней самой зачатков плана разложения» (Григорьев Ап., с. 115).
В русском литературном языке второй половины XIX в. новое употребление слов разложение, разложиться укореняется в языке революционно- демократической печати и затем входит в общую норму русского литературно-книжного языка.
Сравните у Ф. М. Достоевского в романе «Преступление и наказание» (1866, в речи студента): «За одну жизнь — тысячи жизней, спасенных от гниения и разложения».
Сравните позднее у М. Арцыбашева в рассказе «Смех» размышления доктора о смерти: «…как художественно ясно представился ему процесс разложения, та слизь и гниль, которая получится из него, представились толстые, ленивые, белые черви, распухшие от его гноя…» (Арцыбашев, с. 198).
В самом конце XIX в. и особенно ярко с 20-х годов XX в. выступает в слове разложение новый семантический оттенок: дезорганизованность, внутренний распад, упадок. В словаре Ушакова этот оттенок иллюстрируется такими примерами: «Оппозиционеры рассчитывали внести разложение в ряды большевистской партии после смерти Ленина… В армии врага полное разложение. Дошел до окончательного разложения» (3, с. 1163).
Опубликовано в кн.: «Доклады и сообщения филологического факультета МГУ. Вып. 5» (Изд-во МГУ, 1948) вместе со статьей «Обобществить» под общим названием «Из истории русской литературной лексики». В архиве сохранилась рукопись (9 листков разного формата). В рукописи статья открывается следующей цитатой: «…литературный язык — это форма выражения, ставшая традиционной; это — остаток, результат всех стилей, усвоенных от разных последовательно сменявшихся поколений, сумма литературных элементов, переваренных коммуникацией. Они образуют часть общего фонда, отличную от непосредственного языка. Литературный язык имеет свой словарь…, свои клише…, условную конструкцию фраз…» (Сh. Ваllу. Lе langagе et la vie, Рауоt, Раris, 1926, р. 44). Здесь печатается по оттиску. — И. У.
Как правильно пишется слово «разлагать»
разлага́ть(ся)
разлага́ть(ся), -а́ю(сь), -а́ет(ся)
Источник: Орфографический
академический ресурс «Академос» Института русского языка им. В.В. Виноградова РАН (словарная база
2020)
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать
Карту слов. Я отлично
умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: шляхтич — это что-то нейтральное, положительное или отрицательное?
Синонимы к слову «разлагать»
Предложения со словом «разлагать»
- Как, господа, присягать правительству, которому не веришь, которое уже сейчас разлагает армию, хотя и пустозвонит о войне до победы?..
- Как только уровень глюкозы в крови падает, наше тело начинает разлагать гликоген, добывая по одной молекуле глюкозы за раз, и сжигать их по мере необходимости.
- Помимо назначения командующих, обе воюющие стороны стали разлагать наименее устойчивых бойцов в стане противника.
- (все предложения)
Цитаты из русской классики со словом «разлагать»
- Антропософия разлагала целость человеческой личности, потрошила душу не менее психоанализа.
- Самый процесс жизни он выдавал и за ее конечную цель. Разлагая материю на составные части, он думал, что разложил вместе с тем и все, что выражает материя.
- Воля у нас не воспитывалась, а подавлялась, извне — государством, а изнутри разлагала ее свободная мысль.
- (все
цитаты из русской классики)
Афоризмы русских писателей со словом «разлагать»
- Мне, как поэту, дела нету,
Откуда будет свет, лишь был бы это свет —
Лишь был бы он, как солнце для природы,
И разлагал бы все, в чем духа больше нет… - (все афоризмы русских писателей)
Отправить комментарий
Дополнительно
Смотрите также
РАЗЛАГА́ТЬ, —а́ю, —а́ешь; прич. наст. разлага́ющий. Несов. к разложить (в 5, 6 в 7 знач.).
Все значения слова «разлагать»
-
Как, господа, присягать правительству, которому не веришь, которое уже сейчас разлагает армию, хотя и пустозвонит о войне до победы?..
-
Как только уровень глюкозы в крови падает, наше тело начинает разлагать гликоген, добывая по одной молекуле глюкозы за раз, и сжигать их по мере необходимости.
-
Помимо назначения командующих, обе воюющие стороны стали разлагать наименее устойчивых бойцов в стане противника.
- (все предложения)
- раскладывать
- разложить
- развешивать
- рассовывать
- рассортировывать
- (ещё синонимы…)
- разложить по тарелкам
- разложить костёр
- разложить по банкам
- (полная таблица сочетаемости…)
- Спряжение глагола «разлагать»
- Разбор по составу слова «разлагать»
Разложить многочлен на множители означает представить его в виде произведения двух или нескольких многочленов.
Примером разложения многочлена на множители является вынесение общего множителя за скобки, поскольку исходный многочлен обращается в произведение двух сомножителей, один из которых является одночленом, а другой многочленом.
Разложение многочлена на множители способом вынесения общего множителя за скобки
При вынесении общего множителя за скобки образуется произведение из двух сомножителей, один из которых является одночленом, а другой многочленом. Например:
6x + 3xy = 3x(2 + y)
В рамках изучения многочленов, одночлен принято считать многочленом, состоящим из одного члена. Поэтому, когда в многочлене выносится за скобки общий множитель, то говорят что исходный многочлен представлен в виде произведения многочленов.
В нашем примере многочлен 6x + 3xy был представлен в виде произведения многочленов 3x и (2 + y). По-другому говорят, что многочлен 6x + 3xy разложен на множители 3x и (2 + y)
Существуют также многочлены, в которых можно вынести за скобки такой общий множитель, который является двучленом. Например, рассмотрим многочлен 5a(x + y) + 7a(x + y). В этом многочлене общим множителем является двучлен (x + y). Вынесем его за скобки:
Разложение многочлена на множители способом группировки
Некоторые многочлены содержат группу членов, имеющих общий множитель. Такие группы можно заключать в скобки и далее выносить общий множитель за эти скобки. В результате получается разложение исходного многочлена на множители, которое называют разложением на множители способом группировки.
Рассмотрим следующий многочлен:
ax + ay + 3x + 3y
Члены ax и ay имеют общий множитель a. Выпишем эти члены и заключим их в скобки:
(ax + ay)
Далее в многочлене ax + ay + 3x + 3y члены 3x и 3y имеют общий множитель 3. Выпишем эти члены и тоже заключим их в скобки:
(3x + 3y)
Теперь соединим выражения (ax + ay) и (3x + 3y) знаком «плюс»
(ax + ay) + (3x + 3y)
В многочлене (ax + ay) вынесем за скобки общий множитель a, а в многочлене (3x + 3y) вынесем за скобки общий множитель 3. Делать это нужно в исходном выражении:
Далее замечаем, что двучлен (x + y) является общим множителем. Вынесем его за скобки. Продолжаем решение в исходном примере. В результате получим:
Запишем решение покороче, не расписывая подробно, как каждый член был разделен на общий множитель. Тогда решение получится более компактным:
Чтобы проверить правильно ли мы разложили многочлен на множители, выполним умножение (x + y)(a + 3). Если мы всё сделали правильно, то получим многочлен ax + ay + 3x + 3y
(x + y)(a + 3) = ax + ay + 3x + 3y
Пример 2. Разложить многочлен 9x + ax − 9y − ay на множители способом группировки.
Члены 9x и −9y имеют общий множитель 9. А члены ax и −ay имеют общий множитель a. Сгруппируем их с помощью скобок, и объединим с помощью знака «плюс»
(9x − 9y) + (ax − ay)
В первой группе (9x − 9y) вынесем за скобки общий множитель 9. Во второй группе (ax − ay) вынесем за скобки за скобки общий множитель a
(9x − 9y) + (ax − ay) = 9(x − y) + a(x − y)
Далее вынесем за скобки двучлен (x − y)
(9x − 9y) + (ax − ay) = 9(x − y) + a(x − y) = (x − y)(9 + a)
Пример 3. Разложить многочлен ab − 3b + b2 − 3a на множители способом группировки.
Сгруппируем первый член ab с четвёртым членом −3a. А второй член −3b сгруппируем с третьим членом b2. Не забываем, что объединять группы нужно с помощью знака «плюс»
(ab − 3a) + (−3b + b2)
В первой группе вынесем за скобки общий множитель a, во второй группе — общий множитель b
(ab − 3a) + (−3b + b2) = a(b − 3) + b(−3 + b)
Во втором произведении b(−3 + b) в сомножителе (−3 + b) изменим порядок следования членов. Тогда получим b(b − 3)
(ab − 3a) + (−3b + b2) = a(b − 3) + b(b − 3)
Теперь вынесем за скобки общий множитель (b − 3)
(ab − 3a) + (−3b + b2) = a(b − 3) + b(b − 3) = (b − 3)(a + b)
Пример 4. Разложить многочлен x2y + x + xy2 + y + 2xy + 2 на множители способом группировки.
Сгруппируем первый член многочлена со вторым, третий с четвёртым, пятый с шестым:
В первой группе вынесем за скобки общий множитель x, во второй группе — общий множитель y, в третьей группе — общий множитель 2
Далее замечаем, что многочлен (xy + 1) является общим множителем. Вынесем его за скобки:
Разложение многочлена на множители по формуле квадрата суммы двух выражений
Формулы сокращённого умножения, которые мы рассматривали в прошлом уроке, можно применять для разложения многочленов на множители.
Вспомним, как выглядит формула квадрата суммы двух выражений:
(a + b)2 = a2 + 2ab + b2
Поменяем местами левую и правую часть, получим:
a2 + 2ab + b2 = (a + b)2
Левая часть этого равенства является многочленом, а правая часть — произведением многочленов, поскольку выражение (a + b)2 представляет собой перемножение двух сомножителей, каждый из которых равен многочлену (a + b).
Стало быть, если нам встретится выражение вида a2 + 2ab + b2, то мы можем представить его в виде произведения (a + b)(a + b). Иными словами, разложить на множители (a + b) и (a + b).
a2 + 2ab + b2 = (a + b)(a + b)
Пример 1. Разложить на множители многочлен 4x2 + 12xy + 9y2
Чтобы воспользоваться формулой a2 + 2ab + b2 = (a + b)2, нужно узнать чему в данном случае равна переменная a и чему равна переменная b.
Первый член многочлена 4x2 + 12xy + 9y2 является результатом возведения в квадрат одночлена 2x, поскольку (2x)2 = 4x2. Третий член 9y2 является результатом возведения в квадрат одночлена 3y, поскольку (3y)2 = 9y2, а член 12xy это есть удвоенное произведение членов 2x и 3y, то есть 2 × 2x × 3y = 12xy.
Очевидно, что переменная a в данном случае равна 2x, а переменная b равна 3y
a = 2x
b = 3y
Тогда можно сделать вывод, что когда-то выражение 4x2 + 12xy + 9y2 выглядело в виде квадрата суммы (2x + 3y)2, но в результате применения формулы квадрата суммы оно обратилось в многочлен 4x2 + 12xy + 9y2. Наша задача — вернуть ему былую форму, то есть представить в виде (2x + 3y)2
4x2 + 12xy + 9y2 = (2x + 3y)2
А поскольку (2x + 3y)2 это произведение двух сомножителей, каждый из которых равен многочлену (2x + 3y), то исходный многочлен 4x2 + 12xy + 9y2 можно представить в виде разложения на множители (2x + 3y) и (2x + 3y)
4x2 + 12xy + 9y2 = (2x + 3y)(2x + 3y)
Полностью решение можно записать так:
4x2 + 12xy + 9y2 = (2x)2 + 2 × 2x × 3y + (3y)2 = (2x + 3y)2 = (2x + 3y)(2x + 3y)
Пример 2. Разложить на множители многочлен x2 + 12x + 36
Первый член данного многочлена является результатом возведения в квадрат одночлена x, поскольку x2 = x2, третий член — результатом возведения в квадрат числа 6, поскольку 62 = 36, а член 12x это удвоенное произведение членов x и 6, поскольку 2 × x × 6 = 12x.
Воспользуемся формулой a2 + 2ab + b2 = (a + b)2. Роль переменной a играет одночлен x, а роль переменной b играет одночлен 6. Отсюда:
x2 + 12x + 36 = (x + 6)2
А поскольку (x + 6)2 это произведение двух сомножителей, каждый из которых равен многочлену (x + 6), то исходный многочлен x2 + 12x + 36 можно представить в виде разложения на множители (x + 6) и (x + 6)
x2 + 12x + 36 = (x + 6)(x + 6)
Разложение многочлена на множители по формуле квадрата разности двух выражений
Как и по формуле квадрата суммы двух выражений, многочлен можно разложить на множители по формуле квадрата разности двух выражений.
Формула квадрата разности двух выражений выглядит так:
(a − b)2 = a2 − 2ab + b2
Если в этой формуле поменять местами левую и правую часть, то получим:
a2 − 2ab + b2 = (a − b)2
Поскольку правая часть это произведение двух сомножителей, каждый из которых равен (a − b), то многочлен вида a2 − 2ab + b2 можно разложить на множители (a − b) и (a − b).
a2 − 2ab + b2 = (a − b)(a − b)
Пример 1. Разложить на множители многочлен 9x2 − 12xy + 4y2
Чтобы воспользоваться формулой a2 − 2ab + b2 = (a − b)2, нужно узнать чему в данном случае равна переменная a и чему равна переменная b.
Первый член данного многочлена является результатом возведения в квадрат одночлена 3x, поскольку (3x)2 = 9x2. Третий член 4y2 является результатом возведения в квадрат одночлена 2y, поскольку (2y)2 = 4y2, а член 12xy это удвоенное произведение членов 3x и 2y, то есть 2 × 3x × 2y = 12xy.
Очевидно, что переменная a в данном случае равна 3x, а переменная b равна 2y
a = 3x
b = 2y
Тогда можно сделать вывод, что когда-то выражение 9x2 − 12xy + 4y2 выглядело в виде квадрата разности (3x − 2y)2, но в результате применения формулы квадрата разности оно обратилось в многочлен 9x2 − 12xy + 4y2. Наша задача — вернуть ему былую форму, то есть представить в виде (3x − 2y)2
9x2 − 12xy + 4y2 = (3x − 2y)2
А поскольку (3x − 2y)2 это произведение двух сомножителей, каждый из которых равен многочлену (3x − 2y), то исходный многочлен 9x2 − 12xy + 4y2 можно представить в виде разложения на множители (3x − 2y) и (3x − 2y)
9x2 − 12xy + 4y2 = (3x − 2y)(3x − 2y)
Полностью решение можно записать так:
9x2 − 12xy + 4y2 = (3x)2 − 2 × 3x × 2y + (2y)2 = (3x − 2y)2 = (3x − 2y)(3x − 2y)
Пример 2. Разложить на множители многочлен x2 − 4x + 4
Воспользуемся формулой квадрата разности двух выражений:
x2 − 4x + 4 = x2 − 2 × x × 2 + 22 = (x − 2)2 = (x − 2)(x − 2)
Разложение многочлена на множители по формуле куба суммы двух выражений
Вспомним, как выглядит формула куба суммы двух выражений:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
Поменяем местами левую и правую часть, получим:
a3 + 3a2b + 3ab2 + b3 = (a + b)3
Левая часть этого равенства является многочленом, а правая часть — произведением многочленов, поскольку выражение (a + b)3 представляет собой перемножение трёх сомножителей, каждый из которых равен многочлену (a + b).
Стало быть, если нам встретится выражение вида a3 + 3a2b +3ab2 + b3, то мы можем представить его в виде произведения (a + b)(a + b)(a + b). Иными словами, разложить на множители (a + b), (a + b) и (a + b).
a3 + 3a2b + 3ab2 + b3 = (a + b)(a + b)(a + b)
Пример 1. Разложить на множители многочлен m3 + 6m2n + 12mn2 + 8n3
Прежде чем применять формулу куба суммы, следует проанализировать данный многочлен. А именно, убедиться что перед нами действительно куб суммы двух выражений.
Чтобы убедиться, что исходное выражение является кубом суммы двух выражений, следует узнать чему в данном случае равна переменная a и чему равна переменная b.
Первый член данного многочлена является результатом возведения в куб одночлена m
m3 = m3
Последний член 8n3 является результатом возведения в куб одночлена 2n
(2n)3 = 8n3
Второй член 6m2n является утроенным произведением квадрата первого выражения m и последнего 2n
3 × m2 × 2n = 6m2n
Третий член 12mn2 является утроенным произведением первого выражения m и квадрата последнего выражения 2n
3 × m × (2n)2 = 3 × m × 4n2 = 12mn2
То есть исходный многочлен m3 + 6m2n + 12mn2 + 8n3 по всем параметрам соответствует кубу суммы двух выражений. Переменной a в данном многочлене соответствует m, а переменной b соответствует 2n
a = m
b = 2n
Тогда можно сделать вывод, что когда-то выражение m3 + 6m2n + 12mn2 + 8n3 выглядело в виде куба суммы (m + 2n)3, но в результате применения формулы куба суммы оно обратилось в многочлен m3 + 6m2n + 12mn2 + 8n3. Наша задача — вернуть ему былую форму, то есть представить в виде (m + 2n)3
m3 + 6m2n + 12mn2 + 8n3 = (m + 2n)3
А поскольку (m + 2n)3 это произведение трёх сомножителей, каждый из которых равен многочлену (m + 2n), то исходный многочлен m3 + 6m2n + 12mn2 + 8n3 можно представить в виде разложения на множители (m + 2n), (m + 2n) и (m + 2n)
m3 + 6m2n + 12mn2 + 8n3 = (m + 2n)(m + 2n)(m + 2n)
Пример 2. Разложить на множители многочлен 125x3 + 75x2 + 15x + 1
Первый член данного многочлена является результатом возведения в куб одночлена 5x
(5x)3 = 125x3
Последний член 1 является результатом возведения в куб одночлена 1
13 = 1
Второй член 75x2 является утроенным произведением квадрата первого выражения 5x и последнего 1
3 × (5x)2 × 1 = 3 × 25x2 = 75x2
Третий член 15x является утроенным произведением первого выражения 5x и квадрата второго выражения 1
3 × 5x × 12 = 15x
Воспользуемся формулой a3 + 3a2b + 3ab2 + b3 = (a + b)3. Роль переменной a играет одночлен 5x, а роль переменной b играет одночлен 1
a = 5x
b = 1
Поэтому,
125x3 + 75x2 + 15x + 1 = (5x + 1)3
А поскольку (5x + 1)3 это произведение трёх сомножителей, каждый из которых равен многочлену (5x + 1), то исходный многочлен 125x3 + 75x2 + 15x + 1 можно представить в виде разложения на множители (5x + 1), (5x + 1) и (5x + 1)
125x3 + 75x2 + 15x + 1 = (5x + 1)(5x + 1)(5x + 1)
Разложение многочлена на множители по формуле куба разности двух выражений
Как и по формуле куба суммы двух выражений, многочлен можно разложить на множители по формуле куба разности двух выражений.
Вспомним, как выглядит формула куба разности двух выражений:
(a − b)3 = a3 − 3a2b + 3ab2 − b3
Если в этой формуле поменять местами левую и правую часть, то получим:
a3 − 3a2b + 3ab2 − b3 = (a − b)3
Поскольку правая часть это произведение трёх сомножителей, каждый из которых равен (a − b), то многочлен вида a3 − 3a2b + 3ab2 − b3 можно разложить на множители (a − b), (a − b) и (a − b).
a3 − 3a2b + 3ab2 − b3 = (a − b)(a − b)(a − b)
Пример 1. Разложить на множители многочлен 64 − 96x + 48x2 − 8x3
Прежде чем применять формулу куба разности, следует проанализировать данный многочлен. А именно, убедиться что перед нами действительно куб разности двух выражений.
Чтобы убедиться, что исходное выражение является кубом разности двух выражений, следует узнать чему в данном случае равна переменная a и чему равна переменная b.
Первый член данного многочлена является результатом возведения в куб одночлена 4
43 = 64
Последний член 8x3 является результатом возведения в куб одночлена 2x
(2x)3 = 8x3
Второй член 96x является утроенным произведением квадрата первого выражения 4 и последнего 2x
3 × 42 × 2x = 3 × 16 × 2x = 96x
Третий член 48x2 является утроенным произведением первого выражения 4 и квадрата второго выражения 2x
3 × 4 × (2x)2 = 3 × 4 × 4x2 = 48x2
Видим, что исходный многочлен 64 − 96x + 48x2 − 8x3 по всем параметрам соответствует кубу разности двух выражений. Переменной a в данном многочлене соответствует 4, а переменной b соответствует 2x
a = 4
b = 2x
Тогда можно сделать вывод, что когда-то выражение 64 − 96x + 48x2 − 8x3 выглядело в виде куба разности (4 − 2x)3, но в результате применения формулы куба разности оно обратилось в многочлен 64 − 96x + 48x2 − 8x3. Наша задача — вернуть ему былую форму, то есть представить в виде (4 − 2x)3
64 − 96x + 48x2 − 8x3 = (4 − 2x)3
А поскольку (4 − 2x)3 это произведение трёх сомножителей, каждый из которых равен (4 − 2x), то исходный многочлен 64 − 96x + 48x2 − 8x3 можно представить в виде разложения на множители (4 − 2x), (4 − 2x) и (4 − 2x)
64 − 96x + 48x2 − 8x3 = (4 − 2x)(4 − 2x)(4 − 2x)
Пример 2. Разложить на множители многочлен 27 − 135x + 225x2 − 125x3
Первый член данного многочлена является результатом возведения в куб одночлена 3
33 = 27
Последний член 125 является результатом возведения в куб одночлена 5x
(5x)3 = 125x3
Второй член 135x является утроенным произведением квадрата первого выражения 3 и последнего 5x
3 × 32 × 5x = 3 × 9 × 5x = 135x
Третий член 225x2 является утроенным произведением первого выражения 3 и квадрата второго выражения 5x
3 × 3 × (5x)2 = 3 × 3 × 25x2 = 225x2
Воспользуемся формулой a3 − 3a2b + 3ab2 − b3 = (a − b)3. Роль переменной a играет одночлен 3, а роль переменной b играет одночлен 5x
a = 3
b = 5x
Поэтому,
27 − 135x + 225x2 − 125x3 = (3 − 5x)3
А поскольку (3 − 5x)3 это произведение трёх сомножителей, каждый из которых равен многочлену (3 − 5x), то исходный многочлен 27 − 135x + 225x2 − 125x3 можно представить в виде разложения на множители (3 − 5x), (3 − 5x) и (3 − 5x)
125x3 + 75x2 + 15x + 1 = (3 − 5x)(3 − 5x)(3 − 5x)
Разложение многочлена на множители по формуле разности квадратов двух выражений
Вспомним, как выглядит формула умножения разности двух выражений на их сумму:
(a − b)(a + b) = a2 − b2
Если в этой формуле поменять местами левую и правую часть, то получим:
a2 − b2 = (a − b)(a + b)
Эту формулу называют разностью квадратов. Она позволяет разложить выражение вида a2 − b2 на множители (a − b) и (a + b).
Пример 1. Разложить на множители многочлен 16x2 − 25y2
Чтобы воспользоваться формулой a2 − b2 = (a − b)(a + b), следует узнать чему в данном случае равна переменная a и чему равна переменная b.
Первый член 16x2 является результатом возведения в квадрат одночлена 4x
(4x)2 = 16x2
Второй член 25y2 является результатом возведения в квадрат одночлена 5y
(5y)2 = 25y2
То есть в данном случае переменной a соответствует одночлен 4x, а переменной b соответствует одночлен 5y
a = 4x
b = 5y
Теперь можно воспользоваться формулой a2 − b2 = (a − b)(a + b). Подставим в неё наши значения a и b
(4x)2 − (5y)2 = (4x − 5y)(4x + 5y)
Полностью решение можно записать так:
16x2 − 25y2 = (4x)2 − (5y)2 = (4x − 5y)(4x + 5y)
Для проверки можно выполнить умножение (4x − 5y)(4x + 5y). Если мы всё сделали правильно, то должны получить 16x2 − 25y2
(4x − 5y)(4x + 5y) = 16x2 − 20xy + 20xy − 25y2 = 16x2 − 25y2
Пример 2. Разложить на множители многочлен x2 − y2
В данном случае переменной a соответствует x, а переменной b соответствует y. Тогда по формуле квадрата разности имеем:
x2 − y2 = (x − y)(x + y)
Случай как в данном примере является наиболее простым, поскольку здесь сразу видно чему равно a и чему равно b.
Чаще всего члены, из которых состоит исходная разность, являются результатами возведения во вторую степень каких-нибудь одночленов. Чтобы узнать чему в таком случае равны a и b, нужно как в первом примере представить члены исходной разности в виде одночленов возведённых в квадрат.
Например, чтобы разложить многочлен 4x4 − 9y6 на множители, нужно исходные члены представить в виде одночленов возведённых в квадрат. Первый член в виде одночлена, возведенного в квадрат, можно записать как (2x2)2, поскольку вычисление этого выражение даёт в результате 4x4
(2x2)2 = 4x4
А член 9y6 в виде одночлена, возведенного в квадрат, можно записать как (3y3)2, поскольку вычисление этого выражение даёт в результате 9y6
(3y3)2 = 9y6
Теперь мы знаем, чему равны a и b. Они равны 2x2 и 3y3 соответственно. Подставим их в формулу a2 − b2 = (a − b)(a + b)
(2x2)2 − (3y3)2 = (2x2 − 3y3)(2x2 + 3y3)
Полностью решение можно записать так:
4x4 − 9y6 = (2x2)2 − (3y3)2 = (2x2 − 3y3)(2x2 + 3y3)
Несмотря на простоту разложения по формуле разности квадратов, частые ошибки приходятся именно на эти задачи. Чтобы убедиться, что задача решена правильно, не мешает выполнить умножение в получившемся разложении. Если задача решена правильно, то должен получиться изначальный многочлен.
Проверим умножением данный пример. У нас должен получиться многочлен 4x4 − 9y6
(2x2 − 3y3)(2x2 + 3y3) = 2x2(2x2 + 3y3) − 3y3(2x2 + 3y3)
= 4x4 + 6x2y3 − 6x2y3 − 9y6 = 4x4 − 9y6
Пример 4. Разложить на множители многочлен 81 − 64
Представим члены исходной разности в виде одночленов возведенных в квадрат. Далее воспользуемся формулой разности квадратов:
81 − 64 = 92 − 82 = (9 − 8)(9 + 
Разложение многочлена на множители по формуле сумме кубов двух выражений
Мы помним, что произведение суммы двух выражений и неполного квадрата их разности равно сумме кубов этих выражений:
(a + b)(a2 − ab + b2) = a3 + b3
Если в этой формуле поменять местами левую и правую часть, то получим формулу, называемую суммой кубов двух выражений:
a3 + b3 = (a + b)(a2 − ab + b2)
Эта формула позволяет разложить выражение вида a3 + b3 на множители (a + b) и (a2 − ab + b2).
Пример 1. Разложить на множители многочлен 27x3 + 64y3
Представим члены 27x3 и 64y3 в виде одночленов, возведённых в куб
27x3 + 64y3 = (3x)3 + (4y)3
Теперь воспользуемся формулой суммы кубов. Переменная a в данном случае равна 3x, переменная b равна 4y
27x3 + 64y3 = (3x)3 + (4y)3 = (3x + 4y)((3x)2 − 3x × 4y + (4y)2) =
(3x + 4y)(9x2 − 12xy + 16y2)
Пример 2. Разложить на множители многочлен 125 + 8
Представим члены 125 и 8 в виде одночленов, возведённых в куб:
125 + 8 = 53 + 23
Далее воспользуемся формулой суммы кубов:
125 + 8 = 53 + 23 = (5 + 2)(25 − 10 + 4)
Разложение многочлена на множители по формуле разности кубов двух выражений
Произведение разности двух выражений и неполного квадрата их суммы равно разности кубов этих выражений:
(a − b)(a2 + ab + b2) = a3 − b3
Если в этой формуле поменять местами левую и правую часть, то получим формулу, называемую разностью кубов двух выражений:
a3 − b3 = (a − b)(a2 + ab + b2)
Эта формула позволяет разложить выражение вида a3 − b3 на множители (a − b) и (a2 + ab + b2).
Пример 1. Разложить на множители многочлен 64x3 − 27y3
Представим члены 64x3 и 27y3 в виде одночленов, возведённых в куб:
64x3 − 27y3 = (4x)3 − (3y)3
Теперь воспользуемся формулой разности кубов. Переменная a в данном случае равна 4x, переменная b равна 3y
64x3 − 27y3 = (4x)3 − (3y)3 = (4x − 3y)((4x)2 + 4x × 3y + (3y)2) =
(4x − 3y)(16x2 + 12xy + 9y2)
Пример 2. Разложить на множители многочлен 64 − 27
Представим члены 64 и 27 в виде одночленов, возведённых в куб:
64 − 27 = 43 − 33 = (4 − 3)(16 + 12 + 9)
Пример 3. Разложить на множители многочлен 125x3 − 1
Представим члены 125x3 и 1 в виде одночленов, возведённых в куб:
125x3 − 1 = (5x)3 − 13
Теперь воспользуемся формулой разности кубов. Переменная a в данном случае равна 5x, переменная b равна 1
125x3 − 1 = (5x)3 − 13 = (5x − 1)((5x)2 + 5x × 1 + 12) =
(5x − 1)(25x2 + 5x + 1)
Разложение многочлена на множители различными способами
К некоторым многочленам можно применять различные способы разложения на множители. Например, к одному многочлену можно применить способ вынесения общего за скобки, а затем воспользоваться одной из формул сокращённого умножения.
Пример 1. Разложить на множители многочлен ax2 − ay2
В данном многочлене содержится общий множитель a. Вынесем его за скобки:
ax2 − ay2 = a(x2 − y2)
При этом в скобках образовался многочлен, который является разностью квадратов. Применив формулу разности квадратов. Тогда получим:
ax2 − ay2 = a(x2 − y2) = a(x − y)(x + y)
Пример 2. Разложить на множители многочлен 3x2 + 6xy + 3y2
Вынесем за скобки общий множитель 3
3x2 + 6xy + 3y2 = 3(x2 + 2xy + y2)
В скобках образовался многочлен, который является квадратом суммы двух выражений, а именно выражений x и y. Тогда этот квадрат суммы можно представить как (x + y)2 и далее записать в виде двух сомножителей, каждый из которых равен (x + y)
3x2 + 6xy + 3y2 = 3(x2 + 2xy + y2) = 3(x + y)2 = 3(x + y)(x + y)
Задания для самостоятельного решения
Задание 1. Следующий многочлен разложите на множители способом группировки:
Решение:
Задание 2. Следующий многочлен разложите на множители способом группировки:
Решение:
Задание 3. Следующий многочлен разложите на множители способом группировки:
Решение:
Задание 4. Следующий многочлен разложите на множители способом группировки:
Решение:
Задание 5. Следующий многочлен разложите на множители способом группировки:
Решение:
Задание 6. Следующий многочлен разложите на множители способом группировки:
Решение:
Задание 7. Разложите на множители многочлен:
x2 + 12x + 36
Решение:
x2 + 12x + 36 = x2 + 2 × x × 6 + 62 = (x + 6)2 = (x + 6)(x + 6)
Задание 8. Разложите на множители многочлен:
8xy + y2 + 16x2
Решение:
8xy + y2 + 16x2 = 16x2 + 8xy + y2 = (4x)2 + 2 × 4x × y + y2 = (4x + y)2 = (4x + y)(4x + y)
Задание 9. Разложите на множители многочлен:
Решение:
Задание 10. Разложите на множители многочлен:
Решение:
Задание 11. Разложите на множители многочлен:
Решение:
Задание 12. Разложите на множители многочлен:
Решение:
Задание 13. Разложите на множители многочлен:
Решение:
Задание 14. Разложите на множители многочлен:
Решение:
Задание 15. Разложите на множители многочлен:
Решение:
Задание 16. Разложите на множители многочлен:
Решение:
Задание 17. Разложите на множители многочлен:
Решение:
Задание 18. Разложите на множители многочлен:
Решение:
Задание 19. Разложите на множители многочлен:
Решение:
Задание 20. Разложите на множители многочлен:
Решение:
Задание 21. Разложите на множители многочлен:
Решение:
Задание 22. Разложите на множители многочлен:
Решение:
Задание 23. Разложите на множители многочлен:
Решение:
Задание 24. Разложите на множители многочлен:
Решение:
Задание 25. Разложите на множители многочлен:
Решение:
Задание 26. Разложите на множители многочлен:
Решение:
Задание 27. Разложите на множители многочлен:
Решение:
Задание 28. Разложите на множители многочлен:
Решение:
Задание 29. Разложите на множители многочлен:
Решение:
Задание 30. Разложите на множители многочлен:
Решение:
Задание 31. Разложите на множители многочлен:
Решение:
Задание 32. Разложите на множители многочлен:
Решение:
Задание 33. Разложите на множители многочлен:
Решение:
Задание 34. Разложите на множители многочлен:
Решение:
Задание 35. Разложите на множители многочлен:
Решение:
Задание 36. Разложите на множители многочлен:
Решение:
Задание 37. Разложите на множители многочлен:
Решение:
Задание 38. Разложите на множители многочлен:
Решение:
Задание 39. Разложите на множители многочлен:
Решение:
Задание 40. Разложите на множители многочлен:
Решение:
Задание 41. Разложите на множители многочлен:
Решение:
Задание 42. Разложите на множители многочлен:
Решение:
Задание 43. Разложите на множители многочлен:
Решение:
Задание 44. Разложите на множители многочлен:
Решение:
Задание 45. Разложите на множители многочлен:
Решение:
Задание 46. Разложите на множители многочлен:
Решение:
Задание 47. Разложите на множители многочлен:
Решение:
Задание 48. Разложите на множители многочлен:
Решение:
Задание 49. Разложите на множители многочлен:
Решение:
Задание 50. Разложите на множители многочлен:
Решение:
Задание 51. В следующем выражении вынесите за скобки общий множитель 2a, затем выражение в скобках разложите на множители:
Решение:
Задание 52. В следующем выражении вынесите за скобки общий множитель 4, затем выражение в скобках разложите на множители:
Решение:
Задание 53. В следующем выражении вынесите за скобки общий множитель 2x2y2, затем выражение в скобках разложите на множители:
Решение:
Задание 54. В следующем выражении вынесите за скобки общий множитель 4x3y3, затем выражение в скобках разложите на множители:
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже