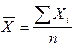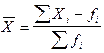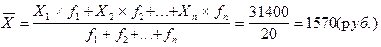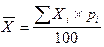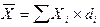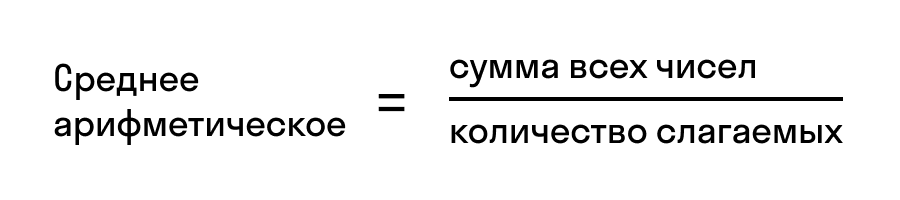Как правильно пишется словосочетание «среднее арифметическое»
- Как правильно пишется слово «средний»
- Как правильно пишется слово «арифметический»
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать
Карту слов. Я отлично
умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: стагнационный — это что-то нейтральное, положительное или отрицательное?
Ассоциации к слову «средний»
Синонимы к словосочетанию «среднее арифметическое»
Предложения со словосочетанием «среднее арифметическое»
- В итоге вывожу среднее арифметическое и рассказываю про жизнь в столицах.
- Самый простой способ уменьшения погрешности – провести измерение не один раз, а несколько, затем вычислить среднее арифметическое из результатов каждого замера.
- Соответственно, рейтинг является средним арифметическим курсов акций этих компаний, взвешенным по весам этих акций в рейтинге.
- (все предложения)
Цитаты из русской классики со словосочетанием «среднее арифметическое»
- — Да, милейший математик, к счастью, к счастью, к счастью! Мы — счастливейшее среднее арифметическое… Как это у вас говорится: проинтегрировать от нуля до бесконечности — от кретина до Шекспира… Так!
- (все
цитаты из русской классики)
Значение словосочетания «среднее арифметическое»
-
Сре́днее арифмети́ческое (в математике и статистике) множества чисел — сумма всех чисел, делённая на их количество. Является одной из наиболее распространённых мер центральной тенденции. (Википедия)
Все значения словосочетания СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ
Афоризмы русских писателей со словом «средний»
- Ни плохих, ни хороших, ни средних…
Все они по своим местам,
Где ни первых нет, ни последних…
Все они опочили там. - У всякого великого писателя свой слог: слога нельзя разделить на три рода — высокий, средний и низкий: слог делится на столько родов, сколько есть на свете великих, по крайней мере, сильнодаровитых писателей.
- (все афоризмы русских писателей)
Отправить комментарий
Дополнительно
Определение. Среднее арифметическое нескольких величин — это отношение суммы величин к их количеству.
Примером среднего арифметического служат такие показатели, как урожайность, производительность, посещаемость, скорость движения на определенном участке. Вычисление среднего арифметического и его составляющих производится по следующему простом правилу.
Правило. Чтобы вычислить среднее арифметическое нескольких чисел, нужно взять сумму этих чисел и разделить все на количество слагаемых. Частное и будет средним арифметическим этих чисел.
Пример 1. У Васи было 2 яблока, у Кати — 10 яблок, а у Саши — 6. Среднее количество яблок:
Пример 2. Средняя посещаемость зала в столовой за неделю высчитывается из посещаемости в течение 7 дней: 145 человек в 1-й день; 152 человека во 2-й день; 158 человек в 3-й лень; 162 человека в 4-й день; 164 человека в 5-й день; 161 человек в 6-й день и 157 человек в 7-й день.
Найдем среднее арифметическое (посещаемость) за
неделю:
Xсреднее = (145 + 152 + 158 + 162 + 164 + 161 + 157) : 7 = 157.
Можно определить среднюю посещаемость и как 1099 : 7 = 157 человек (1099 человек за 7 дней). Т. с. можно фиксировать общее количество посетителей за неделю без учета посещаемости по дням. Но тогда мы не будем знать, что наибольшее количество посетителей в день — 164 человека, а наименьшее — 145 человек, что в этом примере важно (кухня должна ориентироваться на максимальное посещение, от количества посетителей зависит выручка столовой н т. д.).
Во втором примере мы вели статистический учет, следовательно, среднее арифметическое — показатель и в статистике. Но вычисление среднего арифметического имеет смысл только в определенных пределах (небольших промежутках). Нам ничего не даст, например, среднее-мировое количество жителей в одной стране. Стран в мире более 200, а число жителей Индии и Китая совершенно несоизмеримо с количеством жителей Нидерландов или Люксембурга. Полученная средняя численность проживающих в одной стране не будет объективной характеристикой каждой из стран (из-за большого расхождения в числах).
Запись опубликована в рубрике Математика с метками арифметическое, среднее. Добавьте в закладки постоянную ссылку.
Для выяснения методики расчета средней арифметической используем следующие обозначения:
X — арифметический признак
X (X1, X2, … X3) — варианты определенного признака
n — число единиц совокупности
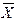
В зависимости от исходных данных средняя арифметическая может быть рассчитана двумя способами:
1. Если данные статистического наблюдения на сгруппированы, или сгруппированные варианты имеют одинаковые частоты, то рассчитывается средняя арифметическая простая:
2. Если частоты сгруппированы в данных разные, то рассчитывается среднее арифметическое взвешанное:
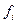
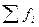
Среднее арифметическое рассчитывается по разному в дискретных и интервальных вариационных рядах.
В дискретных рядах варианты признака умножаются на частоты, эти произведения суммируются и полученная сумма произведений делится на сумму частот.
Рассмотрим пример вычисления средней арифметической в дискретном ряду:
| Заработная плата, руб. Xi | Число сотрудников, чел. fi | Произведение вариант на веса (частоты) Xi*fi |
| Итого: |
В интервальных рядах значение признака задано, как известно, в виде интервалов, поэтому, прежде чем рассчитывать среднюю арифметическую, нужно перейти от интервального ряда к дискретному.
В качестве вариантов Xi используется середина соответствующих интервалов. Они определяются как полусумма нижней и верхней границ.
Если у интервала отсутствует нижняя граница, то его середина определяется как разность между верхней границей и половиной величины следующих интервалов. При отсутствии верхних границ, середина интервала определяется как сумма нижней границы и половины величины предыдущего интервала. После перехода к дискретному ряду дальнейшие вычисления происходят по методике рассмотренной выше.
Если веса fi заданы не в абсолютных показателях, а в относительных, то формула расчета средней арифметической будет следующей:
pi — относительные величины структуры, показывающие, какой процент составляют частоты вариантов в сумме всех частот.
Если относительные величины структуры заданы не в процентах, а в долях, то среднее арифметическое будет рассчитываться по формуле:
Сре́днее арифмети́ческое (в математике и статистике) — разновидность среднего значения. Определяется как число, равное сумме всех чисел множества, делённой на их количество. Является одной из наиболее распространённых мер центральной тенденции.
Предложена (наряду со средним геометрическим и средним гармоническим) ещё пифагорейцами[1].
Частными случаями среднего арифметического являются среднее (генеральной совокупности) и выборочное среднее (выборки).
На случай, если количество элементов множества чисел стационарного случайного процесса бесконечное, в качестве среднего арифметического играет роль математическое ожидание случайной величины.
Введение[править | править код]
Обозначим множество чисел X = (x1, x2, …, xn) — тогда выборочное среднее обычно обозначается горизонтальной чертой над переменной (, произносится «x с чертой»).
Для обозначения среднего арифметического всей совокупности чисел обычно используется греческая буква μ. Для случайной величины, для которой определено среднее значение, μ есть вероятностное среднее, или математическое ожидание случайной величины. Если множество X является совокупностью случайных чисел с вероятностным средним μ, тогда для любой выборки xi из этой совокупности μ = E{xi} есть математическое ожидание этой выборки.
На практике разница между μ и в том, что μ является типичной переменной, потому что видеть можно скорее выборку, а не всю генеральную совокупность. Поэтому, если выборку представлять случайным образом (в терминах теории вероятностей), тогда (но не μ) можно трактовать как случайную переменную, имеющую распределение вероятностей на выборке (вероятностное распределение среднего).
Обе эти величины вычисляются одним и тем же способом:
Если X — случайная переменная, тогда математическое ожидание X можно рассматривать как среднее арифметическое значений в повторяющихся измерениях величины X. Это является проявлением закона больших чисел. Поэтому выборочное среднее используется для оценки неизвестного математического ожидания.
В элементарной алгебре доказано, что среднее n + 1 чисел больше среднего n чисел тогда и только тогда, когда новое число больше чем старое среднее, меньше тогда и только тогда, когда новое число меньше среднего, и не меняется тогда и только тогда, когда новое число равно среднему. Чем больше n, тем меньше различие между новым и старым средними значениями.
Заметим, что имеется несколько других «средних» значений, в том числе среднее степенное, среднее Колмогорова, гармоническое среднее, арифметико-геометрическое среднее и различные средне-взвешенные величины (например, среднее арифметическое взвешенное, среднее геометрическое взвешенное, среднее гармоническое взвешенное).
Примеры[править | править код]
- Для получения среднего арифметического трёх чисел необходимо сложить их и разделить на 3:
- Для получения среднего арифметического четырёх чисел необходимо сложить их и разделить на 4:
Непрерывная случайная величина[править | править код]
Если существует интеграл от некоторой функции одной переменной, то среднее арифметическое этой функции на отрезке определяется через определённый интеграл:
Здесь для определения отрезка подразумевается, что причём чтобы знаменатель не был равен 0.
Некоторые проблемы применения среднего[править | править код]
Отсутствие робастности[править | править код]
Хотя среднее арифметическое часто используется в качестве средних значений или центральных тенденций, это понятие не относится к робастной статистике, то есть среднее арифметическое подвержено сильному влиянию «больших отклонений». Примечательно, что для распределений с большим коэффициентом асимметрии среднее арифметическое может не соответствовать понятию «среднего», а значения среднего из робастной статистики (например, медиана) может лучше описывать центральную тенденцию.
Классическим примером является подсчёт среднего дохода. Арифметическое среднее может быть неправильно истолковано в качестве медианы, из-за чего может быть сделан вывод, что людей с большим доходом больше, чем на самом деле. «Средний» доход истолковывается таким образом, что доходы большинства людей находятся вблизи этого числа. Этот «средний» (в смысле среднего арифметического) доход является выше, чем доходы большинства людей, так как высокий доход с большим отклонением от среднего делает сильный перекос среднего арифметического (в отличие от этого, средний доход по медиане «сопротивляется» такому перекосу). Однако этот «средний» доход ничего не говорит о количестве людей вблизи медианного дохода (и не говорит ничего о количестве людей вблизи модального дохода). Тем не менее если легкомысленно отнестись к понятиям «среднего» и «большинство народа», то можно сделать неверный вывод о том, что большинство людей имеют доходы выше, чем они есть на самом деле. Например, отчёт о «среднем» чистом доходе в Медине, штат Вашингтон, подсчитанный как среднее арифметическое всех ежегодных чистых доходов жителей, даст на удивление большое число — из-за Билла Гейтса. Рассмотрим выборку (1, 2, 2, 2, 3, 9). Среднее арифметическое равно 3.17, но пять значений из шести ниже этого среднего.
Сложный процент[править | править код]
Если числа перемножать, а не складывать, нужно использовать среднее геометрическое, а не среднее арифметическое. Наиболее часто этот казус случается при расчёте окупаемости инвестиций в финансах.
Например, если акции в первый год упали на 10 %, а во второй год выросли на 30 %, тогда вычислять «среднее» увеличение за эти два года как среднее арифметическое (−10 % + 30 %) / 2 = 10 % некорректно, а правильное среднее значение в этом случае дают совокупные ежегодные темпы роста: годовой рост получается около 8,16653826392 % ≈ 8,2 %.
Причина этого в том, что проценты имеют каждый раз новую стартовую точку: 30 % — это 30 % от меньшего, чем цена в начале первого года, числа: если акции в начале стоили $30 и упали на 10 %, они в начале второго года стоят $27. Если акции выросли на 30 %, они в конце второго года стоят $35,1. Арифметическое среднее этого роста 10 %, но, поскольку акции выросли за 2 года всего на $5,1, средний рост в 8,2 % даёт конечный результат $35,1:
$30 × (1 – 0,1) (1 + 0,3) = $30 × (1 + 0,082) (1 + 0,082) = $35,1. Если же использовать таким же образом среднее арифметическое значение 10 %, мы не получим фактическое значение: $30 × (1 + 0,1) (1 + 0,1) = $36.3.
Сложный процент в конце 2 года: 90 % * 130 % = 117 %, то есть общий прирост 17 %, а среднегодовой сложный процент , то есть среднегодовой прирост 8,2 %.
Направления[править | править код]
При расчёте среднего арифметического значений некоторой переменной, изменяющейся циклически (например, фаза или угол), следует проявлять особую осторожность. Например, среднее чисел 1° и 359° будет равно 180°. Этот результат неверен по двум причинам.
Среднее значение для циклической переменной, рассчитанное по приведённой формуле, будет искусственно сдвинуто относительно настоящего среднего к середине числового диапазона. Из-за этого среднее рассчитывается другим способом, а именно, в качестве среднего значения выбирается число с наименьшей дисперсией (центральная точка). Также вместо вычитания используется модульное расстояние (то есть, расстояние по окружности). Например, модульное расстояние между 1° и 359° равно 2°, а не 358° (на окружности между 359° и 360° = 0° — один градус, между 0° и 1° — тоже 1°, в сумме — 2°).
Примечания[править | править код]
См. также[править | править код]
- Арифметическая пропорция
- Арифметическая прогрессия
- Неравенство Швейцера
Ссылки[править | править код]
- Арифметическая средняя // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Финансовая математика. Дисперсия. Среднее арифметическое. Среднеквадратическое отклонение. Коэффициент вариации Архивная копия от 19 сентября 2020 на Wayback Machine / Методики финансового анализа
- Среднее арифметическое — показатель центральной тенденции / Теория вероятностей и математическая статистика
Понятие среднего арифметического
Среднее арифметическое нескольких чисел — это сумма этих чисел, которую разделили на количество слагаемых. Формула среднего арифметического, которую обычно проходят в 5 классе, выглядит так:
Потренируемся использовать формулу среднего арифметического.
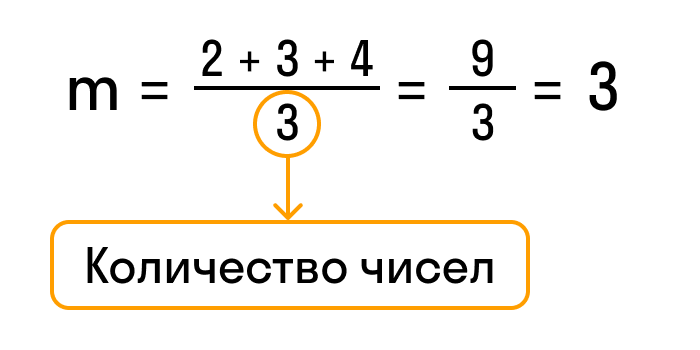
Например, найдем среднее арифметическое чисел 2, 3 и 4. Обозначим среднее значение латинской буквой «m» и посчитаем сумму этих чисел.
- 2 + 3 + 4 = 9
Разделим результат на количество чисел в задании, то есть на 3, и получим ответ — 3.
Применить эти знания можно в любой сфере жизни, где нужно обобщить и дать среднюю оценку: узнать среднюю цену товара в разных магазинах, вычислить среднюю зарплату сотрудников компании, сравнить среднюю посещаемость занятий учениками 5А и 5Б.
Средняя скорость движения — это весь пройденный путь, поделенный на время движения. Формула:
Так мы рассмотрели самые основные методы нахождения среднего значения. Теперь осталось попрактиковаться на примерах, чтобы быстро решать задачки на контрольной.
Примеры расчета среднего арифметического
Пример 1. Вычислить среднее арифметическое 33,3 и 55,5.
Как решаем:
Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат разделить на 2: (33,3 + 55,5) : 2 = 88,8 : 2 = 44,4.
Пример 2. Подсчитать среднее арифметическое 7,5 и 8 и 0,5.
Как решаем:
Чтобы найти среднее арифметическое трех чисел, надо сложить эти числа и результат разделить на 3: (7,5 + 8 + 0,5) : 3 = 16 : 3 = 5,33.
Пример 3. Найти среднее арифметическое 202, 105, 67 и 9.
Как решаем:
Чтобы найти среднее арифметическое четырех чисел, надо сложить эти числа и результат разделить на 4: (202 + 105 + 67 + 9) : 4 = 383 : 4 = 95,75.
Пример 4. Сколько в среднем тратит школьник денег в неделю, если в понедельник он потратил 80 рублей, во вторник 75 рублей, в среду и четверг по 100 рублей, в пятницу 50 рублей.
Как решаем:
Чтобы найти сколько в среднем школьник потратил за пять дней, надо сложить эти суммы и результат разделить на 5: (80 + 75 + 100 + 100 + 50) : 5 = 405 : 5 = 81.
Ответ: школьник в неделю тратит в среднем 81 рубль.
Еще больше интересных практических заданий — на курсах математики в онлайн-школе Skysmart. Вводный урок — бесплатно!
среднеарифметический
- среднеарифметический
-
СРЕДНЕАРИФМЕТИ́ЧЕСКИЙ -ая, -ое. Полученный в результате сложения частей и последующего деления на количество этих частей. С. результат.
◁ Среднеарифмети́ческое, -ого;
ср.
Вычислить с.
Энциклопедический словарь.
2009.
Смотреть что такое «среднеарифметический» в других словарях:
-
среднеарифметический — среднеарифметический … Орфографический словарь-справочник
-
Среднеарифметический радиус частиц — Отношение суммарной длины радиусов частиц к количеству этих частиц Источник: ГОСТ 22023 76: Материалы строительные. Метод микроскопического количественного анализа структуры … Словарь-справочник терминов нормативно-технической документации
-
Среднеарифметический частиц на шлифе — радиус Отношение суммарной длины радиусов всех частиц данного компонента на срезе к количеству этих частиц Источник: ГОСТ 22023 76: Материалы строительные. Метод микроскопического количественного анализа структуры … Словарь-справочник терминов нормативно-технической документации
-
Среднеарифметический реверберационный коэффициент звукопоглощения — 5. Среднеарифметический реверберационный коэффициент звукопоглощения Реверберационный коэффициент звукопоглощения, усредняемый по двум или более октавным полосам частот Источник … Словарь-справочник терминов нормативно-технической документации
-
среднеарифметический — среднеарифмет ический … Русский орфографический словарь
-
среднеарифметический — … Орфографический словарь русского языка
-
среднеарифметический — среднеарифмети/ческий … Слитно. Раздельно. Через дефис.
-
среднеарифметический — ая, ое. см. тж. среднеарифметическое Полученный в результате сложения частей и последующего деления на количество этих частей. Среднеарифмети/ческий результат … Словарь многих выражений
-
среднеарифметический — средн/е/арифмет/ич/еск/ий … Морфемно-орфографический словарь
-
среднеарифметический реверберационный коэффициент звукопоглощения — реверберационный коэффициент звукопоглощения, усредняемый по двум или более октавным полосам частот. (Смотри: ГОСТ 23499 79. Материалы и изделия строительные звукопоглощающие и звукоизоляционные. Классификация и общие технические требования.)… … Строительный словарь
Смотреть что такое СРЕДНЕАРИФМЕТИЧЕСКИЙ в других словарях:
СРЕДНЕАРИФМЕТИЧЕСКИЙ
1) Орфографическая запись слова: среднеарифметический2) Ударение в слове: среднеарифмет`ический3) Деление слова на слоги (перенос слова): среднеарифмет… смотреть
СРЕДНЕАРИФМЕТИЧЕСКИЙ
Деистический Деист Дачник Датчик Датский Дари Дарение Дар Дантес Данте Дант Даний Дан Дамский Даменит Дакий Дак Дайм Ачитский Ачинский Ачинск Афт Афинский Аферистский Аферист Атрий Атрек Атм Астр Астериск Астерий Астенический Астеник Асснер Асс Аскет Аскер Аск Асидерит Арчинский Арфист Артинский Артемий Артем Артек Арт Арский Арсин Арсентий Арсенит Арсений Арсенид Арсен Арник Арменист Арк Арифметический Арифметик Арифм Аритмический Аристид Арин Арест Арен Арек Арден Анфис Антиримский Антимир Антик Анти Антефикс Антеридий Ант Анри Анкист Анкетер Анкерит Анкер Анк Анисим Анисий Анис Анимист Анимикит Аним Аникий Аникей Аник Анид Анемический Андский Андрис Андрей Андре Амт Амин Амид Амер Актиний Актинид Актин Актер Акт Аксис Аксен Акридин Акрид Акр Акмеист Акм Дейксис Акие Айрес Дек Декаметр Декан Декарт Аир Адский Адрес Деметр Аднексит Демин Админ Ден Адермин Адентий Аденский Аденит Аден Дементий Декстрин Декрет Декремент Аист Аистник Дейнека Аки Аким… смотреть
СРЕДНЕАРИФМЕТИЧЕСКИЙ
корень — СРЕДН; соединительная гласная — Е; корень — АРИФМЕТ; суффикс — ИЧ; суффикс — ЕСК; окончание — ИЙ; Основа слова: СРЕДНЕАРИФМЕТИЧЕСКВычисленный … смотреть
СРЕДНЕАРИФМЕТИЧЕСКИЙ
Ударение в слове: среднеарифмет`ическийУдарение падает на букву: иБезударные гласные в слове: среднеарифмет`ический
СРЕДНЕАРИФМЕТИЧЕСКИЙ
Начальная форма — Среднеарифметический, винительный падеж, единственное число, мужской род, неодушевленное
СРЕДНЕАРИФМЕТИЧЕСКИЙ ДОХОД
Среднее арифметическое доходов за второстепенный период, рассчитываемое как сумма доходов за периоды, деленная на количество периодов.
Русский[править]
Морфологические и синтаксические свойства[править]
| падеж | ед. ч. | мн. ч. | |||
|---|---|---|---|---|---|
| муж. р. | ср. р. | жен. р. | |||
| Им. | среднеарифмети́ческий | среднеарифмети́ческое | среднеарифмети́ческая | среднеарифмети́ческие | |
| Р. | среднеарифмети́ческого | среднеарифмети́ческого | среднеарифмети́ческой | среднеарифмети́ческих | |
| Д. | среднеарифмети́ческому | среднеарифмети́ческому | среднеарифмети́ческой | среднеарифмети́ческим | |
| В. | одуш. | среднеарифмети́ческого | среднеарифмети́ческое | среднеарифмети́ческую | среднеарифмети́ческих |
| неод. | среднеарифмети́ческий | среднеарифмети́ческие | |||
| Т. | среднеарифмети́ческим | среднеарифмети́ческим | среднеарифмети́ческой среднеарифмети́ческою | среднеарифмети́ческими | |
| П. | среднеарифмети́ческом | среднеарифмети́ческом | среднеарифмети́ческой | среднеарифмети́ческих |
сред—не—а—риф—ме—ти́—чес—кий
Прилагательное, относительное, тип склонения по классификации А. Зализняка — 3a✕~.
Корень: -средн-; интерфикс: -е-; корень: -арифмет-; суффиксы: -ич-еск; окончание: -ий [Тихонов, 1996].
Произношение[править]
- МФА: [ˌsrʲedʲnʲɪərʲɪf⁽ʲ⁾mʲɪˈtʲit͡ɕɪskʲɪɪ̯]
Семантические свойства[править]
Значение[править]
- матем. полученный в результате сложения частей и последующего деления на количество этих частей ◆ Отсутствует пример употребления (см. рекомендации).
- перен. рядовой, обыкновенный, ничем не выделяющийся в ряду других ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы[править]
Антонимы[править]
Гиперонимы[править]
- средний, усреднённый
Гипонимы[править]
Родственные слова[править]
| Ближайшее родство | |
Этимология[править]
Происходит от ??
Фразеологизмы и устойчивые сочетания[править]
Перевод[править]
| Список переводов | |
Библиография[править]
- Словарь новых слов русского языка (середина 50-х — середина 80-х годов) / Под ред. Н. З. Котеловой. — СПб. : Дмитрий Буланин, 1995. — ISBN 5-86007-016-0.
- среднее арифметическое,
Существительное
мн. средние арифметические
Склонение существительного среднее арифметическоеср.р.,
Единственное число
Множественное число
Единственное число
Именительный падеж
(Кто? Что?)
среднее арифметическое
средние арифметические
Родительный падеж
(Кого? Чего?)
среднего арифметического
средних арифметических
Дательный падеж
(Кому? Чему?)
среднему арифметическому
средним арифметическим
Винительный падеж
(Кого? Что?)
среднее арифметическое
средние арифметические
Творительный падеж
(Кем? Чем?)
средним арифметическим
средними арифметическими
Предложный падеж
(О ком? О чем?)
среднем арифметическом
средних арифметических
Множественное число
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Среднее арифметическое — очень важное понятие из мира математики, используемое во многих других дисциплинах. Например, среднее арифметическое используют для того чтобы найти какое-то усреднённое значение. В частности, в экономических дисциплинах можно воспользоваться этим понятием для расчёта среднего дохода в месяц и других показателей.
Часто понятием среднего арифметического пользуются и учёные: химики с помощью него могут посчитать, сколько в среднем получается необходимого вещества при повторных проведениях опыта, а специалисты агропромышленности — среднюю урожайность яблок или другой сельскохозяйственной культуры.
Что такое среднеарифметическое значение
Определение 1
Средним арифметическим называют сумму всех чисел (например, полученных при повторном проведении одного и того же опыта), поделённых на количество этих чисел.

Английский язык для начинающих
Не откладывай мечты — начни говорить под руководством опытного преподавателя
Узнать подробнее
Замечание 1
Важно! Нельзя складывать и искать среднее арифметическое между величинами с разными единицами измерения и разной размерностью.
Примерами величин, которые нельзя складывать так как они имеют разную размерность, являются масса и расстояние. Масса измеряется в килограммах или граммах, а расстояние измеряется в сантиметрах, метрах и других единицах измерения.
Если значения какой-либо величины заданы с помощью разных единиц измерения, то в таком виде их также нельзя складывать и, соответственно, искать среднее арифметическое между ними.
Если же привести их к одинаковой единице измерения, то можно сложить их между собой.
В качестве примера можно привести длину двух некоторых объектов. Для одного объекта длина равна $70$ см, а для второго — $0, 9$ м. Чтобы найти среднее арифметическое, необходимо перевести один из них в единицу измерения второго, например, метры в сантиметры или наоборот.
«Среднее арифметическое» 👇
Как посчитать среднее арифметическое
Чтобы посчитать среднее арифметическое, нужно сложить все имеющиеся значения какой-либо величины и разделить на количество этих значений. Для четырёх значений $a, b, c, d$ среднее арифметическое равно
$frac{a+b+c+d}{4}$.
Если же $a, b, c$ и $d$ заданы не в одной единице измерения, а, например, в метрах и сантиметрах, то сначала нужно выбрать общую единицу измерения и привести все значения к ней.
Пример 1
Эдуард прыгнул в длину $5$ раз. Первый раз он прыгнул на расстояние $173$ см, второй раз на $169$ см, третий раз на $1,7$ м, а четвёртый и пятый соответственно — на $168$ и $175$ см. Посчитайте, на какую длину в среднем прыгает Эдуард.
Решение:
Длина третьего прыжка Эдуарда дана в метрах, а остальные его результаты — в сантиметрах. Поэтому переведём длину третьего результата также в сантиметры. Для этого умножим метры на $100$, так как в одном метре содержится 100 сантиметров:
$l_3=1,7 м = 1,7 cdot 100 см= 170$ см.
Теперь мы можем найти среднюю длину его прыжка:
$l_{ср.}=frac{173+169+170+168+175}{5}=171$ см.
Ответ: В среднем Эдуард прыгает на длину в 171 см.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме