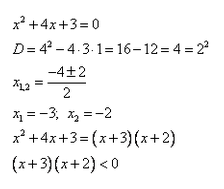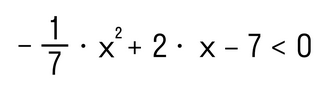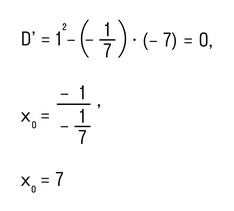строго математический
- строго математический
-
строго математический
Слитно или раздельно? Орфографический словарь-справочник. — М.: Русский язык.
.
1998.
Смотреть что такое «строго математический» в других словарях:
-
Математический сопроцессор — 80×287 в колодке на базовой плате персонального компьютера … Википедия
-
Математический анализ — У этого термина существуют и другие значения, см. Анализ. Математический анализ совокупность разделов математики, посвящённых исследованию функций и их обобщений методами дифференциального и интегрального исчислений. При столь общей… … Википедия
-
Вольф Христиан — (барон Wolf, чаще Wolff) знаменитый немецкий философ; род. в 1679 г. в Бреславле, в семье простого ремесленника; изучал в Йене сначала богословие, потом математику и философию. Примечания его к сочинению Чирнгаузена (Tschirnhausen) Medicina… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
-
Герца опыты — Теория электрических и магнитных явлений, созданная трудами лучших математиков первой половины настоящего столетия и до недавнего времени принимавшаяся почти всеми учеными, допускала в основе своей существование особых невесомых электрических и… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
-
Вольф, Христиан — (барон Wolf, чаще Wolff) знаменитый немецкий философ; род. в 1679 г. в Бреславле, в семье простого ремесленника; изучал в Йене сначала богословие, потом математику и философию. Примечания его к сочинению Чирнгаузена (Tschirnhausen) Medicina… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
-
Вольф — (Христиан барон Wolf, чаще Wolff) знаменитый нем. философ,род. в 1679 г. в Бреславле, в семье простого ремесленника, изучал в Йенесначала богословие, потом математику и философию. Примечания его ксочинению Чирнгаузена (Tschirnhausen) Medicina… … Энциклопедия Брокгауза и Ефрона
-
Циклоидальный маятник — математический Маятник, который, совершая под действием силы тяжести колебания, описывает дугу циклоиды (см. в ст. Линия) с вертикальной осью и выпуклостью, обращенной вниз. Ц. м. можно осуществить, подвесив грузик В на нити длиной 4а и… … Большая советская энциклопедия
-
Университет — (от лат. universitas совокупность). В настоящее время с понятием У. соединяют представление о высшем учебном заведении, которое, имея целью свободное преподавание и развитие всех отраслей науки (universitas litterarum), независимо от их… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
-
Александр II (часть 2, XIII-XIX) — XIII. Дела внутренние (1866—1871). 4 го апреля 1866 года, в четвертом часу дня, Император Александр, после обычной прогулки в Летнем саду, садился в коляску, когда неизвестный человек выстрелил в него из пистолета. В эту минуту, стоявший в… … Большая биографическая энциклопедия
-
МАТЕМАТИКА — Математику обычно определяют, перечисляя названия некоторых из ее традиционных разделов. Прежде всего, это арифметика, которая занимается изучением чисел, отношений между ними и правил действий над числами. Факты арифметики допускают различные… … Энциклопедия Кольера
Предложения с «математически строгое»
| Другие результаты |
|
Строгая математическая основа метода конечных элементов была обеспечена в 1973 году публикацией Strang and Fix. |
|
Применение преобразования Фолди-Вутюйзена в акустике очень естественно; всесторонние и математически строгие расчеты. |
|
Математически строгий анализ сходимости итерационного метода обычно выполняется; однако эвристические итерационные методы также распространены. |
|
В рамках петлевого квантово-гравитационного представления Тим сформулировал математически строгий оператор как предложение в качестве такого ограничения. |
|
Хотя метод является математически строгим, он полностью зависит от точности используемых параметров. |
|
Любые аргументы, которые не могут быть связаны с основными определениями, не будут считаться строгими в математическом сообществе. |
|
Есть много способов показать это равенство, от интуитивных аргументов до математически строгих доказательств. |
|
До публикации Сидерея Нунция Католическая Церковь считала гелиоцентрическую систему Коперника строго математической и гипотетической. |
|
Кроме того, строго говоря, FST не является расстоянием в математическом смысле, поскольку оно не удовлетворяет неравенству треугольника. |
|
Строго говоря, теорема применима только к классу математических функций, имеющих преобразование Фурье, которое равно нулю вне конечной области частот. |
|
Поскольку он использует строго математический подход, LSI по своей сути не зависит от языка. |
|
Бернхард Риман дал строгое математическое определение интегралов. |
|
В большинстве математической литературы доказательства написаны в терминах строгой неформальной логики. |
|
Этот подход может быть подвергнут строгому математическому доказательству с помощью математической индукции и часто используется в качестве примера рекурсии при обучении программированию. |
|
Аргументы правдоподобия с использованием эвристических приемов, таких как изображения и аналогии, предшествовали строгому математическому доказательству. |
|
Первая попытка математической строгости в области вероятности, которую отстаивал Пьер-Симон Лаплас, теперь известна как классическое определение. |
|
Наличие греческих букв является верным признаком математической строгости, а классические соединения указывают на то, что здесь действует наука. |
|
Математическое доказательство-это в основном вопрос строгости. |
|
Греки использовали логику для вывода выводов из определений и аксиом и использовали математическую строгость для их доказательства. |
|
При контролируемом обучении алгоритм строит математическую модель из набора данных, который содержит как входные данные, так и желаемые выходные данные. |
|
При неконтролируемом обучении алгоритм строит математическую модель из набора данных, который содержит только входные данные и не содержит желаемых выходных меток. |
|
Будучи инженером-строителем по образованию, Кэмпинг заявил, что он десятилетиями пытался разработать математически обоснованные пророчества в Библии. |
|
Свойство полноты вещественных чисел является основой, на которой строится исчисление и, в более общем смысле, математический анализ. |
|
Математическое обозначение, обозначаемое замкнутой системой S, строится из начального поведения ⊥S и аппроксимирующей поведение прогрессии функции. |
|
Для меня гистограмма-это математический метод оценки распределения, который обычно строится с помощью гистограммы. |
|
Код более высокого уровня, как математическое программное обеспечение, работает на основе свободного написания строк и использования их в любом порядке. |
|
Однако неявное преобразование между, например, числами и строками отсутствует; строка является недопустимым аргументом математической функции, ожидающей число. |
|
Его описание также звучит как намеренно бессмысленная строка математических слов. |
|
Пользователи могут задавать простые математические соотношения между строками и столбцами. |
|
Сложность Колмогорова может быть определена для любого математического объекта, но для простоты объем этой статьи ограничен строками. |
На основании Вашего запроса эти примеры могут содержать грубую лексику.
На основании Вашего запроса эти примеры могут содержать разговорную лексику.
Перевод «строго математический» на английский
Строго математический ответ на этот вопрос дать невозможно.
Слово «почти» имеет строго математический смысл.
Слово «почти» имеет строго математический смысл.
Это приводит их к выведению вероятности, отличной от собственно математической, так как строго математический ответ обессмыслил бы данный образ личности.
That leads them to infer a definition of «probability» that is different from the strict mathematical one, because giving the mathematical answer would render the personality sketch pointless.
Другие результаты
Многие её тезисы на сегодняшний день строго математически доказаны.
Когда я строю математическую модель, делаю вывод на основе расчетов.
Любая часть функциональной модели может быть принципиально выражена и в строго математической форме.
Any part of functional model can be principally expressed in a strict mathematical form as well.
Первоначально её основные понятия не имели строго математического вида.
Со строго математической точки зрения указанные выше предположение нужно использовать с осторожностью.
Ислими и гирих всегда строго математически выверены и рассчитаны.
Благодаря исследованиям П.Л.Чебышева и его учеников теория вероятностей стала строго математической наукой.
Due to works of P.L. Chebyshev and his successors the probability theory has became a strong mathematical science.
Идеальные пропорции человеческого тела такжерассчитывались строго математически.
Со строго математической точки зрения здесь мы имеем дело с пределом.
В строго математическом плане — нет.
Закон этот, включающий в себя группу теорем, доказан строго математически.
Используя наброски чертежей Эйнштейна и Розена, Торн создал алгоритм, описывающий физику работающей машины времени в строго математическом выражении.
Starting from the rough sketch that Einstein and Rosen left behind, Thorne created an algorithm that describes in strict mathematical terms the physics of a working time machine.
Использование подобного подхода позволяет строго математически доказать, что парадокс Эпименида ровно на 50% истинен и на 50% ложен.
Using this reasoning, one could mathematically prove that the Epimenides Paradox is exactly 50% true and 50% false.
Рассуждения, приведенные здесь, нельзя считать строго математически обоснованными.
The evidence here cannot reasonably be regarded as closely balanced.
Вся остальная часть задания является строго математической.
Его работа была строго математически обоснована.
Результатов: 116. Точных совпадений: 4. Затраченное время: 187 мс
Documents
Корпоративные решения
Спряжение
Синонимы
Корректор
Справка и о нас
Индекс слова: 1-300, 301-600, 601-900
Индекс выражения: 1-400, 401-800, 801-1200
Индекс фразы: 1-400, 401-800, 801-1200
Определение квадратного неравенства
Неравенство — алгебраическое выражение, в котором используются знаки ≠, <, >, ≤, ≥.
Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит найти множество, для которых оно выполняется.
Квадратное неравенство выглядит так:
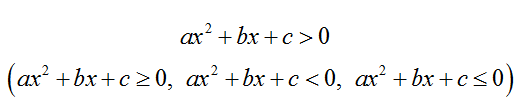
где x — переменная,
a, b, c — числа,
при этом а ≠ 0.
Квадратное неравенство можно решить двумя способами:
- графический метод;
- метод интервалов.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Решение неравенства графическим методом
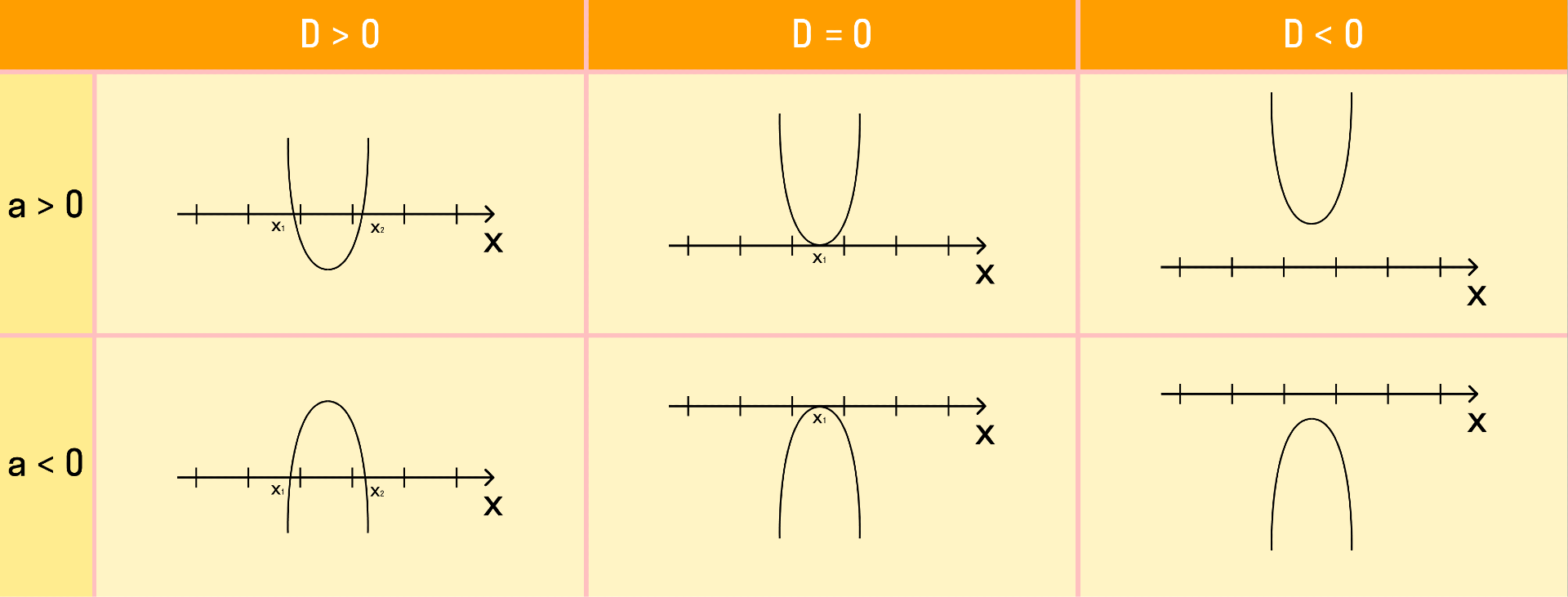
При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.
Как дискриминант влияет на корни уравнения:
- D = 0. Если дискриминант равен нулю, тогда у квадратного уравнения есть один корень;
- D > 0. Если дискриминант больше нуля, тогда у квадратного уравнения есть два различных корня;
- D < 0. Если дискриминант меньше нуля, тогда у квадратного уравнения нет корней.
В зависимости от полученных корней и знака коэффициента a, возможно одно из шести расположений графика функции у = ax2 + bx + c.
Если требуется найти числовой промежуток, на котором квадратный трехчлен ax2 + bx + c больше нуля, то этот числовой промежуток находится там, где парабола лежит выше оси ОХ.
Если нужно найти числовой промежуток, на котором квадратный трехчлен ax2 + bx + c меньше нуля — это числовой промежуток, где парабола лежит ниже оси ОХ.
Если квадратное неравенство нестрогое, то корни входят в числовой промежуток. А если строгое — не входят.
Обучение на курсах по математике в онлайн-школе Skysmart сделает сложные темы понятными, а высокий балл на экзаменах — достижимым!
Решение неравенства методом интервалов
Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.
Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: >, <, ≤, ≥.
Сейчас мы узнаем про интервалы в контексте решения квадратных неравенств.
Интервал — это некий промежуток числовой прямой, то есть все возможные числа, заключенные между двумя числами — концами интервала. Представить эти промежутки не так просто, поэтому интервалы принято рисовать.
Алгоритм решения квадратных неравенств методом интервалов:
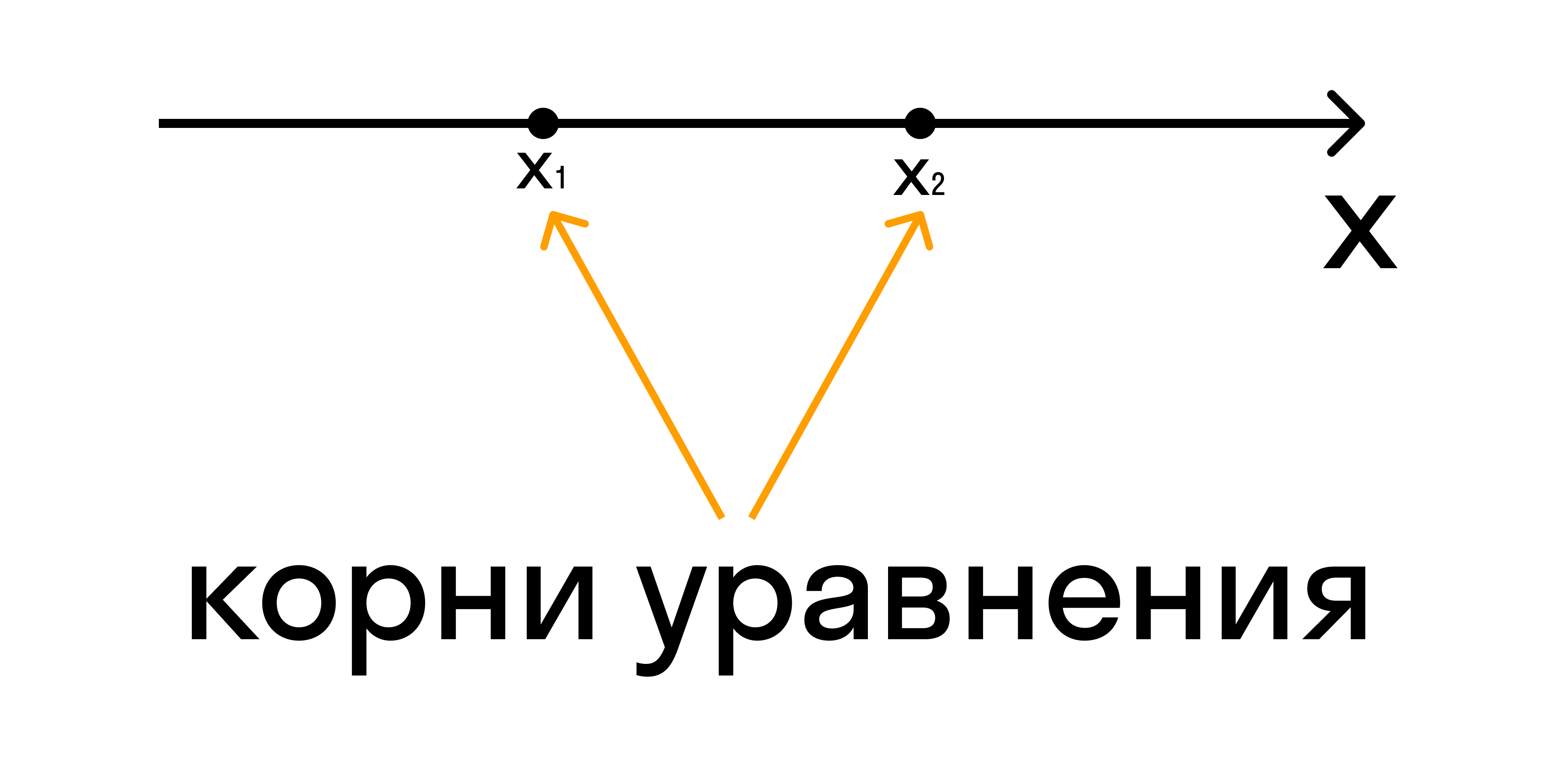
- Найти нули квадратного трехчлена ax2 + bx + c из левой части квадратного неравенства.
- Изобразить координатную прямую и при наличии корней отметить их на ней.
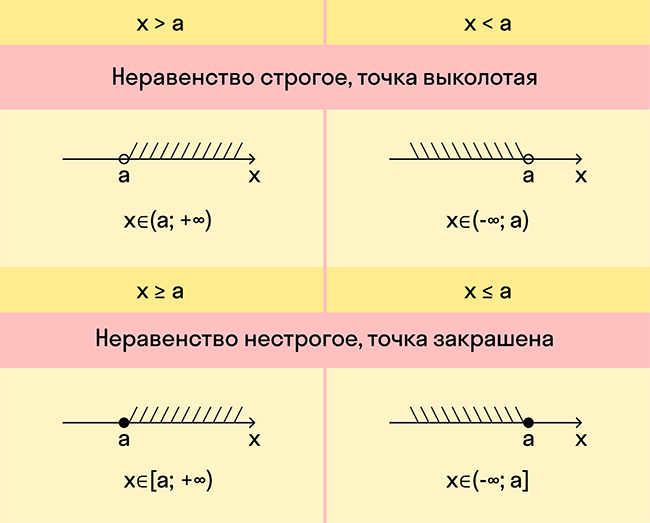
Если неравенство строгое, нужно отметить корни пустыми (выколотыми) точками. Если нестрогое — обычными точками. Именно эти точки разбивают координатную ось на промежутки.
- Определить, какие знаки имеют значения трехчлена на каждом промежутке (если на первом шаге нашли нули) или на всей числовой прямой (если нулей нет). И проставить над этими промежутками + или − в соответствии с определенными знаками.
- Если квадратное неравенство со знаком > или ≥ — наносим штриховку над промежутками со знаками +.
Если неравенство со знаком < или ≤, то наносим штриховку над промежутками со знаком −.
В результате получаем геометрический образ некоторого числового множества — это и есть решение неравенства.
Либо вместо штриховки можно нарисовать «арки» для интервалов. Справа налево, начиная с +, проставить чередуя знаки + и −.
- Выбрать необходимые интервалы и записать ответ.
Расскажем подробнее про третий шаг алгоритма. Существует несколько подходов для определения знаков на промежутках.
Для примера возьмем трехчлен x2 + 4x — 5, его корнями являются числа -5 и 1, они разбивают числовую ось на три промежутка: (-∞, -5), (-5, 1) и (1, +∞).
Определим знак трехчлена x2 + 4x — 5 на промежутке (1, +∞). Для этого вычислим значение данного трехчлена при некотором значении x из этого промежутка. Можно брать любое значение переменной, главное — чтобы вычисления были простыми. В нашем случае, возьмем x = 2. Подставим его в трехчлен вместо переменной x:
- 22 + 4 * 2 — 5 = 4 + 8 — 5 = 7.
7 — положительное число. Это значит, что любое значение квадратного трехчлена на интервале (1, +∞) будет положительным. Так мы определили знак плюс.
Определим знаки на оставшихся двух промежутках. Начнем с интервала (-5, 1). Из этого интервала можем взять x = 0 и вычислить значение квадратного трехчлена при этом значении переменной:
- 02 + 4 * 0 — 5 = 0 + 0 — 5 = -5.
Так как -5 — отрицательное число, то на этом интервале все значения трехчлена будут отрицательными. Так мы определили знак минус.
Осталось определиться со знаком на промежутке (-∞, -5). Возьмем x = -6, подставляем:
- (-6)2 + 4 * (-6) — 5 = 36 — 24 — 5 = 7.
Следовательно, искомый знак — плюс.
Можно расставить знаки быстрее, если запомнить эти факты:
Плюс или минус: как определить знаки
Можно сделать вывод о знаках по значению старшего коэффициента a:
если a > 0, последовательность знаков: +, −, +,
если a < 0, последовательность знаков: −, +, −.
Можно также сделать вывод о знаках по значению старшего коэффициента a:
если a > 0, последовательность знаков: +, +,
если a < 0, последовательность знаков: −, −.
Например -4x2 — 7 не имеет корней и на промежутке (−∞, +∞) его значения отрицательны, так как коэффициент при x2 есть отрицательное число -4, и свободный член -7 тоже отрицателен.
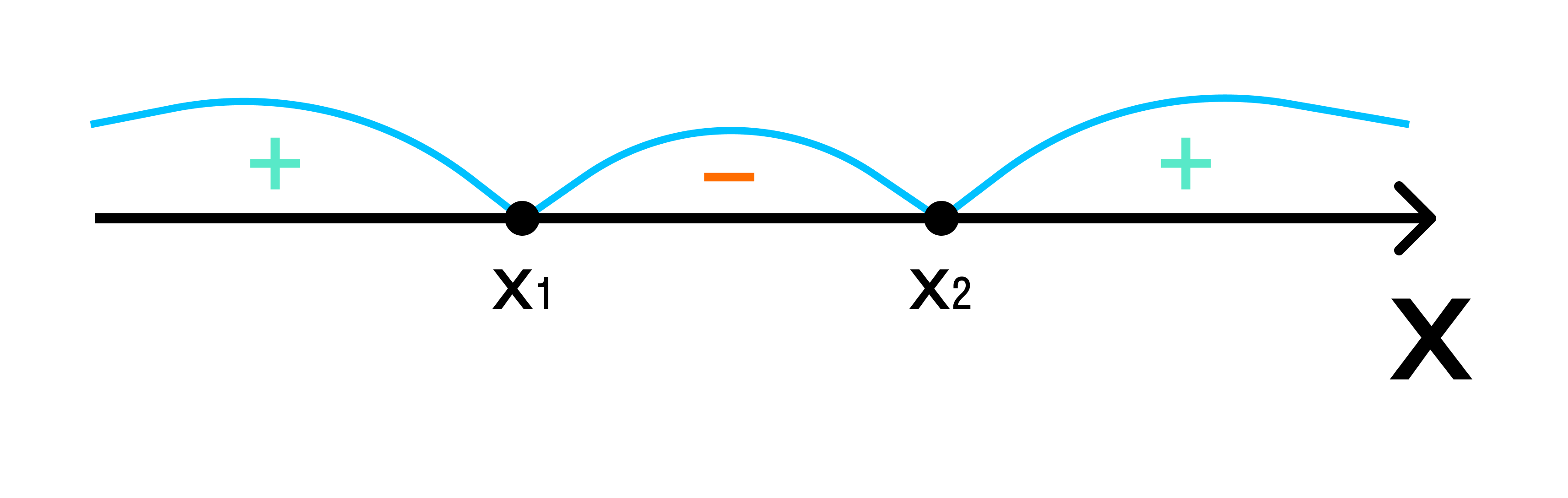
- Когда квадратный трехчлен при D > 0 имеет два корня, то знаки его значений на промежутках чередуются. Это значит, что достаточно определить знак на одном из трех промежутков и расставить знаки над оставшимися промежутками, чередуя их. В результате возможна одна из двух последовательностей: +, −, + или −, +, −.
- Если квадратный трехчлен при D = 0 имеет один корень, то этот корень разбивает числовую ось на два промежутка, а знаки над ними будут одинаковыми. Это значит, что достаточно определить знак над одним из них и над другим поставить такой же. При этом получится, либо +, +, либо −, −.
- Когда квадратный трехчлен корней не имеет (D < 0), то знаки его значений на всей числовой прямой совпадают как со знаком старшего коэффициента a, так и со знаком свободного члена c.
Теперь мы знаем пошаговый алгоритм. Чтобы закрепить материал потренируемся на примерах и научимся использовать метод интервалов для квадратных неравенств.
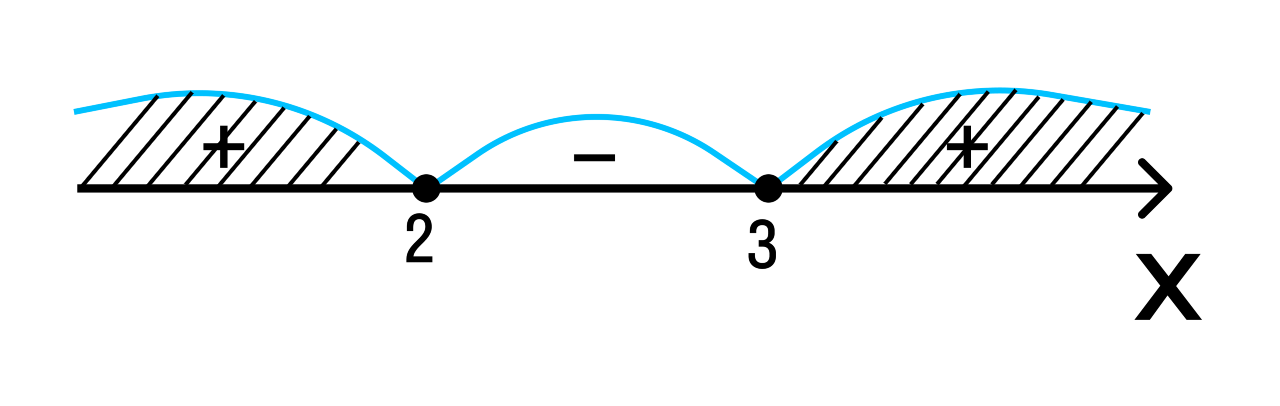
Пример 1. Решить неравенство методом интервалов: x^2 — 5x + 6 ≥ 0.
Как решаем:
-
Приравняем квадратный трехчлен к 0 и найдем нули:
x2 — 5x + 6 = 0
(x — 3) (x -2) = 0
x — 3 = 0
x — 2 = 0
x = 3
x = 2 -
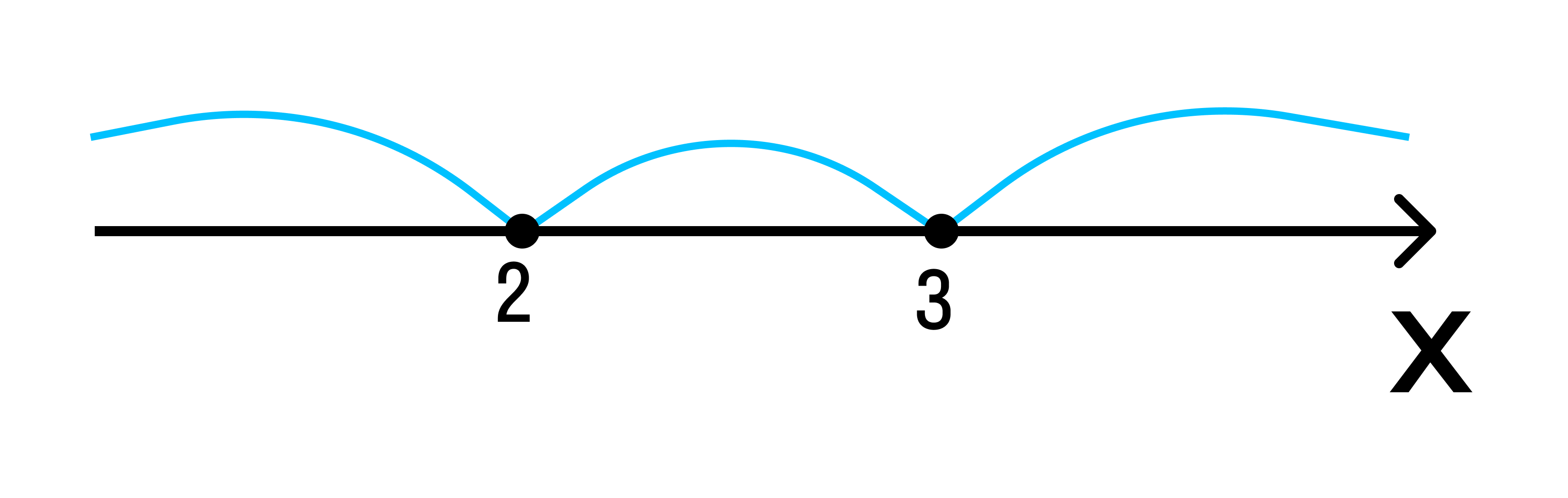
Отметим полученные значения на числовой прямой:
-
Расставим знаки на полученных промежутках:
Ответ: х ≤ 2, х ≥ 3.
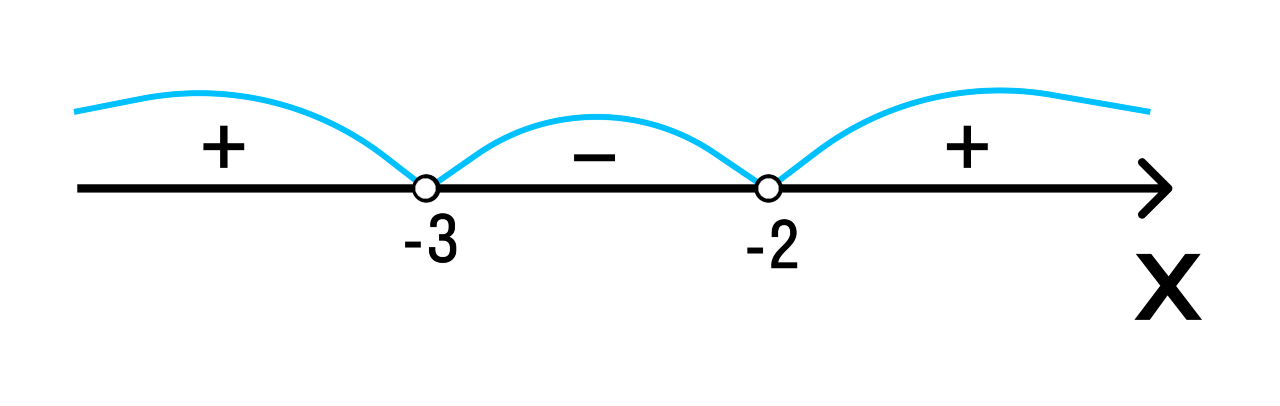
Пример 2. Применить метод интервалов для решения неравенства х2+4х+3 < 0.
Как решить неравенство методом интервалов, нам уже известно. Поэтому можем оформить решение кратко:
Ответ: -3 < x < -2.
Пример 3. Выполнить решение квадратного неравенства методом интервалов:
Как решаем:
- Находим корни квадратного трехчлена, который находится в левой части:
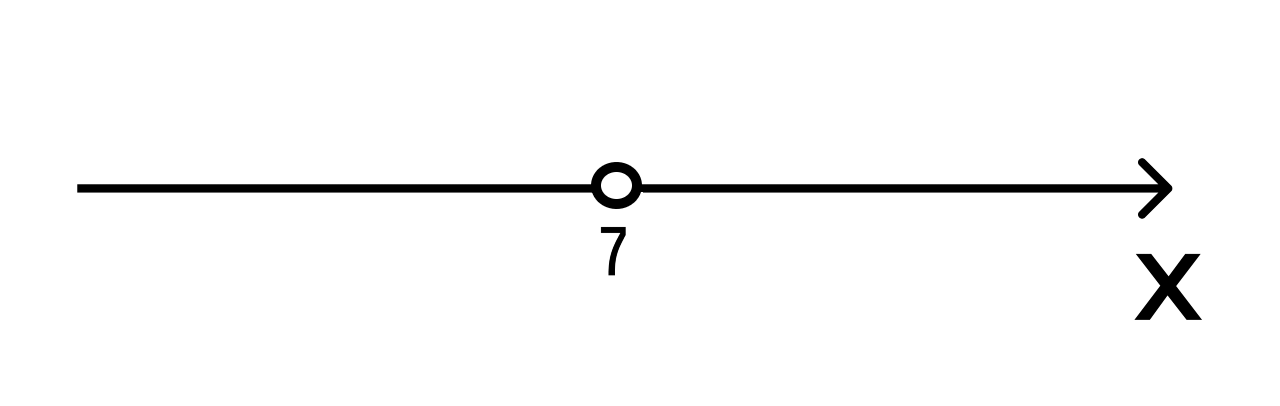
- Так как мы решаем строгое неравенство, то на координатной прямой изображаем выколотую точку с координатой 7:
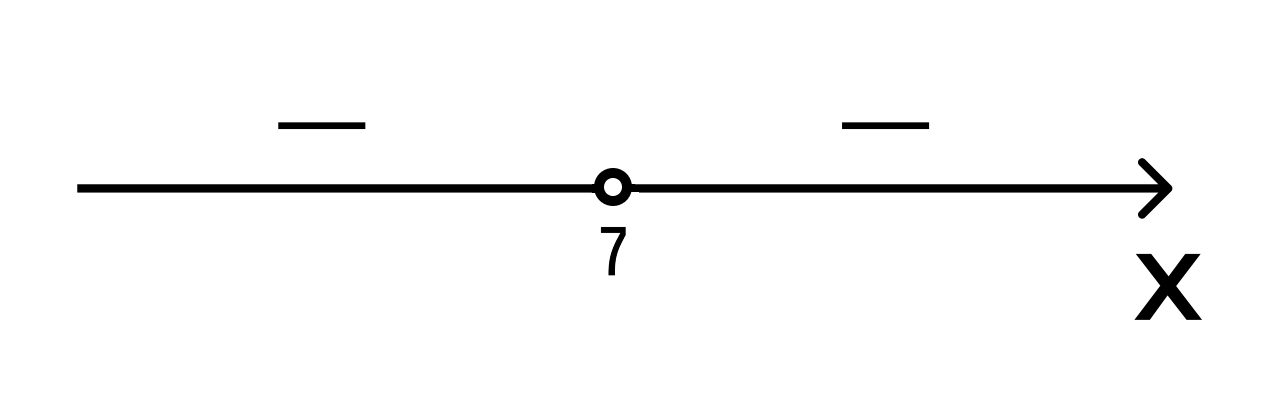
- Теперь определим знаки на двух полученных промежутках (−∞, 7) и (7, +∞).
Это легко сделать, потому что дискриминант квадратного трехчлена равен нулю, а старший коэффициент со знаком минус. Фиксируем знаки: −, −:
- Так как мы решаем неравенство со знаком <, то изобразим штриховку над интервалами со знаками минус:
Очевидно, решениями являются оба промежутка (−∞, 7), (7, +∞).
Ответ: (−∞, 7), (7, +∞).