Судоку как правильно пишется

Судоку (яп. 数独 су:доку, произношение ) — головоломка с числами. Иногда судоку называют «магическим квадратом», что в общем-то неверно, так как судоку является латинским квадратом 9-го порядка. Судоку активно публикуют газеты и журналы разных стран мира, сборники судоку издаются большими тиражами. Решение судоку — популярный вид досуга.

Все значения слова «судоку»

• фанты
• буриме
• бейгл
• авиамоделизм
• спикерфон
• (ещё синонимы…)

• журнал
• ребус
• (ещё ассоциации…)

Решать сложные судоку это просто, если понять алгоритмы и методы решения судоку описанные в этой статье. Заметка в первую очередь рассчитана для новичков судоку, поэтому подробно и пошагово разберу ход мыслей на конкретном примере сложного судоку.

Мой метод как решать сложные судоку для новичка не претендует на оригинальность, но за годы скучных лекций и долгих поездок в электричках я хорошо натренировался разгадывать судоку и вывел определенные закономерности.

Решение судоку это не только способ скоротать время, но и отличная зарядка для нашего ума. Да, да тренировать надо не только тело, но и мозги.

Зачем решать судоку?

При разгадывании задач на логику активно работает левое полушарие головного мозга, а заполняя японский кроссворд карандашом на бумаге, мы еще задействуем правое полушарие мозга.

Получается комплексная зарядка для ума, поэтому я предпочитаю разгадывать судоку на листке бумаге, кому больше нравится вариант на компьютере – в конце этой заметки найдете игру судоку-онлайн.

Судоку к нам пришло в 21-м веке из Японии, поэтому другое популярное название судоку – японский квадрат. В саму Японию головоломка пришла в 20-м веке из США.

Впервые судоку упоминается в 18 веке швейцарским математиком Леонардом Эйлер, под названием латинский квадрат – таблица, в каждой строке которой, одно число встречается только один раз.

Если каждый день решать по одному судоку, то всех существующих комбинаций вам хватит на 17 миллионов лет вперёд!!!

Классический вариант судоку представляет собой квадрат размерами 9х9, состоит из 9 горизонтальных строк, 9 вертикальных строк, внутри делится на 9 блоков размерами 3х3.

По горизонтали строки пронумерованы буквами от А до И, по вертикали нумерация от 1 до 9, внутренние блоки пронумерованы от 1 до 9, центр квадрата находится в блоке №5 с координатами Д5.

Квадрат заполняется цифрами от 1 до 9. Судоку считается решенным, если заполнена 81 ячейка квадрата, таким образом, чтоб ни одно число не повторялось по горизонтали или по вертикали и внутри маленького блока 3х3 встречалось только один раз.

Из этого условия вытекает еще одно правило – сумма всех чисел в каждой строке хоть по вертикали, хоть по горизонтали и в отдельном маленьком квадрате равняется 45.

Видео ролик с решением судоку для тех, кому на слух проще воспринимать информацию.

С Чего Начать Решать Судоку

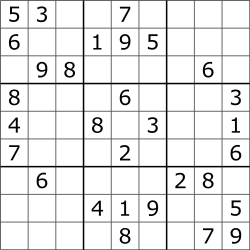
Для разбора я взял сложный судоку, который мне выдала программа. Вам для лучшего понимания алгоритма рекомендую этот японский кроссворд скачать здесь, распечатать или перерисовать на листок бумаги, после чего заполнять вместе со мной.

Вместо объяснений алгоритмов на отдельных кусочках судоку, покажу полностью решение японского кроссворда от А до Я, только так у вас появится целостная картина методов решения судоку.

Сложность судоку определяется количеством изначально заполненных ячеек. Чем меньше цифр известно, тем судоку считается сложнее. Минимальное количество известных цифр это 17 из 81. Если их меньше 17, то задачу решить невозможно.

Есть разные методы решения судоку – пробовать разгадывать по блокам или цифрам в порядке возрастания, начать заполнять пустые клетки всеми возможными вариантами. Сразу проставлять с первого хода возможные варианты во всех пустых клетках, я считаю пустой тратой времени, не приближающей нас к разгадке.

Почему-то многие авторы методичек по решению судоку, цифры, которые предположительно могут стоять в клетке, называют кандидатами. Я предполагаемые числа буду называть вариантами.

Очевидные варианты (одиночки)

Решать судоку начинают с анализа и заполнения клеток, в которых есть один единственно верный вариант. Ещё такие числа и клетки называют одиночками.

Чем больше мы таких клеток одиночек заполним на первоначальном этапе, тем легче будет решать дальше. Каждая правильно заполненная ячейка увеличивает число «одиночек» в соседних блоках.

Рассмотрим центральный блок №5 и горизонтальные строки Г, Д, Е, по условиям задачи цифры не должны повторяться в строках.
По условиям задачи, число 1 проставлено в строке Г блока №4 и в строке Д блока №6, поэтому в блоке №5 единица будет находиться в строке Е, при этом в строке Е вертикальные ряды 4 и 6 уже заняты (рис. 3, 4).

Единственное место, где может находиться 1 в блоке №5 это ячейка с координатами Е5, туда и запишем найденную нами 1.
Следующий важный навык для решения судоку – это находить клетки, где число не может быть. Нашли в отдельном квадратике 8 чисел, которые в нём не могут быть и останется одно число, которое точно будет здесь стоять.

Закрашивыаю красным цветом ячейки, где цифра 7 не может быть по условиям задачи — это все свободные клетки в строках и блоках, где уже есть семерка (рис. 5, 6):

1. ряд А, Б, Е, З, И по горизонтали
2. столбы 1, 3, 5, 6, 9 по вертикали
3. блоки №№ 2, 3, 4, 7, 8

В блоках №1 и №5 осталось по одной не закрашенной клетке, там и находится семерка, это ячейки с координатами В2 и Г4 – смело пишем в них число 7.

В блоках №6 и №9 получается по два взаимоисключающих варианта, где может находиться 7, это ячейки с координатами Д7, Д8 и Ж7, Ж8. Возьмем эти варианты на заметку. Ячейку Г8 мы исключили, потому что уже поставили ранее 7 на пересечении строки Г и столбца 4

После того как мы проставили семерки, в блоках №1 и №5 осталось по одному месту, где может находиться единица, это ячейки Б2 и Е5

Возвращаемся к центральному блоку №5, в нем осталось не закрытыми 4 клетки, не хватает чисел 2, 3 и 5, 6. Пара 5, 6 есть в вертикальном столбе №6, поэтому пара 5, 6 будет в столбе 5 в ячейках Г5, Д5. В какой именно будет 5, а в какой 6 пока не известно.

Но при этом известно, что число 2 уже есть в строке Д, поэтому 2 ставим в клетку Г6, и для клетки Д6 остается единственный вариант – 3.

Теперь в столбце 6 осталось не заполненными три клетки В6, Ж6, И6 и не хватает проставить три числа 1, 4, 9. Число 4 уже есть в блоках №5, 8 и в столбцах 4, 5.

Единственное место под 4 это клетка В6, куда можно было бы поставить 4 сразу, в самом начале. Я заранее этот судоку не решал, и сейчас его решаю на ходу, попутно записывая ход своих мыслей. Так что решение судоку действительно тренирует внимание, сейчас я уже заметил очевидную комбинацию, которую с самого начала пропустил.

Поставить единицу в Ж6 мы не можем, потому что в ряду Ж уже есть 1 – Ж1, и единственное место в столбце 6 для однёрки это И6, так же как и для девятки единственное место Ж6.

После того как заполнили столбец 6, в блоке № 2 остался один квадратик, где может находится 9 – А5, потому что ряд В уже содержит 9 в клетке В9, ряд Б в блоке №2 полностью занят и в столбце 4 тоже есть 9 – Е4.

В блоке №1 появилось место для 9 – клетка Б1, так как строки А и В уже содержат 9, а в строке Б одна не занятая клетка.
В ряду Б остается не заполненными три числа – 2, 3, 4 и все они находятся в блоке №3, я их произвольно запишу в клетки Б7, Б8, Б9, что бы ориентироваться какие числа в каком ряду (рис. 14).

В блоке №3 числа 5 и 6 могут располагаться только в нижнем ряду на местах В7 и В8, потому что строки А и Б содержит 5 и 6 в первом и втором блоке.

Таким образом получается, что в двух верхних клетках блока №3 А7 и А8 находятся числа 1 и 8. В столбце 7 уже есть 8, чтоб не было повтора восьмерку пишем в А8, единицу в А7 и наши предположения относительно 2, 3, 4, 5, 6 убираем.

Кроме этого, мы сразу можем методом исключения определить, где находится 1 в блоках №2 и №9.
Вам уже понятно, почему ячейки В4 и З8 единственные варианты, чтоб записать последние две цифры 1 в этом судоку?

На этом моменте я буквально завис, ни как не мог увидеть логического решения, а делать подстановки наугад – тупиковый метод. Сделав маленький перерыв, я вернулся к решению задачи и сразу увидел куда ставить девятки. В блоке 7 был только один возможный вариант – З2, в строках Ж, И и столбце №1 есть девятки, в столбце №3 нет места под 9.

Порой бывает так, что целый день не получается с места сдвинуться в решении судоку. Отложишь его в сторону, когда через пару дней к нему возвращаешься, судоку оказывается не сложным и решается за несколько минут.

Так же и в жизни, когда затрудняешься принять верное решение, нужно переключиться на другую задачу, а потом на свежую голову всё осмыслить. Как гласит народная мудрость – утро вечера мудренее…

Со свежим взглядом продолжаю решать числовой кроссворд и сразу вижу, что в квадрате №4 единственно возможное место, где может стоять 8 это клетка Д1, т.к. горизонтали Г и Е уже содержат число 8.

Постановка 8 в Д1 сразу сокращает число вариантов в секции №1 – горизонтальные ряды А и Б уже содержат 8, теперь добавилась 8 в вертикальном столбце №1, нам остается только В3, куда и пишем 8.

Теперь посмотрим на ряд З, в котором пустых три ячейки – З1, З4, З7 и в одной из них должна быть не достающая 8. Вертикали №1 и №7 уже содержат восьмерки на Д1и Г7, поэтому в строке З остается один вариант куда поставить 8, этоЗ4.

Метод подстановки 50/50

К этому шагу я начал топтаться на месте, у судоку, так легко разгадывавшегося с самого начала, в глаза больше не бросаются очевидные ходы.

Записал в пустые клетки возможные варианты, какие там могут находиться числа, но однозначной закономерности не выявил.
В решении сложных судоку бывают моменты, когда приходится заполнять ячейку с допущением, чтоб хоть как-то продолжить движение вперед, главное допущение должно быть разумным и не превращаться в гадание на кофейной гуще.

Максимально заполненная секция на данный момент – это горизонтальная строка З, в которой всего две свободные ячейки с координатами З1 и З7 с отсутствующими числами 2 и 3.

В любой из этих ячеек с одинаковой вероятностью может находиться как 2, так и 3. Если в ячейку З1 поставить 3, нам это ничего не даст, потому что в соседних блоках нет числа 3, и дальше снова не отчего будет отталкиваться.

Если в квадрате №7 в свободное место З1 поставить 2, то тогда можно будет записать 2 в квадрате №1 в клетку А3.

С момента, когда я сделал допущение, что координаты З1 принадлежат числу 2, я числа начал писать другим цветом. Это позволит в случае ошибки легко убрать все неверные выводы.

В квадрате №1 заполняем оставшиеся ячейки А1 – 4, Б1 – 3 и переходим заполнять по методу очевидных одиночек квадрат №2. В клеточке А4 будет стоять 3 и в клеточке В5 – 2, в квадрате №7 ставим в Ж5 3.

Возвращаемся к горизонтальной строке Г, где появились две явные одиночки – 4 в клетке Г2, и единственный вариант, где в этой строке может находиться 3 это клетка Г9.

К этому моменту у меня накопилось четыре клетки, где никак не получается сделать выбор 5 или 6? Это координаты Г1, Г5, Д5 и И1. При разгадывании числового квадрата встречаются такие пары, когда решение будет верным во всех случаях, но обычно такие моменты бывают в самом конце решения.

На первый взгляд в квадрате №5 ничего не меняется от того поставить 5 в центр на Д5 или на Г5 – соблюдаются все условия для решения, в каждом ряду и столбце и секции нет повторов одинаковых чисел.

Уже опираясь больше на интуицию, ставлю 5 по центру, в клетку Д5. Тогда получается, что цифра 6 будет в клетках Г5, И1, Ж4, Е2, цифра 3 – Е3, И2, 5 пишем в Г1 и 2 в И4.

В горизонтальном столбе №2 остается не заполненной одна клетка – Ж2 и для полного числового ряда не хватает цифры 8. Пишем 8, и смотрим квадрат №9. В нём для 8 остается только одна клетка – И9.

В самом нижнем горизонтальном ряду И теперь осталось заполнить две клетки И3 и И8, и два числа – 4, 5. В клетку И8 мы не можем записать 4, потому что в столбце 8 уже есть 4 по координатам Е8.

Тогда в клетку И8 ставим 5 и в клетку И3 пишем 4. Тогда в квадрате №7 в оставшейся ячейке Ж3 будет стоять 5. И в квадрате №3 для 5 остаются координаты В7, последнюю клетку с ряда В, В8 заполняем единственно возможным числом – 6.

Завершение разгадывания Судоку

Для полного решения судоку осталось проставить числа всего 9 клеток и начинается мандраж – сойдется или нет? Если была допущена ошибка, придется делать возврат на много шагов назад и начинать всё заново.

Переходим к квадрату №6, образованному пересечением горизонтальных рядов Г, Д, Е и вертикальных столбов 7, 8, 9.
Число 6 уже есть в рядах Г, Е и строках 8, 9. Поэтому, по условиям правильного решения судоку – числа не повторяются в рядах, столбцах и блоках, число 6 в квадрате №6 будет иметь координаты Д7.

В строке Д есть одна пустая клетка Д8 и для заполнения ряда нет одного числа – 7, поэтому ставим в Д8 искомую 7. Тогда в блоке №9, число 7 будет стоять в клетке Ж7, т.к. вертикали №8 и №9 уже содержат 7.

В вертикальном ряду №8 получается одна свободная клетка Ж8 и одно недостающее число – 2, которое заполняем в эту клетку.
В строке Ж и блоке №9 одно пустое место – Ж9. И там, и там не хватает числа 4, в вертикальном столбе №9 тоже еще нет 4. Проставляем в квадратик Ж9 нашу 4.

Чем меньше свободных клеток остается, тем легче решать судоку. Осталось четыре пустые клетки и в каждой очевидные одиночки. В блоке №3 в пустой клетке Б9 у нас помечено два возможных варианта – 2 и 4.

Число 4 исключаем, потому что только что поставили 4 в столбике №9 на пересечении с рядом Ж. Тогда Б9 будет 2 и в клетке Б7 – 4. Для окончательного решения сложного судоку осталось заполнить две взаимоисключающие клетки в квадрате №6 – это Е7 и Е9, где у нас проставлены варианты 2 или 5. В столбе №9 ранее записали 2 в клетку Б9, поэтому записываем в Е9 число 5 и в последнюю пустую клетку Е7 пишем 2.

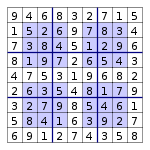
Все клетки заполнены и все числа проставлены, но прежде чем радоваться, что мы решили сложный судоку надо проверить на соблюдения обязательного условия правильного решения:

• Каждое число от 1 до 9 во всем судоку встречается всего 9 раз.
• Число не повторяется дважды в одной горизонтальной или вертикальной строке.
• В каждом маленьком квадрате число встречается только один раз.

Как вы помните, красным цветом заполнять судоку я начал с того момента, как было сомнение в правильности ответа. Я это сделал, чтоб в случае ошибки было легче вернуться к моменту, когда я ошибся и продолжить решение с того места, а не с самого начала судоку.

Обязательное условия не повторяемости чисел по горизонтали, вертикали соблюдено, теперь снимаем выделение красным цветом и можно радоваться:

Бинго, ура — судоку полностью решен

Поздравляю вас, вы прошли курс «Как решать сложные судоку для новичка», предлагаю закрепить результат — оформить подписку на рассылку новых выпусков и получить в подарок электронную книгу «Набор судоку с решениями + судоку для печати».

Понравился материал?! Подпишитесь на рассылку!!!

Игра судоку-онлайн была любезно предоставлена вэб мастером сайта судокуонлайн.ру, за что ему большое спасибо. Для игры с компьютера выбираете мышкой нужную ячейку и проставляете цифру с клавиатуры. В случае ошибки еще раз выбирите ячейку и поставьте новое число.

Благодарю всех за внимание и жду вас на новых тренировках для мозга, искренне ваш, Александр Утышев.

В Википедии есть статья «судоку».

Русский[править]

В Викиданных есть лексема судоку (L167490).

Морфологические и синтаксические свойства[править]

падеж	ед. ч.	мн. ч.
Им.	судо́ку	судо́ку
Р.	судо́ку	судо́ку
Д.	судо́ку	судо́ку
В.	судо́ку	судо́ку
Тв.	судо́ку	судо́ку
Пр.	судо́ку	судо́ку

су—до́—ку

Существительное, неодушевлённое, средний род, несклоняемое (тип склонения 0 по классификации А. А. Зализняка).

Корень: -судоку-.

Произношение[править]

• МФА: [sʊˈdokʊ]

Семантические свойства[править]

Значение[править]

1. головоломка с числами ◆ Судоку начали печатать не только специализированные, но и массовые газеты и журналы. О. Леонтьева, «Головоломки судоку» // «Наука и жизнь», 2006 г.

Синонимы[править]

1. —

Антонимы[править]

1. —

Гиперонимы[править]

1. головоломка

Гипонимы[править]

1. —

Родственные слова[править]

Ближайшее родство

Этимология[править]

От яп. 数独 (sūdoku).

Фразеологизмы и устойчивые сочетания[править]

Перевод[править]

Список переводов
Японскийja: 数独

Библиография[править]

This article is about the puzzle. For the disease, see Sodoku.

Sudoku (; Japanese: 数独, romanized: sūdoku, lit. ‘digit-single’; originally called Number Place)^[1] is a logic-based,^[2][3] combinatorial^[4] number-placement puzzle. In classic Sudoku, the objective is to fill a 9 × 9 grid with digits so that each column, each row, and each of the nine 3 × 3 subgrids that compose the grid (also called «boxes», «blocks», or «regions») contain all of the digits from 1 to 9. The puzzle setter provides a partially completed grid, which for a well-posed puzzle has a single solution.

French newspapers featured variations of the Sudoku puzzles in the 19th century, and the puzzle has appeared since 1979 in puzzle books under the name Number Place.^[5] However, the modern Sudoku only began to gain widespread popularity in 1986 when it was published by the Japanese puzzle company Nikoli under the name Sudoku, meaning «single number».^[6] It first appeared in a U.S. newspaper, and then The Times (London), in 2004, thanks to the efforts of Wayne Gould, who devised a computer program to rapidly produce unique puzzles.

History[edit]

Predecessors[edit]

Number puzzles appeared in newspapers in the late 19th century, when French puzzle setters began experimenting with removing numbers from magic squares. Le Siècle, a Paris daily, published a partially completed 9×9 magic square with 3×3 subsquares on November 19, 1892.^[7] It was not a Sudoku because it contained double-digit numbers and required arithmetic rather than logic to solve, but it shared key characteristics: each row, column, and subsquare added up to the same number.

On July 6, 1895, Le Siècle‘s rival, La France, refined the puzzle so that it was almost a modern Sudoku and named it carré magique diabolique (‘diabolical magic square’). It simplified the 9×9 magic square puzzle so that each row, column, and broken diagonals contained only the numbers 1–9, but did not mark the subsquares. Although they were unmarked, each 3×3 subsquare did indeed comprise the numbers 1–9, and the additional constraint on the broken diagonals led to only one solution.^[8]

These weekly puzzles were a feature of French newspapers such as L’Écho de Paris for about a decade, but disappeared about the time of World War I.^[9]

Modern Sudoku[edit]

The modern Sudoku was most likely designed anonymously by Howard Garns, a 74-year-old retired architect and freelance puzzle constructor from Connersville, Indiana, and first published in 1979 by Dell Magazines as Number Place (the earliest known examples of modern Sudoku).^[1] Garns’s name was always present on the list of contributors in issues of Dell Pencil Puzzles and Word Games that included Number Place and was always absent from issues that did not.^[10] He died in 1989 before getting a chance to see his creation as a worldwide phenomenon.^[10] Whether or not Garns was familiar with any of the French newspapers listed above is unclear.

The puzzle was introduced in Japan by Maki Kaji (鍜治 真起, Kaji Maki), president of the Nikoli puzzle company, in the paper Monthly Nikolist in April 1984^[10] as Sūji wa dokushin ni kagiru (数字は独身に限る), which can be translated as «the digits must be single», or as «the digits are limited to one occurrence» (In Japanese, dokushin means an «unmarried person»). The name was later abbreviated to Sudoku (数独), taking only the first kanji of compound words to form a shorter version.^[10] «Sudoku» is a registered trademark in Japan^[11] and the puzzle is generally referred to as Number Place (ナンバープレース, Nanbāpurēsu) or, more informally, a shortening of the two words, Num(ber) Pla(ce) (ナンプレ, Nanpure). In 1986, Nikoli introduced two innovations: the number of givens was restricted to no more than 32, and puzzles became «symmetrical» (meaning the givens were distributed in rotationally symmetric cells). It is now published in mainstream Japanese periodicals, such as the Asahi Shimbun.

Spread outside Japan[edit]

In 1997, Hong Kong judge Wayne Gould saw a partly completed puzzle in a Japanese bookshop. Over six years, he developed a computer program to produce unique puzzles rapidly.^[5] Knowing that British newspapers have a long history of publishing crosswords and other puzzles, he promoted Sudoku to The Times in Britain, which launched it on November 12, 2004 (calling it Su Doku). The first letter to The Times regarding Su Doku was published the following day on November 13 from Ian Payn of Brentford, complaining that the puzzle had caused him to miss his stop on the tube.^[12] Sudoku puzzles rapidly spread to other newspapers as a regular feature.^[5][13]

The rapid rise of Sudoku in Britain from relative obscurity to a front-page feature in national newspapers attracted commentary in the media and parody (such as when The Guardian‘s G2 section advertised itself as the first newspaper supplement with a Sudoku grid on every page).^[14] Recognizing the different psychological appeals of easy and difficult puzzles, The Times introduced both, side by side, on June 20, 2005. From July 2005, Channel 4 included a daily Sudoku game in their teletext service. On August 2, the BBC’s program guide Radio Times featured a weekly Super Sudoku with a 16×16 grid.

In the United States, the first newspaper to publish a Sudoku puzzle by Wayne Gould was The Conway Daily Sun (New Hampshire), in 2004.^[15]

The world’s first live TV Sudoku show, Sudoku Live, was a puzzle contest first broadcast on July 1, 2005, on Sky One. It was presented by Carol Vorderman. Nine teams of nine players (with one celebrity in each team) representing geographical regions competed to solve a puzzle. Each player had a hand-held device for entering numbers corresponding to answers for four cells. Phil Kollin of Winchelsea, England, was the series grand prize winner, taking home over £23,000 over a series of games. The audience at home was in a separate interactive competition, which was won by Hannah Withey of Cheshire.

Later in 2005, the BBC launched SUDO-Q, a game show that combined Sudoku with general knowledge. However, it used only 4×4 and 6×6 puzzles. Four seasons were produced before the show ended in 2007.

In 2006, a Sudoku website published songwriter Peter Levy’s Sudoku tribute song,^[16] but quickly had to take down the MP3 file due to heavy traffic. British and Australian radio picked up the song, which is to feature^[when?] in a British-made Sudoku documentary. The Japanese Embassy also nominated the song for an award, with Levy doing talks with Sony in Japan to release the song as a single.^[17]

Sudoku software is very popular on PCs, websites, and mobile phones. It comes with many distributions of Linux. The software has also been released on video game consoles, such as the Nintendo DS, PlayStation Portable, the Game Boy Advance, Xbox Live Arcade, the Nook e-book reader, Kindle Fire tablet, several iPod models, and the iPhone. Many Nokia phones also had Sudoku. In fact, just two weeks after Apple Inc. debuted the online App Store within its iTunes Store on July 11, 2008, nearly 30 different Sudoku games were already in it, created by various software developers, specifically for the iPhone and iPod Touch. One of the most popular video games featuring Sudoku is Brain Age: Train Your Brain in Minutes a Day!. Critically and commercially well-received, it generated particular praise for its Sudoku implementation^[18][19][20] and sold more than 8 million copies worldwide.^[21] Due to its popularity, Nintendo made a second Brain Age game titled Brain Age², which has over 100 new Sudoku puzzles and other activities.

In June 2008, an Australian drugs-related jury trial costing over A$ 1 million was aborted when it was discovered that five of the twelve jurors had been playing Sudoku instead of listening to the evidence.^[22]

Variants[edit]

Variations of grid sizes or region shapes[edit]

Although the 9×9 grid with 3×3 regions is by far the most common, many other variations exist. Sample puzzles can be 4×4 grids with 2×2 regions; 5×5 grids with pentomino regions have been published under the name Logi-5; the World Puzzle Championship has featured a 6×6 grid with 2×3 regions and a 7×7 grid with six heptomino regions and a disjoint region. Larger grids are also possible, or different irregular shapes (under various names such as Suguru, Tectonic, Jigsaw Sudoku etc.). The Times offers a 12×12-grid «Dodeka Sudoku» with 12 regions of 4×3 squares. Dell Magazines regularly publishes 16×16 «Number Place Challenger» puzzles (using the numbers 1–16 or the letters A-P). Nikoli offers 25×25 «Sudoku the Giant» behemoths. A 100×100-grid puzzle dubbed Sudoku-zilla was published in 2010.^[23]

Mini Sudoku[edit]

Under the name «Mini Sudoku», a 6×6 variant with 3×2 regions appears in the American newspaper USA Today and elsewhere. The object is the same as that of standard Sudoku, but the puzzle only uses the numbers 1 through 6. A similar form, for younger solvers of puzzles, called «The Junior Sudoku», has appeared in some newspapers, such as some editions of The Daily Mail.

Imposing additional constraints[edit]

Another common variant is to add limits on the placement of numbers beyond the usual row, column, and box requirements. Often, the limit takes the form of an extra «dimension»; the most common is to require the numbers in the main diagonals of the grid to also be unique. The aforementioned «Number Place Challenger» puzzles are all of this variant, as are the Sudoku X puzzles in The Daily Mail, which use 6×6 grids.

Killer Sudoku[edit]

The Killer Sudoku variant combines elements of Sudoku and Kakuro.

Different symbols[edit]

Since standard Sudoku does not involve arithmetic, the digits 1 to 9 can be replaced with nine arbitrary symbols, such as geometric shapes, Roman numerals (e.g. Quadratum latinum, published in the Latin puzzle magazine Hebdomada aenigmatum) or letters, and there is no functional difference.

When letters are used, the puzzle is sometimes known as Wordoku. Some variants, such as in the TV Guide Magazine, include a word reading along a main diagonal, row, or column once solved; determining the word in advance can be viewed as a solving aid. A Wordoku might contain words other than the main word.

Hyper Sudoku / Windoku[edit]

Hyper Sudoku or Windoku uses the classic 9×9 grid with 3×3 regions, but defines four additional interior 3×3 regions in which the numbers 1–9 must appear exactly once. It was invented by Peter Ritmeester and first published by him in Dutch Newspaper NRC Handelsblad in October 2005, and since April 2007 on a daily basis in The International New York Times (International Herald Tribune). The first time it was called Hyper Sudoku was in Will Shortz’s Favorite Sudoku Variations (February 2006). It is also known as Windoku because with the grid’s four interior regions shaded, it resembles a window with glazing bars.^[24]

Twin Sudoku[edit]

In Twin Sudoku two regular grids share a 3×3 box. This is one of many possible types of overlapping grids. The rules for each individual grid are the same as in normal Sudoku, but the digits in the overlapping section are shared by each half. In some compositions neither individual grid can be solved alone – the complete solution is only possible after each individual grid has at least been partially solved.

Other variants[edit]

Puzzles constructed from more than two grids are also common. Five 9×9 grids that overlap at the corner regions in the shape of a quincunx is known in Japan as Gattai 5 (five merged) Sudoku. In The Times, The Age, and The Sydney Morning Herald, this form of puzzle is known as Samurai Sudoku. The Baltimore Sun and the Toronto Star publish a puzzle of this variant (titled High Five) in their Sunday edition. Often, no givens are placed in the overlapping regions. Sequential grids, as opposed to overlapping, are also published, with values in specific locations in grids needing to be transferred to others.

A tabletop version of Sudoku can be played with a standard 81-card Set deck (see Set game). A three-dimensional Sudoku puzzle was published in The Daily Telegraph in May 2005. The Times also publishes a three-dimensional version under the name Tredoku. Also, a Sudoku version of the Rubik’s Cube is named Sudoku Cube.

Many other variants have been developed.^[25][26][27] Some are different shapes in the arrangement of overlapping 9×9 grids, such as butterfly, windmill, or flower.^[28] Others vary the logic for solving the grid. One of these is «Greater Than Sudoku». In this, a 3×3 grid of the Sudoku is given with 12 symbols of Greater Than (>) or Less Than (<) on the common line of the two adjacent numbers.^[10] Another variant on the logic of the solution is «Clueless Sudoku», in which nine 9×9 Sudoku grids are each placed in a 3×3 array. The center cell in each 3×3 grid of all nine puzzles is left blank and forms a tenth Sudoku puzzle without any cell completed; hence, «clueless».^[28] A new variant mixes Sudoku with the sliding tile puzzle in Sudoku Slide Extreme. In this variant, all of the positions are filled in. Tiles are moved to the proper position to solve the puzzle. This variant contains power-ups and a campaign mode.^{[citation needed]} Examples and other variants can be found in the Glossary of Sudoku.

Mathematics of Sudoku[edit]

This section refers to classic Sudoku, disregarding jigsaw, hyper, and other variants.

A completed Sudoku grid is a special type of Latin square with the additional property of no repeated values in any of the nine blocks (or boxes of 3×3 cells). The relationship between the two theories is known, after it was proven that a first-order formula that does not mention blocks is valid for Sudoku if and only if it is valid for Latin squares.^[29]

The general problem of solving Sudoku puzzles on n²×n² grids of n×n blocks is known to be NP-complete.^[30] Many computer algorithms, such as backtracking and dancing links can solve most 9×9 puzzles efficiently, but combinatorial explosion occurs as n increases, creating limits to the properties of Sudokus that can be constructed, analyzed, and solved as n increases. A Sudoku puzzle can be expressed as a graph coloring problem.^[31] The aim is to construct a 9-coloring of a particular graph, given a partial 9-coloring.

The fewest clues possible for a proper Sudoku is 17 (proven January 2012, and confirmed September 2013).^[32][33] Over 49,000 Sudokus with 17 clues have been found, many by Japanese enthusiasts.^[34][35] Sudokus with 18 clues and rotational symmetry have been found, and there is at least one Sudoku that has 18 clues, exhibits two-way diagonal symmetry and is automorphic. The maximum number of clues that can be provided while still not rendering a unique solution is four short of a full grid (77); if two instances of two numbers each are missing from cells that occupy the corners of an orthogonal rectangle, and exactly two of these cells are within one region, the numbers can be assigned two ways. Since this applies to Latin squares in general, most variants of Sudoku have the same maximum.

The number of classic 9×9 Sudoku solution grids is 6,670,903,752,021,072,936,960 (sequence A107739 in the OEIS), or around 6.67×10²¹. This is roughly 1.2×10⁻⁶ times the number of 9×9 Latin squares.^[36] Various other grid sizes have also been enumerated—see the main article for details. The number of essentially different solutions, when symmetries such as rotation, reflection, permutation, and relabelling are taken into account, was shown to be just 5,472,730,538^[37] (sequence A109741 in the OEIS).

Unlike the number of complete Sudoku grids, the number of minimal 9×9 Sudoku puzzles is not precisely known. (A minimal puzzle is one in which no clue can be deleted without losing the uniqueness of the solution.) However, statistical techniques combined with a puzzle generator^[38] show that about (with 0.065% relative error) 3.10 × 10³⁷ minimal puzzles and 2.55 × 10²⁵ nonessentially equivalent minimal puzzles exist.

Competitions[edit]

• The first World Sudoku Championship was held in Lucca, Italy, from March 10 to 11, 2006. The winner was Jana Tylová of the Czech Republic.^[39] The competition included numerous variants.^[40]
• The second World Sudoku Championship was held in Prague, Czech Republic, from March 28 to April 1, 2007.^[41] The individual champion was Thomas Snyder of the US. The team champion was Japan.^[42]
• The third World Sudoku Championship was held in Goa, India, from April 14 to 16, 2008. Thomas Snyder repeated as the individual overall champion and also won the first-ever Classic Trophy (a subset of the competition counting only classic Sudoku). The Czech Republic won the team competition.^[43]
• The fourth World Sudoku Championship was held in Žilina, Slovakia, from April 24 to 27, 2009. After past champion Thomas Snyder of the US won the general qualification, Jan Mrozowski of Poland emerged from a 36-competitor playoff to become the new World Sudoku Champion. Host nation Slovakia emerged as the top team in a separate competition of three-membered squads.^[44]
• The fifth World Sudoku Championship was held in Philadelphia, Pennsylvania, from April 29 to May 2, 2010. Jan Mrozowski of Poland successfully defended his world title in the individual competition, while Germany won a separate team event. The puzzles were written by Thomas Snyder and Wei-Hwa Huang, both past U.S. Sudoku champions.^[45]
• The 12th World Sudoku Championship (WSC) was held in Bangalore, India, from October 15 to 22, 2017. Kota Morinishi of Japan won the Individual WSC and China won the team event.^[46]
• The 13th World Sudoku Championship took place in the Czech Republic.^[47]
• In the United States, The Philadelphia Inquirer Sudoku National Championship has been held three times, each time offering a $10,000 prize to the advanced division winner and a spot on the U.S. National Sudoku Team traveling to the world championships. The winners of the event were Thomas Snyder (2007),^[48] Wei-Hwa Huang (2008), and Tammy McLeod (2009).^[49] In the 2009 event, the third-place finalist in the advanced division, Eugene Varshavsky, performed quite poorly onstage after setting a very fast qualifying time on paper, which caught the attention of organizers and competitors including past champion Thomas Snyder, who requested organizers reconsider his results due to a suspicion of cheating.^[50] Following an investigation and a retest of Varshavsky, the organizers disqualified him and awarded the third-place to Chris Narrikkattu.^[51]

See also[edit]

References[edit]

Further reading[edit]

• Delahaye, Jean-Paul, «The Science Behind Sudoku», Scientific American, June 2006.
• Provan, J. Scott, «Sudoku: Strategy Versus Structure», American Mathematical Monthly, October 2009. Published also as a University of North Carolina technical report UNC/STOR/08/04, 2008.

External links[edit]

• ‘Sudoku Variations’ from Fun With Puzzles
• ‘Father of Sudoku’ puzzles next move (BBC)

This article is about the puzzle. For the disease, see Sodoku.

Sudoku (; Japanese: 数独, romanized: sūdoku, lit. ‘digit-single’; originally called Number Place)^[1] is a logic-based,^[2][3] combinatorial^[4] number-placement puzzle. In classic Sudoku, the objective is to fill a 9 × 9 grid with digits so that each column, each row, and each of the nine 3 × 3 subgrids that compose the grid (also called «boxes», «blocks», or «regions») contain all of the digits from 1 to 9. The puzzle setter provides a partially completed grid, which for a well-posed puzzle has a single solution.

French newspapers featured variations of the Sudoku puzzles in the 19th century, and the puzzle has appeared since 1979 in puzzle books under the name Number Place.^[5] However, the modern Sudoku only began to gain widespread popularity in 1986 when it was published by the Japanese puzzle company Nikoli under the name Sudoku, meaning «single number».^[6] It first appeared in a U.S. newspaper, and then The Times (London), in 2004, thanks to the efforts of Wayne Gould, who devised a computer program to rapidly produce unique puzzles.

History[edit]

Predecessors[edit]

Number puzzles appeared in newspapers in the late 19th century, when French puzzle setters began experimenting with removing numbers from magic squares. Le Siècle, a Paris daily, published a partially completed 9×9 magic square with 3×3 subsquares on November 19, 1892.^[7] It was not a Sudoku because it contained double-digit numbers and required arithmetic rather than logic to solve, but it shared key characteristics: each row, column, and subsquare added up to the same number.

On July 6, 1895, Le Siècle‘s rival, La France, refined the puzzle so that it was almost a modern Sudoku and named it carré magique diabolique (‘diabolical magic square’). It simplified the 9×9 magic square puzzle so that each row, column, and broken diagonals contained only the numbers 1–9, but did not mark the subsquares. Although they were unmarked, each 3×3 subsquare did indeed comprise the numbers 1–9, and the additional constraint on the broken diagonals led to only one solution.^[8]

These weekly puzzles were a feature of French newspapers such as L’Écho de Paris for about a decade, but disappeared about the time of World War I.^[9]

Modern Sudoku[edit]

The modern Sudoku was most likely designed anonymously by Howard Garns, a 74-year-old retired architect and freelance puzzle constructor from Connersville, Indiana, and first published in 1979 by Dell Magazines as Number Place (the earliest known examples of modern Sudoku).^[1] Garns’s name was always present on the list of contributors in issues of Dell Pencil Puzzles and Word Games that included Number Place and was always absent from issues that did not.^[10] He died in 1989 before getting a chance to see his creation as a worldwide phenomenon.^[10] Whether or not Garns was familiar with any of the French newspapers listed above is unclear.

The puzzle was introduced in Japan by Maki Kaji (鍜治 真起, Kaji Maki), president of the Nikoli puzzle company, in the paper Monthly Nikolist in April 1984^[10] as Sūji wa dokushin ni kagiru (数字は独身に限る), which can be translated as «the digits must be single», or as «the digits are limited to one occurrence» (In Japanese, dokushin means an «unmarried person»). The name was later abbreviated to Sudoku (数独), taking only the first kanji of compound words to form a shorter version.^[10] «Sudoku» is a registered trademark in Japan^[11] and the puzzle is generally referred to as Number Place (ナンバープレース, Nanbāpurēsu) or, more informally, a shortening of the two words, Num(ber) Pla(ce) (ナンプレ, Nanpure). In 1986, Nikoli introduced two innovations: the number of givens was restricted to no more than 32, and puzzles became «symmetrical» (meaning the givens were distributed in rotationally symmetric cells). It is now published in mainstream Japanese periodicals, such as the Asahi Shimbun.

Spread outside Japan[edit]

In 1997, Hong Kong judge Wayne Gould saw a partly completed puzzle in a Japanese bookshop. Over six years, he developed a computer program to produce unique puzzles rapidly.^[5] Knowing that British newspapers have a long history of publishing crosswords and other puzzles, he promoted Sudoku to The Times in Britain, which launched it on November 12, 2004 (calling it Su Doku). The first letter to The Times regarding Su Doku was published the following day on November 13 from Ian Payn of Brentford, complaining that the puzzle had caused him to miss his stop on the tube.^[12] Sudoku puzzles rapidly spread to other newspapers as a regular feature.^[5][13]

The rapid rise of Sudoku in Britain from relative obscurity to a front-page feature in national newspapers attracted commentary in the media and parody (such as when The Guardian‘s G2 section advertised itself as the first newspaper supplement with a Sudoku grid on every page).^[14] Recognizing the different psychological appeals of easy and difficult puzzles, The Times introduced both, side by side, on June 20, 2005. From July 2005, Channel 4 included a daily Sudoku game in their teletext service. On August 2, the BBC’s program guide Radio Times featured a weekly Super Sudoku with a 16×16 grid.

In the United States, the first newspaper to publish a Sudoku puzzle by Wayne Gould was The Conway Daily Sun (New Hampshire), in 2004.^[15]

The world’s first live TV Sudoku show, Sudoku Live, was a puzzle contest first broadcast on July 1, 2005, on Sky One. It was presented by Carol Vorderman. Nine teams of nine players (with one celebrity in each team) representing geographical regions competed to solve a puzzle. Each player had a hand-held device for entering numbers corresponding to answers for four cells. Phil Kollin of Winchelsea, England, was the series grand prize winner, taking home over £23,000 over a series of games. The audience at home was in a separate interactive competition, which was won by Hannah Withey of Cheshire.

Later in 2005, the BBC launched SUDO-Q, a game show that combined Sudoku with general knowledge. However, it used only 4×4 and 6×6 puzzles. Four seasons were produced before the show ended in 2007.

In 2006, a Sudoku website published songwriter Peter Levy’s Sudoku tribute song,^[16] but quickly had to take down the MP3 file due to heavy traffic. British and Australian radio picked up the song, which is to feature^[when?] in a British-made Sudoku documentary. The Japanese Embassy also nominated the song for an award, with Levy doing talks with Sony in Japan to release the song as a single.^[17]

Sudoku software is very popular on PCs, websites, and mobile phones. It comes with many distributions of Linux. The software has also been released on video game consoles, such as the Nintendo DS, PlayStation Portable, the Game Boy Advance, Xbox Live Arcade, the Nook e-book reader, Kindle Fire tablet, several iPod models, and the iPhone. Many Nokia phones also had Sudoku. In fact, just two weeks after Apple Inc. debuted the online App Store within its iTunes Store on July 11, 2008, nearly 30 different Sudoku games were already in it, created by various software developers, specifically for the iPhone and iPod Touch. One of the most popular video games featuring Sudoku is Brain Age: Train Your Brain in Minutes a Day!. Critically and commercially well-received, it generated particular praise for its Sudoku implementation^[18][19][20] and sold more than 8 million copies worldwide.^[21] Due to its popularity, Nintendo made a second Brain Age game titled Brain Age², which has over 100 new Sudoku puzzles and other activities.

In June 2008, an Australian drugs-related jury trial costing over A$ 1 million was aborted when it was discovered that five of the twelve jurors had been playing Sudoku instead of listening to the evidence.^[22]

Variants[edit]

Variations of grid sizes or region shapes[edit]

Although the 9×9 grid with 3×3 regions is by far the most common, many other variations exist. Sample puzzles can be 4×4 grids with 2×2 regions; 5×5 grids with pentomino regions have been published under the name Logi-5; the World Puzzle Championship has featured a 6×6 grid with 2×3 regions and a 7×7 grid with six heptomino regions and a disjoint region. Larger grids are also possible, or different irregular shapes (under various names such as Suguru, Tectonic, Jigsaw Sudoku etc.). The Times offers a 12×12-grid «Dodeka Sudoku» with 12 regions of 4×3 squares. Dell Magazines regularly publishes 16×16 «Number Place Challenger» puzzles (using the numbers 1–16 or the letters A-P). Nikoli offers 25×25 «Sudoku the Giant» behemoths. A 100×100-grid puzzle dubbed Sudoku-zilla was published in 2010.^[23]

Mini Sudoku[edit]

Under the name «Mini Sudoku», a 6×6 variant with 3×2 regions appears in the American newspaper USA Today and elsewhere. The object is the same as that of standard Sudoku, but the puzzle only uses the numbers 1 through 6. A similar form, for younger solvers of puzzles, called «The Junior Sudoku», has appeared in some newspapers, such as some editions of The Daily Mail.

Imposing additional constraints[edit]

Another common variant is to add limits on the placement of numbers beyond the usual row, column, and box requirements. Often, the limit takes the form of an extra «dimension»; the most common is to require the numbers in the main diagonals of the grid to also be unique. The aforementioned «Number Place Challenger» puzzles are all of this variant, as are the Sudoku X puzzles in The Daily Mail, which use 6×6 grids.

Killer Sudoku[edit]

The Killer Sudoku variant combines elements of Sudoku and Kakuro.

Different symbols[edit]

Since standard Sudoku does not involve arithmetic, the digits 1 to 9 can be replaced with nine arbitrary symbols, such as geometric shapes, Roman numerals (e.g. Quadratum latinum, published in the Latin puzzle magazine Hebdomada aenigmatum) or letters, and there is no functional difference.

When letters are used, the puzzle is sometimes known as Wordoku. Some variants, such as in the TV Guide Magazine, include a word reading along a main diagonal, row, or column once solved; determining the word in advance can be viewed as a solving aid. A Wordoku might contain words other than the main word.

Hyper Sudoku / Windoku[edit]

Hyper Sudoku or Windoku uses the classic 9×9 grid with 3×3 regions, but defines four additional interior 3×3 regions in which the numbers 1–9 must appear exactly once. It was invented by Peter Ritmeester and first published by him in Dutch Newspaper NRC Handelsblad in October 2005, and since April 2007 on a daily basis in The International New York Times (International Herald Tribune). The first time it was called Hyper Sudoku was in Will Shortz’s Favorite Sudoku Variations (February 2006). It is also known as Windoku because with the grid’s four interior regions shaded, it resembles a window with glazing bars.^[24]

Twin Sudoku[edit]

In Twin Sudoku two regular grids share a 3×3 box. This is one of many possible types of overlapping grids. The rules for each individual grid are the same as in normal Sudoku, but the digits in the overlapping section are shared by each half. In some compositions neither individual grid can be solved alone – the complete solution is only possible after each individual grid has at least been partially solved.

Other variants[edit]

Puzzles constructed from more than two grids are also common. Five 9×9 grids that overlap at the corner regions in the shape of a quincunx is known in Japan as Gattai 5 (five merged) Sudoku. In The Times, The Age, and The Sydney Morning Herald, this form of puzzle is known as Samurai Sudoku. The Baltimore Sun and the Toronto Star publish a puzzle of this variant (titled High Five) in their Sunday edition. Often, no givens are placed in the overlapping regions. Sequential grids, as opposed to overlapping, are also published, with values in specific locations in grids needing to be transferred to others.

A tabletop version of Sudoku can be played with a standard 81-card Set deck (see Set game). A three-dimensional Sudoku puzzle was published in The Daily Telegraph in May 2005. The Times also publishes a three-dimensional version under the name Tredoku. Also, a Sudoku version of the Rubik’s Cube is named Sudoku Cube.

Many other variants have been developed.^[25][26][27] Some are different shapes in the arrangement of overlapping 9×9 grids, such as butterfly, windmill, or flower.^[28] Others vary the logic for solving the grid. One of these is «Greater Than Sudoku». In this, a 3×3 grid of the Sudoku is given with 12 symbols of Greater Than (>) or Less Than (<) on the common line of the two adjacent numbers.^[10] Another variant on the logic of the solution is «Clueless Sudoku», in which nine 9×9 Sudoku grids are each placed in a 3×3 array. The center cell in each 3×3 grid of all nine puzzles is left blank and forms a tenth Sudoku puzzle without any cell completed; hence, «clueless».^[28] A new variant mixes Sudoku with the sliding tile puzzle in Sudoku Slide Extreme. In this variant, all of the positions are filled in. Tiles are moved to the proper position to solve the puzzle. This variant contains power-ups and a campaign mode.^{[citation needed]} Examples and other variants can be found in the Glossary of Sudoku.

Mathematics of Sudoku[edit]

This section refers to classic Sudoku, disregarding jigsaw, hyper, and other variants.

A completed Sudoku grid is a special type of Latin square with the additional property of no repeated values in any of the nine blocks (or boxes of 3×3 cells). The relationship between the two theories is known, after it was proven that a first-order formula that does not mention blocks is valid for Sudoku if and only if it is valid for Latin squares.^[29]

The general problem of solving Sudoku puzzles on n²×n² grids of n×n blocks is known to be NP-complete.^[30] Many computer algorithms, such as backtracking and dancing links can solve most 9×9 puzzles efficiently, but combinatorial explosion occurs as n increases, creating limits to the properties of Sudokus that can be constructed, analyzed, and solved as n increases. A Sudoku puzzle can be expressed as a graph coloring problem.^[31] The aim is to construct a 9-coloring of a particular graph, given a partial 9-coloring.

The fewest clues possible for a proper Sudoku is 17 (proven January 2012, and confirmed September 2013).^[32][33] Over 49,000 Sudokus with 17 clues have been found, many by Japanese enthusiasts.^[34][35] Sudokus with 18 clues and rotational symmetry have been found, and there is at least one Sudoku that has 18 clues, exhibits two-way diagonal symmetry and is automorphic. The maximum number of clues that can be provided while still not rendering a unique solution is four short of a full grid (77); if two instances of two numbers each are missing from cells that occupy the corners of an orthogonal rectangle, and exactly two of these cells are within one region, the numbers can be assigned two ways. Since this applies to Latin squares in general, most variants of Sudoku have the same maximum.

The number of classic 9×9 Sudoku solution grids is 6,670,903,752,021,072,936,960 (sequence A107739 in the OEIS), or around 6.67×10²¹. This is roughly 1.2×10⁻⁶ times the number of 9×9 Latin squares.^[36] Various other grid sizes have also been enumerated—see the main article for details. The number of essentially different solutions, when symmetries such as rotation, reflection, permutation, and relabelling are taken into account, was shown to be just 5,472,730,538^[37] (sequence A109741 in the OEIS).

Unlike the number of complete Sudoku grids, the number of minimal 9×9 Sudoku puzzles is not precisely known. (A minimal puzzle is one in which no clue can be deleted without losing the uniqueness of the solution.) However, statistical techniques combined with a puzzle generator^[38] show that about (with 0.065% relative error) 3.10 × 10³⁷ minimal puzzles and 2.55 × 10²⁵ nonessentially equivalent minimal puzzles exist.

Competitions[edit]

• The first World Sudoku Championship was held in Lucca, Italy, from March 10 to 11, 2006. The winner was Jana Tylová of the Czech Republic.^[39] The competition included numerous variants.^[40]
• The second World Sudoku Championship was held in Prague, Czech Republic, from March 28 to April 1, 2007.^[41] The individual champion was Thomas Snyder of the US. The team champion was Japan.^[42]
• The third World Sudoku Championship was held in Goa, India, from April 14 to 16, 2008. Thomas Snyder repeated as the individual overall champion and also won the first-ever Classic Trophy (a subset of the competition counting only classic Sudoku). The Czech Republic won the team competition.^[43]
• The fourth World Sudoku Championship was held in Žilina, Slovakia, from April 24 to 27, 2009. After past champion Thomas Snyder of the US won the general qualification, Jan Mrozowski of Poland emerged from a 36-competitor playoff to become the new World Sudoku Champion. Host nation Slovakia emerged as the top team in a separate competition of three-membered squads.^[44]
• The fifth World Sudoku Championship was held in Philadelphia, Pennsylvania, from April 29 to May 2, 2010. Jan Mrozowski of Poland successfully defended his world title in the individual competition, while Germany won a separate team event. The puzzles were written by Thomas Snyder and Wei-Hwa Huang, both past U.S. Sudoku champions.^[45]
• The 12th World Sudoku Championship (WSC) was held in Bangalore, India, from October 15 to 22, 2017. Kota Morinishi of Japan won the Individual WSC and China won the team event.^[46]
• The 13th World Sudoku Championship took place in the Czech Republic.^[47]
• In the United States, The Philadelphia Inquirer Sudoku National Championship has been held three times, each time offering a $10,000 prize to the advanced division winner and a spot on the U.S. National Sudoku Team traveling to the world championships. The winners of the event were Thomas Snyder (2007),^[48] Wei-Hwa Huang (2008), and Tammy McLeod (2009).^[49] In the 2009 event, the third-place finalist in the advanced division, Eugene Varshavsky, performed quite poorly onstage after setting a very fast qualifying time on paper, which caught the attention of organizers and competitors including past champion Thomas Snyder, who requested organizers reconsider his results due to a suspicion of cheating.^[50] Following an investigation and a retest of Varshavsky, the organizers disqualified him and awarded the third-place to Chris Narrikkattu.^[51]

See also[edit]

References[edit]

Further reading[edit]

• Delahaye, Jean-Paul, «The Science Behind Sudoku», Scientific American, June 2006.
• Provan, J. Scott, «Sudoku: Strategy Versus Structure», American Mathematical Monthly, October 2009. Published also as a University of North Carolina technical report UNC/STOR/08/04, 2008.

External links[edit]

• ‘Sudoku Variations’ from Fun With Puzzles
• ‘Father of Sudoku’ puzzles next move (BBC)